ИНЖЕНЕРНАЯ И КОМПЬЮТЕОНАЯ ГРАФИКА Проецирование Лекция 1

«ИНЖЕНЕРНАЯ И КОМПЬЮТЕОНАЯ ГРАФИКА» Проецирование. Лекция 1

Начертательная геометрия изучает способы построения изображений пространственных фигур на плоскости и решения пространственных задач. Проекционное черчение рассматривает практические вопросы построения чертежей и решает задачи сначала на чертежах геометрических тел, а затем на чертежах моделей и технических деталей

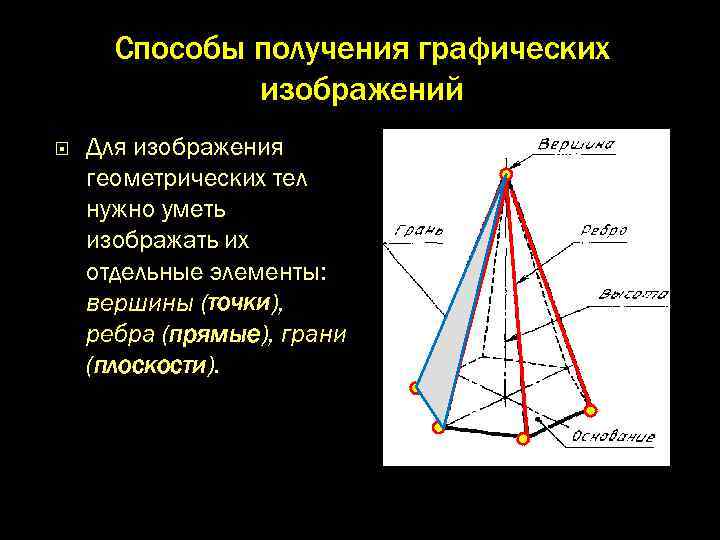Способы получения графических изображений Для изображения геометрических тел нужно уметь изображать их отдельные элементы: вершины (точки), ребра (прямые), грани (плоскости).

Обозначения П 1, П 2, П 3 – основные плоскости проекций; П 4, П 5, … - дополнительные плоскости проекций; Q, G, D, Y, L, S – поверхности (плоскости ); А, В, С, … 1, 2, 3, … - точки в пространстве; а, b, c … - линии в пространстве; а, b, g… - углы; А 1, А 2, А 3 - проекции точек, а 1, а 2, а 3, линий, Q 1, Q 2, Q 3, поверхностей на соответствующие плоскости

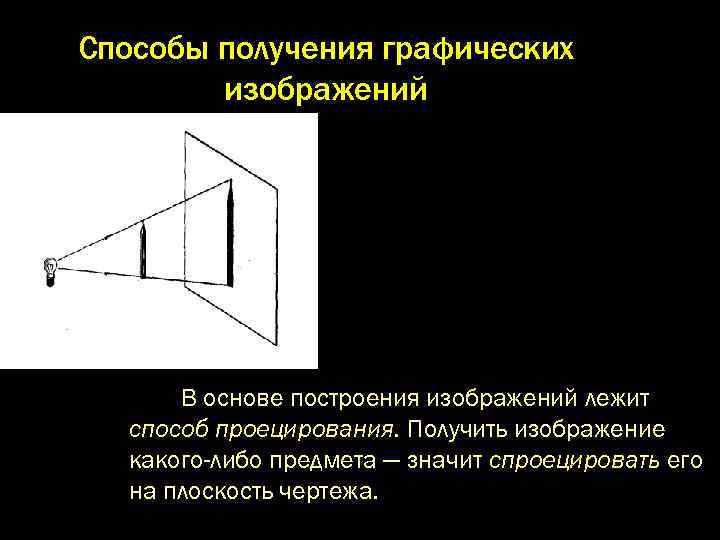Способы получения графических изображений В основе построения изображений лежит способ проецирования. Получить изображение какого-либо предмета — значит спроецировать его на плоскость чертежа.

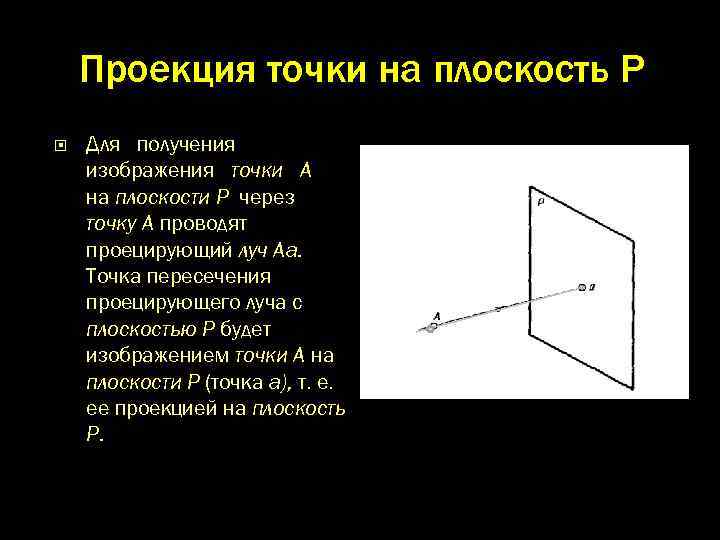Проекция точки на плоскость Р Для получения изображения точки А на плоскости Р через точку А проводят проецирующий луч Аа. Точка пересечения проецирующего луча с плоскостью Р будет изображением точки А на плоскости Р (точка а), т. е. ее проекцией на плоскость Р.

Центральное и параллельное проецирование В зависимости от взаимного расположения проецирующих лучей проецирование делят на центральное и параллельное

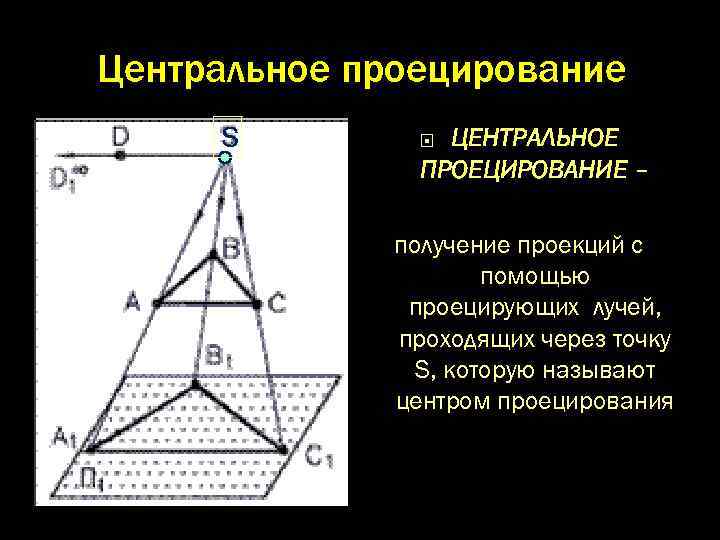Центральное проецирование S ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ – получение проекций с помощью проецирующих лучей, проходящих через точку S, которую называют центром проецирования

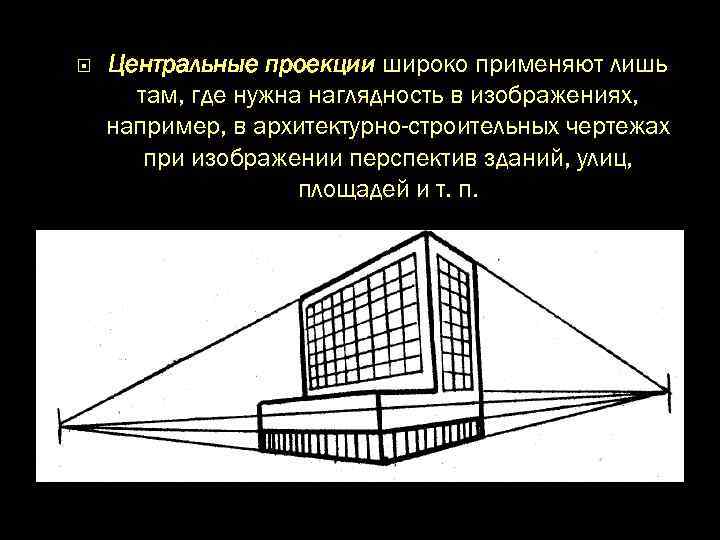Центральные проекции широко применяют лишь там, где нужна наглядность в изображениях, например, в архитектурно-строительных чертежах при изображении перспектив зданий, улиц, площадей и т. п.

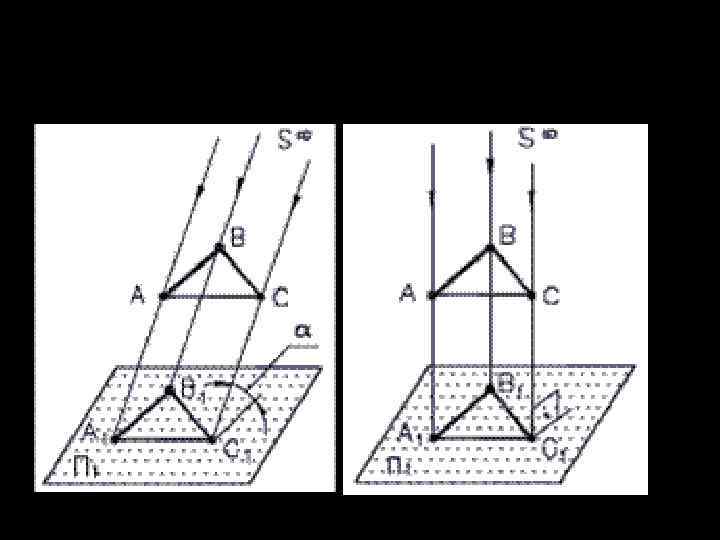
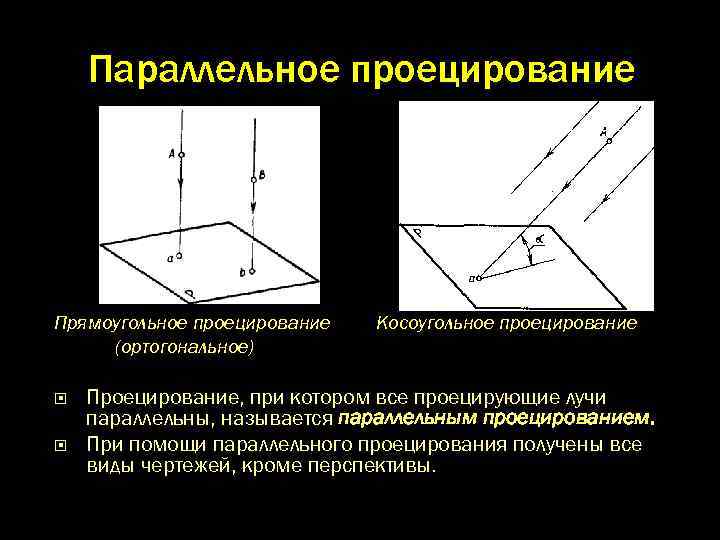Параллельное проецирование Прямоугольное проецирование (ортогональное) Косоугольное проецирование Проецирование, при котором все проецирующие лучи параллельны, называется параллельным проецированием. При помощи параллельного проецирования получены все виды чертежей, кроме перспективы.

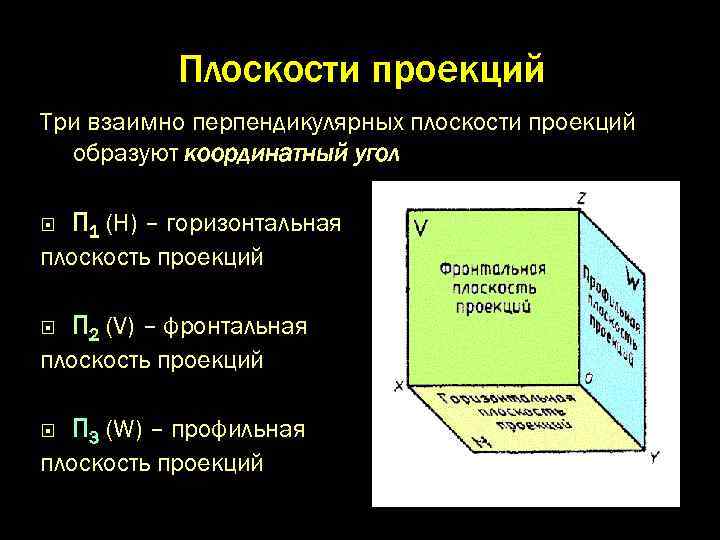Плоскости проекций Три взаимно перпендикулярных плоскости проекций образуют координатный угол П 1 (Н) – горизонтальная плоскость проекций П 2 (V) – фронтальная плоскость проекций П 3 (W) – профильная плоскость проекций

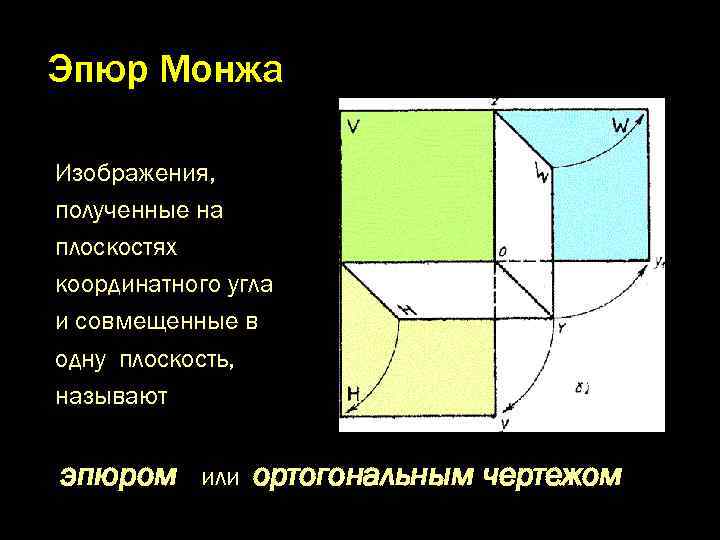Эпюр Монжа Изображения, полученные на плоскостях координатного угла и совмещенные в одну плоскость, называют эпюром или ортогональным чертежом

Проецируя предмет в системе трех плоскостей проекций, его рассматривают с трех сторон, в направлениях перпендикулярных трем плоскостям проекций

Проекция точки Горизонтальная проекция точки Проецирование точки на три плоскости проекций начинают с получения ее изображения на плоскости П 1 (Н) Отрезок АА 1 к плоскости П 1 (Н) и || оси Оz и является расстоянием от точки А до плоскости П 1 (Н) Точка А 1 называется горизонтальной проекцией точки А

Фронтальная проекция точки Для получения изображения точки А на плоскости П 2 (V) через точку А проводят проецирующий луч фронтальной плоскости проекций П 2 (V), который || оси Оу. Точка А 2 является прямоугольной проекцией точки А на плоскость П 2 (V) и называется фронтальной проекцией точки А

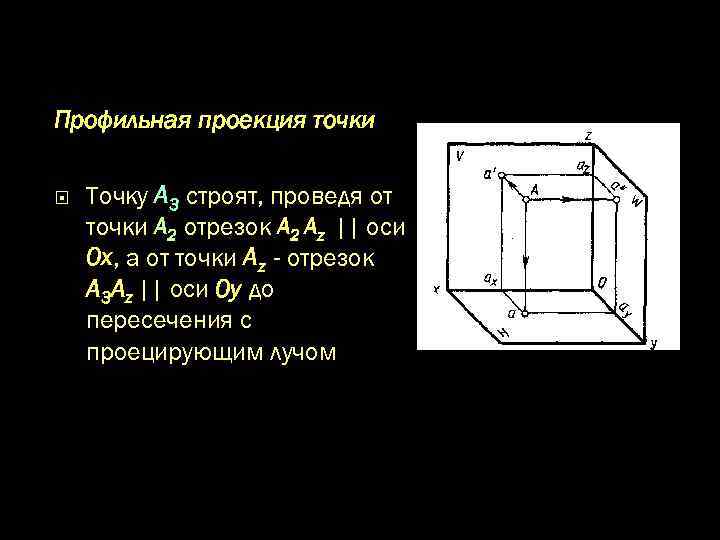Профильная проекция точки Точку А 3 строят, проведя от точки А 2 отрезок А 2 Аz || оси 0 x, а от точки Аz - отрезок А 3 Аz || оси 0 y до пересечения с проецирующим лучом

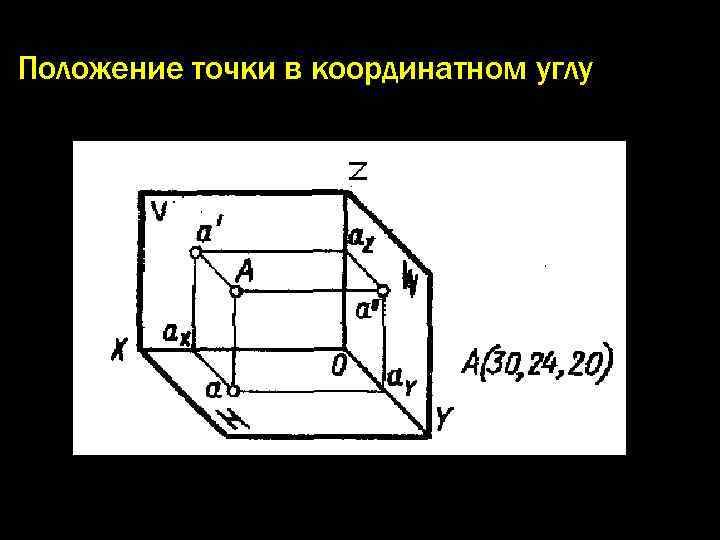Положение точки в координатном углу

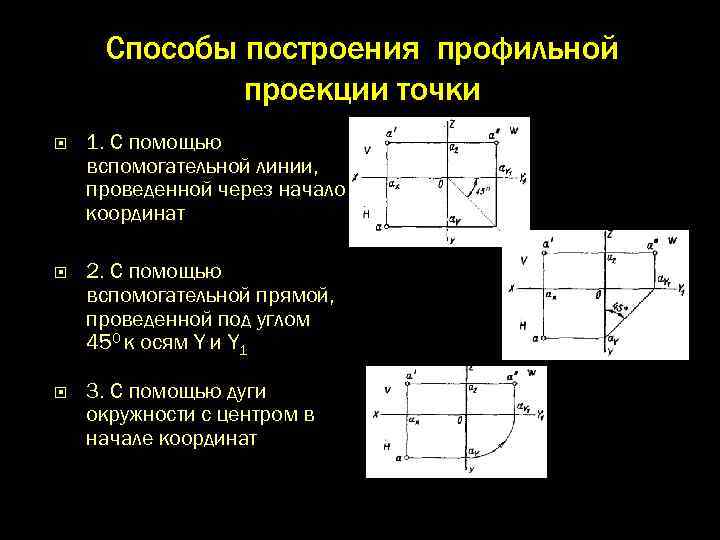Способы построения профильной проекции точки 1. С помощью вспомогательной линии, проведенной через начало координат 2. С помощью вспомогательной прямой, проведенной под углом 450 к осям Y и Y 1 3. C помощью дуги окружности с центром в начале координат

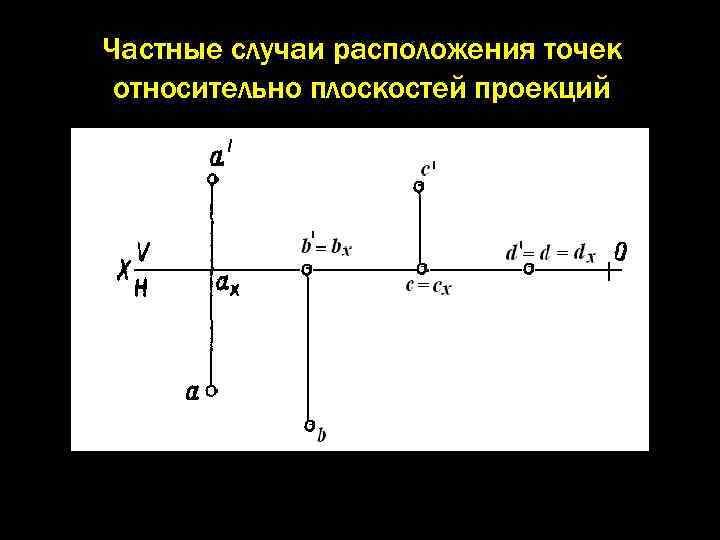Частные случаи расположения точек относительно плоскостей проекций