Golovanova InveSTIGATION oF Two SPIN.pptx
- Количество слайдов: 24
 INVESTIGATION OF TWO SPIN STATES AMPLITUDES ROLE IN DESCRIPTION OF ELASTIC P-P SCATTERING DATA IN ENERGY RANGE 2 - 7000 GEV IN MATHEMATICAL EICONAL METHOD Nina F. Golovanova Moscow State University of Design and Technology Moscow, Russia E-mail: nina 4110@yandex. ru July 2015
INVESTIGATION OF TWO SPIN STATES AMPLITUDES ROLE IN DESCRIPTION OF ELASTIC P-P SCATTERING DATA IN ENERGY RANGE 2 - 7000 GEV IN MATHEMATICAL EICONAL METHOD Nina F. Golovanova Moscow State University of Design and Technology Moscow, Russia E-mail: nina 4110@yandex. ru July 2015
 The results from theoretical calculations of the different cross section of elastic p-p scattering in the mathematical eikonal method with two relativistic amplitudes for two spin states S=0 and S=1 of pair are presented and the input of each one in the differential cross-section is analyzed using comparison with experimental data. July 2015
The results from theoretical calculations of the different cross section of elastic p-p scattering in the mathematical eikonal method with two relativistic amplitudes for two spin states S=0 and S=1 of pair are presented and the input of each one in the differential cross-section is analyzed using comparison with experimental data. July 2015
 Relativistic amplitudes and cross-sections of elastic p-p scattering in mathematical eikonal method There were obtained in works [1, 2, 4, 5] formula for T-matrix as solution of Lippman-Shwinger equation with complex potential (1) that conserves unitarity in the mathematical eikonal method (MEM). The MEM is based on presenting the Т – matrix in the form of a gradated expansion of the mathematical eikonal (ME) matrix that similar to the Sugar- Blanckenbecler one [8] for the common physical eikonal, but includes . In (2) the defect function is July 2015
Relativistic amplitudes and cross-sections of elastic p-p scattering in mathematical eikonal method There were obtained in works [1, 2, 4, 5] formula for T-matrix as solution of Lippman-Shwinger equation with complex potential (1) that conserves unitarity in the mathematical eikonal method (MEM). The MEM is based on presenting the Т – matrix in the form of a gradated expansion of the mathematical eikonal (ME) matrix that similar to the Sugar- Blanckenbecler one [8] for the common physical eikonal, but includes . In (2) the defect function is July 2015
 Green’s free function of ME is associtated with axis X perpendicular to the plane in which vectors and lie: (3) A special system of coordinates is used in the MEM, in which the direction of vectors where are the initial and final scattering momenta in the system of the center of mass, is taken as the direction of axis OZ. In Green’s function (3), the positive sign corresponds to a divergent wave and the negative sign denotes a convergent wave. This function reflects the kinematic for both elastic and inelastic scattering; and are the coordinates of initial momentum and momentum in the intermediate state of the scattering particle, respectively, in the direction of axis OX. The values of ME parameter β and parameter are not specified beforehand. July 2015
Green’s free function of ME is associtated with axis X perpendicular to the plane in which vectors and lie: (3) A special system of coordinates is used in the MEM, in which the direction of vectors where are the initial and final scattering momenta in the system of the center of mass, is taken as the direction of axis OZ. In Green’s function (3), the positive sign corresponds to a divergent wave and the negative sign denotes a convergent wave. This function reflects the kinematic for both elastic and inelastic scattering; and are the coordinates of initial momentum and momentum in the intermediate state of the scattering particle, respectively, in the direction of axis OX. The values of ME parameter β and parameter are not specified beforehand. July 2015
 The profile ME function corresponding to Green’s function (3) is determined as where is the mathematical eikonal. Two-dimensional vector is introduced into formulas below. Formulas below differ from the PEA first by describing both elastic and inelastic scattering, since the mathematical eikonal (in contrast to the physical eikonal) is selected in the direction perpendicular to the scattering plane. No limiting of the narrowness of scattering angles is required. Second, the value of mathematical eikonal parameter β is not specified beforehand (as it is for the physical eikonal) but is determined from the optical theorem. July 2015
The profile ME function corresponding to Green’s function (3) is determined as where is the mathematical eikonal. Two-dimensional vector is introduced into formulas below. Formulas below differ from the PEA first by describing both elastic and inelastic scattering, since the mathematical eikonal (in contrast to the physical eikonal) is selected in the direction perpendicular to the scattering plane. No limiting of the narrowness of scattering angles is required. Second, the value of mathematical eikonal parameter β is not specified beforehand (as it is for the physical eikonal) but is determined from the optical theorem. July 2015
 Comparing the explicit expression for and expansion (2) in the δ approximation, where Green’s function is replaced with. we derive the following expansion for Green’s function in the ME with the help of formula Inserting (6) into the expansion of the Sugar–Blanckenbecler type and introducing a restriction on the profile function we derive the convergent expansion for an onshell T-matrix that allows us to obtain the analytical formula for T-matrix elements in the form where is the transferred momentum. July 2015
Comparing the explicit expression for and expansion (2) in the δ approximation, where Green’s function is replaced with. we derive the following expansion for Green’s function in the ME with the help of formula Inserting (6) into the expansion of the Sugar–Blanckenbecler type and introducing a restriction on the profile function we derive the convergent expansion for an onshell T-matrix that allows us to obtain the analytical formula for T-matrix elements in the form where is the transferred momentum. July 2015
![We use in calculations the profile function of Chou-Yang tape [8] (8) and two We use in calculations the profile function of Chou-Yang tape [8] (8) and two](https://present5.com/presentation/261655423_404554906/image-7.jpg) We use in calculations the profile function of Chou-Yang tape [8] (8) and two relativistic invariant amplitudes of proton -proton pair: the triplet spin amplitude (S=1) (9) and the singlet amplitude (S=0) (10) in model with the structure that describes the experimental form factor found from experiments on scattering high – energy electrons by protons [7] (11) July 2015
We use in calculations the profile function of Chou-Yang tape [8] (8) and two relativistic invariant amplitudes of proton -proton pair: the triplet spin amplitude (S=1) (9) and the singlet amplitude (S=0) (10) in model with the structure that describes the experimental form factor found from experiments on scattering high – energy electrons by protons [7] (11) July 2015
 The triplet differential cross- section (12) The singlet cross- section (13) The summary differential cross - section (14) July 2015
The triplet differential cross- section (12) The singlet cross- section (13) The summary differential cross - section (14) July 2015
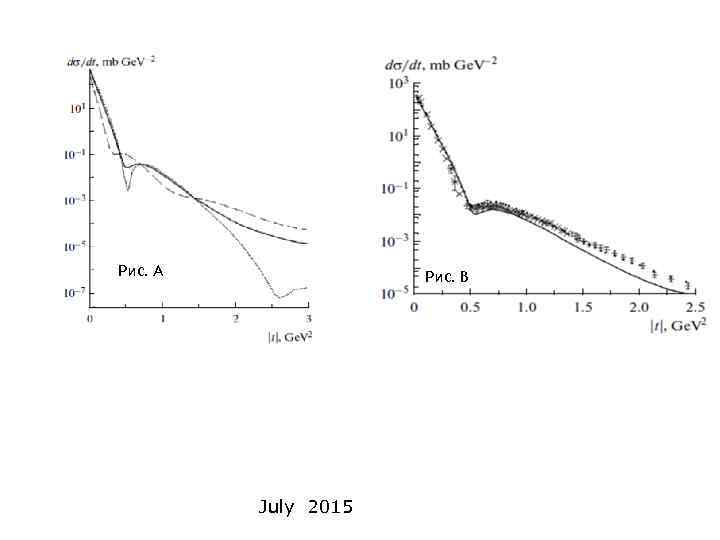 Рис. A Рис. B July 2015
Рис. A Рис. B July 2015
 Рис. А. Теоретические дифференциальные сечения упругого рррассеяния при энергии 7 Тэв. Точечной линией изображено сечение для триплетного состояния протонной пары (12), пунктирной – для синглетного состояния (13) и сплошной – суммарное сечение (14). Рис. В. Экспериментальное (звездочки и кресты) [3] и теоретические дифференциальные сечения упругого рррассеяния при той же энергии, что и на рис. А. Сплошная кривая – сечение, в котором амплитуда упругого рассеяния задаётся в рамках эйконального Редже-подхода [3] с пятнадцатью параметрами; точечная–суммарное в ММЭ (14), вычисленное в работе [2].
Рис. А. Теоретические дифференциальные сечения упругого рррассеяния при энергии 7 Тэв. Точечной линией изображено сечение для триплетного состояния протонной пары (12), пунктирной – для синглетного состояния (13) и сплошной – суммарное сечение (14). Рис. В. Экспериментальное (звездочки и кресты) [3] и теоретические дифференциальные сечения упругого рррассеяния при той же энергии, что и на рис. А. Сплошная кривая – сечение, в котором амплитуда упругого рассеяния задаётся в рамках эйконального Редже-подхода [3] с пятнадцатью параметрами; точечная–суммарное в ММЭ (14), вычисленное в работе [2].
 July 2015
July 2015
 Выбраны значения параметров: А=1, 32, B=-0, 0005, параметр математческого эйконала равен 0, 681 для обеих амплитуд
Выбраны значения параметров: А=1, 32, B=-0, 0005, параметр математческого эйконала равен 0, 681 для обеих амплитуд
 . July 2015
. July 2015
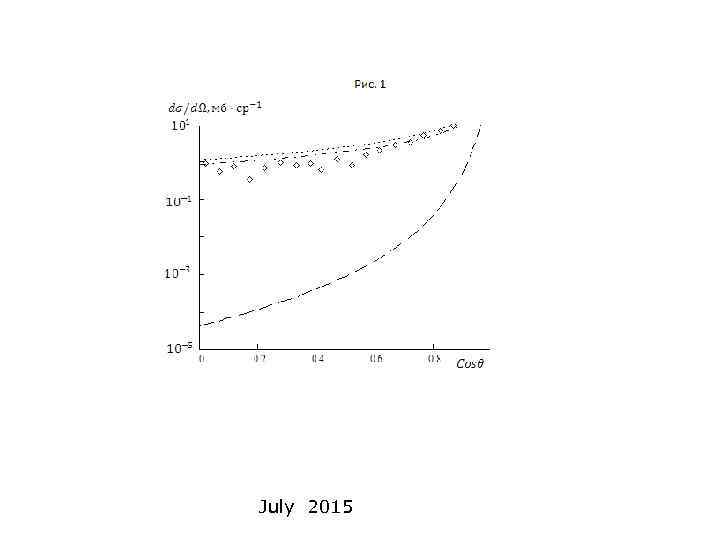
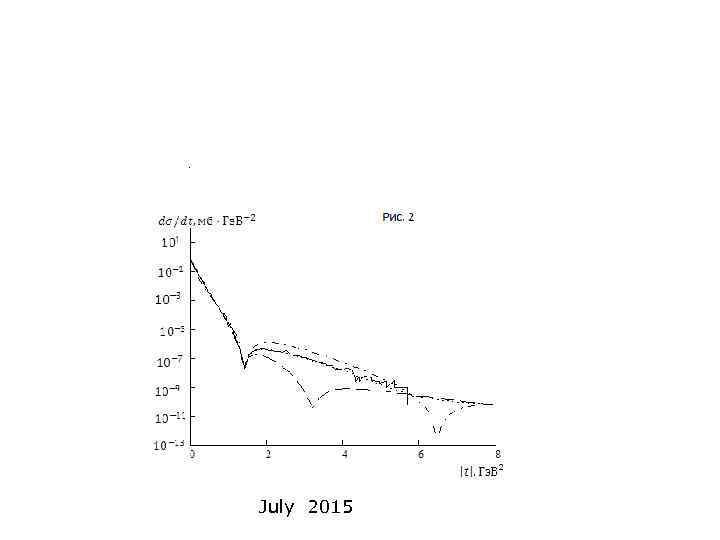
 Рис. 2. Дифференциальные сечения упругого р-р рассеяния при энергии 30, 7 Гэ. В. Сплошной линией представлено экспериментальное [9] дифференциальное сечение упругого. р-р рассеяния. Пунктирной линией изображено триплетное теоретическое сечение (12), штрихпунктирной – синглетное сечение (13) и точечной линией суммарное теоретическое дифференциальное сечение (14). По оси ординат отложены сечения, деленные на 100
Рис. 2. Дифференциальные сечения упругого р-р рассеяния при энергии 30, 7 Гэ. В. Сплошной линией представлено экспериментальное [9] дифференциальное сечение упругого. р-р рассеяния. Пунктирной линией изображено триплетное теоретическое сечение (12), штрихпунктирной – синглетное сечение (13) и точечной линией суммарное теоретическое дифференциальное сечение (14). По оси ординат отложены сечения, деленные на 100
 July 2015
July 2015
 Все сечения разделены на 10000
Все сечения разделены на 10000
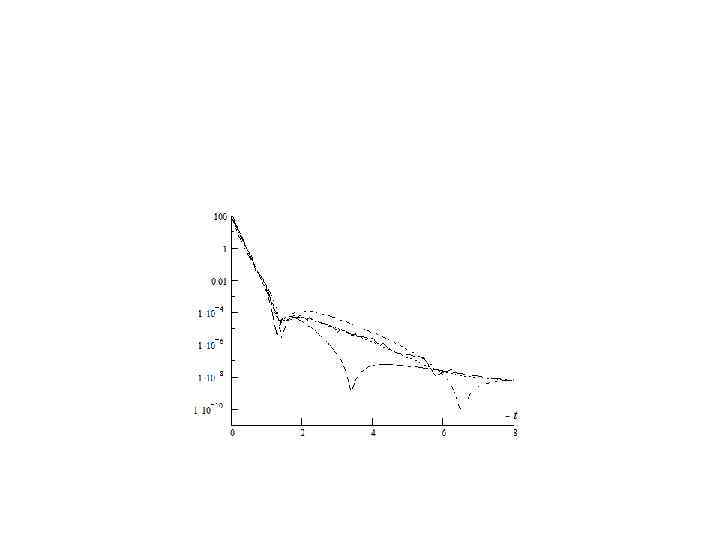
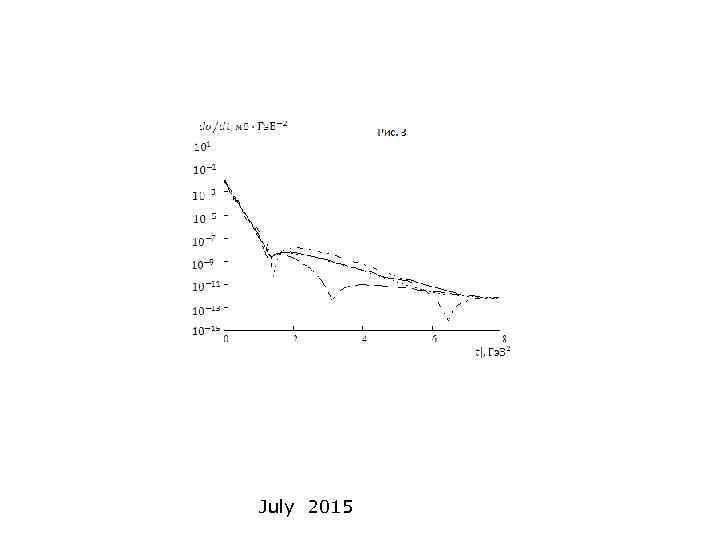
 Рис. 5. Дифференциальные сечения упругого рр − рассеяния при энергии 62 Гэв. По оси ординат отложены значения экспериментального и теоретических дифференциальных сечений в тех же единицах, что и на предыдущем рисунке. Инвариантная передача импульса в системе центра масс двух протонов как на рис. 4. Пунктирная линия есть триплетное сечение (12), штрихпунктирная-синглетное (13), точечная – суммарное (14) и сплошной линией нанесено экспериментальное сечение.
Рис. 5. Дифференциальные сечения упругого рр − рассеяния при энергии 62 Гэв. По оси ординат отложены значения экспериментального и теоретических дифференциальных сечений в тех же единицах, что и на предыдущем рисунке. Инвариантная передача импульса в системе центра масс двух протонов как на рис. 4. Пунктирная линия есть триплетное сечение (12), штрихпунктирная-синглетное (13), точечная – суммарное (14) и сплошной линией нанесено экспериментальное сечение.
 July 2015
July 2015
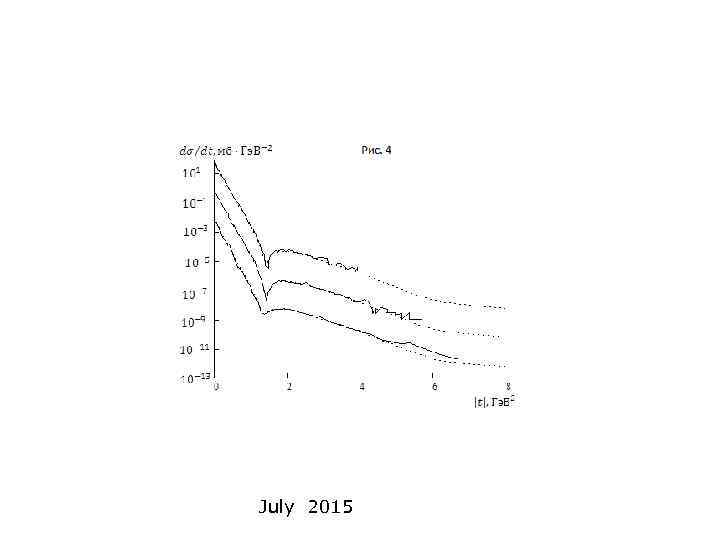
 Рис. 4 Дифференциальные сечения упругого р-р рассеяния при энергиях: 23, 5; 30, 7 и 52, 8 Гэ. В. Экспериментальные данные [9] нанесены сплошными линиями, а точечными линиями даны теоретические кривые суммарных дифференциальных сечений упругого р-р рассеяния (14). Верхняя пара относится к энергии 23, 5 Гэ. В. Средняя пара есть деленные на 100 экспериментальное и теоретическое дифференциальное сечения при энергии 30, 7 Гэ. В. Нижняя пара– экспериментальное и теоретическое распределения, деленные на 10000 для энергии 52, 8 Гэ. В. По осям координат отложено тоже, что на рис. 2 и 3.
Рис. 4 Дифференциальные сечения упругого р-р рассеяния при энергиях: 23, 5; 30, 7 и 52, 8 Гэ. В. Экспериментальные данные [9] нанесены сплошными линиями, а точечными линиями даны теоретические кривые суммарных дифференциальных сечений упругого р-р рассеяния (14). Верхняя пара относится к энергии 23, 5 Гэ. В. Средняя пара есть деленные на 100 экспериментальное и теоретическое дифференциальное сечения при энергии 30, 7 Гэ. В. Нижняя пара– экспериментальное и теоретическое распределения, деленные на 10000 для энергии 52, 8 Гэ. В. По осям координат отложено тоже, что на рис. 2 и 3.
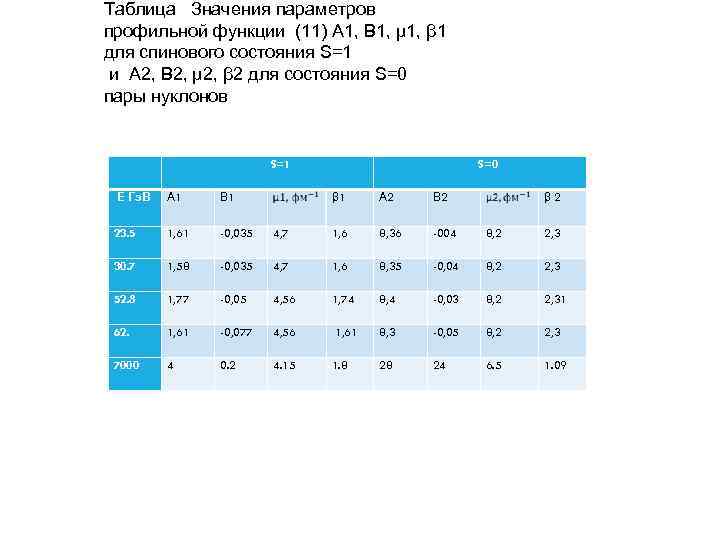 Таблица Значения параметров профильной функции (11) А 1, В 1, µ 1, β 1 для спинового состояния S=1 и А 2, В 2, µ 2, β 2 для состояния S=0 пары нуклонов S=1 Е Гэ. В А 1 В 1 23. 5 1, 61 -0, 035 30. 7 1, 58 52. 8 S=0 β 1 А 2 В 2 β 2 4, 7 1, 6 8, 36 -004 8, 2 2, 3 -0, 035 4, 7 1, 6 8, 35 -0, 04 8, 2 2, 3 1, 77 -0, 05 4, 56 1, 74 8, 4 -0, 03 8, 2 2, 31 62. 1, 61 -0, 077 4, 56 1, 61 8, 3 -0, 05 8, 2 2, 3 7000 4 0. 2 4. 15 1. 8 28 24 6. 5 1. 09
Таблица Значения параметров профильной функции (11) А 1, В 1, µ 1, β 1 для спинового состояния S=1 и А 2, В 2, µ 2, β 2 для состояния S=0 пары нуклонов S=1 Е Гэ. В А 1 В 1 23. 5 1, 61 -0, 035 30. 7 1, 58 52. 8 S=0 β 1 А 2 В 2 β 2 4, 7 1, 6 8, 36 -004 8, 2 2, 3 -0, 035 4, 7 1, 6 8, 35 -0, 04 8, 2 2, 3 1, 77 -0, 05 4, 56 1, 74 8, 4 -0, 03 8, 2 2, 31 62. 1, 61 -0, 077 4, 56 1, 61 8, 3 -0, 05 8, 2 2, 3 7000 4 0. 2 4. 15 1. 8 28 24 6. 5 1. 09
 CONCLUSIONS The MEM, having two relativistic amplitudes for the singlet and triplet spin states of the proton–proton pair and allowing for the structure of nucleons through shape factor (19) in the singlet state, provides a realis tic proton scattering pattern for both at high and ultra high energies. The experimental data on elastic p–p scattering with the isolation of spin states of the proton pair can be considered thorough validation of the proposed description. July 2015
CONCLUSIONS The MEM, having two relativistic amplitudes for the singlet and triplet spin states of the proton–proton pair and allowing for the structure of nucleons through shape factor (19) in the singlet state, provides a realis tic proton scattering pattern for both at high and ultra high energies. The experimental data on elastic p–p scattering with the isolation of spin states of the proton pair can be considered thorough validation of the proposed description. July 2015
 СПИСОК ЛИТЕРАТУРЫ 1. Голованова Н. Ф. // Известия вузов. Физика 2013. т. 56. № 6. С. 97 Golovanova N. F. // Russian Physics Journal, 2013, Т. 56. № 6 р. 715 2. Голованова Н. Ф. // Известия РАН. Серия физическая 2014. т. 78. № 6. С. 1425 Golovanova N. F. // Bulletin of the Russian Academy of Sciences. Physics, 2014, Vol. 78, № 11, p. 1425 3. Donnachie A, Landshoff P V // ar. Xiv: 1112. 2485 v 1[hep-ph] 12 Dec 2011 4. Golovanova N. F. , Golovanov A. A. // Rus. J. Math. Phys. 2003. V. 10. Р. 31. 5. Golovanova N. F. & Iskra V. //Phys. Lett. B 1987. V. 187. № 1, 2. Р. 7. 6. Sugar R. L. & Blanckenbecler R. //Phys. Rev. 1969. V. 183 № 5. Р. 1387. 7. Де Бенедетти С. Ядерные взаимодействия. Атомиздат, Москва, 1968 8. Durand L. , Lipes R. //Phys. Rev. Lett. 1968. V. 20. № 12. P. 402 9. Бертини М. , Жиффон М. // ФЭЧАЯ. 1997. Т. 26. Вып. 1. С. 32
СПИСОК ЛИТЕРАТУРЫ 1. Голованова Н. Ф. // Известия вузов. Физика 2013. т. 56. № 6. С. 97 Golovanova N. F. // Russian Physics Journal, 2013, Т. 56. № 6 р. 715 2. Голованова Н. Ф. // Известия РАН. Серия физическая 2014. т. 78. № 6. С. 1425 Golovanova N. F. // Bulletin of the Russian Academy of Sciences. Physics, 2014, Vol. 78, № 11, p. 1425 3. Donnachie A, Landshoff P V // ar. Xiv: 1112. 2485 v 1[hep-ph] 12 Dec 2011 4. Golovanova N. F. , Golovanov A. A. // Rus. J. Math. Phys. 2003. V. 10. Р. 31. 5. Golovanova N. F. & Iskra V. //Phys. Lett. B 1987. V. 187. № 1, 2. Р. 7. 6. Sugar R. L. & Blanckenbecler R. //Phys. Rev. 1969. V. 183 № 5. Р. 1387. 7. Де Бенедетти С. Ядерные взаимодействия. Атомиздат, Москва, 1968 8. Durand L. , Lipes R. //Phys. Rev. Lett. 1968. V. 20. № 12. P. 402 9. Бертини М. , Жиффон М. // ФЭЧАЯ. 1997. Т. 26. Вып. 1. С. 32
 Thank you! Questions? Голованова Нина Федотовна Dr. Nina F. Golovanova nina 4110@yandex. ru www. ninagolovanova. ru July 2015
Thank you! Questions? Голованова Нина Федотовна Dr. Nina F. Golovanova nina 4110@yandex. ru www. ninagolovanova. ru July 2015


