80b04d55246471a428f6b6b4f1161751.ppt
- Количество слайдов: 40
 Inventory Control
Inventory Control
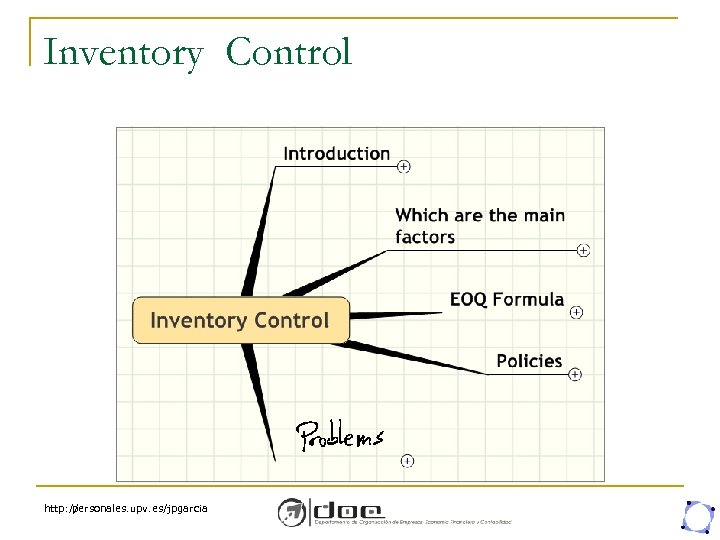 Inventory Control http: // personales. upv. es/jpgarcia
Inventory Control http: // personales. upv. es/jpgarcia
 Inventory Control is everywhere. n n n Fuel for the Car Milk to Drink Milk to Sell Mother. Boards to Assemble Computers Production with Setups http: // personales. upv. es/jpgarcia
Inventory Control is everywhere. n n n Fuel for the Car Milk to Drink Milk to Sell Mother. Boards to Assemble Computers Production with Setups http: // personales. upv. es/jpgarcia
 Some youtube videos n n http: //es. youtube. com/watch? v=qk. ZQx. XJuq. Ko http: //es. youtube. com/watch? v=_Vr. BKF 6 SUCA http: // personales. upv. es/jpgarcia
Some youtube videos n n http: //es. youtube. com/watch? v=qk. ZQx. XJuq. Ko http: //es. youtube. com/watch? v=_Vr. BKF 6 SUCA http: // personales. upv. es/jpgarcia
 Why we do store? n n n n Unplanned shocks (labor strikes, natural disasters, surges in demand, etc. ) To maintain independence of supply chain Economies of production Improve customer service Economies of purchasing Transportation savings Hedge against future http: // personales. upv. es/jpgarcia
Why we do store? n n n n Unplanned shocks (labor strikes, natural disasters, surges in demand, etc. ) To maintain independence of supply chain Economies of production Improve customer service Economies of purchasing Transportation savings Hedge against future http: // personales. upv. es/jpgarcia
 Costs Related with Inventory Control n n n Inventory deteriorates, becomes obsolete, lost, stolen, etc. Order processing q Shipping q Handling Carrying Costs q Capital (opportunity) costs q Inventory risk costs q Space costs q Inventory service costs Out-of- Stock Costs q Lost sales cost q Back-order cost Complacency http: // personales. upv. es/jpgarcia
Costs Related with Inventory Control n n n Inventory deteriorates, becomes obsolete, lost, stolen, etc. Order processing q Shipping q Handling Carrying Costs q Capital (opportunity) costs q Inventory risk costs q Space costs q Inventory service costs Out-of- Stock Costs q Lost sales cost q Back-order cost Complacency http: // personales. upv. es/jpgarcia
 Nature of Inventory: Adding Value through Inventory n Speed q n Cost q q n direct: purchasing, delivery, manufacturing indirect: holding, stockout. Quality q n location of inventory has gigantic effect on speed inventory can be a “buffer” against poor quality; conversely, low inventory levels may force high quality Flexibility q location, level of anticipatory inventory both have effects http: // personales. upv. es/jpgarcia
Nature of Inventory: Adding Value through Inventory n Speed q n Cost q q n direct: purchasing, delivery, manufacturing indirect: holding, stockout. Quality q n location of inventory has gigantic effect on speed inventory can be a “buffer” against poor quality; conversely, low inventory levels may force high quality Flexibility q location, level of anticipatory inventory both have effects http: // personales. upv. es/jpgarcia
 Nature of Inventory: Functional Roles of Inventory n n n n Transit Buffer Seasonal Decoupling Speculative Lot Sizing or Cycle Mistakes Promotional http: // personales. upv. es/jpgarcia
Nature of Inventory: Functional Roles of Inventory n n n n Transit Buffer Seasonal Decoupling Speculative Lot Sizing or Cycle Mistakes Promotional http: // personales. upv. es/jpgarcia
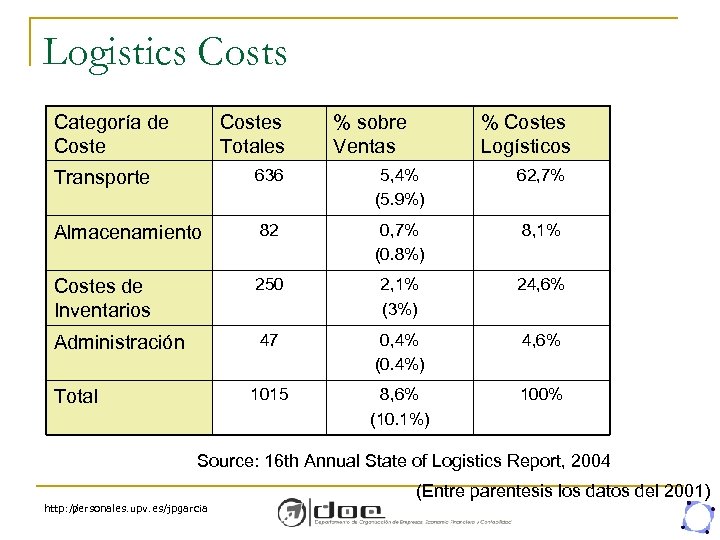 Logistics Costs Categoría de Costes Totales % sobre Ventas % Costes Logísticos Transporte 636 5, 4% (5. 9%) 62, 7% Almacenamiento 82 0, 7% (0. 8%) 8, 1% Costes de Inventarios 250 2, 1% (3%) 24, 6% Administración 47 0, 4% (0. 4%) 4, 6% 1015 8, 6% (10. 1%) 100% Total Source: 16 th Annual State of Logistics Report, 2004 (Entre parentesis los datos del 2001) http: // personales. upv. es/jpgarcia
Logistics Costs Categoría de Costes Totales % sobre Ventas % Costes Logísticos Transporte 636 5, 4% (5. 9%) 62, 7% Almacenamiento 82 0, 7% (0. 8%) 8, 1% Costes de Inventarios 250 2, 1% (3%) 24, 6% Administración 47 0, 4% (0. 4%) 4, 6% 1015 8, 6% (10. 1%) 100% Total Source: 16 th Annual State of Logistics Report, 2004 (Entre parentesis los datos del 2001) http: // personales. upv. es/jpgarcia
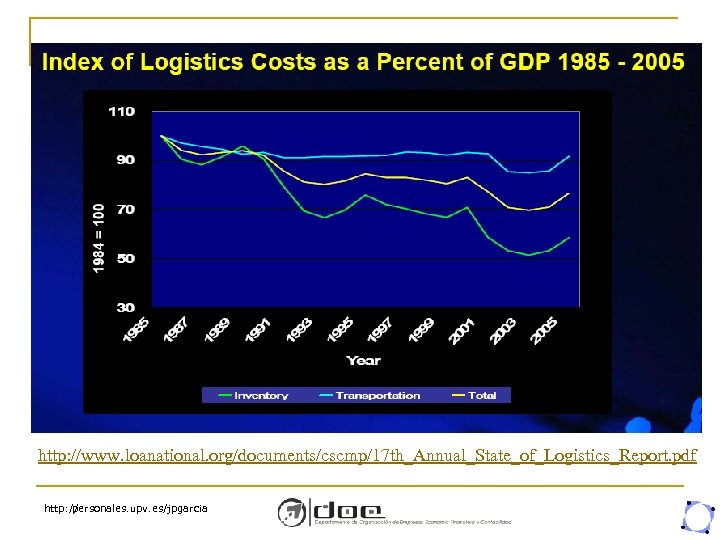 http: //www. loanational. org/documents/cscmp/17 th_Annual_State_of_Logistics_Report. pdf http: // personales. upv. es/jpgarcia
http: //www. loanational. org/documents/cscmp/17 th_Annual_State_of_Logistics_Report. pdf http: // personales. upv. es/jpgarcia
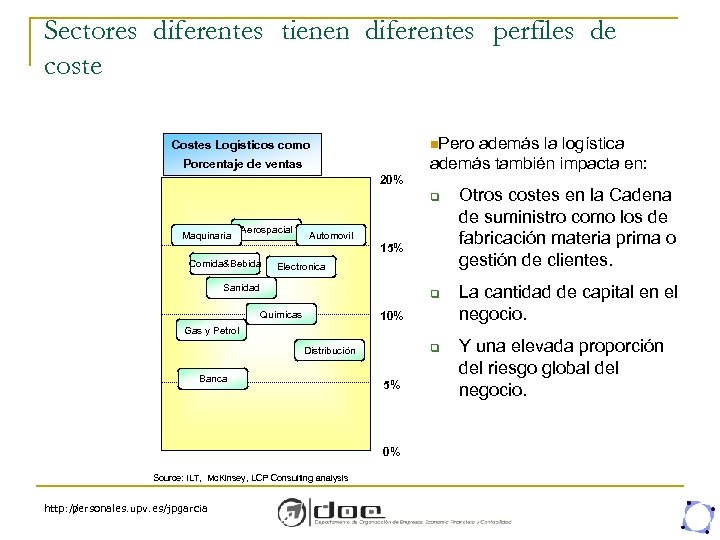 Sectores diferentes tienen diferentes perfiles de coste n. Pero además la logística además también impacta en: Costes Logísticos como Porcentaje de ventas 20% q Maquinaría Aerospacial Automovil 15% Comida&Bebida Electronica Sanidad q Químicas 10% Otros costes en la Cadena de suministro como los de fabricación materia prima o gestión de clientes. La cantidad de capital en el negocio. Gas y Petrol q Distribución Banca 5% 0% Source: ILT, Mc. Kinsey, LCP Consulting analysis http: // personales. upv. es/jpgarcia Y una elevada proporción del riesgo global del negocio.
Sectores diferentes tienen diferentes perfiles de coste n. Pero además la logística además también impacta en: Costes Logísticos como Porcentaje de ventas 20% q Maquinaría Aerospacial Automovil 15% Comida&Bebida Electronica Sanidad q Químicas 10% Otros costes en la Cadena de suministro como los de fabricación materia prima o gestión de clientes. La cantidad de capital en el negocio. Gas y Petrol q Distribución Banca 5% 0% Source: ILT, Mc. Kinsey, LCP Consulting analysis http: // personales. upv. es/jpgarcia Y una elevada proporción del riesgo global del negocio.
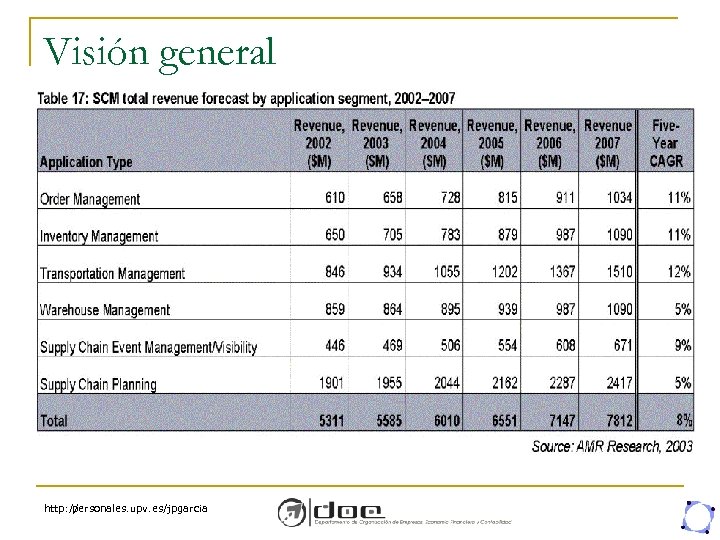 Visión general http: // personales. upv. es/jpgarcia
Visión general http: // personales. upv. es/jpgarcia
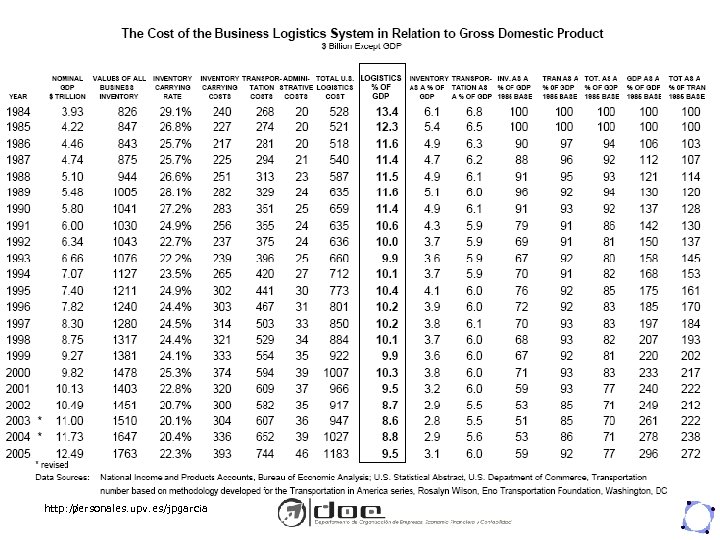 http: // personales. upv. es/jpgarcia
http: // personales. upv. es/jpgarcia
 Which are the main factors http: // personales. upv. es/jpgarcia
Which are the main factors http: // personales. upv. es/jpgarcia
 Main Factors defining an Inventory Demand Policy Forecasted Demand Average n q q n Setup q q n Cost Time Storage q q q n Error on Forecasted Demand Cost Capacity Expiration Time q q q q Lead Time (LT) Basic Period of Forecasting Horizon Finite and Infinite Horizon Finite or Infinite Production Rate http: // personales. upv. es/jpgarcia
Main Factors defining an Inventory Demand Policy Forecasted Demand Average n q q n Setup q q n Cost Time Storage q q q n Error on Forecasted Demand Cost Capacity Expiration Time q q q q Lead Time (LT) Basic Period of Forecasting Horizon Finite and Infinite Horizon Finite or Infinite Production Rate http: // personales. upv. es/jpgarcia
 EOQ Formula http: // personales. upv. es/jpgarcia
EOQ Formula http: // personales. upv. es/jpgarcia
 Why to do it with Formulae what has always been done by head? n n Reduce Cost Number of Different units Time to do Added Value tasks Computer Aid Management http: // personales. upv. es/jpgarcia
Why to do it with Formulae what has always been done by head? n n Reduce Cost Number of Different units Time to do Added Value tasks Computer Aid Management http: // personales. upv. es/jpgarcia
 Assumptions to derive the EOQ formula n n n Production is Instantaneous. Delivery is inmediate Demand is deterministic Demand is constant over time A production run incurs a fixed setup cost Products can be analyzed individually http: // personales. upv. es/jpgarcia
Assumptions to derive the EOQ formula n n n Production is Instantaneous. Delivery is inmediate Demand is deterministic Demand is constant over time A production run incurs a fixed setup cost Products can be analyzed individually http: // personales. upv. es/jpgarcia
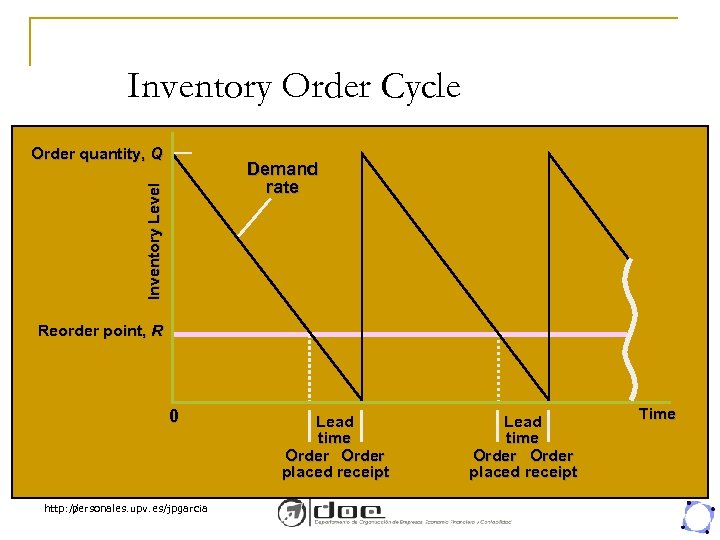 Inventory Order Cycle Order quantity, Q Inventory Level Demand rate Reorder point, R 0 http: // personales. upv. es/jpgarcia Lead time Order placed receipt Time
Inventory Order Cycle Order quantity, Q Inventory Level Demand rate Reorder point, R 0 http: // personales. upv. es/jpgarcia Lead time Order placed receipt Time
 EOQ Cost Model Co - cost of placing order Cc - annual per-unit carrying cost D - annual demand Q - order quantity Annual ordering cost = Co D Q Annual carrying cost = Cc Q 2 Co D Cc Q Total cost = + Q 2 http: // personales. upv. es/jpgarcia
EOQ Cost Model Co - cost of placing order Cc - annual per-unit carrying cost D - annual demand Q - order quantity Annual ordering cost = Co D Q Annual carrying cost = Cc Q 2 Co D Cc Q Total cost = + Q 2 http: // personales. upv. es/jpgarcia
 EOQ Cost Model Deriving Qopt Co D Cc Q TC = + Q 2 Co D Cc TC = + Q 2 2 Q C 0 D Cc 0= + Q 2 2 Qopt = http: // personales. upv. es/jpgarcia 2 Co. D Cc Proving equality of costs at optimal point Co D Cc Q = Q 2 2 Co. D = Cc Qopt = 2 Co. D Cc
EOQ Cost Model Deriving Qopt Co D Cc Q TC = + Q 2 Co D Cc TC = + Q 2 2 Q C 0 D Cc 0= + Q 2 2 Qopt = http: // personales. upv. es/jpgarcia 2 Co. D Cc Proving equality of costs at optimal point Co D Cc Q = Q 2 2 Co. D = Cc Qopt = 2 Co. D Cc
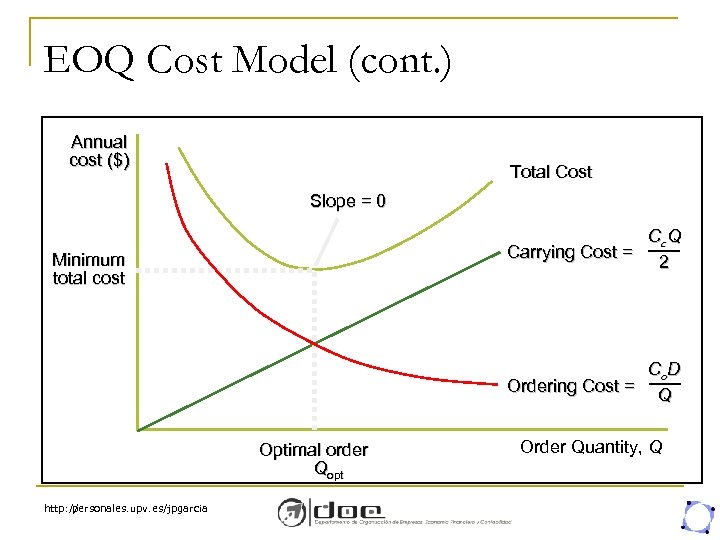 EOQ Cost Model (cont. ) Annual cost ($) Total Cost Slope = 0 Cc. Q Carrying Cost = 2 Minimum total cost Co D Ordering Cost = Q Optimal order Qopt http: // personales. upv. es/jpgarcia Order Quantity, Q
EOQ Cost Model (cont. ) Annual cost ($) Total Cost Slope = 0 Cc. Q Carrying Cost = 2 Minimum total cost Co D Ordering Cost = Q Optimal order Qopt http: // personales. upv. es/jpgarcia Order Quantity, Q
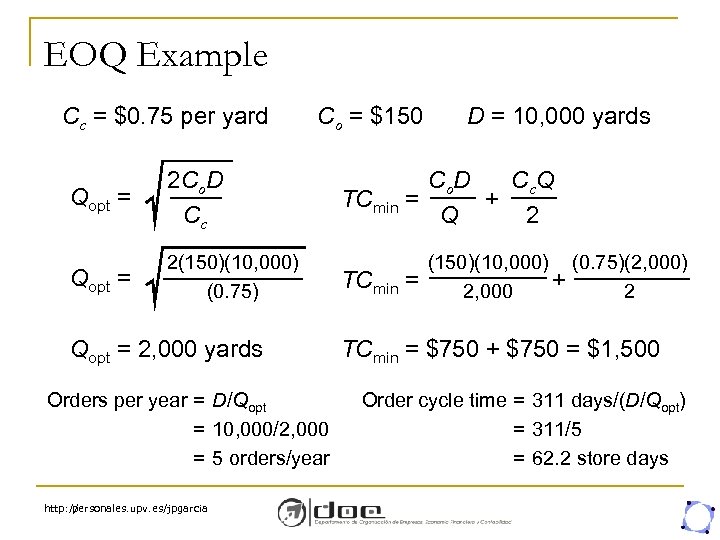 EOQ Example Cc = $0. 75 per yard Qopt = 2 Co. D Cc Qopt = Co = $150 2(150)(10, 000) (0. 75) Qopt = 2, 000 yards Orders per year = D/Qopt = 10, 000/2, 000 = 5 orders/year http: // personales. upv. es/jpgarcia D = 10, 000 yards Co. D Cc Q TCmin = + Q 2 TCmin = (150)(10, 000) (0. 75)(2, 000) + 2, 000 2 TCmin = $750 + $750 = $1, 500 Order cycle time = 311 days/(D/Qopt) = 311/5 = 62. 2 store days
EOQ Example Cc = $0. 75 per yard Qopt = 2 Co. D Cc Qopt = Co = $150 2(150)(10, 000) (0. 75) Qopt = 2, 000 yards Orders per year = D/Qopt = 10, 000/2, 000 = 5 orders/year http: // personales. upv. es/jpgarcia D = 10, 000 yards Co. D Cc Q TCmin = + Q 2 TCmin = (150)(10, 000) (0. 75)(2, 000) + 2, 000 2 TCmin = $750 + $750 = $1, 500 Order cycle time = 311 days/(D/Qopt) = 311/5 = 62. 2 store days
 Required Data to generate a Policy n n Time q Forecast Period q Horizon q Lead Time Demand for a given Period (average and Standard Deviation) q Demand during Horizon Cost q holding Cost (€ per unit per year) =K·Cu q Unit Cost (€ per unit) q Setup Cost S (€) q Total Cost =Holding Cost + Setup Cost Service Level (max % of runouts that we are willing to afford) http: // personales. upv. es/jpgarcia
Required Data to generate a Policy n n Time q Forecast Period q Horizon q Lead Time Demand for a given Period (average and Standard Deviation) q Demand during Horizon Cost q holding Cost (€ per unit per year) =K·Cu q Unit Cost (€ per unit) q Setup Cost S (€) q Total Cost =Holding Cost + Setup Cost Service Level (max % of runouts that we are willing to afford) http: // personales. upv. es/jpgarcia
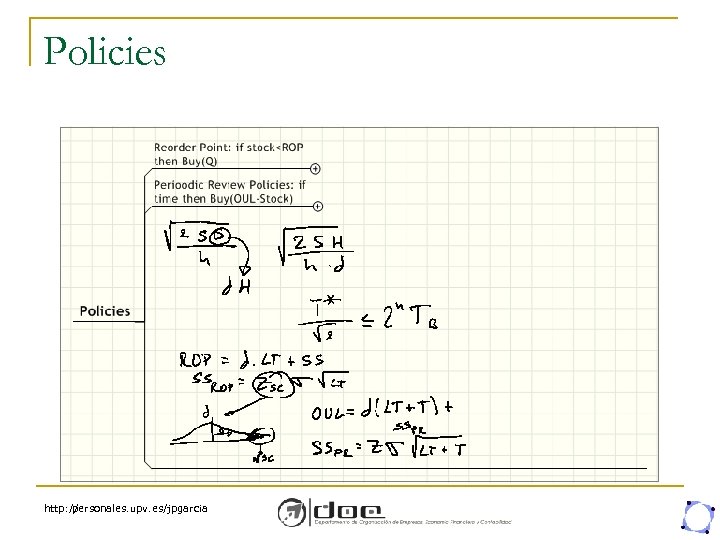 Policies http: // personales. upv. es/jpgarcia
Policies http: // personales. upv. es/jpgarcia
 Reorder Point: if stock
Reorder Point: if stock
 Safety Stocks. Basic Concepts § Safety stock § buffer added to on hand inventory during lead time § Stockout § an inventory shortage § Service level § probability that the inventory available during lead time will meet demand http: // personales. upv. es/jpgarcia
Safety Stocks. Basic Concepts § Safety stock § buffer added to on hand inventory during lead time § Stockout § an inventory shortage § Service level § probability that the inventory available during lead time will meet demand http: // personales. upv. es/jpgarcia
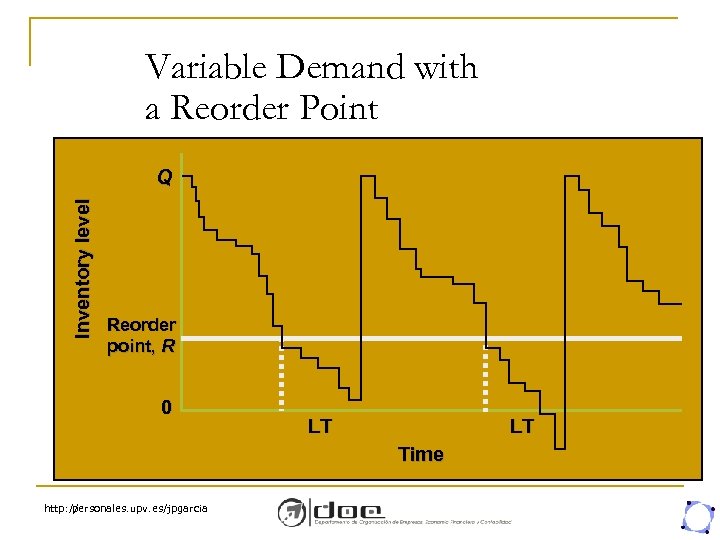 Variable Demand with a Reorder Point Inventory level Q Reorder point, R 0 LT LT Time http: // personales. upv. es/jpgarcia
Variable Demand with a Reorder Point Inventory level Q Reorder point, R 0 LT LT Time http: // personales. upv. es/jpgarcia
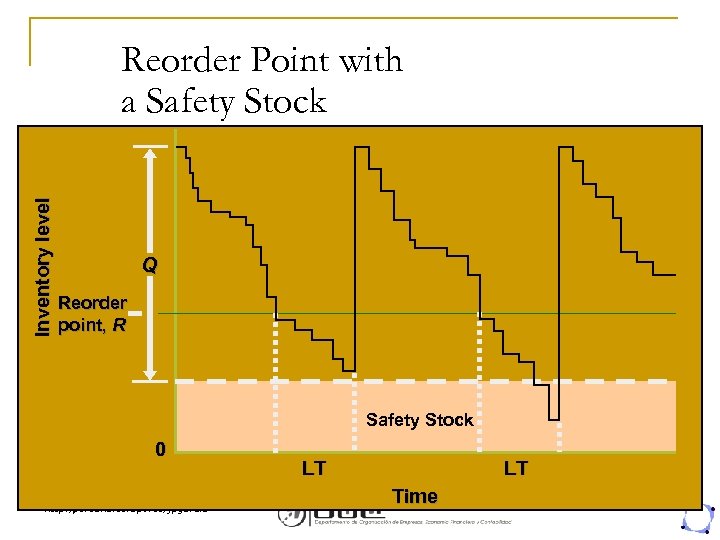 Inventory level Reorder Point with a Safety Stock Q Reorder point, R Safety Stock 0 http: // personales. upv. es/jpgarcia LT LT Time
Inventory level Reorder Point with a Safety Stock Q Reorder point, R Safety Stock 0 http: // personales. upv. es/jpgarcia LT LT Time
 Reorder Point With Variable Demand R = d. L + z d L where d = average daily demand L = lead time d = the standard deviation of daily demand z = number of standard deviations corresponding to the service level probability z d L = safety stock http: // personales. upv. es/jpgarcia
Reorder Point With Variable Demand R = d. L + z d L where d = average daily demand L = lead time d = the standard deviation of daily demand z = number of standard deviations corresponding to the service level probability z d L = safety stock http: // personales. upv. es/jpgarcia
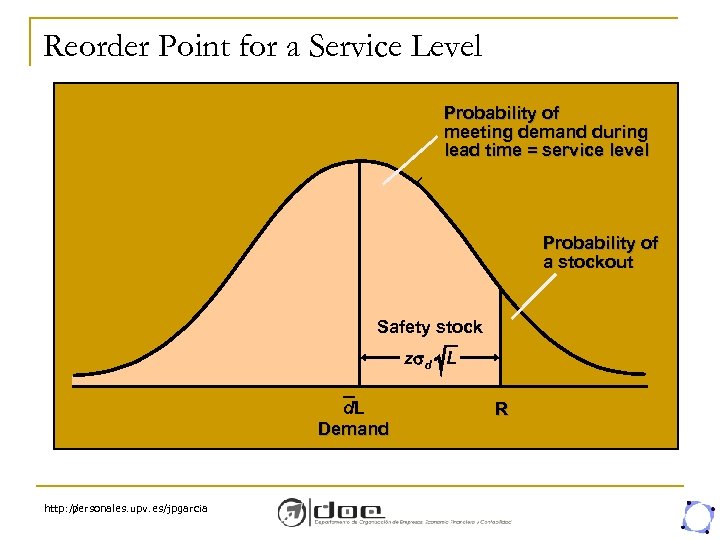 Reorder Point for a Service Level Probability of meeting demand during lead time = service level Probability of a stockout Safety stock z d L d. L Demand http: // personales. upv. es/jpgarcia R
Reorder Point for a Service Level Probability of meeting demand during lead time = service level Probability of a stockout Safety stock z d L d. L Demand http: // personales. upv. es/jpgarcia R
 Reorder Point for Variable Demand The carpet store wants a reorder point with a 95% service level and a 5% stockout probability d = 30 yards per day L = 10 days d = 5 yards per day For a 95% service level, z = 1. 65 R = d. L + z d L Safety stock = z d L = 30(10) + (1. 65)(5)( 10) = 326. 1 yards = 26. 1 yards http: // personales. upv. es/jpgarcia
Reorder Point for Variable Demand The carpet store wants a reorder point with a 95% service level and a 5% stockout probability d = 30 yards per day L = 10 days d = 5 yards per day For a 95% service level, z = 1. 65 R = d. L + z d L Safety stock = z d L = 30(10) + (1. 65)(5)( 10) = 326. 1 yards = 26. 1 yards http: // personales. upv. es/jpgarcia
 Periodic Review Policies: if time then Buy(OUL -Stock) n n OUL: Max Demand we cover during next Review Period + Lead Time Review Period that minimizes Total Cost q q Economic Order Period (T*) Power of Two Policies http: // personales. upv. es/jpgarcia
Periodic Review Policies: if time then Buy(OUL -Stock) n n OUL: Max Demand we cover during next Review Period + Lead Time Review Period that minimizes Total Cost q q Economic Order Period (T*) Power of Two Policies http: // personales. upv. es/jpgarcia
 Order Quantity for a Periodic Inventory System Q = d(tb + L) + z d tb + L - I where d tb L d z d = average demand rate = the fixed time between orders = lead time = standard deviation of demand tb + L = safety stock I = inventory level http: // personales. upv. es/jpgarcia
Order Quantity for a Periodic Inventory System Q = d(tb + L) + z d tb + L - I where d tb L d z d = average demand rate = the fixed time between orders = lead time = standard deviation of demand tb + L = safety stock I = inventory level http: // personales. upv. es/jpgarcia
 Fixed-Period Model with Variable Demand d d tb L I z = 6 bottles per day = 1. 2 bottles = 60 days = 5 days = 8 bottles = 1. 65 (for a 95% service level) Q = d(tb + L) + z d tb + L - I = (6)(60 + 5) + (1. 65)(1. 2) = 397. 96 bottles http: // personales. upv. es/jpgarcia 60 + 5 - 8
Fixed-Period Model with Variable Demand d d tb L I z = 6 bottles per day = 1. 2 bottles = 60 days = 5 days = 8 bottles = 1. 65 (for a 95% service level) Q = d(tb + L) + z d tb + L - I = (6)(60 + 5) + (1. 65)(1. 2) = 397. 96 bottles http: // personales. upv. es/jpgarcia 60 + 5 - 8
 Problem n A toy manufacturer uses aproximately 32000 silicon chips annually. The Chips are used at a steady rate during the 240 days a year that the plant operates. Annual holding cost is 60 cents per chip and ordering cost is 24$. A year has 288 days. q q n How muchh should we order each time? How many times per year are we to order? What is the length of an order cycle. What is the total cost? If the supplier has a lead time of 20 days? q q Which is the reorder point? Should do we have a safety stock? To prevent what? http: // personales. upv. es/jpgarcia
Problem n A toy manufacturer uses aproximately 32000 silicon chips annually. The Chips are used at a steady rate during the 240 days a year that the plant operates. Annual holding cost is 60 cents per chip and ordering cost is 24$. A year has 288 days. q q n How muchh should we order each time? How many times per year are we to order? What is the length of an order cycle. What is the total cost? If the supplier has a lead time of 20 days? q q Which is the reorder point? Should do we have a safety stock? To prevent what? http: // personales. upv. es/jpgarcia
 Problem n n Determine optimal number to order D = 1, 000 units S = $10 per order H = $. 50 per unit per year The pack has 150 units each Management underestimated demand by 50% C = $5/unit There is a discount of 5% per unit if you buy more than 500 units http: // personales. upv. es/jpgarcia
Problem n n Determine optimal number to order D = 1, 000 units S = $10 per order H = $. 50 per unit per year The pack has 150 units each Management underestimated demand by 50% C = $5/unit There is a discount of 5% per unit if you buy more than 500 units http: // personales. upv. es/jpgarcia
 Problem n n n A company substitutes in a regular way a component of a given machine to ensure quality parameters of the product. Machine works during the whole year and needs 40 parts per week. The component supplier offers a price of 10 € per unit for orders with less than 300 units, and a price of 9. 70 € per unit for bigger orders. The cost of setting each order is stimated on 25 €, and the holding cost is of 0. 26 €/ €/ year. How many units should you request each time? If the supplier wants you to make orders bigger than 500 units ¿which is maximum unit price that should stablish for orders bigger than 500 units? http: // personales. upv. es/jpgarcia
Problem n n n A company substitutes in a regular way a component of a given machine to ensure quality parameters of the product. Machine works during the whole year and needs 40 parts per week. The component supplier offers a price of 10 € per unit for orders with less than 300 units, and a price of 9. 70 € per unit for bigger orders. The cost of setting each order is stimated on 25 €, and the holding cost is of 0. 26 €/ €/ year. How many units should you request each time? If the supplier wants you to make orders bigger than 500 units ¿which is maximum unit price that should stablish for orders bigger than 500 units? http: // personales. upv. es/jpgarcia
 Karbonicas Ju. Pe n n n Karbonicas Ju. Pe is a company bottling drinks where you work. To simplify we are to consider only one product. Our company has a warehouse where store product just manufactured and from where we serve three logistics platforms that our client holds. The logistics platforms are cross-dock warehouses, where storing products has a high cost, and from where there associated retail stores are served. The lead time at the manufacturing side for Karbonicas Ju. Pe is 7 days (i. e. it takes one week from we have been asked to produce until the product is ready at the warehouse. Each of the logistics platforms faces a demand (measured in pallets) that might be approximated by a normal distribution. (Data can be found at Table I). Each logistic platform knows the demand the stock levels of each associated retail store. It takes two (2) days since the platform asks for products until the product reaches each retail store through the logistic platform. The inventory system is Reorder Point at each echelon. (i. e. the platforms work with ROP logic to the central warehouse of Karbonicas Ju. Pe, and the central warehouse works with ROP to the manufacturing facility). The relation between the logistic platform and the retail stores is not considere in this problem. You are considering the posibility of eliminate the central warehouse echelon. To do that the three logistics platforms should agree a joint review period (considering all the costs) with a power-of-two policy. The factory consolidates the three orders (that have been done simultaneously) and will bottle them together. From the factory docks and without passing through the central warehouse the product will be sent directly to each logistic platform. Key questions are: how much does it cost now, how much will it cost the new system. http: // personales. upv. es/jpgarcia
Karbonicas Ju. Pe n n n Karbonicas Ju. Pe is a company bottling drinks where you work. To simplify we are to consider only one product. Our company has a warehouse where store product just manufactured and from where we serve three logistics platforms that our client holds. The logistics platforms are cross-dock warehouses, where storing products has a high cost, and from where there associated retail stores are served. The lead time at the manufacturing side for Karbonicas Ju. Pe is 7 days (i. e. it takes one week from we have been asked to produce until the product is ready at the warehouse. Each of the logistics platforms faces a demand (measured in pallets) that might be approximated by a normal distribution. (Data can be found at Table I). Each logistic platform knows the demand the stock levels of each associated retail store. It takes two (2) days since the platform asks for products until the product reaches each retail store through the logistic platform. The inventory system is Reorder Point at each echelon. (i. e. the platforms work with ROP logic to the central warehouse of Karbonicas Ju. Pe, and the central warehouse works with ROP to the manufacturing facility). The relation between the logistic platform and the retail stores is not considere in this problem. You are considering the posibility of eliminate the central warehouse echelon. To do that the three logistics platforms should agree a joint review period (considering all the costs) with a power-of-two policy. The factory consolidates the three orders (that have been done simultaneously) and will bottle them together. From the factory docks and without passing through the central warehouse the product will be sent directly to each logistic platform. Key questions are: how much does it cost now, how much will it cost the new system. http: // personales. upv. es/jpgarcia
 Karbonicas Ju. Pe (ctnd ) n Data http: // personales. upv. es/jpgarcia
Karbonicas Ju. Pe (ctnd ) n Data http: // personales. upv. es/jpgarcia


