Инвариантные свойства ортогонального проецирования Свойства геометрических фигур которые

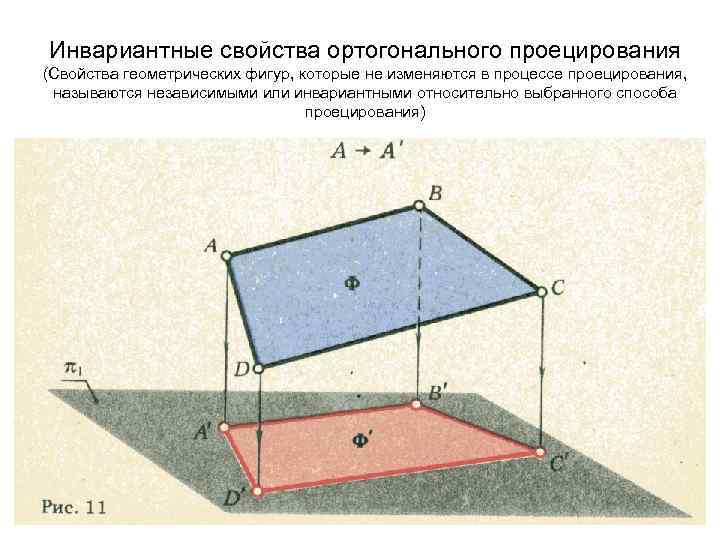Инвариантные свойства ортогонального проецирования (Свойства геометрических фигур, которые не изменяются в процессе проецирования, называются независимыми или инвариантными относительно выбранного способа проецирования)

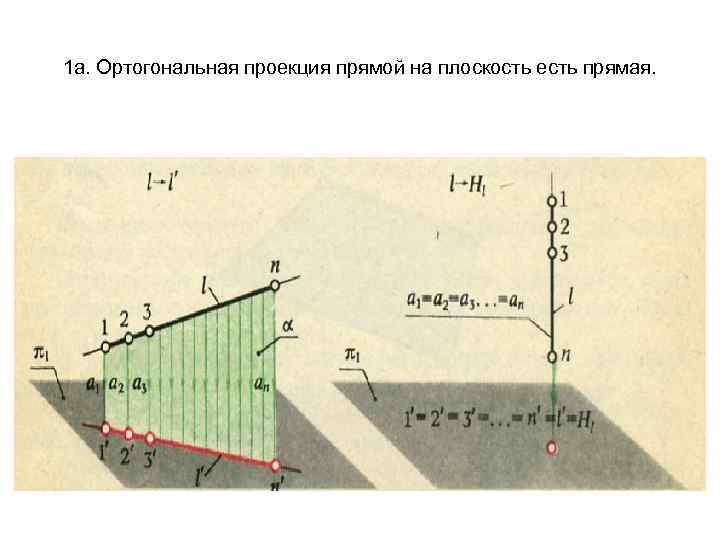1 а. Ортогональная проекция прямой на плоскость есть прямая.

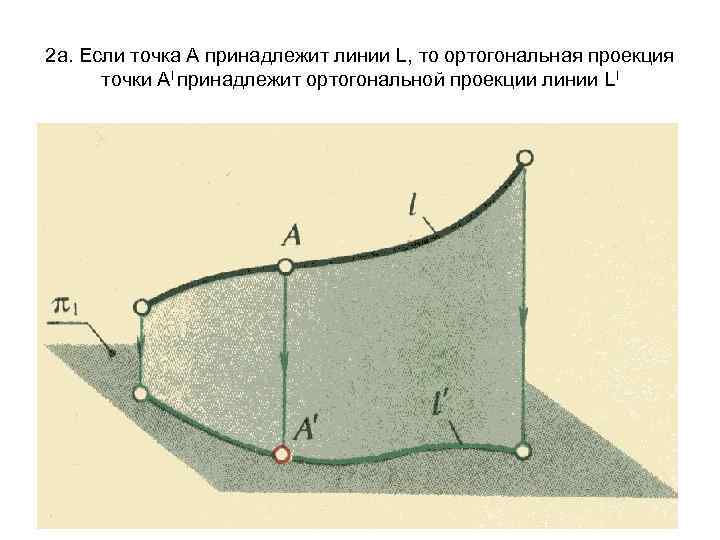2 а. Если точка А принадлежит линии L, то ортогональная проекция точки Аl принадлежит ортогональной проекции линии Ll

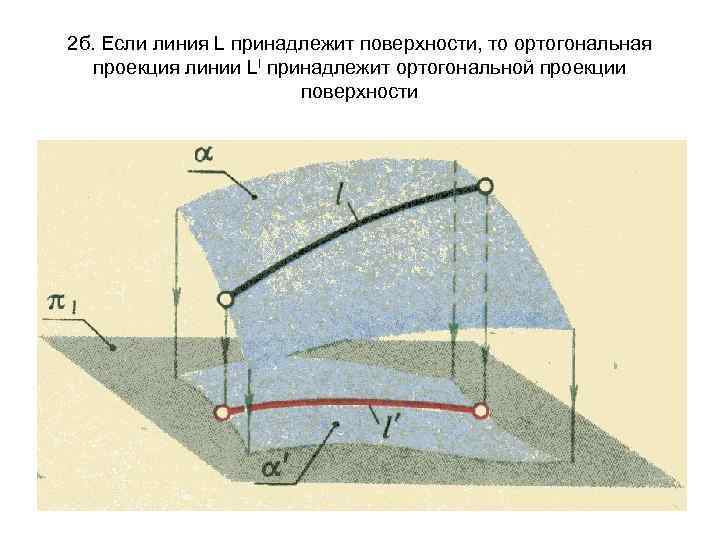2 б. Если линия L принадлежит поверхности, то ортогональная проекция линии Ll принадлежит ортогональной проекции поверхности

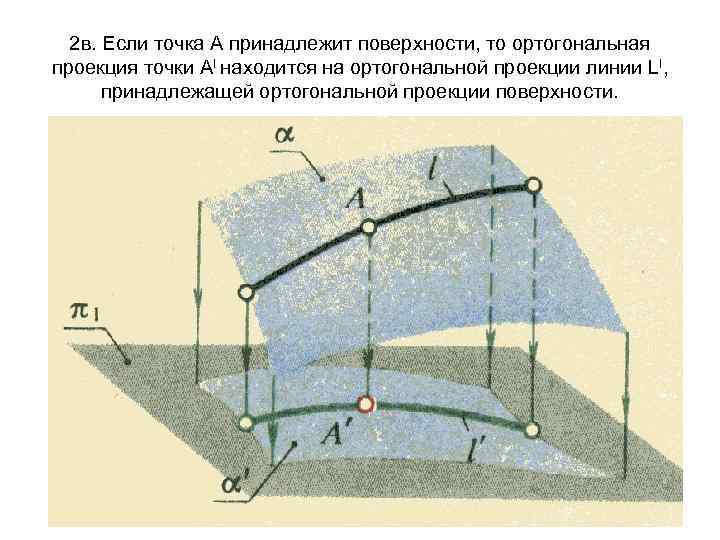2 в. Если точка А принадлежит поверхности, то ортогональная проекция точки АI находится на ортогональной проекции линии LI, принадлежащей ортогональной проекции поверхности.

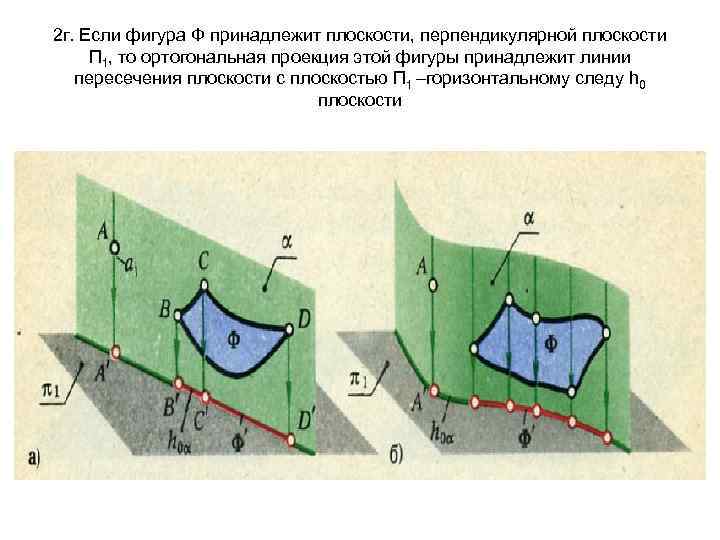2 г. Если фигура Ф принадлежит плоскости, перпендикулярной плоскости П 1, то ортогональная проекция этой фигуры принадлежит линии пересечения плоскости с плоскостью П 1 –горизонтальному следу h 0 плоскости

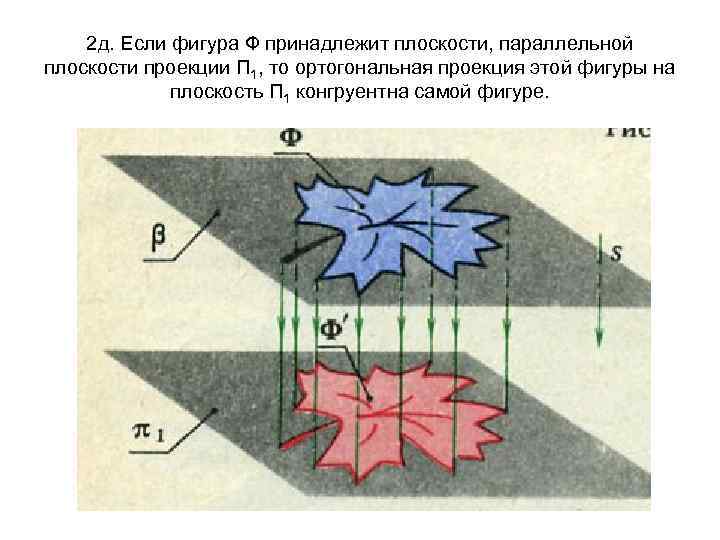2 д. Если фигура Ф принадлежит плоскости, параллельной плоскости проекции П 1, то ортогональная проекция этой фигуры на плоскость П 1 конгруентна самой фигуре.

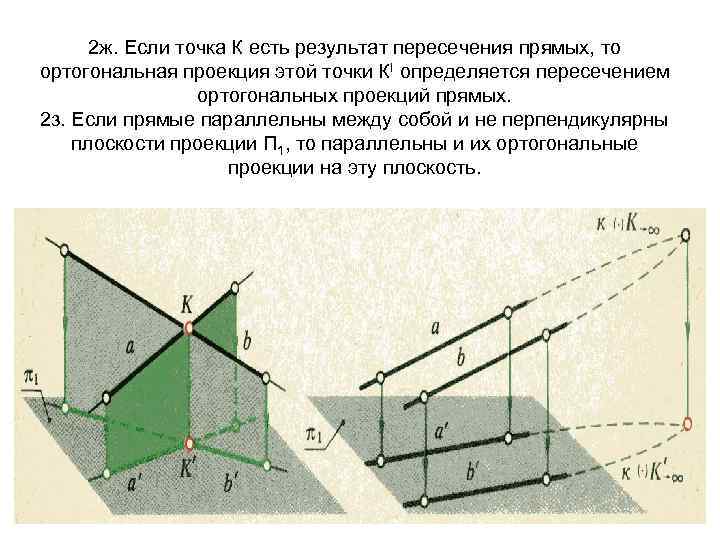2 ж. Если точка К есть результат пересечения прямых, то ортогональная проекция этой точки КI определяется пересечением ортогональных проекций прямых. 2 з. Если прямые параллельны между собой и не перпендикулярны плоскости проекции П 1, то параллельны и их ортогональные проекции на эту плоскость.

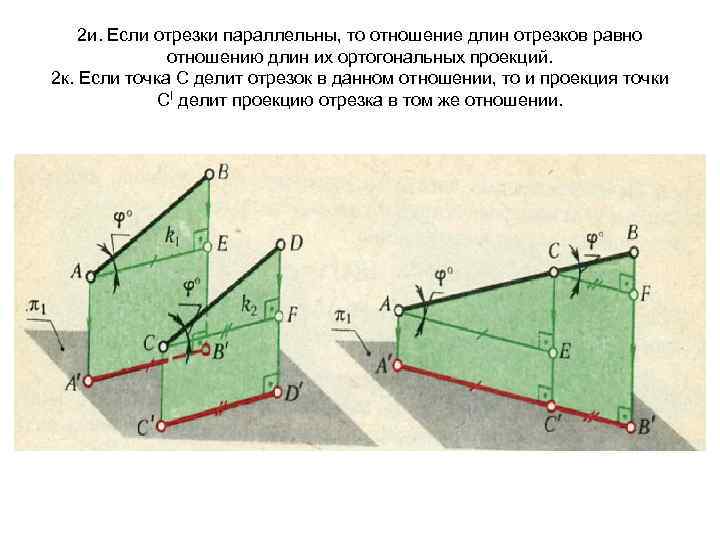2 и. Если отрезки параллельны, то отношение длин отрезков равно отношению длин их ортогональных проекций. 2 к. Если точка С делит отрезок в данном отношении, то и проекция точки СI делит проекцию отрезка в том же отношении.

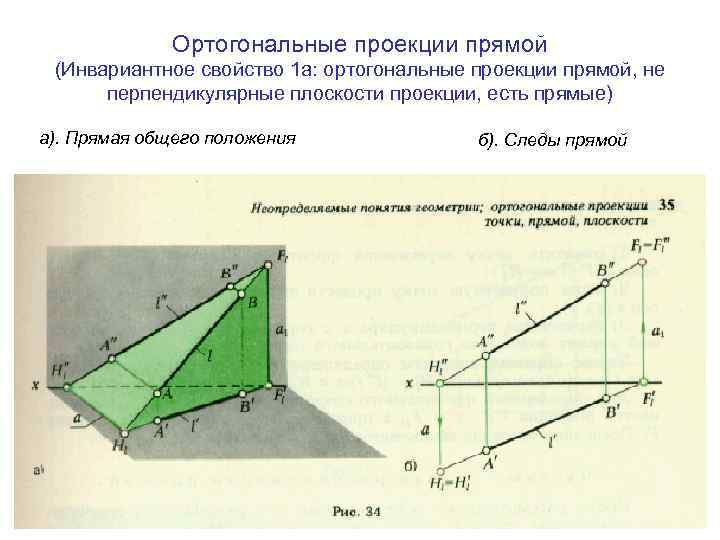Ортогональные проекции прямой (Инвариантное свойство 1 а: ортогональные проекции прямой, не перпендикулярные плоскости проекции, есть прямые) а). Прямая общего положения б). Следы прямой

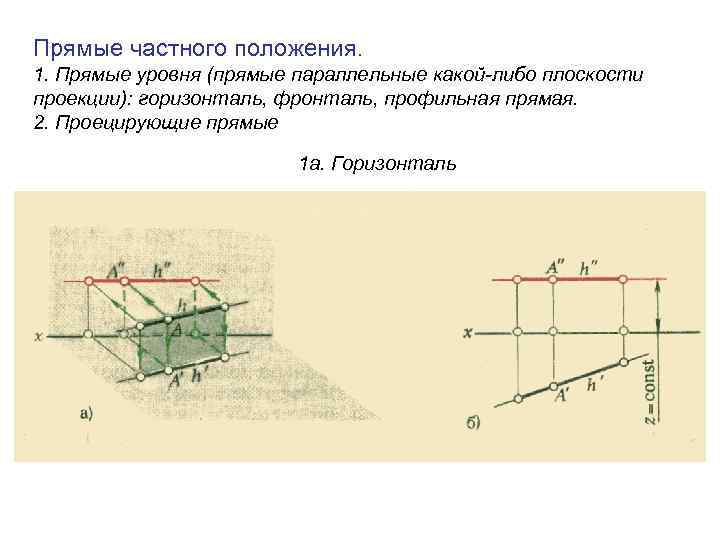Прямые частного положения. 1. Прямые уровня (прямые параллельные какой-либо плоскости проекции): горизонталь, фронталь, профильная прямая. 2. Проецирующие прямые 1 а. Горизонталь

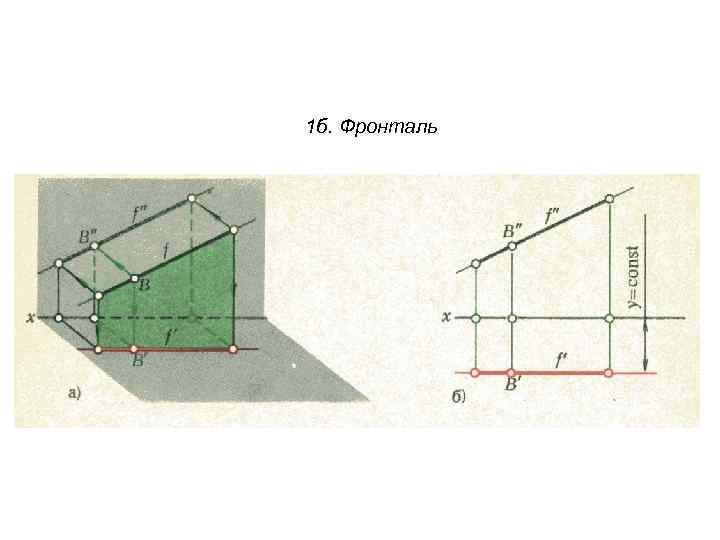1 б. Фронталь

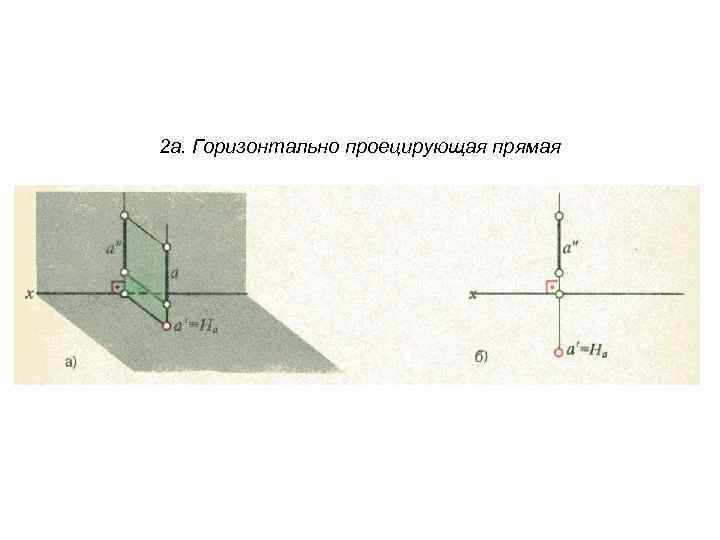2 а. Горизонтально проецирующая прямая

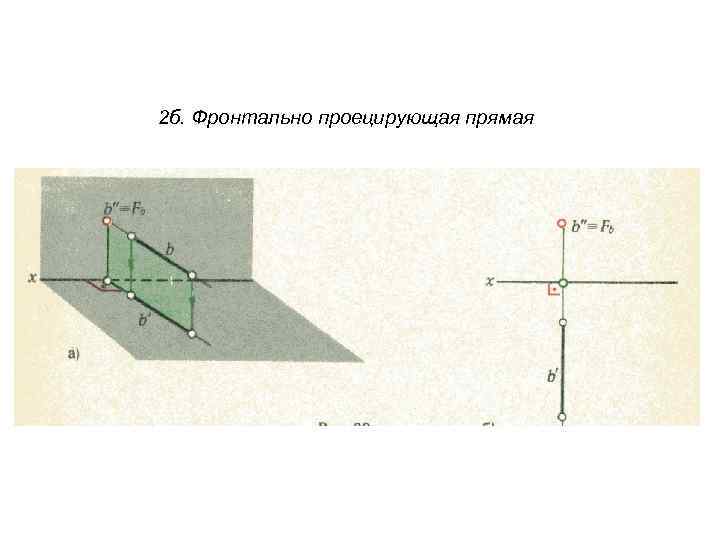2 б. Фронтально проецирующая прямая

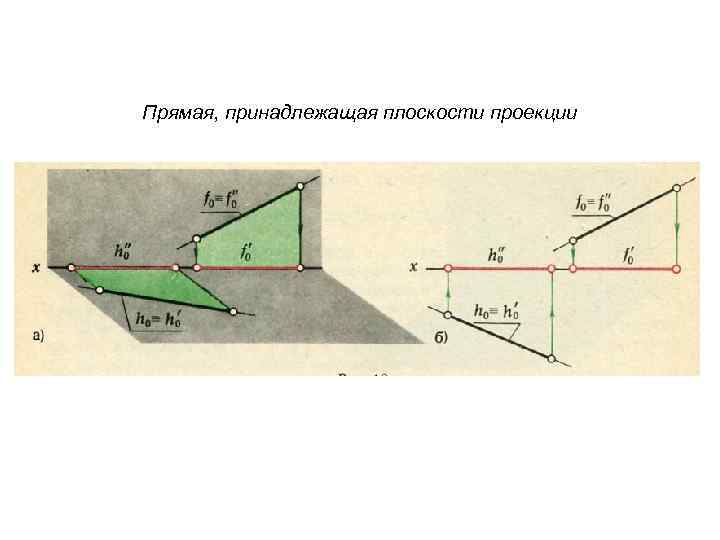Прямая, принадлежащая плоскости проекции

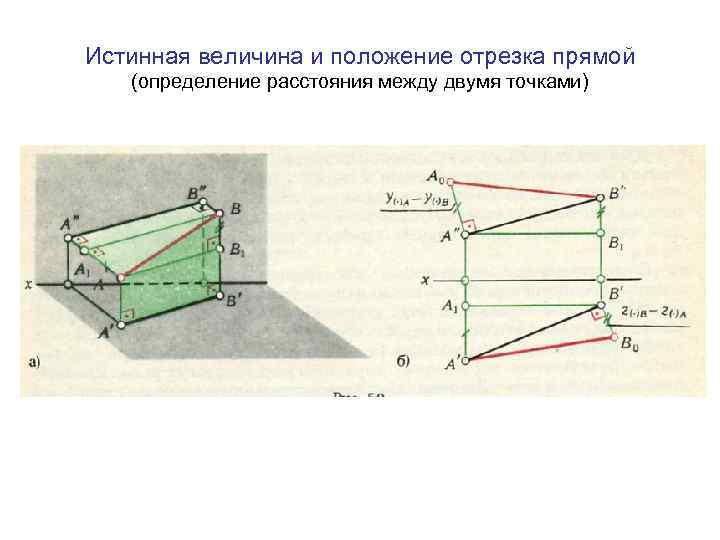Истинная величина и положение отрезка прямой (определение расстояния между двумя точками)

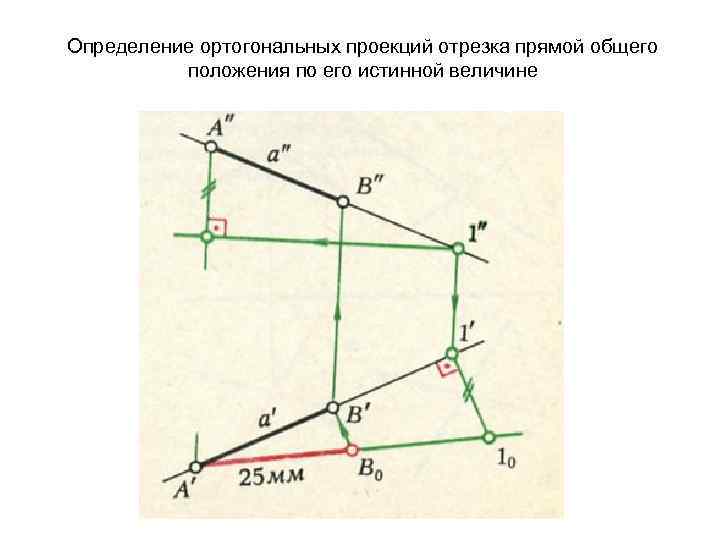Определение ортогональных проекций отрезка прямой общего положения по его истинной величине

Ортогональные проекции плоскости

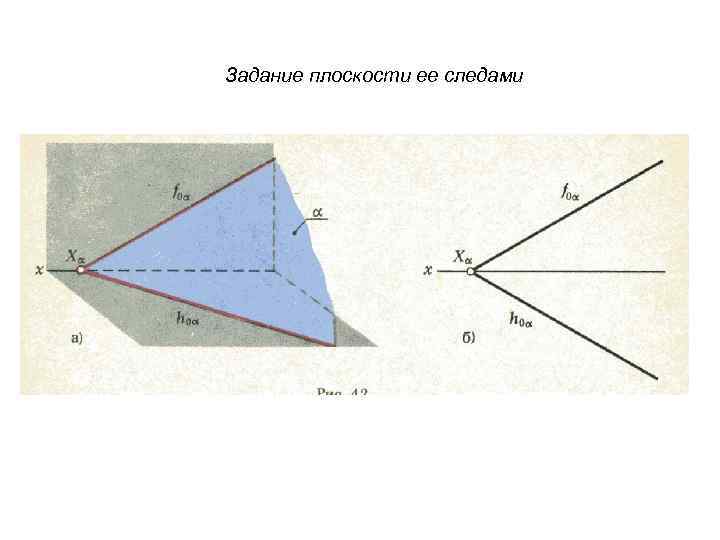Задание плоскости ее следами

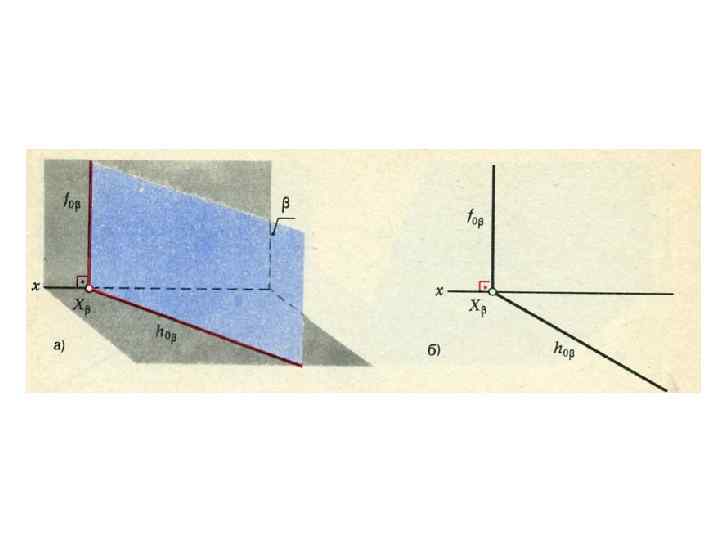
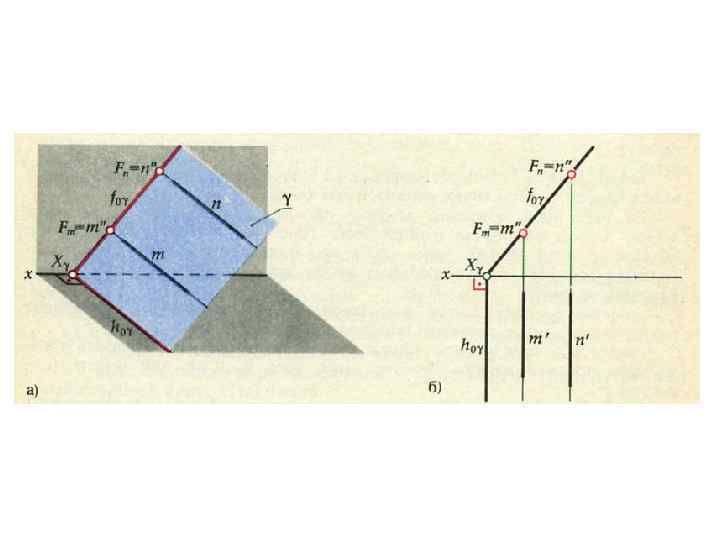
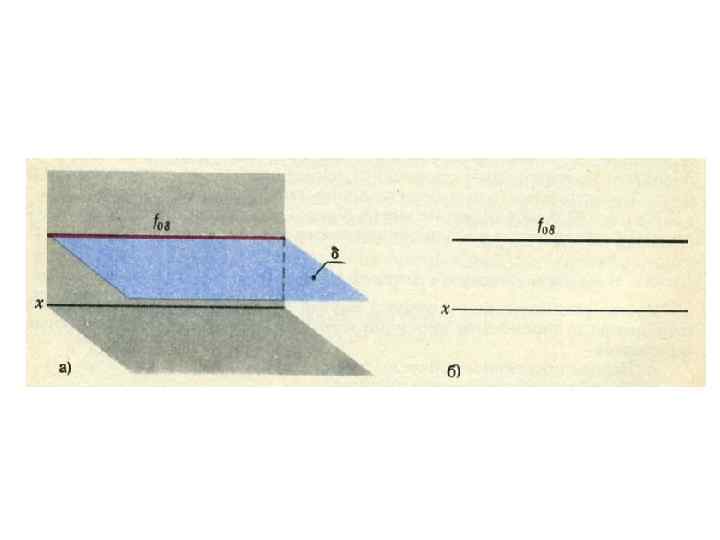
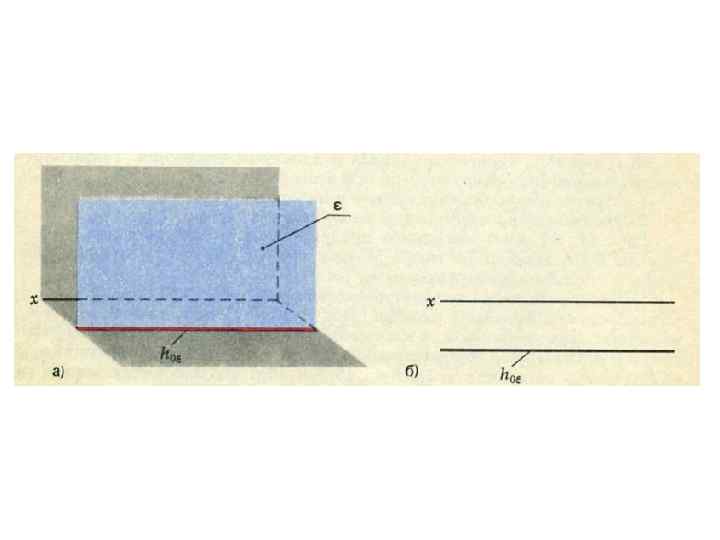
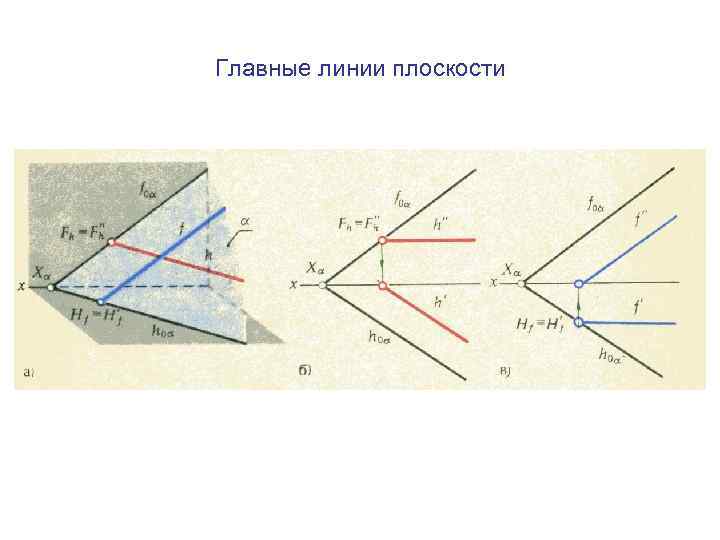Главные линии плоскости

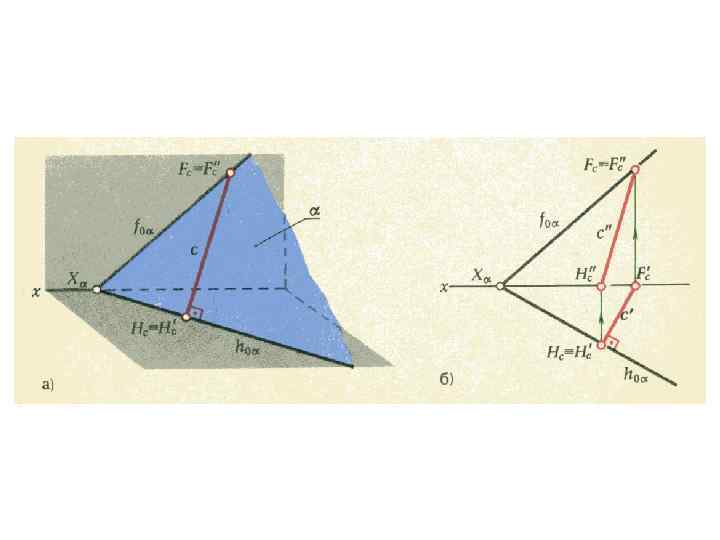
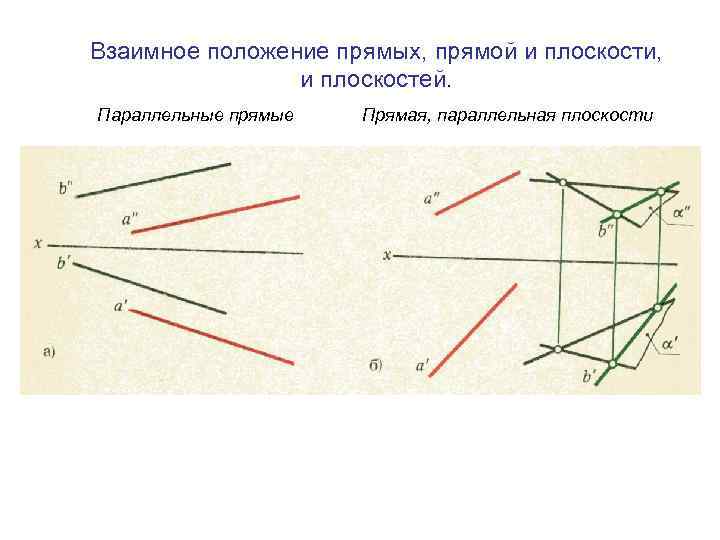Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельные прямые Прямая, параллельная плоскости

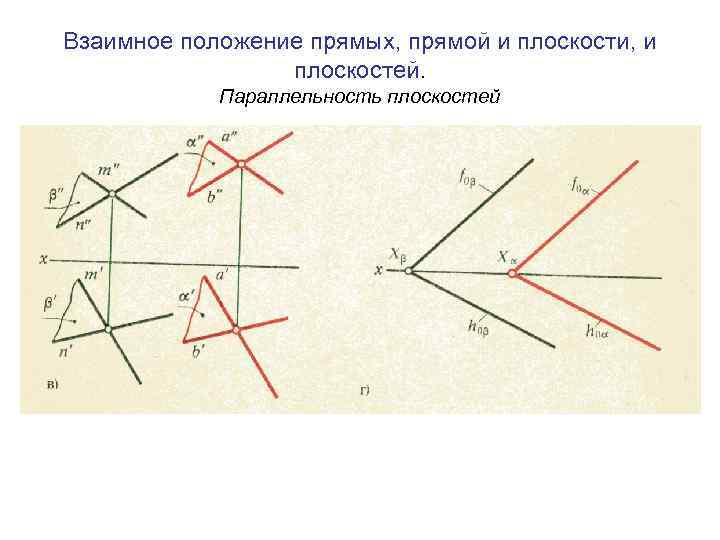Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельность плоскостей

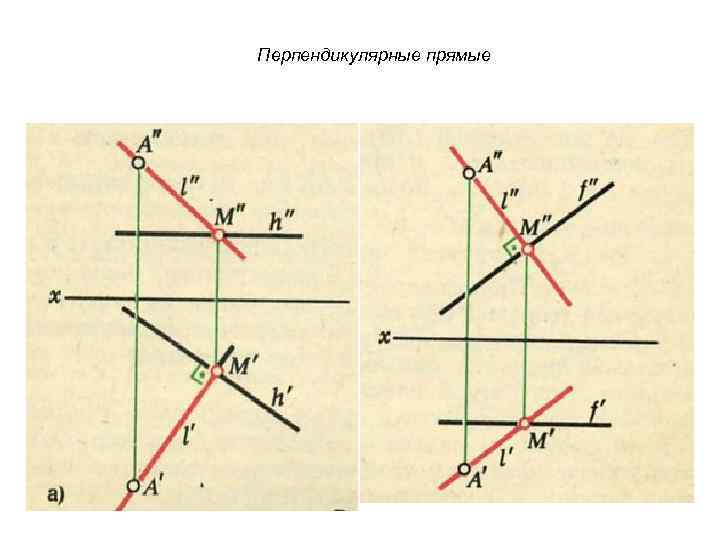Перпендикулярные прямые

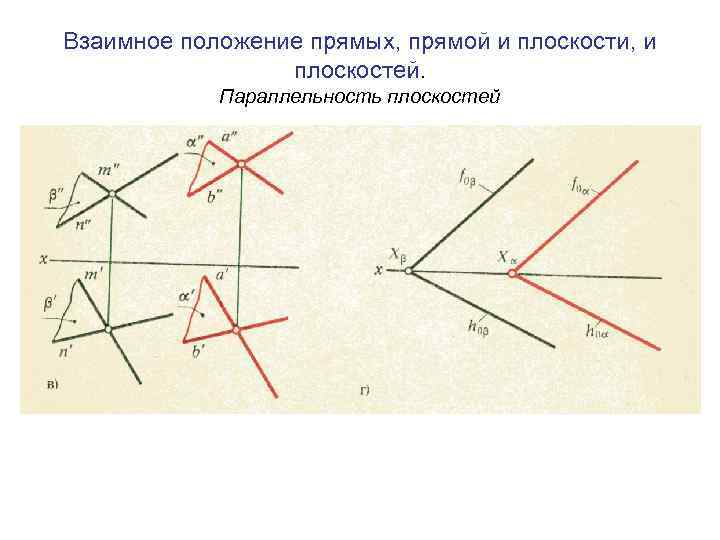Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельность плоскостей

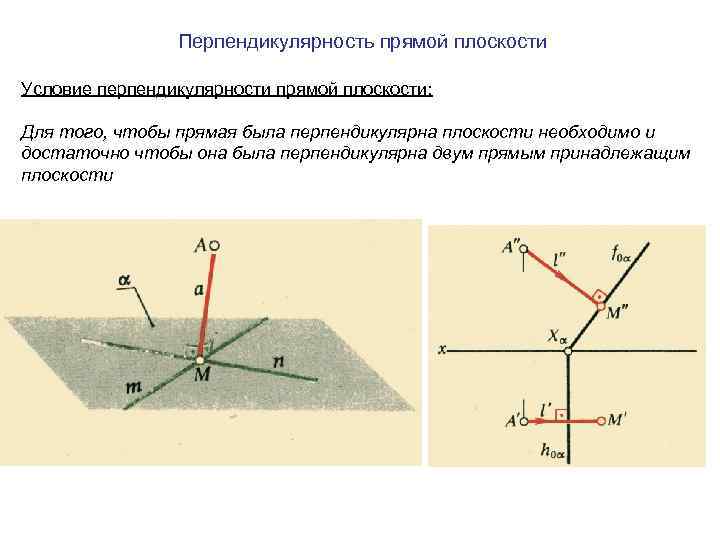Перпендикулярность прямой плоскости Условие перпендикулярности прямой плоскости: Для того, чтобы прямая была перпендикулярна плоскости необходимо и достаточно чтобы она была перпендикулярна двум прямым принадлежащим плоскости

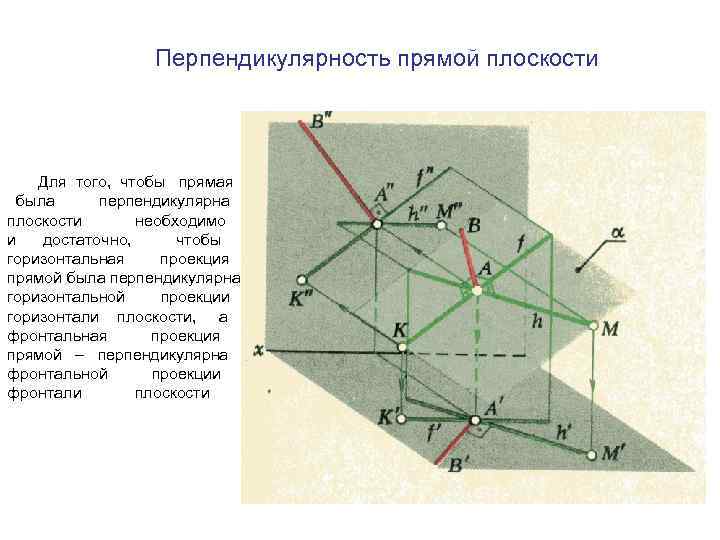Перпендикулярность прямой плоскости Для того, чтобы прямая была перпендикулярна плоскости необходимо и достаточно, чтобы горизонтальная проекция прямой была перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой – перпендикулярна фронтальной проекции фронтали плоскости

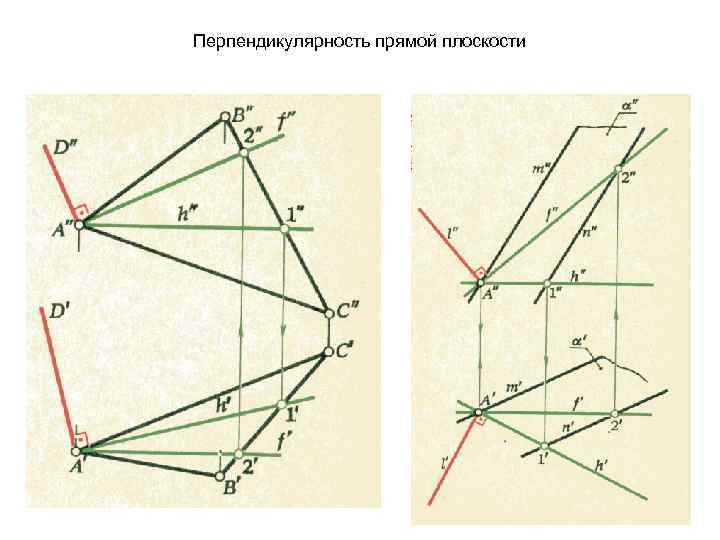Перпендикулярность прямой плоскости

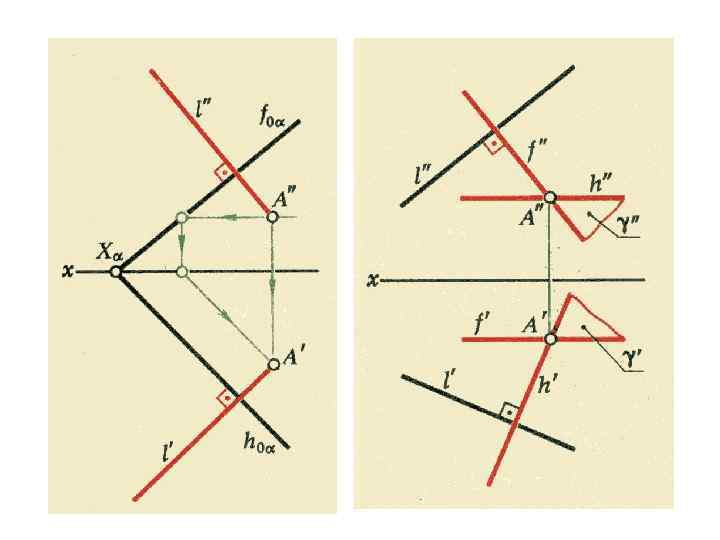
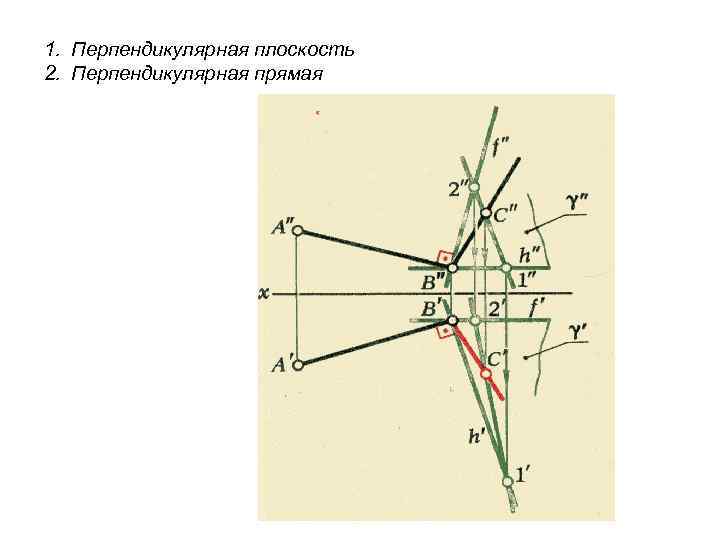1. Перпендикулярная плоскость 2. Перпендикулярная прямая

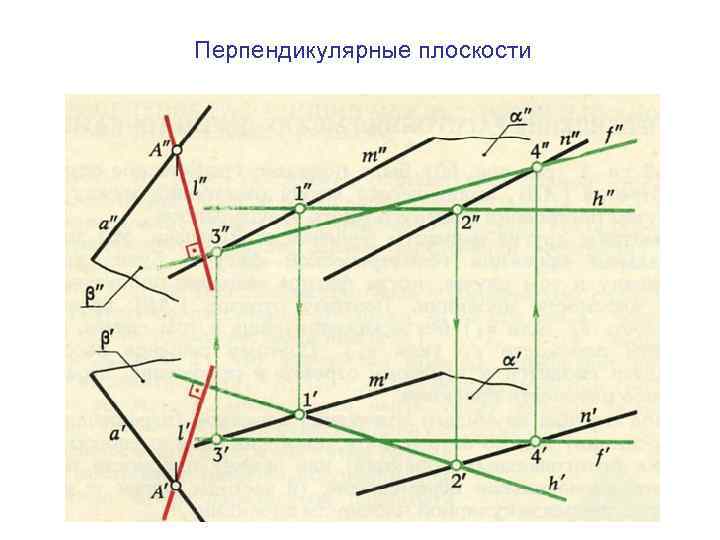Перпендикулярные плоскости

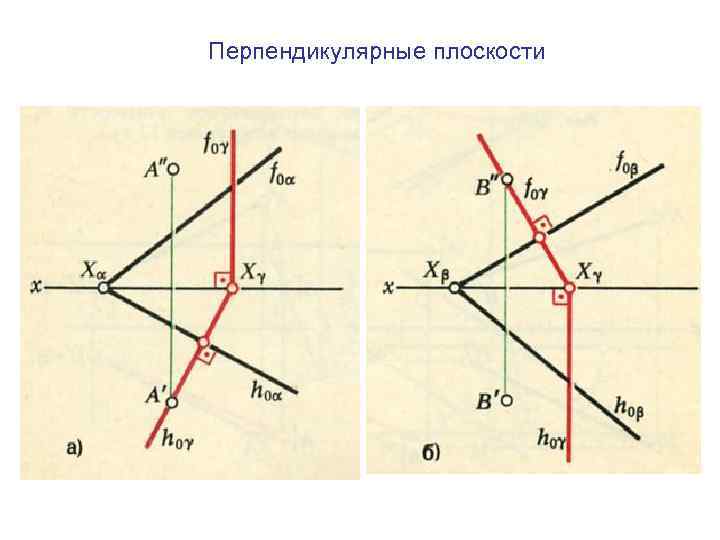Перпендикулярные плоскости