Introductory Microeconomics ES 10001 Topic 2 Consumer Theory

Introductory Microeconomics (ES 10001) Topic 2: Consumer Theory

1. Introduction n We have seen how demand curves may be used to represent consumer behaviour. n But we said very little about the nature of the demand curve; why it slopes down for example. n Now we go ‘behind’ the demand curve n i. e. we investigate how buyers reconcile what they want with what they can get 2

1. Introduction n N. B. We can use this theory in many ways - not simply as household consumer buying goods. n For example: n Modelling decision of worker as regards his supply of labour (i. e. demand for leisure) n Allocation of income across time (saving and investment) 3

2. Theory of Consumer Choice n Four elements: (i) Consumer’s income (ii) Prices of goods (iii) Consumer’s tastes (iv) Rational Maximisation 4

3. The Budget Constraint n The first two elements define the budget constraint n The feasibility of the consumer’s desired consumption bundle depends upon two factors: (i) Income (ii) Prices n Note: We assume, for the time being, that both are exogenous (i. e. beyond consumer's control) 5

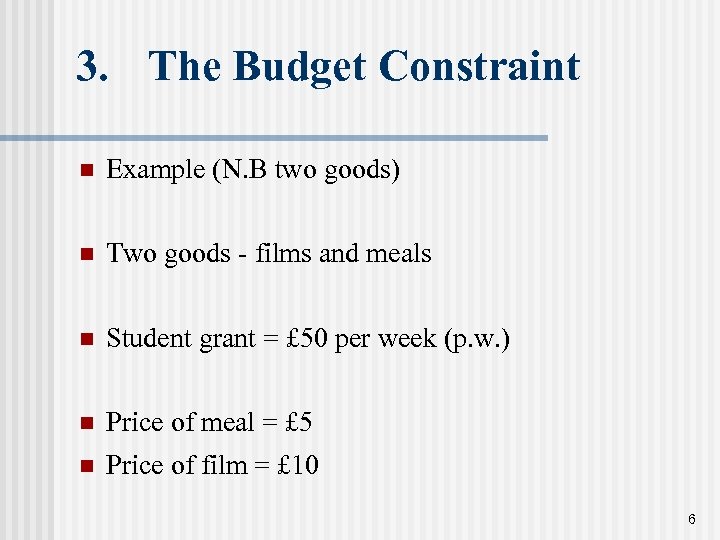3. The Budget Constraint n Example (N. B two goods) n Two goods - films and meals n Student grant = £ 50 per week (p. w. ) n Price of meal = £ 5 n Price of film = £ 10 6

3. The Budget Constraint n Thus student can ‘consume’ maximum p. w. of 10 meals or 5 films by devoting all of his grant to the consumption of only one of these goods. n Alternatively, he can consume some combination of the two goods n For example, giving up one film a week (saving £ 10) enables student to buy two additional meals (costing £ 5 each) . 7

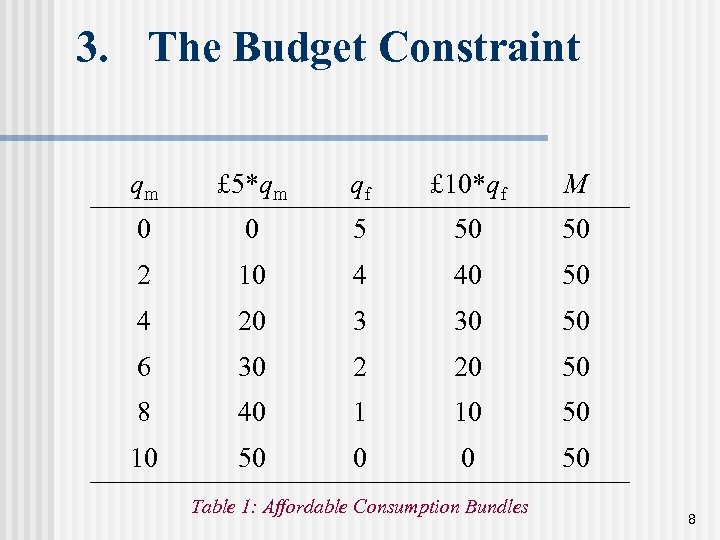3. The Budget Constraint qm £ 5*qm qf £ 10*qf M 0 0 5 50 50 2 10 4 40 50 4 20 3 30 50 6 30 2 20 50 8 40 1 10 50 0 0 50 Table 1: Affordable Consumption Bundles 8

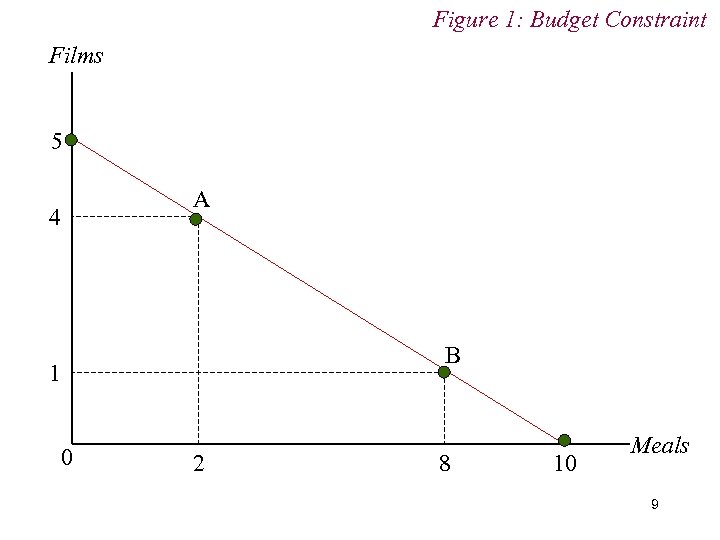Figure 1: Budget Constraint Films 5 4 A B 1 0 2 8 10 Meals 9

3. The Budget Constraint n The budget constraint defines the maximum affordable quantity of one good available to the consumer given the quantity of the other good that is being consumed. n N. B. Trade-off! n Trade-off is represented slope of budget constraint. 10

3. The Budget Constraint n Intercepts Determined by income divided by the appropriate price of the good Define maximum quantity of a particular good available to an individual n Slope Independent of income Determined only by relative prices 11

3. The Budget Constraint n If consumer is devoting all income to films (qf = £ 50/£ 10 = 5), then 1 meal can only be obtained by sacrificing consumption of some films. n How many films must consumer give up? n pm = £ 5; thus to obtain that £ 5, the consumer must give up 1/2 a film 12

3. The Budget Constraint n The slope of the budget constraint in this example is thus: 13

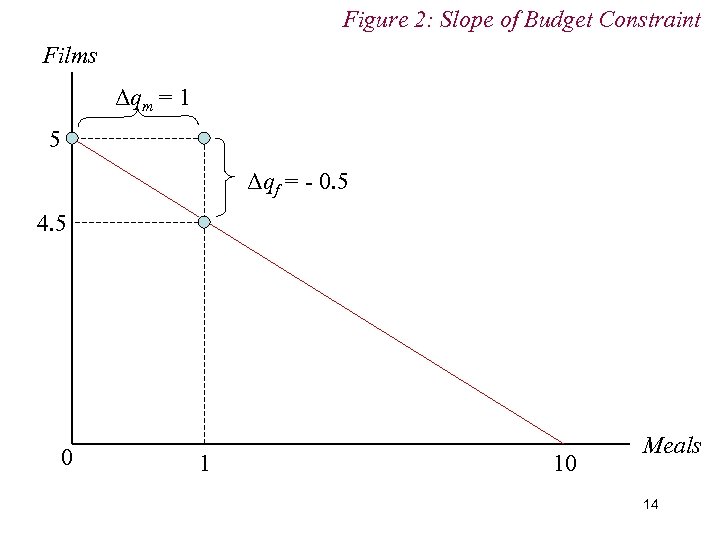Figure 2: Slope of Budget Constraint Films Δqm = 1 5 Δqf = - 0. 5 4. 5 0 1 10 Meals 14

3. The Budget Constraint n More generally: n Two goods (x, y), prices (px, py) and money income (m) n n m = pxx + pyy Slope of budget constraint: - px/py 15

3. The Budget Constraint n Proof: 16

3. The Budget Constraint n Thus: n Such that 17

3. The Budget Constraint n That is: 18

3. The Budget Constraint n Or by calculus: 19

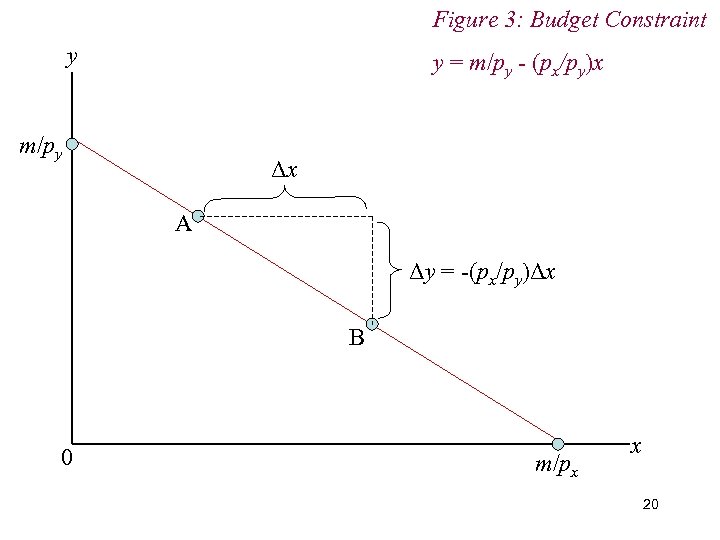Figure 3: Budget Constraint y y = m/py - (px/py)x m/py Δx A Δy = -(px/py)Δx B 0 m/px x 20

3. The Budget Constraint n Intuition: n If additional unit of x costs px n Then its purchase requires a change in consumption of y of –(px/py) (i. e. a sacrifice of y) in order to maintain the budget constraint. 21

3. The Budget Constraint n Economic Rate of Substitution (ERS) Amount of y the consumer is obliged to sacrifice for one extra unit of x n ERS = –(px/py) n Slope of budget line

3. Budget Constraint n Taxes and Subsidies Taxes can be imposed per unit (i. e. p + t) or ad valorem [i. e. p(1+ t)] n Subsidies are ‘negative’ taxes n Rationing causes budget constraint to become vertical or horizontal

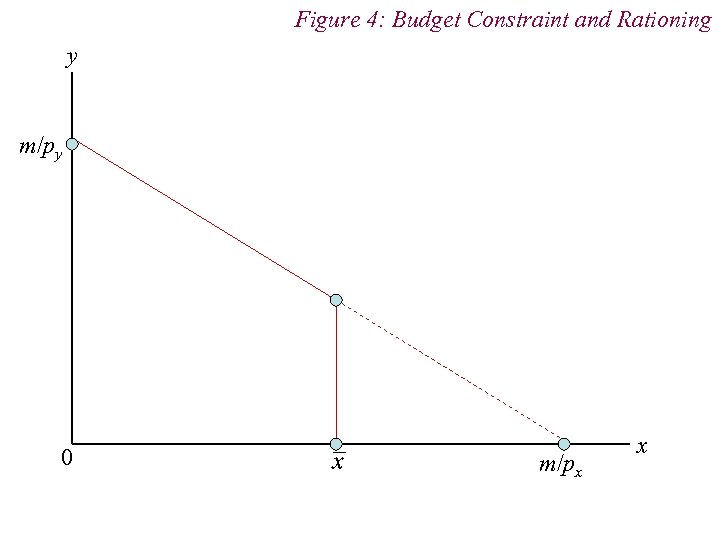Figure 4: Budget Constraint and Rationing y m/py 0 m/px x

Figure 5: Budget Constraint and Taxation y m/py Slope = -(px/py) Slope = -[(px+t)/py] 0 xt m/px x

3. Budget Constraint n Calculating new intercept …

3. Budget Constraint n Calculating new intercept …

3. Budget Constraint n Calculating new intercept …

4. Preferences n Consider now the consumer preferences n Given what consumer can do, what would he like to do? n Four assumptions: (i) Completeness (ii) Consistency (iii) Non-satiation (iv) Diminishing Marginal Rate of Substitution 29

4. Preferences n Completeness Consumers can rank alternative bundles according to the satisfaction or utility they provide Thus given two bundles a and b, then or , Preferences assumed only to be ordinal, not cardinal; i. e. consumer simply has to be able to say he prefers a to b, not to say by how much. 30

IV. Preferences n Consistency Preferences are also assumed to be consistent Thus if and , then we would infer that We assume consumer is logically consistent 31

4. Preferences n Non-satiation Consumers assumed to always prefer more ‘goods’ to less. We can accommodate economics ‘bads’ (e. g. pollution) in this assumption by interpreting then as ‘negative’ goods n We can illustrate the first three assumptions graphically as follows 32

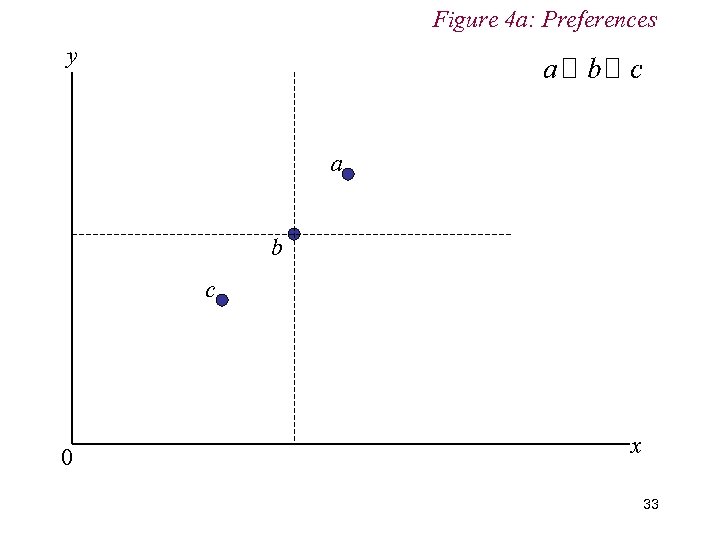Figure 4 a: Preferences y a b c 0 x 33

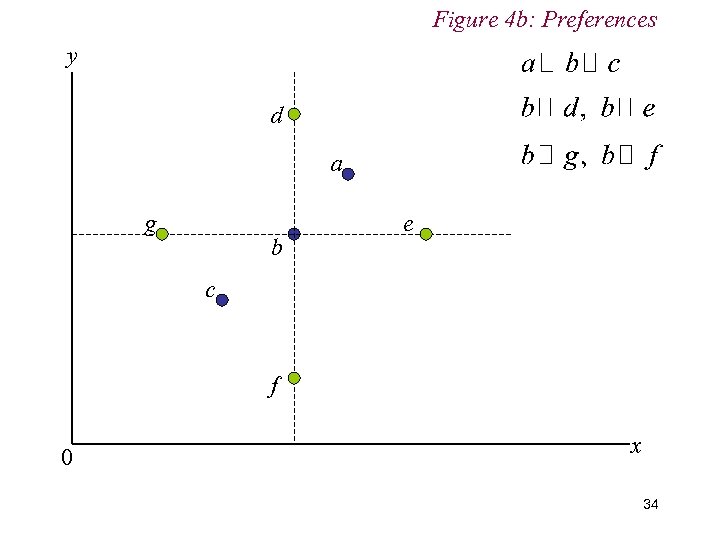Figure 4 b: Preferences y d a g b e c f 0 x 34

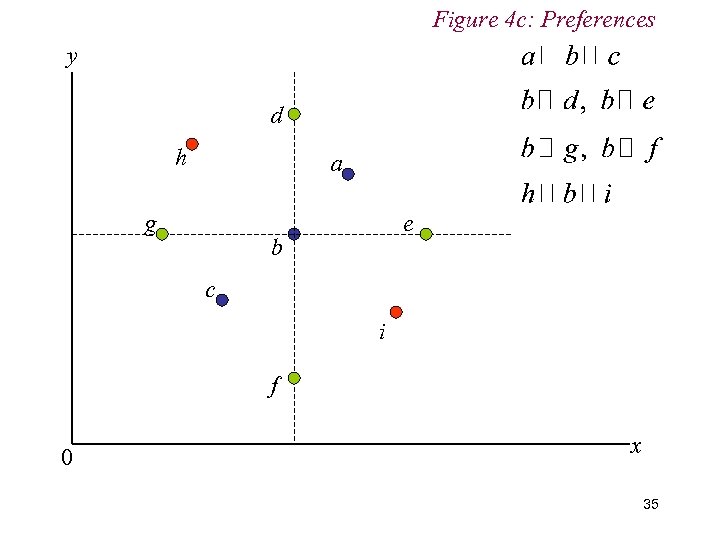Figure 4 c: Preferences y d h a g e b c i f 0 x 35

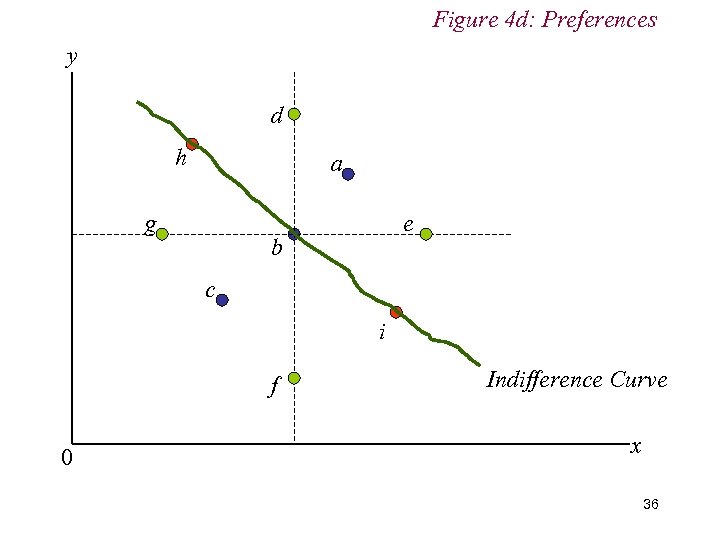Figure 4 d: Preferences y d h a g e b c i f 0 Indifference Curve x 36

4. Preferences n Marginal Rate of Substitution (MRS) The quantity of y (i. e. the ‘vertical’ good) the consumer must sacrifice to increase the quantity of x (i. e. ‘the horizontal’ good) by one unit without changing total utility. n We generally assume (smooth) diminishing MRS n To hold utility constant, diminishing quantities of one good must be sacrificed to obtain successive equal increases in the quantity of the other good. 37

4. Preferences n Diminishing MRS derives from underlying assumption of diminishing marginal utility n Marginal utility of a good is defined as the change in a consumer’s total utility from consuming the good divided by the change in his consumption of the good n Diminishing MRS assumes that the increase in utility from consuming additional units of a good 38 is declining

4. Preferences n Non-satiation implies downward sloping indifference curves; increases in one good require sacrifices in the other good to hold total utility constant. n However, we can go further; diminishing MRS implies that indifference curves are convex to origin, becoming flatter as we move to the right. n Indeed, the MRS of x for y is simply the slope of 39 the indifference curve

Figure 5: Indifference Curves y I 0 0 40 x

Figure 5: Indifference Curves y A B 0 I 0 41 x

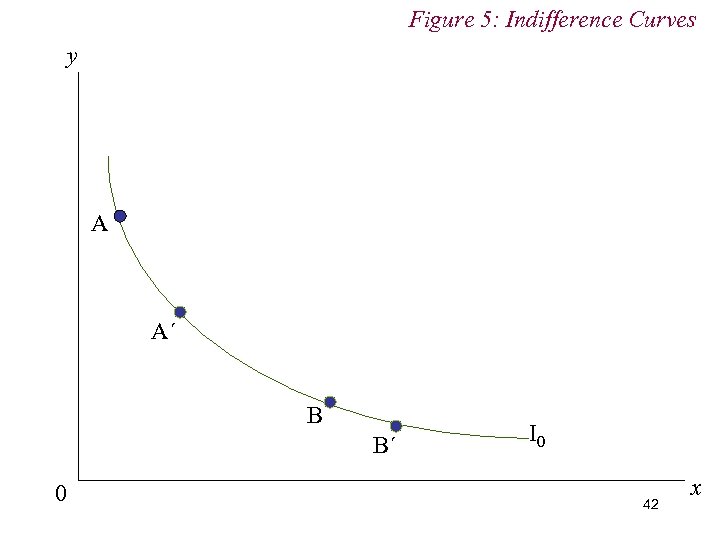Figure 5: Indifference Curves y A A´ B B´ 0 I 0 42 x

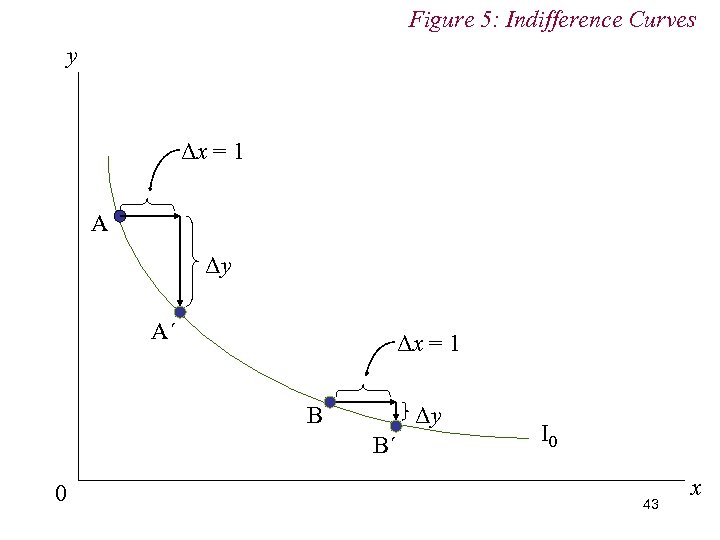Figure 5: Indifference Curves y Δx = 1 A Δy A´ Δx = 1 B Δy B´ 0 I 0 43 x

4. Preferences n Diminishing MRS implies consumers prefer consumption bundles containing mixtures of goods rather than extremes n i. e. Bundle C = (5, 5) preferred to both Bundle A = (2, 8) and Bundle B = (8, 2) n Diminishing MRS (i. e. diminishing marginal utility) 44

Figure 6: Indifference Curves y A B 0 I 0 45 x

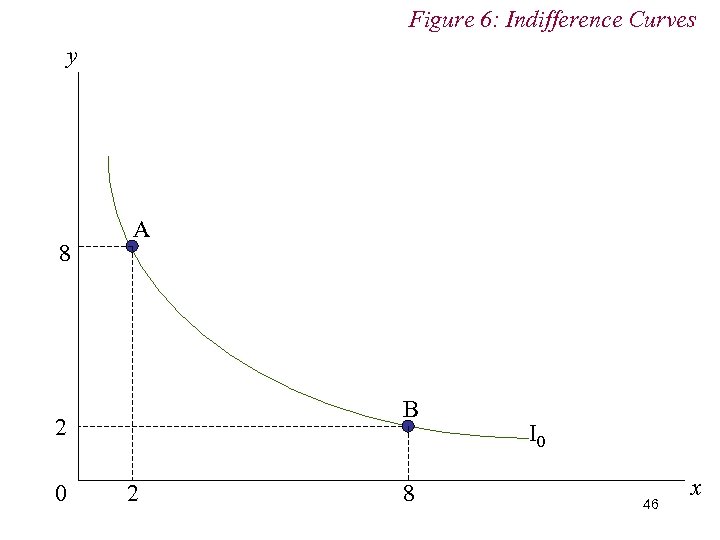Figure 6: Indifference Curves y 8 A B 2 0 2 8 I 0 46 x

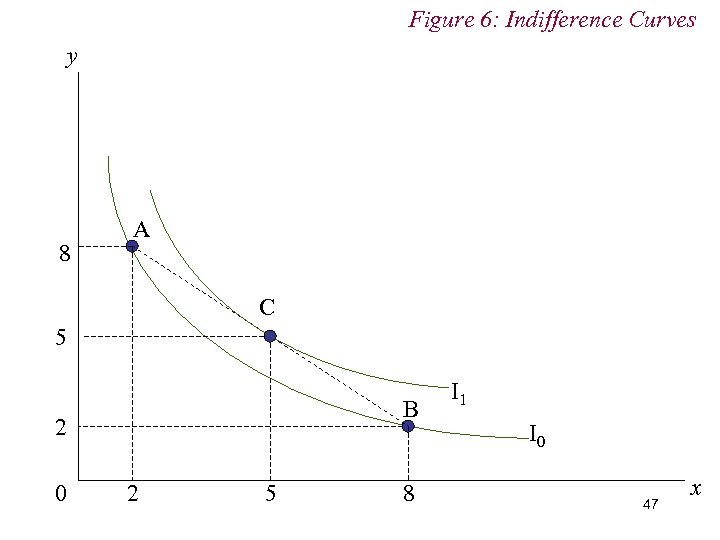Figure 6: Indifference Curves y 8 A C 5 B 2 0 2 5 8 I 1 I 0 47 x

4. Preferences n Note: (i) Any point on the indifference map must lay on an indifference curve. (ii) indifference curves cannot cross n Thus every point on the indifference map must lay on one and only one indifference curve. 48

Figure 7: Indifference Curves y I 2 I 1 I 0 0 49 x

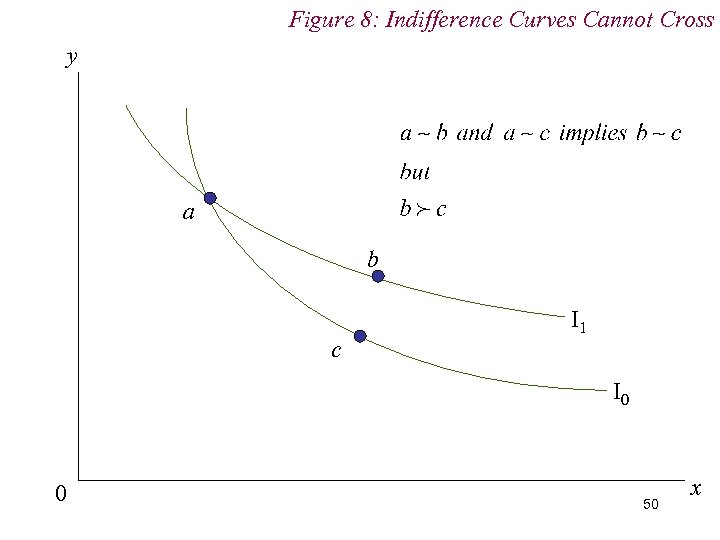Figure 8: Indifference Curves Cannot Cross y a b c I 1 I 0 0 50 x

4. Preferences n Comparing preferences n Slope of indifference curve (MRS) measures relative intensity of consumer’s demand n Steeper (flatter) indifference curves implies relatively higher (lower) demand for horizontal good (x)

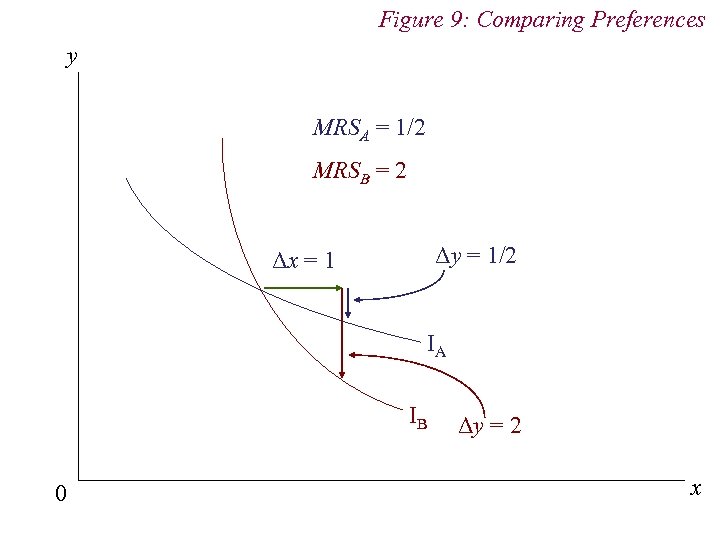Figure 9: Comparing Preferences y MRSA = 1/2 MRSB = 2 Δy = 1/2 Δx = 1 IA IB 0 Δy = 2 x

4. Preferences n Non-Standard Preferences n Perfect Substitutes n Perfect Complements n Neutral Goods n Satiation and Bliss Points

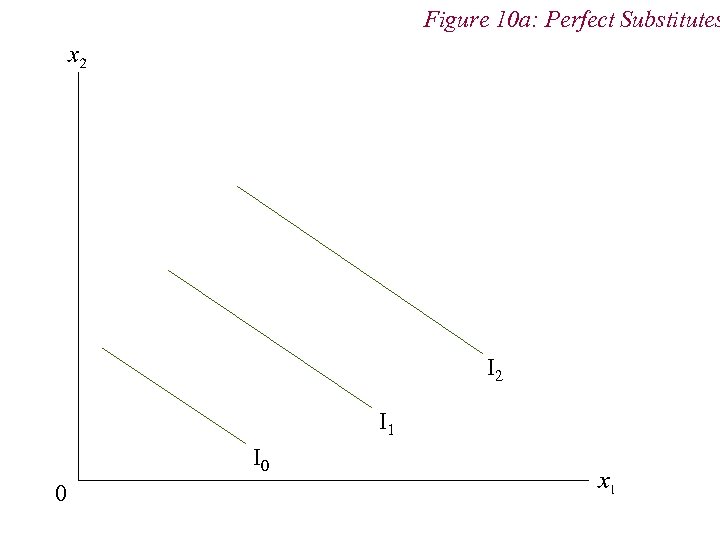Figure 10 a: Perfect Substitutes I 2 I 1 I 0 0

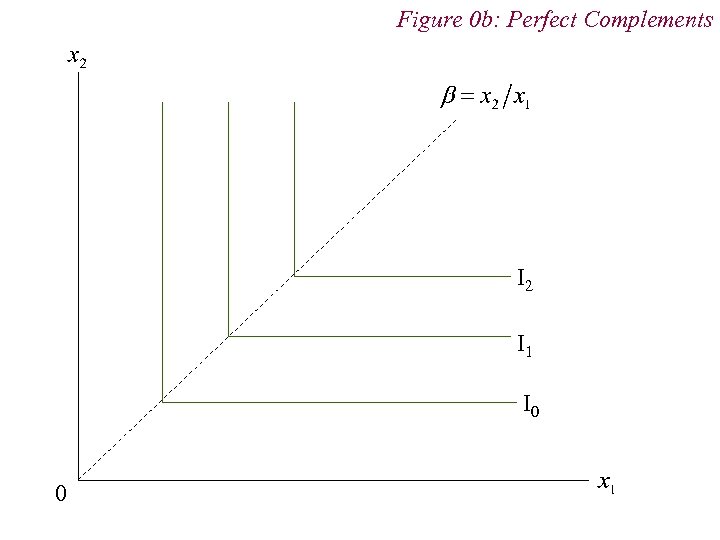Figure 0 b: Perfect Complements I 2 I 1 I 0 0

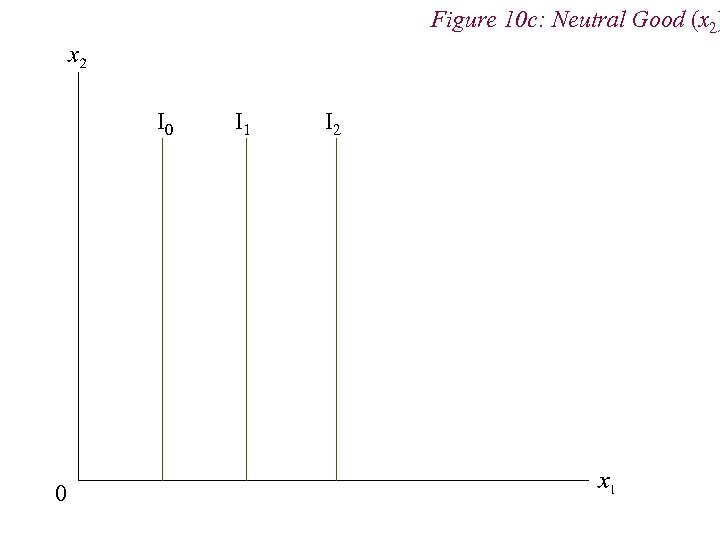Figure 10 c: Neutral Good (x 2) I 0 0 I 1 I 2

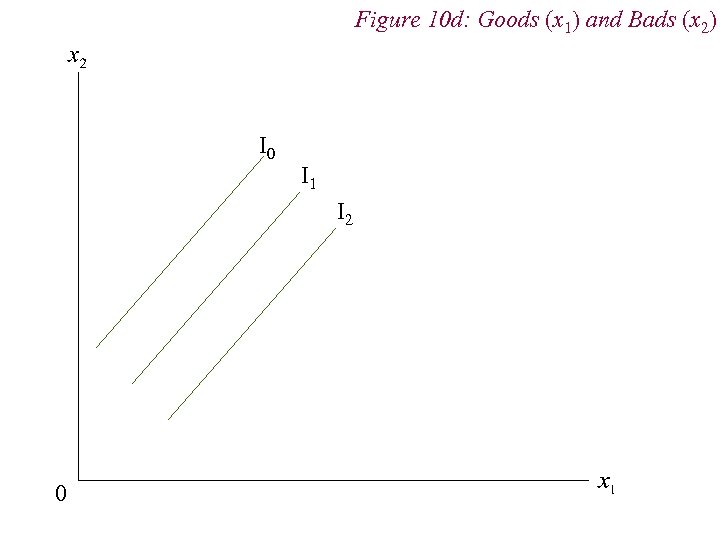Figure 10 d: Goods (x 1) and Bads (x 2) I 0 I 1 I 2 0

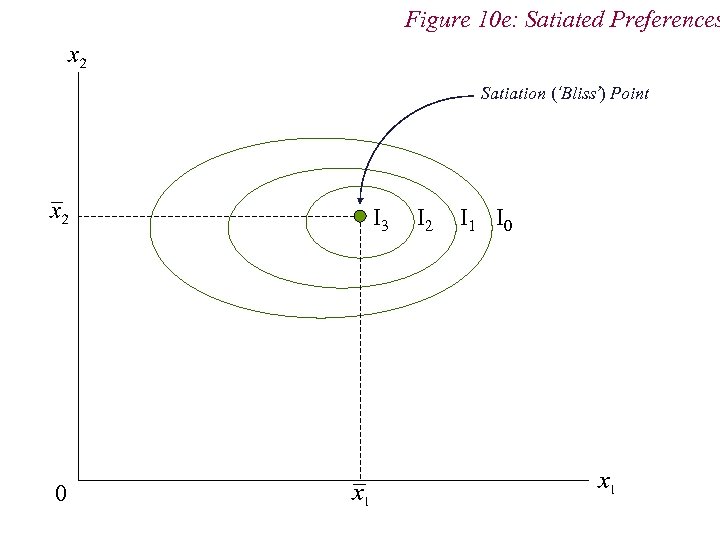Figure 10 e: Satiated Preferences Satiation (‘Bliss’) Point I 3 0 I 2 I 1 I 0

5. Utility Maximisation n Budget line shows the consumer’s affordable bundles given the market environment. n The indifference map shows the consumer’s desired bundles n To complete the model we assume rational maximisation - i. e. the consumer chooses the affordable bundle that maximises his utility. 59

5. Utility Maximisation n This is a non-trivial point. We are implicitly assuming that the consumer only derives utility from the consumption of x and y. n Moreover, rational maximisation implies consumer processes huge amount of information before choosing his most preferred bundle n In reality, perhaps we ‘satisfice’ 60

5. Utility Maximisation n The optimal choice bundle will be that point at which an indifference curve just touches the budget line n That is, where an indifference curve is tangent to the budget line n In words, where the consumer’s marginal rate of substitution (MRS) and economic rate of substitution (ERS) are in accord 61

5. Utility Maximisation n Marginal Rate of Substitution (MRS) Amount of y consumer willing to sacrifice for one extra unit of x Slope of indifference curve n Economic Rate of Substitution (ERS) Amount of y the consumer is obliged to sacrifice for one extra unit of x Slope of budget line 62

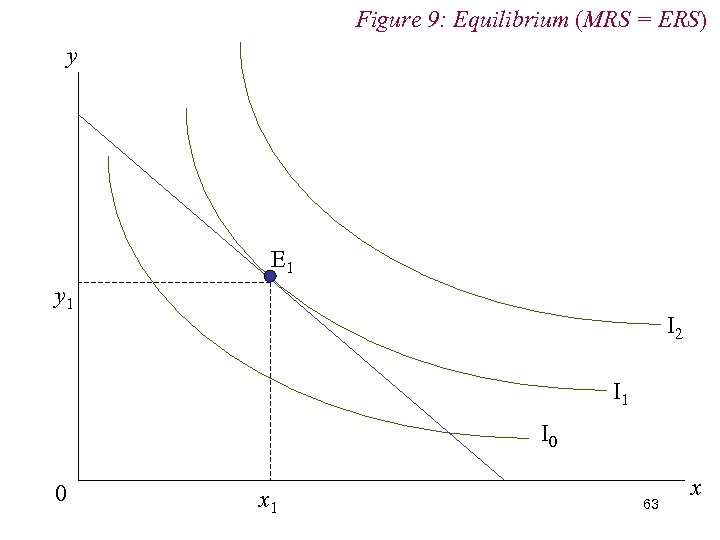Figure 9: Equilibrium (MRS = ERS) y E 1 y 1 I 2 I 1 I 0 0 x 1 63 x

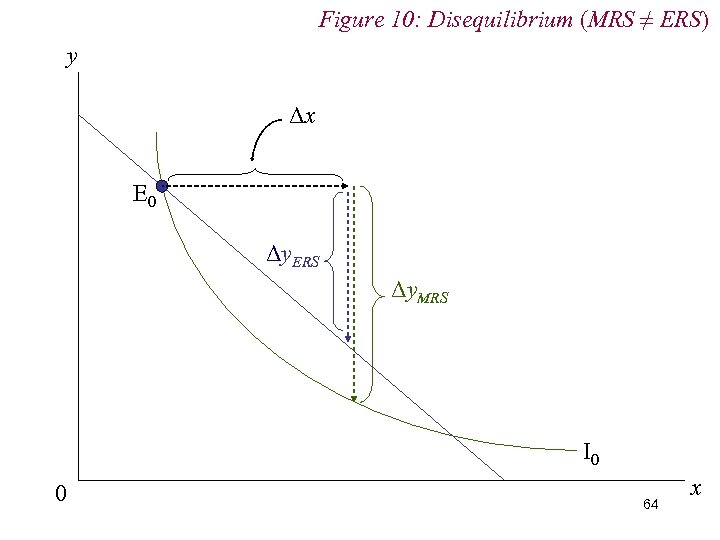Figure 10: Disequilibrium (MRS ≠ ERS) y Δx E 0 Δy. ERS Δy. MRS I 0 0 64 x

5. Utility Maximisation n Since preferences are unique, individuals will not choose identical bundles, even when confronted by same market environment n But they will all move to point where MRS = ERS n Even with different preferences, since ERS is the same for everyone (i. e. we all face same relative prices), it must be the case that in equilibrium: n MRS 1 = ERS = MRS 2 65

6. Comparative Statics n We now consider how the consumer responds to changes in his market environment n That is, to changes in: (i) Endowment income; (ii) Prices. n N. B, Comparative Statics / Dynamics 66

6. Comparative Statics n Changes in Income n An increase in endowment income causes a parallel shift out of the budget constraint n A decrease in endowment income causes a parallel shift in of the budget constraint 67

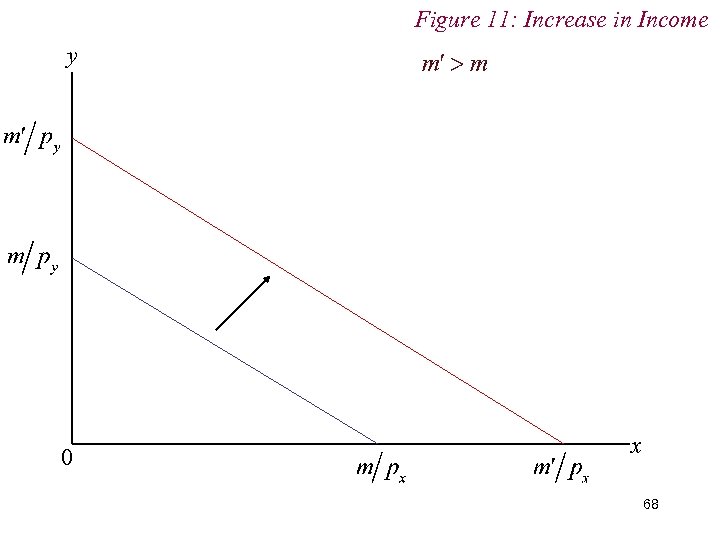Figure 11: Increase in Income y 0 x 68

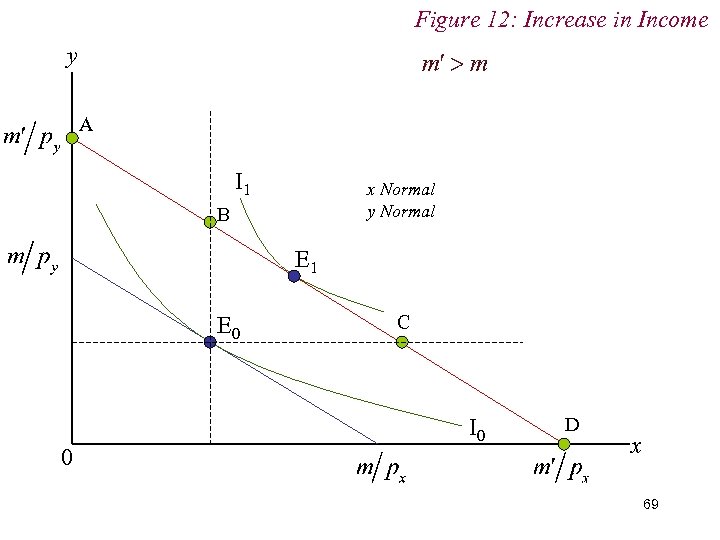Figure 12: Increase in Income y A I 1 x Normal y Normal B E 1 E 0 0 C I 0 D x 69

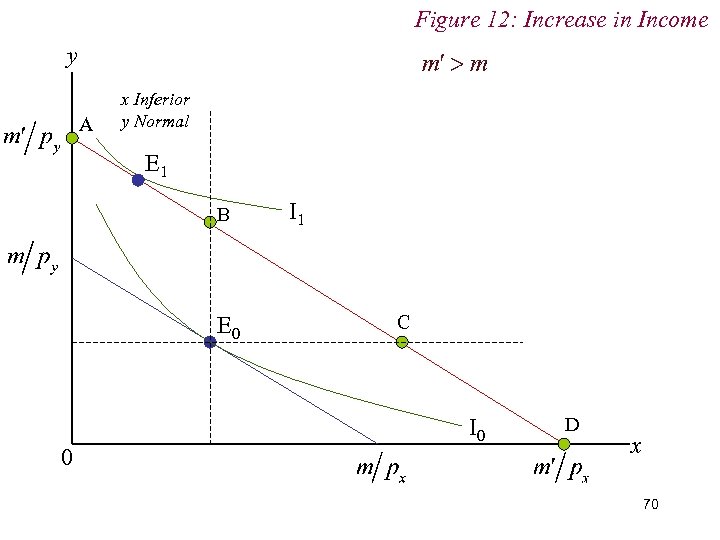Figure 12: Increase in Income y A x Inferior y Normal E 1 B E 0 0 I 1 C I 0 D x 70

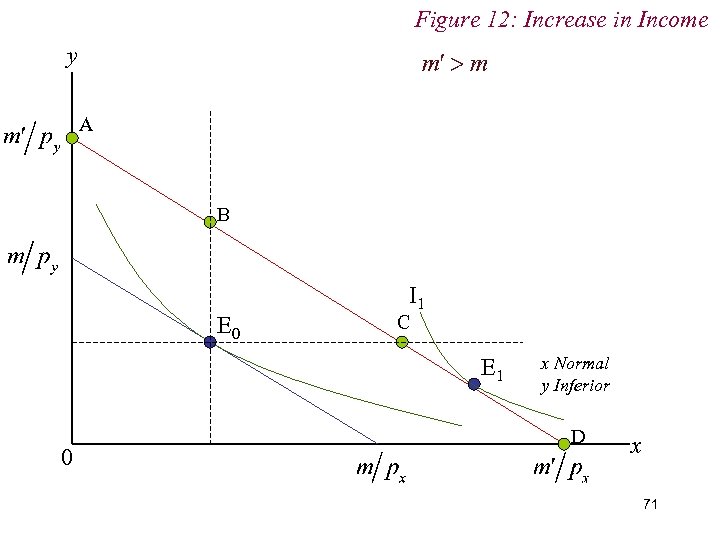Figure 12: Increase in Income y A B E 0 I 1 C E 1 0 x Normal y Inferior D x 71

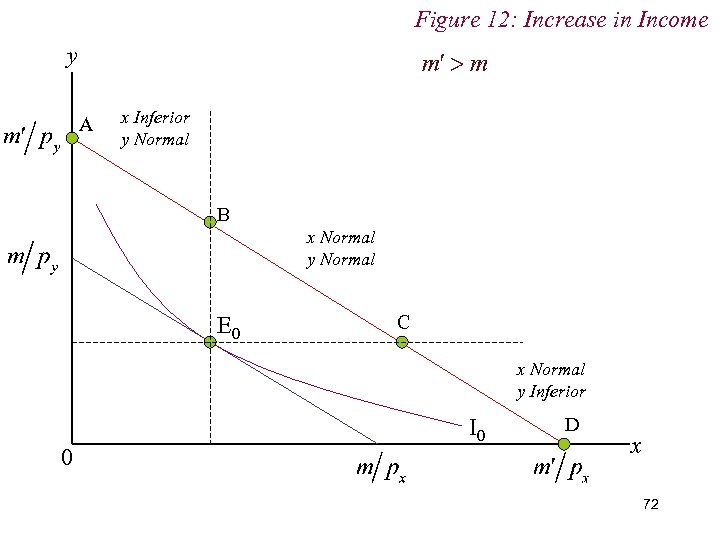Figure 12: Increase in Income y A x Inferior y Normal B x Normal y Normal E 0 C x Normal y Inferior 0 I 0 D x 72

6. Comparative Statics n Changes in Prices n An increase in price causes a pivot inwards of the budget constraint n An decrease price causes a pivot outwards of the budget constraint. 73

Figure 13: Fall in Price y 0 x 74

7. Income & Substitution Effects n Price changes affects the optimal choice bundle in two distinct ways: n First, there is a change in relative prices as represented by a change in the slope of the budget constraint. n Second, there is a change in purchasing power (i. e. real income). The same level of money income is now worth more to the consumer in terms of its 75 ability to purchase both goods.

Figure 13: Fall in Price y 0 x 76

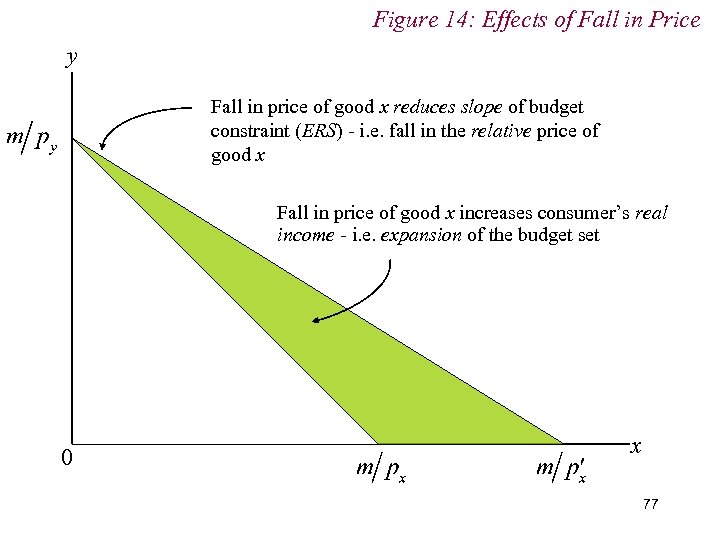Figure 14: Effects of Fall in Price y Fall in price of good x reduces slope of budget constraint (ERS) - i. e. fall in the relative price of good x Fall in price of good x increases consumer’s real income - i. e. expansion of the budget set 0 x 77

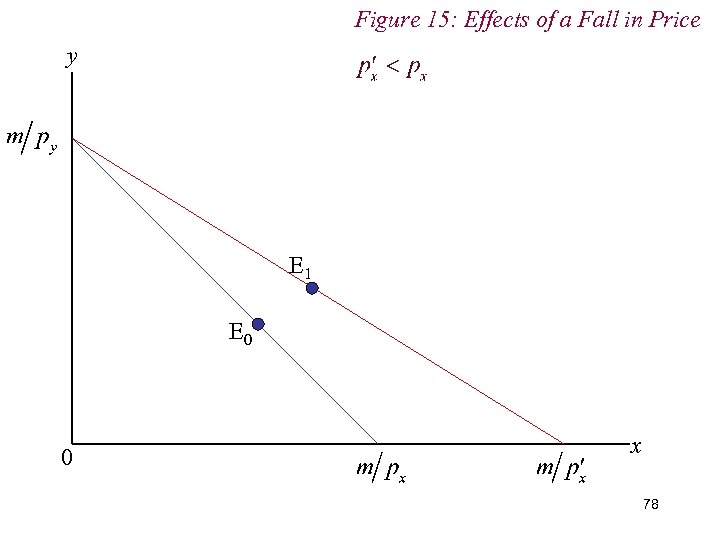Figure 15: Effects of a Fall in Price y E 1 E 0 0 x 78

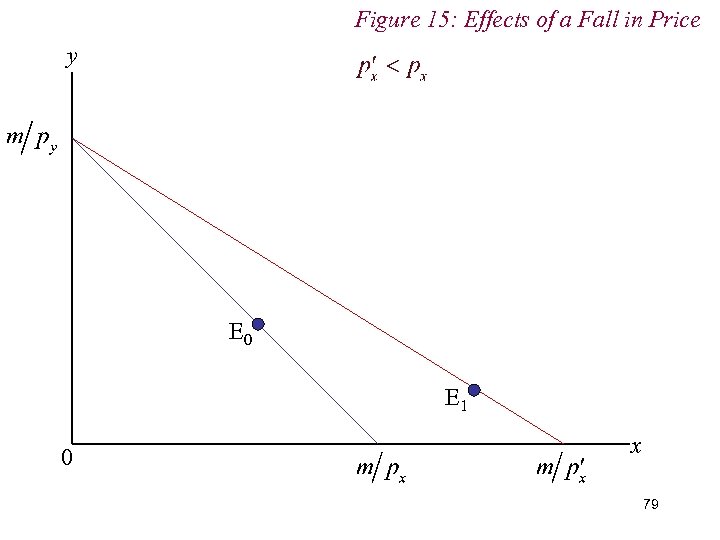Figure 15: Effects of a Fall in Price y E 0 E 1 0 x 79

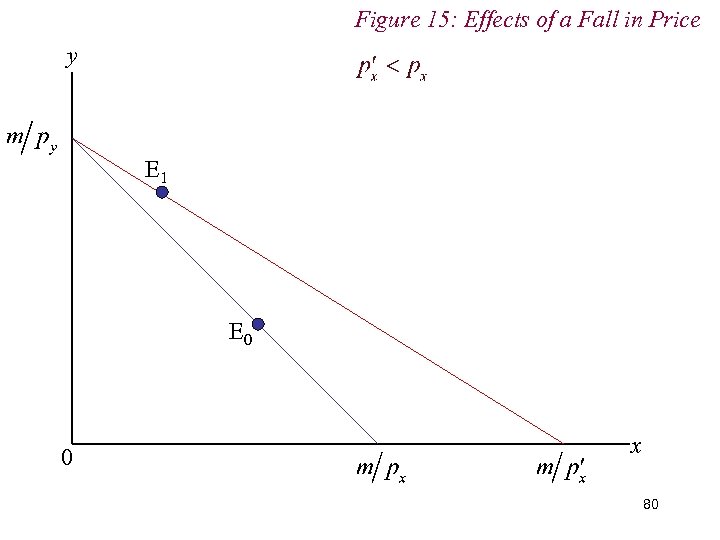Figure 15: Effects of a Fall in Price y E 1 E 0 0 x 80

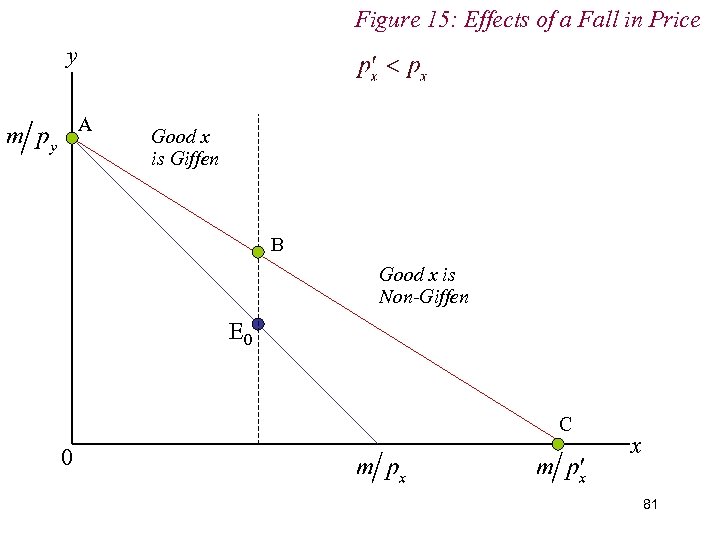Figure 15: Effects of a Fall in Price y A Good x is Giffen B Good x is Non-Giffen E 0 C 0 x 81

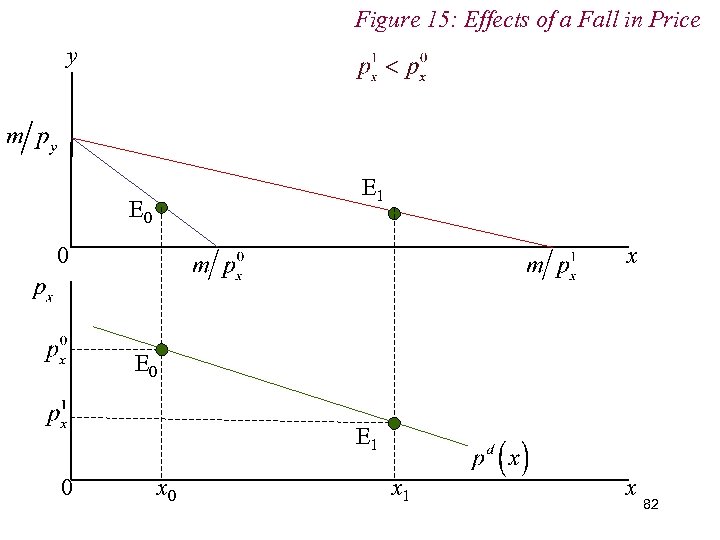Figure 15: Effects of a Fall in Price y E 1 E 0 0 x E 0 E 1 0 x 1 x 82

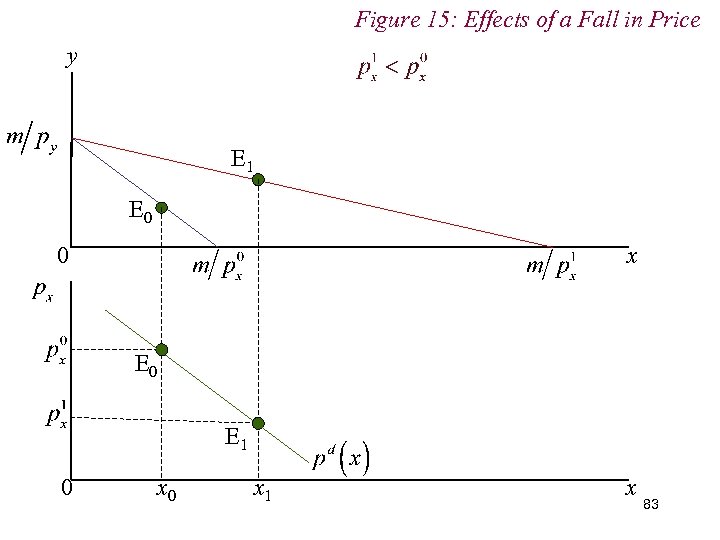Figure 15: Effects of a Fall in Price y E 1 E 0 0 x E 0 E 1 0 x 1 x 83

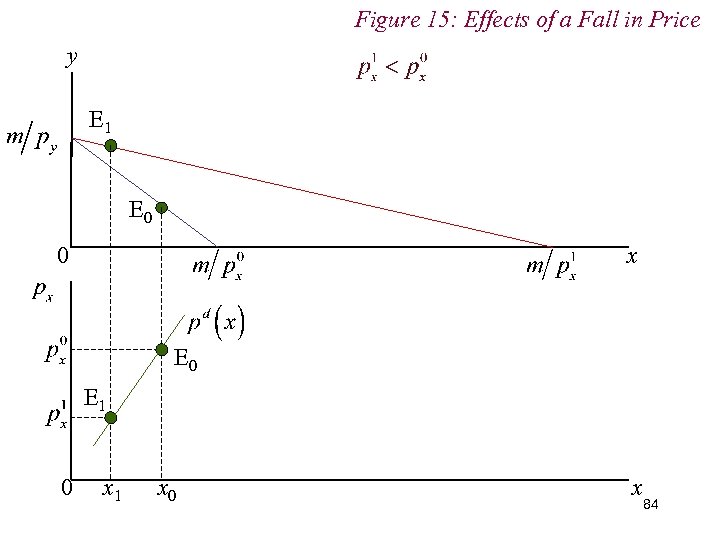Figure 15: Effects of a Fall in Price y E 1 E 0 0 x E 0 E 1 0 x 1 x 0 x 84

7. Income & Substitution Effects n We decompose total effect of price change into: (i) Income Effect (ii) Substitution Effect n The income effect is the adjustment of demand to the change in real income. n The substitution effect is the adjustment of demand 85 to the change in relative prices.

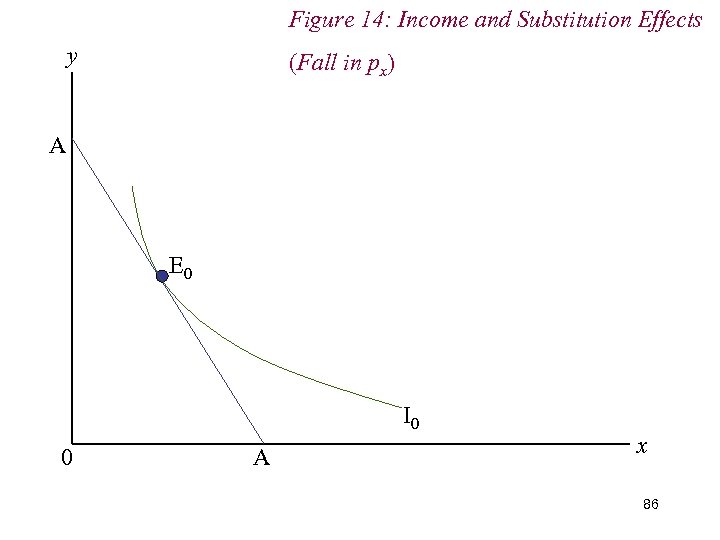Figure 14: Income and Substitution Effects y (Fall in px) A E 0 I 0 0 A x 86

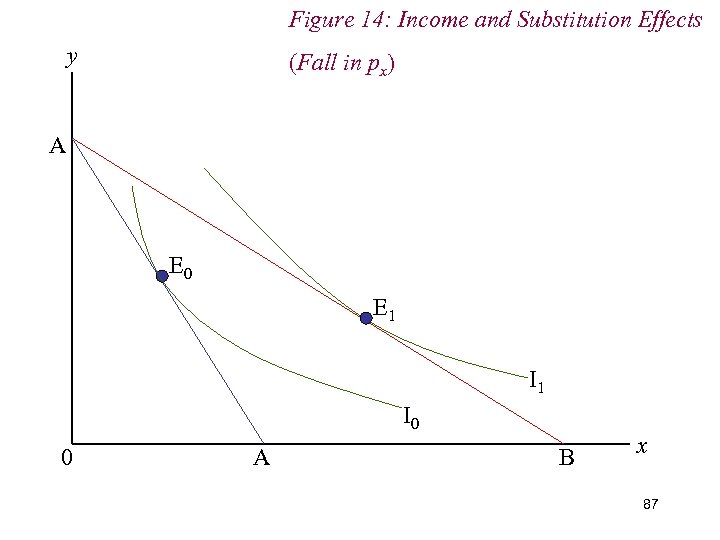Figure 14: Income and Substitution Effects y (Fall in px) A E 0 E 1 I 0 0 A B x 87

7. Income & Substitution Effects n We decompose the overall change in demand into income and substitution effects by (hypothetically) adjusting the consumer’s income to restore him to the level of real income he enjoyed before the price change n Given the fall in px and the subsequent increase in real income, we therefore reduce the consumer’s real income; mechanically, we drag the new budget line back until it is just tangent to the original indifference curve. 88

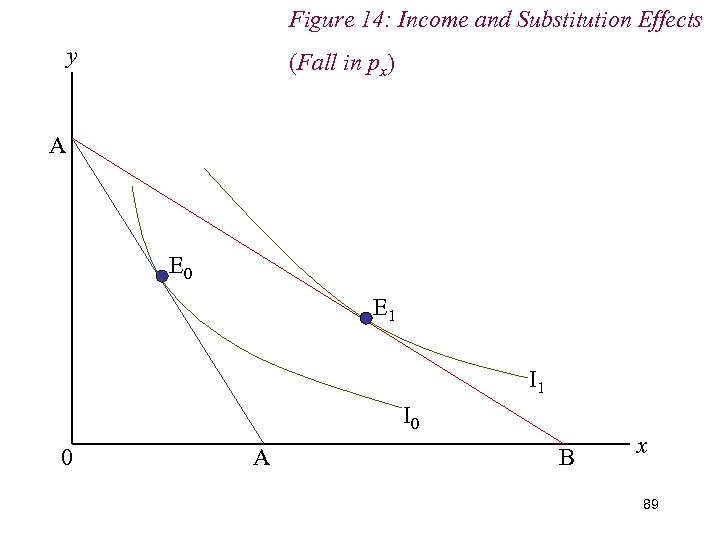Figure 14: Income and Substitution Effects y (Fall in px) A E 0 E 1 I 0 0 A B x 89

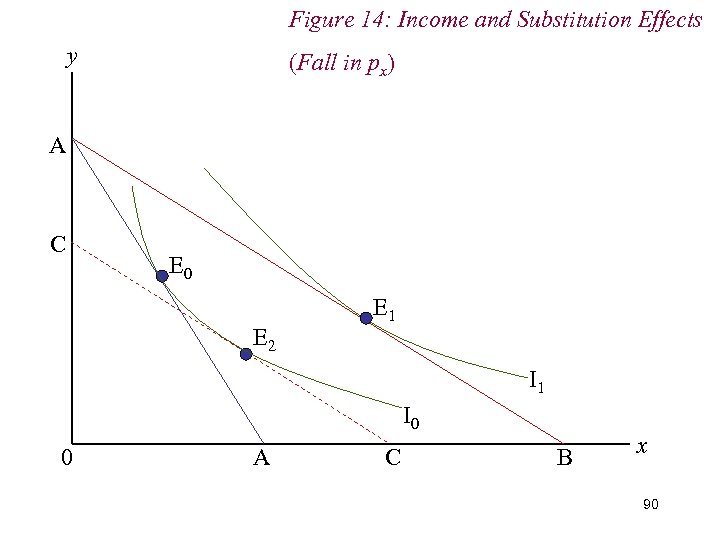Figure 14: Income and Substitution Effects y (Fall in px) A C E 0 E 2 E 1 I 0 0 A C B x 90

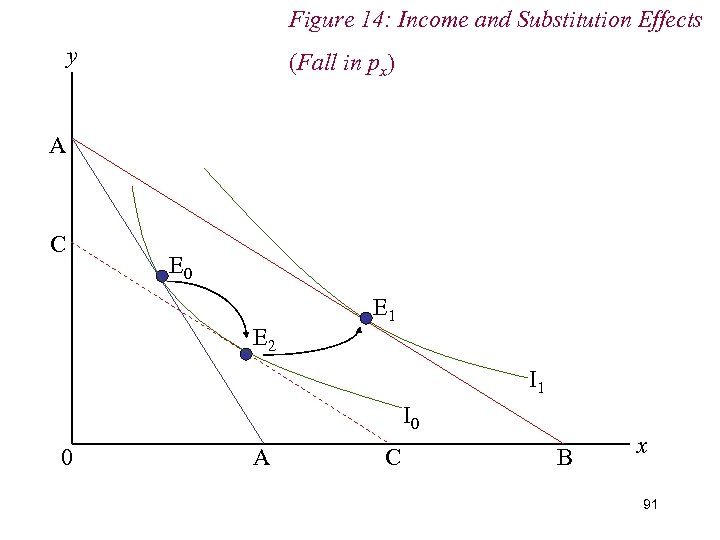Figure 14: Income and Substitution Effects y (Fall in px) A C E 0 E 2 E 1 I 0 0 A C B x 91

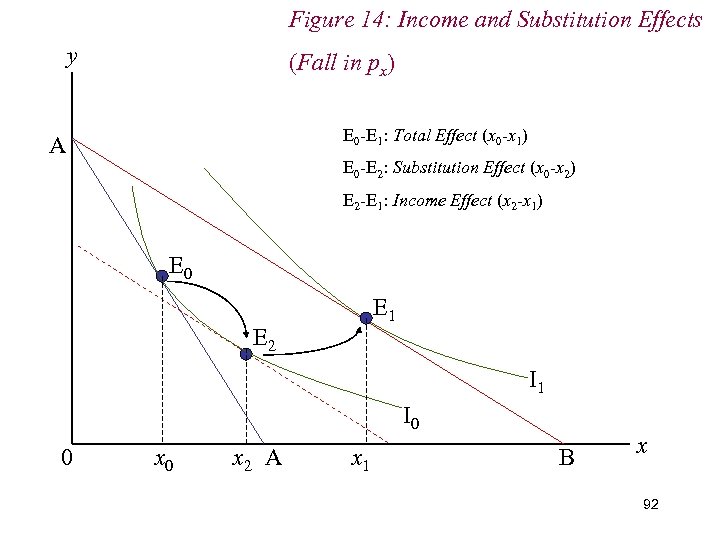Figure 14: Income and Substitution Effects y (Fall in px) E 0 -E 1: Total Effect (x 0 -x 1) A E 0 -E 2: Substitution Effect (x 0 -x 2) E 2 -E 1: Income Effect (x 2 -x 1) E 0 E 1 E 2 I 1 I 0 0 x 2 A x 1 B x 92

8. Inferior and Giffen Goods n In a two good model, a price change always induces a substitution effect in the opposite direction of the change in price n Thus, an increase (decrease) in px induces a substitution away (towards) good x ceteris paribus n We usually say that ‘… the own price substitution effect is negative. ’ (N. B. implicit assumption of price increase) 93

8. Inferior and Giffen Goods n The income effect, however, can be positive or negative n Positive Income Effect. . . n Change in income induces an increase in demand n Thus, increase (decrease) in income induces an increase in demand for a normal (inferior) good 94

8. Inferior and Giffen Goods n In contrast. . . n Negative Income Effect. . . n Change in income induces a decrease in demand n Thus, decrease (increase) in income induces an decrease in demand for a normal (inferior) good 95

8. Inferior and Giffen Goods n Recall that an increase (decrease) in price induces a decrease (increase) in real income n Thus, an increase in price of a normal good induces a negative substitution effect and a negative income effect, both of which act to reduce the demand for good x n An increase in price of an inferior good, however, induces a negative substitution effect but a positive income effect, thus the overall effect is ambiguous 96

8. Inferior and Giffen Goods n If, when the price of an inferior good changes, the income effect dominates the substitution effect, we have the case of a Giffen Good n That is, a good for which demand rises (falls) when price rises (falls) n Giffen goods are very inferior good 97

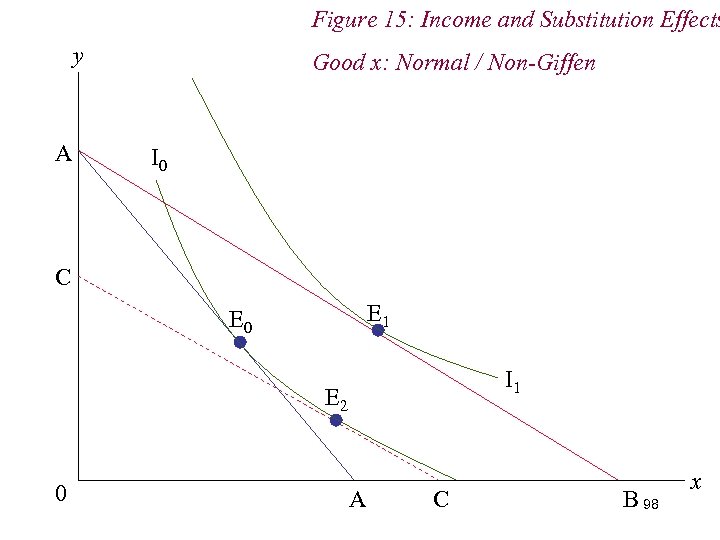Figure 15: Income and Substitution Effects y A Good x: Normal / Non-Giffen I 0 C E 1 E 0 I 1 E 2 0 A C B 98 x

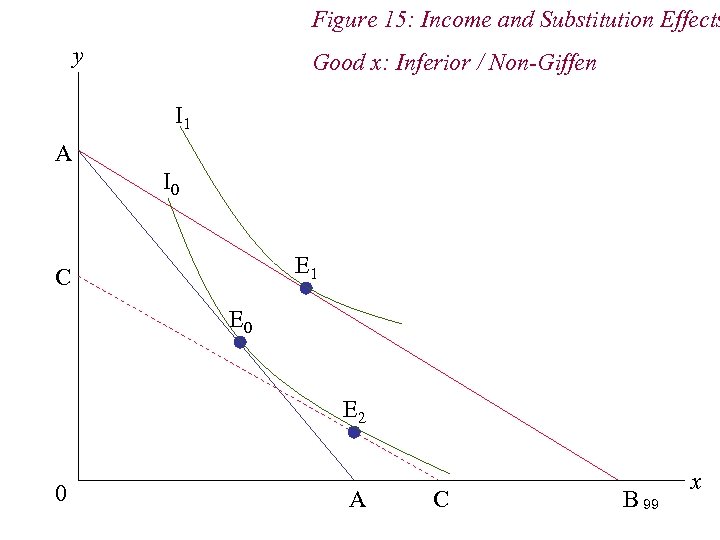Figure 15: Income and Substitution Effects y Good x: Inferior / Non-Giffen I 1 A I 0 E 1 C E 0 E 2 0 A C B 99 x

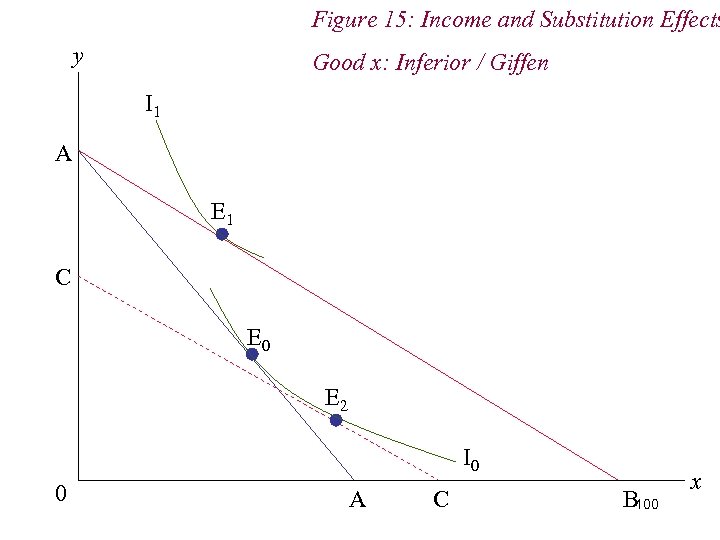Figure 15: Income and Substitution Effects y Good x: Inferior / Giffen I 1 A E 1 C E 0 E 2 I 0 0 A C B 100 x

9. Measuring Real Income n When we decomposed the change in demand resulting from a change in price into an income and substitution effect, we did so by varying money income n Specifically, when the price of good x fell, we ‘varied’ the consumer’s money income to hold his real income constant, where real income was defined as the consumer’s ability to enjoy a particular level of utility 101

9. Measuring Real Income n Varying money income is this way is known as a Hicks Compensating Variation in money income (HCV) n HCV allows consumer to enjoy original level of utility at the new relative price ratio n We ‘compensate’ the consumer for the change in price n Sounds odd in respect of a price fall. 102

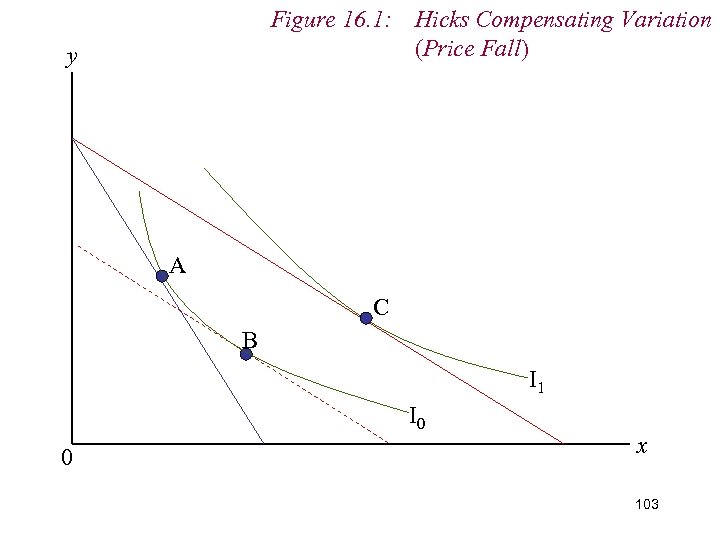Figure 16. 1: Hicks Compensating Variation (Price Fall) y A C B I 1 I 0 0 x 103

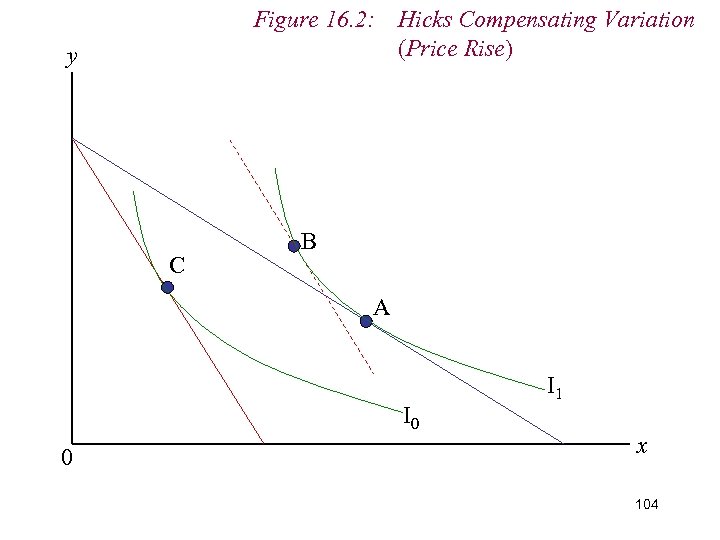Figure 16. 2: Hicks Compensating Variation (Price Rise) y C B A I 0 0 I 1 x 104

9. Measuring Real Income n An alternative definition of real income is the ability to consumer not a particular level of utility, but a particular bundle of goods n i. e. we vary the consumer’s money income following a change in price to permit him to consumer his original bundle of goods at the new relative price ratio n The is know as the Slutsky Compensating Variation (SCV) in money income. 105

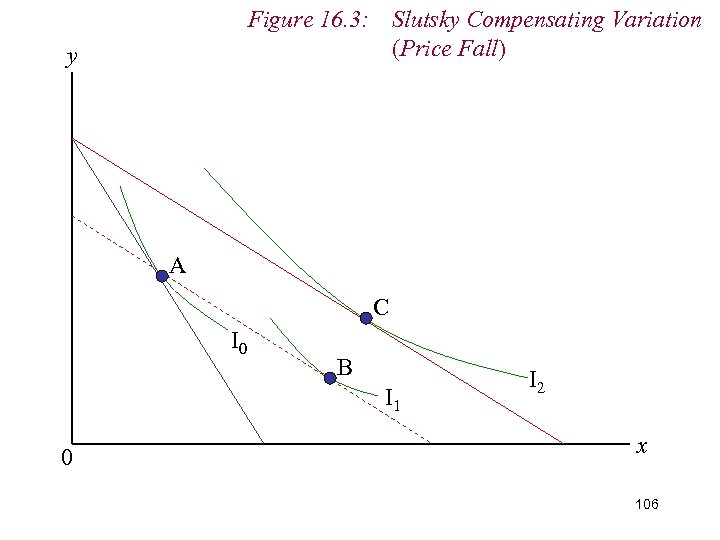Figure 16. 3: Slutsky Compensating Variation (Price Fall) y A C I 0 B I 1 0 I 2 x 106

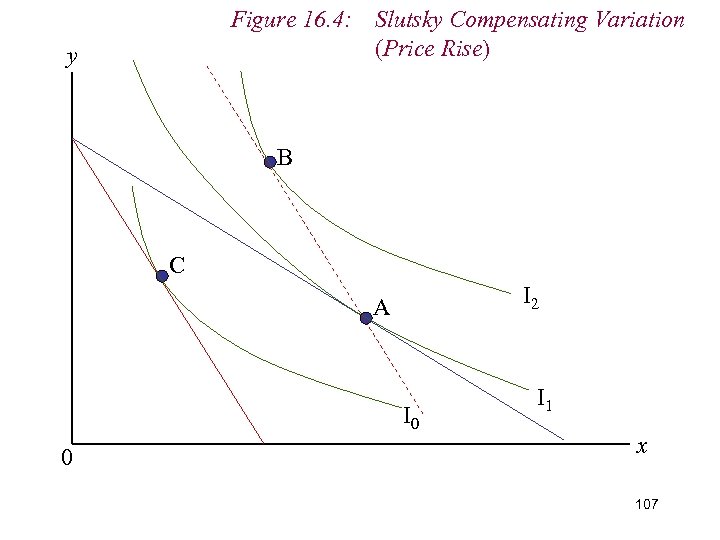Figure 16. 4: Slutsky Compensating Variation (Price Rise) y B C I 2 A I 0 0 I 1 x 107

9. Measuring Real Income n Both Hicks and Slutsky compensating variations adjust the consumer’s new level of income (i. e. the level following the price change) such that he is able to enjoy either his original level of utility (Hicks) or his original consumption bundle (Slutsky) n An alternative approach is to adjust the consumer’s original level of income in such a way that he is able to enjoy the level of utility (Hicks) or the consumption bundle (Slutsky) that he would have been able to enjoy were he to face the change in prices 108

9. Measuring Real Income n That is, we vary the consumer’s money income at the original relative price ratio to enable him to enjoy the level of real income (i. e. utility or consumption bundle) that he would have been able to enjoy from the price change n i. e. we provide the consumer with an Equivalent Variation in money income n A variation in money income that will adjust the consumer’s real income in a manner analogous to the price change 109

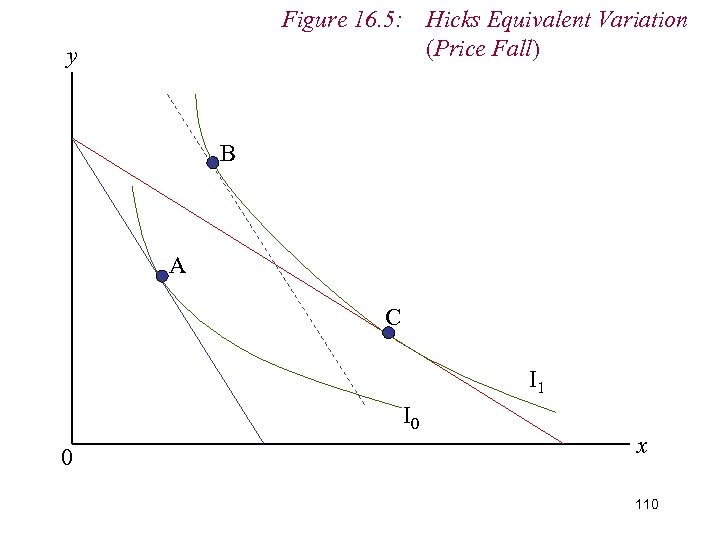Figure 16. 5: Hicks Equivalent Variation (Price Fall) y B A C I 1 I 0 0 x 110

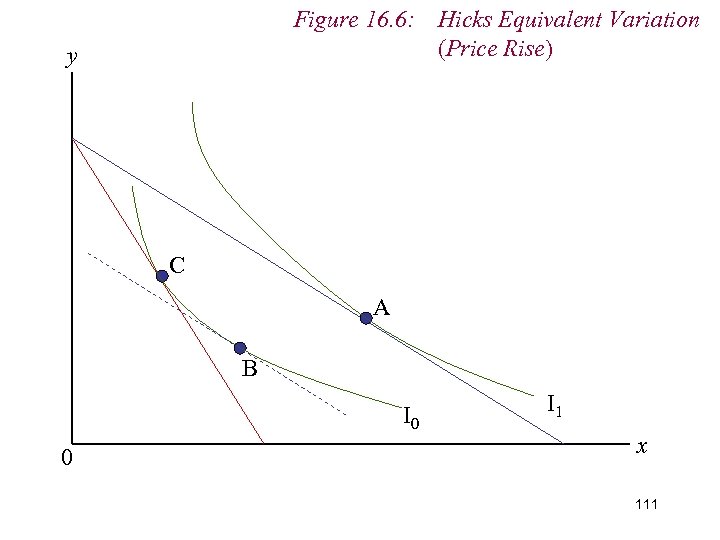Figure 16. 6: Hicks Equivalent Variation (Price Rise) y C A B I 0 0 I 1 x 111

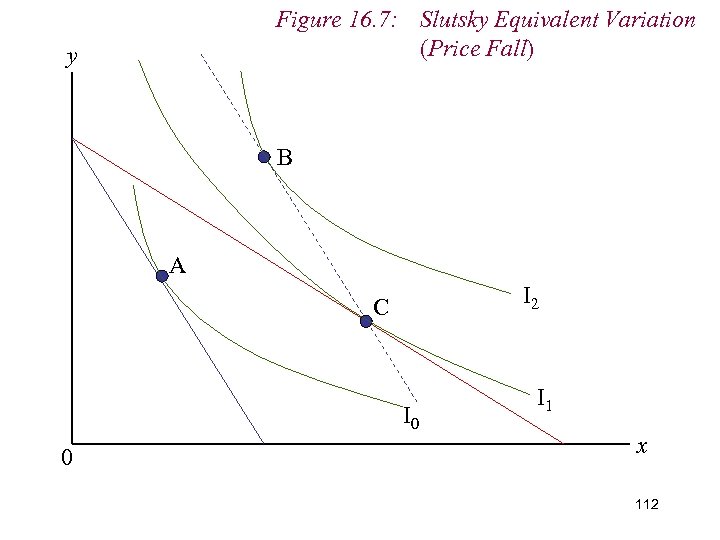Figure 16. 7: Slutsky Equivalent Variation (Price Fall) y B A I 2 C I 0 0 I 1 x 112

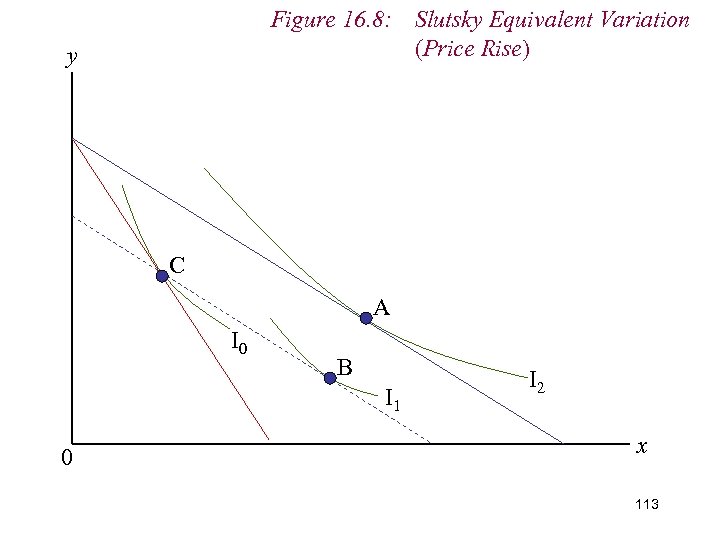Figure 16. 8: Slutsky Equivalent Variation (Price Rise) y C A I 0 B I 1 0 I 2 x 113

9. Measuring Real Income n To summarise, we have eight cases n Hicks / Slutsky n Compensating Variation / Equivalent Variation n Price Rise / Price Fall 114

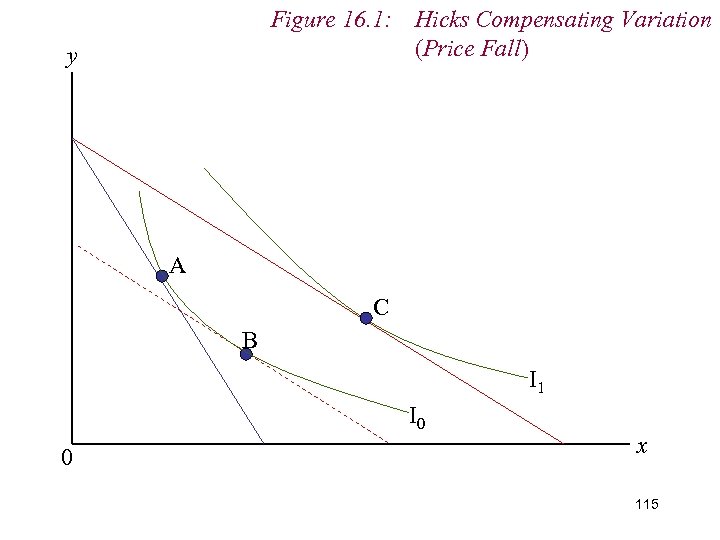Figure 16. 1: Hicks Compensating Variation (Price Fall) y A C B I 1 I 0 0 x 115

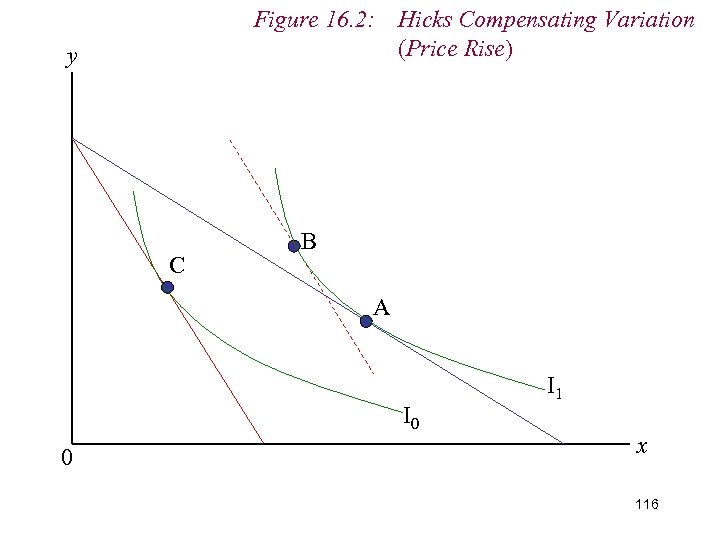Figure 16. 2: Hicks Compensating Variation (Price Rise) y C B A I 0 0 I 1 x 116

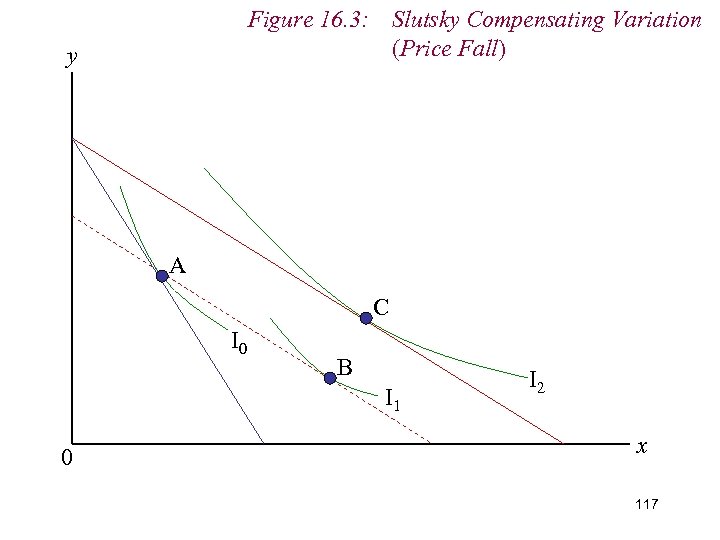Figure 16. 3: Slutsky Compensating Variation (Price Fall) y A C I 0 B I 1 0 I 2 x 117

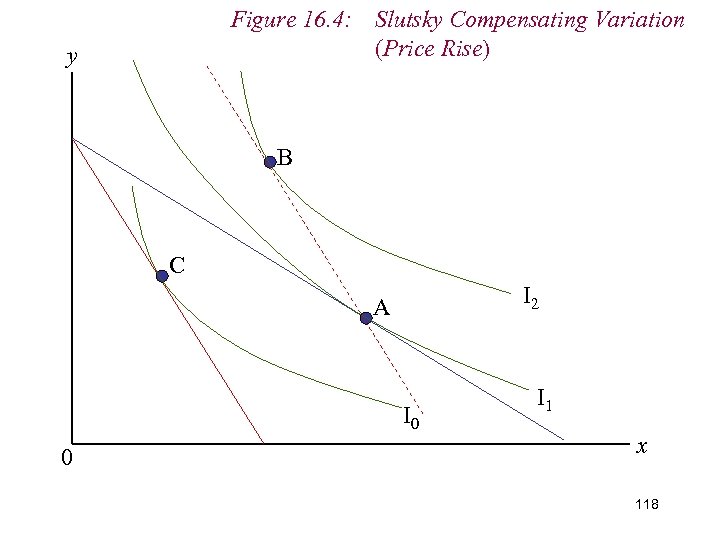Figure 16. 4: Slutsky Compensating Variation (Price Rise) y B C I 2 A I 0 0 I 1 x 118

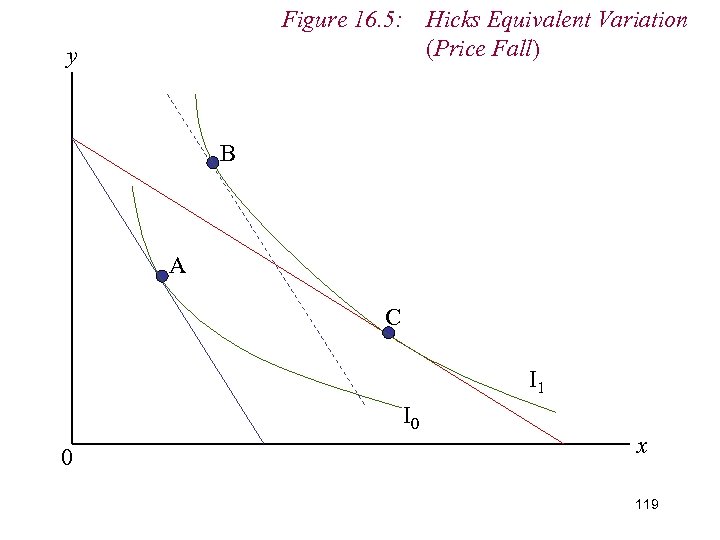Figure 16. 5: Hicks Equivalent Variation (Price Fall) y B A C I 1 I 0 0 x 119

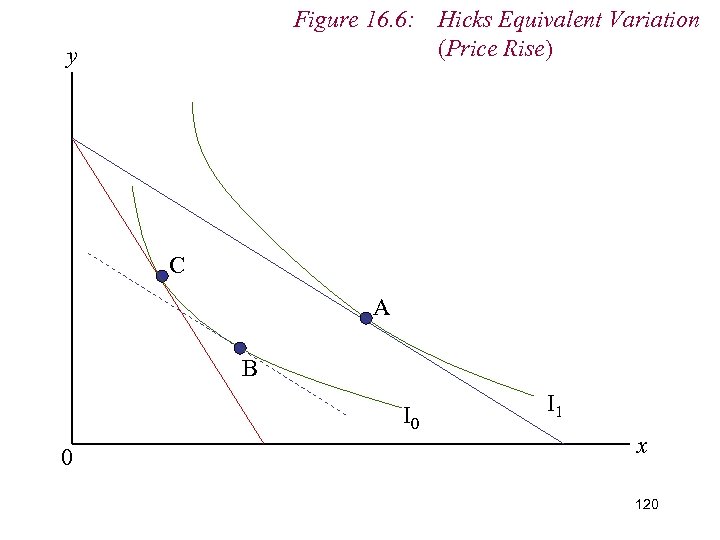Figure 16. 6: Hicks Equivalent Variation (Price Rise) y C A B I 0 0 I 1 x 120

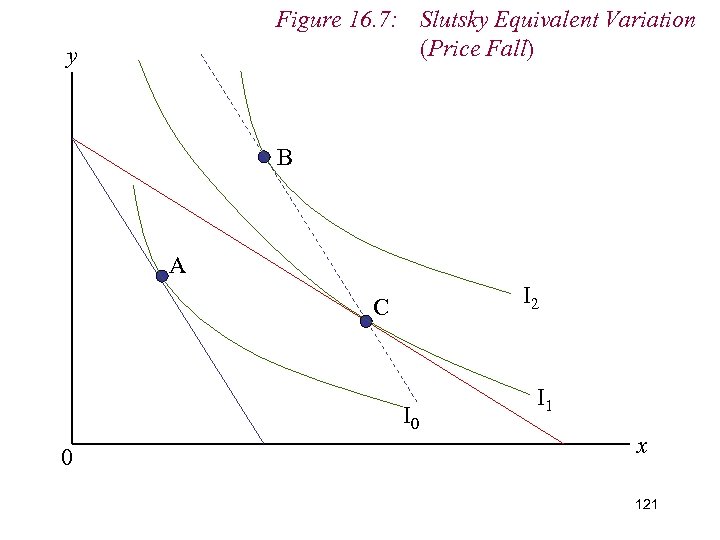Figure 16. 7: Slutsky Equivalent Variation (Price Fall) y B A I 2 C I 0 0 I 1 x 121

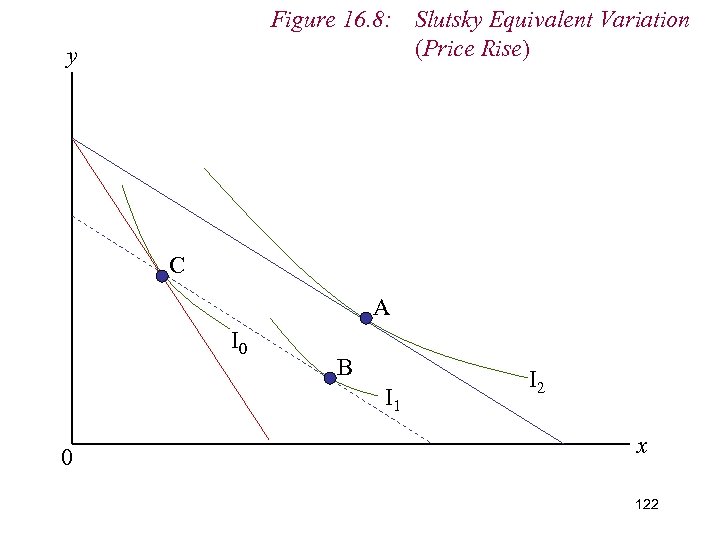Figure 16. 8: Slutsky Equivalent Variation (Price Rise) y C A I 0 B I 1 0 I 2 x 122

9. Measuring Real Income: Aide Memoire § Hicks moves budget line to indifference curve § Slutsky moves budget line to consumption bundle § Compensating Variation moves new budget line to original indifference curve / bundle § Equivalent Variation moves original budget line to new indifference curve / bundle 123

10. Applications n Two key areas: (i) Labour Supply; (ii) Intertemporal Choice. 124

10. 1 Labour Supply n Consider individual’s role as a supplier of factor services n Individuals sell their labour to firms in return for a wage. n Individual makes a choice between income and leisure given the dual constraints of time and the wage 125

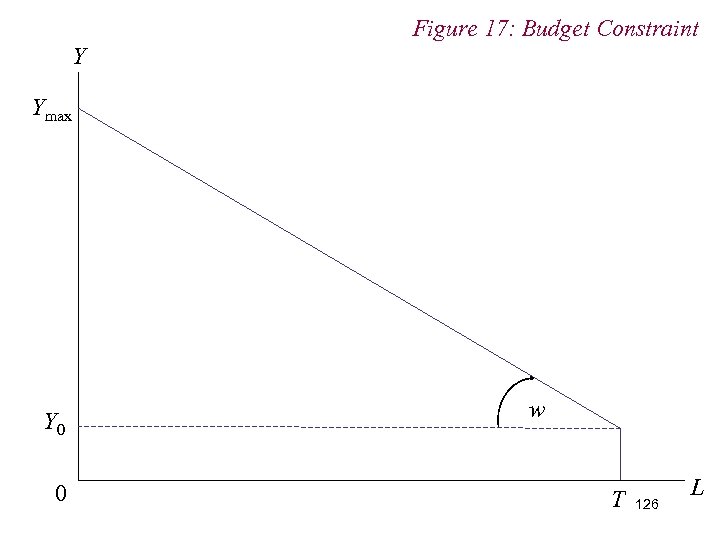Figure 17: Budget Constraint Y Ymax Y 0 0 w T 126 L

Figure 18: Preferences Y I 2 I 1 I 0 0 127 L

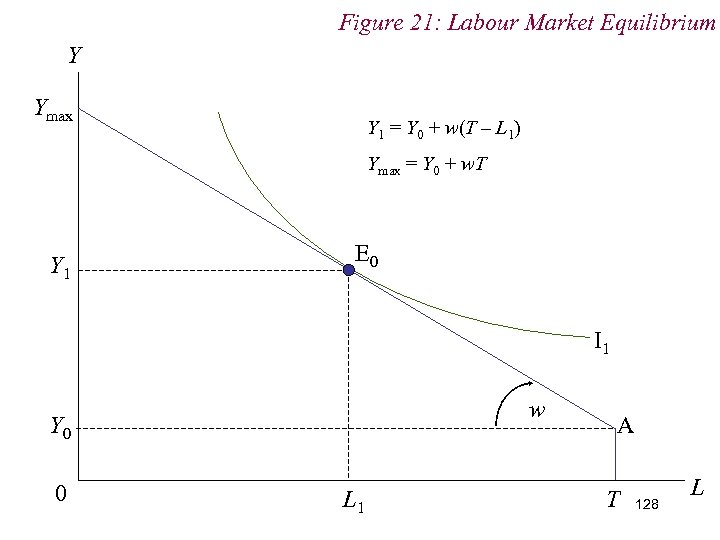Figure 21: Labour Market Equilibrium Y Ymax Y 1 = Y 0 + w(T – L 1) Ymax = Y 0 + w. T Y 1 E 0 I 1 w Y 0 0 L 1 A T 128 L

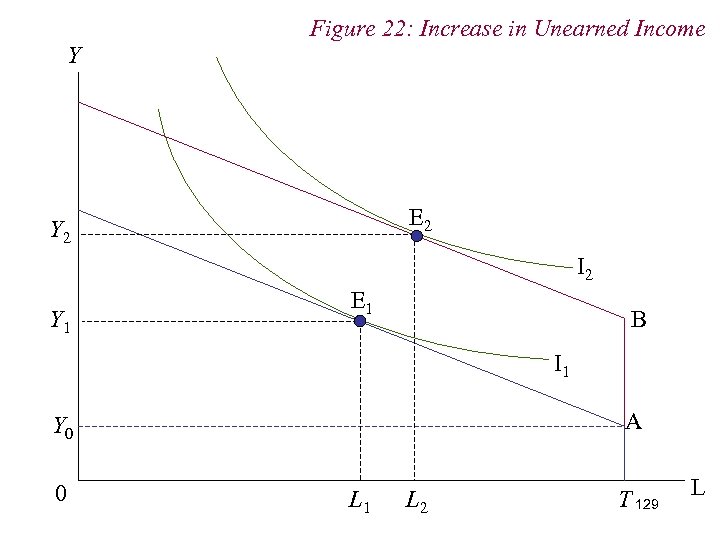Figure 22: Increase in Unearned Income Y E 2 Y 2 I 2 Y 1 E 1 B I 1 A Y 0 0 L 1 L 2 T 129 L

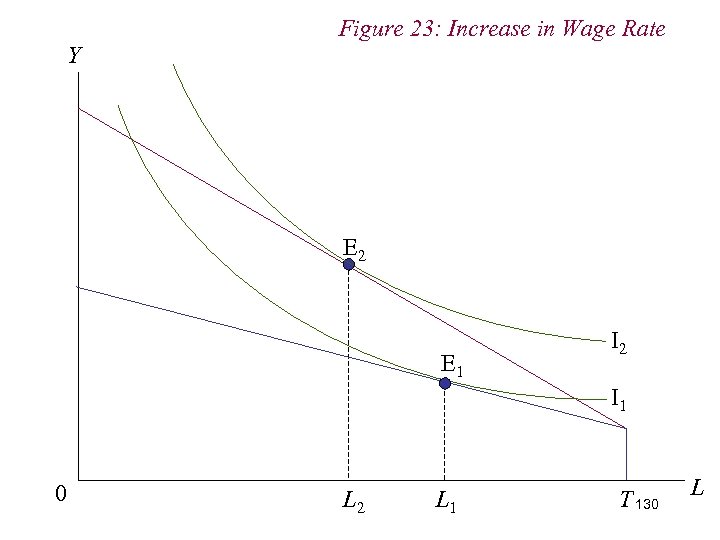Figure 23: Increase in Wage Rate Y E 2 E 1 I 2 I 1 0 L 2 L 1 T 130 L

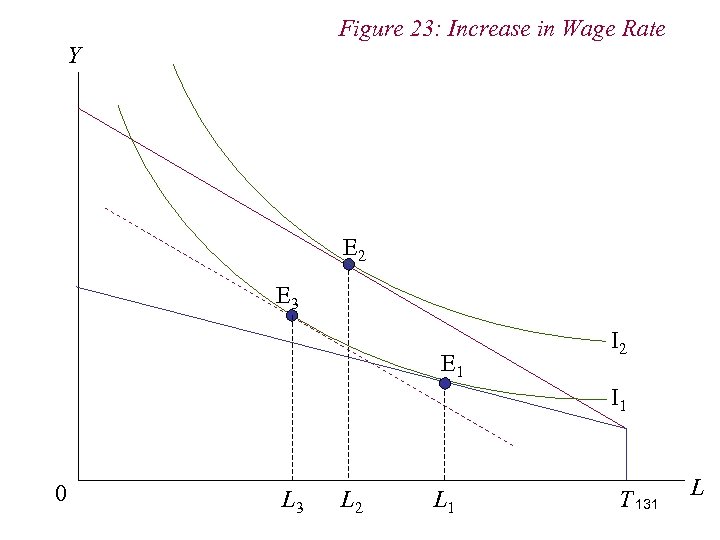Figure 23: Increase in Wage Rate Y E 2 E 3 E 1 I 2 I 1 0 L 3 L 2 L 1 T 131 L

10. 1 Labour Supply n Note that the income and substitution effects work against one another n Because leisure is a normal good, the income effect from the increase in wage increases the demand for leisure n But the wage rate is the opportunity cost, or price, of leisure. Thus, an increase in the wage rate / price of leisure induces a substitution away from leisure 132

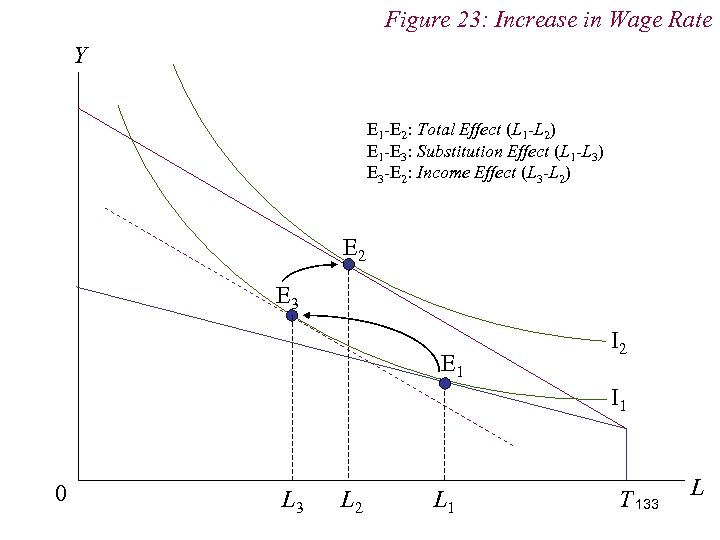Figure 23: Increase in Wage Rate Y E 1 -E 2: Total Effect (L 1 -L 2) E 1 -E 3: Substitution Effect (L 1 -L 3) E 3 -E 2: Income Effect (L 3 -L 2) E 2 E 3 E 1 I 2 I 1 0 L 3 L 2 L 1 T 133 L

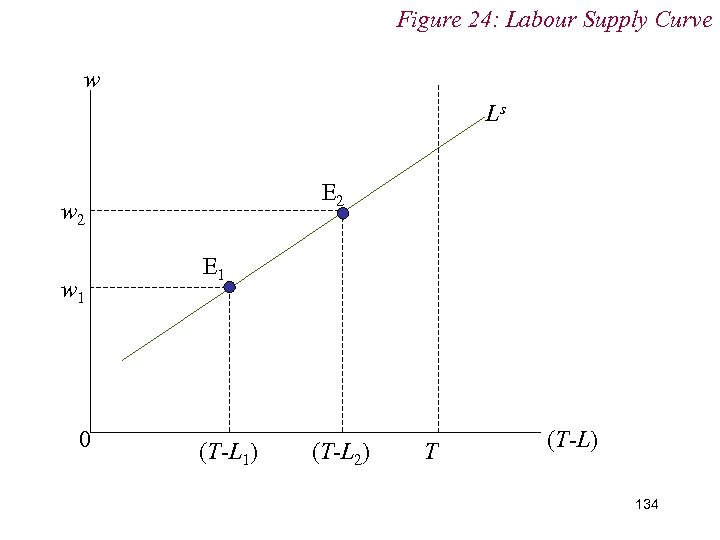Figure 24: Labour Supply Curve w Ls E 2 w 1 0 E 1 (T-L 1) (T-L 2) T (T-L) 134

10. 1 Labour Supply n If the income effect dominates the substitution effect, then we have a situation in which an increase in the wage (i. e. the price of leisure) leads to an increase in the demand for leisure n That is: n Leisure is Giffen … but Normal! 135

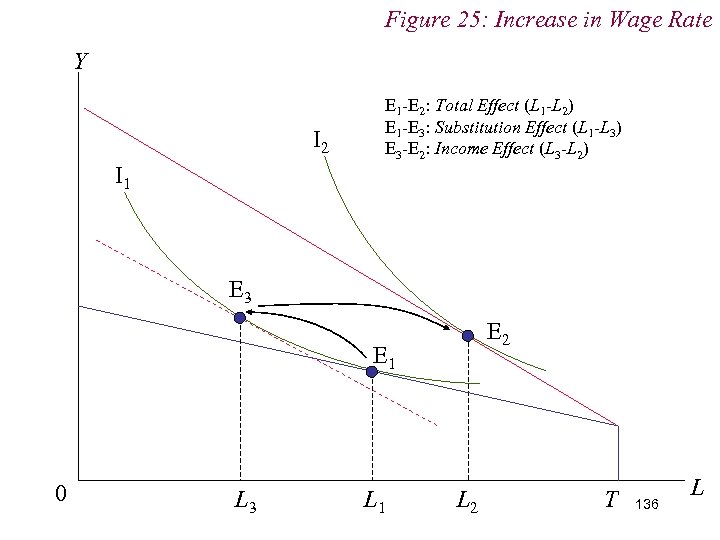Figure 25: Increase in Wage Rate Y I 2 E 1 -E 2: Total Effect (L 1 -L 2) E 1 -E 3: Substitution Effect (L 1 -L 3) E 3 -E 2: Income Effect (L 3 -L 2) I 1 E 3 E 2 E 1 0 L 3 L 1 L 2 T 136 L

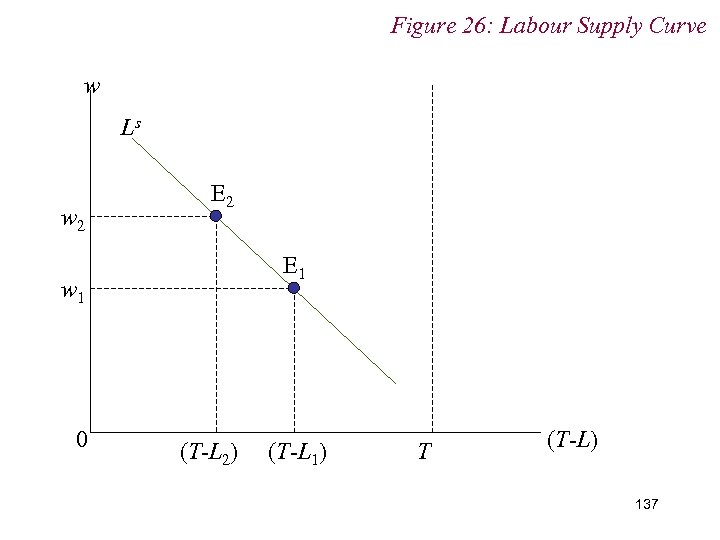Figure 26: Labour Supply Curve w Ls w 2 E 1 w 1 0 (T-L 2) (T-L 1) T (T-L) 137

10. 1 Labour Supply n This is possible because there is also an Endowment Effect in operation … n The Individual is entering the market with an endowment of leisure which he is selling to the firm n The presence of endowment effects complicates the relationship between inferiority and Gifffeness 138

10. 1 Labour Supply n Empirically, we tend to see labour supply curves bending backwards at high wage rates n i. e. 139

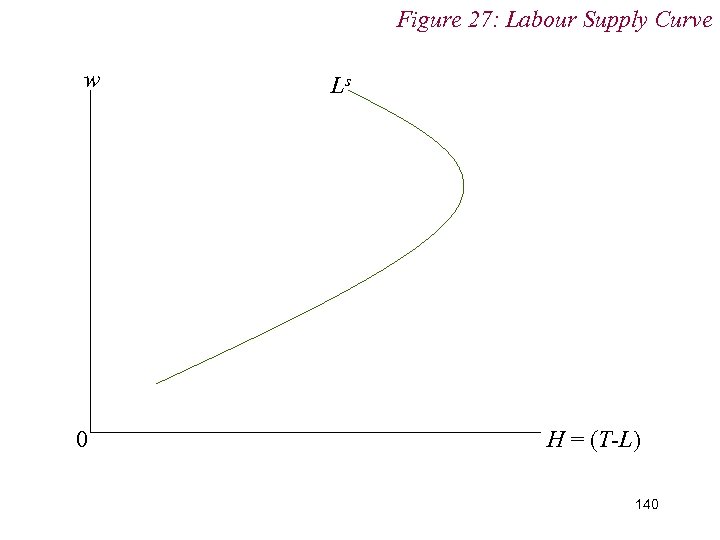Figure 27: Labour Supply Curve w 0 Ls H = (T-L) 140

10. 1 Labour Supply n Rather than at low wage rates n i. e. 141

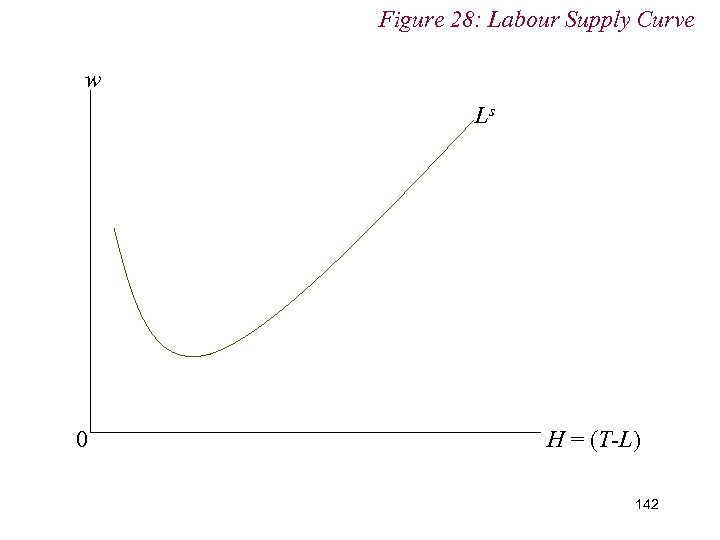Figure 28: Labour Supply Curve w Ls 0 H = (T-L) 142

10. 1 Labour Supply n Moreover, backward bending labour supply curves are usually observed for males but nor females n i. e. 143

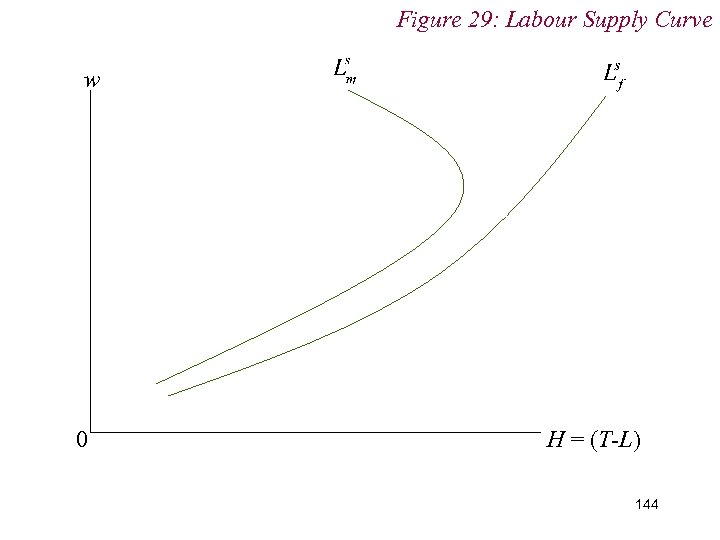Figure 29: Labour Supply Curve w 0 H = (T-L) 144

10. 1 Labour Supply n Implications of backward bending labour supply curve n Multiple equilibria n Unstable equilibria n What happens to w if it is perturbed slightly above / below its equilibirum level, w*? Do forces of excess demand / excess supply force w back to w* 145

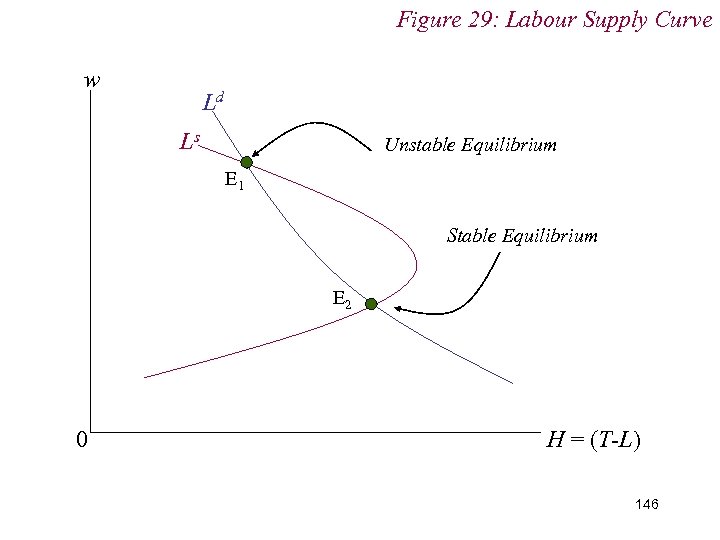Figure 29: Labour Supply Curve w Ld Ls Unstable Equilibrium E 1 Stable Equilibrium E 2 0 H = (T-L) 146

10. 2 Intertemporal Choice n Assume individual lives for two periods with a lifetime income endowment of y = (y 1, y 2) n Consumption over time is c = (c 1, c 2) n Now, £x saved today (i. e. period 1) will yield £(1+r)x tomorrow (i. e. period 2) n The future value of £x today is thus £(1+r)x 147

10. 2 Intertemporal Choice n Conversely, the present value of £x received tomorrow (i. e. period 2) is: n Intuitively, if we receive £x tomorrow, can borrow £z today, where: 148

10. 2 Intertemporal Choice n Thus, given an income endowment of: n Then the maximum period 1 income is: n And the maximum period 2 income is: 149

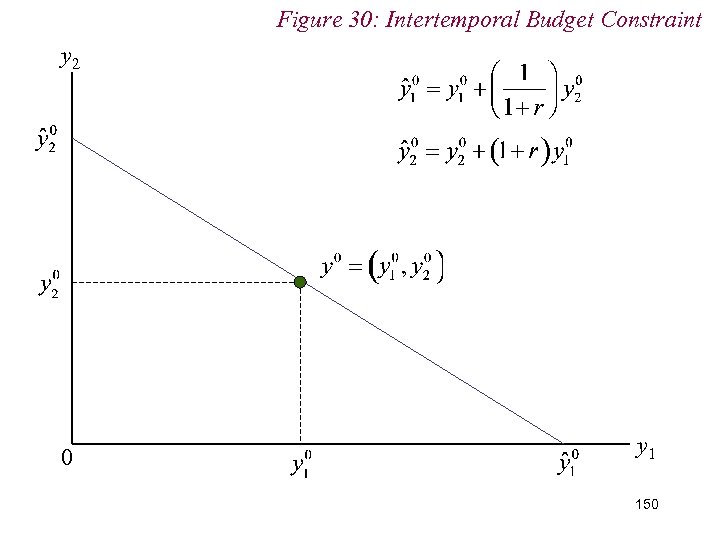Figure 30: Intertemporal Budget Constraint y 2 0 y 1 150

10. 2 Intertemporal Choice n Assume individual consumes in both periods n If the value of consumption in period 1 is , then can save in period 1 for period 2 consumption in excess of period 2 income, : 151

10. 2 Intertemporal Choice 152

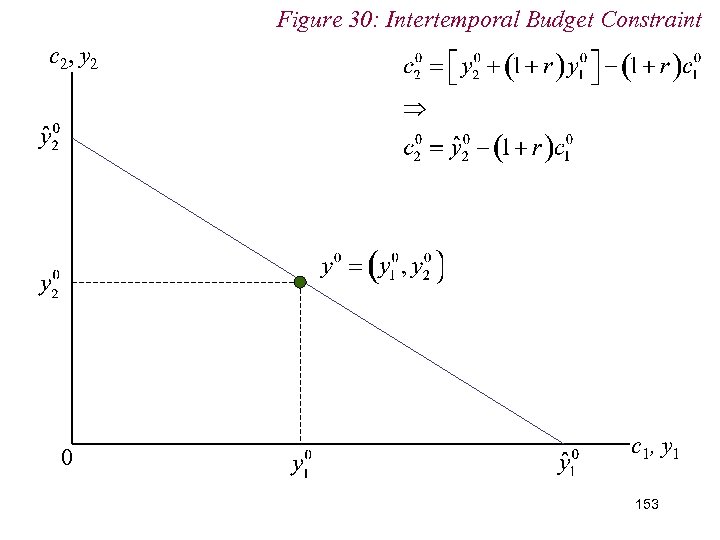Figure 30: Intertemporal Budget Constraint c 2, y 2 0 c 1, y 1 153

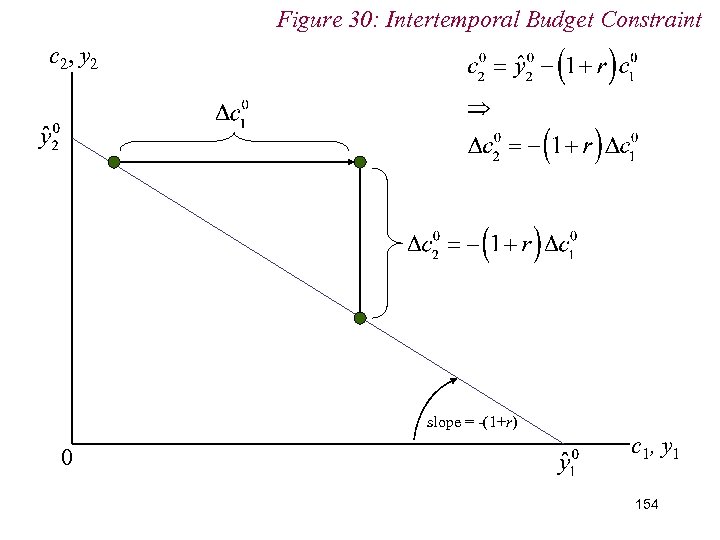Figure 30: Intertemporal Budget Constraint c 2, y 2 slope = -(1+r) 0 c 1, y 1 154

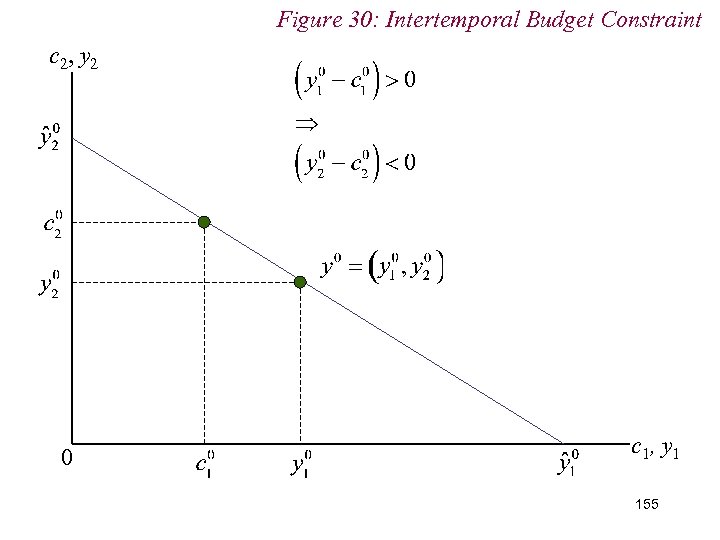Figure 30: Intertemporal Budget Constraint c 2, y 2 0 c 1, y 1 155

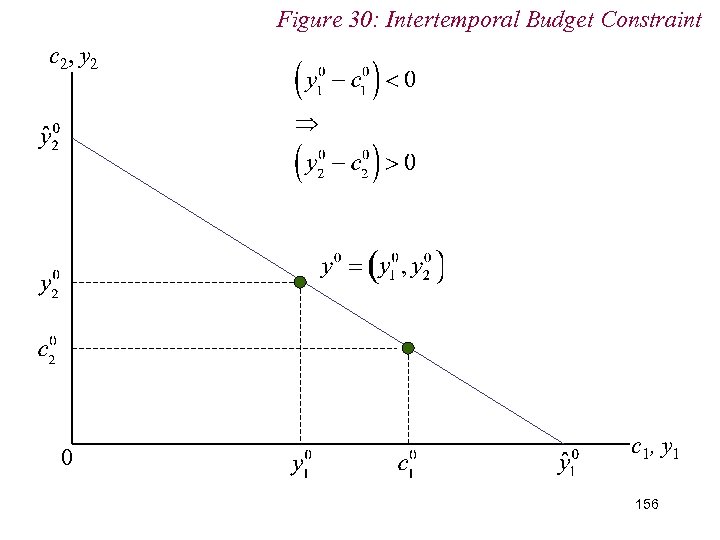Figure 30: Intertemporal Budget Constraint c 2, y 2 0 c 1, y 1 156

10. 2 Intertemporal Choice n Note the effects of changes in income endowment or interest rate n Change in income endowment shifts the intertemporal budget constraint parallel n Changes in interest rate pivot the budget constraint around the initial income endowment 157

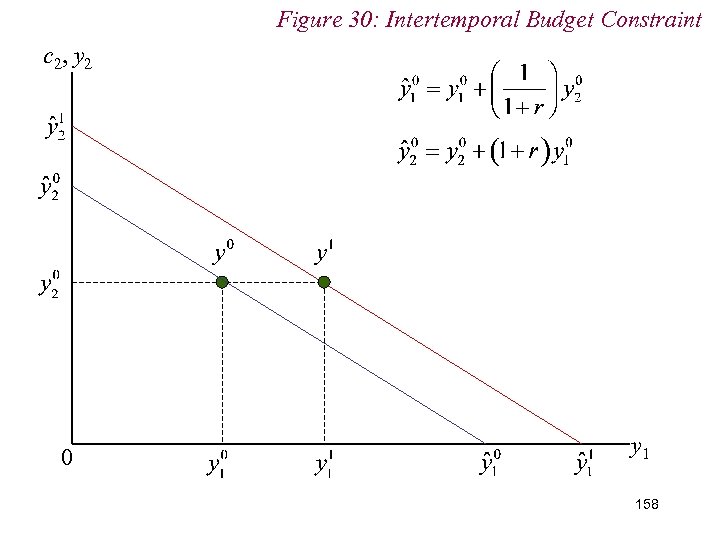Figure 30: Intertemporal Budget Constraint c 2, y 2 0 y 1 158

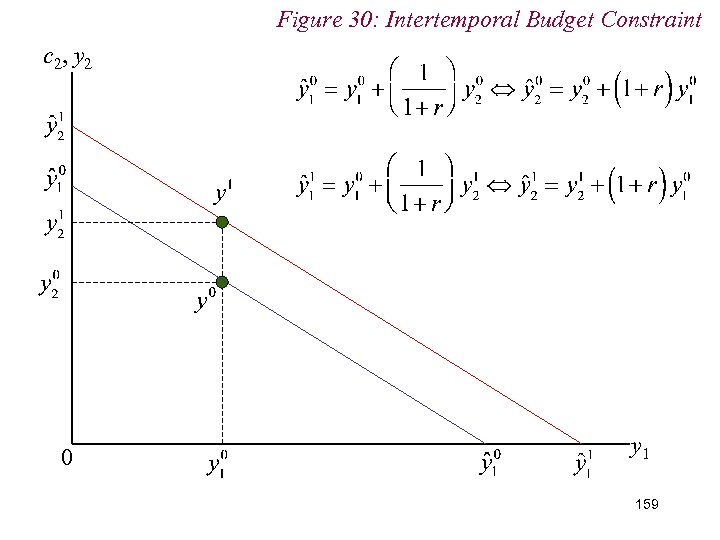Figure 30: Intertemporal Budget Constraint c 2, y 2 0 y 1 159

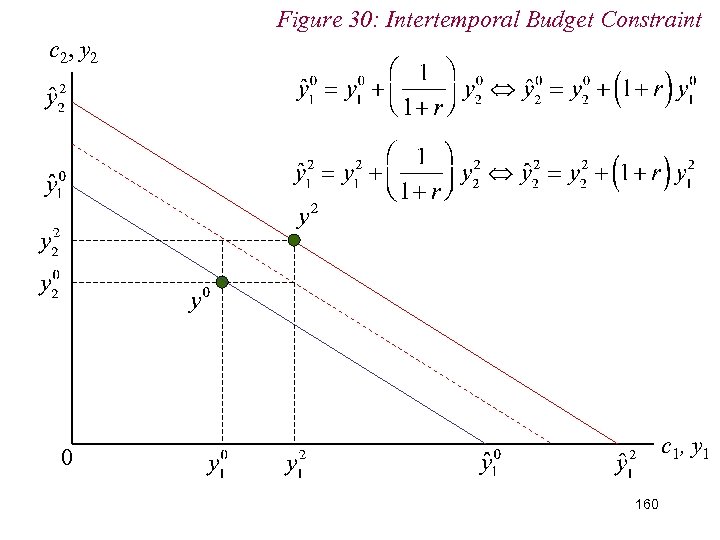Figure 30: Intertemporal Budget Constraint c 2, y 2 c 1, y 1 0 160

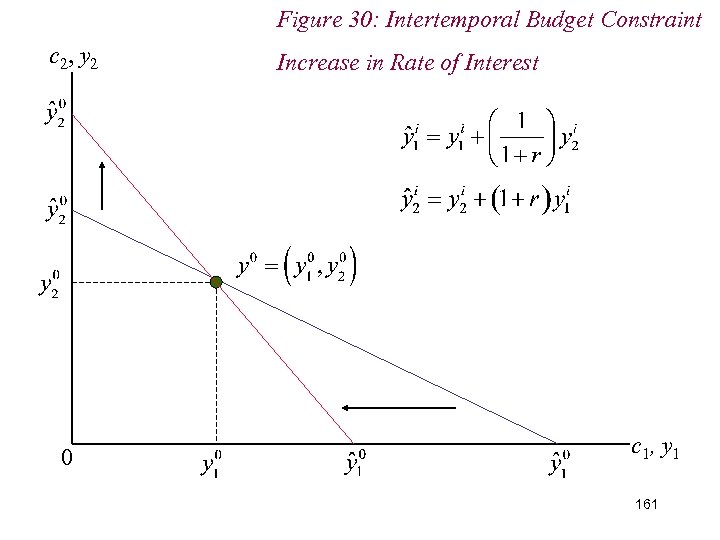Figure 30: Intertemporal Budget Constraint c 2, y 2 0 Increase in Rate of Interest c 1, y 1 161

10. 2 Intertemporal Choice n Consider a (period 1) borrower n That is: n (c 1 - y 1) > 0 n How does he react to changes in interest rate? 162

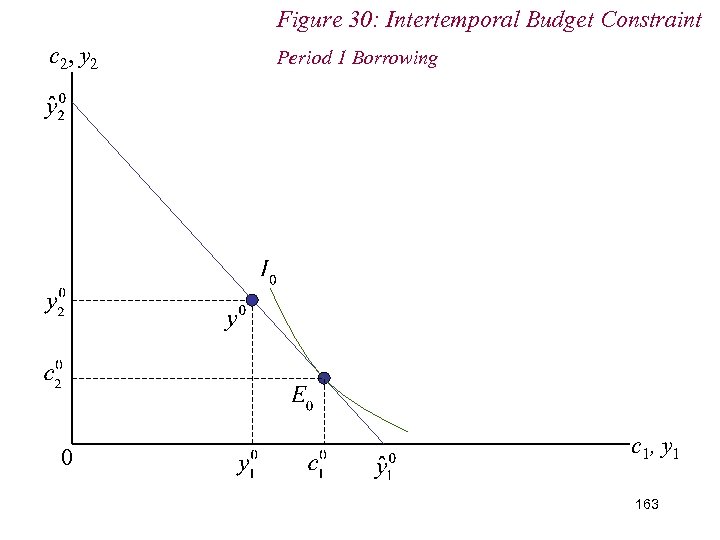Figure 30: Intertemporal Budget Constraint c 2, y 2 0 Period 1 Borrowing c 1, y 1 163

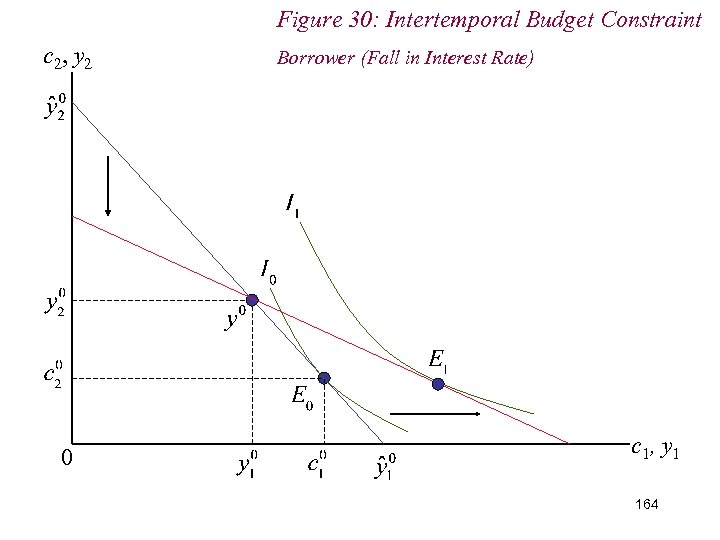Figure 30: Intertemporal Budget Constraint c 2, y 2 0 Borrower (Fall in Interest Rate) c 1, y 1 164

10. 2 Intertemporal Choice n Thus, if interest rate falls: (i) (Period 1) Borrower remains a (period 1) borrower; (ii) Is better-off; (iii) Increases (period 1) borrowing if c 1 a normal good 165

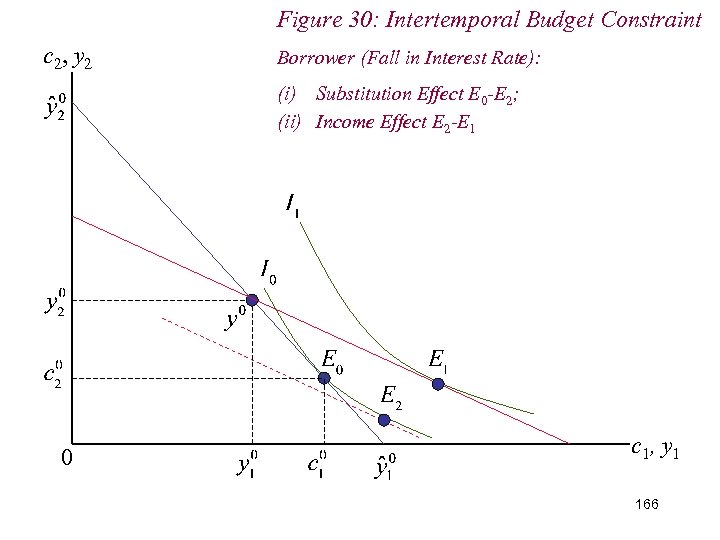Figure 30: Intertemporal Budget Constraint c 2, y 2 Borrower (Fall in Interest Rate): (i) Substitution Effect E 0 -E 2; (ii) Income Effect E 2 -E 1 0 c 1, y 1 166

10. 2 Intertemporal Choice n If interest rate falls, then borrower reduces borrowing and is worse-off; 167

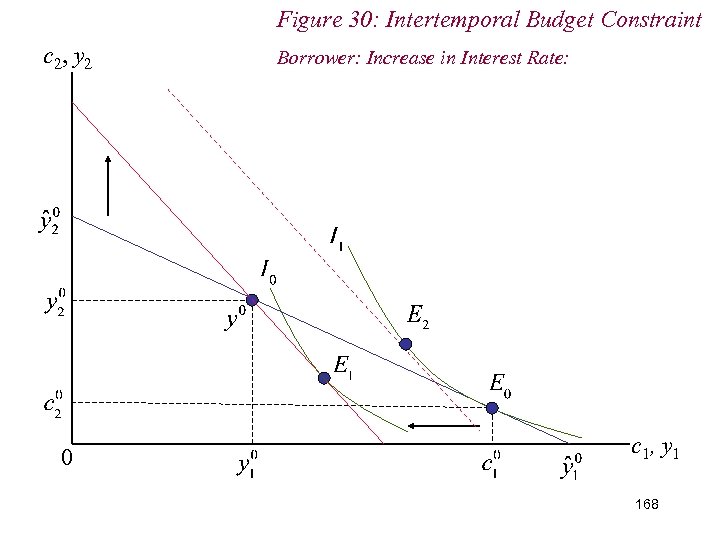Figure 30: Intertemporal Budget Constraint c 2, y 2 0 Borrower: Increase in Interest Rate: c 1, y 1 168

10. 2 Intertemporal Choice n Conversely, for savers (c 1 - y 1) < 0: n Rise in interest rates: (i) Remain savers; (ii) Better off; (iii) Increase saving if c 1 is an inferior good 169

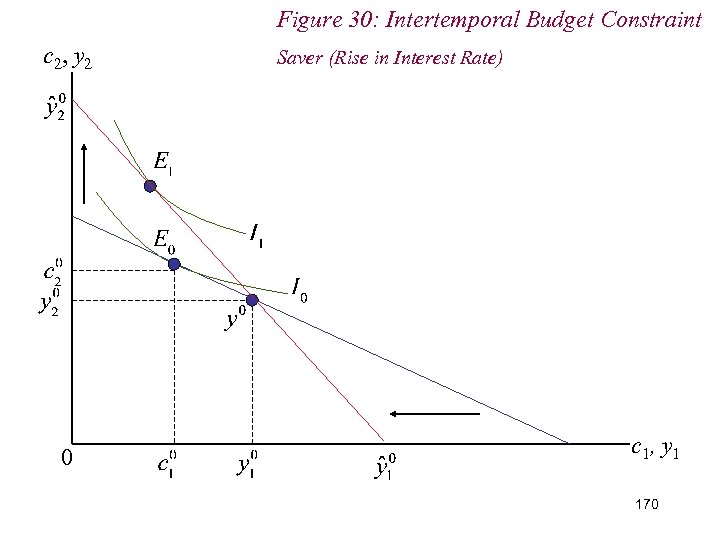Figure 30: Intertemporal Budget Constraint c 2, y 2 0 Saver (Rise in Interest Rate) c 1, y 1 170

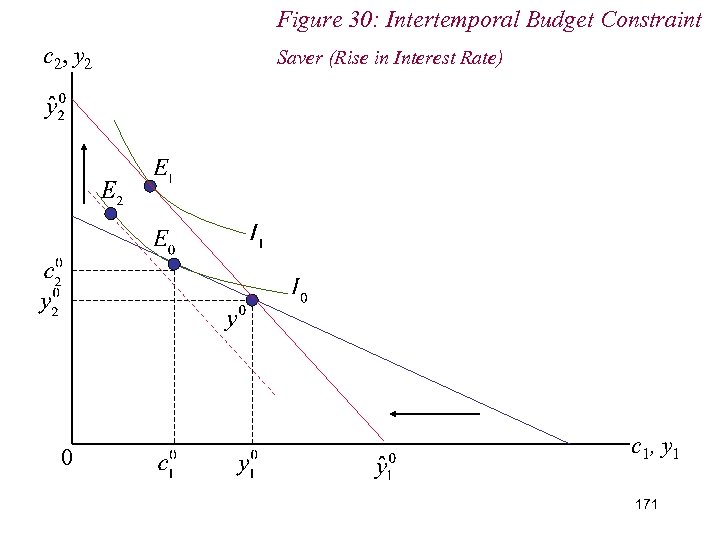Figure 30: Intertemporal Budget Constraint c 2, y 2 0 Saver (Rise in Interest Rate) c 1, y 1 171