Introduction to Statistics Political Science Class 5 Non-Linear

Introduction to Statistics: Political Science (Class 5) Non-Linear Relationships

Thus far • Focus on examining and controlling for linear relationships – Each one unit increase in an IV is associated with the same expected change in the DV – Ordinary-least-squares regression can only estimate linear relationships • But, we can “trick” regression into estimating non-linear relationships buy transforming our independent (and/or dependent) variables

When to transform an IV • Theoretical expectation • Look at the data (sometimes tricky in multivariate analysis or when you have thousands of cases) • Today: three types of transformations – Logarithm – Squared terms – Converting to indicator variables

Logarithm • The power to which a base must be raised to produce a given value • We’ll focus on natural logarithms where ln(x) is the power to which e (2. 718281) must be raised to get x – ln(4) = 1. 386 because e 1. 386 = 4

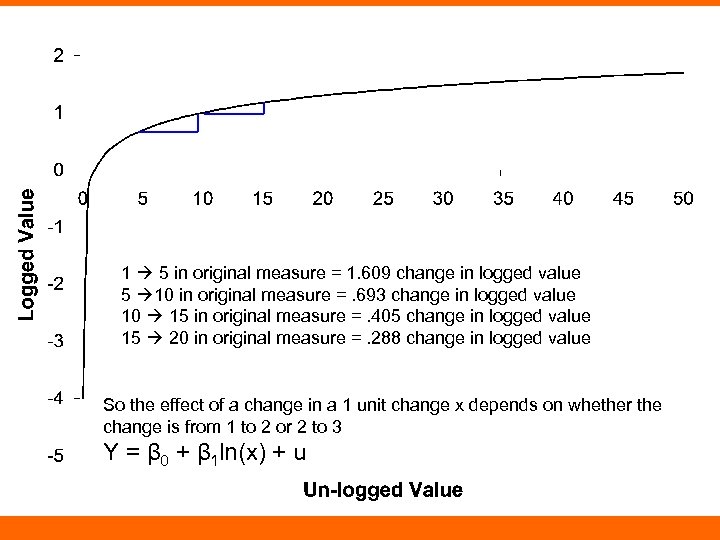1 5 in original measure = 1. 609 change in logged value 5 10 in original measure =. 693 change in logged value 10 15 in original measure =. 405 change in logged value 15 20 in original measure =. 288 change in logged value So the effect of a change in a 1 unit change x depends on whether the change is from 1 to 2 or 2 to 3 Υ = β 0 + β 1 ln(x) + u

When to log an IV • “Diminishing returns” as X gets large – Data is skewed – e. g. , income

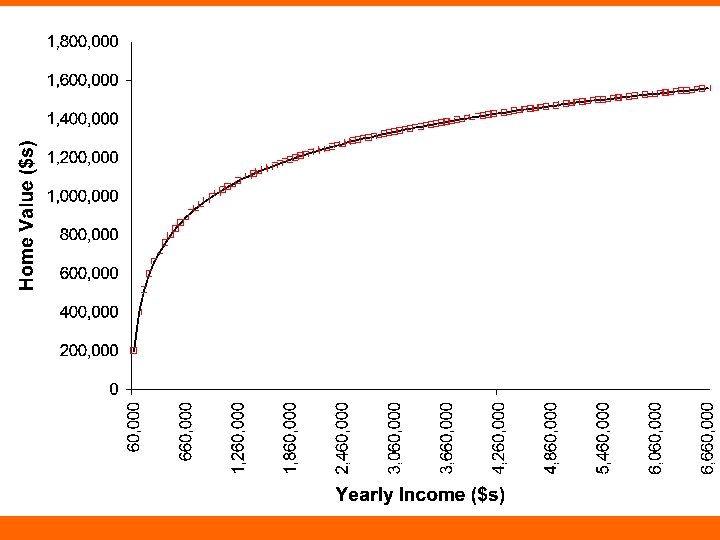
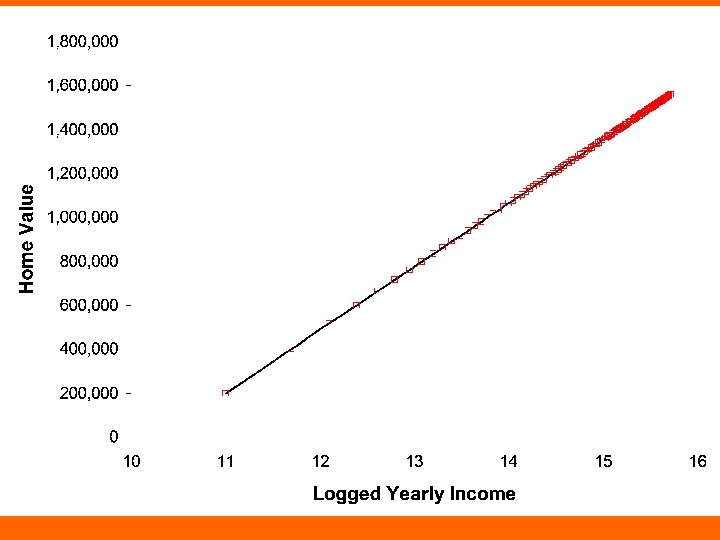
Income and home value • $60, 000/year $200, 000 home • $120, 000/year $400, 000 home • Bill Gates makes about $175 million/year – $175, 000 = 2917 x $60, 000 – Should we expect him to have a 2917 x $200, 000 ($583, 400, 000) home?

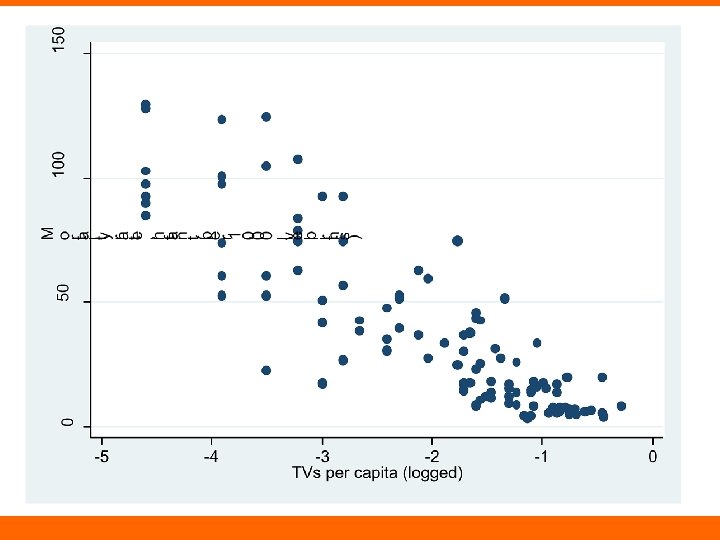
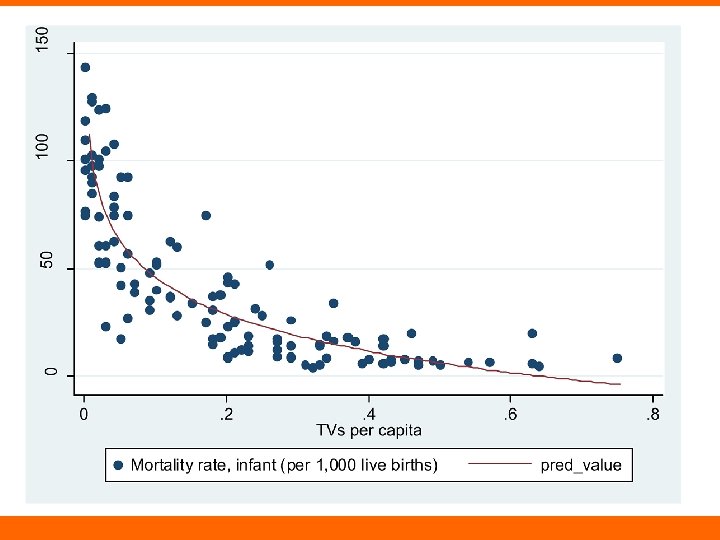
TVs and Infant Mortality • TVs as proxy for resources or wealth • Biggest differences at the low end? – E. g. , “there a couple of TVs in town” and “some people have TVs in their private homes”

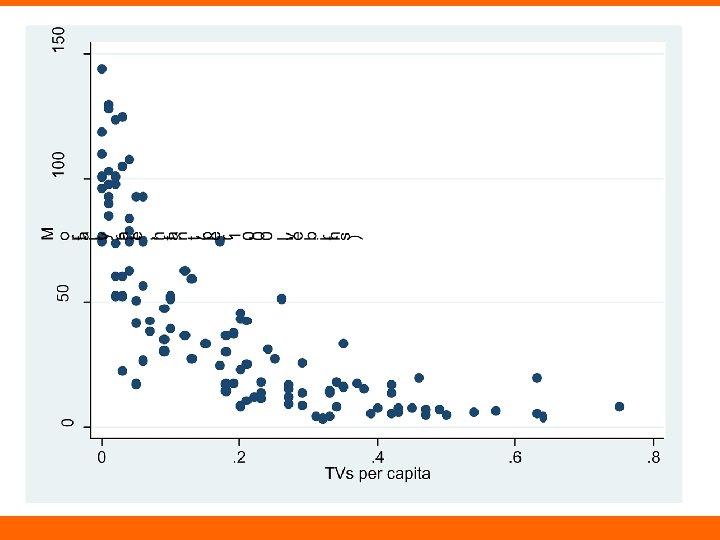
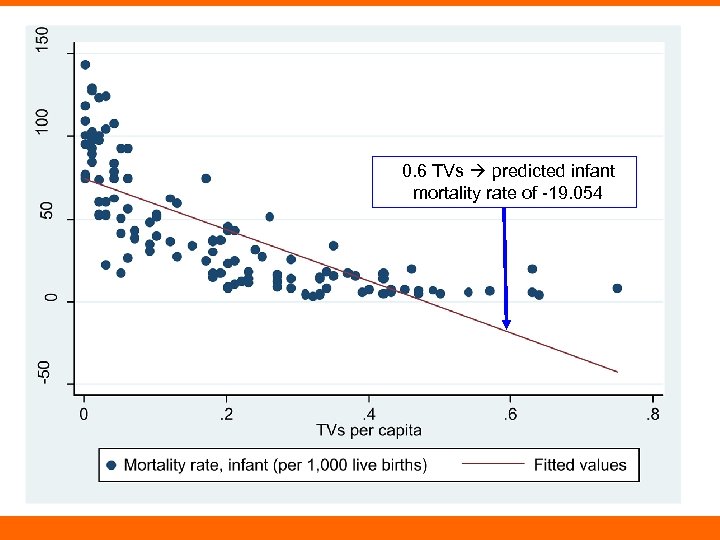0. 6 TVs predicted infant mortality rate of -19. 054

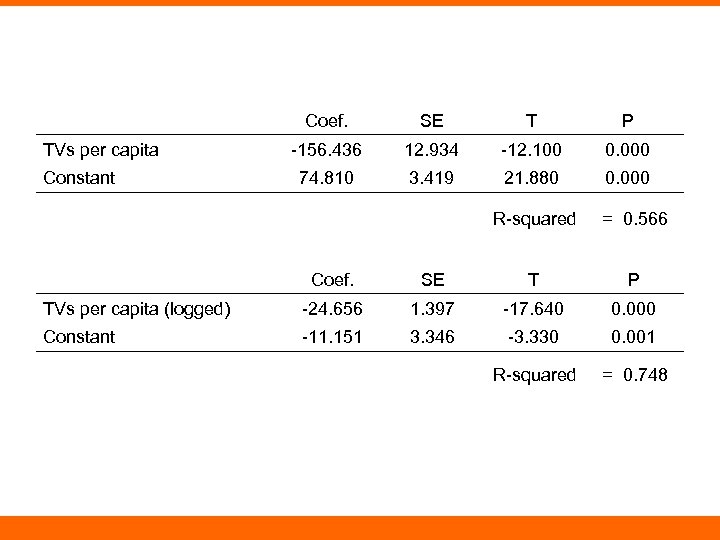Coef. TVs per capita Constant SE T P -156. 436 12. 934 -12. 100 0. 000 74. 810 3. 419 21. 880 0. 000 R-squared = 0. 566 Coef. SE T P TVs per capita (logged) -24. 656 1. 397 -17. 640 0. 000 Constant -11. 151 3. 346 -3. 330 0. 001 R-squared = 0. 748

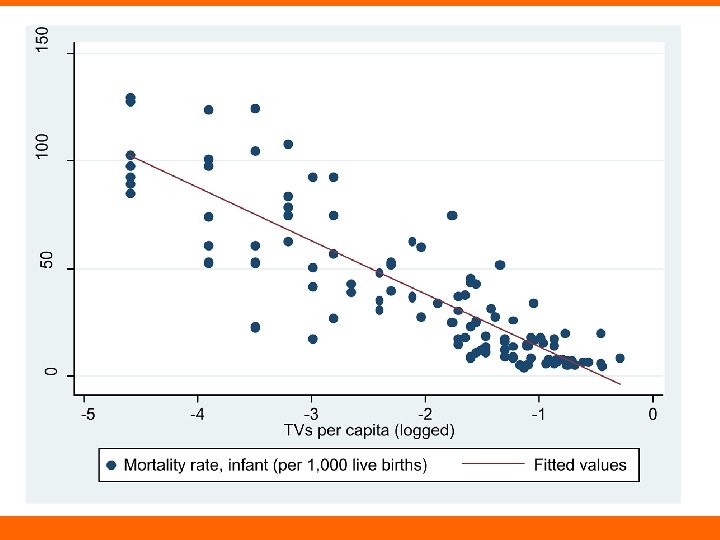
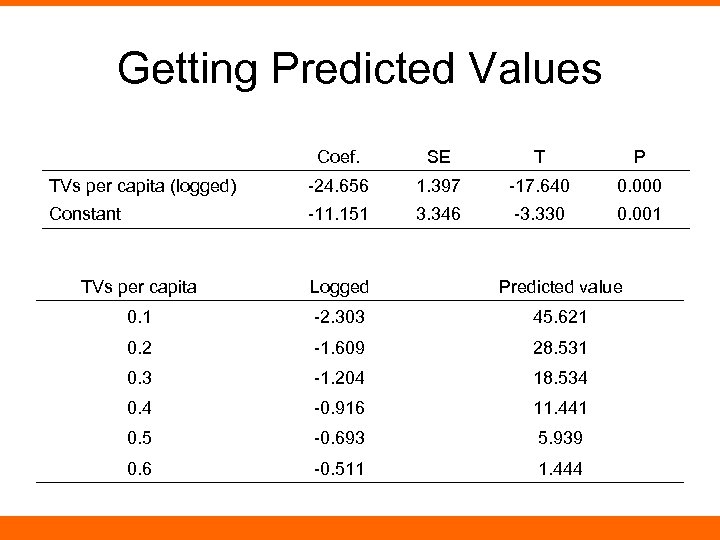Getting Predicted Values Coef. SE T P TVs per capita (logged) -24. 656 1. 397 -17. 640 0. 000 Constant -11. 151 3. 346 -3. 330 0. 001 TVs per capita Logged Predicted value 0. 1 -2. 303 45. 621 0. 2 -1. 609 28. 531 0. 3 -1. 204 18. 534 0. 4 -0. 916 11. 441 0. 5 -0. 693 5. 939 0. 6 -0. 511 1. 444

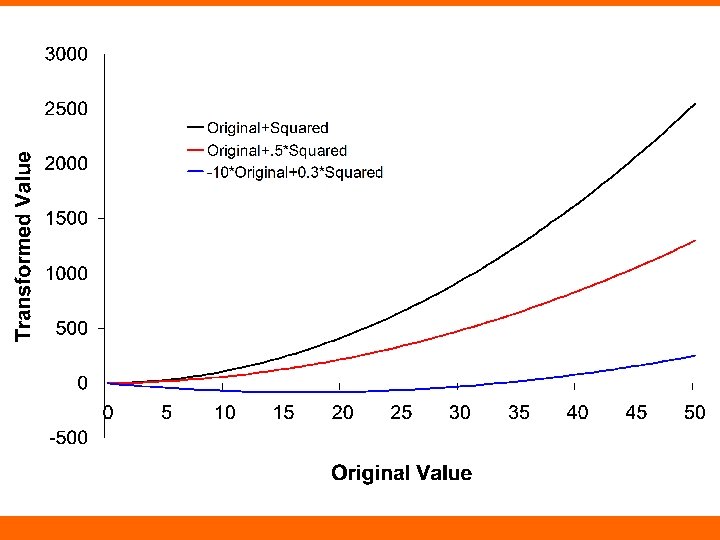
Quadratic (squared) models • Curved like logarithm – Key difference: quadratics allow for “U-shaped” relationship • Enter original variable and squared term – Allows for a direct test of whether allowing the line to curve significantly improves the predictive power of the model

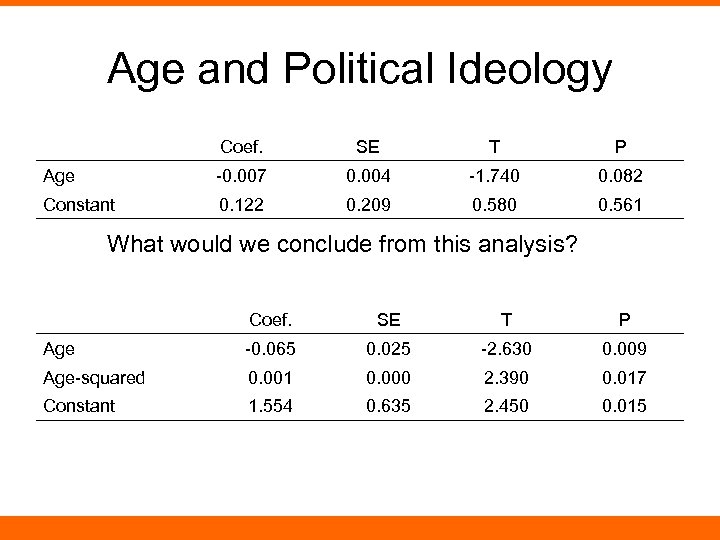Age and Political Ideology Coef. SE T P Age -0. 007 0. 004 -1. 740 0. 082 Constant 0. 122 0. 209 0. 580 0. 561 What would we conclude from this analysis? Coef. SE T P Age -0. 065 0. 025 -2. 630 0. 009 Age-squared 0. 001 0. 000 2. 390 0. 017 Constant 1. 554 0. 635 2. 450 0. 015

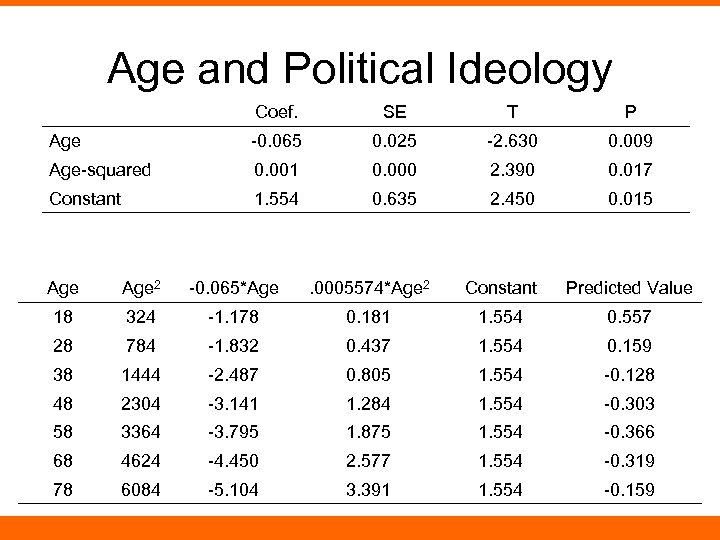Age and Political Ideology Coef. SE T P Age -0. 065 0. 025 -2. 630 0. 009 Age-squared 0. 001 0. 000 2. 390 0. 017 Constant 1. 554 0. 635 2. 450 0. 015 Age 2 -0. 065*Age . 0005574*Age 2 Constant Predicted Value 18 324 -1. 178 0. 181 1. 554 0. 557 28 784 -1. 832 0. 437 1. 554 0. 159 38 1444 -2. 487 0. 805 1. 554 -0. 128 48 2304 -3. 141 1. 284 1. 554 -0. 303 58 3364 -3. 795 1. 875 1. 554 -0. 366 68 4624 -4. 450 2. 577 1. 554 -0. 319 78 6084 -5. 104 3. 391 1. 554 -0. 159

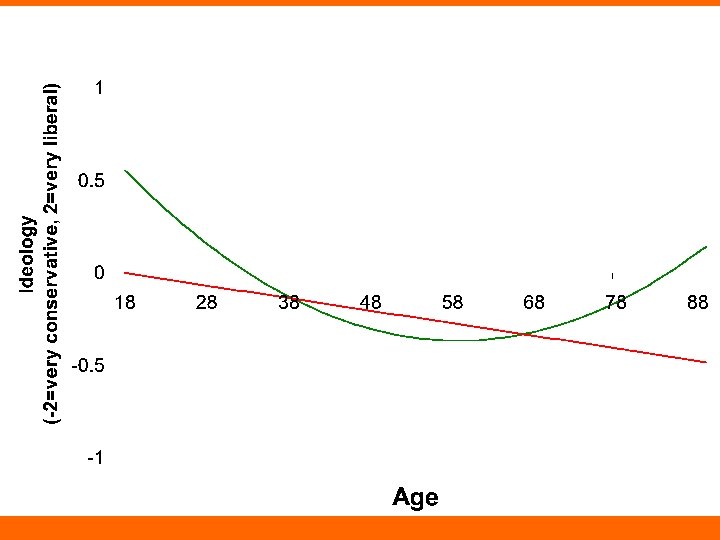
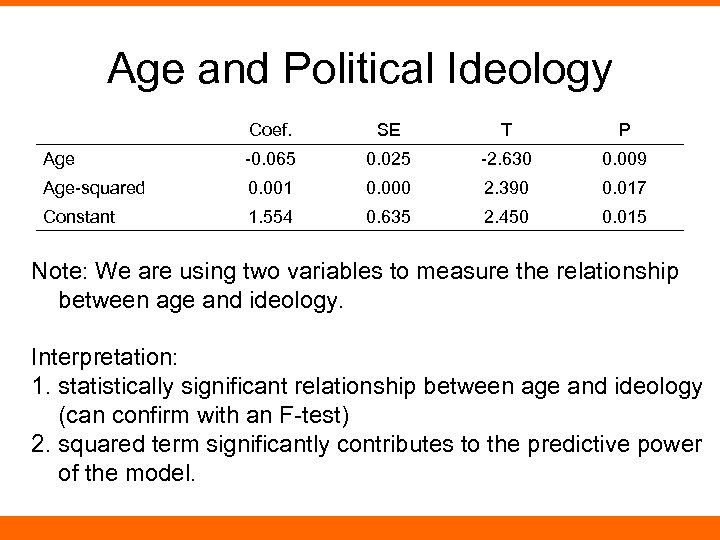Age and Political Ideology Coef. SE T P Age -0. 065 0. 025 -2. 630 0. 009 Age-squared 0. 001 0. 000 2. 390 0. 017 Constant 1. 554 0. 635 2. 450 0. 015 Note: We are using two variables to measure the relationship between age and ideology. Interpretation: 1. statistically significant relationship between age and ideology (can confirm with an F-test) 2. squared term significantly contributes to the predictive power of the model.

If you add a linear and squared term (e. g. , age and age 2) to a model and neither is independently statistically significant • This does not necessarily mean that age is not significantly related to the outcome Why? • What we want to know is whether age and age 2 jointly improve the predictive power of the model. How can we test this?

Formula F= (SSRr - SSRur)/q SSRur/(n-(k+1) • q = # of variables being tested • n = number of cases • k = number of IVs in unrestricted Check whether value is above critical value in the F-distribution [depends on degrees of freedom: Numerator = number of IVs being tested; Denominator = N-(number of IVs)-1 ]

Don’t worry about the F-test formula • The point is: – F-tests are a way to test whether adding a set of variables reduces the sum of squared residuals enough to justify throwing these new variables into the model • Depends on: – How much sum of squared residuals is reduced – How many variables we’re adding – How many cases we have to work with • More “acceptable” to add variables if you have a lot of cases • Intuition: explaining 10 cases with 10 variables v. explaining 1000 cases with 10 variables?

TVs and Infant Mortality • Squared term or logarithm? Coef. SE T P TVs per capita -380. 088 29. 949 -12. 690 0. 000 TVs per capita (squared) 410. 957 51. 629 7. 960 0. 000 Constant 90. 197 3. 353 26. 900 0. 000

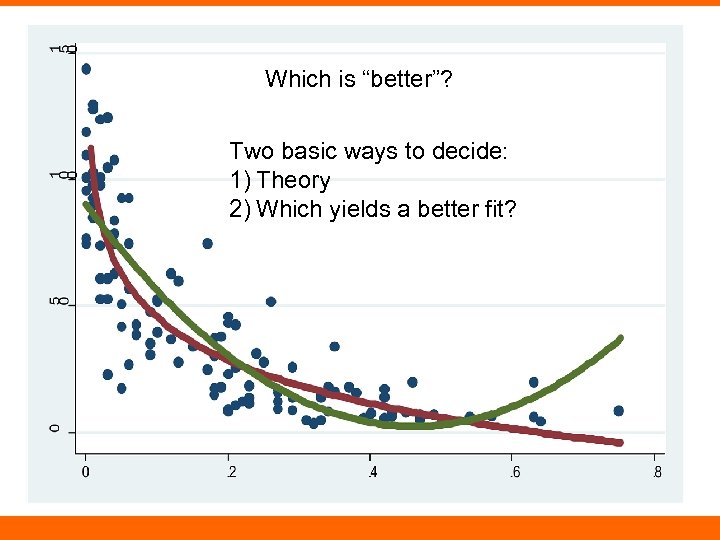Which is “better”? Two basic ways to decide: 1) Theory 2) Which yields a better fit?

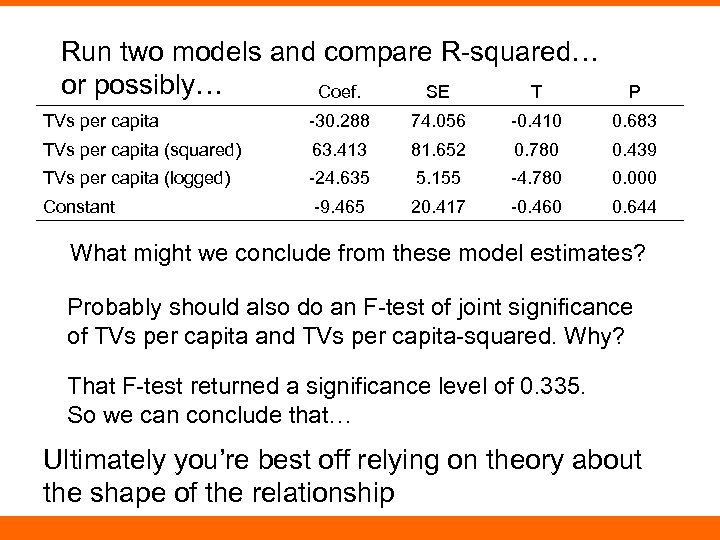Run two models and compare R-squared… or possibly… Coef. SE T P TVs per capita -30. 288 74. 056 -0. 410 0. 683 TVs per capita (squared) 63. 413 81. 652 0. 780 0. 439 TVs per capita (logged) -24. 635 5. 155 -4. 780 0. 000 Constant -9. 465 20. 417 -0. 460 0. 644 What might we conclude from these model estimates? Probably should also do an F-test of joint significance of TVs per capita and TVs per capita-squared. Why? That F-test returned a significance level of 0. 335. So we can conclude that… Ultimately you’re best off relying on theory about the shape of the relationship

Ordered IVs Indicators • Sometimes we have reason to expect the relationship between an IV and outcome to be more complex • Can address this using more polynomials (e. g. , variable 3, variable 4, etc) – We won’t go there… instead… • Example: Party identification and evaluations of candidates and issues

Standard “branching” PID Items • Generally speaking, do you usually think of yourself as a Republican, a Democrat, an Independent, or something else? – If Republican or Democrat ask: Would you call yourself a strong (Republican/Democrat) or a not very strong (Republican/Democrat)? – If Independent or something else ask: Do you think of yourself as closer to the Republican or Democratic party?

Party Identification Measure People who say Democrat or Republican in response to first question Strong Republican Weak Republican Lean Republican -3 -2 -1 Independent Lean Democrat Weak Democrat Strong Democrat 0 1 2 3 Question: Is the change from -2 to -1 (or 1 to 2) the same as the change from 0 to 1 or 2 to 3?

Create Indicators Party Identification (-3 to 3) Seven Variables: Strong Republican (1=yes) Weak Republican (1=yes) Lean Republican (1=yes) Pure Independent (1=yes) Lean Democrat (1=yes) Weak Democrat (1=yes) Strong Democrat (1=yes)

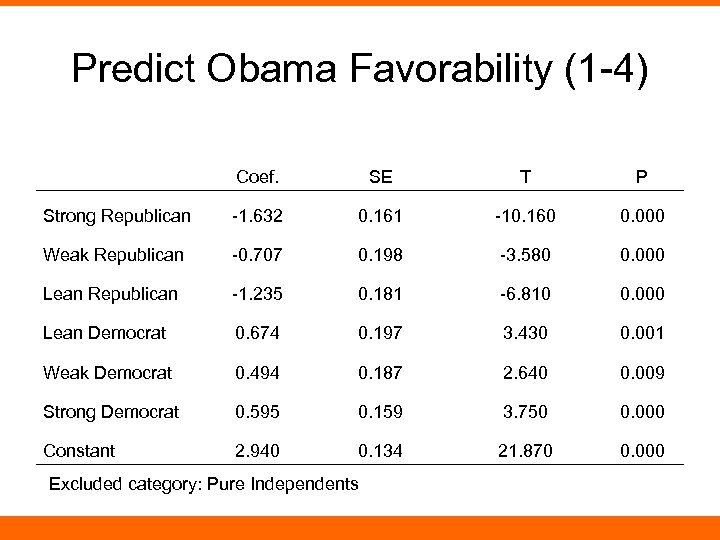Predict Obama Favorability (1 -4) Coef. SE T P Strong Republican -1. 632 0. 161 -10. 160 0. 000 Weak Republican -0. 707 0. 198 -3. 580 0. 000 Lean Republican -1. 235 0. 181 -6. 810 0. 000 Lean Democrat 0. 674 0. 197 3. 430 0. 001 Weak Democrat 0. 494 0. 187 2. 640 0. 009 Strong Democrat 0. 595 0. 159 3. 750 0. 000 Constant 2. 940 0. 134 21. 870 0. 000 Excluded category: Pure Independents

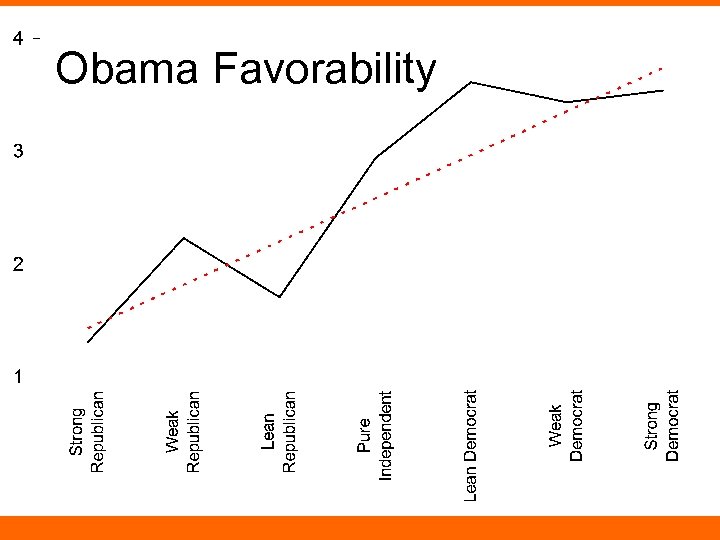Obama Favorability

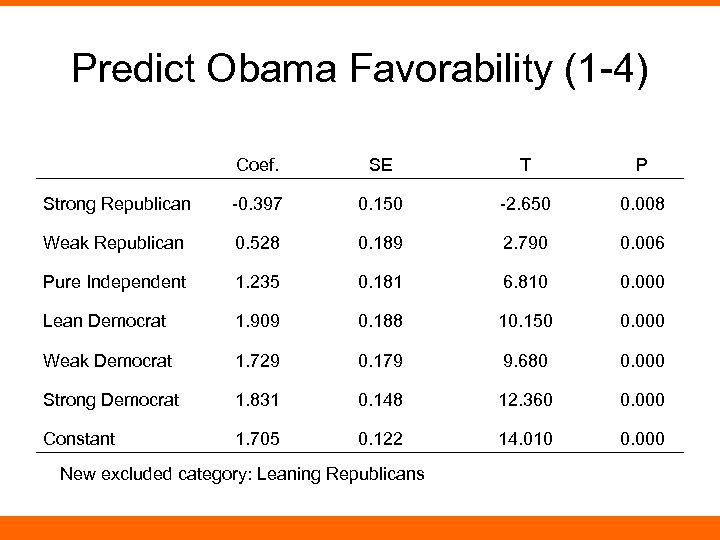Predict Obama Favorability (1 -4) Coef. SE T P Strong Republican -0. 397 0. 150 -2. 650 0. 008 Weak Republican 0. 528 0. 189 2. 790 0. 006 Pure Independent 1. 235 0. 181 6. 810 0. 000 Lean Democrat 1. 909 0. 188 10. 150 0. 000 Weak Democrat 1. 729 0. 179 9. 680 0. 000 Strong Democrat 1. 831 0. 148 12. 360 0. 000 Constant 1. 705 0. 122 14. 010 0. 000 New excluded category: Leaning Republicans

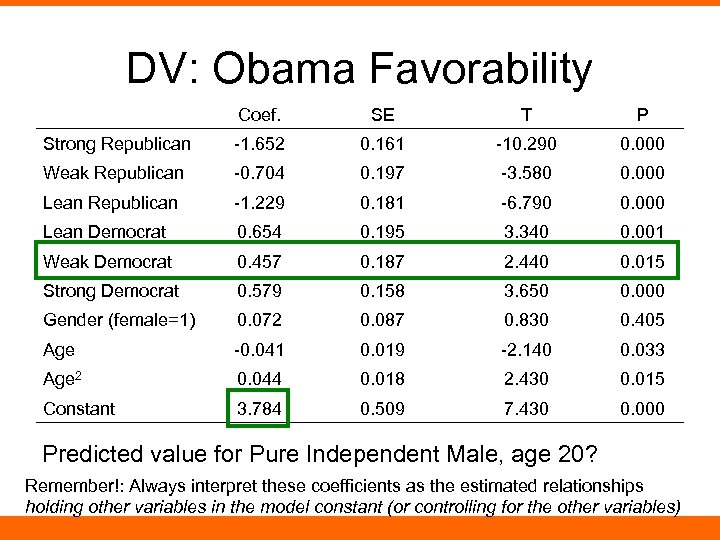DV: Obama Favorability Coef. SE T P Strong Republican -1. 652 0. 161 -10. 290 0. 000 Weak Republican -0. 704 0. 197 -3. 580 0. 000 Lean Republican -1. 229 0. 181 -6. 790 0. 000 Lean Democrat 0. 654 0. 195 3. 340 0. 001 Weak Democrat 0. 457 0. 187 2. 440 0. 015 Strong Democrat 0. 579 0. 158 3. 650 0. 000 Gender (female=1) 0. 072 0. 087 0. 830 0. 405 Age -0. 041 0. 019 -2. 140 0. 033 Age 2 0. 044 0. 018 2. 430 0. 015 Constant 3. 784 0. 509 7. 430 0. 000 Predicted value for Pure Independent Male, age 20? Remember!: Always interpret these coefficients as the estimated relationships holding other variables in the model constant (or controlling for the other variables)

Notes and Next Time • Homework due next Thursday (11/18) • Next homework handed out next Tuesday – Not due until Tuesday after Fall Break • Next time: – Dealing with situations where you expect the relationship between an IV and a DV to depend on the value of another IV