Introduction to SPSS Data types and SPSS data

Introduction to SPSS Data types and SPSS data entry and analysis 1

In this session l l l l What does SPSS look like? Types of data (revision) Data Entry in SPSS Simple charts in SPSS Summary statistics Contingency tables and crosstabulations Scatterplots and correlations Tests of differences of means 2

SPSS/PASW 3

Aspects of SPSS l l Menus - Analyse and Charts esp. Spreadsheet view of data l l l Rows are cases (people, respondents etc. ) Columns are Variables Variable view of data l Shows detail of each variable type 4

Questionnaire Data Coding 5

In SPSS l l l We change ticks etc. on a questionnaire into numbers One number for each variable for each case How we do this depends on the type of variable/data 6

Types of data l l l Nominal Ranked Scales/measures Mixed types Text answers (open ended questions) 7

Nominal (categorical) l l l order is arbitrary e. g. sex, country of birth, personality type, yes or no. Use numeric in SPSS and give value labels. (e. g. 1=Female, 2=Male, 99=Missing) (e. g. 1=Yes, 2=No, 99=Missing) (e. g. 1=UK, 2=Ireland, 3=Pakistan, 4=India, 5=other, 99=Missing) 8

Ranks or Ordinal l in order, 1 st, 2 nd, 3 rd etc. e. g. status, social class Use numeric in SPSS with value labels l l E. g. 1=Working class, 2=Middle class, 3=Upper class E. g. Class of degree, 1=First, 2=Upper second, 3=Lower second, 4=Third, 5=Ordinary, 99=Missing 9

Measures, scales Interval - equal units 1. l e. g. IQ Ratio - equal units, zero on scale 2. l l e. g. height, income, family size, age Makes sense to say one value is twice another Use numeric (or comma, dot or scientific) in SPSS l l l E. g. family size, 1, 2, 3, 4 etc. E. g. income per year, 25000, 14500, 18650 etc. 10

Mixed type l l Categorised data Actually ranked, but used to identify categories or groups l l l e. g. age groups = ratio data put into groups Use numeric in SPSS and use value labels. l E. g. Age group, 1=‘Under 18’, 2=‘ 18 -24’, 3=‘ 2534’, 4=‘ 35 -44’, 5=‘ 45 -54’, 6=‘ 55 or greater’ 11

Text answers l l E. g. answers to open-ended questions Either enter text as given (Use String in SPSS) Or Code or classify answers into one of a small number types. (Use numeric/nominal in SPSS) 12

Data Entry in SPSS l Video by Andy Field 13

Frequency counts l l Used with categorical and ranked variables e. g. gender of students taking Health and Illness option 14

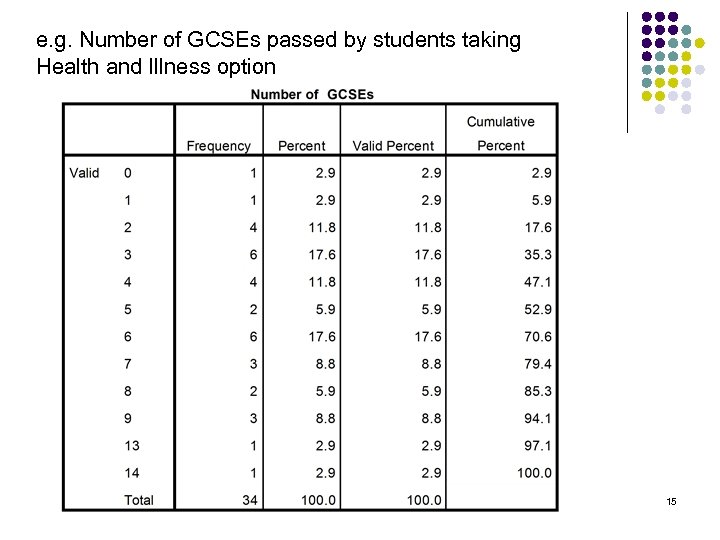e. g. Number of GCSEs passed by students taking Health and Illness option 15

Central Tendency l Mean l l l Mode l l l = average value sum of all the values divided by the number of values = the most frequent value in a distribution (N. B. it is possible to have 2 or more modes, e. g. bimodal distribution) Median l l l = the half-way value, or the value that divides the ordered distribution in the middle The middle score when scores are ordered N. B. need to put values into order first 16

Dispersion and variability l Quartiles l l l The three values that split the sorted data into four equal parts. Second Quartile = median. Lower quartile = median of lower half of the data Upper quartile = median of upper half of the data Need to order the individuals first One quarter of the individuals are in each interquartile range 17

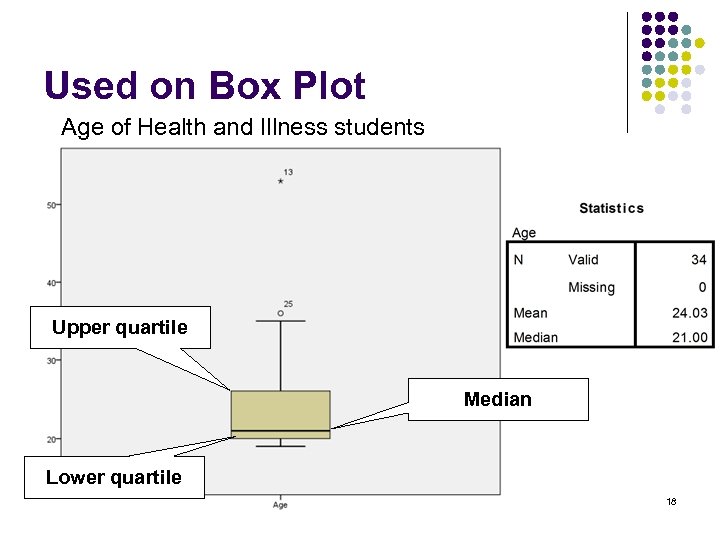Used on Box Plot Age of Health and Illness students Upper quartile Median Lower quartile 18

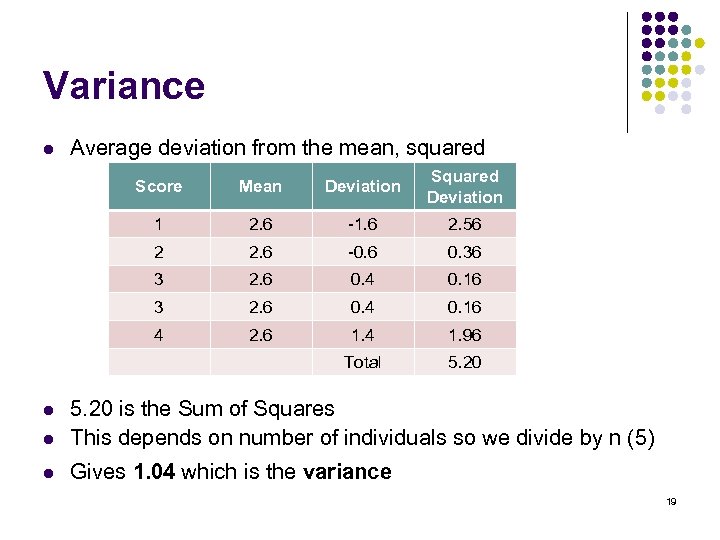Variance l Average deviation from the mean, squared Score Mean Deviation Squared Deviation 1 2. 6 -1. 6 2. 56 2 2. 6 -0. 6 0. 36 3 2. 6 0. 4 0. 16 4 2. 6 1. 4 1. 96 Total 5. 20 is the Sum of Squares This depends on number of individuals so we divide by n (5) l Gives 1. 04 which is the variance l 19

Standard Deviation l The variance has one problem: it is measured in units squared. l This isn’t a very meaningful metric so we take the square root value. l This is the Standard Deviation 20

Using SPSS l l l ‘Analyse>Descriptive>Explore’ menu. Gives mean, median, SD, variance, min, max, range, skew and kurtosis. Can also produce stem and leaf, and histogram. 21

Charts in SPSS l l l Use ‘Chart Builder’ from ‘Graph’ menu or the Legacy menu And/or double click chart to edit it. E. g. double click to edit bars (e. g. to change from colour to fill pattern). Do this in SPSS first before cut and paste to Word Label the chart (in SPSS or in Word) 22

Stem and leaf plots l l e. g. age of students taking Health and Illness option good at showing l l l distribution of data outliers range 23

Stem and leaf plots e. g. 24

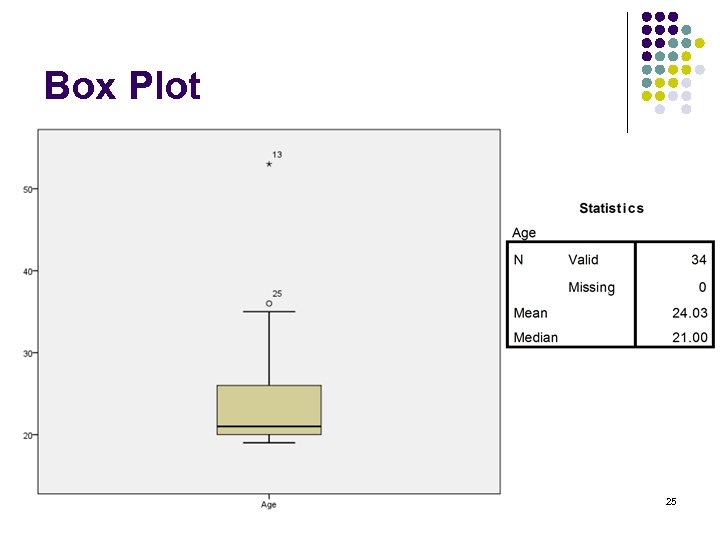Box Plot 25

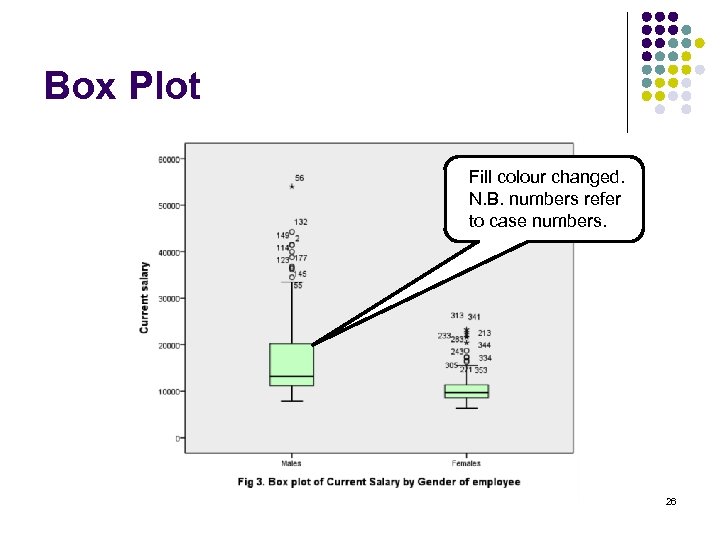Box Plot Fill colour changed. N. B. numbers refer to case numbers. 26

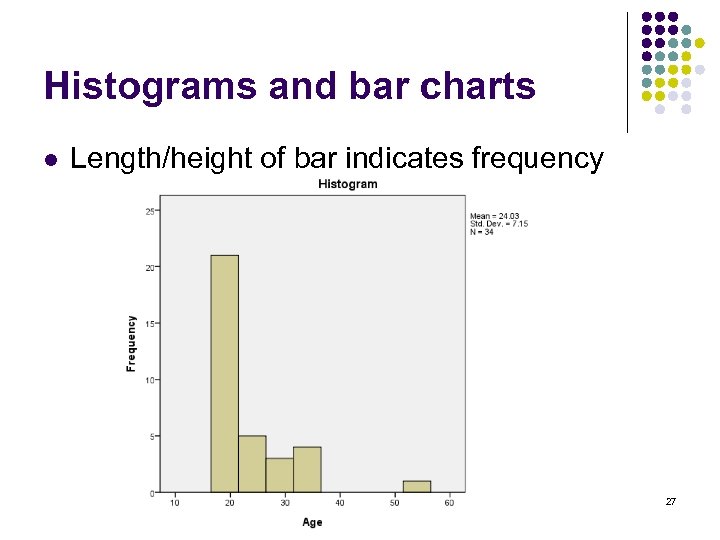Histograms and bar charts l Length/height of bar indicates frequency 27

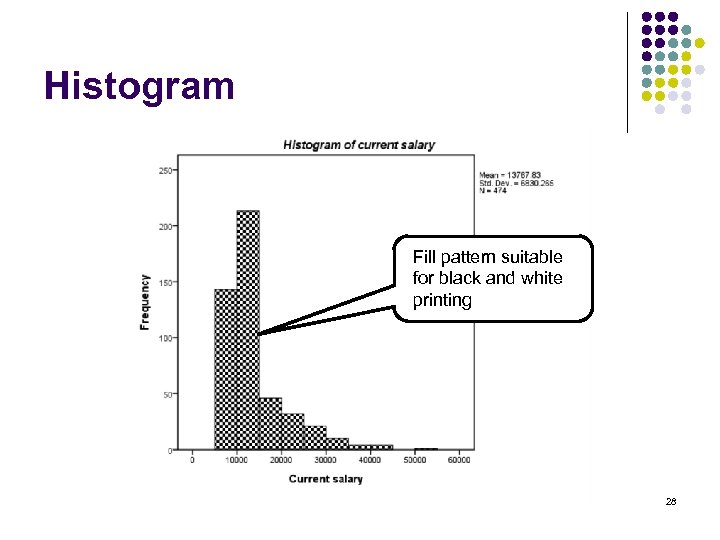Histogram Fill pattern suitable for black and white printing 28

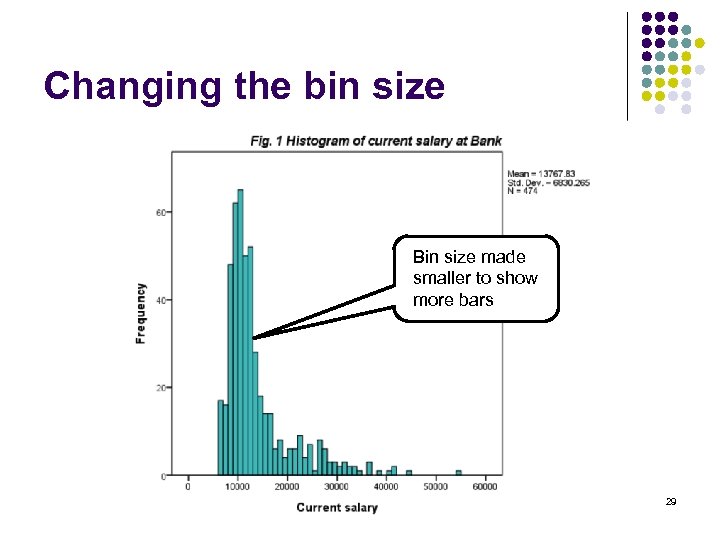Changing the bin size Bin size made smaller to show more bars 29

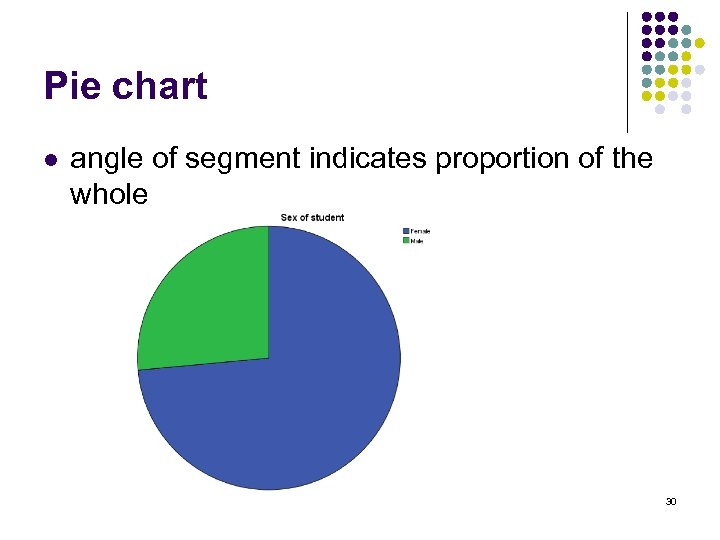Pie chart l angle of segment indicates proportion of the whole 30

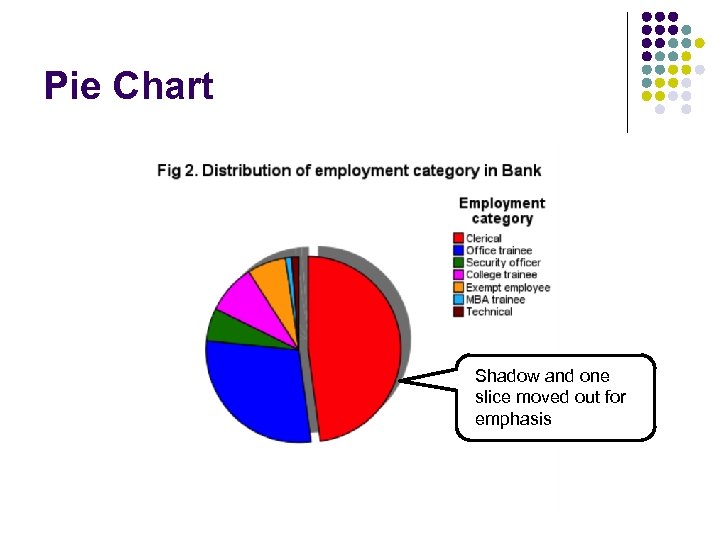Pie Chart Shadow and one slice moved out for emphasis

Analysing relationships l Contingency tables or crosstabulations l Compares nominal/categorical variables l l l But can include ordinal variables N. B. table contains counts (= frequency data) One variable on horizontal axis One variable on vertical axis Row and column total counts known as marginals

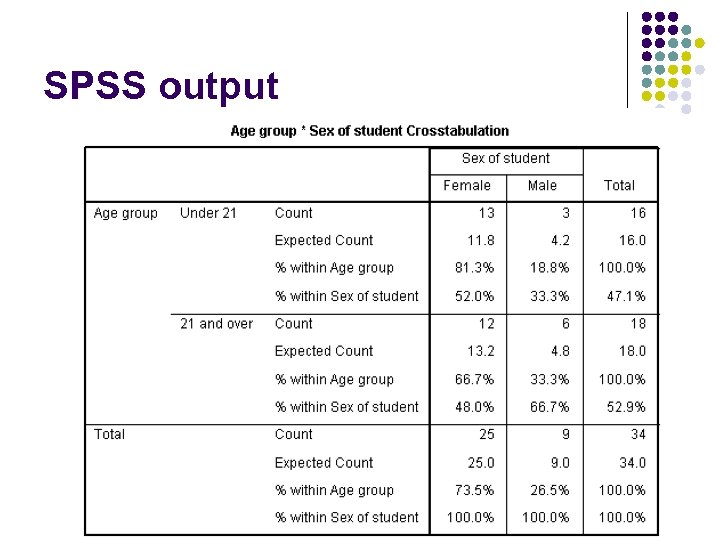
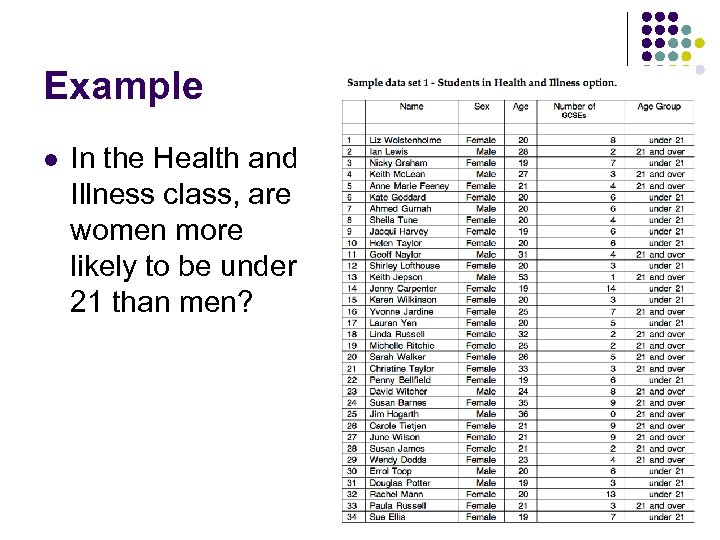Example l In the Health and Illness class, are women more likely to be under 21 than men?

Crosstabulations l e. g. l Use column and row percentages to look for relationships

SPSS output

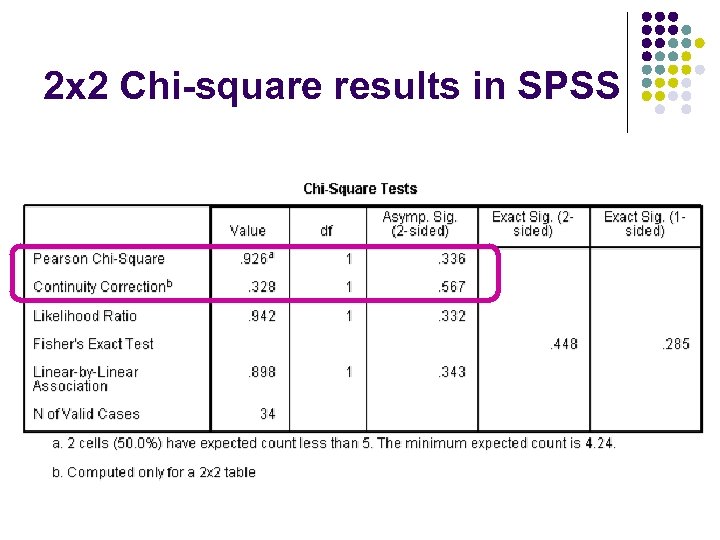
Chi-square ² Cross tabulations and Chi-square tests that can be used to look for a relationship between two variables: l When the variables are categorical so the data are nominal (or frequency). l For example, if we wanted to look at the relationship between gender and age. l There are several different types of Chi-square ( ²), we will be using the 2 x 2 Chi-square

2 x 2 Chi-square results in SPSS

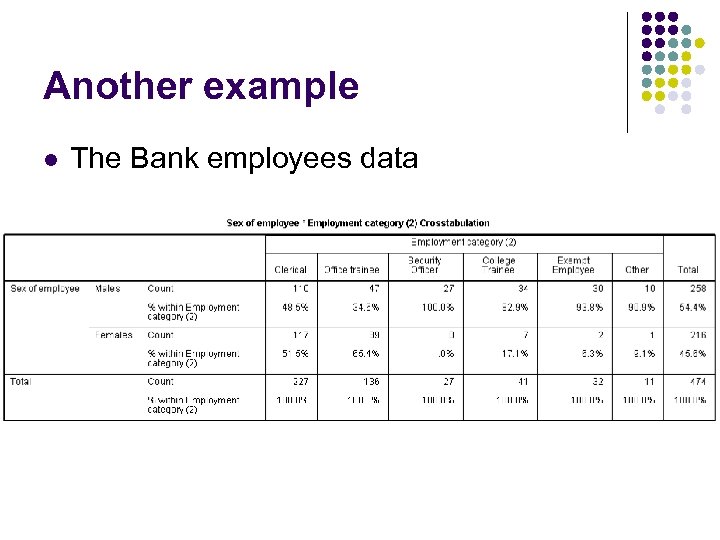Another example l The Bank employees data

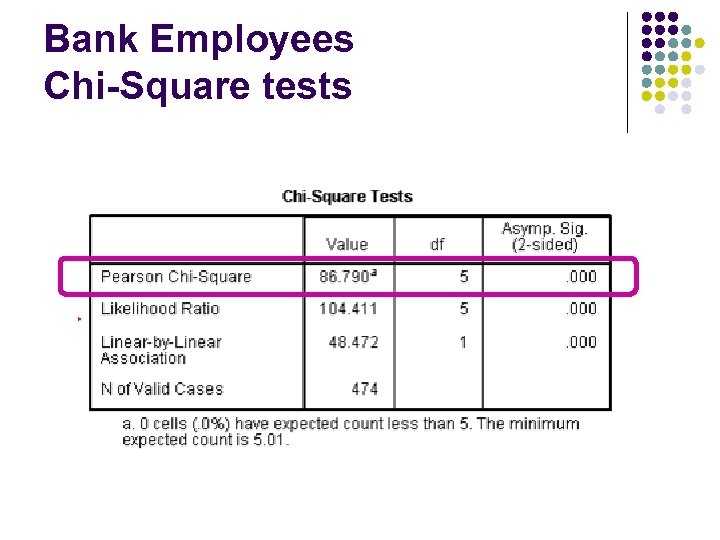Bank Employees Chi-Square tests

Chi-Square analysis on SPSS l l http: //www. youtube. com/watch? v=Ahs 8 j. S 5 m JKk 4 m 15 s http: //www. youtube. com/watch? v=IRCz. OD 27 NQU l l From 6 m: 30 s to 9 m: 50 s http: //www. youtube. com/watch? v=532 QXt 1 P MQ&feature=plcp&context=C 3 ba 91 a 4 UDOEgs To. PDsk. J-ABupdp-Yfvuf 4 j 4 f. JGz. V 12 m 30 s

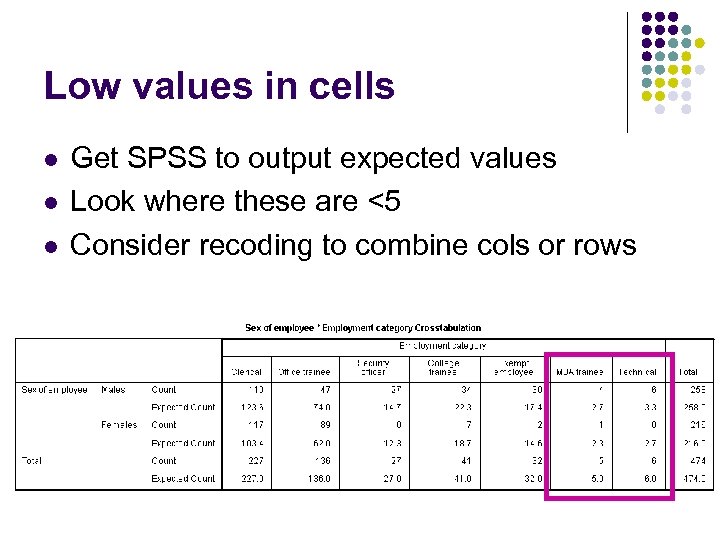Low values in cells l l l Get SPSS to output expected values Look where these are <5 Consider recoding to combine cols or rows

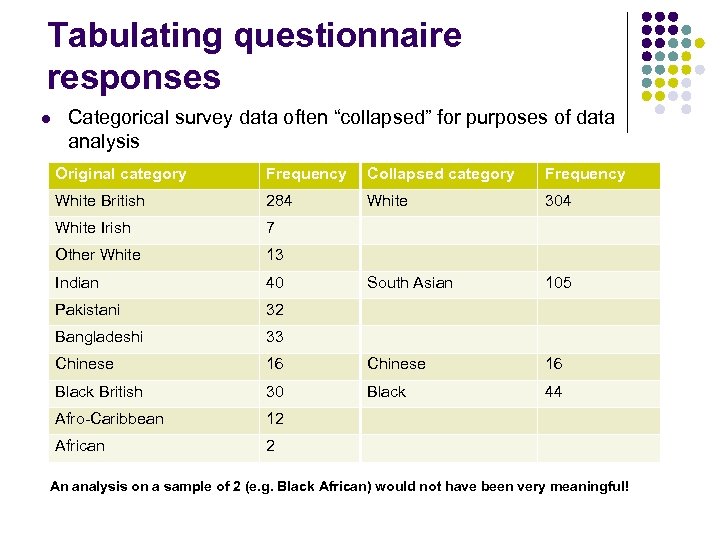Tabulating questionnaire responses l Categorical survey data often “collapsed” for purposes of data analysis Original category Frequency Collapsed category Frequency White British 284 White 304 White Irish 7 Other White 13 Indian 40 South Asian 105 Pakistani 32 Bangladeshi 33 Chinese 16 Black British 30 Black 44 Afro-Caribbean 12 African 2 An analysis on a sample of 2 (e. g. Black African) would not have been very meaningful!

Recoding variables l http: //www. youtube. com/watch? v=uz. Q_522 F 2 SM&feature=related l l Ignore t-test for now 6 m 11 s http: //www. youtube. com/watch? v=FUo. YZ_f 6 Lxc l Uses old version of SPSS, no submenu now. 6 m

Scatterplots and correlations l Looks for association between variables, e. g. l l l Population size and GDP crime and unemployment rates height and weight Both variables must be rank, interval or ratio (scale or ordinal in SPSS). Thus cannot use variables like, gender, ethnicity, town of birth, occupation. 44

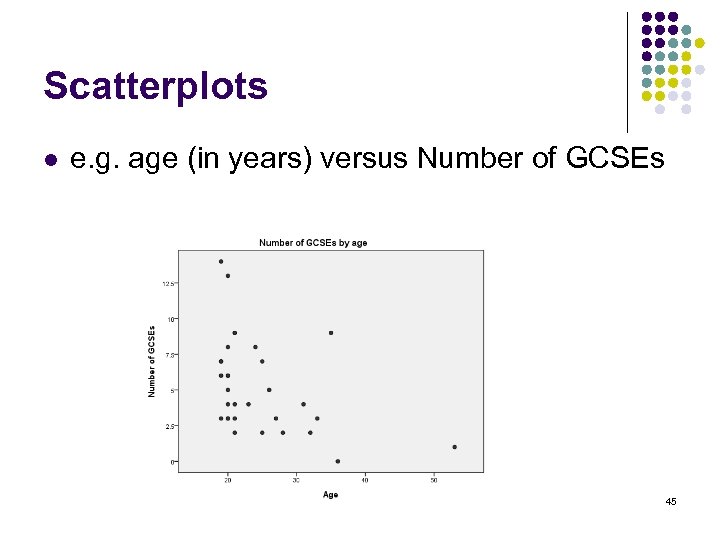Scatterplots l e. g. age (in years) versus Number of GCSEs 45

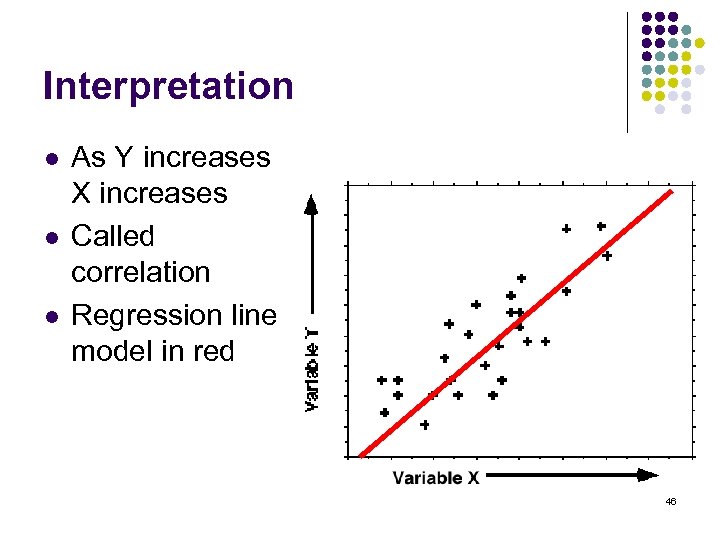Interpretation l l l As Y increases X increases Called correlation Regression line model in red 46

Correlation measures association not causation l l l Height correlates with weight l l l The older the child the better s/he is at reading The less your income the greater the risk of schizophrenia But weight does not cause height Height is one of the causes of weight (also body shape, diet, fitness level etc. ) Numbers of ice creams sold is correlated with the rate of drowning l l Ice creams do not cause drowning (nor vice versa) Third variable involved – people swim more and buy more ice creams when it’s warm 47

Scatterplot in SPSS l l Use Graph menu http: //www. youtube. com/watch? v=74 Bjg. PQv. I Eg 8 m 34 s http: //www. youtube. com/watch? v=blffl. A 34 p. Q&feature=related 4 m 04 s http: //www. youtube. com/watch? v=UVyl. Qo. G 4 h. ZM 1 m 50 s, ignore polynomial regression 48

Modifying the Scatterplot l l http: //www. youtube. com/watch? v=803 YCYA 2 Ao. Q&feature=related 4 m 04 s http: //www. youtube. com/watch? v=v. Pzvu. Mu. V Xk 8&feature=related 3 m 40 s 49

If mixed data sets l l Change point icon and/or colour to see different subsets. Overall data may have no relationship but subsets might. E. g. show male and female respondents. Use Chart builder 50

Correlation l l Correlation coefficient = measure of strength of relationship, e. g. Pearson’s r varies from 0 to 1 with a plus or minus sign 51

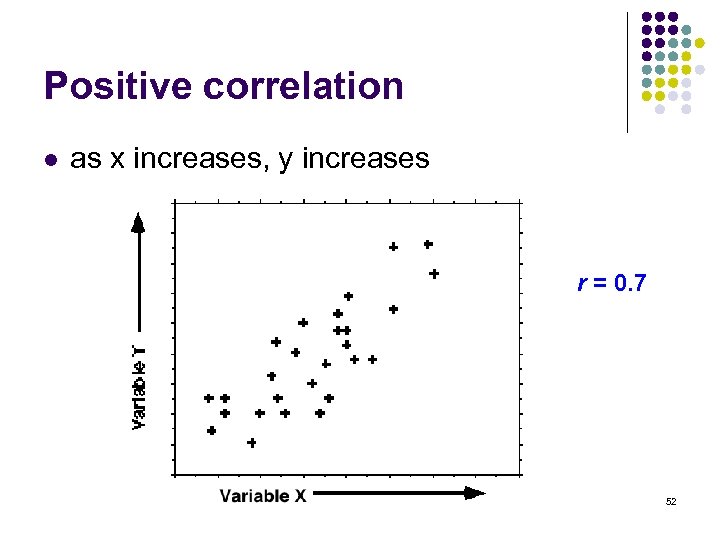Positive correlation l as x increases, y increases r = 0. 7 52

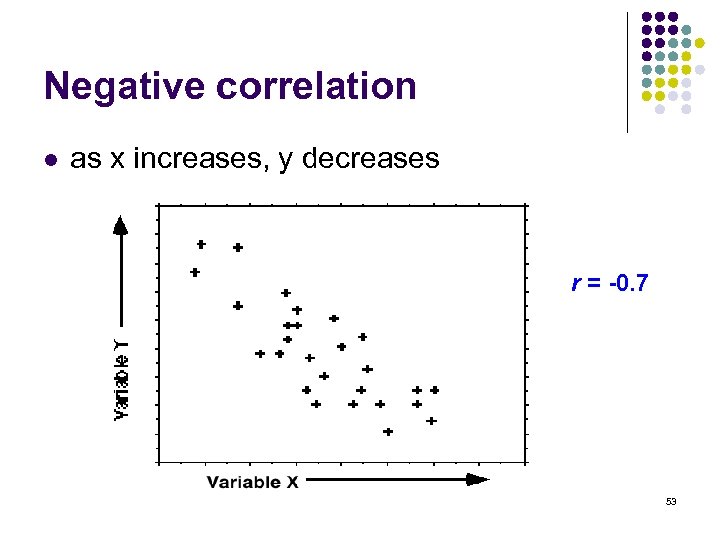Negative correlation l as x increases, y decreases r = -0. 7 53

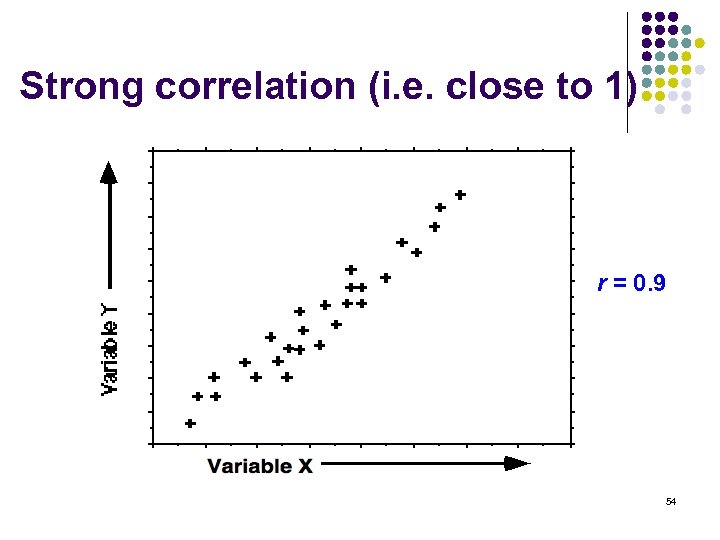Strong correlation (i. e. close to 1) r = 0. 9 54

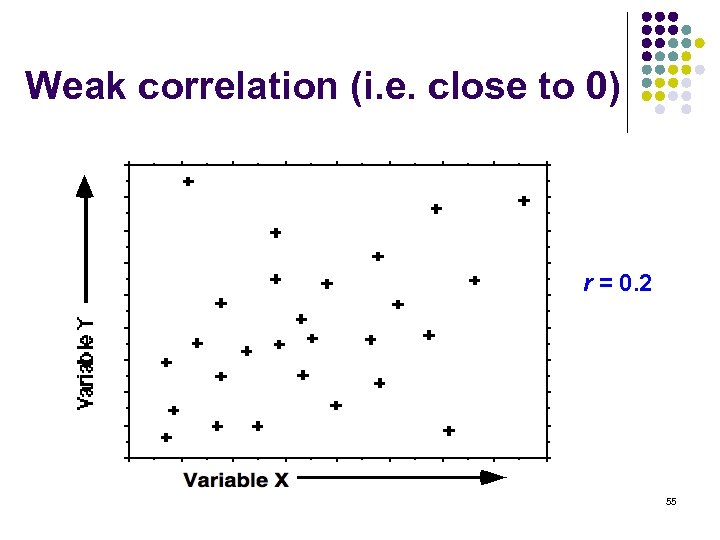Weak correlation (i. e. close to 0) r = 0. 2 55

Interpretation cont. l r 2 l l is a measure of degree of variation in one variable accounted for by variation in the other. E. g. If r=0. 7 then r 2=. 49 i. e. just under half the variation is accounted for (rest accounted for by other factors). If r=0. 3 then r 2=0. 09 so 91% of the variation is explained by other things. 56

Significance of r l l SPSS reports if r is significant at α=0. 05 N. B. this is dependent on sample size to a large extent. Other things being equal, larger samples more likely to be significant. Usually, size of r is more important than its significance 57

Pearson’s r in SPSS l http: //www. youtube. com/watch? v=lo. FLq. Zmvf z. U 6 m 57 s 58

Parametric and non-parametric l l Some statistics rely on the variables being investigated following a normal distribution. – Called Parametric statistics Others can be used if variables are not distributed normally – called Non-parametric statistics. Pearson’s r is a parametric statistic Kendal’s tau and Spearman’s rho (rank correlation) are non-parametric. 59

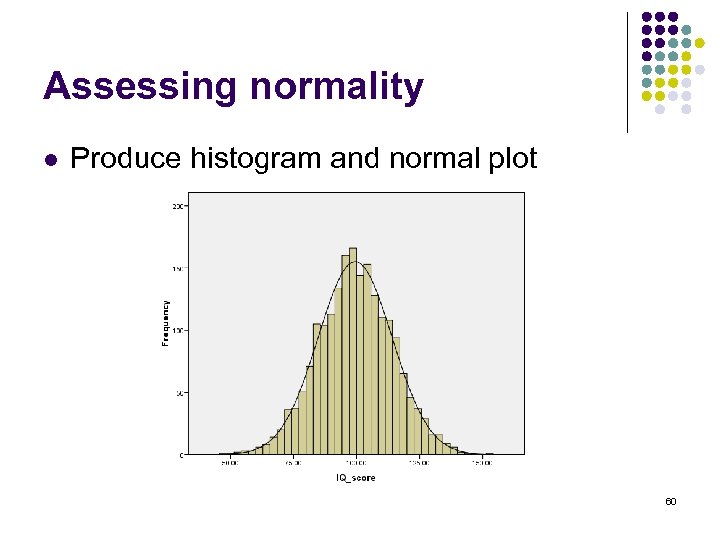Assessing normality l Produce histogram and normal plot 60

Use statistical test l SPSS provides two formal tests for normality : Kolmogorov-Smirnov (K-S) and Shapiro. Wilks (S-W) l l But, there is debate about KS Extremely sensitive to departure from normality May erroneously imply parametric test not suitable – especially in small sample So, always use a histogram as well. 61

Often can use parametric tests l l l Parametric tests (e. g. Pearson’s r) are robust to departures from normality Small, non-normal samples OK But use non-parametric if l l Data are skewed (questionnaire data often is) Data are bimodal 62

Spearmans’s rho l l http: //www. youtube. com/watch? v=r_WQe 2 c. ISU From 4. 14 to 4. 56 http: //www. youtube. com/watch? v=POk. Fi 5 v. Kv I 8&feature=fvwrel 6 m 16 s 63

So far… l Looked at relationships between nominal variables l l Looked at relationships between scale variables l l l Gender vs age group Height vs. Weight Now combine the two Groups vs a scale variable l E. g. Gender vs income 64

Reminder – IV vs DV l l l IV = independent variable What makes a difference, causes effects, is responsible for differences. DV = dependent variable What is affected by things, what is changed by the IV. Gender vs income. Gender = IV, income = DV So we investigate the effect of gender on income 65

Example 1 Age group vs. no. of GCSEs l l Using the Health and Illness class data Age group defines 2 groups l l l Under 21 21 and over Just two groups Can use independent samples t-test Independent because the two groups consist of different people. t-test compares the means of the 2 groups. 66

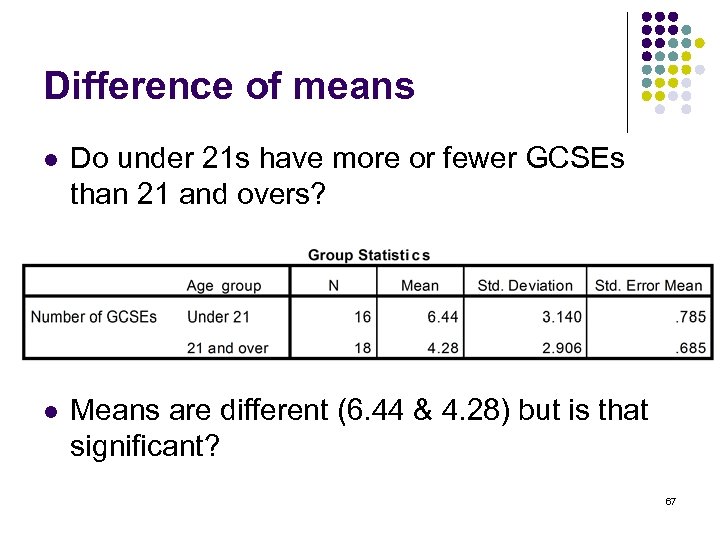Difference of means l Do under 21 s have more or fewer GCSEs than 21 and overs? l Means are different (6. 44 & 4. 28) but is that significant? 67

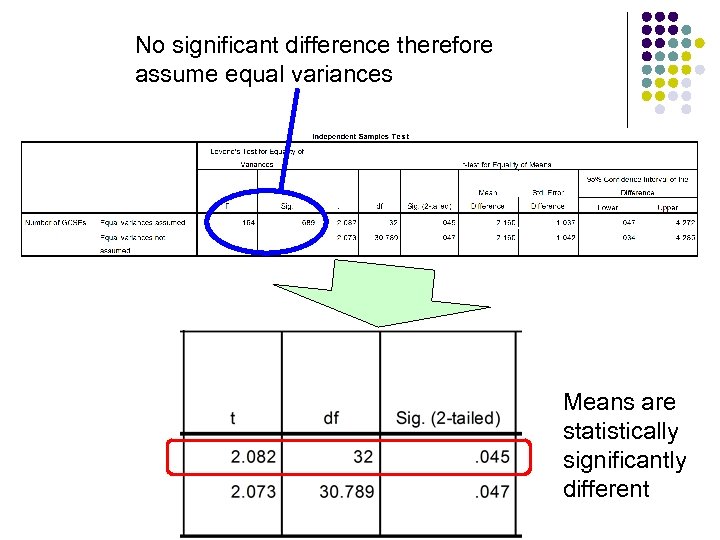No significant difference therefore assume equal variances Means are statistically significantly different 68

Parametric vs non-parametric l l Just as in the case of correlations, there are both kinds of tests. Need to check if DV is normally distributed. Do this visually Also use statistical tests 69

Tests for normality l l l Kolmogorov-Smirnov and Shapiro-Wilk If n>50 use KS If n≤ 50 use SW Null hypothesis is ‘data are normally distributed’. So if p<0. 05 then data are significantly different from a normal distribution – use non-parametric tests If p≥ 0. 05 then no significant difference – use parametric tests 70

Checking normality l l l Produce histogram of DV Tick box to undertake statistical test Interpret results. 71

t-test l l Identify your two groups. Determine what values in the data indicate those two groups (e. g. 1=female, 2=male) Select Analyze: Compare Means: Independent samples t-test http: //www. youtube. com/watch? v=_KHI 3 Sc. O 8 sc 9 m 40 s 72

Mann-Whitney U test l l Use this when comparing two groups and the DV is not normally distributed http: //www. youtube. com/watch? v=7 i. Tvv 3 m 9 d _g 3 m 45 s 73

Comparing 3 or more groups ANOVA = Analysis of Variance l Analyze: Compare Means: One-way ANOVA l http: //www. youtube. com/watch? v=w. Fq 1 b 3 Qj. I 1 U 4 m 04 s Useful to get table of means (descriptives) and means plots from ANOVA options. l 74

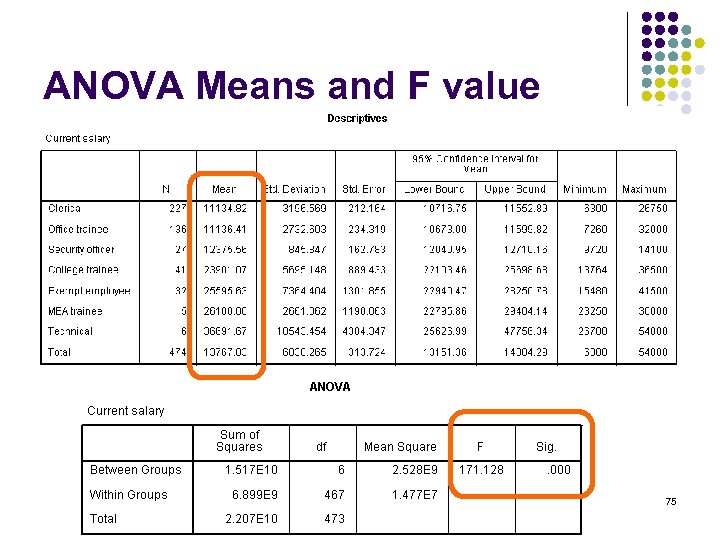ANOVA Means and F value 75

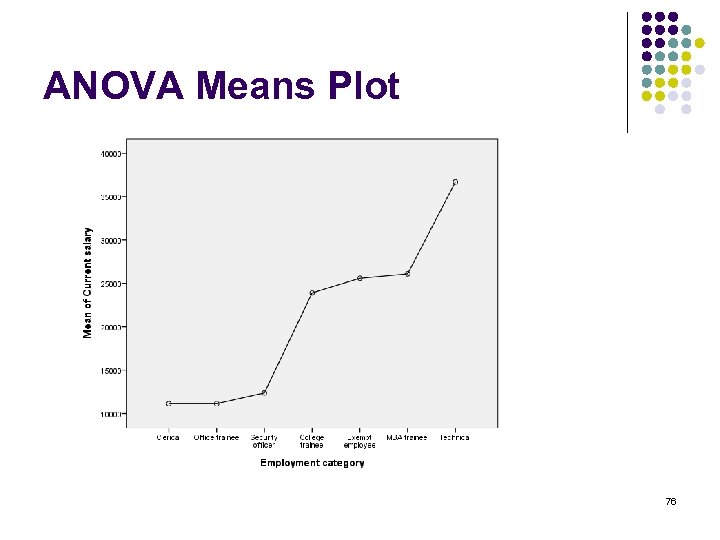ANOVA Means Plot 76