7b3168c6abdb1444f32ba1bde2023263.ppt
- Количество слайдов: 93

Introduction to Practical Cryptography Lecture 2 Public Key Cryptography

Overview • Some math • Public key ciphers – RSA – Diffie-Hellman – El. Gamal – Feige-Fiat-Shamir – Elliptic curve cryptography (general idea) • Certificate Authorities

Some Math • • (only 21 slides) Modular arithmetic Fermat’s little theorem Euler’s Totient Function Groups Euclid – greatest common divisor Extended Euclidean – computing inverses Chinese Remainder Theorem

Modular Arithmetic • x mod n = remainder x/n 12 mod 9 = 3 • Reduce intermediate results mod n (a+b) mod n = a mod n + b mod n (ab) mod n = (a mod n) (b mod n) mod n (a(b+c))mod n = (ab mod n + ac mod n) mod n

Fermat’s Little Theorem • Any prime p and any a 1 a < p: ap-1 mod p = 1 Also note that: • For any x such that ax mod p = 1 x is a multiple of p-1; therefore, x = 0 mod p-1

Euler’s Totient Function • (n) = # of integers < n that are relatively prime to n • If p is prime, (p) = p-1 • If n = pq, p and q are prime then (n) = (p − 1)(q − 1) • If gcd(a, n) = 1 then a (n) mod n = 1

Inverse Example • a-1 mod n • x = a (n) -1 mod n • 5 -1 mod 7 (7) = 6 56 -1 mod 7 = 55 mod 7 = (((52) mod 7)((52)mod 7)5 mod 7) mod 7 = (4)(4)(5) mod 7 = 3 5*3 mod 7 = 15 mod 7= 1

Group Definition • A group (G, * ) is a set G together with a operator * satisfying: • Associative: a, b and c in G, (a * b) * c = a * (b * c). • Identity element e in G: For all a in G, e * a = a * e = a. • Invertible: a in G, there is a b in G such that a * b = b * a = e. • Closure: a and b in G, a * b belongs to G.

Multiplicative Group • p prime • Z*p = 1, 2, 3 …. p-1, p • Let g Z*p – order of g: smallest x for which gx = 1 mod p – 1, g, g 2, g 3, … gx-1 • There is at least one g Z*p that generates the entire group – a Z*p , a = gi for some i {0, 1, 2 … p-2} – 1, g, g 2, g 3, … gp-2
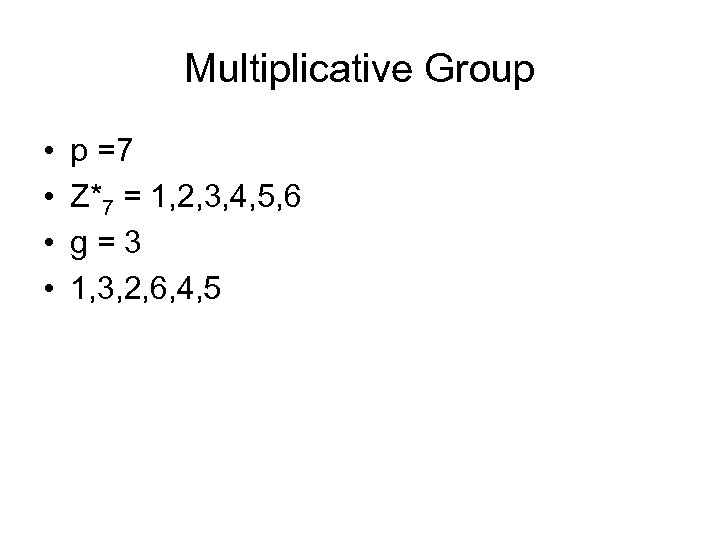
Multiplicative Group • • p =7 Z*7 = 1, 2, 3, 4, 5, 6 g = 3 1, 3, 2, 6, 4, 5

Multiplicative Group • Order of any element g is a divisor of p-1 • Let g be generator of Z*p • Let h Z*p and h ≠ g • h = gx for some x • h 0, h 1, h 2, … = 1, gx, g 2 x, g 3 x … • Let q = order of h: hq = 1 = gqx qx = 0 mod (p-1) (by Fermat) q = (p-1)/gcd(x, p-1)

Multiplicative Group • Consider again Z*7 = 1, 2, 3, 4, 5, 6 • h = 2: – subgroup: 1, h, h 2 = 1, 2, 4 – order 3 (h 3 = 8 mod 7 = 1) • h = 6 – subgroup: 1, h = 1, 6 – Order 2 (h 2 = 36 mod 7 = 1) • 2 and 3 are divisors of p-1 (7 -1 = 6)
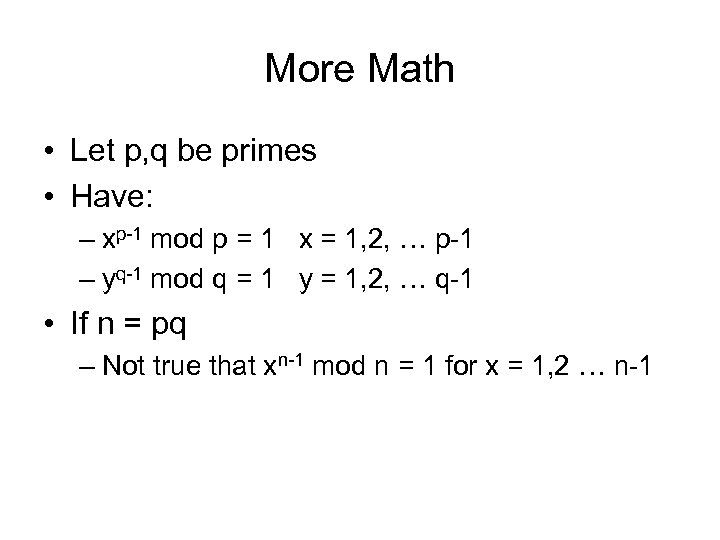
More Math • Let p, q be primes • Have: – xp-1 mod p = 1 x = 1, 2, … p-1 – yq-1 mod q = 1 y = 1, 2, … q-1 • If n = pq – Not true that xn-1 mod n = 1 for x = 1, 2 … n-1

More Math • Want t such that xt mod n = 1 for most x • Requires xt mod p = 1 and xt mod q = 1 • From earlier, know this means p-1 divides t and q-1 divides t • Smallest t with property is lcm(p-1, q-1) = (p-1)(q-1)/gcd(p-1, q-1)

GCD - Euclid’s Algorithm gcd of x and y, x, y 0 g = y while (x > 0) { g = x x = y % x y = g } g is gcd

Inverses: Extended Euclidean • Want to find x such that ax mod n = 1 • a-1 = x mod n has unique solution only if a and n are relatively prime; otherwise, no solution • Extended Euclid’s algorithm is one way to find inverse

Extended Euclidean Find inverse (x) of a mod n n 0 = n a 0 = a x 0 = 0 x = 1 q = n 0/a 0 r = n 0 – qa 0 while (r > 0) { tmp = x 0 -qx if (tmp 0) { tmp = tmp mod n} if (tmp < 0) { tmp = n – ((-tmp)mod n)} } x 0 = x x = tmp n 0 = a 0 = r q = n 0/a 0 r = n 0 -qa 0 if (a 0 ≠ 1) then no inverse else a-1 = x mod n

Chinese Remainder Theorem • Why? • Way of representing keys in RSA – will see later • Composite number n = pq • p, q are primes, p ≠ q • (a, b) = (x mod p, x mod q)

Chinese Remainder Theorem • First, check there is no x’ such that x’ mod p = a and x’ mod q = b • Because x, x’ result in same (a, b) • Won’t know unique answer • x’ ≠ x does not exist • Proof: d = x – x’ d mod p = (x –x’) mod p = x mod p – x’ mod p = a – a = 0 d is a multiple of p Likewise, d is a multiple of q

Chinese Remainder Theorem • Proof continued d is a multiple of p and d is a multiple of q d is a multiple of lcm(p, q) p ≠ q, p and q are primes, pq = n lcm(p, q) = n d is a multiple of n x –x’ is a multiple of n x, x’ {0, 1, 2 … n-1} x – x’ {-n+1, -n +2, … n-2, n-1} x –x’ = 0 (no other multiple of n in the range) x = x’ For any (a, b); there is at most one solution for x such that a = x mod p, b = x mod q

Chinese Remainder Theorem – Finding x • Garner’s Formula Let x = q(((a –b)(q-1 mod p)) mod p) + b • won’t show this equation was obtained, only that it works: (a, b) = (x mod p, x mod q) • First show 0 x n-1 x 0 since both terms are 0 First term, call it t, is in range 0 to p-1 because of mod p; b is in range 0 to q-1 by definition t p-1 tq (p-1)q x = tq + b (p-1)q + (q-1) = pq -1 = n-1

Chinese Remainder Theorem – Finding x • Now show x mod q = b x mod q = (q(((a –b)(q-1 mod p)) mod p) + b) mod q = (zq + b) mod q for some z = zq mod q + b mod q = 0 + b mod q = b

Chinese Remainder Theorem – Finding x • Now show x mod p = a x mod p = (q(((a –b)(q-1 mod p)) mod p) + b) mod p = (((a - b) q-1)q + b) mod p = ((a - b) (q-1 q) + b) mod p = a –b + b mod p = a

Chinese Remainder Theorem - Usefulness • RSA uses n = pq • If n is k bits, p and q are ~ k/2 bits • Addition: – Addition mod n requires k bit addition and maybe k bit subtraction if addition result > n – (a, b) representation uses two k/2 bit additions and possibly subtractions, so same amount of work • Multiplication – multiplying two k bit numbers more than twice the work of multiplying two k/2 bit numbers • Exponentiation – even more savings

Trapdoor Function • easy to compute in one direction • believed to be hard to compute in the opposite direction (inverse) without secret information (the trapdoor)

Public Key Cryptography • Uses a key pair – one component is public, one component is private • Algorithms used in practice depend on the mathematical hardness of factoring or of computing discrete logs.

Uses • Signatures – Non-repudiation: signature had to generated by someone with private key • Encrypt small amounts of data, such as in key exchange protocols • Establish shared secret (Diffie-Hellman)

Distribution • Publishing public keys – Certificates – Web site – Send as needed

RSA • Generate two large distinct (at least 1024 bits) primes p and q; let n = pq • Compute (n) = (p − 1)(q − 1). • Pick two integers e and d such that ed = 1 mod (n) where 1 < e < (n) and e and (n) are coprime • The public key is <e, n>; the private key is <d, n>. • The security of the system relies on the difficulty of factoring n. • Finding such primes is easy; factoring n is believed to be hard.

RSA • • message m of length < n bits Encrypt: c = me mod n Decrypt: m = cd mod n Why? cd mod n = med mod n but ed = 1 mod (n) = m k (n)+1 mod n = (m (n))km mod n = (1 k)m mod n = m (n) is t in the “xt mod n = 1” from earlier

RSA for Signatures • Encryption with RSA is expensive. • Typically used to encrypt short data: – Key for symmetric key cipher • Signature: – Hash message, encrypt result with RSA – To verify: recipient decrypts signature, hashes original data and compares results

RSA • If encrypt m 1, m 2 – c 1 = m 1 e mod n – c 2 = m 2 e mod n • If m 3 = m 1 m 2, • c 3 = (m 1 m 2)e mod n = c 1 c 2 mod n • Solution – Padding: append to message before encrypting – Hashing: hash data to shorten before signing

RSA Parameter sizes • n of 3072 bits equivalent security of 128 -bit key in AES • n of 15360 bits equivalent to 256 -bit key in AES • NIST SP 800 -57, May 2006 Recommendation for Key Management – Part 1

Diffie-Hellman Key Exchange • Allows two entities, Alice and Bob, to establish a secret key • p is a large prime • g < p – With condition that: • The multiplicative group Zp* denotes the numbers coprime to p • Zp* is cyclic since p is prime • g is a primitive root mod p every q < p is coprime to p q < p, q = gi mod p for some i • g, p known in advance, can be public

Diffie-Hellman • • Alice picks x, secret Bob picks y, secret Alice computes Ta =gx mod p Bob compute Tb = gy mod p Alice and Bob exchange Ta, Tb Alice computes k = Tbx mod p Bob computes k = Tay mod p Shared key = k: Tbx = gyx = gxy = Tay

Diffie-Hellman • Example (values are too small for use in practice) – p = 19, g =2 – x = 3, y = 8 – Ta = 23 = 8 (mod 19) – Tb = 28 = 256 = 9 (mod 19) – k = 93 = 729 = 7 (mod 19) = 88 = 7 (mod 19) Note: 88 mod 19 = 40962 mod 19 = 112 mod 19 = 7 4096 mod 19 = 11

Diffie-Hellman Key Exchange • If intercept TA and TB , • Can’t find x or y (discrete log problem) • Thus can’t compute k
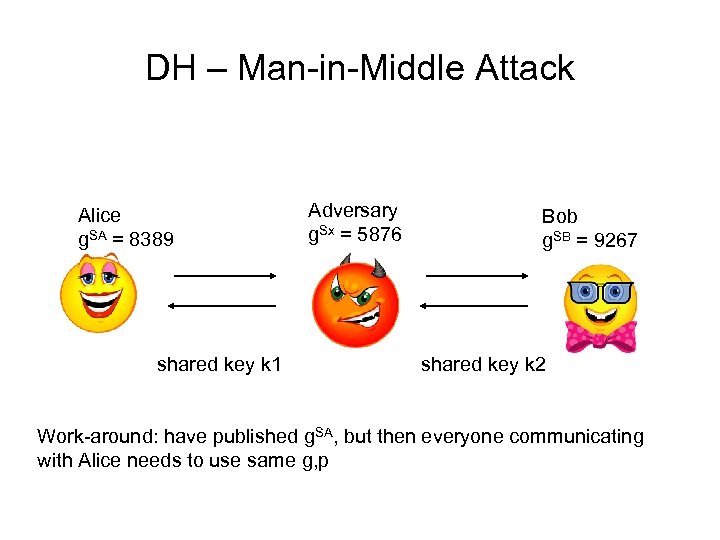
DH – Man-in-Middle Attack Alice g. SA = 8389 shared key k 1 Adversary g. Sx = 5876 Bob g. SB = 9267 shared key k 2 Work-around: have published g. SA, but then everyone communicating with Alice needs to use same g, p

Diffie-Hellman Parameter Sizes: • p of 3072 bits, x, y of 256 bits equivalent to the security of a 128 -bit key in AES • p of 15360, x, y of 512 bits equivalent to the security of a 256 -bit key in AES

El. Gamal • • • Prime p Random g, x g < p, x < p y = gx mod p Public key: (y, g, p) Private key: x

El. Gamal Signature • • • Message M Choose k < p-1 and relatively prime to p-1 k is secret and unique per message a = gk mod p Solve for b in M = [xa+kb] mod (p-1) Signature of M is (a, b) Verification: yaab mod p = g. M mod p If k reused or obtained, x can be obtained

El. Gamal Signature Example • Parameters p = 11, g = 2, x = 8 y = 28 mod 11 = 3 Public key is (y, g, p) = (3, 2, 11) M = 5 Suppose choose k = 9 • Signature of M a = 29 mod 11 = 6 5 = (8*6+9 b) mod 10 results in b = 3 Signature of M is (6, 3) • Verification 3663 mod 11 = 25 mod 11 ((36 mod 11) (63 mod 11) = 32 mod 11 3*7 mod 11 = 10

El. Gamal Encryption • Encrypt Choose random k relatively prime to p-1 y = gx mod p a = gk mod p b = yk. M mod p Ciphertext = (a, b) • Decrypt M = b/ax mod p ax = gkx mod p b/ax = yk. M/ax = gxk. M/gxk = M mod p

Feige-Fiat-Shamir Basics • n = product of two large primes • Trusted entity selects v, a quadratic residue mod n (i. e. x 2 = v mod n has a solution and v-1 mod n exists) • v is Alice’s public key. • s = sqrt(v-1) mod n (smallest such s) is Alice’s private key • Alice picks random r, r < n – Computes x = r 2 mod n • Bob sends Alice a random bit, b • If b = 0, Alice sends Bob r; else sends y = rs mod n • Bob verifies: – If b = 0, Bob verifies that x = r 2 mod n (Proves to Bob that Alice knows sqrt (x)). – If b = 1, Bob verifies x = y 2 v mod n (y 2 v = r 2 s 2 v = r 2 v-1 v = r 2 mod n = x) • Repeat number of times until Bob is sure Alice knows s (and wasn’t lucky in guessing a few times)

FFS - Identification • n as before • Trusted entity selects k v values this time instead of just one: v = (v 1, v 2, … vk) • v is Alice’s public key (a sequence of k values) • Corresponding s= (s 1, s 2, … sk) is Alice’s private key • Alice picks random r, r < n – Computes x = r 2 mod n • • • Bob sends Alice a random bit string, b = (b 1, b 2, … bk) Alice computes stmp = product of all si’s for which bi = 1 Alice sends y = r(stmp) mod n to Bob computes vtmp = product of all vi’s for which bi = 1 Bob verifies x = y 2(vtmp) mod n Repeat number of times, t, until Bob is sure Alice knows s (and wasn’t lucky in guessing a few times) • Probability Alice fools Bob is 2 -kt

FFS - Example n = 35 (= 5*7) vi, vi-1, si 1, 1, 1 4, 9, 3 9, 4, 2 11, 16, 4 16, 11, 9 29, 8 k=4 Don’t use 1 4, 9 are inverses, so can only use one of them

FFS - Example • Public key: (4, 11, 16, 29) • Private key: (3, 4, 9, 8) • One round of protocol: – Alice picks r = 16, 162 mod 35 = 11 – Alice sends 11 to Bob – Bob picks b = (1, 1, 0, 1) and sends to Alice – Alice computes (16)(3)(4)(8) mod 35 = 31 and sends to Bob – Bob computes (31)2(4)(11)(29) mod 35 = 11

FFS - Signature Scheme • • v, s as before (public key) Alice picks t random r’s between 1 and n: r 1, r 2, . . rt Computes xi = ri 2 mod n for each I H = hash m = message to sign Alice: – – – • • computes h = H(m, x 1, x 2. . xt) uses first kt bits of h as values for bij for i = 1 to t, j = 1 to k computes ytmpi = product of si’s mod n where bij = 1 computes yi = (ri)(ytmpi) mod n sends Bob m, all bij’s and all yi’s Bob: computes ztmpi =product of vi’s mod n where bij = 1 computes zi = (yi 2)(ztmpi) mod n Verifies first kt bits of H(m, z 1, z 2, . . zt) are the bij’s

Elliptic Curve • • Public key algorithm Elliptic curves over finite fields Just want to mention – won’t go into math Tutorial on elliptic curves: http: //www. certicom. com/index. php? action=ecc_ tutorial, home

Elliptic Curve • set of points (x, y) such that y 2 = x 3 + ax + b • x, y, a, b R • If x 3 + ax + b has no repeated factors, then the curve is a group (under addition) • Example: y 2 = x 3 - 4 x + 0. 67

Elliptic Curve • negative of a point P = (x, y) is its reflection over the xaxis: -P = (x, -y) • P on elliptic curve, -P is on the curve. P, Q are on the curve • P+Q (when Q ≠ P, -P) draw line through P and Q the line will intersect the curve at a third point: -R P+Q = R (negative of the third point)

Additive Identity • vertical line from P to -P does not intersect the elliptic curve at a third point • additive identity: O = point at infinity P + (-P) = O P + O = P

P+P • When y coordinate ≠ 0 • Use line tangent to P
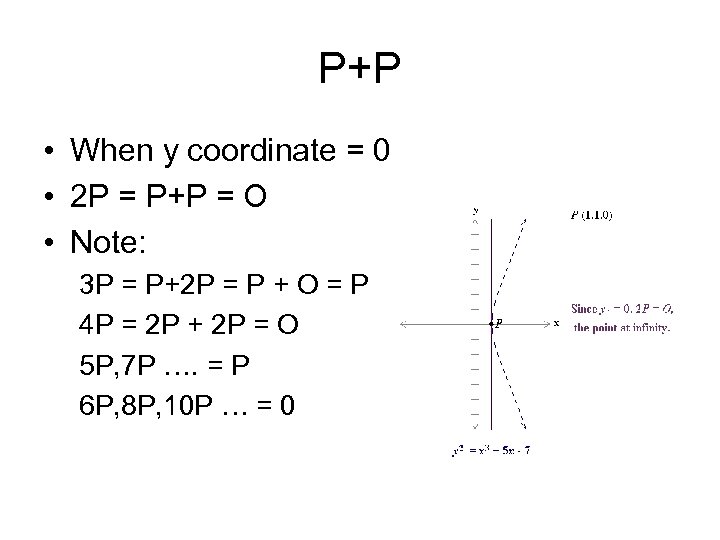
P+P • When y coordinate = 0 • 2 P = P+P = O • Note: 3 P = P+2 P = P + O = P 4 P = 2 P + 2 P = O 5 P, 7 P …. = P 6 P, 8 P, 10 P … = 0

Elliptic Curve • • Raise points to powers – repeated multiplication (gx)y = gxy = (gy)x Factoring hard Discrete log hard

Elliptic Curve • Public key, private key § k = private key § G is a point § P = k. G is public key • DH: § PA = k. AG § PB = k. BG § Shared secret k. Bk. AG

ECC Key Size • Key size: order of base point G • 256 -383 bits 128 bit AES key • 512 256 bit AES key

Public Key Infrastructure (PKI)

PKI Overview • Public Key Infrastructure: components necessary to distribute public keys – Certificates – Repository for obtaining/retrieving certificates – Certificate revocation – Evaluation of train of certificates using public keys known/trusted in advance

Certificate Authority • Central point for certificates • Signs cert for Alice containing her public key • Others need only CA’s public key • Revocation? – Online real time – Offline CA –expiration date, certificate revocation list
![PKI Overview - Chains • Bob receives certificate saying [Alice’s public key is X]Carol PKI Overview - Chains • Bob receives certificate saying [Alice’s public key is X]Carol](https://present5.com/presentation/7b3168c6abdb1444f32ba1bde2023263/image-61.jpg)
PKI Overview - Chains • Bob receives certificate saying [Alice’s public key is X]Carol signed by Carol • Suppose Bob doesn’t know/trust Carol, but trusts Ted, use chain [Carol’s public key is Y] Ted [Alice’s public key is X]Carol

PKI Overview - Terms • Certificate: contains name, public key (and other information) • CA: certificate authority, required components • Issuer: signer of certificate, vouches for it • Target: entity want to find path to • Verifier: evaluates chain of certificates • Principal: any entity with public key • Trust chain: verifiable chain, 1 st certificate signed by trust anchor

PKI Models - Monopoly • 1 CA trusted by everyone – CA public key embedded in all software, hardware – Issues all certificates • Simple model, not practical – Infeasible to change key – How to remotely certify everyone – Security relies on trust in single entity

Monopoly + Help • Registration authorities (RA) • Distributed, verifies identities of entities requesting certificates • CA trusts RAs • All certificates signed by CA

Delegated CAs Anchor CA CA 1 CA 2 CAn • Principals obtain certificates from delegates • Chain: • Certificates signed by delegate • Delegate CA has certificate signed by anchor CA

Oligarchy • List of trust anchors • Example: Default list in browsers • Users don’t know what a valid list is

Anarchy • Example: PGP • Each user has to define own list of trust anchors • If receive certificate from someone not in own list, go to public database and see if can find a chain from someone in own list • Infeasible if every person participates – contributes certificates to public database • Can chain derived from database really be trusted? – Alice gets certificate signed by Ted. Alice has Bob in her anchor list. – Database tells her Bob trusts Carol, Carol trusts Dave, Dave trusts Eve, Eve trusts Fred, Fred trusts Ted. – What if someone added fake certificates to database? – In contrast, more likely to trust a few CAs weren’t compromised.

CAs and Names • CA can only vouch for certain names • Hierarchy CA for edu CA for Columbia Alumni Students Faculty CA for Johns Hopkins Alumni Students Faculty CA for gov CA for whitehouse, congress CA for agencies

Revocation • Why needed? – – Stolen private key Person leaves company Division spun off from company Moore’s law – processing power increasing, recommend size of key increases – Attacker falsely obtains valid certificate • Methods – Expiration dates – Certificate revocation list (CRL)

Expiration date • Time required to issue certificates, so most valid for months or years • Too long to wait if key is stolen • Systems may not use CRLs and wait for expiration date • Principals not renewing certificates due to cost – Browsers may avoid checking expiration date because servers never bother to renew certificates – Don’t want it to appear to the end user as if browser is broken

CRLs • CA periodically issues signed list of revoked CRLs – Can quickly become large – Delta CRL – only changes since last CRL – Timing still an issue • Online Certificate Status Protocol (OCSP) – used for obtaining the revocation status of X. 509 certificate – RFC 2560 – Send query to responder asking if certificate is valid, responder checks database and replies – Timing still an issue - requires up-to-date list

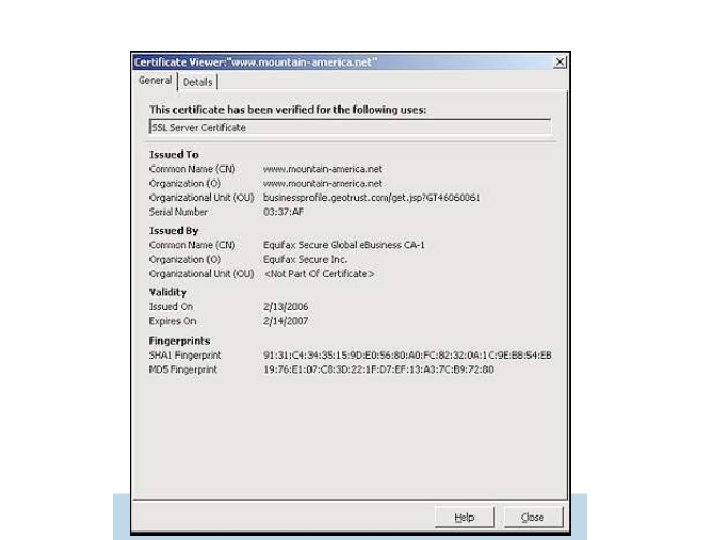
Obtaining Certificate • Issuers responsible for ensuring entity requesting a certificate is authorized to request it on the company's behalf – remote – physically present with id • Errors happen • Example: Geotrust's (Equifax) cert verification process – automated: request a cert for a particular website triggers Geotrust to send an e-mail to the address included in the Web site's registrar records, includes code the recipient needs to phone in to complete the process – mountain-america. net vs mountainamerica. net – http: //blog. washingtonpost. com/securityfix/2006/02/the_new_fac e_of_phishing_1. html

Styles of Certification • • At least 3 major styles X. 509/PKIX — traditional hierarchical CA SPKI/SDSI — authorization certificates PGP web of trust (primarily for email)

What is in a Certificate? • Public key • Technical information, such as algorithm identifiers • More identification information — company, location, etc. • Expiration date • Logos • Certificate role

X. 509 • • • Version Serial Number Algorithm ID Issuer Validity – Not Before – Not After • • Subject Public Key Info – Public Key Algorithm – Subject Public Key • • • Issuer Unique Identifier (Optional) Subject Unique Identifier (Optional) Extensions (Optional) –. . . • • Certificate Signature Algorithm Certificate Signature

Examples • Cs department certificate fall 2006 • Columbia University certificate fall 2006

Example • Signer Issuer: C=US, O=Equifax, OU=Equifax Secure Certificate Authority • Validity dates Not Before: Jul 7 19: 51: 50 2005 GMT Not After : Oct 7 19: 51: 50 2006 GMT • Algorithms (RSA, SHA 1, MD 5) Signature Algorithm: sha 1 With. RSAEncryption • Certificate Revocation List (CRL) X 509 v 3 CRL Distribution Points: URI: http: //crl. geotrust. com/crls/secureca. crl

Example • Certificate usage — encryption and authentication, but not for issuing other certificates X 509 v 3 extensions: X 509 v 3 Key Usage: critical Digital Signature, Non Repudiation, Key Encipherment, Data Encipherment … X 509 v 3 Extended Key Usage: TLS Web Server Authentication, TLS Web Client Authentication

Example • If certificate was for vouching for other certificates, would contain: X 509 v 3 extensions: X 509 v 3 Basic Constraints: critical CA: TRUE

Root Certificate • Issuer and subject are the same • Manually install in application/installed in default list (example: browsers)

Utilities • JAVA keytool • openssl

keytool • generate a new public/private key pair and put the public key in a self-signed certificate keytool -genkey -alias alice -keypass alicekey • Use - keystore to specify keystore Default is. keystore • keytool –h for options • http: //java. sun. com/j 2 se/1. 5. 0/docs/tooldocs/win dows/keytool. html

openssl • Generate key openssl genrsa -out privkey. pem 2048 bit RSA private key, also contains public key • Self-signed cetificate openssl req -new -x 509 -key privkey. pem -out cacert. pem -days 1095 http: //www. openssl. org/docs/HOWTO

TSL/HTTPS not Always Sufficient • Consider phishing • Use of https not sufficient in preventing

Phishing Example 1: Chase Dear Customer, CONGRATULATIONS !!! We are very satisfied about the Reward Survey results and we've made improvements to JPMorgan Chase Bank Online web page. To make all the customers happy we will credit every account that uses every day our online banking service with 100$. Helping us better understand how our customers feel, benefits everyone. With the information collected we can decide to direct a number of changes to improve and expand our online services. We kindly ask you to spare two minutes of your time in taking part with this unique offer! This offer expires in 24 h after you recieve this message. To Continue click on the link below: https: //chaseonline. chase. com/chaseonline/signup/sso_signup_filter. jsp? LOB=RBGSurvey © 2006 JPMorgan Chase & Co. Link is then mapped to another url in href tag

Chase -header From security@chaseonline. chase. com Fri Oct 6 12: 22: 46 2006 Return-Path: <security@chaseonline. chase. com> Received: from cs. columbia. edu (cs. columbia. edu [128. 59. 16. 20]) by parker. cs. columbia. edu (8. 12. 10/8. 12. 10) with ESMTP id k 96 GMij. M 008316 (version=TLSv 1/SSLv 3 cipher=DHE-RSA-AES 256 -SHA bits=256 verify=NOT) for <joesmith@parker. cs. columbia. edu>; Fri, 6 Oct 2006 12: 22: 44 -0400 (EDT) Received: from exchange. rremc. local (mail. rremc. com [216. 199. 214. 82]) by cs. columbia. edu (8. 12. 10/8. 12. 10) with ESMTP id k 96 GMg 5 P 026987 for <joesmith@cs. columbia. edu>; Fri, 6 Oct 2006 12: 22: 43 -0400 (EDT) Received: from User ([62. 81. 199. 90] RDNS failed) by exchange. rremc. local with Microsoft SMTPSVC(6. 0. 3790. 1830); Fri, 6 Oct 2006 12: 24: 52 -0400 Reply-To: <do-not-reply@chaseonline. chase. com> From: "Chase Bank"<security@chaseonline. chase. com> Subject: Chase Online. SM $100 Reward Survey. Date: Fri, 6 Oct 2006 18: 22: 28 +0200 MIME-Version: 1. 0 Content-Type: text/html; charset="Windows-1251" Content-Transfer-Encoding: 7 bit X-Priority: 1 X-MSMail-Priority: High X-Mailer: Microsoft Outlook Express 6. 00. 2600. 0000 X-Mime. OLE: Produced By Microsoft Mime. OLE V 6. 00. 2600. 0000 Bcc: Message-ID: <EXCHANGEd. NCx. LYxrw. Zn 00000776@exchange. rremc. local> X-Original. Arrival. Time: 06 Oct 2006 16: 24: 52. 0667 (UTC) FILETIME=[F 3 B 928 B 0: 01 C 6 E 963] X-Perl. Mx-Spam: Gauge=XIIIIII, Probability=16%, X-Seen-By filter 2. cs. columbia. edu Status: RO X-Status: A X-Keywords: X-UID: 19426

Phishing Example 2: ebay • <img src="http: //pics. ebaystatic. com/aw/pics/logos/ebay_95 x 39. gif" border="0" alt="e. Bay"> • <a href="http: //pages. ebay. com/securitycenter/selling_safely. html"> • href="http: //pages. ebay. com">http: //pages. ebay. com/education/spoo ftutorial</a> • “Respond Now” link href="http: //www. google. com/pagead/iclk? sa=l&ai=Br 3 yc. NQz 5 Q -f. XBJGSi. QLU 0 e. DSAue. Hk. Arnht. WZAu. Fm. QWgjlk. QAxg. FKAg 4 AEDKEUi. FOVD-4 r 2 f. P____8 Bo. AGyqor_A 8 g. BAZUCCap. CCqk. Cx. U 7 NLQH 0 sz 4&num= 5&adurl=http: //host 217 -37 -160 -25. inaddr. btopenworld. com: 82/ebay. com/reg. php" border="0"><img src="http: //pics. ebaystatic. com/aw/pics/buttons/btn. Respond. Now. gif" width="120" height="32" alt="Respond Now" border="0"></a></td>
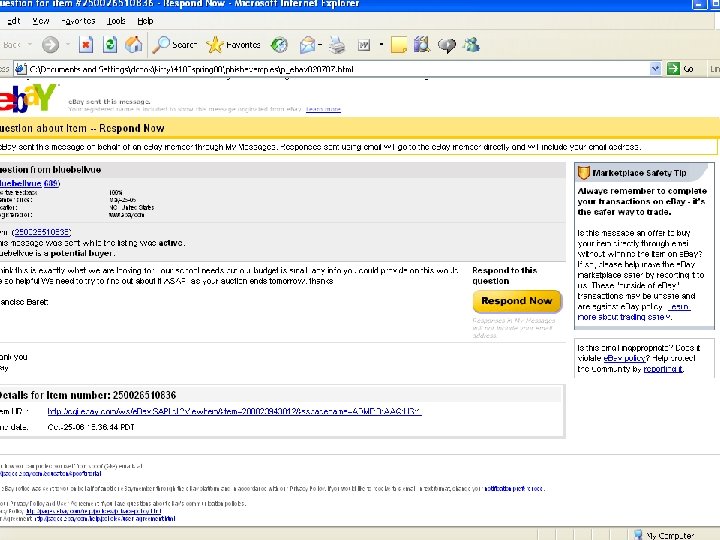

ebay - header Received: from hoemail 1. lucent. com (hoemail 1. dmz. lucent. com [192. 11. 226. 41]) by ihmail. ih. lucent. com (8. 11. 7 p 1+Sun/8. 12. 11) with ESMTP id l 1769 Lu 07527 for <joesmith@ihmail. ih. lucent. com>; Wed, 7 Feb 2007 00: 09: 21 -0600 (CST) Received: from mail. com (pd 95 b 3 a 19. dip 0. t-ipconnect. de [217. 91. 58. 25]) by hoemail 1. lucent. com (8. 13. 8/IER-i) with SMTP id l 1769 EFE 002509 for <joesmith@lucent. com>; Wed, 7 Feb 2007 00: 09: 15 -0600 (CST) Message-Id: <200702070609. l 1769 EFE 002509@hoemail 1. lucent. com> From: "e. Bay member" <aw. member@e. Bay. com> Subject: Question about Item -- Respond Now Date: Wed, 7 Feb 2007 07: 17: 33 +0100 MIME-Version: 1. 0 Content-Type: text/html; charset="Windows-1251" Content-Transfer-Encoding: 7 bit X-Priority: 3 X-MSMail-Priority: Normal X-Mailer: Microsoft Outlook Express 6. 00. 2600. 0000 X-Mime. OLE: Produced By Microsoft Mime. OLE V 6. 00. 2600. 0000 X-Scanned-By: MIMEDefang 2. 57 on 192. 11. 226. 161 Content-Length: 14656

TLS/HTTPS not Sufficient • Most phishing emails display “https” link in email but href to http • Sophisticated Phishers get certificate, use https – Phisher’s link https: //www. rbcbanking. com – Real Bank’s link (Royal Bank of Canada) https: //www 1. royalbank. com and https: //www 1. rbcroyalbank. com • Mountain America example • In general https: //www. joephisher. com/banksname. com vs https: //www. banksname. com

TLS/HTTPS not Sufficient • If certificate signed by “trusted” CA, no warning displayed to user – Recall browser may have 100+ “trusted CAs” • If certificate not signed by trusted CA, most people click to ok/proceed when warning pops up – Most people also ignore http vs https

Social Engineering • Not Detected by tools/filters • Someone persuaded a reputable CA to issue them a certificate for Mountain America, a credit union – The DNS name was www. mountain-america. net – looks legitimate, but real credit union site is at www. mtnamerica. org. – (There’s also www. mountainamerica. com, a Las Vegas travel site) – Which site was intended by the user?
7b3168c6abdb1444f32ba1bde2023263.ppt