Introduction to Practical Cryptography Lecture 1 Overview Debbie

Introduction to Practical Cryptography Lecture 1 Overview Debbie Cook dcook ATcs. columbia. edu

Agenda • Course Outline • Topics in cryptography – Basic • • Terms Privacy - Encryption Authentication - Signatures Integrity – Hash, MAC – Not-so Basic • Zero knowledge • Oblivious transfer • Proxy cryptography – Some Applications • Multiparty computation • Searchable encryption • Redaction – Current “hot” items • Hash Function • Pairings • Universal composability • Gap between theory and practice

Course Outline 1. Overview - today 2. Basics: lectures 2 -6 • • • Public key Block ciphers Stream ciphers Hash functions Cryptanalysis Protocols 3. General topics: lectures 7 -9 • • Forward key security Oblivious transfer Zero knowledge Multiparty computation Searchable encryption Redaction Proxy cryptography Universal composability 4. Exam

Grading + Contact Info • One homework (50% - tentative) • One 2 hour exam during last class (50% - tentative) • My email: dcook AT cs. columbia. edu • Slides for lectures are available at http: //www. cs. columbia. edu/~dcook/forth • All lecture slides are currently posted, but are subject to small modifications

Agenda • Course Outline • Topics in cryptography – Basic • • Terms Privacy - Encryption Authentication - Signatures Integrity – Hash, MAC – Not-so Basic • Zero knowledge • Oblivious transfer • Proxy cryptography – Some Applications • Multiparty computation • Searchable encryption • Redaction – Current “hot” items • Hash Function • Pairings • Universal composability • Gap between theory and practice

Terms • Private Key (symmetric key) • Public Key (asymmetric key) • Hash Function

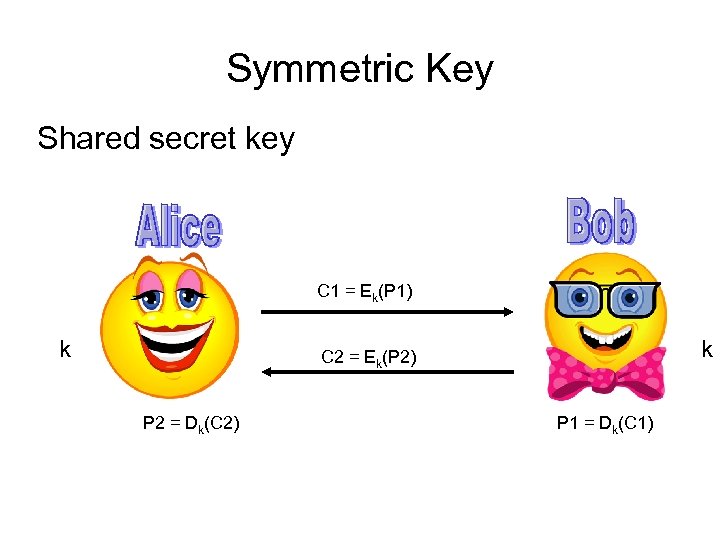
Symmetric Key Shared secret key C 1 = Ek(P 1) k k C 2 = Ek(P 2) P 2 = Dk(C 2) P 1 = Dk(C 1)

Symmetric Key Cryptography • Secret key – one key • General categories of algorithms • Block Ciphers • Stream Ciphers • Heuristics • Well analyzed • Components based on defined properties • But, unlike public key, no formal security proof exists • Faster than public key algorithms

Uses • Encryption of data • Files, disk, large plaintext, streaming data • Random number generator for OTPs • RSA token, VASCO digipass

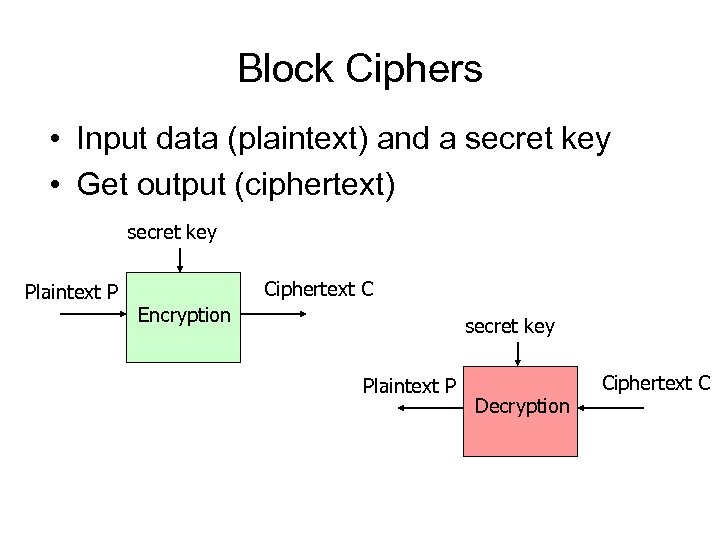
Block Ciphers • Input data (plaintext) and a secret key • Get output (ciphertext) secret key Plaintext P Ciphertext C Encryption secret key Plaintext P Decryption Ciphertext C

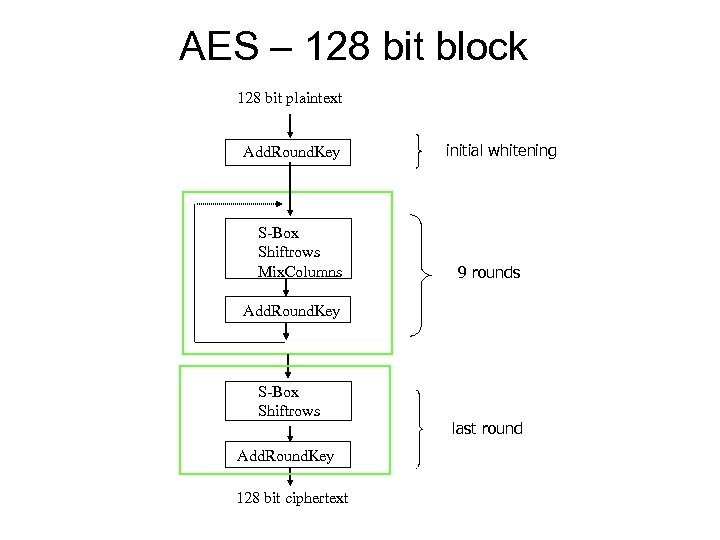
AES – 128 bit block 128 bit plaintext Add. Round. Key S-Box Shiftrows Mix. Columns initial whitening 9 rounds Add. Round. Key S-Box Shiftrows Add. Round. Key 128 bit ciphertext last round

Stream Ciphers • Stream cipher outputs keystream, KS • KS produced by a function, F, that is initialized with a key, k • C = Ek(P) = P KS • P = C KS • k can be used only once • C 1 = Ek 1(P 1); C 2 = Ek 2(P 2) • C 1 C 2 = P 1 KS 1 P 2 KS 2 = P 1 P 2 if KS 1 = KS 2 • Will know when P 1 and P 2 have identical bits • If know part of P 1 (if packet headers, format information), then can obtain part of P 2 • Period – how long is KS before it starts repeating? • repeating is equivalent to reusing a key • Period of 232 repeats after ~ 8. 5 minutes when encrypting 1 MB/sec

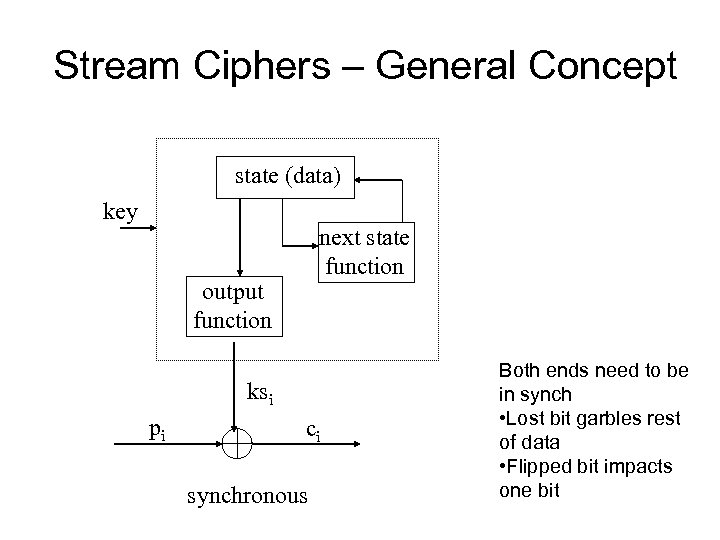
Stream Ciphers – General Concept state (data) key next state function output function ksi pi ci synchronous Both ends need to be in synch • Lost bit garbles rest of data • Flipped bit impacts one bit

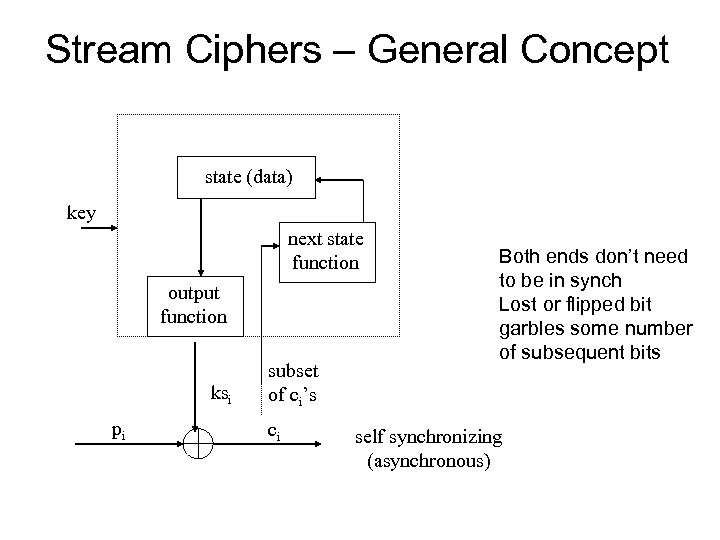
Stream Ciphers – General Concept state (data) key next state function output function ksi pi subset of ci’s ci Both ends don’t need to be in synch Lost or flipped bit garbles some number of subsequent bits self synchronizing (asynchronous)

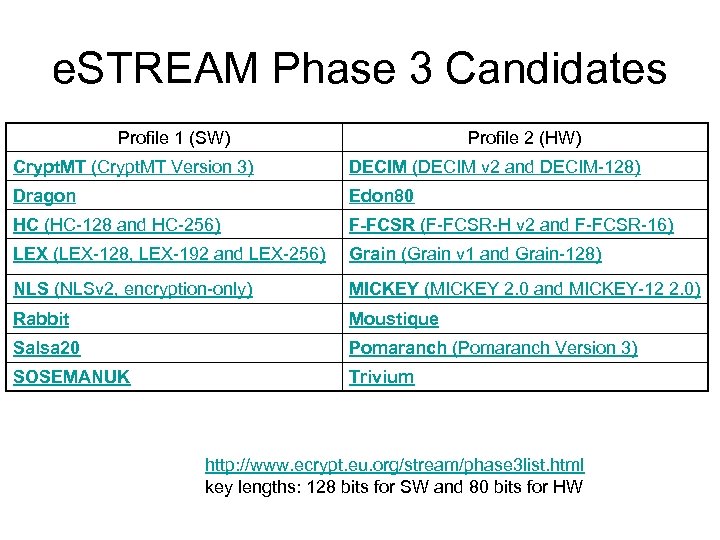
e. STREAM Phase 3 Candidates Profile 1 (SW) Profile 2 (HW) Crypt. MT (Crypt. MT Version 3) DECIM (DECIM v 2 and DECIM-128) Dragon Edon 80 HC (HC-128 and HC-256) F-FCSR (F-FCSR-H v 2 and F-FCSR-16) LEX (LEX-128, LEX-192 and LEX-256) Grain (Grain v 1 and Grain-128) NLS (NLSv 2, encryption-only) MICKEY (MICKEY 2. 0 and MICKEY-12 2. 0) Rabbit Moustique Salsa 20 Pomaranch (Pomaranch Version 3) SOSEMANUK Trivium http: //www. ecrypt. eu. org/stream/phase 3 list. html key lengths: 128 bits for SW and 80 bits for HW

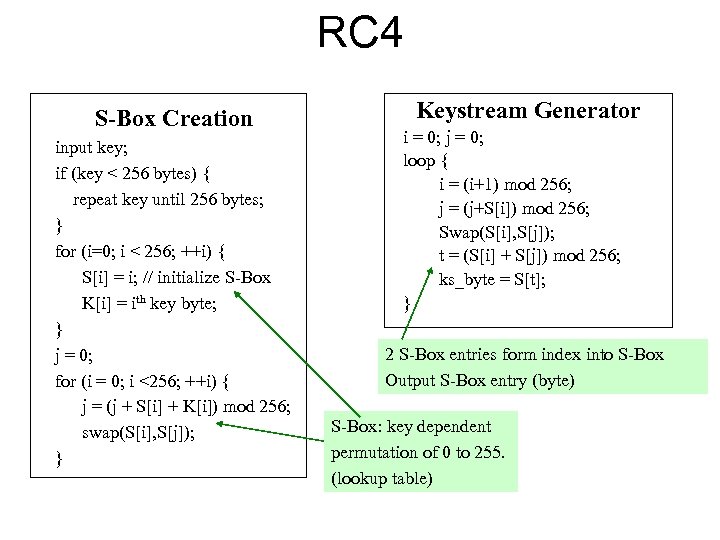
RC 4 S-Box Creation input key; if (key < 256 bytes) { repeat key until 256 bytes; } for (i=0; i < 256; ++i) { S[i] = i; // initialize S-Box K[i] = ith key byte; } j = 0; for (i = 0; i <256; ++i) { j = (j + S[i] + K[i]) mod 256; swap(S[i], S[j]); } Keystream Generator i = 0; j = 0; loop { i = (i+1) mod 256; j = (j+S[i]) mod 256; Swap(S[i], S[j]); t = (S[i] + S[j]) mod 256; ks_byte = S[t]; } 2 S-Box entries form index into S-Box Output S-Box entry (byte) S-Box: key dependent permutation of 0 to 255. (lookup table)

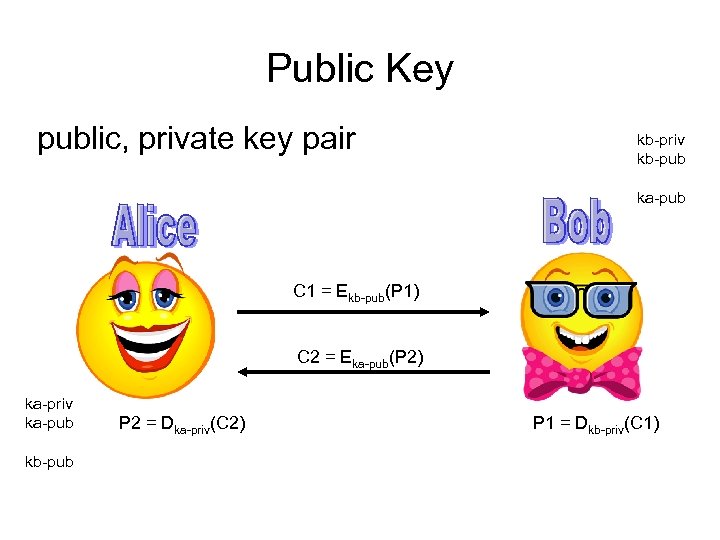
Public Key public, private key pair kb-priv kb-pub ka-pub C 1 = Ekb-pub(P 1) C 2 = Eka-pub(P 2) ka-priv ka-pub kb-pub P 2 = Dka-priv(C 2) P 1 = Dkb-priv(C 1)

Public Key Cryptography • Uses a key pair – one component is public, one component is private • Algorithms used in practice depend on the mathematical hardness of factoring or of computing discrete logs.

Uses • Signatures – Non-repudiation: signature had to generated by someone with private key • Encrypt small amounts of data, such as in key exchange protocols • Establish shared secret (Diffie-Hellman)

RSA • Generate two large distinct (at least 1024 bits) primes p and q; let n = pq • Compute (n) = (p − 1)(q − 1). • Pick two integers e and d such that ed = 1 mod (n) where 1 < e < (n) and e and (n) are coprime • The public key is <e, n>; the private key is <d, n>. • The security of the system relies on the difficulty of factoring n. • Finding such primes is easy; factoring n is believed to be hard.

RSA • • message m of length < n Encrypt: c = me mod n Decrypt: m = cd mod n Why? cd mod n = med mod n but ed = 1 mod (n) = m k (n)+1 mod n = (m (n))km mod n = (1 k)m mod n = m

RSA Parameter sizes • n of 3072 bits equivalent security of 128 -bit key in AES • n of 15360 bits equivalent to 256 -bit key in AES • NIST SP 800 -57, May 2006 Recommendation for Key Management – Part 1

Privacy - Encryption • Considerations – Type of data/application - suitable for public or private key – Supported algorithms – Performance – Key distribution – Key security

Authentication - Signatures • Signature: typically hash data, encrypt with public key algorithm using private key • Verification: decrypt with public key, hash original data, compare results • Non-repudiation – can’t refute validity of signed data • Issues – Time – signed it, but when? – Key security

Integrity - MACs • Want to know the data has not changed • Hash function • Message Authentication Code (MAC)

Hash Properties • Map bit strings of arbitrary length to fixedlength outputs h = hash(m), h is fixed-length, short • Not injective, but collisions unlikely – Example: 2160 possible values • Computationally infeasible to generate collisions • Computationally infeasible to invert

Hash Properties • Preimage resistant: given h, hard to find m such that h = hash(m) • Second preimage resistant: given m 1, hard to find m 2 (≠ m 1) such that hash(m 1) = hash(m 2) • Collision-resistant: hard to find m 1 and m 2, m 2 ≠ m 1, such that hash(m 1) = hash(m 2)

MAC • Message Authentication Code – keyed hash • Examples: – Encrypt hash with symmetric key cipher – HMAC H((K c 1) || H((K c 2) || m)) where c 1 = 0 x 5 c 5 c 5 c …, c 2 = 0 x 363636 …

Hash - Uses • Integrity – Hash file/message – Changes detectable provided attacker can’t recompute and replace hash value after modifying file/message • Authentication – Signature: hash data to shorten (for efficiency) then encrypt with public key algorithm – Append shared secret to unencrypted data then hash • Random bits – OATH OTP standard

In Practice • Heuristics • Simple operations, performance: – Iterative, series of rounds – Diffusion through logical operations, addition, shifts, rotates

Agenda • Course Outline • Topics in cryptography – Basic • • Terms Privacy - Encryption Authentication - Signatures Integrity – Hash, MAC – Not-so Basic • Zero knowledge • Oblivious transfer • Proxy cryptography – Some Applications • Multiparty computation • Searchable encryption • Redaction – Current “hot” items • Hash Function • Pairings • Universal composability • Gap between theory and practice

Zero Knowledge I know X X Prove it Some exchange, but which does not provide X • Interactive method for Alice to prove to Bob that she has/knows x without revealing x to Bob. • Motivation: authentication • Alice wants to prove her identity to Bob via some secret but doesn't want Bob to learn anything about this secret – Login methods where password is not stored on server (maybe hash of password is stored) – Alice (user/client) proves to Bob (server) that she knows the password without giving Bob the password

Zero Knowledge • Jean-Jacques Quisquater, et. al "How to Explain Zero-Knowledge Protocols to Your Children“ • Peggy (prover) has uncovered the secret password to open a magic door in a cave. The cave is shaped like a circle, with the entrance in one side and the magic door blocking the opposite side. • Victor (verifier) will pay Peggy for the secret, but not until he's sure that she really knows it. Peggy says she'll tell him the secret, but not until she receives the money. • Zero knowledge – need a method by which Peggy proves to Victor that she knows the word without telling it to him door A B enter

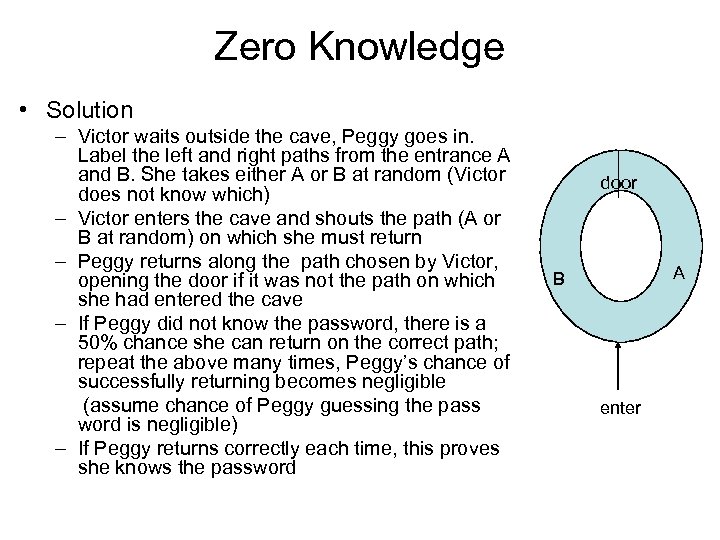
Zero Knowledge • Solution – Victor waits outside the cave, Peggy goes in. Label the left and right paths from the entrance A and B. She takes either A or B at random (Victor does not know which) – Victor enters the cave and shouts the path (A or B at random) on which she must return – Peggy returns along the path chosen by Victor, opening the door if it was not the path on which she had entered the cave – If Peggy did not know the password, there is a 50% chance she can return on the correct path; repeat the above many times, Peggy’s chance of successfully returning becomes negligible (assume chance of Peggy guessing the pass word is negligible) – If Peggy returns correctly each time, this proves she knows the password door A B enter

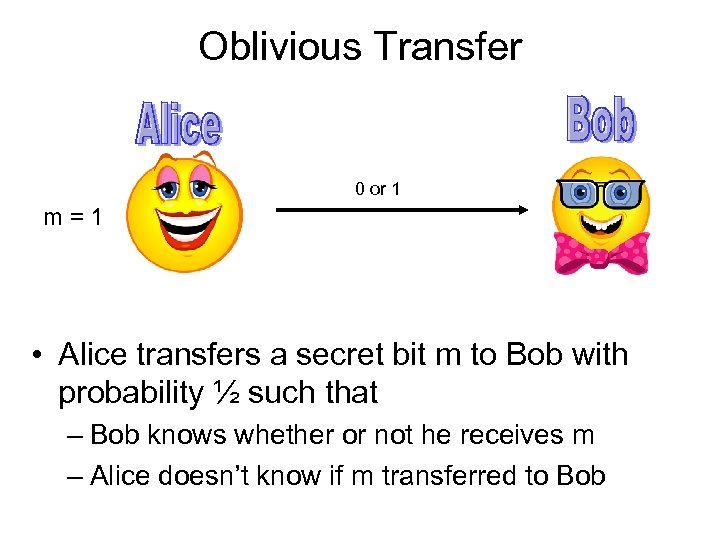
Oblivious Transfer 0 or 1 m = 1 • Alice transfers a secret bit m to Bob with probability ½ such that – Bob knows whether or not he receives m – Alice doesn’t know if m transferred to Bob

Oblivious Transfer – Application • Alice and Bob will each sign a contract only if the other also signs it • Idea – If names are of equal length, could sign a letter at a time, alternating • But someone must go last and could abort – not complete last letter – Sign small fragment at a time – bit, pixel • Don’t know who will be last • If one stops, both are approximately at same point – But one could send garbage in a fragment • Oblivious transfer solves the problem

Proxy Cryptography • Convert ciphertext from encryption with one key to encryption with another key: – Encrypt with one key, let recipient decrypt with some other key • Similar notion for signatures: sign with one key, let recipient verify with another key.

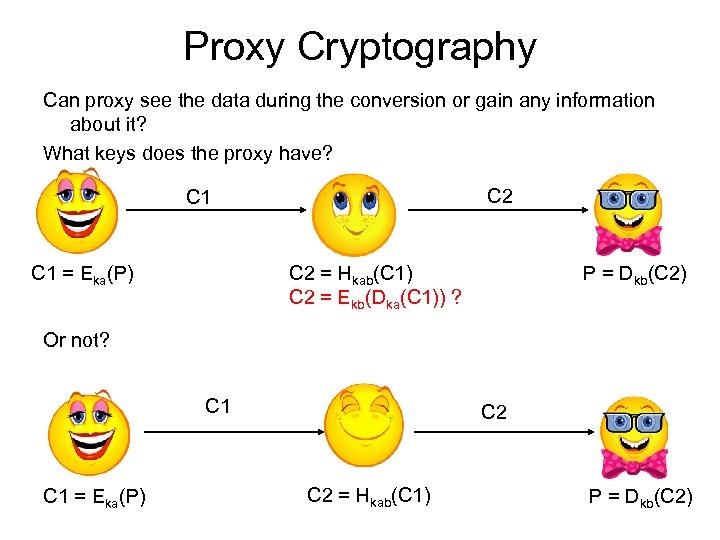
Proxy Cryptography Can proxy see the data during the conversion or gain any information about it? What keys does the proxy have? C 2 C 1 = Eka(P) C 2 = Hkab(C 1) C 2 = Ekb(Dka(C 1)) ? P = Dkb(C 2) Or not? C 1 = Eka(P) C 2 = Hkab(C 1) P = Dkb(C 2)

Proxy Cryptography • VPNs • File servers • Transform A’s signature into B’s signature

Secure Multi-Party Computation • A set of parties with private inputs wish to compute some joint function of their inputs. • Parties wish to preserve some security properties. E. g. , privacy and correctness. – Example: secure election protocol • Security must be preserved in the face of adversarial behavior by some of the participants

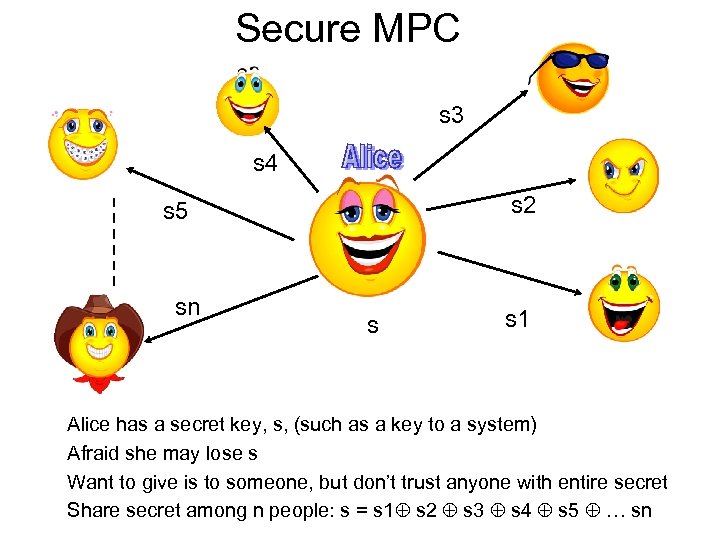
Secure MPC s 3 s 4 s 2 s 5 sn s s 1 Alice has a secret key, s, (such as a key to a system) Afraid she may lose s Want to give is to someone, but don’t trust anyone with entire secret Share secret among n people: s = s 1 s 2 s 3 s 4 s 5 … sn

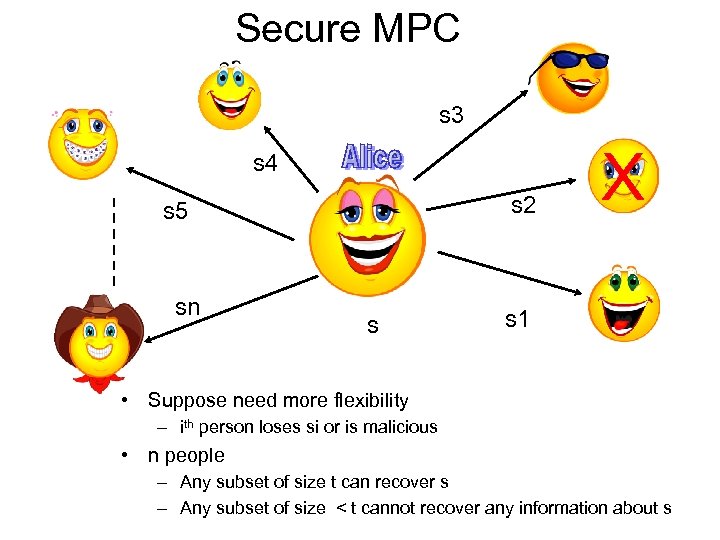
Secure MPC s 3 s 4 s 2 s 5 sn s X s 1 • Suppose need more flexibility – ith person loses si or is malicious • n people – Any subset of size t can recover s – Any subset of size < t cannot recover any information about s

Application of 2 PC • On-line Bidding – If seller’s price buyer’s price, sell at average of the two – Privacy: don’t want to announce exact prices – Correctness: don’t sell for less than asking price

Application of MPC • Auctions – Parties: 1 auctioneer, (n-1) bidders. – Consider secret bids: • An adversary may wish to learn the bids of all parties – to prevent this, requires privacy • An adversary may wish to win with a lower bid than the highest – to prevent this, requires correctness • Elections – – Many voters Correctness: outcome (election winner) determined by votes Privacy: no information about individual votes revealed Can’t say Alice voted for Bob • But what can be said: town called Sandy Hook had majority vote for Bob when only 20 people reside there?

Searchable Encryption query response encrypted data repository

Untrusted Remote Storage Remote storage is ubiquitous: E-mail, backups, CVS, Department servers

Searchable Encryption • Store data externally – encrypted – want to search data easily – avoid downloading everything then decrypt – allow others to search data without having access to plaintext

Searchable Encryption - Factors • When searching, what must be protected? – retrieved data – search query outcome (was anything found? ) • Scenario – single query vs multiple queries – non-adaptive: series of queries, each independent of the others – adaptive: form next query based on previous results • # of participants – single user (owner of data) can query data – multiple users can query the data, possibly with access rights defined by the owner

Redaction • Removal of information from documents, media … The project involved people with a budget of • Image with brand name that must be removed

Redaction Example • Original content: – John Doe testified that Al Smith did not commit the crime. • After redaction: – [REDACTED] testified that Al Smith did not commit the crime. – testified that Al Smith did not commit the crime. • If redaction is not indicated, the meaning can be changed: – John Doe testified that Al Smith did not commit the crime. – John Doe testified that Al Smith did commit the crime.

Redaction - Examples • Government documents • classified information is removed prior to public release • Financial documents • mortgage application: different people need subsets of the information - appraiser doesn’t need to see income • Legal documents • some information remains under attorney-client privilege • Medical Records • Different employees access different information • Corporations • different employees have access to subsets of information • Public records • towns in US that place mortgage, property tax information online – remove personal information

Issues • Information leakage • Length of redacted area. • Inferred content: from remainder of document or possibly google remaining terms • Human error - forget to redact/overlook one or more pieces • Formatting • Altering length of redacted area to reduce information leakage changes format – length, paragraph/page alignment • How to sign a document • Need to authenticate non-redacted information is unchanged from the original • Need to authenticate that information was not improperly removed

Agenda • Course Outline • Topics in cryptography – Basic • • Terms Privacy - Encryption Authentication - Signatures Integrity – Hash, MAC – Not-so Basic • Zero knowledge • Oblivious transfer • Proxy cryptography – Some Applications • Multiparty computation • Searchable encryption • Redaction – Current “hot” items • Hash Function • Pairings • Universal composability • Gap between theory and practice

Hash Functions x

Algorithms - Broken • MD 4 (no longer in use) – can form collisions on paper (will see later) • MD 5 – designed to replace MD 4 • SHA-0 • SHA-1

SHS • Replaced SHA-0 • NIST FIPS 180 -2, Secure Hash Standard (SHS) 2002 • SHA-1: message < 264 bits, 160 -bit output • SHA-256: message < 264 bits, 256 -bit output • SHA-384: message < 2128 bits, 384 -bit output • SHA-512: message < 2128 bits, 512 -bit output

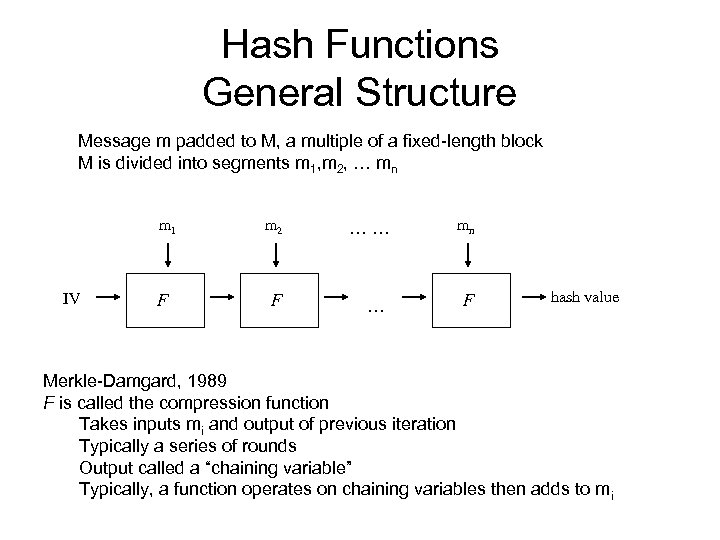
Hash Functions General Structure Message m padded to M, a multiple of a fixed-length block M is divided into segments m 1, m 2, … mn m 1 IV F m 2 …… mn F … F hash value Merkle-Damgard, 1989 F is called the compression function Takes inputs mi and output of previous iteration Typically a series of rounds Output called a “chaining variable” Typically, a function operates on chaining variables then adds to mi

Collisions - Uses • Generate meaningful files with the same hash – Code download – replace code, hash file remains unchanged – Signed files – replace one file with another, signature unchanged

Collisions Differentials • Differential cryptanalysis from block ciphers – Look at of inputs, of outputs after each round • In block ciphers, 1 to 1 mapping, – Never have in ≠ 0 out = 0 • In hash functions, round output shorter than input – There exists in ≠ 0 out = 0 – Need to find these ‘s

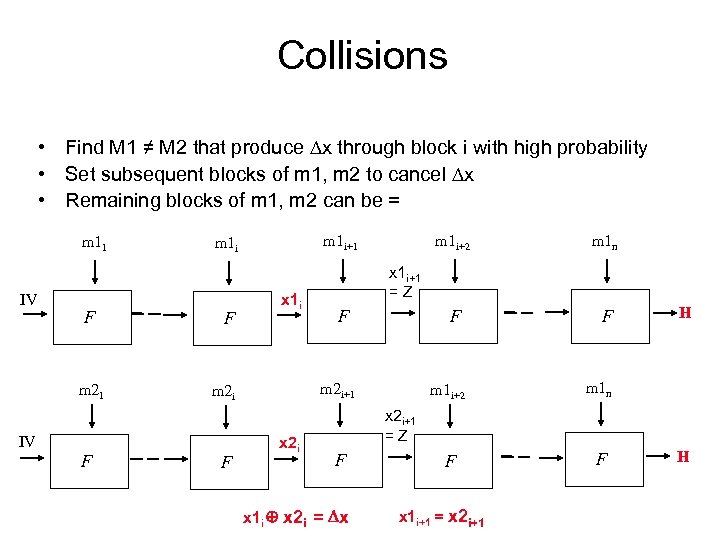
Collisions • Find M 1 ≠ M 2 that produce x through block i with high probability • Set subsequent blocks of m 1, m 2 to cancel x • Remaining blocks of m 1, m 2 can be = m 11 IV F m 21 F x 1 i F m 1 i+2 x 2 i m 1 n F F m 1 i+2 m 1 n F F x 1 i+1 = Z F m 2 i+1 m 2 i IV F m 1 i+1 m 1 i H x 2 i+1 = Z F x 1 i x 2 i = x x 1 i+1 = x 2 i+1 H

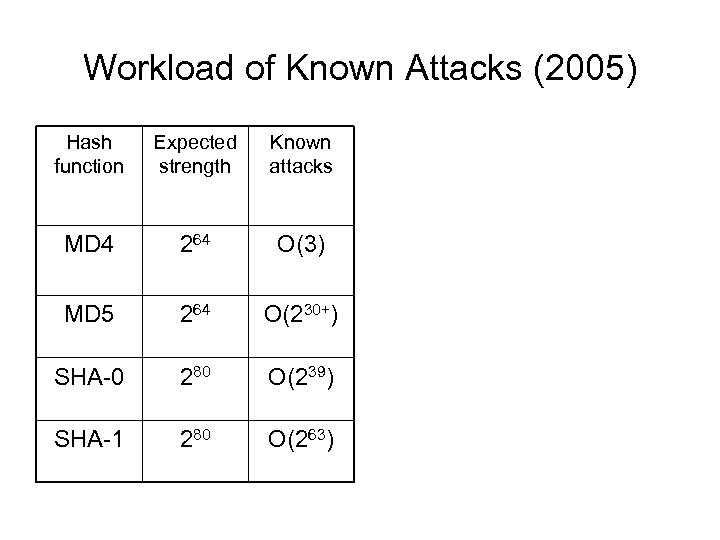
Workload of Known Attacks (2005) Hash function Expected strength Known attacks MD 4 264 O(3) MD 5 264 O(230+) SHA-0 280 O(239) SHA-1 280 O(263)

MD 4 Collisions M’ = M + C C = (0, 231, -228+231, 0, 0, 0, -216, 0, 0, 0) MD 4(M) = MD 4(M’) mi for i = 1, 2, 12 differ between M and M’

MD 4 Collision Example m 0[16] = { 0 xa 8 b 1 b 641, 0 x 88 d 2 ecaf, 0 xb 7 d 7 c 1 a 1, 0 x 99044241, 0 xffef 1639, 0 x 1934 bdcf, 0 x 30 e 2 adb 8, 0 x 252 ac 4 b 4, 0 x 7 bad 86 a 5, 0 x 7883 f 30 e, 0 x 8 b 37 f 23 b, 0 xd 694 dce 0, 0 x 701 d 8 b 69, 0 x 045095 eb, 0 x 92012 e 03, 0 x 71 ed 419 e } m 1[16] = { 0 xa 8 b 1 b 641, 0 x 08 d 2 ecaf, 0 x 27 d 7 c 1 a 1, 0 x 99044241, 0 xffef 1639, 0 x 1934 bdcf, 0 x 30 e 2 adb 8, 0 x 252 ac 4 b 4, 0 x 7 bad 86 a 5, 0 x 7883 f 30 e, 0 x 8 b 37 f 23 b, 0 xd 694 dce 0, 0 x 701 c 8 b 69, 0 x 045095 eb, 0 x 92012 e 03, 0 x 71 ed 419 e }

NIST Hash Workshop • Proposed competition – SHA 3 – – – • • Call for proposals – Nov. 2007 Allow time for public comments on hash function requirements Review submissions starting in 2009 Select winner end of 2011 Standard released in 2012 Then time to integrate into applications 6+ years before standard replacement

SHA 3 Requirements • NIST does not currently plan to withdraw SHA-2 • SHA-3 can be directly substituted for SHA-2 in current applications – must provide message digests of 224, 256, 384 and 512 -bits to allow substitution for the SHA-2 family • 160 -bit hash value produced by SHA-1 is becoming too small to use for digital signatures – a 160 -bit replacement hash algorithm is not contemplated.

SHA 3 Requirements • Certain properties of the SHA-2 hash functions must be preserved – – input parameters, output sizes collision resistance, preimage resistance, second-preimage resistance “one-pass” streaming mode of execution successful attack on the SHA-2 hash functions is unlikely to be applicable to SHA -3. – be suitably flexible for a wide variety of implementations, • May offer additional properties – – – • randomized hashing parallelizable more efficient to implement on some platforms more suitable for certain applications may avoid some of the incidental “generic” properties (such as length extension) of the Merkle-Damgard construct that often result in insecure applications For interoperability, prefer a single hash algorithm family (different size message digests be internally generated in as similar a manner as possible)

Approaches • Augment existing hash functions: – Add bit count to input – part of chaining value – Padding: 1, 0’s, hash size, message length • New algorithms, with approach similar to past hashes – chaining • New approaches that avoid Merkle. Damgard chaining • Algorithm related to mathematically hard problems

Pairings

Secret Sharing - DH What if 3 people want to agree on a shared secret K using DH? Three-party Diffie-Hellman key exchange: • Alice, Bob, and Charlie pick secret integers a, b, and c • Round 1: – Alice sends Bob ga – Bob sends Charlie gb – Charlie sends Alice gc • Round 2: – Alice sends Bob gac – Bob sends Charlie gab – Charlie sends Alice gbc • The shared secret is gabc

Secret Sharing • Three-way key agreement requires two rounds of communication – can we do better? • Yes, by using a cryptographic pairing

Pairing Definition A cryptographic pairing is a map e between two cyclic groups G 1 and G 2 with the following properties: • For each pair of elements (x, y) in G 1, the map gives an element e(x, y) in G 2. • The map preserves the structure of the group operation: – e(x 1 x 2 , y) = e(x 1, y) e(x 2, y) – e(x, y 1 y 2) = e(x, y 1) e(x, y 2) – e(xa, yb) = e(x, y)ab • The map is non-degenerate: – If x 1 in G 1, then e(x, x) 1 in G 2

Secret Sharing with Pairings Pairing-based 3 -way key exchange: Given a pairing e between groups G 1 and G 2, and an element g of G 1: • Alice, Bob, and Charlie think of secret integers a, b, c, respectively • Alice broadcasts ga; Bob broadcasts gb; Charlie broadcasts gc • Shared key is e(g, g)abc – Alice computes e(gb, gc)a – Bob computes e(ga, gc)b – Charlie computes e(ga, gb)c

UC - Universal Composability • framework for defining the security of cryptographic protocols • instances of such protocols remain secure when arbitrarily composed with other instances of the same or other protocols • First defined in – R. Canetti. Security and Composition of Multiparty Cryptographic Protocols. Journal of Cryptology, 13(1): 143– 202, 2000

UC - Protocol Composition • Participants involved in multiple protocol executions • Honest parties do not coordinate between executions (no state, no history maintained) • Adversaries may coordinate between executions

UC - Types of Protocol Composition • Considerations – Context in which the protocol runs – Participants – Schedule

UC - Types of Protocol Composition • Context in which the protocol runs: – What protocols are being run together • Self composition: – A single protocol is executed alone multiple times (no other protocols are being executed) – Protocol said to “self compose” if it remains secure in this scenario – Example: concurrent zero-knowledge • General composition – Many different protocols executed. – Protocols may have been designed independent of each other – Protocol is secure under general composition if it remains secure even when executed with arbitrary other protocols

UC - Protocol Composition • Self composition – protocol designed has complete control • General composition – no control over other protocols, they may have been intentionally designed to be malicious

UC - Participants • Single set of participants – Same participants in all executions – Same roles in all executions – Self composition typically assumes single set • Arbitrary set of participants – Arbitrary participants in each execution – Some may participant in multiple executions, others may not – May not have the same role

UC - Scheduling • Sequential – Next execution begins only when previous one has terminated • Parallel – All executions begin at same time and progress at the same rate • Concurrent – Executions start at any time, proceed at different rates • Example: protocol X run twice, messages for one execution may be held until certain messages for the other execution are sent – Controlled by adversary

UC - Paradigms • Ideal execution - trusted third party – All exchanges go through trusted third party, which computes function(s) according to the protocol and sends outputs to participants. • Real environment is secure if adversary cannot do more damage than in ideal environment

UC - Paradigms • In secure computation, adversary controls set of corrupt participants • In UC, environment, Z, – generates all inputs to all participants – reads all outputs – interacts with adversary in arbitrary manner

UC Security • No environment Z can tell if it is interacting with adversary in real world or the ideal world • Under concurrent general composition • Arbitrary set of parties

UC Security • If majority of participants are honest, UC security exists for any multi-party function (Canetti, A new Paradigm for Cryptographic Protocols, FOCs, 2001) • Not possible for some two-party protocols (such as the millionaires problem)

UC vs Real World • How to relate to real world? • What constitutes a protocol? – Any data exchange? • What privacy is required? – Know which entities communicate? • What is a participant? What time frame? – Client exchanges data with web server, are all clients that ever exchange data with the same server participants?

Agenda • Course Outline • Topics in cryptography – Basic • • Terms Privacy - Encryption Authentication - Signatures Integrity – Hash, MAC – Not-so Basic • Zero knowledge • Oblivious transfer • Proxy cryptography – Some Applications • Multiparty computation • Searchable encryption • Redaction – Current “hot” items • Hash Function • Pairings • Universal composability • Gap between theory and practice

Gap Between Theory and Practice Too often hear things such as “well that is a practical issue or an implementation issue and is of no concern to me”

Gap Between Theory and Practice Some “practical” things just require a need to consider the environment (public key and certificates – nice in theory, not so nice in reality, part is logistics, human factors, costs)

Certificates in Practice – TLS/HTTPS • The cryptography itself seems correct • But what about human factors? – Many users don’t know what a certificate is or how to verify one – Even when they do know, it’s hard to know what it should say in any given situation – There is no rational basis for deciding whether or not to trust a given CA

TLS/HTTPS • Sophisticated Phishers get certificate, use https – Phisher’s link https: //www. rbcbanking. com – Real Bank’s link (Royal Bank of Canada) https: //www 1. royalbank. com and https: //www 1. rbcroyalbank. com • In general https: //www. joephisher. com/banksname. com vs https: //www. banksname. com

TLS/HTTPS • If certificate signed by “trusted” CA, no warning displayed to user – Browser may have 100+ “trusted CAs” • If certificate not signed by trusted CA, most people click to ok/proceed when warning pops up – Most people also ignore http vs https

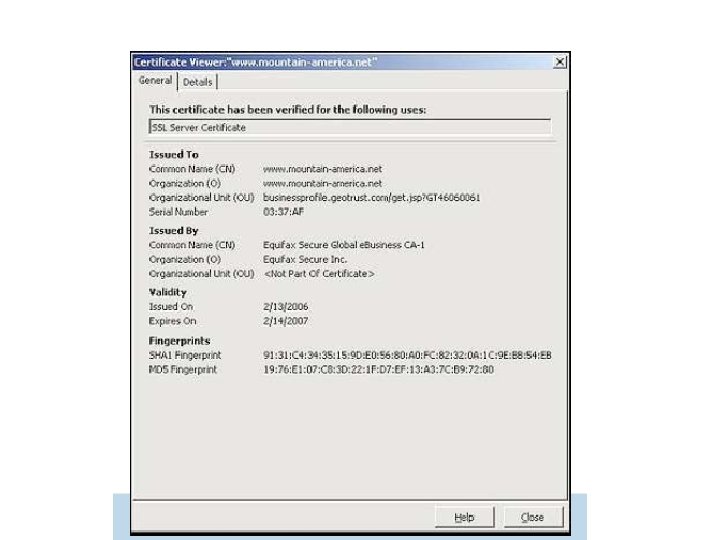
TLS/HTTPS - Social Engineering • Not Detected by tools/filters • Someone persuaded a reputable CA to issue them a certificate for Mountain America, a credit union – The DNS name was www. mountain-america. net – looks legitimate, but real credit union site is at www. mtnamerica. org. – (There’s also www. mountainamerica. com, a Las Vegas travel site) – Which site was intended by the user?

Gap Between Theory and Practice Some “practical” things should be addressed when the method is developed – searchable encryption method encrypting list nodes with a block cipher

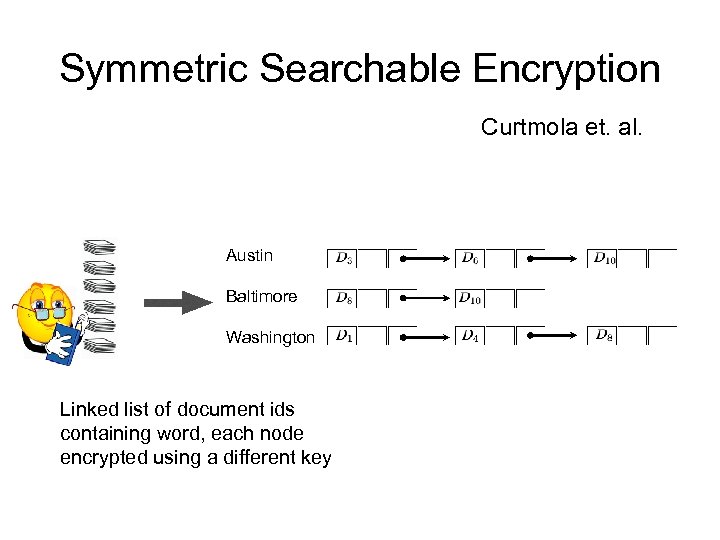
Symmetric Searchable Encryption Curtmola et. al. Austin Baltimore Washington Linked list of document ids containing word, each node encrypted using a different key

Gap Between Theory and Practice But each node is encrypted under a different key – key schedule run for each “block” What about block size? Overhead due to padding

Protocols and Universal Composability • Protocols may be secure in theory – it is the environment and/or usability that often is the problem • Separating functions/data across applications on same server – not a protocol interaction issue but more of a system security issue – How to limit access – How to secure memory • Malware on clients/servers – Participate may not necessarily be acting maliciously, but all data and inputs is passively read • Usability – Wireless – easy for users just to connect to whatever network is available and forget security – Certificates