Introduction to Practical Cryptography Forward Key Security Zero

Simple Schemes: Efficiency? • Long Public and Long Private Keys – – – T pairs (p 1, s 1), (p 2, s 2), ……. (pt, st) PK= (p 1, p 2, …. , pt) SK= (s 1, s 2, …. . , st) Update= erase si for period i Drawback: public and private key linear in t = number of periods 13

Anderson: Long Secret Key Only • • • T pairs as before and an additional pair (p, s) Sig(j)=SIG( j || pj) with key s, j =1, …, t [“certificate”] Public key now = p (only) Secret key = (sj, Sig(j)) j=1, . . , t [Still linear] The public key p is like a CA key and a signature will include the period, the certificate, the message, signature on the message with period’s secret key 14

Long Signatures Only • • Have (p, s) In period j get (pj, sj) and Let Cert(j)= sig_s[j-1] (j || pj) A signature is the entire certificate chain + signature, it is of the form: (j, sig_sj(m), p 1, Cert(1), …pj, Cert(j)) • Think about it as a tree of degree one and height t for t periods • (signer memory still linear in t) 15

Binary Certification tree [BM] • • Now (s 0, p 0) Each element certifies two children left and right We have a tree of height log t (for t periods) At each point only a log branch of certificate is used in the signature • Only leaves are used to sign • Keys whose children are not going to be used in future periods are erased. • We get O(log t) key sizes, signature size 16

Concrete Scheme • • • Use a scheme based on Fiat-Shamir variant Have the public key be a point x raised to 2 t Have the initial private key at period zero be x Sign based on FS paradigm Update by squaring the current key The verifier is aware of the period so it knows that currently the private key is raised to the power 2 t-1 (and the identification proofs are adjusted accordingly). 17

Replace keys Pseudorandomness • Have future keys derived from a forward secure pseudorandom generator • Pseudorandom generators which are forward secure are easy: replace the seed with an iteration of the function. • Possibilities in practice: – Block cipher – use previous output as next input – Stream cipher – previous output as next state 18

Agenda • • Forward Key Security Zero Knowledge Oblivious Transfer Multi-party Computation 19

Zero Knowledge I know X X Prove it Some exchange, but which does not provide X • Interactive method for Alice to prove to Bob that she has/knows x without revealing x to Bob. • Motivation: authentication • Alice wants to prove her identity to Bob via some secret but doesn't want Bob to learn anything about this secret – Login methods where password is not stored on server (maybe hash of password is stored) – Alice (user/client) proves to Bob (server) that she knows the password without giving Bob the password 20

Zero Knowledge • Interactive method for Alice to prove to Bob that she has/knows x without revealing x to Bob. • Zero-knowledge proof must satisfy three properties: • Statement is “alice knows x” – Completeness: if the statement is true, the honest verifier (that is, one following the protocol properly) will be convinced of this fact by an honest prover. – Soundness: if the statement is false, no cheating prover can convince the honest verifier that it is true, except with some small probability. – Zero-knowledge: if the statement is true, no cheating verifier learns anything other than this fact. • Completeness and soundness needed for any interactive proof 21

Zero Knowledge • Example use: enforce honest behavior while maintaining privacy • Force a user to prove that its behavior is correct according to the protocol. • Used in secure multiparty computation 22

Zero Knowledge • • • Jean-Jacques Quisquater, et. al "How to Explain Zero-Knowledge Protocols to Your Children“ Peggy (prover) has uncovered the secret password to open a magic door in a cave. The cave is shaped like a circle, with the entrance in one side and the magic door blocking the opposite side. Victor (verifier) will pay Peggy for the secret, but not until he's sure that she really knows it. Peggy says she'll tell him the secret, but not until she receives the money. Zero knowledge – need a method by which Peggy proves to Victor that she knows the word without telling it to him Solution – Victor waits outside the cave, Peggy goes in. Label the left and right paths from the entrance A and B. She takes either A or B at random (Victor does not know which) – Victor enters the cave and shouts the path (A or B at random) on which she must return – Peggy returns along the path chosen by Victor, opening the door if it was not the path on which she had entered the cave – If Peggy did not know the word, there is a 50% chance she can return on the correct path; repeat the above many times, Peggy’s chance of successfully returning becomes negligible (assume chance of Peggy guessing the word is negligible) – If Peggy returns correctly each time, this proves she knows the word door A B enter 23

Agenda • • Forward Key Security Zero Knowledge Oblivious Transfer Multi-party Computation 24

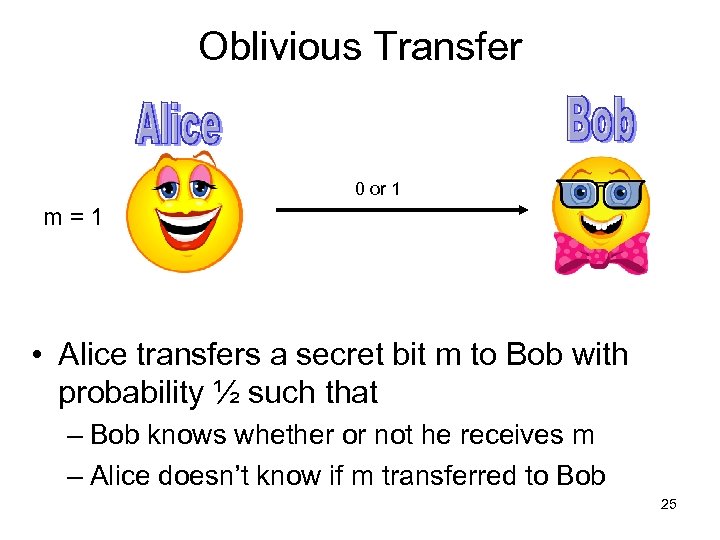Oblivious Transfer 0 or 1 m=1 • Alice transfers a secret bit m to Bob with probability ½ such that – Bob knows whether or not he receives m – Alice doesn’t know if m transferred to Bob 25

Oblivious Transfer – Example Method • Alice oblivious transfer to Bob • Alice – – picks 2 random primes p, q, set n = pq encrypt message m using n (such as with RSA) c = resulting ciphertext sends n and c to Bob • Bob – picks a Z*n at random – sends w = a 2 mod n to Alice • Alice – computes square roots of w: S = {x, -x, y, -y} – picks one of the four at random, s S and sends to Bob (probability s = a or –a is ½) • Bob – if s ≠ a, -a: Bob can factor n and obtain m (and will know he has m) – Won’t walk through why – see Rabin cryptosystem • Bob obtains m with probability ½ and Alice doesn’t know result 26

Oblivious Transfer – Example Method • Works if Bob selects a at random (doesn’t cheat) • Not known if Bob gains any advantage (can cheat) if intentionally selects a specific a 27

Oblivious Transfer – Application • Alice and Bob will each sign a contract only if the other also signs it • Idea – If names are of equal length, could sign a letter at a time, alternating • But someone must go last and could abort – not complete last letter – Sign small fragment at a time – bit, pixel • Don’t know who will be last • If one stops, both are approximately at same point – But one could send garbage in a fragment • Oblivious transfer solves the problem 28

Oblivious Transfer – Application • Alice and Bob will each sign a contract only if the other also signs it • Idea – If names are of equal length, could sign a letter at a time, alternating • But someone must go last and could abort – not complete last letter – Sign small fragment at a time – bit, pixel • Don’t know who will be last • If one stops, both are approximately at same point – But one could send garbage in a fragment • Oblivious transfer solves the problem 29

Oblivious Transfer – Application • Alice and Bob each – create 2 signatures, pick 2 random keys and encrypt each signature (such as with a block cipher) • Alice – – LA = “Alice, this is my signature of the left half of the contract” RA = “Alice, this is my signature of the right half of the contract” Keys KLA, KRA CLA = EKLA(LA), CRA = EKRA(RA) • Bob – – LB = “Bob, this is my signature of the left half of the contract” RB = “Bob, this is my signature of the right half of the contract” Keys KLB, KRB CLB = EKLB(LB), CRB = EKRB(RB) • Contract is considered signed only if Alice and Bob each have both halves of other’s signature 30

Oblivious Transfer – Application • Alice sends one of KLA, KRA to Bob using oblivious transfer • Bob sends one of KLB, KRB to Alice using oblivious transfer • Alice and Bob exchange bits of both keys, one bit at a time from each key, in order, until all bits are sent. • If Alice sees a mistake in key bits received, Alice aborts – Likewise if Bob sees a mistake • Bob does not know if Alice has KBL or KBR, so he cannot risk sending an incorrect value for either key – Likewise for Alice • Must exchange bits simultaneously; otherwise, last one could flip last bit 31

Agenda • • Forward Key Security Zero Knowledge Oblivious Transfer Multi-party Computation Some slides are modified from a presentation by Juan Garay, Bell Labs 32

Secure MPC • A set of parties with private inputs wish to compute some joint function of their inputs. • Parties wish to preserve some security properties. E. g. , privacy and correctness. – Example: secure election protocol • Security must be preserved in the face of adversarial behavior by some of the participants 33

Secure MPC Multi-party computation (MPC) [Goldreich-Micali-Wigderson 87] : – – n parties {P 1, P 2, …, Pn}: each Pi holds a private input xi One public function f (x 1, x 2, …, xn) All want to learn y = f (x 1, x 2, …, xn) (Correctness) Nobody wants to disclose his private input (Privacy) 2 -party computation (2 PC) [Yao 82, Yao 86] : n=2 Studied for a long time. Focus has been security. 34

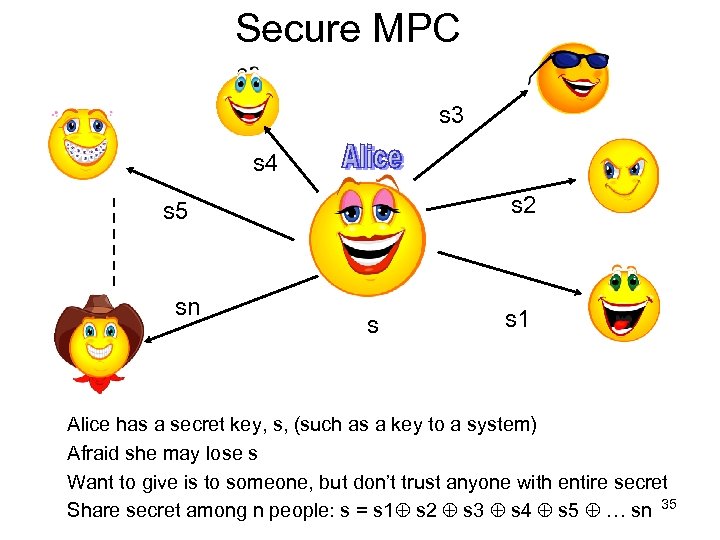Secure MPC s 3 s 4 s 2 s 5 sn s s 1 Alice has a secret key, s, (such as a key to a system) Afraid she may lose s Want to give is to someone, but don’t trust anyone with entire secret Share secret among n people: s = s 1 s 2 s 3 s 4 s 5 … sn 35

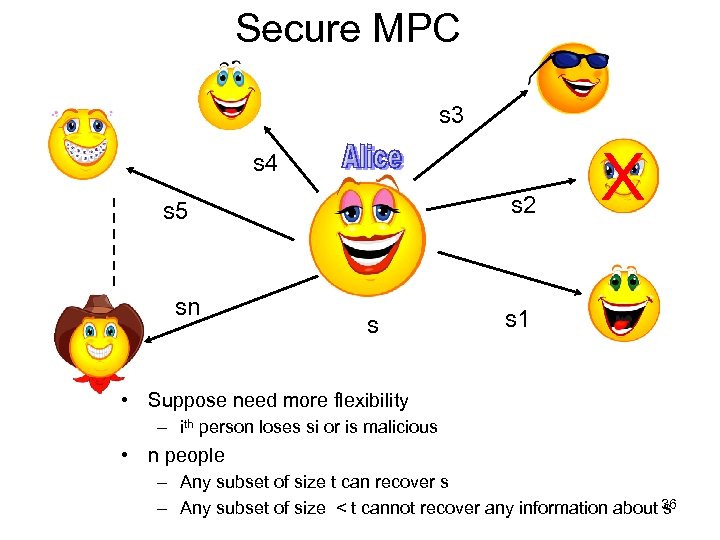Secure MPC s 3 s 4 s 2 s 5 sn s X s 1 • Suppose need more flexibility – ith person loses si or is malicious • n people – Any subset of size t can recover s – Any subset of size < t cannot recover any information about 36 s

Secure MPC • Use polynomials • Finite field F (such as some Z*p for prime p) • F(x) = a 0 x 0 + a 1 x 1 + a 2 x 2 + … atxt • Coefficients a 0, a 1, a 2 … at F • t+1 terms (degree is t) 37

Secure MPC • Polynomials properties: • Interpolation: given t+1 distinct points, (x 1, y 1), (x 2, y 2) … (xt+1, yt+1) , can find a 0, a 1, a 2 , … at • Secrecy: if have only t (or fewer) distinct points, can’t determine anything about a 0 38

Secure MPC • Coefficients – Pick a 1, a 2. . at at random – set a 0 = s • Each person is associated with a distinct point – Person i assigned distinct xi – Set si = f(xi) : (xi, si) is point for person i 39

Secure MPC • Polynomial construction requires honesty – Entity choosing ai’s, xi’s is dishonest – Collusion – person 2 may give (x 2, s 2) to person 10 • Verifiable secret sharing – Each person can verify piece received is a proper piece – Allows for O(log n) colluders – Based on factoring [Chor, Goldwasser, Micali, Awerbuch] 40

Instances of 2 PC • Authentication – Parties: 1 server, 1 client. – Function : if (server. passwd == client. passwd), then return “succeed, ” else return “fail. ” • On-line Bidding – Parties: 1 seller, 1 buyer. – Function: if (seller. price <= buyer. price), then return (seller. price + buyer. price)/2, else return “no transaction. ” – Intuition: In NYSE, the trading price is between the ask (selling) price and bid (buying) price. 41

Instances of MPC • Auctions – Parties: 1 auctioneer, (n-1) bidders. – Function: Many possibilities (e. g. , Vickrey*). • Consider a secure auction (with secret bids): – An adversary may wish to learn the bids of all parties – to prevent this, requires privacy – An adversary may wish to win with a lower bid than the highest – to prevent this, requires correctness *sealed-bid, bidders submit written bids without knowing the bid of the others. Highest bidder wins, but pays secondhighest bid. Intent: bidders bid true value. 42

MPC Protocols Consider 2 PC (MPC is similar). Two parties: P 0 and P 1. Encode function as a Boolean circuit of ANDs and XORs Bits on each wire are shared using XOR Per-gate evaluation: (Shared) Inputs: x = x 0 x 1 , y = y 0 y 1 XOR: No interaction needed ( x y ) = ( x 0 y 0 ) ( x 1 y 1 ) AND: More complex (needs interaction) Each party reveals his shares 43

MPC – Elections • • m voters: v 1, v 2, … vm ith voter inputs xi Result: function, f, of xi’s Required properties – – – – Only authorized voters can vote Each can only vote once Each vote is secret No vote can be duplicated by another voter Vote tally correctly computed Anyone can check the tally is correct Fault tolerate protocol: works if some number of “bad” parties Cannot coerce a voter into revealing how he/she voted (no vote-buying) • Meeting all requirements tricky, especially last • In real life – system, logistical problems main issues as opposed to protocols 44

MPC –Digital Cash • Required properties – Prevent forgery – Prevent or detect duplication – Preserve customer’s anonymity • Practical: – operationally feasible (ex. no large single database of all issued digital cash) 45

Digital Cash • 3 protocols – Withdrawal – user can obtain a digital coin – Payment – user buys goods from vendor using digital coin – Deposit – vendor gives digital coin to bank to be credited to the vendors account • Notation: – – – U = user B = Bank V = vendor D = digital coin of $100 SKB{x} = signature of B on x 46

Digital Cash - Withdrawal • U notifies B wants to withdraw D • B gives D to U D = SKB{I am a $100 bill, #4527} • U checks signature – accepts D if it is valid – else rejects D • Bank deducts D from U’s account if U accepts D 47

Digital Cash - Payment • U pays V with D • V checks signature – accepts D if it is valid – else rejects D 48

Digital Cash - Deposit • V gives D to B • B checks signature – accepts D if it is valid and credits V’s account – else rejects D 49

Digital Cash – Do Properties Hold? • Prevent forgery – ok, infeasible under basic assumptions of signature schemes • Prevent or detect duplication – Very easy to duplicate coins, double spend • Preserve customer’s anonymity – No anonymity – know U and where D was spent 50

Digital Cash – Fix Properties • Blind signature – U presents D to B – B signs D without seeing its contents (i. e. can’t associate with U) • Analogy: U covers check with carbon paper and seals both inside an envelope. Bank signs outside of envelop – But how does B know D is not fake? 51

Digital Cash – Fix Properties • RSA Blind signature – – – – Have key pair (e, n) (d, n) U picks random r mod n U computes D’ = D – re mod n presents D’ to B B signs D’: s’ = (D’)d mod n (= Md (re)d = Mdr mod n ) B deducts D from U’s account U computes signature on M: s = Md mod n by dividing s’ by r • Now anonymity: no link between U and D • But – B can be tricked into signing fake D – D can be duplicated and double spent 52

Digital Cash – Fix Properties • One denomination or one public key per denomination, feasible – not many denominations • Probability method – – – U makes up 100 D’s Blind signature on all 100 and gives all to B B signs one, requires U to unblind the rest (reveal r’s) U has 1/100 chance of successfully cheating U spends 1 remaining D, anonymous 53

Digital Cash – Fix Properties • Now have anonymity and no (or small) chance of cheating • How to prevent double spending? • B has database of all D, records D’s as they are returned spent from V – not too practical – large database, V must wait for B to ok each D at time of purchase 54

Digital Cash – Fix Properties • What if just detect double spending? • Random identity string (RIS) – Different for every payment of D – Only U can create a valid RIS – Two different RIS’s on same D allows B to retrieve U’s name • If B receives two identical D’s with different RIS values, U cheated • If B receives two different D’s with same RIS values, V cheated 55

Digital Cash – Fix Properties • H = hash • U creates 100 D’s – Di = (I’m a $100 bill, #4527 i, yi, 1 y’i, 1, yi, 2, y’i, 2, …yi, k, y’i, k) – where yi, j = H(xi, j); y’i, j = H(x’i, j) xi, j and x’i, j are randomly chosen but such that xi, j x’i, j = U’s name i, j 56

Digital Cash – Fix Properties • Withdrawal – U blinds each Di, get D’i – B has U unblind all but one D’i and reveals appropriate xi, j and x’i, j – B checks for each yi, j = H(xi, j); y’i, j = H(x’i, j) xi, j x’i, j = U’s name – B signs remaining blind D’i and gives to U 57

Digital Cash – Fix Properties • Payment – – – U gives D’i to V V checks B’s signature on D’i V creates a challenge: random bit string b 1, b 2, … bk If bj = 0, U reveals xi, j , else reveals x’i, j V checks yi, j = H(xi, j) or y’i, j = H(x’i, j) and accepts if yes, else rejects • Probability in a different payment that same RIS is produced is 2 -k because V creates challenge at random • Only U can produce valid RIS – H is computationally infeasible to invert • Two different RIS values on same D’I leaks U’s name: have xi, j and x’i, j for some j (due two different challenges) 58

Digital Cash – Fix Properties • Deposit – V gives D’i, s’, RIS to B – B verifies signature, checks if already returned – If already in database, B compares RIS values – If different, U double spent – If equal, V trying to deposit twice 59

Other MPC Applications • Database Query: – Alice has a string q; Bob has a database of strings – Alice wants to know whethere exists a string ti in Bob's database that matches q (exact or close) – Privacy: – Bob cannot know Alice's q or the response – Alice cannot know the database contents except for what can be known from the query result 60

Other MPC Applications • Profile Matching – Alice has a database of known hacker's behaviors – Bob has a hacker's behavior from a recent break-in – How can Bob check if his hacker is in Alice’s database while • Not disclosing the hacker's actual behavior to Alice – doing so that might disclose the vulnerability in his system. • Not obtaining contents of Alice’s database – it contains confidential information. 61

Other MPC Applications • Companies want to cooperate in preventing intrusions into their networks. – Need to share data patterns, but this is sensitive information • Real data for IDS/security research – None exists – Outdated/now irrelevant MIT Lincoln Laboratory IDS Evaluation Data Set 19982000 62

Other MPC Applications • In general, many database applications – Simple queries – Determining intersection – Sharing of patterns without revealing actual content 63

Backup 64

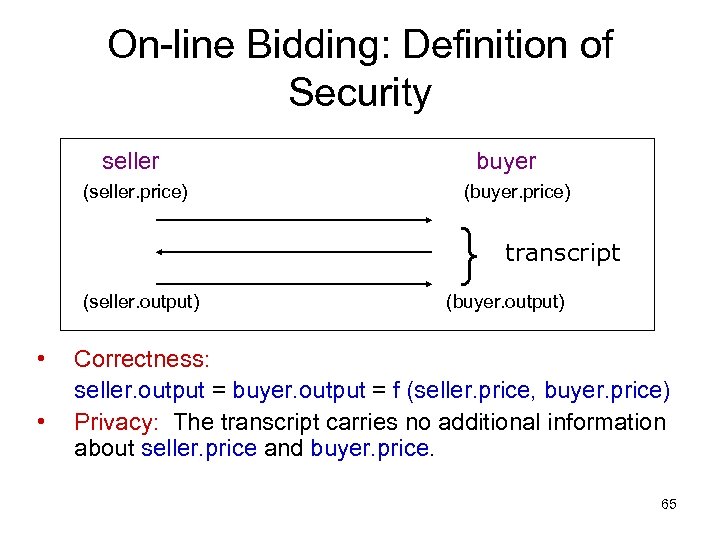On-line Bidding: Definition of Security seller (seller. price) (seller. output) • • buyer (buyer. price) } transcript (buyer. output) Correctness: seller. output = buyer. output = f (seller. price, buyer. price) Privacy: The transcript carries no additional information about seller. price and buyer. price. 65

“Privacy” is a little tricky… On-line Bidding Function if (seller. price <= buyer. price), then return (seller. price + buyer. price)/2, else return “no transaction. ” • • • If seller. price ≤ buyer. price, then both parties can learn each other’s private input. If seller. price > buyer. price, then both parties should learn nothing more than this fact. Privacy: Each party should only learn whatever can be inferred from the output (which can be a lot sometimes). 66

Fair Secure Multi-Party Computation (FMPC) Parties P 1, P 2, …, Pn (some corrupted), each holding private input xi, wish to compute y = f(x 1, x 2, …, xn) privately and correctly. Security is about absolute information gain. “At the end of the protocol, each party learns y (and anything inferable from y). ” Fairness is about relative information gain. “At the end of the protocol, either all parties learn y, or no party learns anything. ” Important in MPC; crucial in some applications (e. g. , two-party contract signing). 67

Security vs. Fairness • The problem of secure MPC/2 PC is well-studied and well-understood. • The problem of fair MPC/2 PC less developed • Security and fairness – different concepts – Fair without being secure 68

Security Fairness On-line Bidding Function if (seller. price <= buyer. price), then return (seller. price + buyer. price)/2 else return “no transaction. ” E. g. , in an unfair on-line bidding protocol, the seller may learn the output (and thus buyer. price) before the buyer learns anything. 69

Cheating with Unfair Protocols A cheating seller: 1. Initiate protocol with price x (originally $999, 999). 2. Run until getting the output (buyer hasn’t got the output yet). 3. if (output == “no transaction”), then abort (e. g. , announce “network failure”), set x x-1, and repeat. A cheating seller can: – find out the buyer’s price (destroys privacy) and – achieve maximum profit (destroys correctness) (the actual function computed is {return buyer. price}) The lack of fairness completely voids the security! 70

Fairness: Positive Results n parties, t corrupted: • t n/3 — possible with p 2 p channels – computational [GMW 87] – information-theoretic [BGW 88, CCD 88] • n/3 t n/2 — possible with broadcast channel – computational [GMW 87] – information-theoretic [RB 89] 71

Unfortunately… • Fairness is impossible with corrupted majority (t n/2): Intuition (2 parties): Party sending the last message may abort early. • Consequently, many security definitions do not consider fai or only consider partial fairness [BG 90, BL 91, FGHHS 02, G 72

Fairness After the Impossibility Result We still need (some form of) fairness, so “tweak” model/definition: “Optimistic” approach (tweak the model) [M 97, ASW 98, CC 0 • Adds a trusted party as an arbiter in case of dispute. • Needs to be (constantly) available. “Gradual Release” approach (tweak the definition) [Blum 83, D 95, BN 00, …] • No trusted party needed. • Parties take turns releasing info’ “little-by-little. ” • Still somewhat unfair, but we can quantify and control the amount of “unfairness. ” 73

The Gradual Release Approach • Reasonably studied – Initial idea by [Blum 83] – Subsequent work: […, Damgard 95, Boneh-Naor 00, Garay-Pomerance 03, Pinkas 03, …] • Not quite well-understood – – – Ad hoc security notions Limited general constructions (only 2 PC) Few practical constructions 74

Security and Fairness A typical gradual release protocol (e. g. , [BN 00, GP 03, P 03]) consists of two phases: 1. Computation phase: “Normal” computation. 2. Revealing phase: Each Pi gradually reveals a “secret” si ; then each Pi computes the result y from s 1, s 2, …, sn. 75

Observation on Existing MPC Protocols Many (unfair) MPC protocols (e. g. , [GMW 87, CDN 01, CLOS 02]) share the same structure: Sharing phase: Parties share data among themselves (simple sharing, or (n, t) threshold sharing) Evaluation phase: “Gate-by-gate” evaluation (all intermediate data are shared or “blinded”) Revealing phase: Each party reveal its secret share ir! fa (all parties learn the result from the shares) n U Honest parties reveal their secrets, and corrupted parties abort (and learn the result). 76

FCPFO : Commit-Prove-Fair-Open • Commit phase: Every party Pi commits to a value xi. • Prove phase: Every party Pi proves a relation about xi. • Open phase: Open x 1, x 2, …, xn simultaneously. Simultaneous opening guarantees fairness — either all parties learn all the committed values, or nobody learns anything. Using FCPFO, the revealing phase becomes fair, and so does MPC protocol. 77

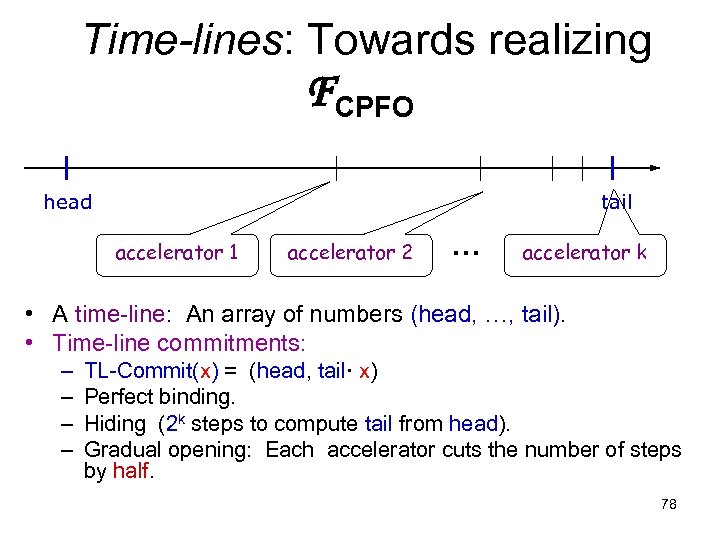Time-lines: Towards realizing FCPFO head tail accelerator 1 accelerator 2 … accelerator k • A time-line: An array of numbers (head, …, tail). • Time-line commitments: – – TL-Commit(x) = (head, tail· x) Perfect binding. Hiding (2 k steps to compute tail from head). Gradual opening: Each accelerator cuts the number of steps by half. 78

A time-line, mathematically [BN 00, GJ 02, GP 03] accelerator 1 g g 2 k-1 2 accelerator 2 g … … (2 k-1+2 k-2) 2 g 2 k 2 • N: “safe Blum modulus, ” N = p·q, where p, q, (p-1)/2, (q-1)/2 are all primes. • g a random element in ZN*. • head = g, tail = g 2 k 2 79

A time-line, mathematically (cont’d) accelerator 1 g G[i] = g g 2 k-1 2 accelerator 2 g … … (2 k-1+2 k-2) 2 g 2 k 2 2 i 2 • Can move forward m positions by doing m squarings • Knowing (N), one can compute G[i] efficiently, for any i. • Hard to move backward, not knowing factorization of N • inefficient to move forward (step-by-step) point “far away” is “unknown”… 80

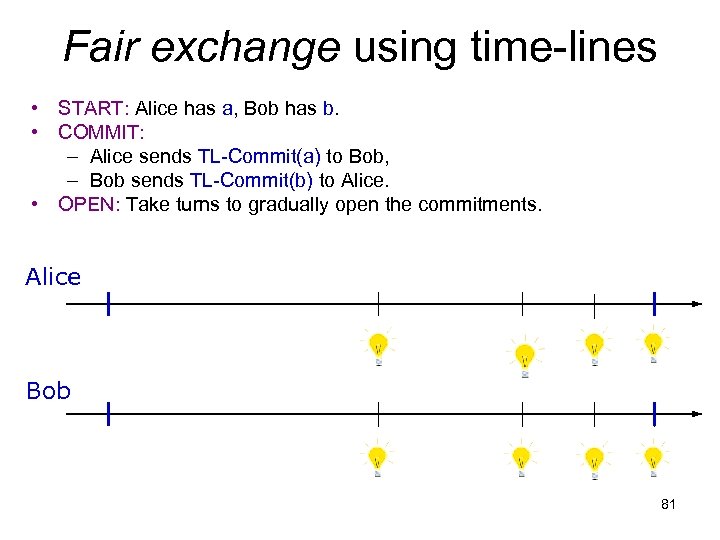Fair exchange using time-lines • START: Alice has a, Bob has b. • COMMIT: – Alice sends TL-Commit(a) to Bob, – Bob sends TL-Commit(b) to Alice. • OPEN: Take turns to gradually open the commitments. Alice Bob 81

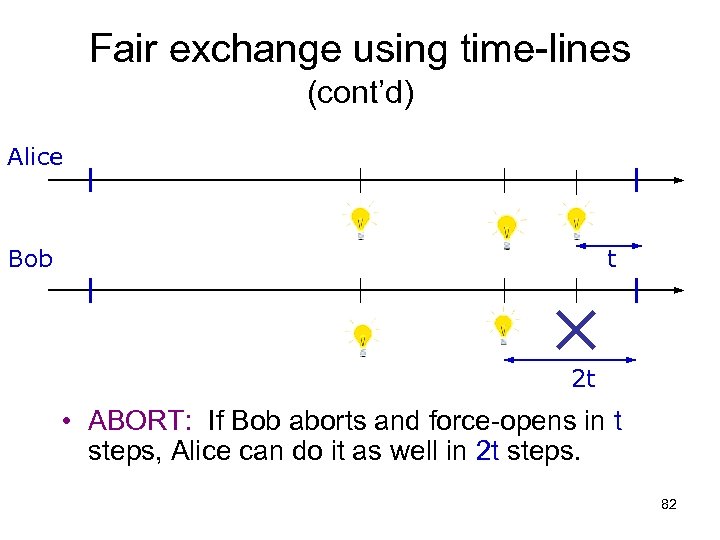Fair exchange using time-lines (cont’d) Alice Bob t 2 t • ABORT: If Bob aborts and force-opens in t steps, Alice can do it as well in 2 t steps. 82

Realizing FCPFO using time-lines • Setup: A “master” time-line T = N; g; G[j], j=1, …, k in CR • Commit: Each party Pi : Derives a time-line Ti= N; gi; Gi[j] ; TL-commits to xi : (gi; Gi[k]· xi), • Prove: Standard ZK proof. • Open: In round m, each party Pi reveals Gi[m] with ZK proo if any party aborts, enter panic mode. Panic mode: Depends on current round m… • If (k-m) is “large, ” then abort. (A does not have enough time to force-open. ) • If (k-m) is “small, ” then force-open. (A has enough time to force-open as well. ) 83

Putting things together… Plug FCPFO into existing MPC protocols Fair MPC protocols 84