dda55dbd4edb62c7c4081a7af7de6253.ppt
- Количество слайдов: 56

Introduction to options Basic and advanced concepts TIP If you do not understand something, ask me!

Today’s plan Introduction of options y. Definition of options y. Position diagrams y. No arbitrage argument y. Put-call parity y. Application of put-call parity y. How parameter values affect option values? 2

Introduction to options What is an option? z An option is a right to do something at a specified price or cost on or before some specified date. z An option, is a contract, and is therefore “written” – just means it exists z Options are everywhere. y. AOL offers its CEO a bonus (stock options) if its stock price exceeds $65 per share y. You have the option to come to my office hours at the cost of walking several extra steps. 3

Brief History z. Options are a form of insurance, so in that sense they have been around for quite some time. z. The first organized exchange on which options were traded was opened in Chicago in 1973. Before that, options were traded over-the-counter. 4

Brief History (cont’d) z. In the same year, the Black-Scholes formulae for option prices was published. The prices predicted by the formulae turned out to be extremely close to actual option prices. z. The popularity of options skyrocketed. They are arguably the most successful derivative security ever! 5

Financial Options vs. Real Options z Financial Options y. Options written on financial asset are called financial options, or simply “options” x(ex: option written on IBM or Dell) z Real options y. Options written on real assets are called real options y. For example, the option to set up a factory or discontinue a division is called real option 6

Now we focus on two types of (financial) options… z. Call y. An option to buy an underlying security (for example, a stock) for a fixed price (that is, the strike or exercise price) on or before a certain date (expiration date or maturity date). z. Put y. An option to sell the underlying security (for example, a stock) for a fixed price (that is the strike or exercise price) on or before a certain date (expiration date or maturity date). 7

Option Terms z. Exercising the Option y. Enforcing the contract, i. e. , buy or selling the underlying asset using the option z. Striking, Strike, or Exercise Price y. The fixed price specified in the option contract for which the holder can buy or sell the underlying asset. z. Expiration Date y. The last date on which the contract is still valid. After this date the contract no longer exists. 8

Option terminology z In-the-money call – a call option whose exercise price is less than the current price of the underlying stock. z Out-of-the-money call – a call option whose exercise price exceeds the current stock price. z Another way to remember whether an option is in the money: if you can make money by immediately exercising your option, the option is in the money. (You may not be able to exercise it, though. ) 9

European vs. American Options z. European y. A European option can only be exercised on the exercise date. z. American y. An American option can be exercised on any date up to the exercise date. 10

Option Obligations z Options are rights (to the buyer), and are obligations (to the seller) z This means that: ythe buyer of an option may or may not exercise the option. y. However, the seller of the option must sell or buy the underlying assets if the buyer decides to exercise the option. 11

What is a short position in an option? y. In this case the other party has the option. y. Is a long position in a call the same as a short position in a put? 12

Payoff or cash flows from options at expiration date z. The payoff of a call option with a strike price K at the expiration date T is y. Where S(T) is the stock price at time T z The payoff of a put option with a strike price K at the expiration date T is y. Where S(T) is the stock price at time T 13
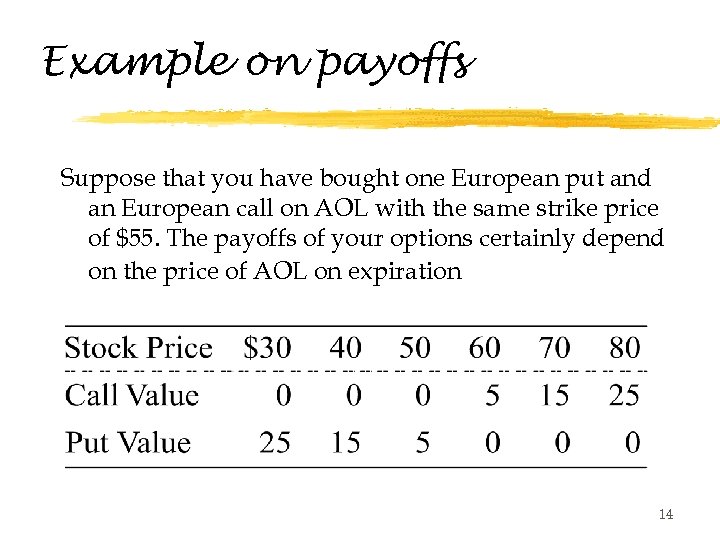
Example on payoffs Suppose that you have bought one European put and an European call on AOL with the same strike price of $55. The payoffs of your options certainly depend on the price of AOL on expiration 14
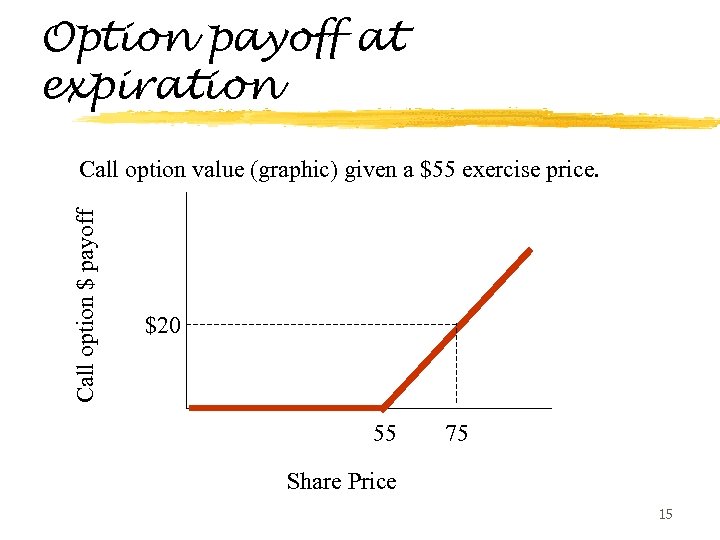
Option payoff at expiration Call option $ payoff Call option value (graphic) given a $55 exercise price. $20 55 75 Share Price 15
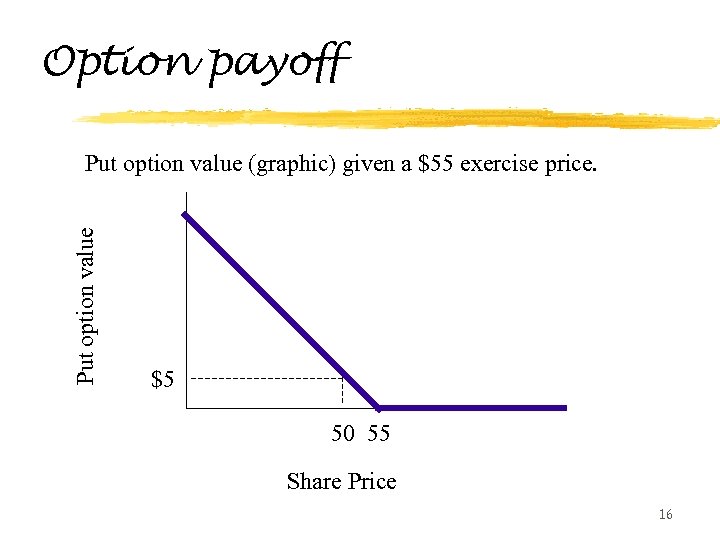
Option payoff Put option value (graphic) given a $55 exercise price. $5 50 55 Share Price 16
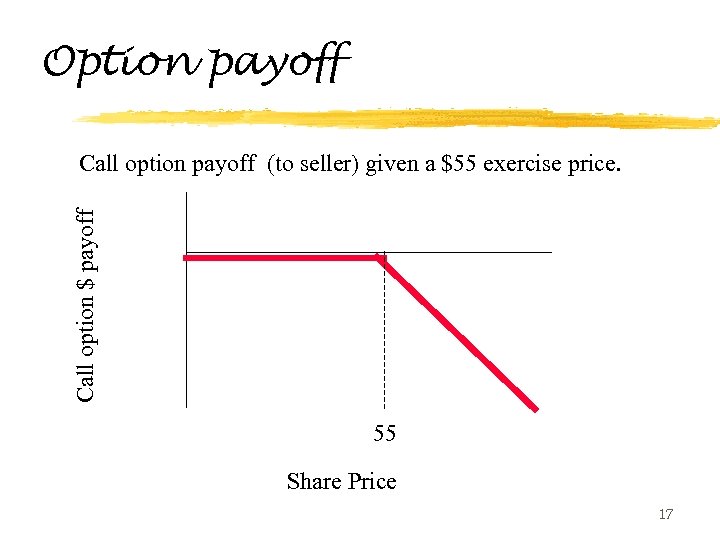
Option payoff Call option $ payoff Call option payoff (to seller) given a $55 exercise price. 55 Share Price 17
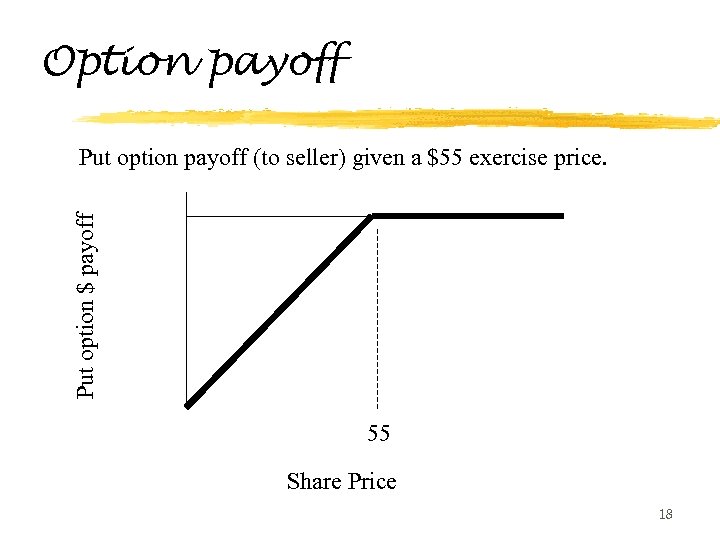
Option payoff Put option $ payoff Put option payoff (to seller) given a $55 exercise price. 55 Share Price 18

Let's do some examples. z. Going short, selling an option you do not own, or writing an option are all the same thing. z. You have written a call with a strike of $50 on GM stock. What is your position if, on the expiration date, GM closes at $55 $45 z. Who has the option in this case? 19
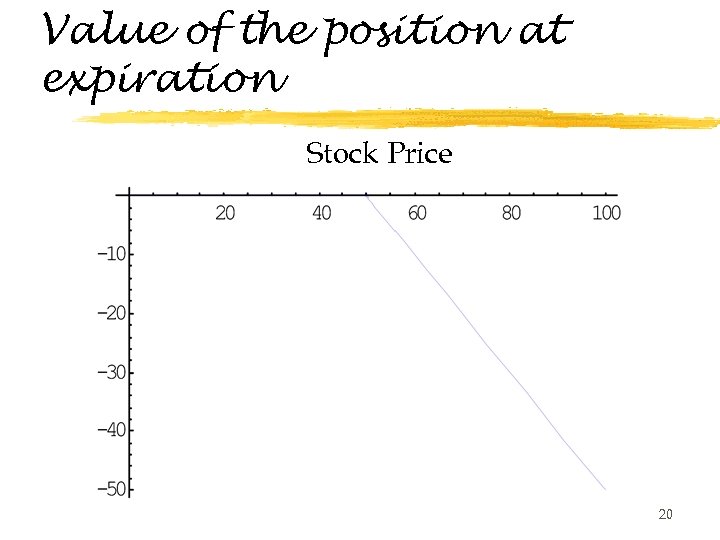
Value of the position at expiration Stock Price 20

Shorting Puts z. You have written a put with a strike of $50 on GM stock. What is your position if, on the expiration date, GM closes at $55 $45 z. Who has the option in this case? 21
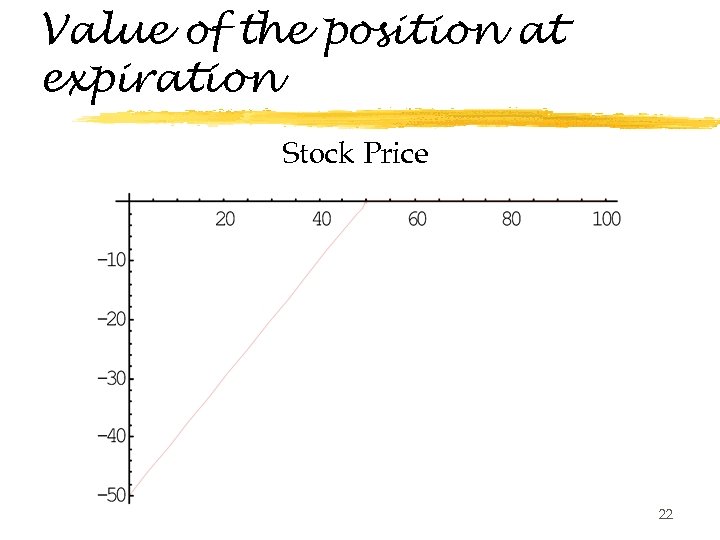
Value of the position at expiration Stock Price 22
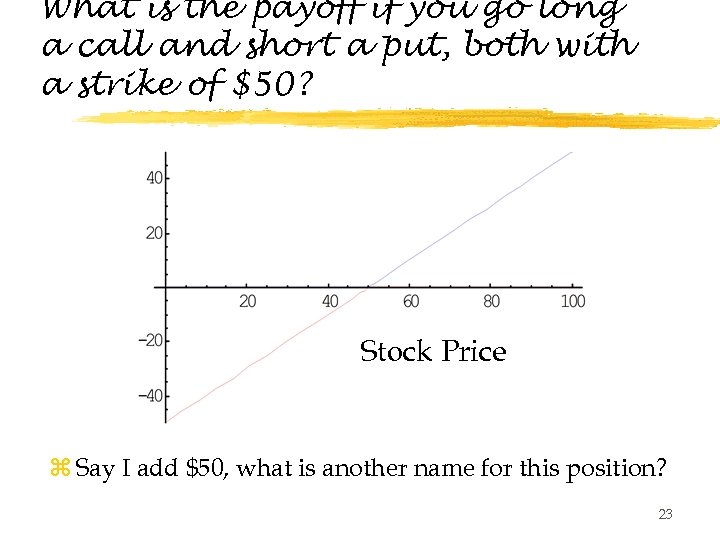
What is the payoff if you go long a call and short a put, both with a strike of $50? Stock Price z Say I add $50, what is another name for this position? 23

Some examples z. Please draw position diagrams for the following investment: y. Buy a call and put with the same strike price and maturity (straddle) 24
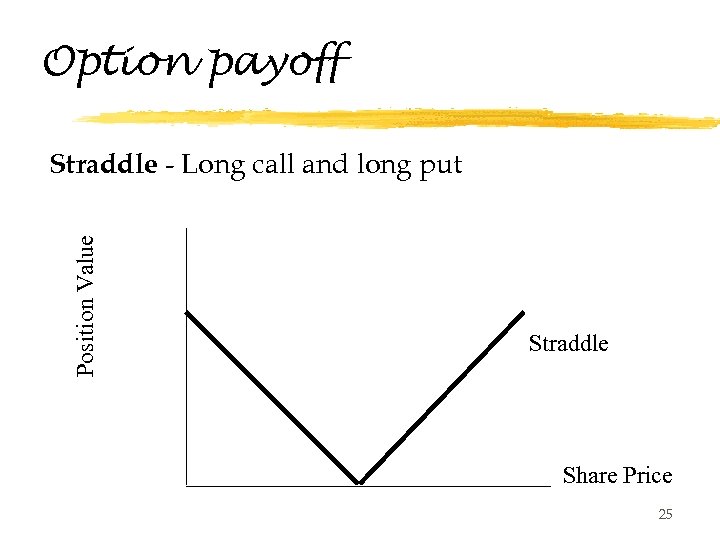
Option payoff Position Value Straddle - Long call and long put Straddle Share Price 25

More examples y. Buy a stock and a put (protective put) 26
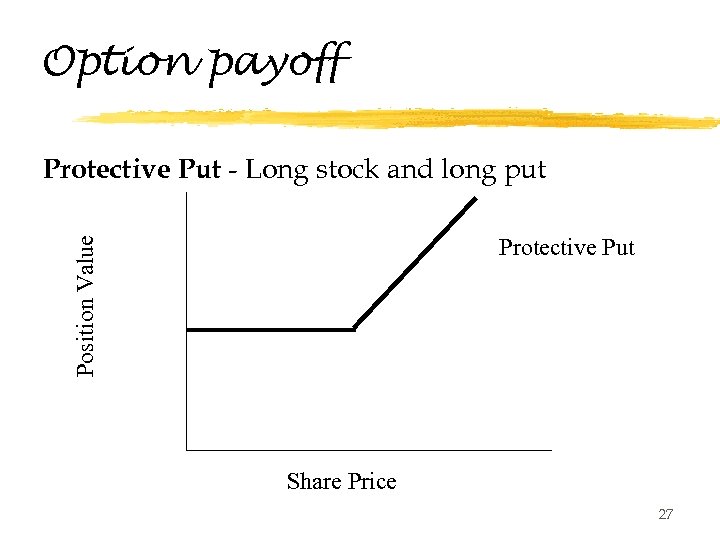
Option payoff Protective Put - Long stock and long put Position Value Protective Put Share Price 27

Valuation of options z. At expiration an option must be worth its exercise value or zero. z. An American option's value is as least as large as its immediate exercise value (why? ) and since it gives an extra right (which can always be ignored) is always at least as valuable as its European counterpart. 28

Valuation of options z. An American call's (put's) value can never exceed the value of the stock (strike price) y. Why? z. Does this principle hold for European options? z. Yes. 29

Valuation of options z. Everything else equal, the longer maturity for An American option, the more valuable. y. Why? z. Does this principle hold for European options? 30

Valuation of options z. An American call (put) with a higher exercise price will be worth less (more). z. Why? z. Does this principle apply to European options? z. Yes. 31

Put-Call Parity z. Let P(K, T) and C(K, T) be the prices of a European put and a call with strike prices of K and maturity of T. S 0 is current stock price. Then we have or Where 32

No arbitrage concept z. If two securities have the exactly the same payoff or cash flows in every state of each future period, these two securities should have the same price; otherwise there is an arbitrage opportunity or money making opportunity. 33

Let’s show put-call parity z. We can first use position diagrams to show put-call parity z. This exercise is a good way of getting used to the ideas of the single price rule or no arbitrage argument. 34
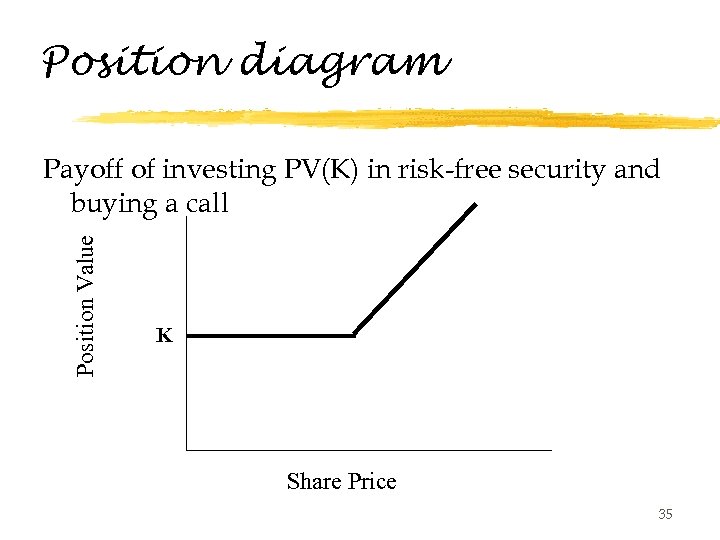
Position diagram Position Value Payoff of investing PV(K) in risk-free security and buying a call K Share Price 35
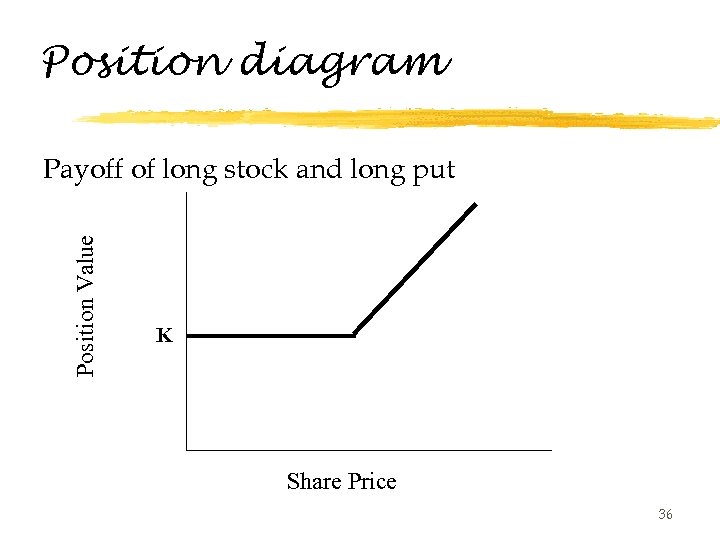
Position diagram Position Value Payoff of long stock and long put K Share Price 36

The conclusion z. Since both portfolios in the previous two slides give you exactly the same payoff, they must have the same price. That is, 37

In the above we have assumed that the stock will not pay any dividend. z Consider dividend payment D before expiration date. For European options: 38

Things to note about Put. Call parity z. Only works for European options. z. Based on arbitrage so it works exactly. This is how brokers created puts out of calls when options were traded over the counter. 39

European vrs American Calls z. It turns out that you would never want to exercise an American call on a nondividend paying stock early. z. Why might you wish to exercise an American call early when the stocks pays dividend? 40

European vs American Puts z. There are times when you will want to exercise an American put on a nondividend paying stock early. z. Why? 41

concepts and put-call parity z. One important application of option concepts and put-call parity is the valuation of corporate bonds. z. For example, suppose that a firm has issued $K million zero-coupon bonds maturing at time T. Let the market value of the firm asset at time t be V(t). 42
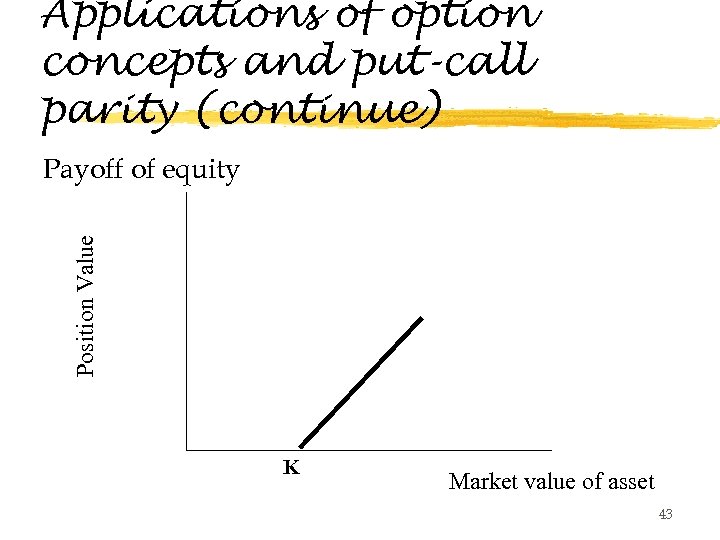
Applications of option concepts and put-call parity (continue) Position Value Payoff of equity K Market value of asset 43

concepts and put-call parity (continue) z So based on the position payoff diagram in the previous slide, we can see that the value of equity is just the value of a call option with strike price K. z Then bond value =Asset value –equity value (value of call: C(K, T) z Using the put-call parity, we have z Bond value=V(A)-(V(A)+P(K, T)-PV(K))=PV(K)P(K, T) (value of put ) 44

concepts and put-call parity (continue) z. What does this result mean? z. The value of risky corporate bonds is equal to the value of the safe corporate bonds minus the cost of default. z. When will the firm default? y. At time T, if the value of asset is less than K, the firm will default. P(K, T) is the cost of this default to bond holders. 45

Some bounds about option values z Since an option is a right to buy or sell securities, its price is always non-negative. z Since at expiration, we have payoff Max(S(T)-K, 0) for a call with a price C(K, T) at time 0 Max(K-S(T), 0) for a put with a price P(K, T) at time 0 z Then 46

Some bounds about option values (continue) z. From put-call parity, we have z. Thus 47

the stock price on the call option z Consider the following two call options written on stocks A and B with the same strike price of $50 and same maturity, respectively: current price SA=SB=$40 and stock A is much more volatile than stock B. Then At maturity, stock A has a much larger chance that the stock price is larger than $50 than stock B. Thus, the payoff from the option on stock A is expected to be larger than from the option A. Thus the option on stock A is more valuable than the option on stock B. 48

Volatility and option values. z. For call options, the larger the volatility of the underlying asset, the larger the value of the option. z. Suppose a firm has both debt and equity. y. If the managers are to take riskier projects than bond holders expect, should the bond holders or equity holders benefit from this? 49
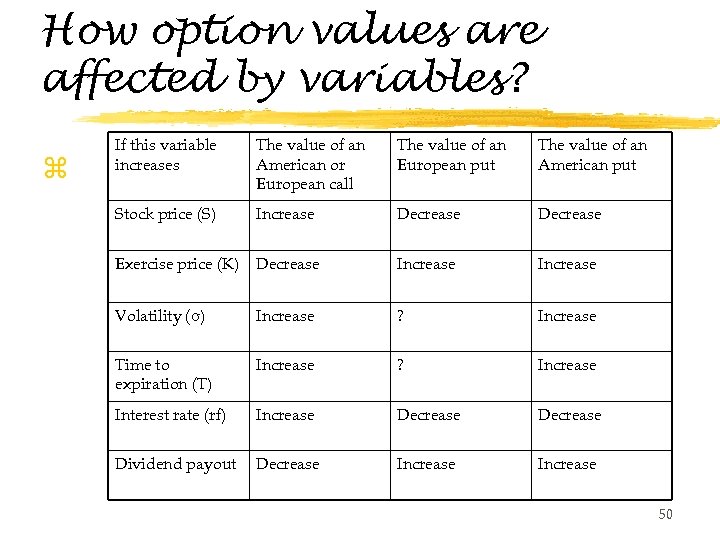
How option values are affected by variables? z If this variable increases The value of an American or European call The value of an European put The value of an American put Stock price (S) Increase Decrease Exercise price (K) Decrease Increase Volatility (σ) Increase ? Increase Time to expiration (T) Increase ? Increase Interest rate (rf) Increase Decrease Dividend payout Decrease Increase 50

The Black-Scholes formula for a call option z The Black-Scholes formula for a European call is z Where 51

The Black-Scholes formula for a put option z The Black-Scholes formula for a European put is z Where 52

Of course, if you already know a call with same maturity and expiration… z. You can get the put price by put-call parity. 53

Intuition for the Black-Scholes formula z One way to understand the Black-Scholes formula is to find the present value of the payoff of the call option if you are sure that you can exercise the option at maturity, i. e. , S - exp(-rt)K. z Comparing this present value of this payoff to the Black-Scholes formula, we know that N(d 1) can be regarded as the probability that the option will be exercised at maturity 54

An example z. Microsoft sells for $50 per share. Its return volatility is 20% annually. What is the value of a call option on Microsoft with a strike price of $70 and maturing two years from now suppose that the risk-free rate is 8%? z. What is the value of a put option on Microsoft with a strike price of $70 and maturing in two years? 55

Solution z. The parameter values are z. Then 56
dda55dbd4edb62c7c4081a7af7de6253.ppt