5540206b3abf7fd0ae012266415fad89.ppt
- Количество слайдов: 20

Introduction to MCMC and BUGS MODELING and DECISION MAKING USING BAYESIAN STATISTICS Part II Samu Mäntyniemi

MCMC and You • To apply Bayesian inference you need to know – What MCMC gives to you – How to use it – That it is not foolproof • You do not (necessarily) need to know – How MCMC works – Why it works – How to implement and program MCMC algorithms 3/17/2018 Biotieteellinen tiedekunta / Henkilön nimi / Esityksen nimi 2

Markov chain Monte Carlo simulation • Method for drawing random numbers from a probability distribution with unknown normalising constant =? • Posterior mean = mean of samples • Posterior sd = sd of samples • Posterior density = kernel density/frequency dist. Of samples

MC and MCMC • Monte Carlo – Direct sampling, Importance sampling, SIR, etc – Independent random numbers – Difficult to implement automatically, some hand tuning typically needed • Markov chain Monte Carlo (MCMC) – Dependent sequence of random numbers – Each simulation depends on the previous one (=Markov chain) – Relatively easy to automate – More simulations (=time) needed compared to well tuned MC – Needs to converge: the first part of the simulation does not represent the true distribution
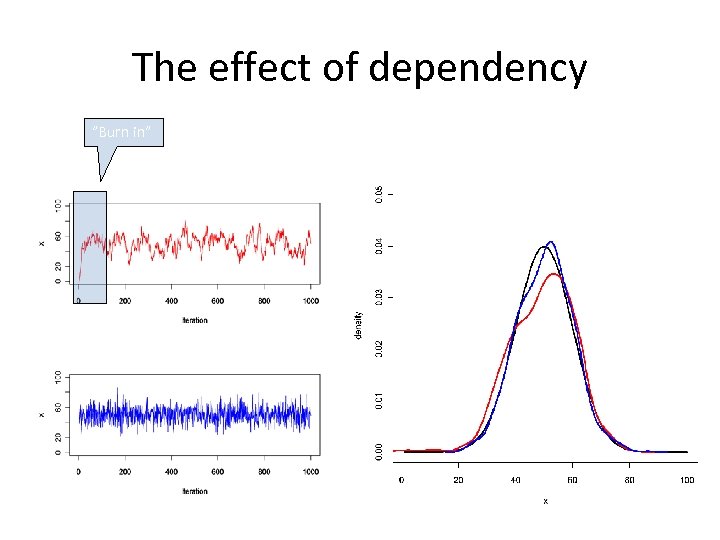
The effect of dependency ”Burn in”

How many samples after ”convergence”? • Depends on the problem – Just want to know roughly where the mean is located : 500 -1000 independent values – Want to know a small tail area probability: much more samples needed • A rule of thumb that is quite often used – Simulate until MC error / posterior sd < 0. 05 – MC error: standard error of the sample mean • Posterior sd / sqrt(number of samples)

Example: The Metropolis algorithm • Target: provide a sample from distribution 1. Choose arbitrary intial value θ 0 2. Draw a candidate value θt’ from a symmetric proposal distribution that is centered on θt-1. 3. Calculate ratio R=q(θt’)/q(θt-1) 4. Draw a number U from a uniform distribution 5. If R > U set θt = θt’, else θt =θt-1 6. Increase t and go to 2

How to implement MCMC for a model? • Use a programming language – Visual Basic (Excel) – C/C++ (AD Model Builder) – R / Matlab /SAS etc • Or use a pre-made toolbox – BUGS (Bayesian inference Using Gibbs Sampling) • Open. BUGS – JAGS (Just Another Gibbs Sampler)

Metropolis demo

Win. BUGS (Open. BUGS, Lin. BUGS, classic. BUGS…) • General purpose MCMC software • Implements MCMC automatically for almost any given model • Performance varies from excellent to non existent • Good for learning Bayesian analysis – As problem complexity increases, hand made samplers may become more efficient (=converge and mix faster) – But programming takes time and skill…

Working with BUGS • Specify the probability model, use the logic of directed acyclic graphs (DAGs) • Load the observed data • Decide how many MCMC chains to run in parallel • Provide or generate initial values for each chain • BUGS sets up all the MCMC algorithms by choosing an updating method for each variable or block of variables – There are 31 MCMC methods to choose from

Working with BUGS • Choose the length of the simulation, and start the simulation • Assess the convergence of MCMC by using diagnostic plots • Remove the burn in • Summarize the posterior distribution with descriptive statistics and plotting tools
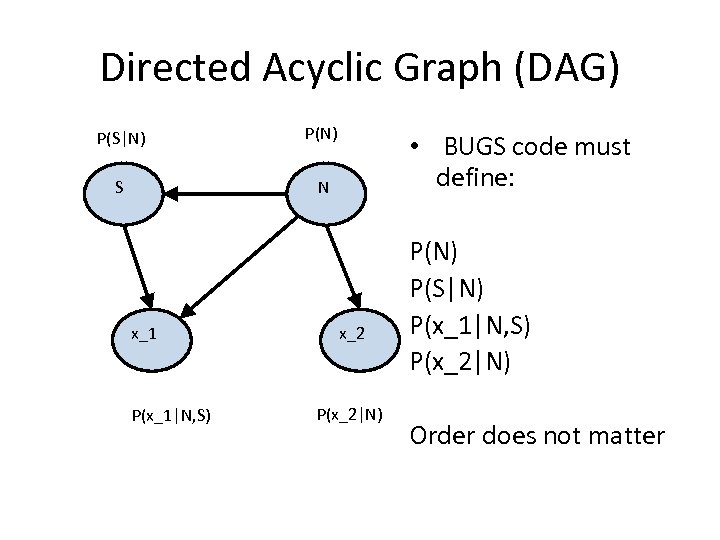
Directed Acyclic Graph (DAG) P(S|N) P(N) S N x_1 P(x_1|N, S) • BUGS code must define: x_2 P(x_2|N) P(S|N) P(x_1|N, S) P(x_2|N) Order does not matter

BUGS model specification language model{ μ # P(mu) mu~dnorm(70, tau_mu) tau_mu<-1/4 x # P(x|mu) x~dnorm(mu, tau_x) tau_x<-1/1 }

Open. BUGS walkthrough
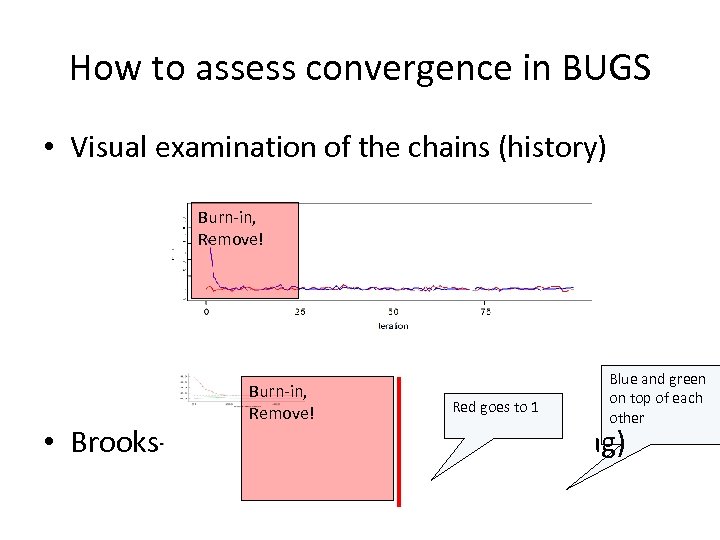
How to assess convergence in BUGS • Visual examination of the chains (history) Burn-in, Remove! Red goes to 1 Blue and green on top of each other • Brooks-Gelman-Rubin diagnostic (bgr diag)

Open. BUGS demo: convergence diagnostics

Problems with MCMC • Guaranteed to converge to posterior – …eventually. Can take thousands of years • Slow mixing – Chains may move slowly, do not mix well – Increases simulation time – Convergence difficult to assess • Generally difficult to estimate model uncertainty – Normalising constants would be needed • Remedies – Reparameterize the model (e. g. standardize covariates) – Use different MCMC algorithm – Buy more powerful computer or try some other ways of sampling from the posterior (IS, SIR, etc)

Problems with BUGS • Slow simulation – Avoid long deterministic calculations: add negligible amount of random variation if in trouble • Slow mixing – Disable/change the sampling algorithm • Error messages while simulating – Check the code • Log( 0 or negative) • Values outside of the range of a distribution – If code and model are logically correct • Try JAGS instead of BUGS – Faster and more stable, but no GUI

First exercise • Recall the example about ”healthy body temperature” • Try to write the model definition in BUGS language • Then run the model without data and explore the dependencies between variables • Finally, use measurement data on 9 individuals and predict the temperature of the 10 th person. Data is on the wiki.
5540206b3abf7fd0ae012266415fad89.ppt