Introduction to Mathematica AE 6381 Special Lecture Prof

Introduction to Mathematica AE 6381 Special Lecture Prof. J. Craig Fall 2008

What is Mathematica? • “A system for doing mathematics by computer” • Also for modeling, simulation, visualization, development, documentation, and deployment. • Available on all public computer clusters. • Can be installed on any GT-owned computer – Current version: 6. 0. 3 – Versions for: • Windows XP, Vista • Mac OS-X • Unix/Linux

Why consider Mathematica? • Powerful system for symbolic mathematical but also handles numerical mathematics, graphics, data visualization, simulation. • Larger community of users than Maple. • Versatile Notebook and Player for flexible documentation & distribution. • CONS: – VERY steep learning curve – Proprietary

What is this introduction? • I’ve been using Mathematica in AE 3125 Aerospace Structural Analysis in order to simplify tedious calculations and solve problems not readily doable by hand. • All homework solutions are in Mathematica. • I’ll try to provide a simple and very basic introduction using this as my reference. • I’ll suggest other uses and point to the Wolfram web pages and Screen. Casts.

References • Wolfram, S. , “Mathematica, ” 2 nd Edition, Addison. Wesley, 1991. • http: //www. wolfram. com is main web site. • Built-in Mathematica documentation (all written in Mathematica Notebook code) • Tutorial screencasts are an excellent source of helpful information and can be found at: http: //www. wolfram. com/broadcast/screencasts/ • Demonstration Project has great user demos at: http: //demonstrations. wolfram. com/ (create your own using File>New>Demonstration) • Mathematica Journal at http: //www. mathematicajournal. com

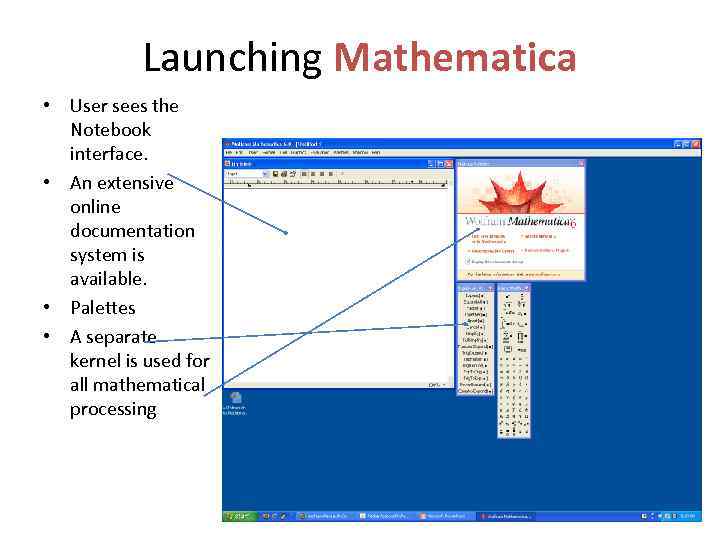Launching Mathematica • User sees the Notebook interface. • An extensive online documentation system is available. • Palettes • A separate kernel is used for all mathematical processing

Basic Notebook Operation • Type an expression; default style is Input – Press Enter (in numeric pad) or Shift-Return which will send Input to kernel – Result will appear on line below – Sequential line numbers are prepended by kernel • Style determines appearance and what happens to line(s). Input is always sent to kernel. • Styles define appearance of blocks of cells shown by brackets at right margin. – Click cell bracket to select (to change, cut, copy…) – Double-click cell bracket to collapse that cell – Can collapse an entire bracket to the first cell

Notebooks • Provide a very readable display of code along with comments to fully document • Can collapse/hide portions (styles are useful here) • Layout is controlled by styles that can be modified by the user to change appearance • Can insert graphics, logos, etc. • Previous output can be saved in Notebook, including plots. • Use Evaluation>Evaluate Notebook to compute Notebook (send code to kernel). • Can also click on style bracket(s) and hit Enter (or Shift. Return) to compute that selected portion of Notebook.

Notebook and Kernel Issues • Kernel retains state of computations and sequentially numbers all input and output lines. • Must manually clear any previous variables – Clear[variables] (* clears values of variables *) – x=. (* same as Clear *) – Remove[“Global`*”] (* removes all variables *) • May need to “quit” local kernel to reset counter. See Evaluation>Quit Kernel

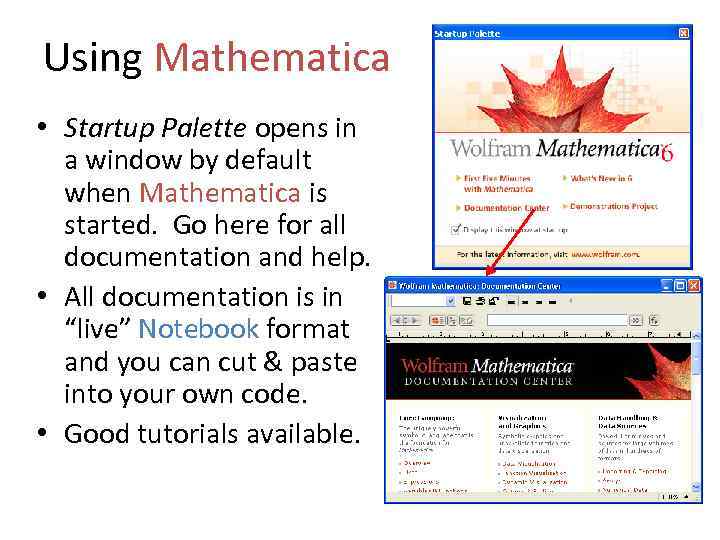Using Mathematica • Startup Palette opens in a window by default when Mathematica is started. Go here for all documentation and help. • All documentation is in “live” Notebook format and you can cut & paste into your own code. • Good tutorials available.

Useful details… • Use of brackets: – – [ ] { } [[n ( ) =function arguments =defines a list (can be nested) ]] =indexes a list (equiv to Part[ ] ) =groups mathematical operations • N[expr]=numeric value =operator postfix notation • expr/. x→ 2 =transformation rule (substitution) • % =previous result (%%=next to previous) • %n =result on Output line n • expr//

Basic operations • • Simple numerical computations Simple symbolic computations Using built-in Functions …

Useful Algebraic Manipulation • Can use Algebraic palette: – Click to apply directly to current expression – Type function and execute – Some functions have optional arguments Simplify[ expr, assum] = Simplify to expression with smallest number of terms. Optional: assumptions, i. e, x>0. Full. Simplify[ ]= same but with more effort… Expand[ expr]= Expand numerators, keeping denominator Expand. All[expr]= Expand numerators and denominators Expand. Numerator[expr]= Expand only numerator (like Expand[ ]) Expand. Denominator[ ]= Expand only denominator Factor[expr] = Factor a polynomial Together[expr] = Puts terms in a sum over a common denominator and cancels factors in the result. Apart[expr] = Rewrites a rational expression as a sum of terms with minimal denominators. Cancel[expr] = Cancels out common factors in the numerator and denominator of expr. Collect[expr, [x 1, . . }]= Collect together terms with same powers of objects matching x 1 …

Examples from AE 3125 • Shear flow in a thin-wall cross-section beam. – Function definitions – Symbolic integration – Plotting • Bending-shear-torsion in a complex thin-wall cross-section beam. – Solve ODE with boundary conditions – Rotational transformation using matrices

Another example… • Needed to explain to undergrad what happens to structural dynamics when you add a tip mass to a cantilever beam: – Set up PDE and use separation of variables – Solve spatial ODE – Compute eigenvalues and modeshapes – Animate?

Graphics • Large and sophisticated collection of graphics functions and objects. • Easy functional evaluation as well as basic numeric data plotting. • Many interesting examples available in Document Center and in “Demonstration Project. ” • Screencasts: http: //www. wolfram. com/broadcast/screencasts/

Data Manipulation • Easy to import data in many different file formats. • Many data sources (lots of new ones in 6. 0). • Computation as well as plotting. • Screencast: http: //www. wolfram. com/broadcast/screencasts/int egrateddata/

Other topics… • • • Programming in Mathematica Developing attractive Notebooks Using Packages Developing Packages Creating Notebook Player files (. nbp)