bc31174fd6651fa36490bb5369639bf0.ppt
- Количество слайдов: 63

Introduction to Management Science 8 th Edition by Bernard W. Taylor III Chapter 8 Project Management Chapter 8 - Project Management 1

Chapter Topics The Elements of Project Management The Project Network Probabilistic Activity Times Activity-on-Node Networks and Microsoft Project Crashing and Time-Cost Trade-Off Formulating the CPM/PERT Network as a Linear Programming Model Chapter 8 - Project Management 2

Overview Uses networks for project analysis. Networks show projects are organized and are used to determine time duration for completion. Network techniques used are: CPM (Critical Path Method) PERT (Project Evaluation and Review Technique) Developed during late 1950’s. Chapter 8 - Project Management 3

Elements of Project Management is generally perceived as concerned with planning, organizing, and control of an ongoing process or activity. Project Management is concerned with control of an activity for a relatively short period of time after which management effort ends. Primary elements of Project Management to be discussed: Project Team Project Planning Project Control Chapter 8 - Project Management 4

The Elements of Project Management The Project Team Project team typically consists of a group of individuals from various areas in an organization and often includes outside consultants. Members of engineering staff often assigned to project work. Most important member of project team is the project manager. Project manager is often under great pressure because of uncertainty inherent in project activities and possibility of failure. Project manager must be able to coordinate various skills of team members into a single focused effort. Chapter 8 - Project Management 5
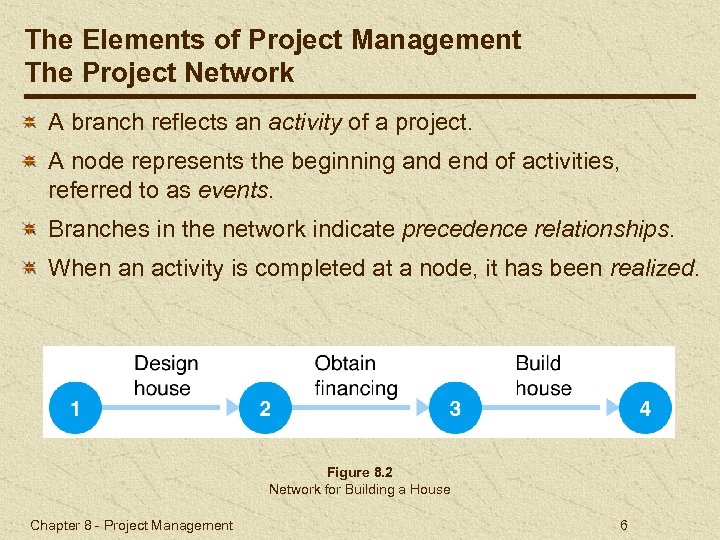
The Elements of Project Management The Project Network A branch reflects an activity of a project. A node represents the beginning and end of activities, referred to as events. Branches in the network indicate precedence relationships. When an activity is completed at a node, it has been realized. Figure 8. 2 Network for Building a House Chapter 8 - Project Management 6
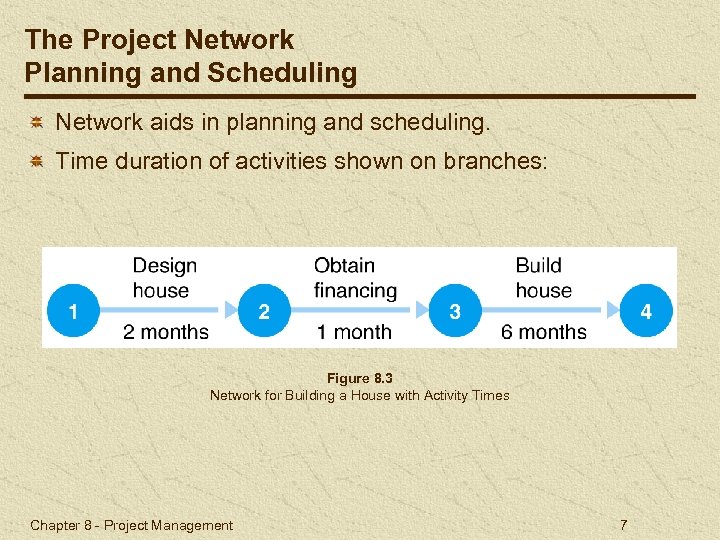
The Project Network Planning and Scheduling Network aids in planning and scheduling. Time duration of activities shown on branches: Figure 8. 3 Network for Building a House with Activity Times Chapter 8 - Project Management 7
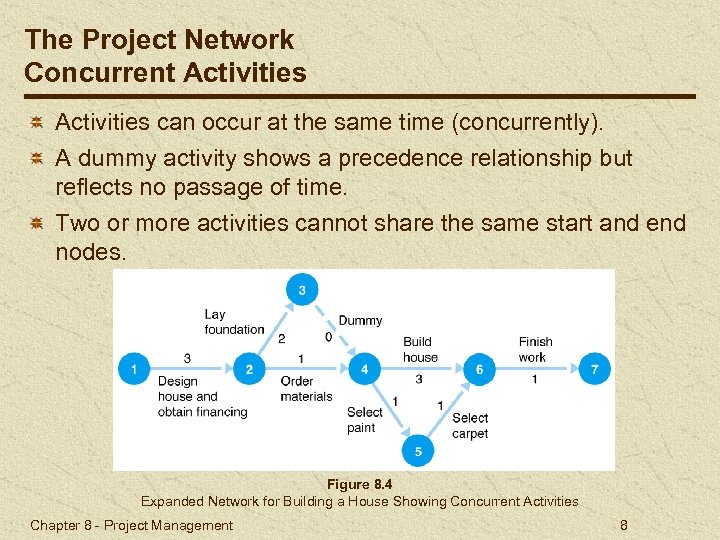
The Project Network Concurrent Activities can occur at the same time (concurrently). A dummy activity shows a precedence relationship but reflects no passage of time. Two or more activities cannot share the same start and end nodes. Figure 8. 4 Expanded Network for Building a House Showing Concurrent Activities Chapter 8 - Project Management 8
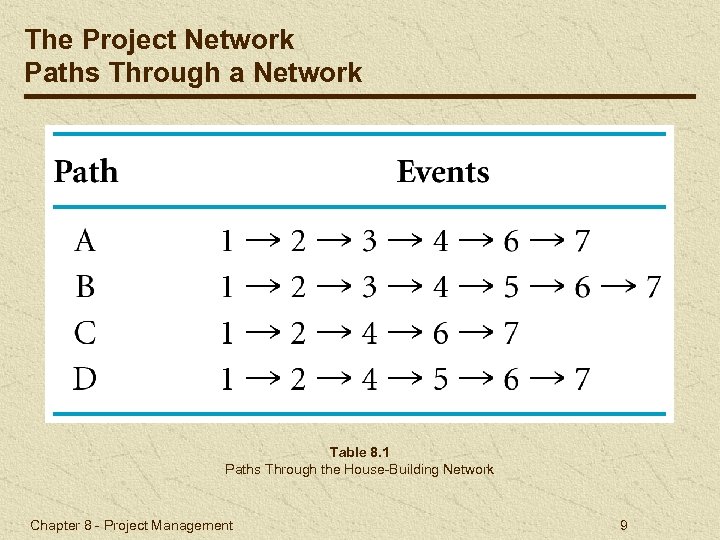
The Project Network Paths Through a Network Table 8. 1 Paths Through the House-Building Network Chapter 8 - Project Management 9
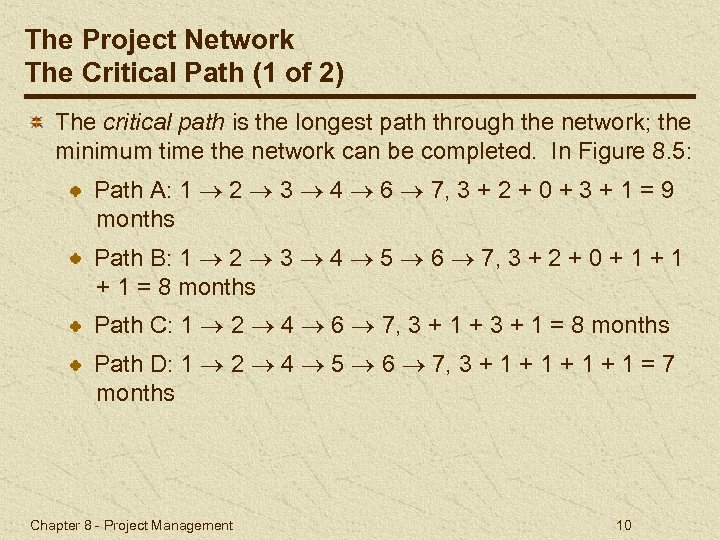
The Project Network The Critical Path (1 of 2) The critical path is the longest path through the network; the minimum time the network can be completed. In Figure 8. 5: Path A: 1 2 3 4 6 7, 3 + 2 + 0 + 3 + 1 = 9 months Path B: 1 2 3 4 5 6 7, 3 + 2 + 0 + 1 + 1 = 8 months Path C: 1 2 4 6 7, 3 + 1 + 3 + 1 = 8 months Path D: 1 2 4 5 6 7, 3 + 1 + 1 = 7 months Chapter 8 - Project Management 10
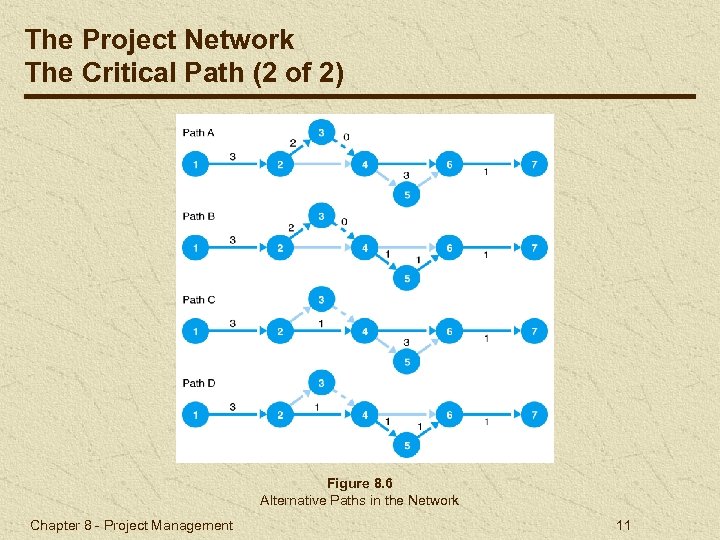
The Project Network The Critical Path (2 of 2) Figure 8. 6 Alternative Paths in the Network Chapter 8 - Project Management 11
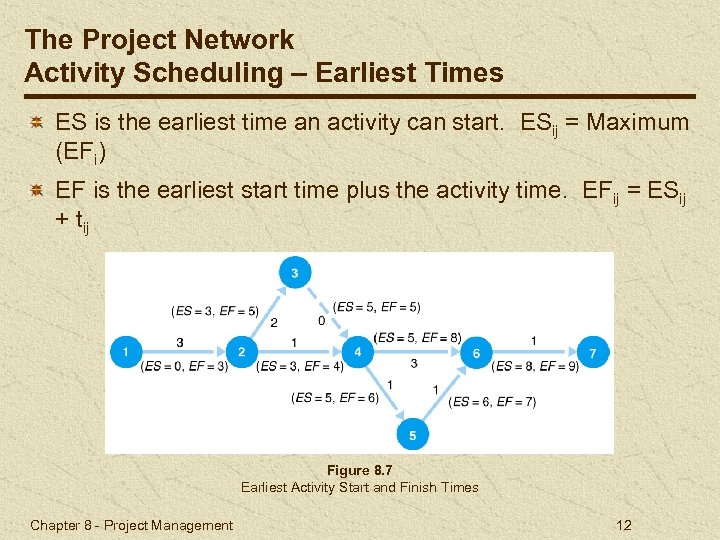
The Project Network Activity Scheduling – Earliest Times ES is the earliest time an activity can start. ESij = Maximum (EFi) EF is the earliest start time plus the activity time. EFij = ESij + tij Figure 8. 7 Earliest Activity Start and Finish Times Chapter 8 - Project Management 12
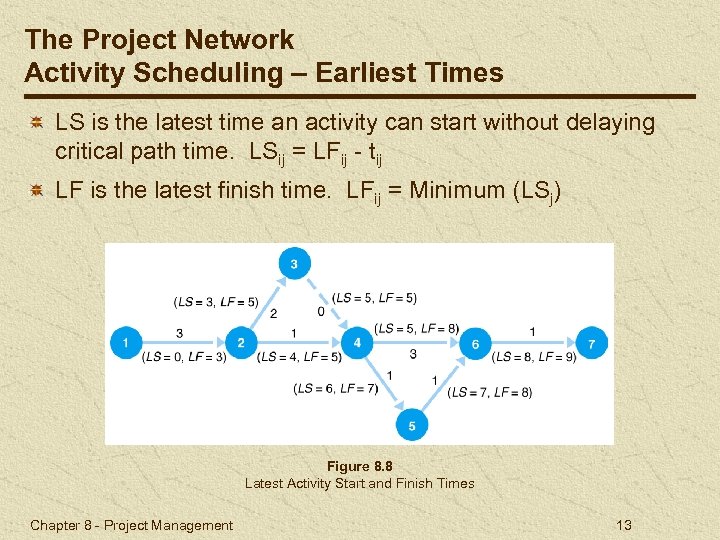
The Project Network Activity Scheduling – Earliest Times LS is the latest time an activity can start without delaying critical path time. LSij = LFij - tij LF is the latest finish time. LFij = Minimum (LSj) Figure 8. 8 Latest Activity Start and Finish Times Chapter 8 - Project Management 13
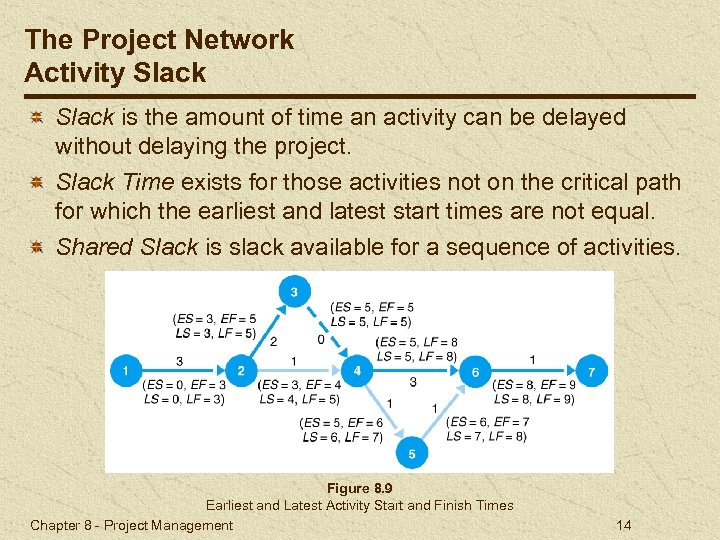
The Project Network Activity Slack is the amount of time an activity can be delayed without delaying the project. Slack Time exists for those activities not on the critical path for which the earliest and latest start times are not equal. Shared Slack is slack available for a sequence of activities. Figure 8. 9 Earliest and Latest Activity Start and Finish Times Chapter 8 - Project Management 14
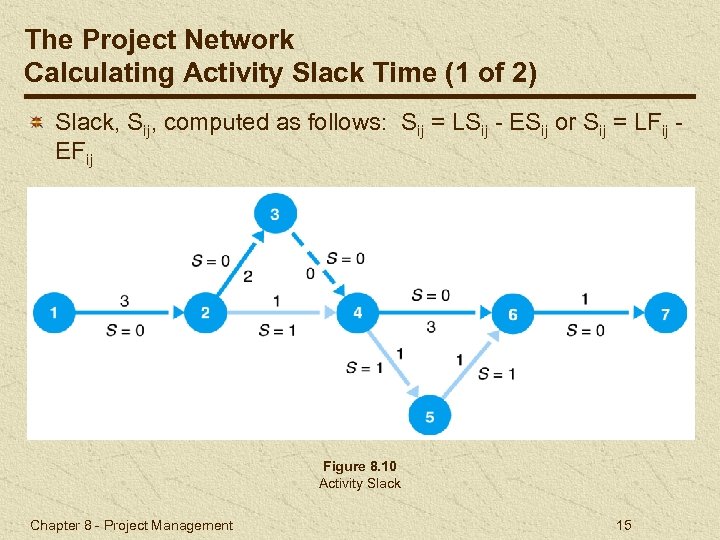
The Project Network Calculating Activity Slack Time (1 of 2) Slack, Sij, computed as follows: Sij = LSij - ESij or Sij = LFij EFij Figure 8. 10 Activity Slack Chapter 8 - Project Management 15
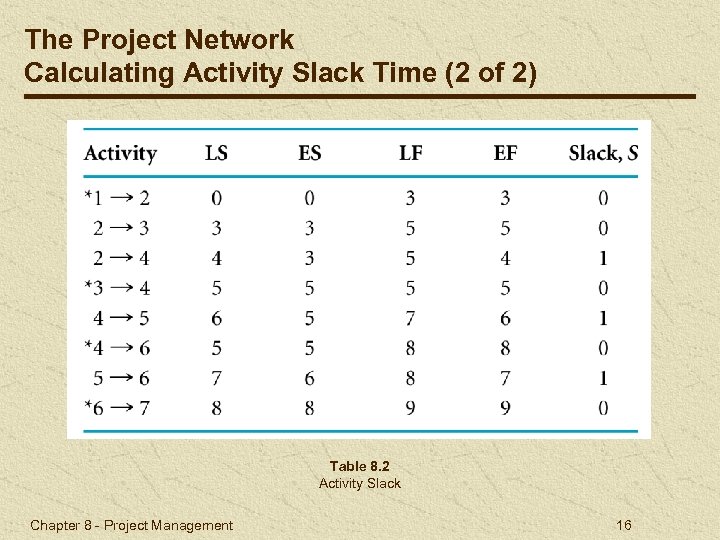
The Project Network Calculating Activity Slack Time (2 of 2) Table 8. 2 Activity Slack Chapter 8 - Project Management 16

Probabilistic Activity Times Activity time estimates usually can not be made with certainty. PERT used for probabilistic activity times. In PERT, three time estimates are used: most likely time (m), the optimistic time (a) , and the pessimistic time (b). These provide an estimate of the mean and variance of a beta distribution: mean (expected time): variance: Chapter 8 - Project Management 17
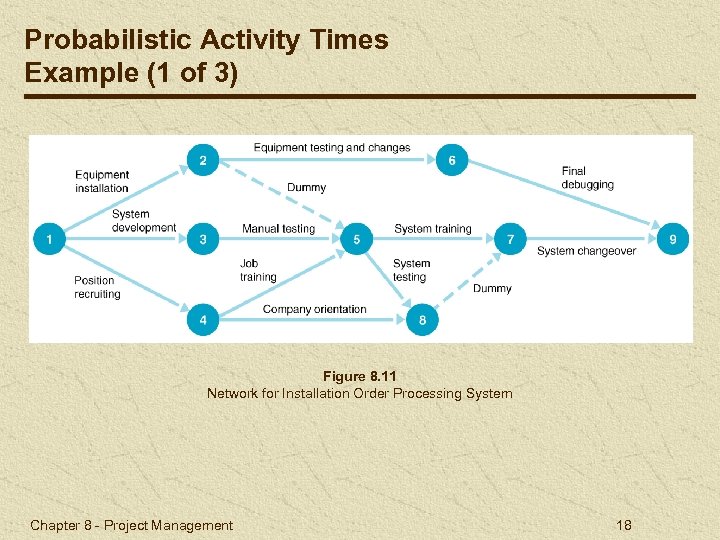
Probabilistic Activity Times Example (1 of 3) Figure 8. 11 Network for Installation Order Processing System Chapter 8 - Project Management 18
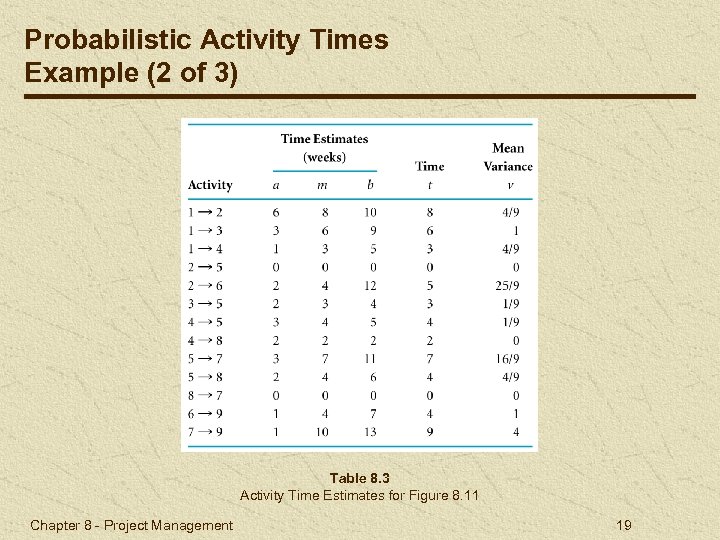
Probabilistic Activity Times Example (2 of 3) Table 8. 3 Activity Time Estimates for Figure 8. 11 Chapter 8 - Project Management 19
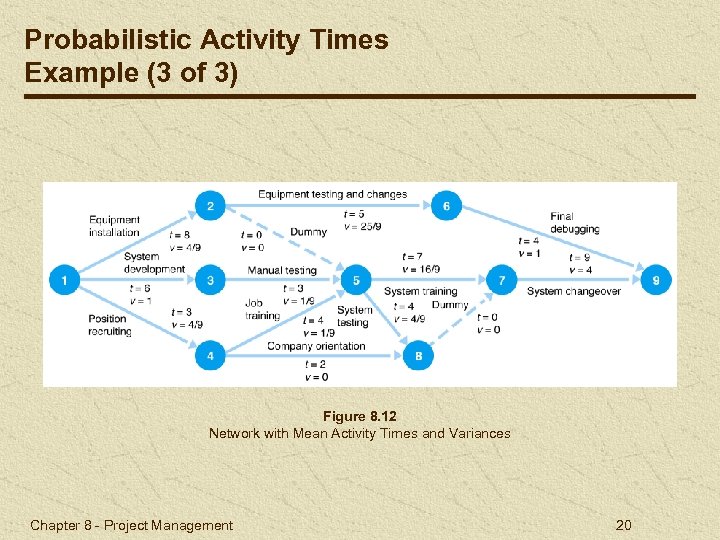
Probabilistic Activity Times Example (3 of 3) Figure 8. 12 Network with Mean Activity Times and Variances Chapter 8 - Project Management 20
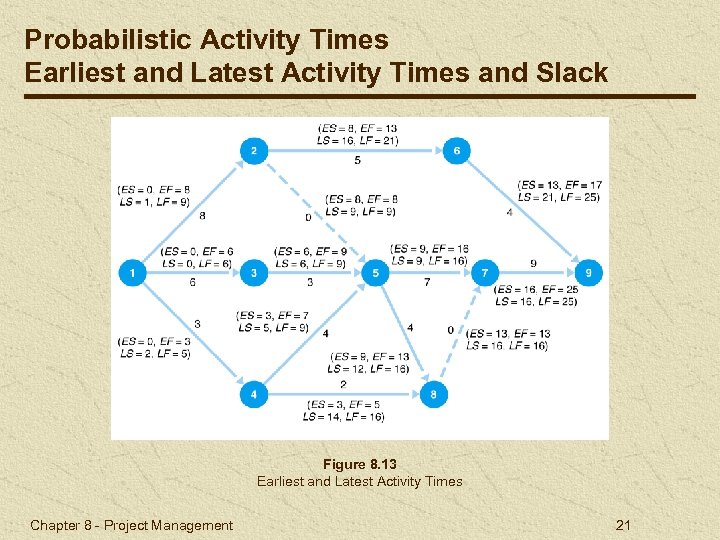
Probabilistic Activity Times Earliest and Latest Activity Times and Slack Figure 8. 13 Earliest and Latest Activity Times Chapter 8 - Project Management 21
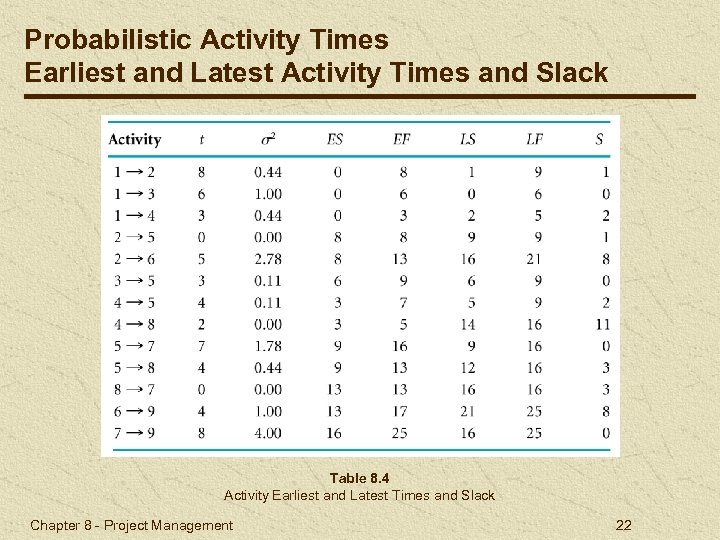
Probabilistic Activity Times Earliest and Latest Activity Times and Slack Table 8. 4 Activity Earliest and Latest Times and Slack Chapter 8 - Project Management 22

Probabilistic Activity Times Expected Project Time and Variance The expected project time is the sum of the expected times of the critical path activities. The project variance is the sum of the variances of the critical path activities. The expected project time is assumed to be normally distributed (based on central limit theorem). In example, expected project time (tp) and variance (vp) interpreted as the mean ( ) and variance ( 2) of a normal distribution: = 25 weeks 2 = 6. 9 weeks Chapter 8 - Project Management 23

Probability Analysis of a Project Network (1 of 2) Using normal distribution, probabilities are determined by computing number of standard deviations (Z) a value is from the mean. Value is used to find corresponding probability in Table A. 1, Appendix A. Chapter 8 - Project Management 24
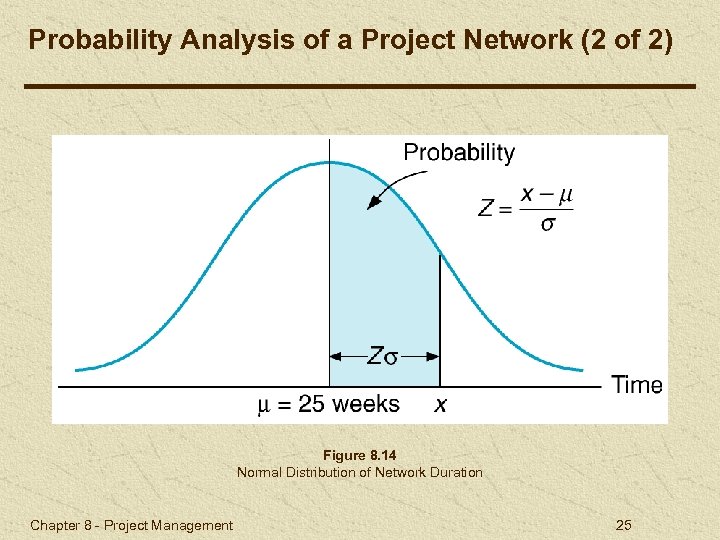
Probability Analysis of a Project Network (2 of 2) Figure 8. 14 Normal Distribution of Network Duration Chapter 8 - Project Management 25

Probability Analysis of a Project Network Example 1 (1 of 2) Z value of 1. 90 corresponds to probability of. 4713 in Table A. 1, Appendix A. Probability of completing project in 30 weeks or less: (. 5000 +. 4713) =. 9713. 2 = 6. 9 = 2. 63 Z = (x- )/ = (30 -25)/2. 63 = 1. 90 Chapter 8 - Project Management 26
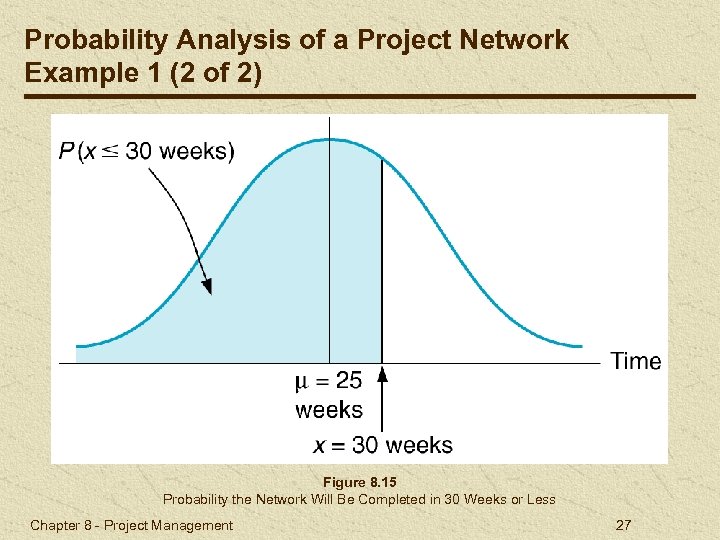
Probability Analysis of a Project Network Example 1 (2 of 2) Figure 8. 15 Probability the Network Will Be Completed in 30 Weeks or Less Chapter 8 - Project Management 27

Probability Analysis of a Project Network Example 2 (1 of 2) Z = (22 - 25)/2. 63 = -1. 14 • Z value of 1. 14 (ignore negative) corresponds to probability of. 3729 in Table A. 1, appendix A. • Probability that customer will be retained is. 1271 Chapter 8 - Project Management 28
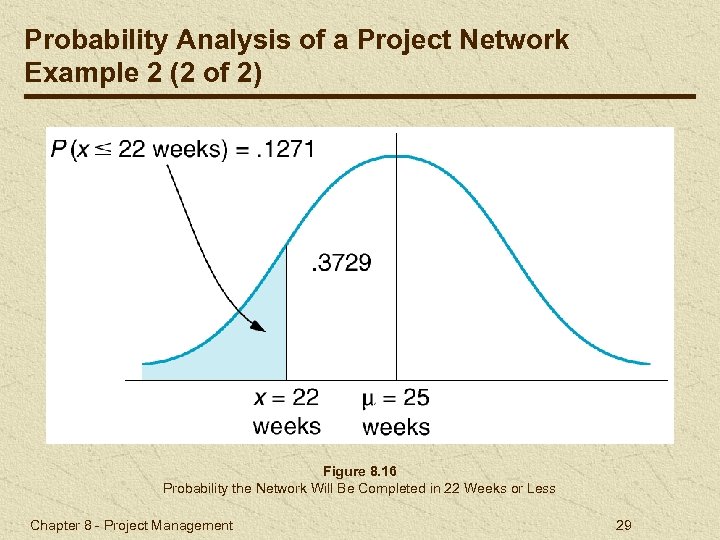
Probability Analysis of a Project Network Example 2 (2 of 2) Figure 8. 16 Probability the Network Will Be Completed in 22 Weeks or Less Chapter 8 - Project Management 29
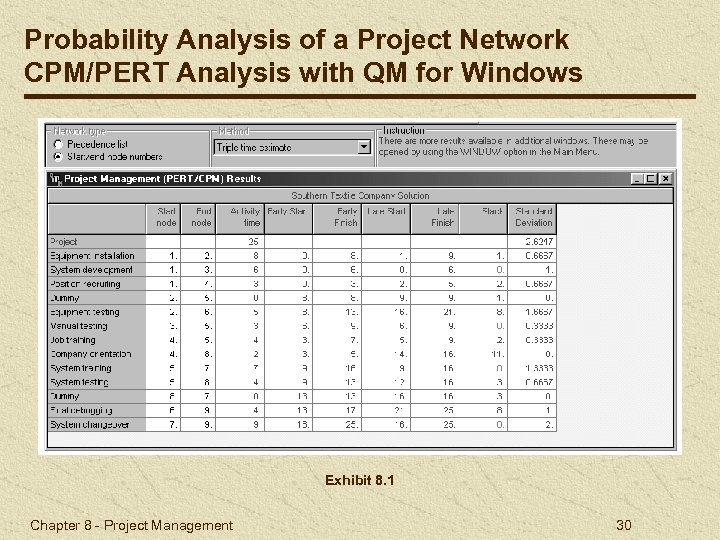
Probability Analysis of a Project Network CPM/PERT Analysis with QM for Windows Exhibit 8. 1 Chapter 8 - Project Management 30

Activity-on-Node Networks and Microsoft Project The project networks developed so far have used the “activity-on-arrow” (AOA) convention. “Activity-on-node” (AON) is another method of creating a network diagram. The two different conventions accomplish the same thing, but there a few differences. An AON diagram will often require more nodes than an AOA diagram. An AON diagram does not require dummy activities because two “activities” will never have the same start and end nodes. Microsoft Project handles only AON networks. Chapter 8 - Project Management 31
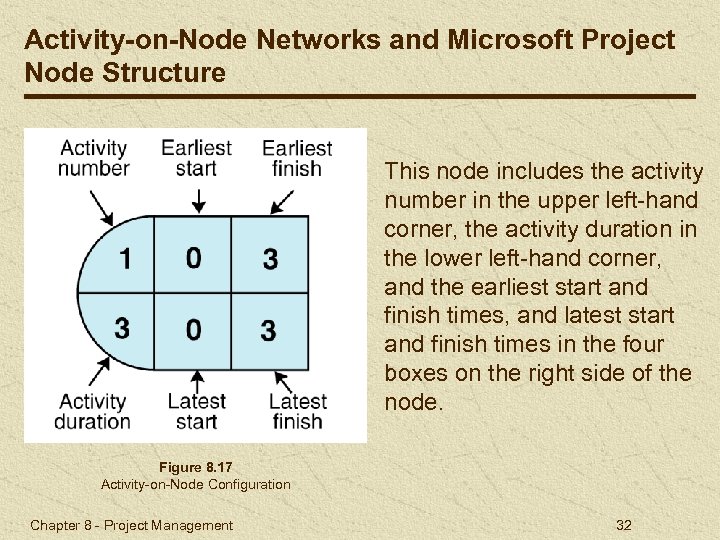
Activity-on-Node Networks and Microsoft Project Node Structure This node includes the activity number in the upper left-hand corner, the activity duration in the lower left-hand corner, and the earliest start and finish times, and latest start and finish times in the four boxes on the right side of the node. Figure 8. 17 Activity-on-Node Configuration Chapter 8 - Project Management 32
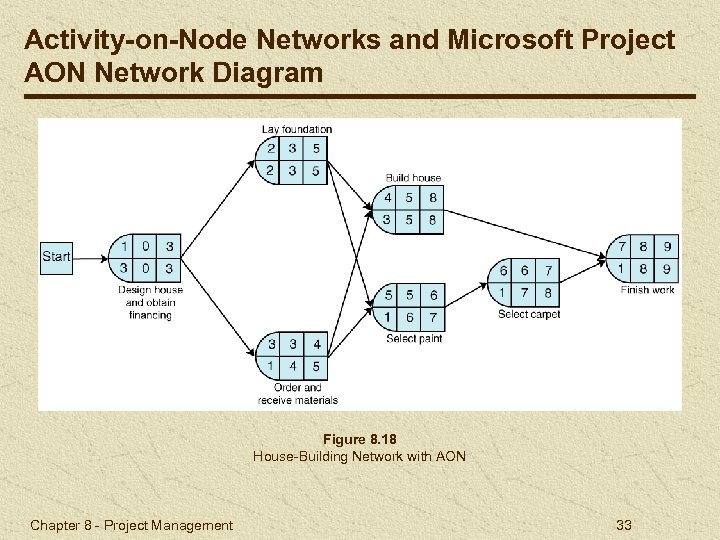
Activity-on-Node Networks and Microsoft Project AON Network Diagram Figure 8. 18 House-Building Network with AON Chapter 8 - Project Management 33

Activity-on-Node Networks and Microsoft Project (1 of 4) Exhibit 8. 2 Chapter 8 - Project Management 34
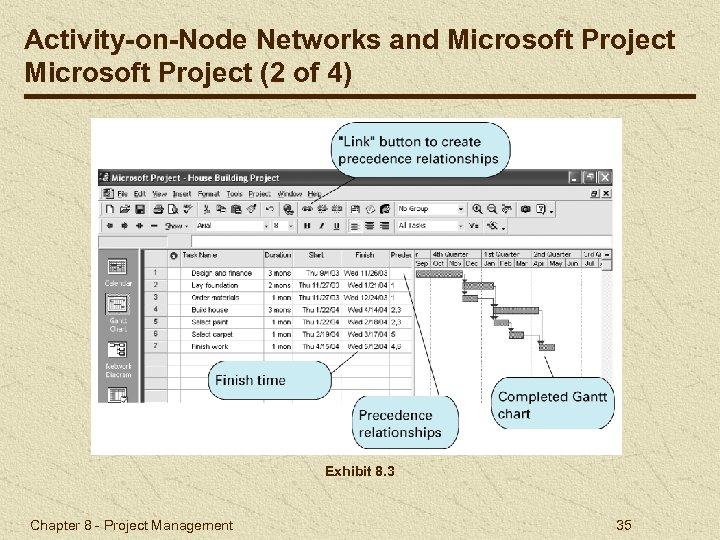
Activity-on-Node Networks and Microsoft Project (2 of 4) Exhibit 8. 3 Chapter 8 - Project Management 35
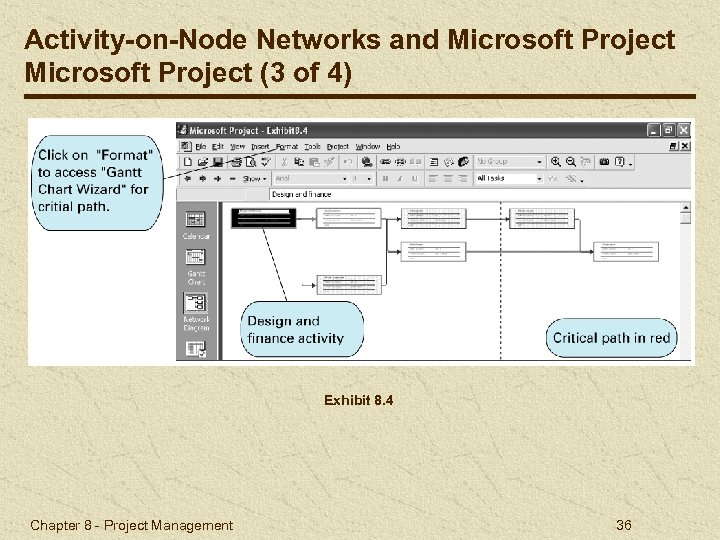
Activity-on-Node Networks and Microsoft Project (3 of 4) Exhibit 8. 4 Chapter 8 - Project Management 36
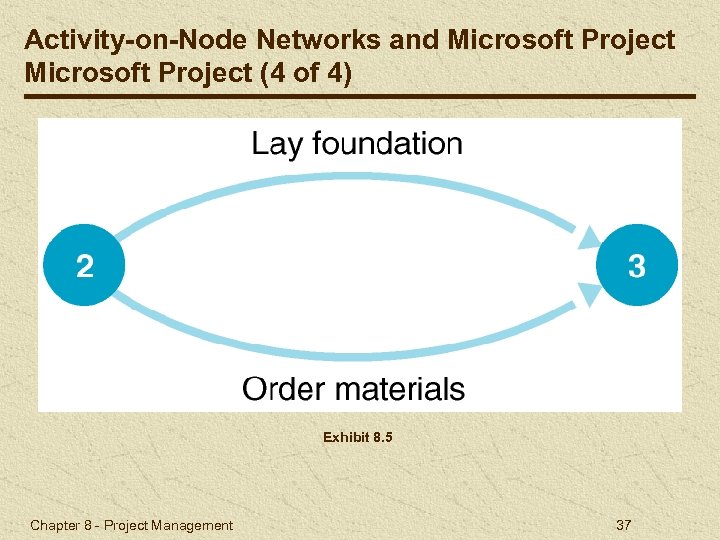
Activity-on-Node Networks and Microsoft Project (4 of 4) Exhibit 8. 5 Chapter 8 - Project Management 37

Project Crashing and Time-Cost Trade-Off Definition Project duration can be reduced by assigning more resources to project activities. Doing this however increases project cost. Decision is based on analysis of trade-off between time and cost. Project crashing is a method for shortening project duration by reducing one or more critical activities to a time less than normal activity time. Crashing achieved by devoting more resources to crashed activities. Chapter 8 - Project Management 38
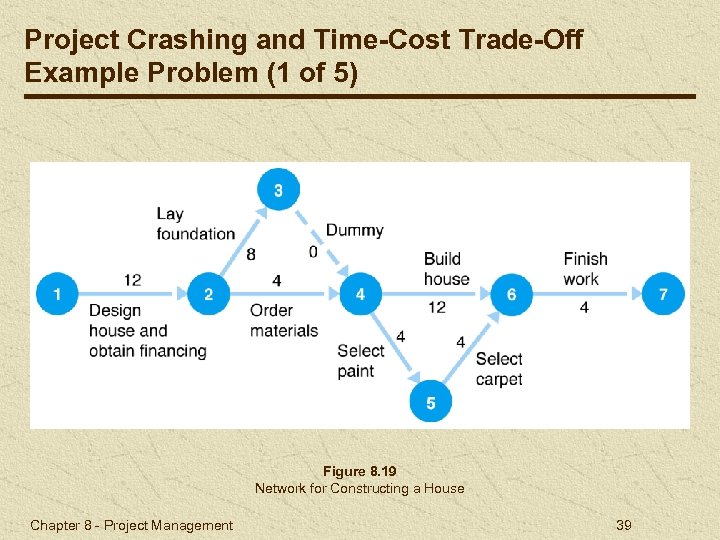
Project Crashing and Time-Cost Trade-Off Example Problem (1 of 5) Figure 8. 19 Network for Constructing a House Chapter 8 - Project Management 39
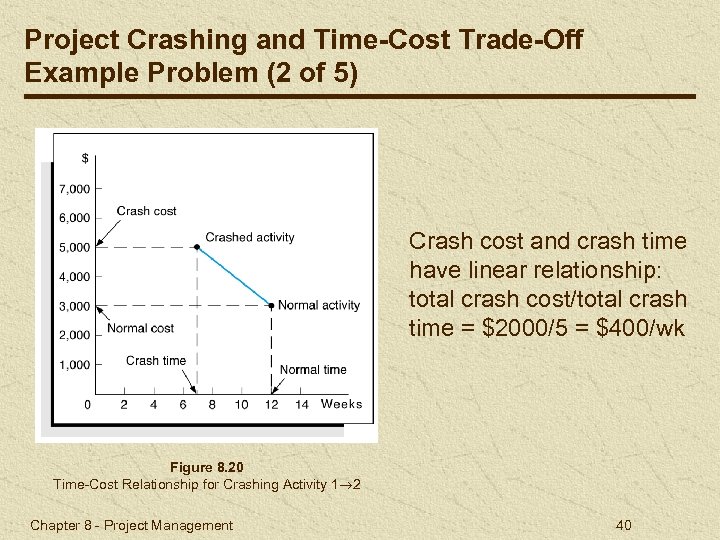
Project Crashing and Time-Cost Trade-Off Example Problem (2 of 5) Crash cost and crash time have linear relationship: total crash cost/total crash time = $2000/5 = $400/wk Figure 8. 20 Time-Cost Relationship for Crashing Activity 1 2 Chapter 8 - Project Management 40
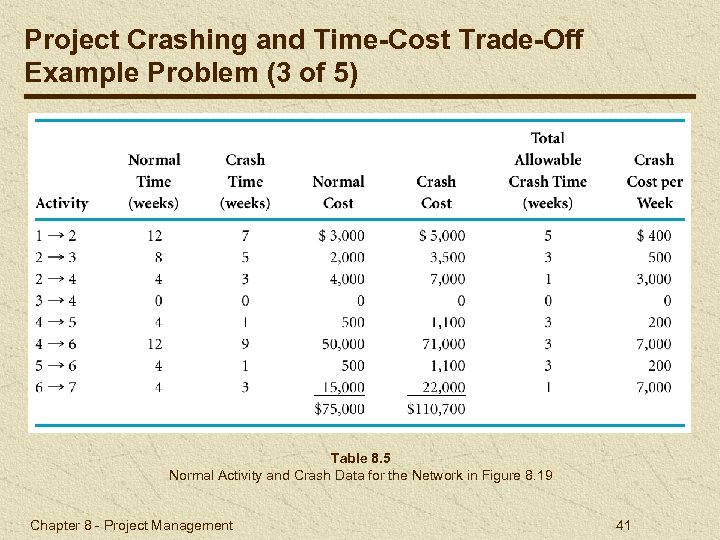
Project Crashing and Time-Cost Trade-Off Example Problem (3 of 5) Table 8. 5 Normal Activity and Crash Data for the Network in Figure 8. 19 Chapter 8 - Project Management 41

Project Crashing and Time-Cost Trade-Off Example Problem (4 of 5) Figure 8. 21 Network with Normal Activity Times and Weekly Activity Crashing Costs Chapter 8 - Project Management 42
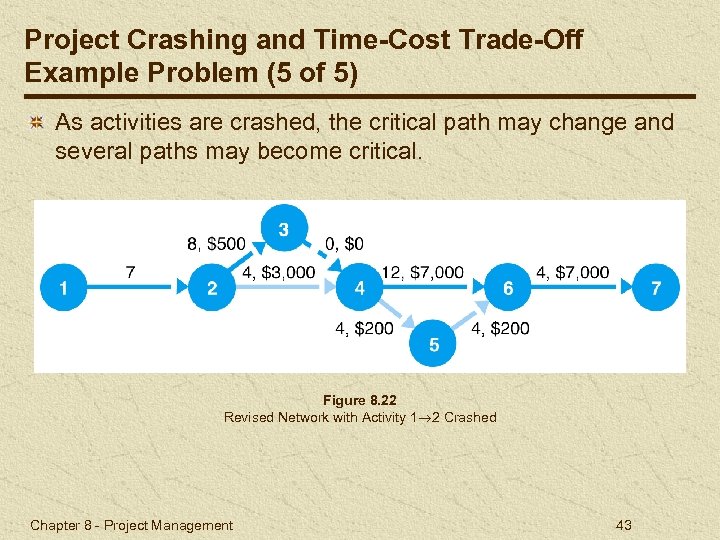
Project Crashing and Time-Cost Trade-Off Example Problem (5 of 5) As activities are crashed, the critical path may change and several paths may become critical. Figure 8. 22 Revised Network with Activity 1 2 Crashed Chapter 8 - Project Management 43
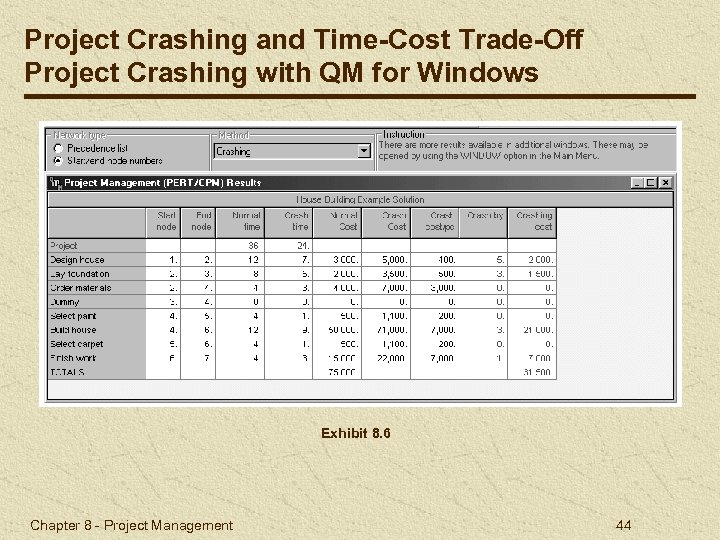
Project Crashing and Time-Cost Trade-Off Project Crashing with QM for Windows Exhibit 8. 6 Chapter 8 - Project Management 44

Project Crashing and Time-Cost Trade-Off General Relationship of Time and Cost (1 of 2) Project crashing costs and indirect costs have an inverse relationship. Crashing costs are highest when the project is shortened. Indirect costs increase as the project duration increases. Optimal project time is at minimum point on the total cost curve. Chapter 8 - Project Management 45
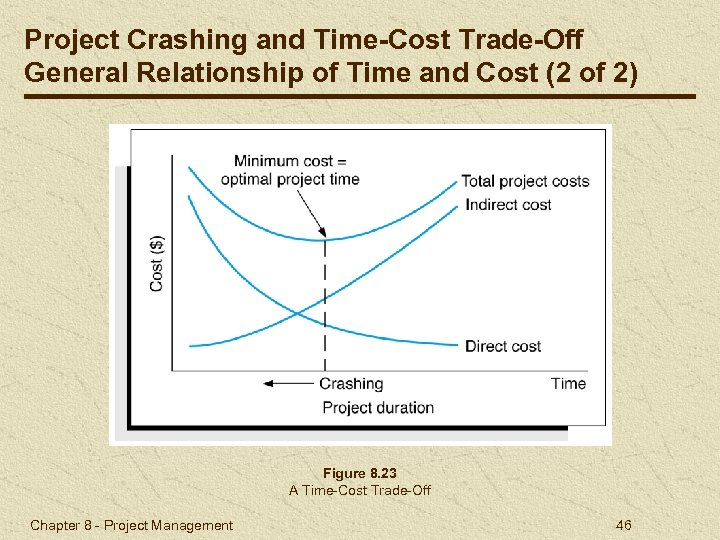
Project Crashing and Time-Cost Trade-Off General Relationship of Time and Cost (2 of 2) Figure 8. 23 A Time-Cost Trade-Off Chapter 8 - Project Management 46

The CPM/PERT Network Formulating as a Linear Programming Model The objective is to determine the earliest time the project can be completed (i. e. , the critical path time). General linear programming model: Minimize Z = xi subject to: xj - xi tij for all activities i j xi, xj 0 Where: xi = earliest event time of node i xj = earliest event time of node j tij = time of activity i j Chapter 8 - Project Management 47

The CPM/PERT Network Example Problem Formulation and Data (1 of 2) Minimize Z = x 1 + x 2 + x 3 + x 4 + x 5 + x 6 + x 7 subject to: x 2 - x 1 12 x 3 - x 2 8 x 4 - x 2 4 x 4 - x 3 0 x 5 - x 4 4 x 6 - x 4 12 x 6 - x 5 4 x 7 - x 6 4 xi, xj 0 Chapter 8 - Project Management 48

The CPM/PERT Network Example Problem Formulation and Data (2 of 2) Figure 8. 24 CPM/PERT Network for the House-Building Project with Earliest Event Times Chapter 8 - Project Management 49
The CPM/PERT Network Example Problem Solution with Excel (1 of 4) Exhibit 8. 7 Chapter 8 - Project Management 50
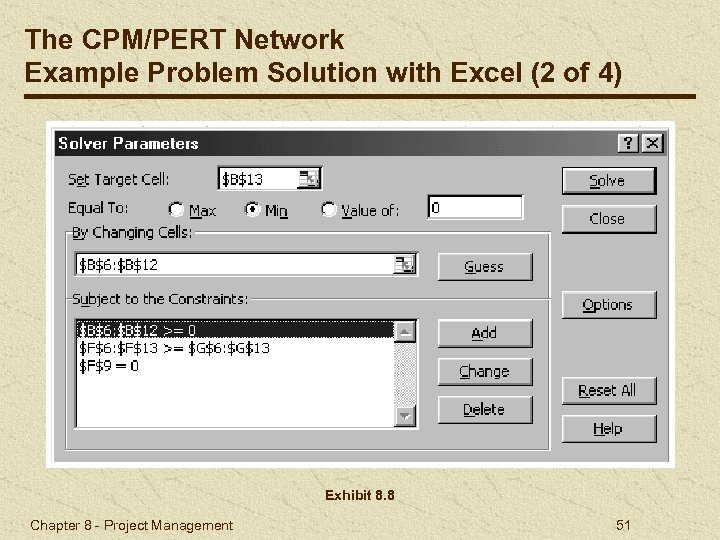
The CPM/PERT Network Example Problem Solution with Excel (2 of 4) Exhibit 8. 8 Chapter 8 - Project Management 51

The CPM/PERT Network Example Problem Solution with Excel (3 of 4) Exhibit 8. 9 Chapter 8 - Project Management 52

The CPM/PERT Network Example Problem Solution with Excel (4 of 4) Exhibit 8. 10 Chapter 8 - Project Management 53
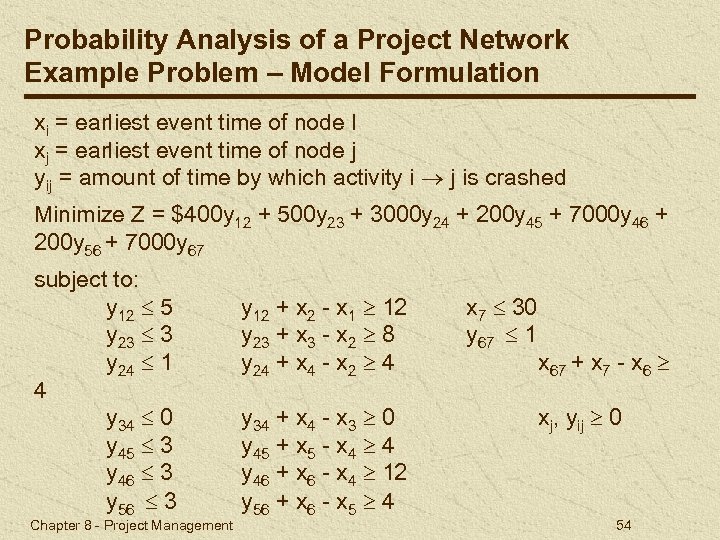
Probability Analysis of a Project Network Example Problem – Model Formulation xi = earliest event time of node I xj = earliest event time of node j yij = amount of time by which activity i j is crashed Minimize Z = $400 y 12 + 500 y 23 + 3000 y 24 + 200 y 45 + 7000 y 46 + 200 y 56 + 7000 y 67 subject to: y 12 5 y 23 3 y 24 1 4 y 34 0 y 45 3 y 46 3 y 56 3 Chapter 8 - Project Management y 12 + x 2 - x 1 12 y 23 + x 3 - x 2 8 y 24 + x 4 - x 2 4 y 34 + x 4 - x 3 0 y 45 + x 5 - x 4 4 y 46 + x 6 - x 4 12 y 56 + x 6 - x 5 4 x 7 30 y 67 1 x 67 + x 7 - x 6 xj, yij 0 54

Probability Analysis of a Project Network Example Problem – Excel Solution (1 of 3) Exhibit 8. 11 Chapter 8 - Project Management 55

Probability Analysis of a Project Network Example Problem – Excel Solution (2 of 3) Exhibit 8. 12 Chapter 8 - Project Management 56
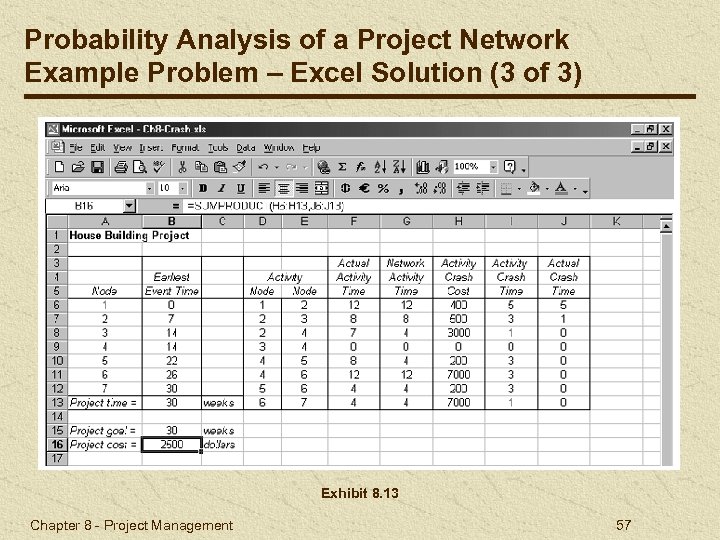
Probability Analysis of a Project Network Example Problem – Excel Solution (3 of 3) Exhibit 8. 13 Chapter 8 - Project Management 57

PERT Project Management Example Problem Statement and Data (1 of 2) Given the following data determine the expected project completion time and variance, and the probability that the project will be completed in 28 days or less. Chapter 8 - Project Management 58

PERT Project Management Example Problem Statement and Data (2 of 2) Chapter 8 - Project Management 59

PERT Project Management Example Problem Solution (1 of 4) Step 1: Compute the expected activity times and variances. Chapter 8 - Project Management 60
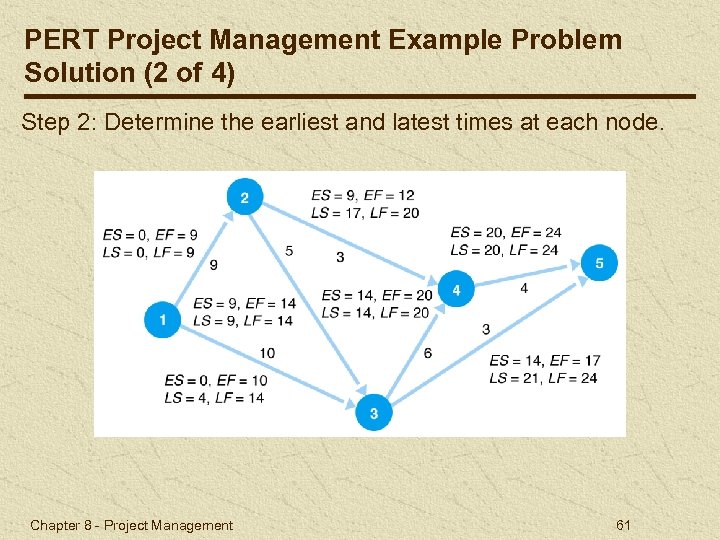
PERT Project Management Example Problem Solution (2 of 4) Step 2: Determine the earliest and latest times at each node. Chapter 8 - Project Management 61

PERT Project Management Example Problem Solution (3 of 4) Step 3: Identify the critical path and compute expected completion time and variance. Critical path (activities with no slack): 1 2 3 4 5 Expected project completion time (tp): 24 days Variance: v = 4 + 4/9 + 1/9 = 5 days Chapter 8 - Project Management 62
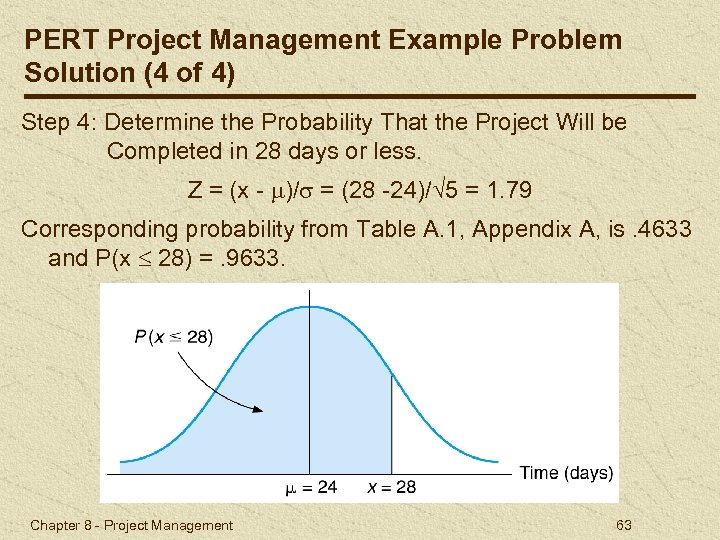
PERT Project Management Example Problem Solution (4 of 4) Step 4: Determine the Probability That the Project Will be Completed in 28 days or less. Z = (x - )/ = (28 -24)/ 5 = 1. 79 Corresponding probability from Table A. 1, Appendix A, is. 4633 and P(x 28) =. 9633. Chapter 8 - Project Management 63
bc31174fd6651fa36490bb5369639bf0.ppt