Introduction to Game Theory Ch 3 Sequential games

Introduction to Game Theory Ch 3. Sequential games Jarek Neneman neneman@uni. lodz. pl 601305093

Sequential games Game trees (extensive form of a game) Nodes, branches and paths of play Nodes: - initial (root) - action (decision) - terminal (no action node) Move - single action taken at a node Moves (actions) are represented by branches Strategy – complete plan of action

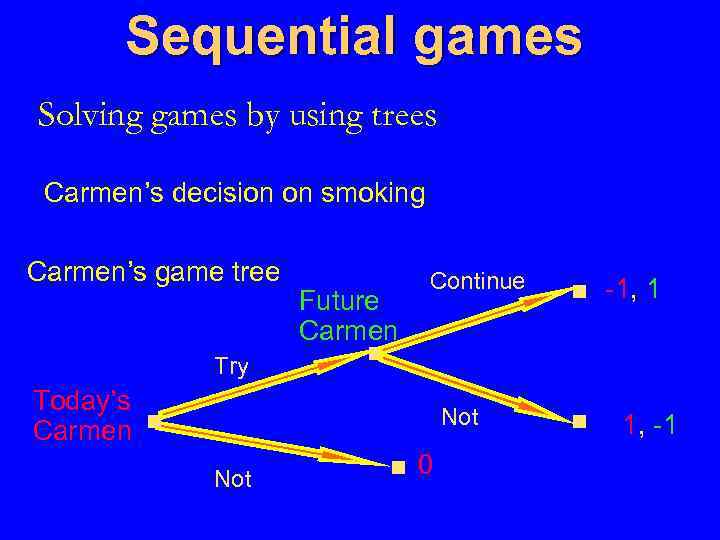Sequential games Solving games by using trees Carmen’s decision on smoking Carmen’s game tree Try Future Carmen ■ Continue Today’s Carmen ■ Not ■ 0 ■ -1, 1 ■ 1, -1

Sequential games 3 Adding more players Preferences: Ø Don’t contribute, both of the others do 4 Ø Contribute, one or two do 3 Ø Don’t contribute, only one or neither does 2 Ø Contribute, neither of the others does 1

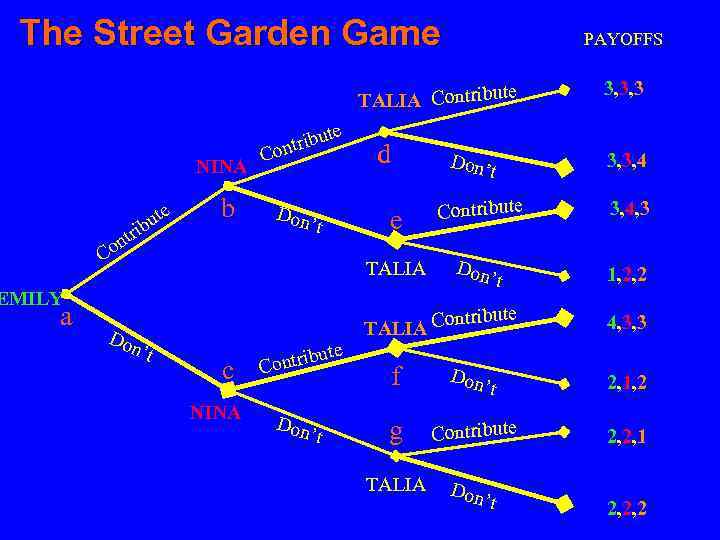The Street Garden Game PAYOFFS TALIA Contribute NINA ute b tri n Co b te tribu on C Don ’t Don’ t e Contribute 3, 3, 4, 3 1, 2, 2 ntribute ’t Don 4, 3, 3 Don 2, 1, 2 TALIA EMILY a d 3, 3, 3 ’t TALIA Co c NINA ute ontrib C Don ’t f g TALIA ’t Contribute Don ’t 2, 2, 1 2, 2, 2

Sequential games 3 Adding more players Strategies: Ø Emily has two choices. For her strategy = move” Her optimal strategy (move) D

Sequential games 3 Adding more players Strategies: ØNina acts at two nodes. Her plan of action has to specify what to do at each node. Strategies available to her: C at b, C at c i. e. CC C at b, D at c i. e. CD D at b, C at c i. e. DC D at b, D at c i. e. DD

Sequential games 3 Adding more players Strategies: ØTalia acts at 4 nodes. Her plan of action has to specify what to do at each node. There are 16 strategies available to her: CCCC, CCCD, CCDC, CCDD, CDCC, CDCD, CDDC, CDDD, DCCC, DCCD, DCDC, DCDD, DDCC, DDCD, DDDC, DDDD

Sequential games 3 Adding more players Strategies: Configuration of strategies: D DC DCCD constitutes rollback equilibrium of the game

Sequential games 3 Adding more players Small summary – three distinct concepts: 1. List of all available strategies for each player. 2. The optimal strategy (complete plan of action) for each player 3. Actual path of play in the rollback equilibrium

Sequential games Homework A firm is quite happy monopolizing its industry with profits of $10 M. A potential competitor considers entering the industry. If the competitor elects not to enter, it earns profits of $0 and the monopolist maintains its profit of $10 M. If the competitor enters, the monopolist must either accommodate the entry or fight. If the monopolist accommodates, both firms earn $5 M. If the monopolist fights, both firms lose $5 M. Suppose that the decision to enter by the competitor is reversible in the following sense: after it has entered, and after the monopolist has chosen to accommodate or fight, the competitor can choose to remain in the industry (and receive either the $5 M profits or $5 M loss) or to exit. Suppose that exiting at this point results in a loss to the entrant of $1 M, and the monopolist regains its $10 M profit. Draw the game tree and find rollback equilibrium of this game.

Sequential games Homework 2 Paying ransom A member of family has been kidnapped. Now family is about to decide if they should pay the ransom. Then kidnapers will decide between release and kill. Preferences are presented below – the lower number, the better. Draw game tree and decide if the family should pay Kidnapers Family Kidnapers’ payoff (ranking) Family’s payoff (ranking) release pay I II release not pay II I kill pay III IV kill not pay IV III