Скачать презентацию Introduction to DSL Yaakov J Stein Chief Scientist
a9152932bd793041a603b0588aa8c05d.ppt
- Количество слайдов: 133
Introduction to DSL Yaakov J. Stein Chief Scientist RAD Data Communications Stein Intro DSL 1
PSTN Stein Intro DSL 2
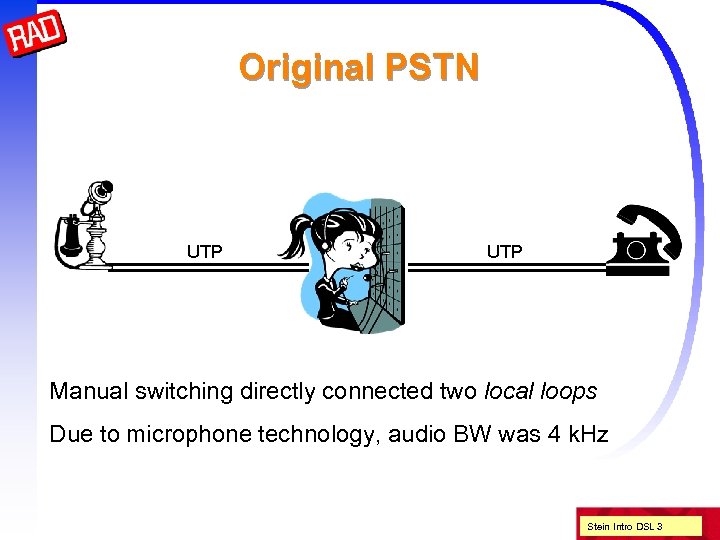Original PSTN UTP Manual switching directly connected two local loops Due to microphone technology, audio BW was 4 k. Hz Stein Intro DSL 3
Analog switched PSTN Invention of tube amplifier enabled long distance Between central offices used FDM spaced at 4 k. Hz (each cable carrying 1 group = 12 channels) Developed into hierarchical network of automatic switches (with supergroups, master groups, supermaster groups) Stein Intro DSL 4
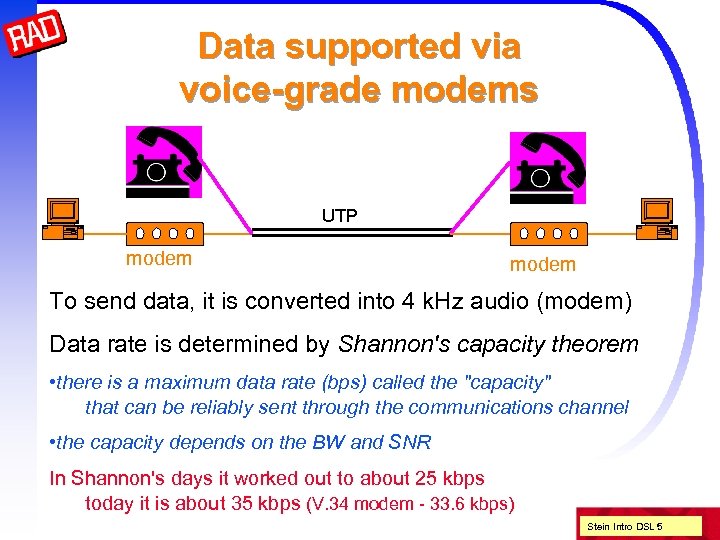Data supported via voice-grade modems UTP modem To send data, it is converted into 4 k. Hz audio (modem) Data rate is determined by Shannon's capacity theorem • there is a maximum data rate (bps) called the "capacity" that can be reliably sent through the communications channel • the capacity depends on the BW and SNR In Shannon's days it worked out to about 25 kbps today it is about 35 kbps (V. 34 modem - 33. 6 kbps) Stein Intro DSL 5
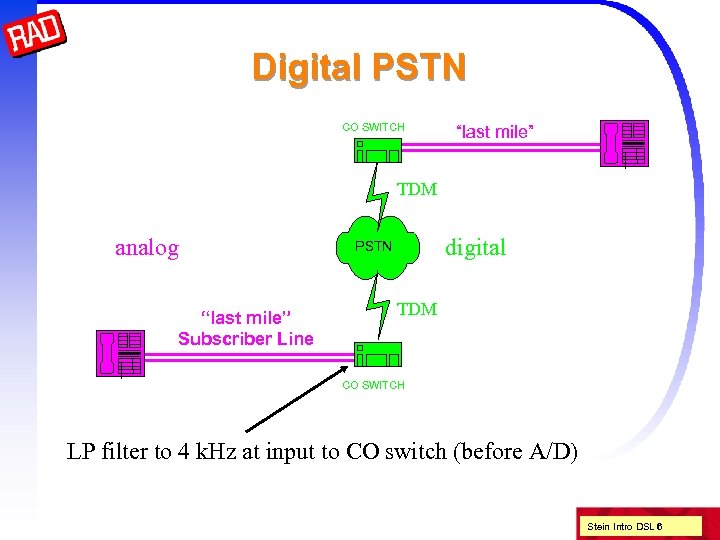Digital PSTN CO SWITCH “last mile” TDM analog “last mile” Subscriber Line digital PSTN TDM CO SWITCH LP filter to 4 k. Hz at input to CO switch (before A/D) Stein Intro DSL 6
Digital PSTN Sample 4 k. Hz audio at 8 k. Hz (Nyquist) Need 8 bits per sample = 64 kbps Multiplexing 64 kbps channels leads to higher and higher rates Only the subscriber line (local loop) remains analog (too expensive to replace) Can switch (cross connect) large number of channels Noise and distortion could be eliminated due to Shannon's theorems 1. Separation theorem 2. Source coding theorem 3. Channel capacity theorem Stein Intro DSL 7
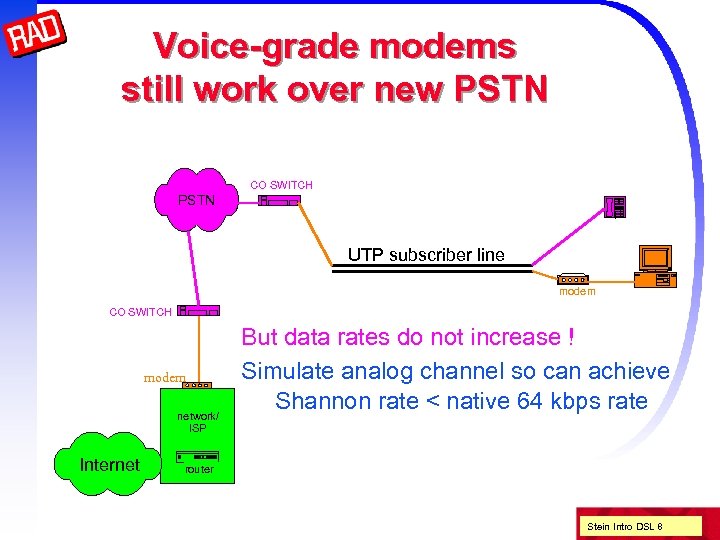Voice-grade modems still work over new PSTN CO SWITCH PSTN UTP subscriber line modem CO SWITCH modem network/ ISP Internet But data rates do not increase ! Simulate analog channel so can achieve Shannon rate < native 64 kbps rate router Stein Intro DSL 8
? Where is the limitation The digital network was developed incrementally No forklift upgrades to telephones, subscriber lines, etc. Evolutionary deployment meant that the new network needed to simulate pre-existing analog network So a 4 k. Hz analog channel is presented to subscriber The 4 k. Hz limitation is enforced by LP filter at input to CO switch (before 8 k. Hz sampling) The actual subscriber line is not limited to 4 k. Hz Is there a better way to use the subscriber line for digital transmissions ? Stein Intro DSL 9
UTP Stein Intro DSL 10
What is UTP? The achievable data rate is limited by physics of the subscriber line The subscriber line is an Unshielded Twisted Pair of copper wires n Two plastic insulated copper wires n Two directions over single pair n Twisted to reduce crosstalk n Supplies DC power and audio signal n Physically, UTP is – distributed resistances in series – distributed inductances in series – distributed capacitances in parallel so the attenuation increases with frequency n Various other problems exist (splices, loading coils, etc. ) Stein Intro DSL 11
UTP characteristics n Resistance per unit distance n Capacitance per unit distance n Inductance per unit distance n Cross-admittance (assume pure reactive) per unit distance Stein Intro DSL 12
UTP resistance Influenced by gauge, copper purity, temperature Resistance is per unit distance n 24 gauge 0. 15 W/kft n 26 gauge 0. 195 W/kft Skin effect: Resistance increases with frequency Theoretical result R~f 1/2 In practice this is a good approximation Stein Intro DSL 13
UTP capacitance Capacitance depends on interconductor insulation About 15. 7 n. F per kft Only weakly dependent on gauge Independent of frequency to high degree Stein Intro DSL 14
UTP inductance Higher for higher gauge 24 gauge 0. 188 m. H per kft 26 gauge 0. 205 m. H per kft Constant below about 10 k. Hz Drops slowly above Stein Intro DSL 15
UTP admittance Insulation good so no resistive admittance Admittance due to capacitive and inductive coupling Self-admittance can usually be neglected Cross admittance causes cross-talk! Stein Intro DSL 16
Propagation loss Voltage decreases as travel along cable Each new section of cable reduces voltage by a factor 1 v 1/2 v 1/4 v So the decrease is exponential Va / Vb = e -g x = H(f, x) where x is distance between points a and b We can calculate g, and hence loss, directly from RCLG model Stein Intro DSL 17
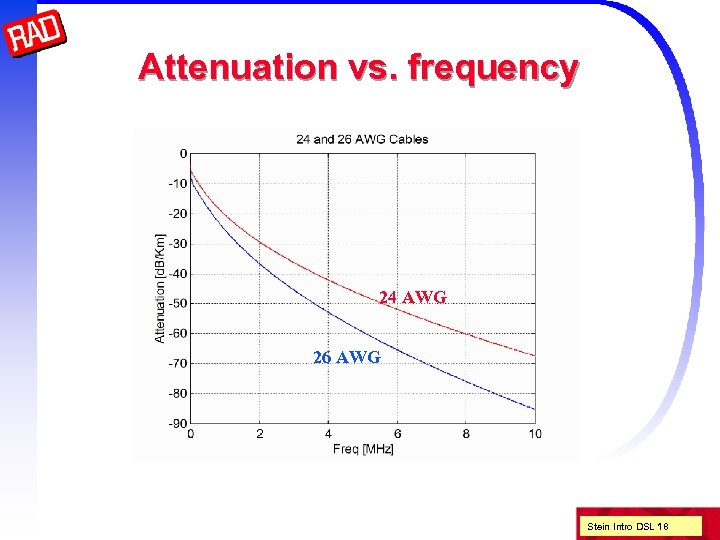Attenuation vs. frequency 24 AWG 26 AWG Stein Intro DSL 18
Why twisted? from Alexander Graham Bell’s 1881 patent To place the direct and return lines close together. To twist the direct and return lines around one another so that they should be absolutely equidistant from the disturbing wires n a V = (a+n) - (b+n) b Stein Intro DSL 19
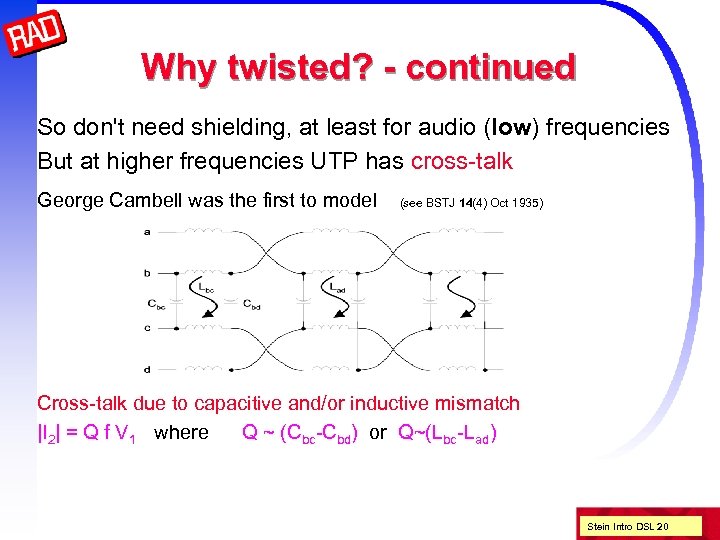Why twisted? - continued So don't need shielding, at least for audio (low) frequencies But at higher frequencies UTP has cross-talk George Cambell was the first to model (see BSTJ 14(4) Oct 1935) Cross-talk due to capacitive and/or inductive mismatch |I 2| = Q f V 1 where Q ~ (Cbc-Cbd) or Q~(Lbc-Lad) Stein Intro DSL 20
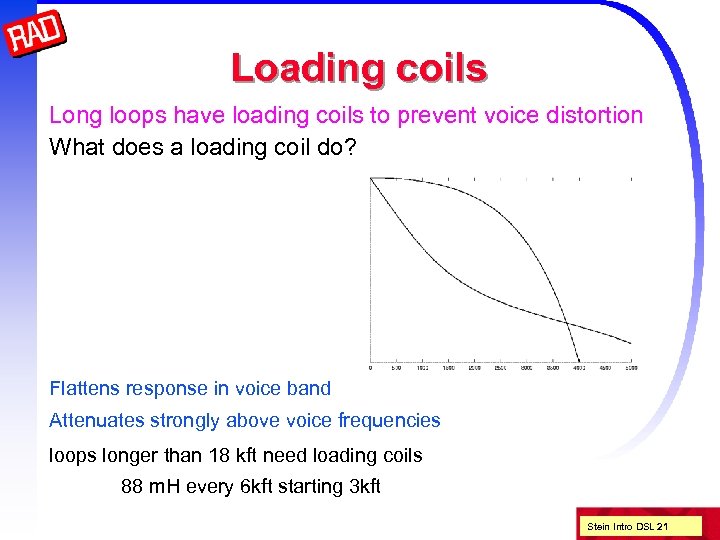Loading coils Long loops have loading coils to prevent voice distortion What does a loading coil do? Flattens response in voice band Attenuates strongly above voice frequencies loops longer than 18 kft need loading coils 88 m. H every 6 kft starting 3 kft Stein Intro DSL 21
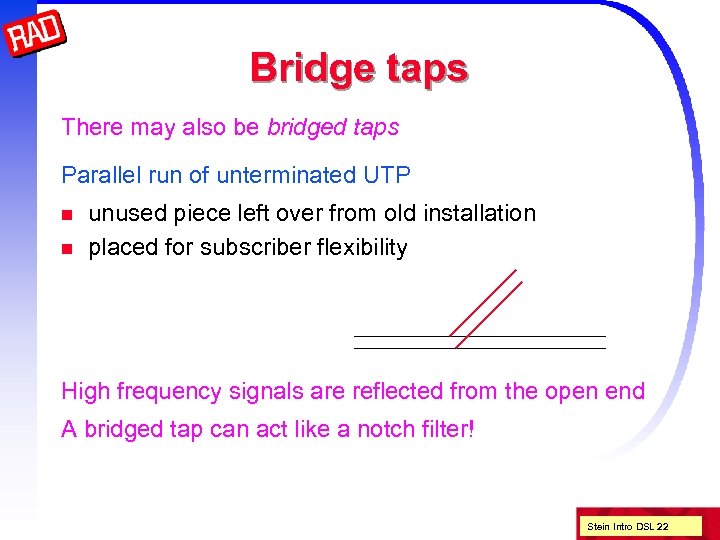Bridge taps There may also be bridged taps Parallel run of unterminated UTP n n unused piece left over from old installation placed for subscriber flexibility High frequency signals are reflected from the open end A bridged tap can act like a notch filter! Stein Intro DSL 22
Other problems Splices Subscriber lines are seldom single runs of cable In the US, UTP usually comes in 500 ft lengths So splices must be made every 500 ft Average line has >20 splices Splices are pressure connections that add to attenuation Over time they corrode and may spark, become intermittent, etc. Gauge changes US binder groups typically start off at 26 AWG Change to 24 AWG after 10 kft In rural areas they may change to 19 AWG after that Stein Intro DSL 23
Binder groups UTP are not placed under/over ground individually In central offices they are in cable bundles with 100 s of other UTP In the outside plant they are in binder groups with 25 or 50 pairs per group We will see that these pairs interfere with each other a phenomenon called cross-talk (XTALK) Stein Intro DSL 24
CSA guidelines 1981 AT&T Carrier Service Area guidelines advise as follows for new deployments n No loading coils n Maximum of 9 kft of 26 gauge (including bridged taps) n Maximum of 12 kft of 24 gauge (including bridged taps) n Maximum of 2. 5 kft bridged taps n Maximum single bridged tap 2 kft n Suggested: no more than 2 gauges In 1991 more than 60% of US lines met CSA requirements Stein Intro DSL 25
Present US PSTN UTP only in the last mile (subscriber line) n n n 70% unloaded < 18 kft 15% loaded > 18 kft 15% optical or digital to remote terminal + DA (distribution area) PIC, 19, 22, 24, 26 gauge Built for 2 W 4 KHz audio bandwidth DC used for powering Above 100 KHz: n n n severe attenuation cross-talk in binder groups (25 - 1000 UTP) lack of intermanufacturer consistency Stein Intro DSL 26
Present US PSTN - continued We will see, that for DSL - basically four cases n Resistance design > 18 Kft loaded line - no DSL possible n Resistance design unloaded <18 Kft <1300 W - ADSL n CSA reach - HDSL n DA (distribution area) 3 -5 kft - VDSL Higher rate - lower reach (because of attenuation and noise!) Stein Intro DSL 27
x. DSL Stein Intro DSL 28
Alternatives for data services Fiber, coax, HFC COST: $10 k-$20 k / mile TIME: months to install T 1/E 1 COST: >$5 k/mile for conditioning TIME: weeks to install DSL COST: @ 0 (just equipment price) TIME: @ 0 (just setup time) Stein Intro DSL 29
x. DSL Need higher speed digital connection to subscribers Not feasible to replace UTP in the last mile Older voice grade modems assume 4 k. Hz analog line Newer (V. 90) modems assume 64 kbps digital line DSL modems don’t assume anything Use whatever the physics of the UTP allows Stein Intro DSL 30
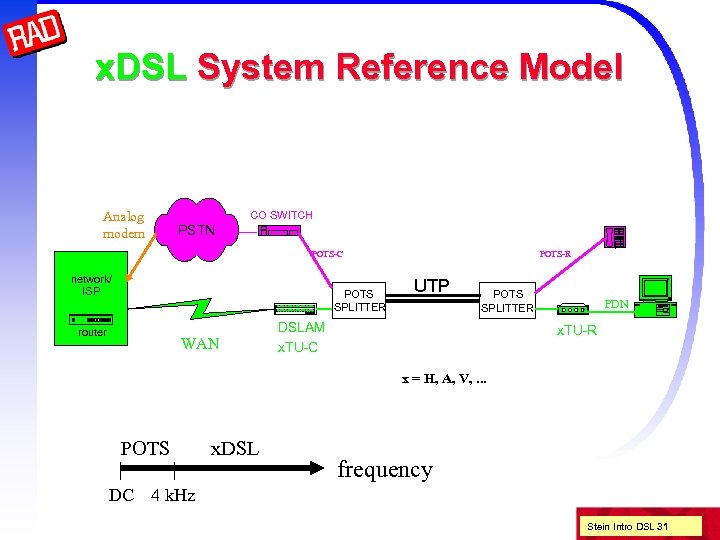x. DSL System Reference Model Analog modem CO SWITCH PSTN POTS-C network/ ISP POTS SPLITTER router WAN POTS-R UTP POTS SPLITTER DSLAM x. TU-C PDN x. TU-R x = H, A, V, . . . POTS x. DSL frequency DC 4 k. Hz Stein Intro DSL 31
Splitter separates POTS from DSL signals n n n Must guarantee lifeline POTS services! Hence usually passive filter Must block impulse noise (e. g. ring) from phone into DSL ADSLforum/T 1 E 1. 4 specified that splitter be separate from modem No interface specification (but can buy splitter and modem from different vendors) Splitter requires installation n Costly technician visit is the major impediment to deployment n ADSL has splitterless versions to facilitate residential deployment Stein Intro DSL 32
Why is DSL better than a voice-grade modem? Analog telephony modems are limited to 4 KHz bandwidth Shannon’s channel capacity theorem gives the maximum transfer rate N S C = BW log 2 ( SNR + 1 ) for SNR >> 1 C(bits/Hz) SNR(d. B) / 3 So by using more BW we can get higher transfer rates! But what is the BW of UTP? Stein Intro DSL 33
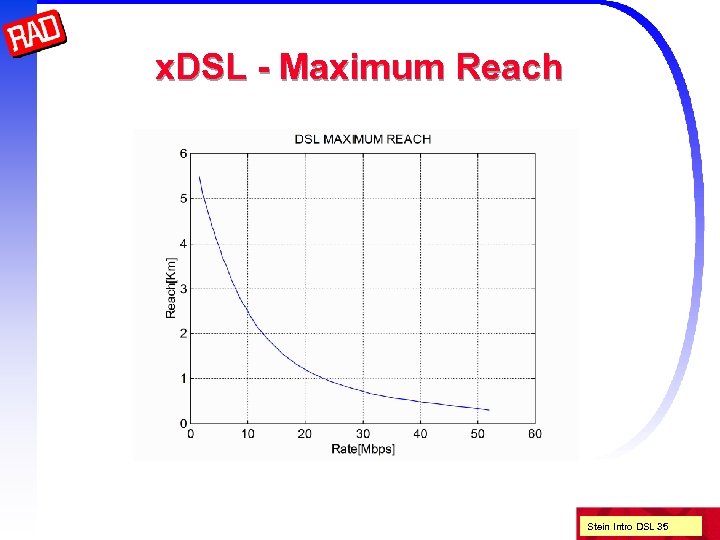
Maximum reach To use Shannon's capacity theorem we need to know how much noise there is One type of noise that is always present (above absolute zero temperature) is thermal noise Maximum reach is the length of cable for reliable communications ASSUMING ONLY THERMAL NOISE Bellcore study in residential areas (NJ) found n n -140 d. Bm / Hz white (i. e. independent of frequency) is a good approximation We can compute the maximum reach from known UTP attenuation Stein Intro DSL 34
x. DSL - Maximum Reach Stein Intro DSL 35
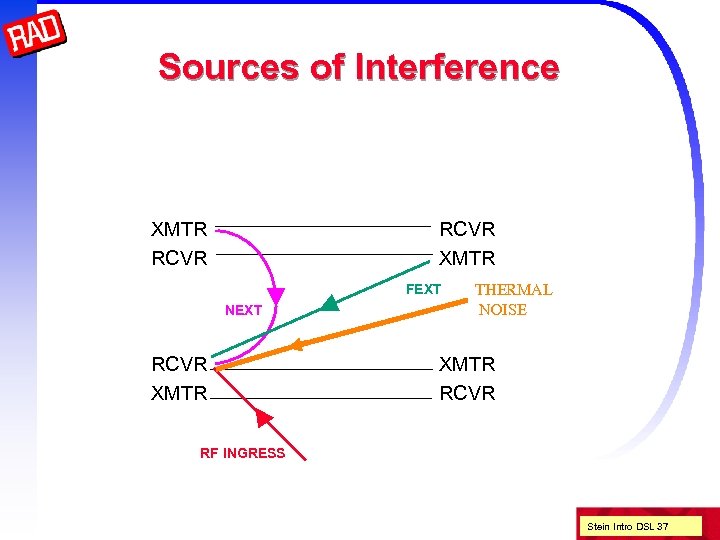
Other sources of noise But real systems have other sources of noise, and thus the SNR will be lower and thus will have lower reach There are three other commonly encountered types of noise n RF ingress n Near End Cross Talk (NEXT) n Far End Cross Talk (FEXT) Stein Intro DSL 36
Sources of Interference XMTR RCVR XMTR FEXT NEXT RCVR XMTR THERMAL NOISE XMTR RCVR RF INGRESS Stein Intro DSL 37
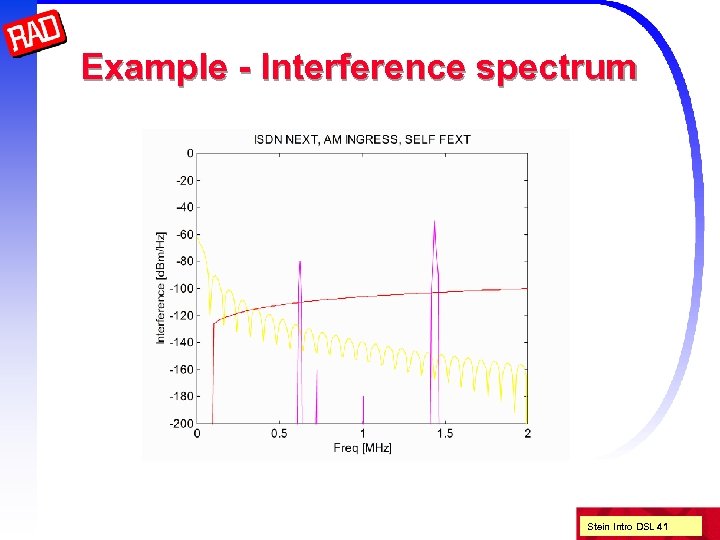
Unger’s discovery What happens with multiple sources of cross-talk? Unger (Bellcore) : 1% worst case NEXT n n n (T 1 D 1. 3 185 -244) 50 pair binders 22 gauge PIC 18 Kft Found empirically that cross-talk only increases as N 0. 6 This is because extra interferers must be further away Stein Intro DSL 38
NEXT Only close points are important n Distant points are twice attenuated by line attenuation |H(f, x)|2 Unger dependence on number of interferers Frequency dependence n Transfer function ~ I 2 Campbell / R ~ f 2 / f 1/2 = f 3/2 n Power spectrum of transmission Total NEXT interference (noise power) KNEXT N 0. 6 f 3/2 PSD(f) Stein Intro DSL 39
FEXT Entire parallel distance important n Thus there will be a linear dependence on L Unger dependence on number of interferers Frequency dependence n Transfer function ~ I 2 Campbell ~ f 2 n Power spectrum of transmission Total FEXT interference (noise power) KFEXT N 0. 6 L f 2 |Hchannel(f)|2 PSD(f) Stein Intro DSL 40
Example - Interference spectrum Stein Intro DSL 41
Examples of Realistic Reach More realistic design goals (splices, some xtalk) n 1. 5 Mbps 18 Kft 5. 5 km (80% US loops) n 2 Mbps 16 Kft 5 km n 6 Mbps 12 Kft 3. 5 km n 10 Mbps 7 Kft n 13 Mbps 4. 5 Kft 1. 4 km n 26 Mbps 3 Kft 900 m n 52 Mbps 1 Kft 300 m (SONET (CSA 50% US loops) 2 km STS-1 = 1/3 STM-1) Stein Intro DSL 42
(Bonding (inverse mux If we need more BW than attainable by Shannon bounds we can use more than one UTP pair (although XT may reduce) This is called bonding or inverse multiplexing There are many ways of using multiple pairs: n ATM - extension of IMA (may be different rates per pair) ATM cells marked with SID and sent on any pair n Ethernet - based on 802. 3(EFM) frames are fragmented, marked with SN, and sent on many pairs n n n Time division inverse mux Dynamic Spectral Management (Cioffi) Ethernet link aggregation Stein Intro DSL 43
Duplexing Up to now we assumed that only one side transmits Bidirectional (full duplex) transmission requires some form of duplexing For asymmetric applications we usually speak of DS downstream and US upstream Four methods are in common use: n Half duplex mode (4 W mode) (as in E 1/T 1) n Echo cancellation mode (ECH) n Time Domain Duplexing (requires syncing all binder contents) n Frequency Domain Duplexing POTS US DS frequency DC 4 k. Hz Stein Intro DSL 44
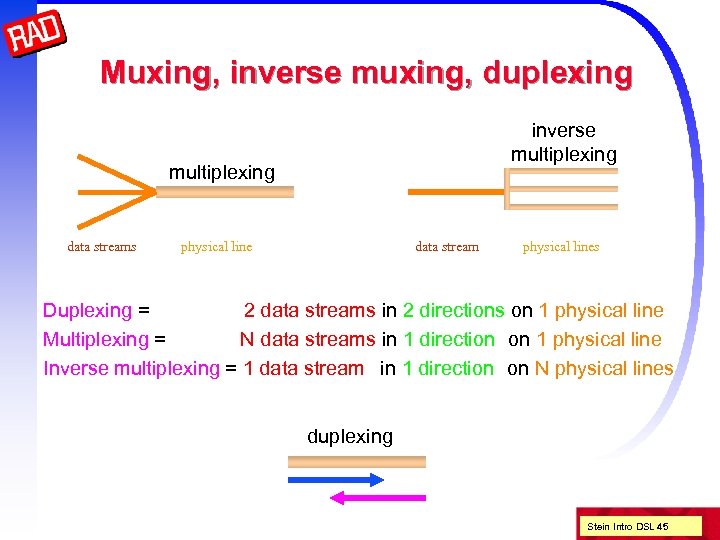Muxing, inverse muxing, duplexing inverse multiplexing data streams physical line data stream physical lines Duplexing = 2 data streams in 2 directions on 1 physical line Multiplexing = N data streams in 1 direction on 1 physical line Inverse multiplexing = 1 data stream in 1 direction on N physical lines duplexing Stein Intro DSL 45
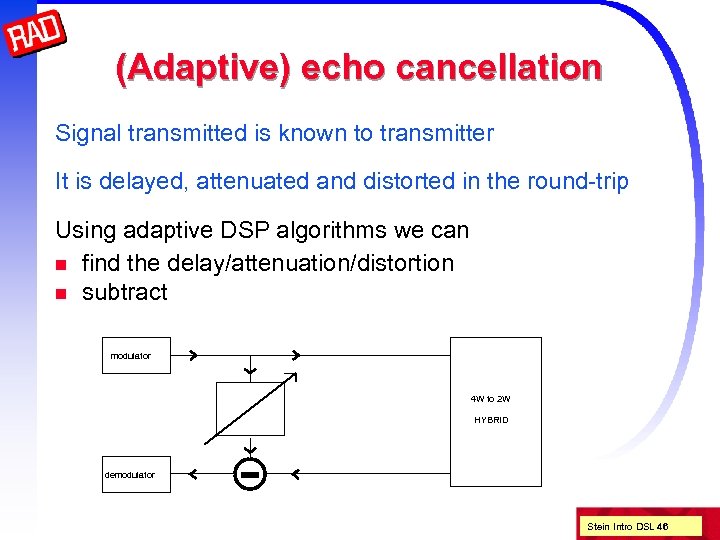(Adaptive) echo cancellation Signal transmitted is known to transmitter It is delayed, attenuated and distorted in the round-trip Using adaptive DSP algorithms we can n find the delay/attenuation/distortion n subtract modulator 4 W to 2 W HYBRID demodulator Stein Intro DSL 46
x. DSL types and history Stein Intro DSL 47
DSL Flavors DSL is often called x. DSL since there are many varieties (different x) e. g. ADSL, HDSL, SHDSL, VDSL, IDSL, etc. There were once many unconnected types but now we divide them into three main families The differentiation is by means of the application scenario n n n HDSL (symmetric, mainly business, data + telephony) ADSL (asymmetric, mainly residential, Internet access) VDSL (very high rate, but short distance) Stein Intro DSL 48
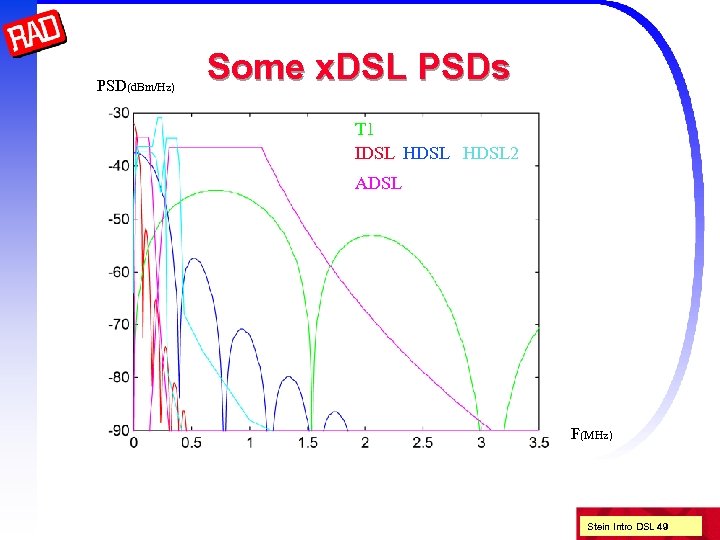PSD(d. Bm/Hz) Some x. DSL PSDs T 1 IDSL HDSL 2 ADSL F(MHz) Stein Intro DSL 49
ITU G. 99 x standards n G. 991 HDSL (G. 991. 1 HDSL G. 991. 2 SHDSL) n G. 992 ADSL (G. 992. 1 ADSL G. 992. 2 splitterless ADSL G. 992. 4 splitterless ADSL 2 G. 992. 3 ADSL 2 G. 992. 5 ADSL 2+) n G. 993 VDSL (G. 993. 1 VDSL n G. 994 HANDSHAKE n G. 995 GENERAL (INFO) n G. 996 TEST n G. 997 PLOAM n G. 998 bonding (G. 998. 1 ATM G. 993. 2 VDSL 2) G. 998. 2 Ethernet G. 998. 3 TDIM) Stein Intro DSL 50
ITU x. DSL layer model n Transport protocol (ATM, STM, PTM) n Transport Protocol Specific - Transmission Convergence (TPS-TC) n Physical Medium Specific - Transmission Convergence (PMS-TC) n Physical Medium Dependent (PMD) n Physical medium Stein Intro DSL 51
More x. DSL flavors Stein Intro DSL 52
More x. DSL flavors (cont. ) Not DSL Stein Intro DSL 53
T 1 service (not DSL) 1963: Coax deployment of T 1 n n n 2 groups in digital TDM AMI line code Beyond CSA range should use DLC (direct loop carrier) Repeaters every 6 Kft Made possible by Bell Labs invention of the transistor 1971: UTP deployment of T 1 (but still not DSL) n n Bring 1. 544 Mbps to customer private lines Use two UTP in half duplex mode Requires expensive line conditioning One T 1 per binder group Stein Intro DSL 54
T 1 line conditioning In order for a subscriber’s line to carry T 1 n n n n Single gauge CSA range No loading coils No bridged taps Repeaters every 6 Kft (starting 3 Kft) One T 1 per binder group Labor intensive (expensive) process Need something better … (DSL) Stein Intro DSL 55
The first true x. DSL! 1984, 88: IDSL n BRI access for ISDN n 4 B 3 T (3 level PAM) or 2 B 1 Q (4 level PAM) modulation n Prevalent in Europe, never really caught on in US n 144 Kbps over CSA range ITU-T G. 961 describes IDSL There are 4 appendices: n Appendix I - 4 B 3 T (AKA MMS 43) n Appendix II - 2 B 1 Q n Appendix III - AMI Time Compression Multiplex (TDD) n Appendix IV - SU 32 (3 B 2 T + ECH) Stein Intro DSL 56
HDSL - NA improved copy of IDSL 1991: HDSL n Replaced T 1/E 1 service, but – full CSA distance w/o line conditioning / repeaters n AMI line code replaced with IDSL's 2 B 1 Q line code n Use 2 UTP pairs, but in ECH mode (DFE) – For T 1 784 kbps on each pair – For E 1, 1, 2, 3 and 4 pair modes (all ECH) n Requires DSP for echo cancellation n Mature DSL technology, now becoming obsolete Stein Intro DSL 57
HDSL 2 With the success of HDSL, customers requested HDSL service that would : n require only a single UTP HDSL n attain at least full CSA reach n be spectrally compatible w/ HDSL, T 1, ADSL, etc. The result, based on high order PAM, was called n n HDSL 2 (ANSI) SDSL Symmetric DSL (ETSI) and is now called n SHDSL Single pair HDSL (ITU) Stein Intro DSL 58
SHDSL Uses Trellis Coded 16 -PAM with various shaping options Does not co-exist with POTS service on UTP Can uses regenerators for extended reach single-pair operation n 192 kbps to 2. 312 Mbps in steps of 8 kbps n 2. 3 Mbps should be achieved for reaches up to 3. 5 km dual-pair operation (4 -wire mode) n 384 kbps to 4. 608 Mbps in steps of 16 kbps n line rate is the same on both pairs Latest standard (G. shdsl. bis - G. 991. 2 2003 version) n bonding up to 4 pairs n rates up to 5696 kbps n optional 32 -PAM (instead of 16 -PAM) n dynamic rate repartitioning Stein Intro DSL 59
ADSL Asymmetric - high rate DS, lower rate US Originally designed for video on demand New modulation type - Discrete Multi. Tone FDD and ECH modes Almost retired due to lack of interest …but then came the Internet Studies - DS: US for both applications can be about 10: 1 Some say ADSL could mean All Data Subscribers Living Stein Intro DSL 60
Why asymmetry? NEXT is the worst interferer stops HDSL from achieving higher rates FEXT much less (attenuated by line) FDD eliminates NEXT All modems must transmit in the SAME direction A reversal would bring all ADSL modems down Upstream(US) at lower frequencies and power density Downstream (DS) at high frequencies and power Stein Intro DSL 61
ADSL Duplexing n US uses low DMT tones (e. g. 8 - 32) n If over POTS / ISDN lowest frequencies reserved n DS uses higher tones – If FDD no overlap – If ECH DS overlaps US P O T S US 8 DS 32 G. 992. 1 FDD mode 256 * 4. 3125 k. Hz Stein Intro DSL 62
Why asymmetry? - continued PSD (d. Bm/Hz) US DS F(MHz) Stein Intro DSL 63
Echo cancelled ADSL FDD gives sweet low frequencies to US only and the sharp filters enhance ISI By overlapping DS on US we can use low frequencies and so increase reach Power spectral density chart Stein Intro DSL 64
ADSL - continued ADSL system design criterion BER 10 -12 (1 error every 2 days at 6 Mbps) Raw modem can not attain this low a BER! For video on demand: n RS and interleaving can deliver (error bursts of 500 msec) n but add 17 msec delay For Internet: n TCP can deliver n high raw delay problematic So the G. 992. 1 standard defines TWO framers fast (noninterleaved ) and slow (interleaved) buffers Stein Intro DSL 65
ADSL standard ITU (G. dmt) G. 992. 1, ANSI T 1. 413 i 2 standard DS - 6. 144 Mbps (minimum) US- 640 kbps First ADSL data implementations were CAP (QAM) ITU/ANSI/ETSI standards are DMT with spacing of 4. 3125 k. Hz n n DMT allows approaching water pouring capacity DMT is robust DMT requires more complex processing DMT may require more power Stein Intro DSL 66
Splitterless ADSL, UAWG, G. lite, G. 992. 2, G. 992. 4 Splitterless operation n fast retrain n power management to eliminate clipping n initialization includes probing telephone sets for power level n microfilters n modems usually store environment parameters G. 992. 2 - cost reduction features n n G. 992. 1 compatible DMT compatible using only 128 tones 512 Kbps US / 1. 5 Mbps DS (still >> V. 34 or V. 90 modems) features removed for simplicity simpler implementation (only 500 MIPS < 2000 MIPS for full rate) Stein Intro DSL 67
ADSL 2 ADSL uses BW from 20 k. Hz to 1. 1 MHz ADSL 2 Increases rate/reach of ADSL by using 20 k. Hz - 4. 4 MHz Also numerous efficiency improvements n better modulation n reduced framing overhead n more flexible format (see next slide) n stronger FEC n reduced power mode n misc. algorithmic improvements for given rate, reach improved by 200 m 3 user data types - STM, ATM and packet (Ethernet) ADSL 2+ dramatically increased rate at short distances Stein Intro DSL 68
More ADSL 2 features Dynamic training features n Bit Swapping (dynamic change of DMT bin bit/power allocations) n Seamless Rate Adaptation (dynamic change of overall rate) Frame bearers n Multiple (up to 4) frame bearers (data flows) n Multiple latencies for different frame bearers (FEC/interleave lengths) n Dynamic rate repartitioning (between different latencies) Stein Intro DSL 69
ADSL annexes (G. 992. 1/3) Annex A ADSL over POTS Annex B ADSL over 2 B 1 Q/4 B 3 T ISDN Annex C ADSL over TDD ISDN Annex D State diagrams (state machine for idle, (re)training, etc) Annex E Splitters (POTS and ISDN) Annex F North America - classification and performance Annex G Europe - classification (interop options) and performance Annex H Synchronized Symmetric DSL with TDD ISDN in binder Stein Intro DSL 70
ADSL annexes (G. 992. 3) Annex I All digital ADSL (i. e. alone on UTP) with POTS in binder Annex J All digital ADSL with ISDN in binder Annex K Transmission Protocol Specific functions (STM, ATM, PTM) Annex L Reach Extended ADSL 2 over POTS Annex M Extended US BW over POTS Stein Intro DSL 71
VDSL Optical network expanding (getting closer to subscriber) Optical Network Unit ONU at curb or basement cabinet FTTC (curb), FTTB (building) These scenarios usually dictates low power Rates can be very high since required reach is minimal! Proposed standard has multiple rates and reaches Stein Intro DSL 72
VDSL - rate goals Symmetric rates 6. 5 4. 5 Kft (1. 4 Km) 13 3 Kft (900 m) 26 1 Kft (300 m) Asymmetric rates (US/DS) 0. 8/ 6. 5 1. 6/13 3. 2/26 6. 4/52 6 Kft 4. 5 Kft 3 Kft 1 Kft (1. 8 Km) (1. 4 Km) (900 m) (300 m) Stein Intro DSL 73
VDSL - Power issues Basic template is -60 d. Bm/Hz from 1. 1 MHz to 20 MHz Notches reduce certain frequencies to -80 d. Bm/Hz Power boost on increase power to -50 d. Bm/Hz Power back-off reduces VTU-R power so that won’t block another user ADSL compatibility off use spectrum down to 300 KHz Stein Intro DSL 74
VDSL 2 DMT line code (same 4. 3125 k. Hz spacing as ADSL) VDSL uses BW of 1. 1 MHz - 12 MHz (spectrally compatible with ADSL) VDSL 2 can use 20 k. Hz - 30 MHz n new band-plans (up to 12 MHz, and 12 -30 MHz) n increased DS transmit power various algorithmic improvements borrowed improvements from ADSL 2 3 user data types - STM, ATM and PTM n n n Stein Intro DSL 75
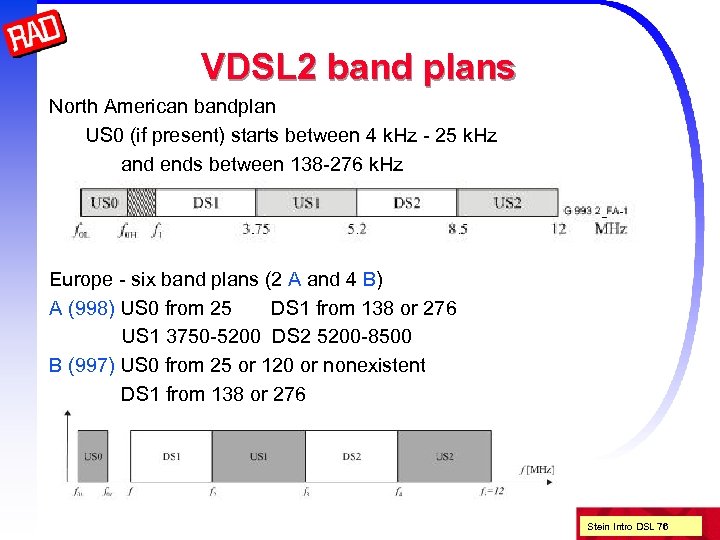VDSL 2 band plans North American bandplan US 0 (if present) starts between 4 k. Hz - 25 k. Hz and ends between 138 -276 k. Hz Europe - six band plans (2 A and 4 B) A (998) US 0 from 25 DS 1 from 138 or 276 US 1 3750 -5200 DS 2 5200 -8500 B (997) US 0 from 25 or 120 or nonexistent DS 1 from 138 or 276 US 1 3000 -5100 DS 2 5100 -7050 Stein Intro DSL 76
HPNA (G. PNT) n Studies show that about 50% of US homes have a PC 30% have Internet access, 20% have more than one PC! n Average consumer has trouble with cabling Home. PNA de facto industry standard for home networking n n Computers, peripherals interconnect (and connect to Internet? ) using internal phone wiring (user side of splitter) Does not interrupt lifeline POTS services Does not require costly or messy LAN wiring of the home Presently 1 Mbps, soon 10 Mbps, eventually 100 Mbps! Stein Intro DSL 77
Shannon Theory Stein Intro DSL 78
Shannon - Game plan Claude Shannon (Bell Labs) 1948 Digital communications never worse than analog and frequently better ! Basic idea: n n Analog signals become contaminated by noise Amplification doesn't help - noise is amplified too Bits can not be degraded in a minor way - either 0 or 1 When bit flip - Error Correcting Codes can fix Rigorous proof: n n n Source - channel separation theorem Source encoding theorems Channel capacity theorems Stein Intro DSL 79
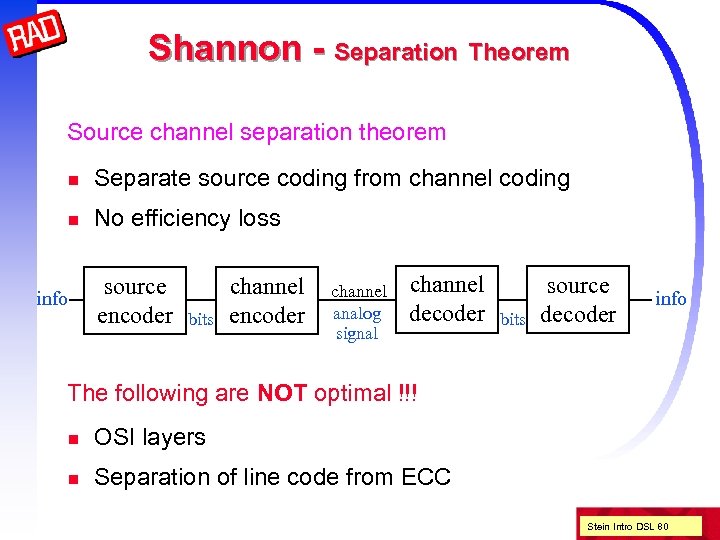Shannon - Separation Theorem Source channel separation theorem n Separate source coding from channel coding n No efficiency loss info source encoder bits channel encoder channel analog signal channel decoder bits source decoder info The following are NOT optimal !!! n OSI layers n Separation of line code from ECC Stein Intro DSL 80
Shannon - Channel Capacity Every bandlimited noisy channel has a capacity Below capacity errorless information reception Above capacity errors Shocking news to analog engineers Previously thought: only increasing power decreases error rate But Shannon didn’t explain HOW! Stein Intro DSL 81
Channel Capacity (continued) Shannon’s channel capacity theorem: If no noise (even if narrow BW): Infinite information transferred instantaneously Just send very precise level If infinite bandwidth (even if high noise): No limitation on how fast switch between bits If both limitations: C = BW log 2 ( SNR + 1 ) Stein Intro DSL 82
Channel Capacity (continued) The forgotten part: All correlations introduce redundancy Maximal information means nonredundant The signal that attains channel capacity looks like white noise filtered to the BW Stein Intro DSL 83
Channel Capacity (continued) That was for an ideal low-pass channel What about a real channel (like DSL)? Shannon says. . . Simply divide channel into subchannels and integrate each bandpass channel obeys regular Shannon law S log 2 (SNR(f) + 1) BW log 2 (SNR(f) + 1) df Only SNR(f) is important ! Stein Intro DSL 84
Water pouring (Gallager) theorem Given total amount of energy, N(f) and A(F) how can we maximize the capacity? N(f) / A(f) f Stein Intro DSL 85
Line Codes Stein Intro DSL 86
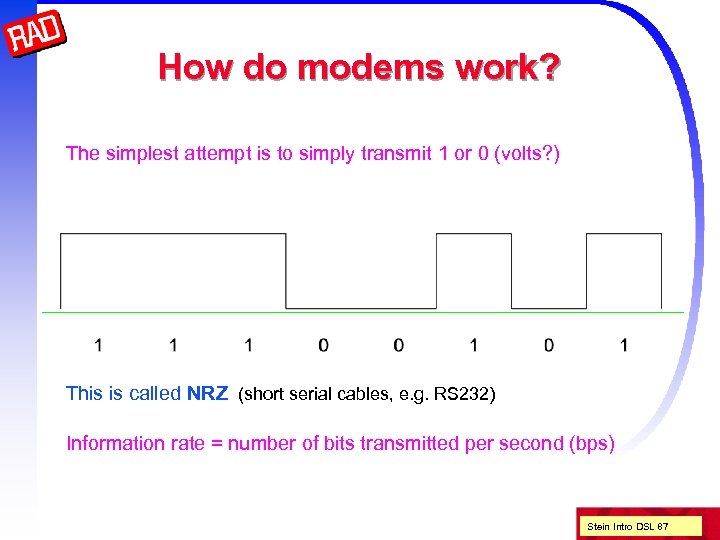How do modems work? The simplest attempt is to simply transmit 1 or 0 (volts? ) This is called NRZ (short serial cables, e. g. RS 232) Information rate = number of bits transmitted per second (bps) Stein Intro DSL 87
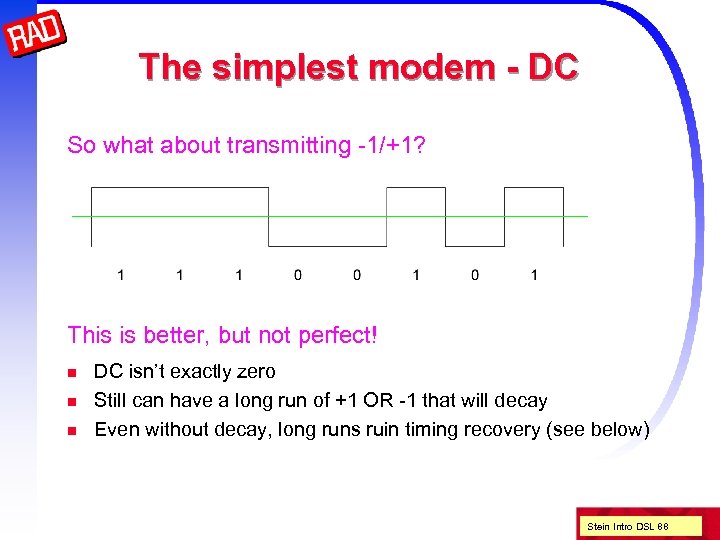The simplest modem - DC So what about transmitting -1/+1? This is better, but not perfect! n n n DC isn’t exactly zero Still can have a long run of +1 OR -1 that will decay Even without decay, long runs ruin timing recovery (see below) Stein Intro DSL 88
The simplest modem - DC What about RZ? n No long +1 runs, so DC decay not important n Still there is DC Half width pulses means twice bandwidth! n Stein Intro DSL 89
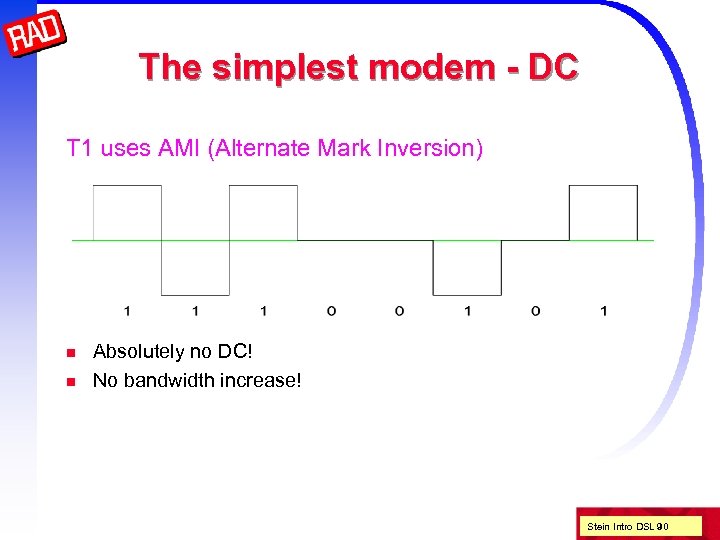The simplest modem - DC T 1 uses AMI (Alternate Mark Inversion) n n Absolutely no DC! No bandwidth increase! Stein Intro DSL 90
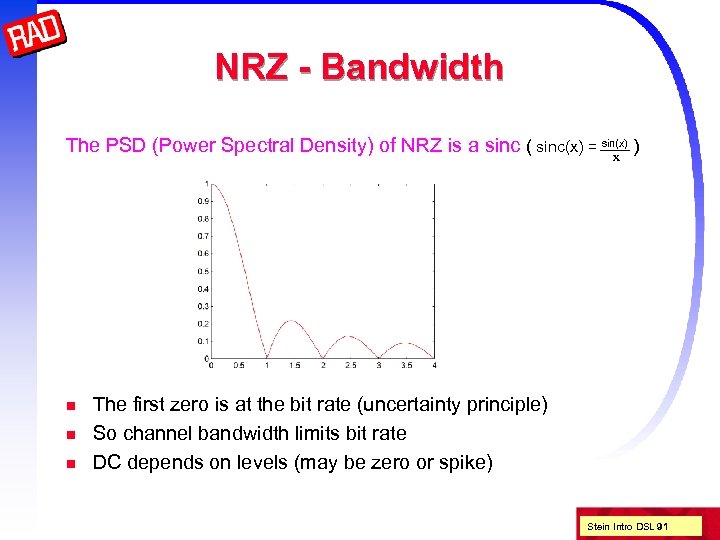NRZ - Bandwidth The PSD (Power Spectral Density) of NRZ is a sinc ( sinc(x) = sin(x) ) x n n n The first zero is at the bit rate (uncertainty principle) So channel bandwidth limits bit rate DC depends on levels (may be zero or spike) Stein Intro DSL 91
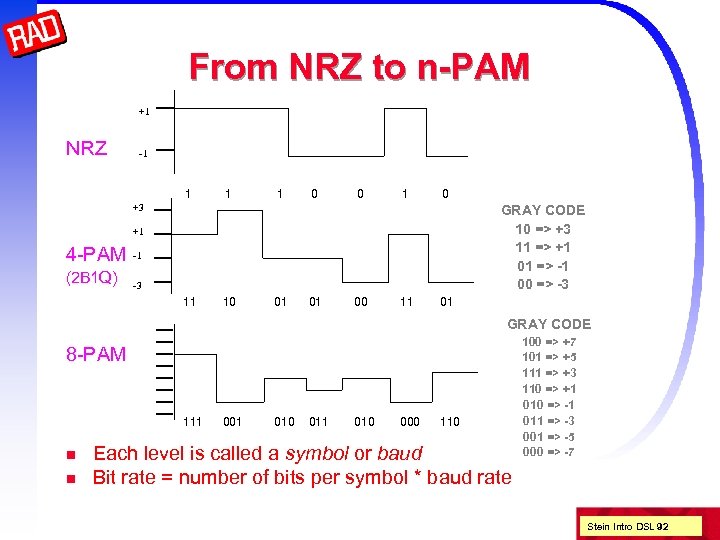From NRZ to n-PAM +1 NRZ -1 1 0 0 1 0 +3 GRAY CODE 10 => +3 11 => +1 01 => -1 00 => -3 +1 4 -PAM (2 B 1 Q) -1 -3 11 10 01 01 00 11 01 GRAY CODE 8 -PAM 111 n n 001 010 011 010 000 110 Each level is called a symbol or baud Bit rate = number of bits per symbol * baud rate 100 => +7 101 => +5 111 => +3 110 => +1 010 => -1 011 => -3 001 => -5 000 => -7 Stein Intro DSL 92
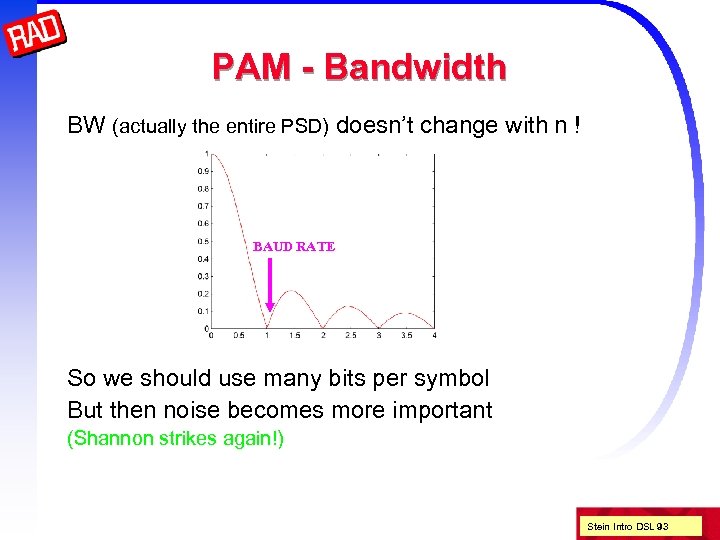PAM - Bandwidth BW (actually the entire PSD) doesn’t change with n ! BAUD RATE So we should use many bits per symbol But then noise becomes more important (Shannon strikes again!) Stein Intro DSL 93
The simplest modem - OOK Even better - use OOK (On Off Keying) n n n Absolutely no DC! Based on sinusoid (“carrier”) Can hear it (morse code) Stein Intro DSL 94
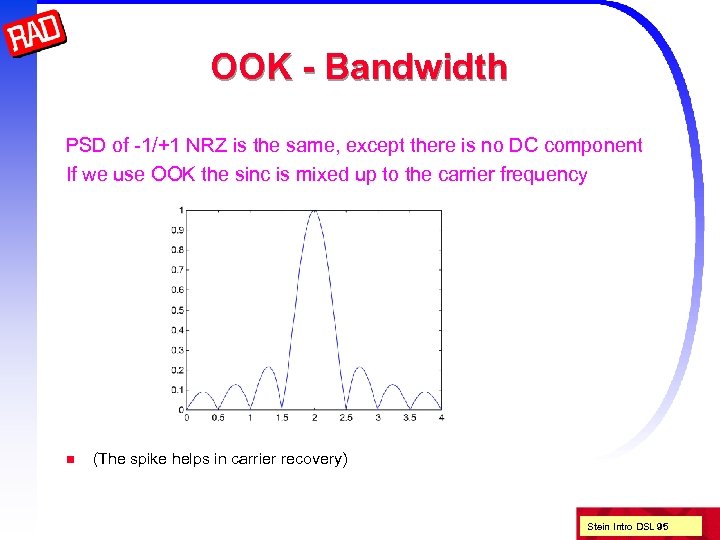OOK - Bandwidth PSD of -1/+1 NRZ is the same, except there is no DC component If we use OOK the sinc is mixed up to the carrier frequency n (The spike helps in carrier recovery) Stein Intro DSL 95
ASK What about Amplitude Shift Keying - ASK ? 2 bits / symbol n n Generalizes OOK like multilevel PAM did to NRZ Not widely used since hard to differentiate between levels Is FSK better? Stein Intro DSL 96
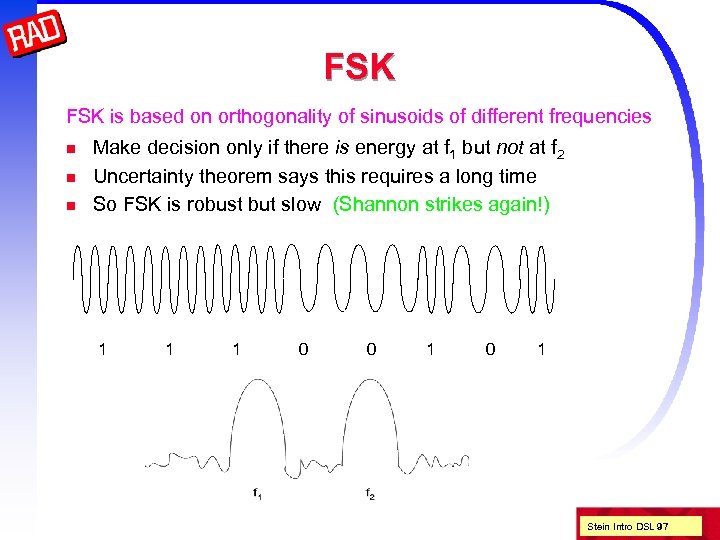FSK is based on orthogonality of sinusoids of different frequencies n n n Make decision only if there is energy at f 1 but not at f 2 Uncertainty theorem says this requires a long time So FSK is robust but slow (Shannon strikes again!) 1 1 1 0 0 1 Stein Intro DSL 97
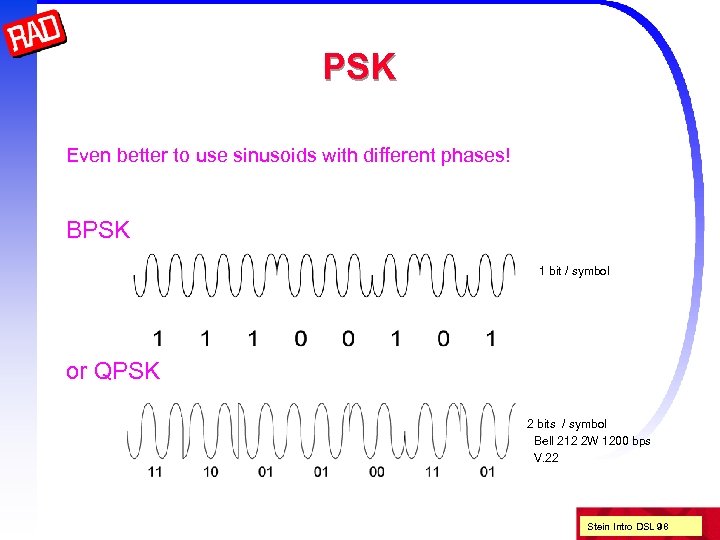PSK Even better to use sinusoids with different phases! BPSK 1 bit / symbol or QPSK 2 bits / symbol Bell 212 2 W 1200 bps V. 22 Stein Intro DSL 98
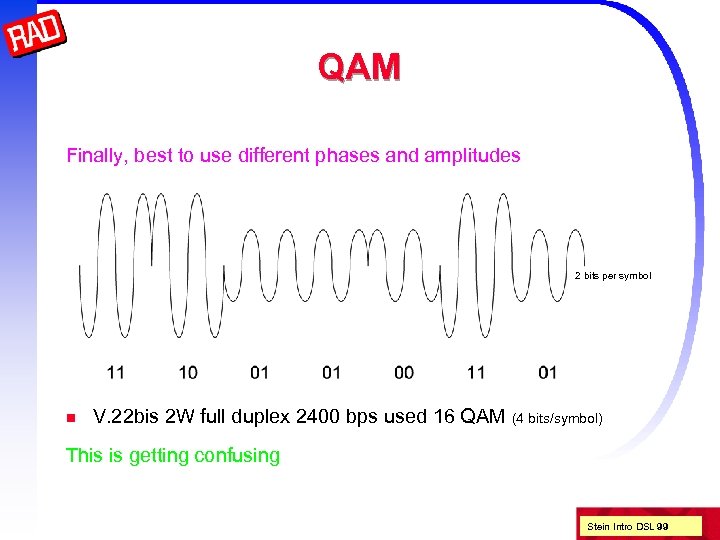QAM Finally, best to use different phases and amplitudes 2 bits per symbol n V. 22 bis 2 W full duplex 2400 bps used 16 QAM (4 bits/symbol) This is getting confusing Stein Intro DSL 99
The secret math behind it all The instantaneous representation n x(t) = A(t) cos ( 2 p fc t + f(t) ) A(t) is the instantaneous amplitude f(t) is the instantaneous phase This obviously includes ASK and PSK as special cases n n n Actually all bandwidth limited signals can be written this way Analog AM, FM and PM FSK changes the derivative of f(t) The way we defined them A(t) and f(t) are not unique n The canonical pair (Hilbert transform) Stein Intro DSL 100
The secret math - continued How can we find the amplitude and phase? The Hilbert transform is a 90 degree phase shifter H cos(f(t) ) = sin(f(t) ) Hence n x(t) = A(t) cos ( 2 p fc t + f(t) ) n y(t) = H x(t) = A(t) sin ( 2 p fc t + f(t) ) n A(t) = n f(t) = arctan( y(t) x 2(t) + y 2(t) x(t) ) Stein Intro DSL 101
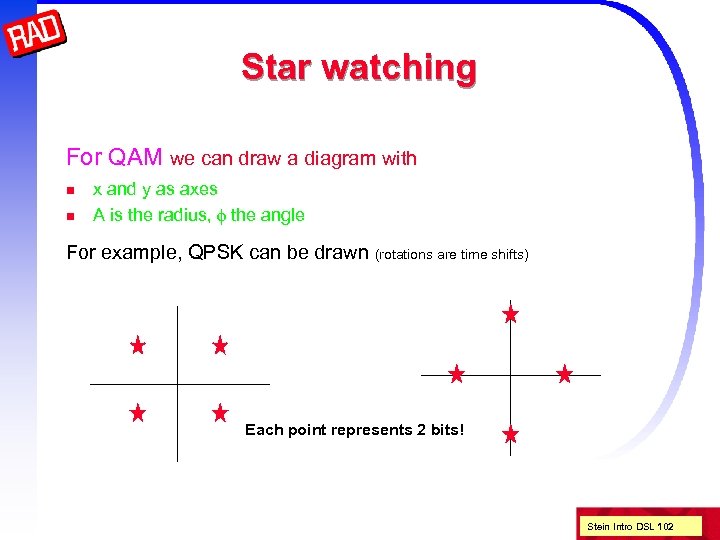Star watching For QAM we can draw a diagram with n n x and y as axes A is the radius, f the angle For example, QPSK can be drawn (rotations are time shifts) Each point represents 2 bits! Stein Intro DSL 102
QAM constellations 16 QAM V. 29 (4 W 9600 bps) V. 22 bis 2400 bps Codex 9600 (V. 29) 2 W first non-Bell modem (Carterphone decision) Adaptive equalizer Reduced PAR constellation Today - 9600 fax! 8 PSK V. 27 4 W 4800 bps Received symbols are not points due to noise and Inter Symbol Interference (ISI removed by equalizer) Stein Intro DSL 103
QAM constellations (cont) 1664 points Stein Intro DSL 104
Multicarrier Modulation n n n n NRZ, etc. have NO carrier PSK, QAM have ONE carrier MCM has MANY carriers Each is essentially an independent, standalone modem Achieve maximum capacity by direct water pouring! PROBLEM Basic FDM requires has Inter Channel Interference To reduce effect require guard frequencies Squanders good bandwidth Stein Intro DSL 105
OFDM n Subsignals are orthogonal if spaced precisely by the baud rate n Sinc function has zero at center of nearby modem This implies that the signals are orthogonal - no ICI No guard frequencies are needed Don’t need N independent modems – efficient digital implementation by FFT algorithm n n n Stein Intro DSL 106
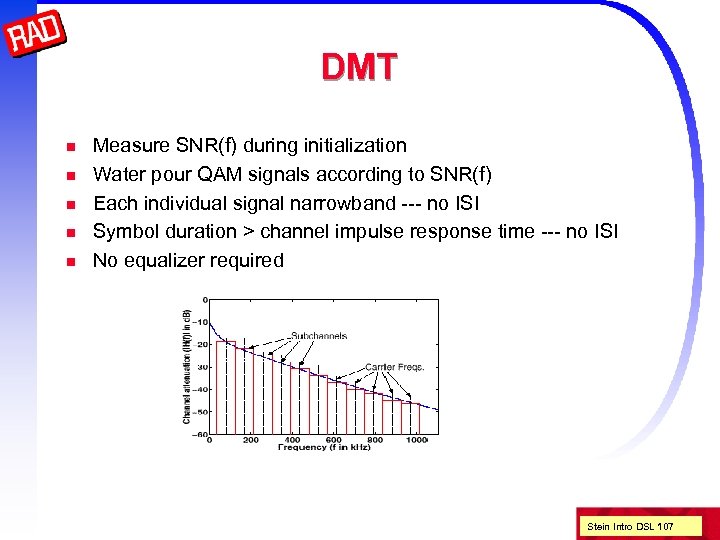DMT n n n Measure SNR(f) during initialization Water pour QAM signals according to SNR(f) Each individual signal narrowband --- no ISI Symbol duration > channel impulse response time --- no ISI No equalizer required Stein Intro DSL 107
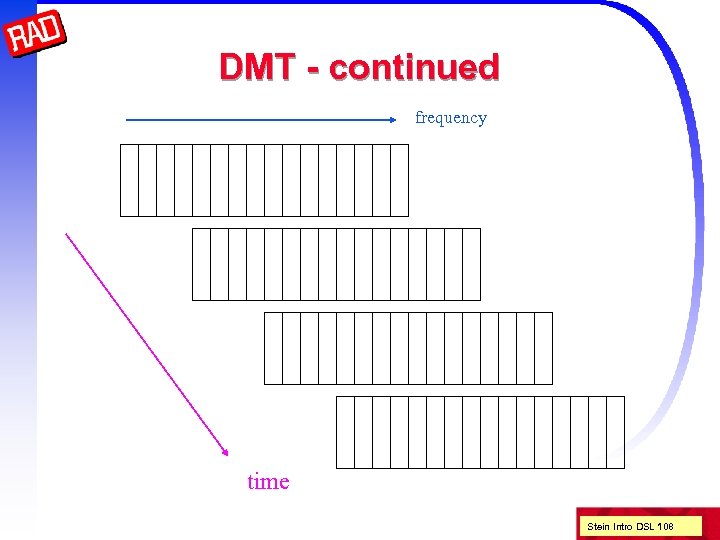DMT - continued frequency time Stein Intro DSL 108
Summary of x. DSL Line Codes PAM n IDSL (2 B 1 Q) n HDSL n SHDSL/HDSL 2 (with TCM and optionally OPTIS) n SDSL QAM/CAP n proprietary HDSL/ADSL/VDSL DMT n n ADSL 2, ADSL 2+ G. lite VDSL 2 Stein Intro DSL 109
Misc. Topics in DSL Modem Theory Stein Intro DSL 110
Bit scrambling We can get rid of long runs that cause DC at the bit level n n n Bits randomized for better spectral properties Self synchronizing Original bits can be recovered by descrambler Still not perfect! (one to one transformation) Stein Intro DSL 111
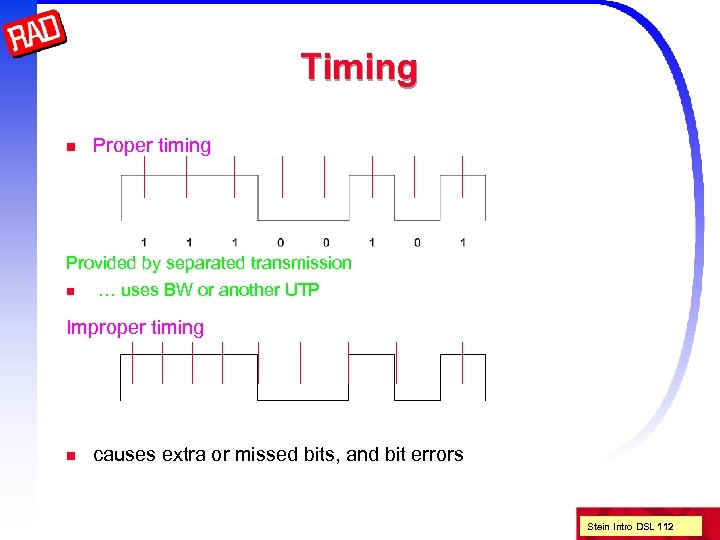Timing n Proper timing Provided by separated transmission n … uses BW or another UTP Improper timing n causes extra or missed bits, and bit errors Stein Intro DSL 112
Timing (baudrate) recovery How do we recover timing (baud rate) for an NRZ signal? n For clean NRZ - find the GCF of observed time intervals n For noisy signals need to filter n PLL b=T/t t = a t + (1 -a) T/b How can we recover the timing for a PSK signal? n n n The amplitude is NOT really constant (energy cut-off) Contains a component at baud rate Sharp filter and appropriate delay Similarly for QAM BUT as constellation gets rounder recovery gets harder Stein Intro DSL 113
Carrier recovery Need carrier recovery for PSK / QAM signals How can we recover the carrier of a PSK signal? X(t) = A(t) cos ( 2 p fc t So X 2(t) = cos 2 ( 2 p fc t ) where A(t) = +/- 1 ) For QPSK X 4(t) eliminates the data and emphasizes the carrier! Old saying “square for baud, to the fourth for carrier” Stein Intro DSL 114
Constellation rotation recovery How can we recover the rotation of the constellation? Simply change phase for best match to the expected constellation! How do we get rid of 90 degree ambiguity? We can’t! We have to live with it! And the easiest way is to use differential coding! DPSK 00 10 11 1 01 NPSK Gray code 000 110 011 101 000 QAM put the bits on the transitions! Stein Intro DSL 115
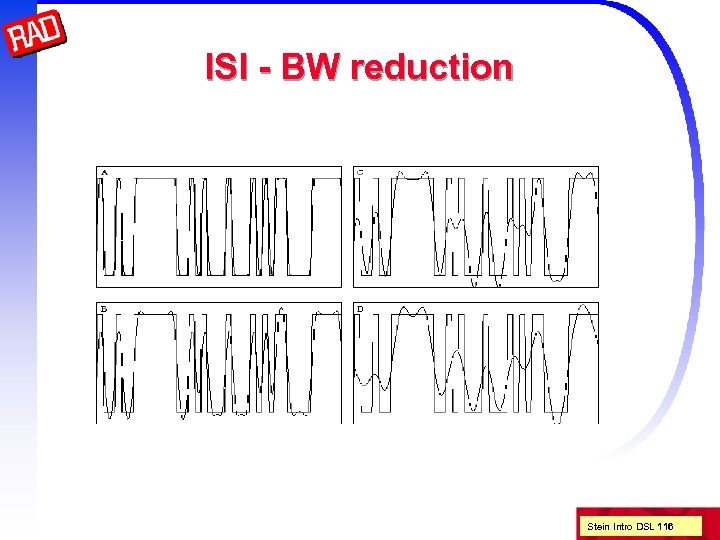ISI - BW reduction Stein Intro DSL 116
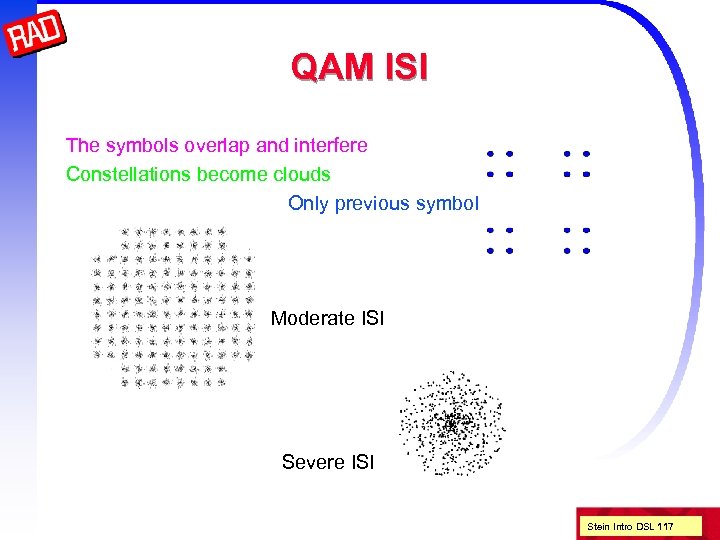QAM ISI The symbols overlap and interfere Constellations become clouds Only previous symbol Moderate ISI Severe ISI Stein Intro DSL 117
Equalizers ISI is caused by the channel acting like a low-pass filter n Can correct by filtering with inverse filter modulator channel filter equalizer demodulator This is called a linear equalizer n Can use compromise (ideal low-pass) equalizer plus an adaptive equalizer n Usually assume the channel is all-pole so the equalizer is all-zero (FIR) How do we find the equalizer coefficients? Stein Intro DSL 118
Training equalizers Basically a system identification problem n n n Initialize during training using known data (can be reduced to solving linear algebraic equations) Update using decision directed technique (e. g. LMS algorithm) once decisions are reliable Sometimes can also use blind equalization e e = e (ai) Stein Intro DSL 119
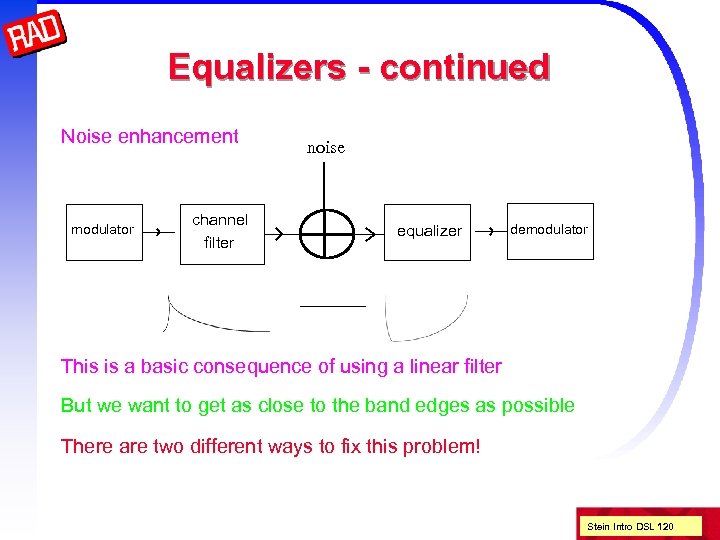Equalizers - continued Noise enhancement modulator channel filter noise equalizer demodulator This is a basic consequence of using a linear filter But we want to get as close to the band edges as possible There are two different ways to fix this problem! Stein Intro DSL 120
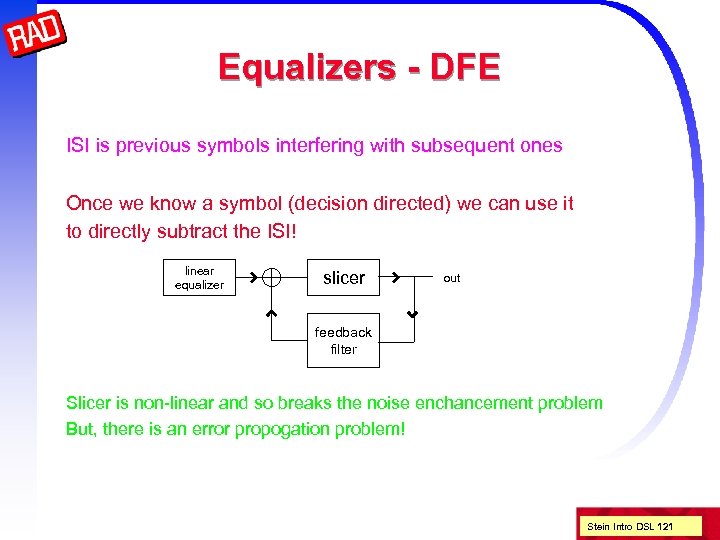Equalizers - DFE ISI is previous symbols interfering with subsequent ones Once we know a symbol (decision directed) we can use it to directly subtract the ISI! linear equalizer slicer out feedback filter Slicer is non-linear and so breaks the noise enchancement problem But, there is an error propogation problem! Stein Intro DSL 121
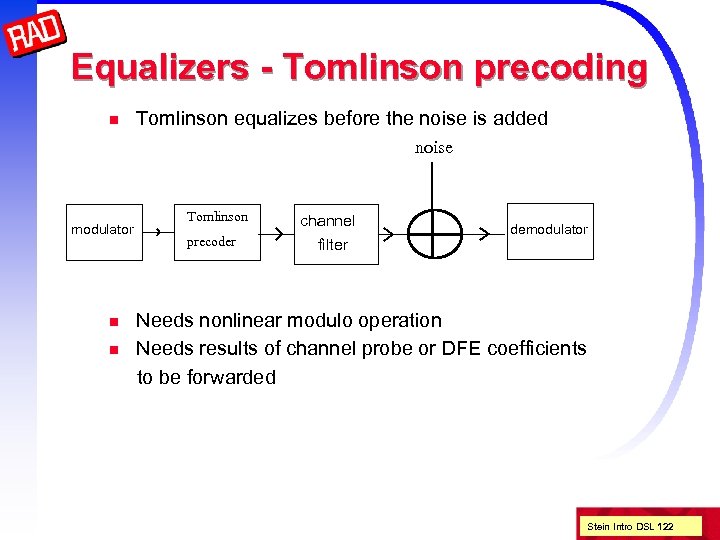Equalizers - Tomlinson precoding n Tomlinson equalizes before the noise is added noise modulator n n Tomlinson precoder channel filter demodulator Needs nonlinear modulo operation Needs results of channel probe or DFE coefficients to be forwarded Stein Intro DSL 122
More on QAM constellations What is important in a constellation? n n The number of points The minimum distance between points N dmin The average squared distance from the center E =
QAM constellations - slicers How do we use the constellation plot? n n n Received point classified to nearest constellation point Each point has associated bits (well that’s a lie, but hold on) Sum of errors is the PDSNR Stein Intro DSL 124
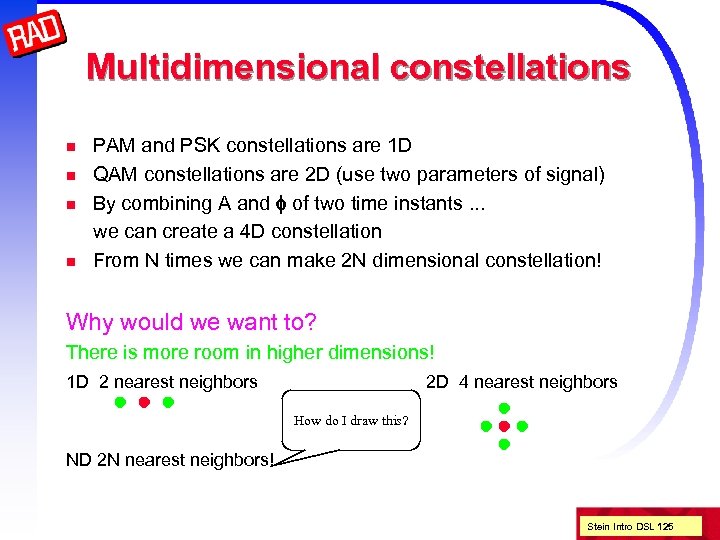Multidimensional constellations n n PAM and PSK constellations are 1 D QAM constellations are 2 D (use two parameters of signal) By combining A and f of two time instants. . . we can create a 4 D constellation From N times we can make 2 N dimensional constellation! Why would we want to? There is more room in higher dimensions! 1 D 2 nearest neighbors 2 D 4 nearest neighbors How do I draw this? ND 2 N nearest neighbors! Stein Intro DSL 125
Trellis coding Modems still make mistakes n Traditionally these were corrected by ECCs (e. g. Reed Solomon) n This separation is not optimal n Proof: incorrect hard decisions - not obvious where to correct soft decisions - correct symbols with largest error How can we efficiently integrate demodulation and ECC? n This was a hard problem since very few people were expert in ECCs and signal processing The key is set partitioning Stein Intro DSL 126
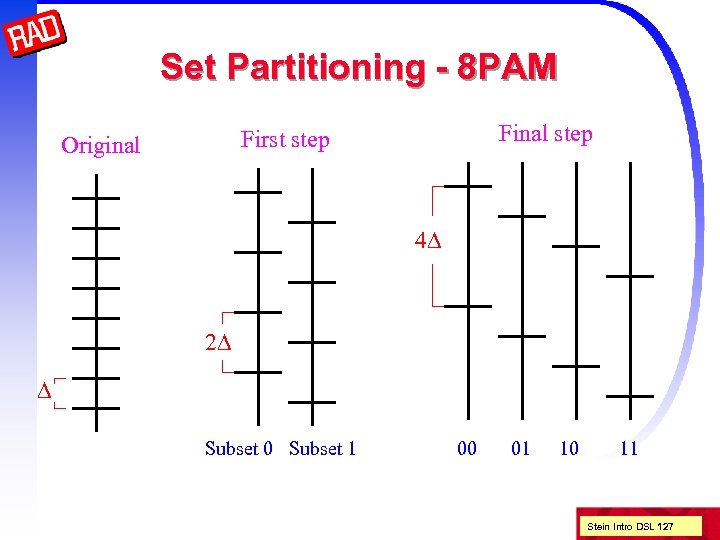Set Partitioning - 8 PAM Final step First step Original 4 D 2 D D Subset 0 Subset 1 00 01 10 11 Stein Intro DSL 127
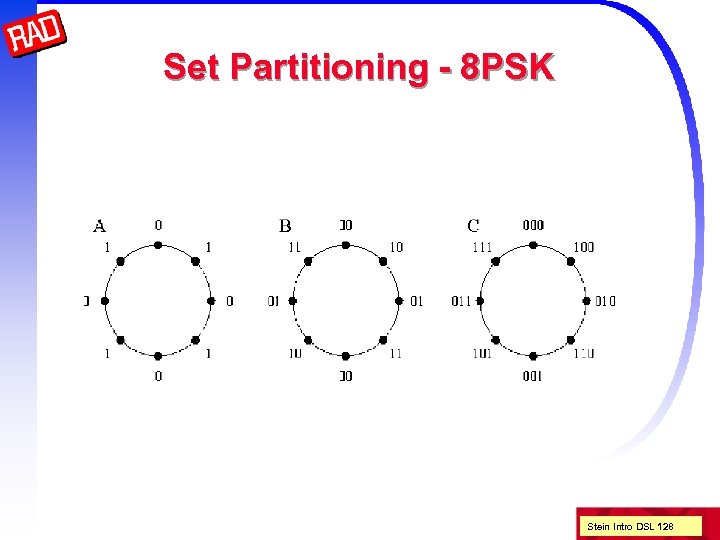Set Partitioning - 8 PSK Stein Intro DSL 128
Trellis coding - continued n If we knew which subset was transmitted, the decision would be easy So we transmit the subset and the point in the subset But we can’t afford to make a mistake as to the subset So we “protect” the subset identifier bits with an ECC n To decode use the Viterbi algorithm (example for 4 states - 2 subsets) n n n Stein Intro DSL 129
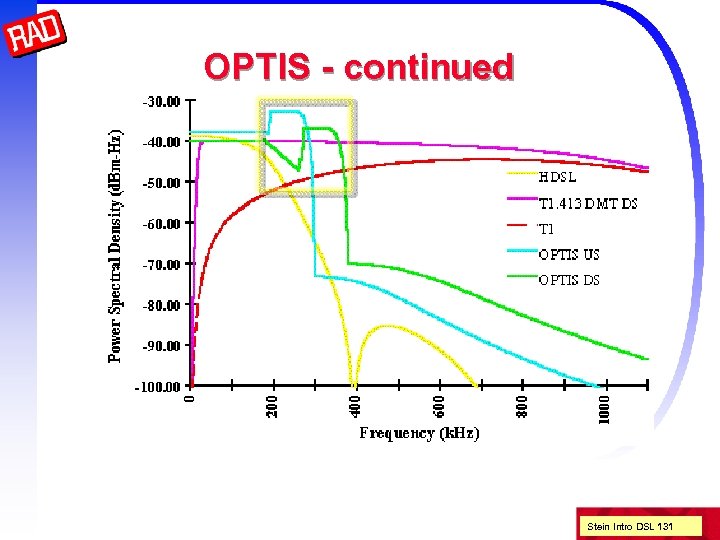
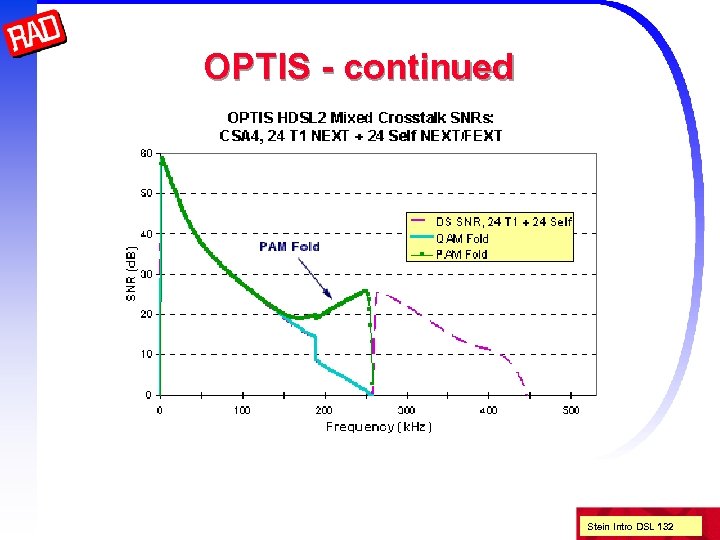
OPTIS Overlapping PAM Transmission with Interlocking Spectra An single pair HDSL replacement that is spectrally compatible with HDSL and T 1 16 level PAM with 517 K baud rate very strong (512 state, >5 d. B) TCM 1 D for low (216 msec) latency (speech) strong DFE tailored spectra (fits between HDSL and T 1) partially overlapped (interlocking) spectra folding (around fb/2) enhances SNR! upstream bump for spectral compatibility Stein Intro DSL 130
OPTIS - continued Stein Intro DSL 131
OPTIS - continued Stein Intro DSL 132
DMT processing bit handling ((de)framer, CRC, (de)scrambler, RS, (de)interleaver) tone handling (bit load, gain scaling, tone ordering, bit swapping) QAM modem (symbolizer, slicer) signal handling (cyclic prefix insertion/deletion, (I)FFT, interpolation, PAR reduction) synchronization (clock recovery) channel handling (probing and training, echo cancelling, FEQ, TEQ) Stein Intro DSL 133