8b5b1668153d74836c23e59eec13ac16.ppt
- Количество слайдов: 79

Introduction to Computer Security Lecture 6 Cryptography October 2, 2003 Courtesy of Professors Chris Clifton & Matt Bishop INFSCI 2935: Introduction of Computer Security 1

Overview of the DES l A block cipher: encrypts blocks of 64 bits using a 64 bit key ¡ outputs 64 bits of ciphertext ¡ A product cipher ¡ l performs both substitution and transposition (permutation) on the bits basic unit is the bit Consists of 16 rounds (iterations) each with a round key generated from the user-supplied key INFSCI 2935: Introduction to Computer Security 2
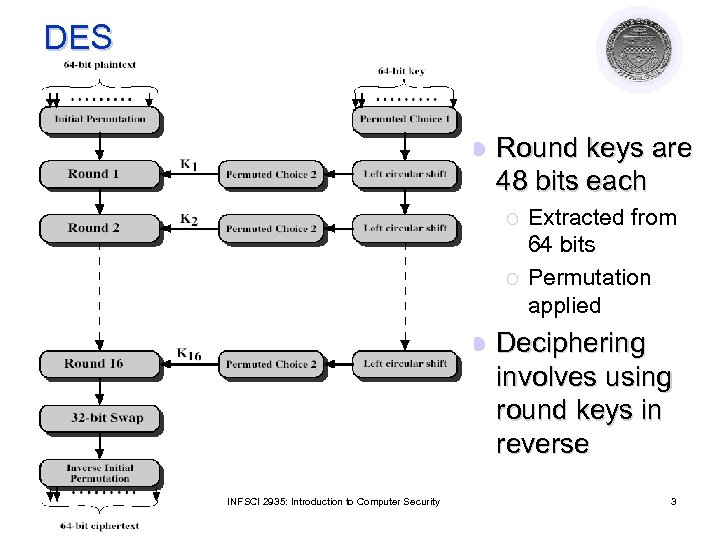
DES l Round keys are 48 bits each ¡ ¡ l INFSCI 2935: Introduction to Computer Security Extracted from 64 bits Permutation applied Deciphering involves using round keys in reverse 3
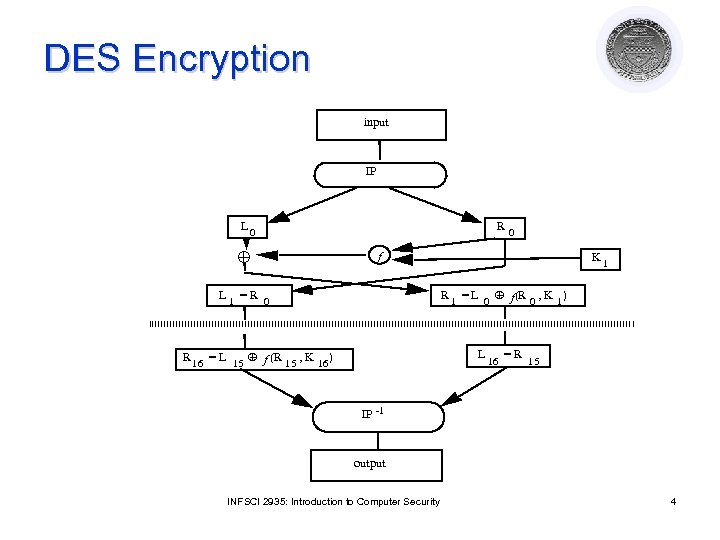
DES Encryption input IP L 0 R 0 f K 1 R 1 = L 0 f (R 0 , K 1) L 1 =R 0 L R 16 = L 15 f (R 15 , K 16 ) 16 =R 15 IP -1 output INFSCI 2935: Introduction to Computer Security 4
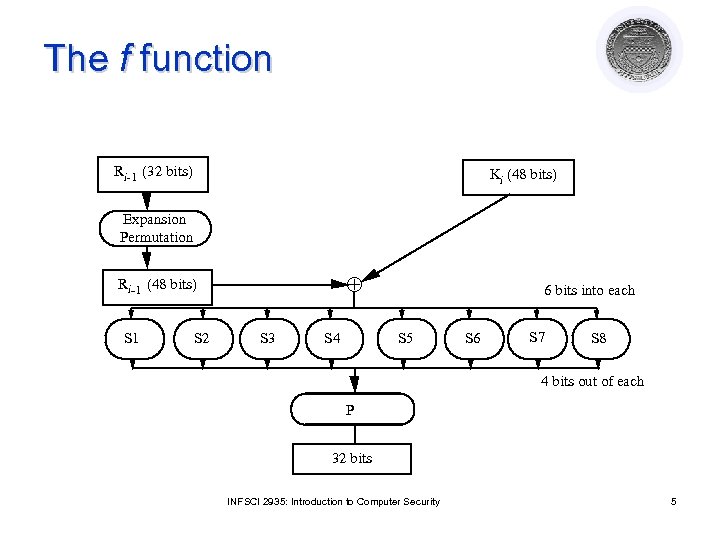
The f function Ri-1 (32 bits) Ki (48 bits) Expansion Permutation Ri-1 (48 bits) S 1 S 2 S 3 S 4 6 bits into each S 5 S 6 S 7 S 8 4 bits out of each P 32 bits INFSCI 2935: Introduction to Computer Security 5

Controversy l Considered too weak ¡ Diffie, Hellman said in a few years technology would allow DES to be broken in days l Design using 1999 technology published ¡ Design l decisions not public S-boxes may have backdoors INFSCI 2935: Introduction to Computer Security 6

Undesirable Properties l 4 weak keys ¡ l 12 semi-weak keys ¡ l Each has another semi-weak key as inverse Complementation property ¡ l They are their own inverses DESk(m) = c DESk´(m´) = c´ S-boxes exhibit irregular properties ¡ ¡ ¡ Distribution of odd, even numbers non-random Outputs of fourth box depends on input to third box Reasons for structure were suspicious INFSCI 2935: Introduction to Computer Security 7

Differential Cryptanalysis l A form of chosen plaintext attack ¡ ¡ l Revealed several properties ¡ ¡ l Involves encrypting many texts that are only slightly different from one another and comparing results Requires 247 plaintext, ciphertext pairs Small changes in S-boxes reduce the number of pairs needed Making every bit of the round keys independent does not impede attack Linear cryptanalysis improves result ¡ Requires 243 plaintext, ciphertext pairs INFSCI 2935: Introduction to Computer Security 8
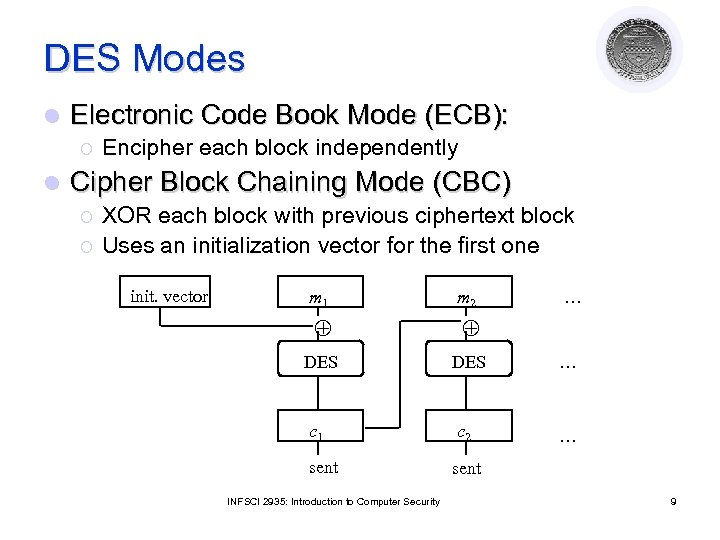
DES Modes l Electronic Code Book Mode (ECB): ¡ l Encipher each block independently Cipher Block Chaining Mode (CBC) ¡ ¡ XOR each block with previous ciphertext block Uses an initialization vector for the first one init. vector m 1 m 2 DES … c 1 c 2 … sent INFSCI 2935: Introduction to Computer Security … 9

CBC Mode Decryption init. vector c 1 c 2 DES m 1 m 2 … … … l CBC has self healing property ¡ If one block of ciphertext is altered, the error propagates for at most two blocks INFSCI 2935: Introduction to Computer Security 10

Self-Healing Property l Initial message ¡ l Received as (underlined 4 c should be 4 b) ¡ l 3231343336353837 ef 7 c 4 cb 2 b 4 ce 6 f 3 b f 6266 e 3 a 97 af 0 e 2 c 746 ab 9 a 6308 f 4256 33 e 60 b 451 b 09603 d Which decrypts to ¡ ¡ efca 61 e 19 f 4836 f 1 3231333336353837 3231343336353837 Incorrect bytes underlined; plaintext “heals” after 2 blocks INFSCI 2935: Introduction to Computer Security 11

Current Status of DES Design for computer system, associated software that could break any DES-enciphered message in a few days published in 1998 l Several challenges to break DES messages solved using distributed computing l NIST selected Rijndael as Advanced Encryption Standard, successor to DES l ¡ Designed to withstand attacks that were successful on DES INFSCI 2935: Introduction to Computer Security 12

Public Key Cryptography l Two keys ¡ Private key known only to individual ¡ Public key available to anyone l Idea ¡ Confidentiality: encipher using public key, l decipher using private key l ¡ Integrity/authentication: encipher using private key, l decipher using public one l INFSCI 2935: Introduction to Computer Security 13

Requirements Given the appropriate key, it must be computationally easy to encipher or decipher a message 2. It must be computationally infeasible to derive the private key from the public key 3. It must be computationally infeasible to determine the private key from a chosen plaintext attack 1. INFSCI 2935: Introduction to Computer Security 14

Diffie-Hellman l Compute a common, shared key ¡ Called a symmetric key exchange protocol l Based on discrete logarithm problem ¡ Given integers n and g and prime number p, compute k such that n = gk mod p ¡ Solutions known for small p ¡ Solutions computationally infeasible as p grows large – hence, choose large p INFSCI 2935: Introduction to Computer Security 15

Algorithm l Constants known to participants ¡ l l prime p; integer g other than 0, 1 or p– 1 Alice: (private = k. A, public = KA) Bob: (private = k. B, public = KB) KA = gk. A mod p ¡ KB = gk. B mod p ¡ l To communicate with Bob, ¡ l To communicate with Alice, ¡ l Anne computes SA, B= KBk. A mod p Bob computes SB, A = KAk. B mod p SA, B = SB, A ? INFSCI 2935: Introduction to Computer Security 16

Example l Assume p = 53 and g = 17 l Alice chooses k. A = 5 ¡ Then KA = 175 mod 53 = 40 l Bob chooses k. B= 7 ¡ Then KB= 177 mod 53 = 6 Let p = 5, g = 3 k. A = 4, k. B = 3 KA = ? , KB = ? , S = ? , l Shared key: ¡ KBk. A mod p = 65 mod 53 = 38 ¡ KAk. B mod p = 407 mod 53 = 38 INFSCI 2935: Introduction to Computer Security 17

RSA Relies on the difficulty of determining the number of numbers relatively prime to a large integer n l Totient function (n) l ¡ Number of + integers less than n and relatively prime to n l l Relatively prime means with no factors in common with n Example: (10) = 4 ¡ 1, 3, 7, 9 are relatively prime to 10 (77) ? l (p) ? l ¡ l When p is a prime number (pq) ? ¡ When p and q are prime numbers INFSCI 2935: Introduction to Computer Security 18

Algorithm l Choose two large prime numbers p, q ¡ Let n = pq; then (n) = (p– 1)(q– 1) ¡ Choose e < n relatively prime to (n). ¡ Compute d such that ed mod (n) = 1 l Public key: (e, n); private key: d (or (d, n)) l Encipher: c = me mod n l Decipher: m = cd mod n INFSCI 2935: Introduction to Computer Security 19
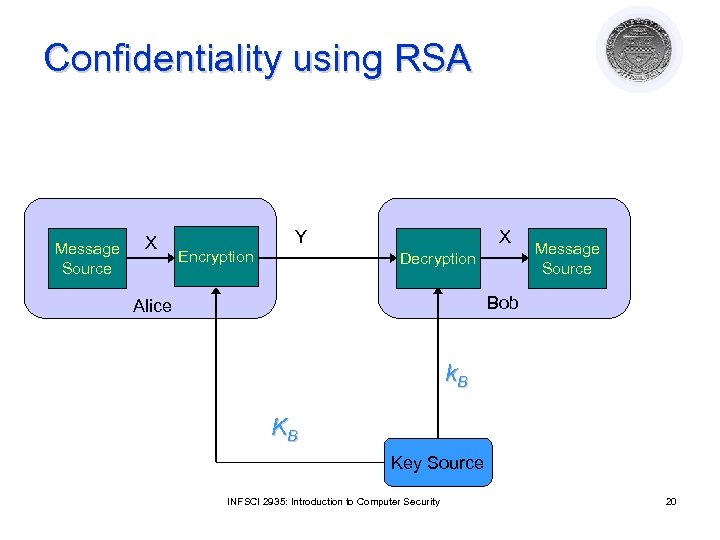
Confidentiality using RSA Message Source X Y Encryption X Decryption Message Source Bob Alice k. B KB Key Source INFSCI 2935: Introduction to Computer Security 20

Example: Confidentiality Take p = 7, q = 11, so n = 77 and (n) = 60 l Say Bob chooses (KB) e = 17, making (k. B) d = 53 l ¡ l Alice wants to send Bob secret message HELLO [07 04 11 11 14] ¡ ¡ ¡ l 17 x 53 mod 60 = ? 0717 mod 77 = 28 0417 mod 77 = 16 1117 mod 77 = 44 1417 mod 77 = 42 Alice sends ciphertext [28 16 44 44 42] INFSCI 2935: Introduction to Computer Security 21
![Example l l Bob receives [28 16 44 44 42] Bob uses private key Example l l Bob receives [28 16 44 44 42] Bob uses private key](https://present5.com/presentation/8b5b1668153d74836c23e59eec13ac16/image-22.jpg)
Example l l Bob receives [28 16 44 44 42] Bob uses private key (k. B), d = 53, to decrypt the message: 2853 mod 77 = 07 ¡ 1653 mod 77 = 04 ¡ 4453 mod 77 = 11 ¡ 4253 mod 77 = 14 ¡ l H E L L O No one else could read it, as only Bob knows his private key and that is needed for decryption INFSCI 2935: Introduction to Computer Security 22
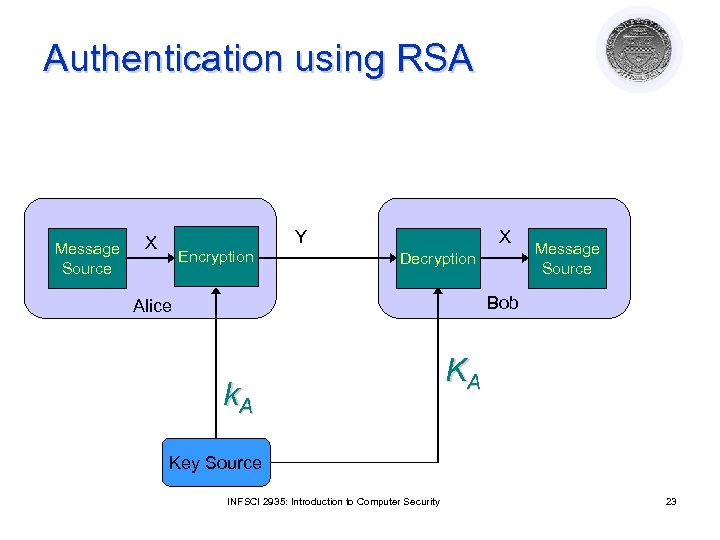
Authentication using RSA Message Source Y X Encryption X Decryption Message Source Bob Alice k. A KA Key Source INFSCI 2935: Introduction to Computer Security 23

Example: Origin Integrity/Authentication l Take p = 7, q = 11, so n = 77 and (n) = 60 Alice chooses (KA) e = 17, making (k. A) d = 53 l Alice wants to send Bob message HELLO [07 04 11 11 14] so Bob knows it is what Alice sent and there was no changes in transit l ¡ ¡ ¡ l 0753 mod 77 = 35 0453 mod 77 = 09 1153 mod 77 = 44 1453 mod 77 = 49 Alice sends [35 09 44 44 49] INFSCI 2935: Introduction to Computer Security 24

Example Bob receives 35 09 44 44 49 l Bob uses Alice’s public key (KA), e = 17, n = 77, to decrypt message: l ¡ ¡ ¡ 3517 mod 77 = 07 0917 mod 77 = 04 4417 mod 77 = 11 4917 mod 77 = 14 H E L L O Alice sent it as only she knows her private key, so no one else could have enciphered it l If (enciphered) message’s blocks (letters) altered in transit, would not decrypt properly l INFSCI 2935: Introduction to Computer Security 25
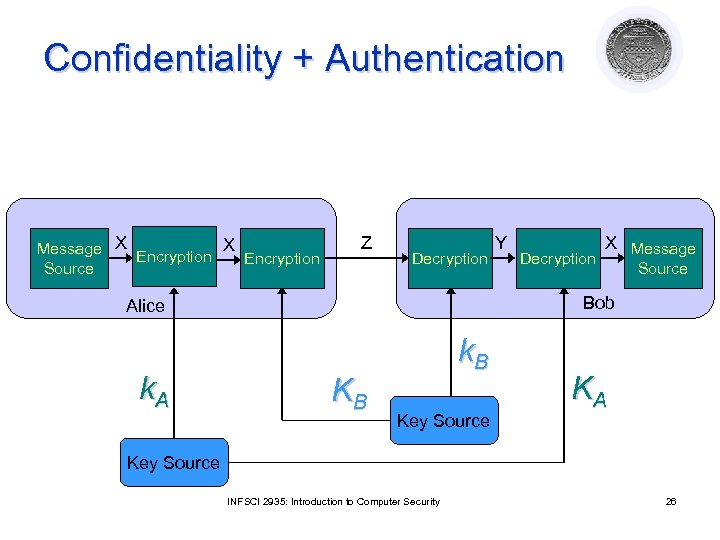
Confidentiality + Authentication Message X Encryption Source Z Decryption X Message Source Bob Alice k. A Y KB k. B Key Source KA Key Source INFSCI 2935: Introduction to Computer Security 26

Example: Confidentiality + Authentication l Alice wants to send Bob message HELLO both enciphered and authenticated (integrity-checked) ¡ ¡ l Alice enciphers HELLO [07 04 11 11 14]: ¡ ¡ ¡ l Alice’s keys: public (17, 77); private: 53 Bob’s keys: public: (37, 77); private: 13 (0753 mod 77)37 mod 77 = 07 (0453 mod 77)37 mod 77 = 37 (1153 mod 77)37 mod 77 = 44 (1453 mod 77)37 mod 77 = 14 Alice sends [07 37 44 44 14] INFSCI 2935: Introduction to Computer Security 27

Example: Confidentiality + Authentication ¡ Alice’s keys: public (17, 77); private: 53 ¡ Bob’s keys: public: (37, 77); private: 13 l Bob deciphers (07 37 44 44 14): ¡ (0713 mod 77)17 mod 77 = 07 ¡ (3713 mod 77)17 mod 77 = 04 ¡ (4413 mod 77)17 mod 77 = 11 ¡ (1413 mod 77)17 mod 77 = 14 INFSCI 2935: Introduction to Computer Security H E L L O 28

Security Services l Confidentiality ¡ Only the owner of the private key knows it, so text enciphered with public key cannot be read by anyone except the owner of the private key l Authentication ¡ Only the owner of the private key knows it, so text enciphered with private key must have been generated by the owner INFSCI 2935: Introduction to Computer Security 29

More Security Services l Integrity ¡ Enciphered letters cannot be changed undetectably without knowing private key l Non-Repudiation ¡ Message enciphered with private key came from someone who knew it INFSCI 2935: Introduction to Computer Security 30

Warnings l Encipher message in blocks considerably larger than the examples here ¡ If 1 character per block, RSA can be broken using statistical attacks (just like classical cryptosystems) ¡ Attacker cannot alter letters, but can rearrange them and alter message meaning l Example: reverse enciphered message of text ON to get NO INFSCI 2935: Introduction to Computer Security 31

Cryptographic Checksums l Mathematical function to generate a set of k bits from a set of n bits (where k ≤ n). ¡ ¡ k is smaller then n except in unusual circumstances Keyed CC: requires a cryptographic key h = CK(M) ¡ Keyless CC: requires no cryptographic key Message Digest or One-way Hash Functions h = H(M) l l Can be used for message authentication ¡ Hence, also called Message Authentication Code (MAC) INFSCI 2935: Introduction to Computer Security 32

Mathematical characteristics Every bit of the message digest function potentially influenced by every bit of the function’s input l If any given bit of the function’s input is changed, every output bit has a 50 percent chance of changing l Given an input file and its corresponding message digest, it should be computationally infeasible to find another file with the same message digest value l INFSCI 2935: Introduction to Computer Security 33

Definition l Cryptographic checksum function h: A B: 1. For any x A, h(x) is easy to compute – 2. For any y B, it is computationally infeasible to find x A such that h(x) = y – 3. Makes hardware/software implementation easy One-way proerpty It is computationally infeasible to find x, x´ A such that x ≠ x´ and h(x) = h(x´) 3’. Alternate form (Stronger): Given any x A, it is computationally infeasible to find a different x´ A such that h(x) = h(x´). INFSCI 2935: Introduction to Computer Security 34

Collisions l If x ≠ x´ and h(x) = h(x´), x and x´ are a collision ¡ Pigeonhole principle: if there are n containers for n+1 objects, then at least one container will have 2 objects in it. ¡ Application: suppose n = 5 and k = 3. Then there are 32 elements of A and 8 elements of B, so at least one element of B has at least 4 corresponding elements of A INFSCI 2935: Introduction to Computer Security 35

Keys l Keyed cryptographic checksum: requires cryptographic key ¡ DES in chaining mode: encipher message, use last n bits. Requires a key to encipher, so it is a keyed cryptographic checksum. l Keyless cryptographic checksum: requires no cryptographic key ¡ MD 5 and SHA-1 are best known; others include MD 4, HAVAL, and Snefru INFSCI 2935: Introduction to Computer Security 36

Message Digest l MD 2, MD 4, MD 5 (Ronald Rivest) ¡ ¡ ¡ l SHA, SHA-1 (Secure Hash Algorithm) ¡ ¡ ¡ l Related to MD 4; used by NIST’s Digital Signature Produces 160 -bit digest SHA-1 may be better SHA-256, SHA-384, SHA-512 ¡ l Produces 128 -bit digest; MD 2 is probably the most secure, longest to compute (hence rarely used) MD 4 is a fast alternative; MD 5 is modification of MD 4 256 -, 384 -, 512 hash functions designed to be use with the Advanced Encryption Standards (AES) Example: ¡ ¡ MD 5(There is $1500 in the blue bo) = f 80 b 3 fde 8 ecbac 1 b 515960 b 9058 de 7 a 1 MD 5(There is $1500 in the blue box) = a 4 a 5471 a 0 e 019 a 4 a 502134 d 38 fb 64729 INFSCI 2935: Introduction to Computer Security 37

Hash Message Authentication Code (HMAC) Make keyed cryptographic checksums from keyless cryptographic checksums l h keyless cryptographic checksum function that takes data in blocks of b bytes and outputs blocks of l bytes. k´ is cryptographic key of length b bytes l ¡ If short, pad with 0 bytes; if long, hash to length b ipad is 00110110 repeated b times l opad is 01011100 repeated b times l HMAC-h(k, m) = h(k´ opad || h(k´ ipad || m)) l ¡ exclusive or, || concatenation INFSCI 2935: Introduction to Computer Security 38

Security Levels l Unconditionally Secure ¡ Unlimited resources + unlimited time ¡ Still the plaintext CANNOT be recovered from the ciphertext l Computationally Secure ¡ Cost of breaking a ciphertext exceeds the value of the hidden information ¡ The time taken to break the ciphertext exceeds the useful lifetime of the information INFSCI 2935: Introduction to Computer Security 39

Key Points l Two main types of cryptosystems: classical and public key l Classical cryptosystems encipher and decipher using the same key ¡ Or one key is easily derived from the other l Public key cryptosystems encipher and decipher using different keys ¡ Computationally the other infeasible to derive one from INFSCI 2935: Introduction to Computer Security 40

Key Management Courtesy of Professors Chris Clifton & Matt Bishop INFSCI 2935: Introduction of Computer Security 41

Issues l Authentication and distribution of keys ¡ Session key ¡ Key exchange protocols ¡ Kerberos l Mechanisms to bind an identity to a key l Generation, maintenance and revoking of keys INFSCI 2935: Introduction to Computer Security 42

Notation l X Y : { Z || W } k. X, Y ¡ l X sends Y the message produced by concatenating Z and W enciphered by key k. X, Y, which is shared by users X and Y A T : { Z } k. A || { W } k. A, T ¡ A sends T a message consisting of the concatenation of Z enciphered using k. A, A’s key, and W enciphered using k. A, T, the key shared by A and T l r 1 , r 2 nonces (nonrepeating random numbers) INFSCI 2935: Introduction to Computer Security 43

Session, Interchange Keys l Alice wants to send a message m to Bob ¡ ¡ Assume public key encryption Alice generates a random cryptographic key ks and uses it to encipher m l l ¡ She enciphers ks with Bob’s public key k. B l l ¡ To be used for this message only Called a session key k. B enciphers all session keys Alice uses to communicate with Bob Called an interchange key Alice sends { m } ks { ks } k. B INFSCI 2935: Introduction to Computer Security 44

Benefits l Limits amount of traffic enciphered with single key ¡ Standard practice, to decrease the amount of traffic an attacker can obtain Makes replay attack less effective l Prevents some attacks l ¡ ¡ ¡ Example: Alice will send Bob message that is either “BUY” or “SELL”. Eve computes possible ciphertexts {“BUY”} k. B and {“SELL”} k. B. Eve intercepts enciphered message, compares, and gets plaintext at once INFSCI 2935: Introduction to Computer Security 45

Key Exchange Algorithms Goal: Alice, Bob use a shared key to communicate secretely l Criteria l ¡ Key cannot be sent in clear l l ¡ ¡ Attacker can listen in Key can be sent enciphered, or derived from exchanged data plus data not known to an eavesdropper Alice, Bob may trust third party All cryptosystems, protocols publicly known l l Only secret data is the keys, ancillary information known only to Alice and Bob needed to derive keys Anything transmitted is assumed known to attacker INFSCI 2935: Introduction to Computer Security 46

Classical Key Exchange l How do Alice, Bob begin? ¡ Alice can’t send it to Bob in the clear! l Assume trusted third party, Cathy ¡ Alice and Cathy share secret key k. A ¡ Bob and Cathy share secret key k. B l Use this to exchange shared key ks INFSCI 2935: Introduction to Computer Security 47
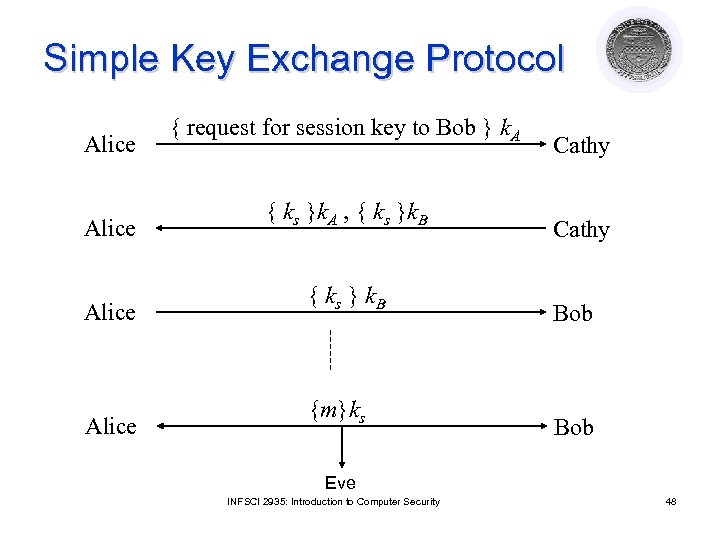
Simple Key Exchange Protocol Alice { request for session key to Bob } k. A { ks }k. A , { ks }k. B { ks } k. B {m}ks Cathy Bob Eve INFSCI 2935: Introduction to Computer Security 48

Problems l How does Bob know he is talking to Alice? ¡ Replay attack: Eve records message from Alice to Bob, later replays it; Bob may think he’s talking to Alice, but he isn’t ¡ Session key reuse: Eve replays message from Alice to Bob, so Bob re-uses session key l Protocols must provide authentication and defense against replay INFSCI 2935: Introduction to Computer Security 49
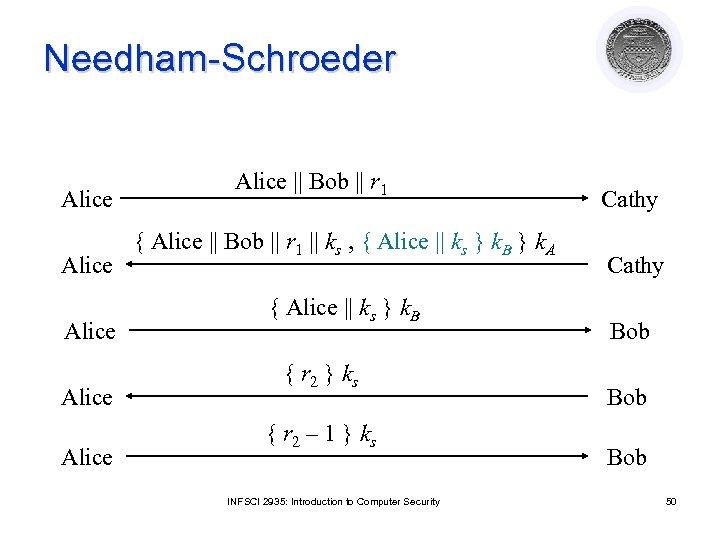
Needham-Schroeder Alice Alice || Bob || r 1 { Alice || Bob || r 1 || ks , { Alice || ks } k. B } k. A { Alice || ks } k. B { r 2 } k s { r 2 – 1 } k s INFSCI 2935: Introduction to Computer Security Cathy Bob Bob 50

Argument: Alice talking to Bob l Second message ¡ Enciphered using key only she, Cathy know l ¡ Response to first message l l So Cathy enciphered it As r 1 in it matches r 1 in first message Third message ¡ Alice knows only Bob can read it l ¡ As only Bob can derive session key from message Any messages enciphered with that key are from Bob INFSCI 2935: Introduction to Computer Security 51

Argument: Bob talking to Alice l Third message ¡ Enciphered using key only he, Cathy know l ¡ Names Alice, session key l l So Cathy enciphered it Cathy provided session key, says Alice is other party Fourth message ¡ Uses session key to determine if it is replay from Eve l l If not, Alice will respond correctly in fifth message If so, Eve can’t decipher r 2 and so can’t respond, or responds incorrectly INFSCI 2935: Introduction to Computer Security 52

Problem with Needham-Schroeder Assumption: all keys are secret l Question: suppose Eve can obtain session key. How does that affect protocol? l ¡ In what follows, Eve knows ks Eve Eve { Alice || ks } k. B { r 3 } k s { r 3 – 1 } k s INFSCI 2935: Introduction to Computer Security [Replay] [Eve intercepts] Bob Bob 53

Solution: Denning-Sacco Modification In protocol above, Eve impersonates Alice l Problem: replay in third step l ¡ l Solution: use time stamp T to detect replay ¡ l First in previous slide Needs synchronized clocks Weakness: if clocks not synchronized, may either reject valid messages or accept replays ¡ ¡ Parties with either slow or fast clocks vulnerable to replay Resetting clock does not eliminate vulnerability INFSCI 2935: Introduction to Computer Security 54

Needham-Schroeder with Denning-Sacco Modification Alice Alice || Bob || r 1 { Alice || Bob || r 1 || ks || { Alice || T || ks } k. B } k. A { Alice || T || ks } k. B { r 2 } k s { r 2 – 1 } k s INFSCI 2935: Introduction to Computer Security Cathy Bob Bob 55

Otway-Rees Protocol l Corrects problem ¡ That is, Eve replaying the third message in the protocol l Does not use timestamps ¡ Not vulnerable to the problems that Denning. Sacco modification has l Uses integer n to associate all messages with a particular exchange INFSCI 2935: Introduction to Computer Security 56
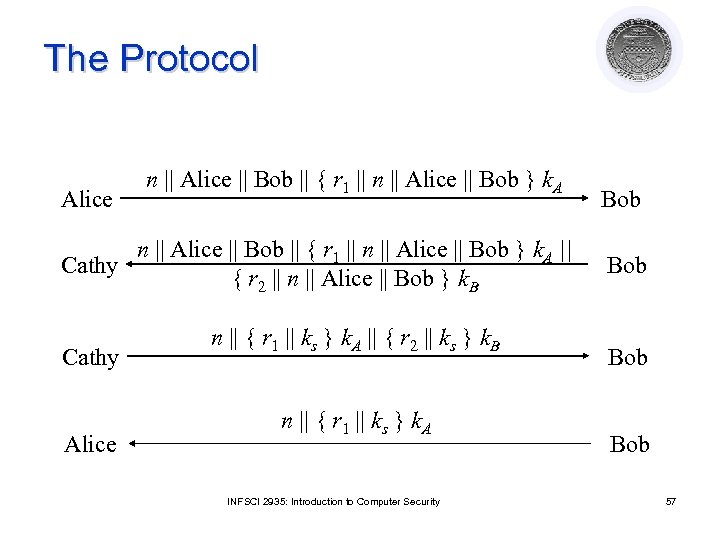
The Protocol Alice n || Alice || Bob || { r 1 || n || Alice || Bob } k. A || Cathy { r 2 || n || Alice || Bob } k. B Cathy Alice n || { r 1 || ks } k. A || { r 2 || ks } k. B n || { r 1 || ks } k. A INFSCI 2935: Introduction to Computer Security Bob Bob 57

Argument: Alice talking to Bob l Fourth message ¡ If n matches first message, Alice knows it is part of this protocol exchange ¡ Cathy generated ks because only she, Alice know k. A ¡ Enciphered part belongs to exchange as r 1 matches r 1 in encrypted part of first message INFSCI 2935: Introduction to Computer Security 58

Argument: Bob talking to Alice l Third message ¡ If n matches second message, Bob knows it is part of this protocol exchange ¡ Cathy generated ks because only she, Bob know k. B ¡ Enciphered part belongs to exchange as r 2 matches r 2 in encrypted part of second message INFSCI 2935: Introduction to Computer Security 59

Replay Attack l Eve acquires old ks, message in third step ¡ l n || { r 1 || ks } k. A || { r 2 || ks } k. B Eve forwards appropriate part to Alice ¡ ¡ Alice has no ongoing key exchange with Bob: n matches nothing, so is rejected Alice has ongoing key exchange with Bob: n does not match, so is again rejected l If replay is for the current key exchange, and Eve sent the relevant part before Bob did, Eve could simply listen to traffic; no replay involved INFSCI 2935: Introduction to Computer Security 60

Kerberos l Authentication system ¡ ¡ l Ticket (credential) ¡ l Issuer vouches for identity of requester of service Authenticator ¡ l Based on Needham-Schroeder with Denning-Sacco modification Central server plays role of trusted third party (“Cathy”) Identifies sender Alice must 1. 2. Authenticate herself to the system Obtain ticket to use server S INFSCI 2935: Introduction to Computer Security 61

Overview l User u authenticates to Kerberos server ¡ l User u wants to use service s: ¡ ¡ ¡ l Obtains ticket Tu, TGS for ticket granting service (TGS) User sends authenticator Au, ticket Tu, TGS to TGS asking for ticket for service TGS sends ticket Tu, s to user User sends Au, Tu, s to server as request to use s Details follow INFSCI 2935: Introduction to Computer Security 62

Ticket Credential saying issuer has identified ticket requester l Example ticket issued to user u for service s l Tu, s = s || { u || u’s address || valid time || ku, s } ks where: ¡ ku, s is session key for user and service ¡ Valid time is interval for which the ticket is valid ¡ u’s address may be IP address or something else l Note: more fields, but not relevant here INFSCI 2935: Introduction to Computer Security 63

Authenticator l Credential containing identity of sender of ticket ¡ l Used to confirm sender is entity to which ticket was issued Example: authenticator user u generates for service s Au, s = { u || generation time || kt } ku, s where: ¡ kt is alternate session key ¡ Generation time is when authenticator generated l Note: more fields, not relevant here INFSCI 2935: Introduction to Computer Security 64
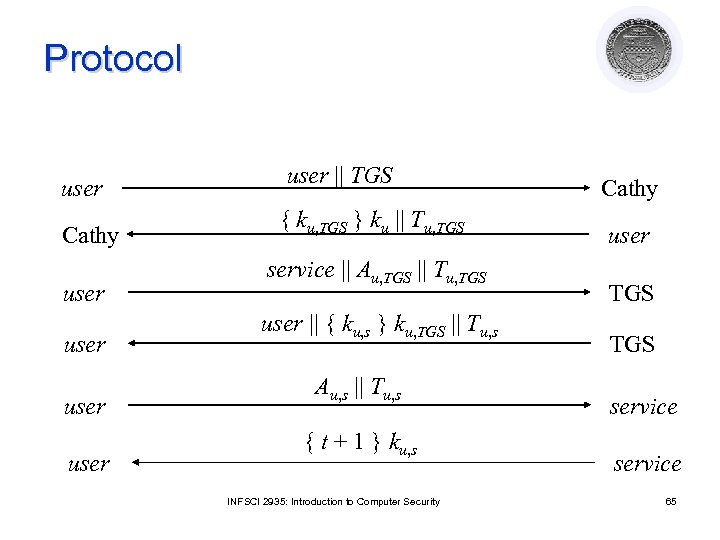
Protocol user Cathy user user || TGS { ku, TGS } ku || Tu, TGS service || Au, TGS || Tu, TGS user || { ku, s } ku, TGS || Tu, s Au, s || Tu, s { t + 1 } ku, s INFSCI 2935: Introduction to Computer Security Cathy user TGS service 65

Analysis l First two steps get user ticket to use TGS ¡ User u can obtain session key only if u knows key shared with Cathy l Next four steps show ticket for service s u gets and uses ¡ Service s validates request by checking sender (using Au, s) is same as entity ticket issued to ¡ Step 6 optional; used when u requests confirmation INFSCI 2935: Introduction to Computer Security 66

Problems l Relies on synchronized clocks ¡ If not synchronized and old tickets, authenticators not cached, replay is possible l Tickets have some fixed fields ¡ Dictionary attacks possible ¡ Kerberos 4 session keys weak (had much less than 56 bits of randomness); researchers at Purdue found them from tickets in minutes INFSCI 2935: Introduction to Computer Security 67

Public Key Exchange l Here interchange keys known ¡ ¡ l e. A, e. B Alice and Bob’s public keys known to all d. A, d. B Alice and Bob’s private keys known only to owner Simple protocol ¡ ks is desired session key Alice { ks } e. B INFSCI 2935: Introduction to Computer Security Bob 68

Problem and Solution l Vulnerable to forgery or replay ¡ l Because e. B known to anyone, Bob has no assurance that Alice sent message Simple fix uses Alice’s private key ¡ ks is desired session key Alice { { ks } d. A } e. B INFSCI 2935: Introduction to Computer Security Bob 69

Notes Can include message enciphered with ks l Assumes Bob has Alice’s public key, and vice versa l If not, each must get it from public server ¡ If keys not bound to identity of owner, attacker Eve can launch a man-in-the-middle attack (next slide; Cathy is public server providing public keys) ¡ INFSCI 2935: Introduction to Computer Security 70
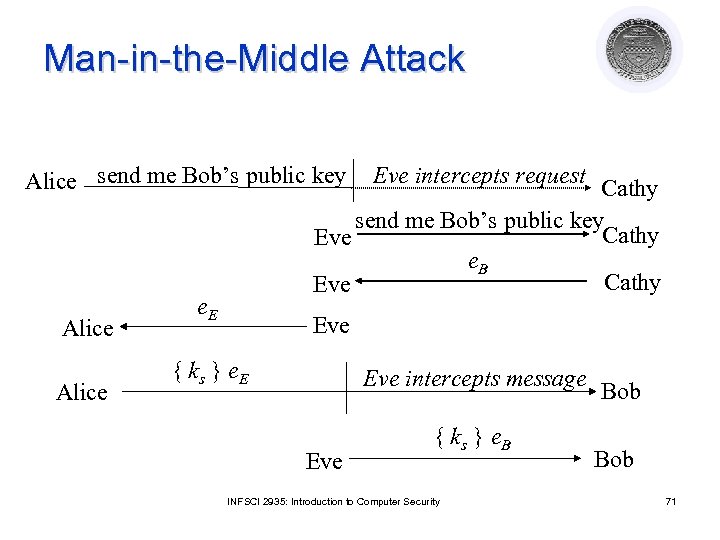
Man-in-the-Middle Attack Alice send me Bob’s public key Alice Eve intercepts request Cathy send me Bob’s public key Cathy Eve e. B Cathy Eve e. E Eve { ks } e. E Eve intercepts message Eve { ks } e. B INFSCI 2935: Introduction to Computer Security Bob 71

Key Generation Goal: generate difficult to guess keys l Problem statement: given a set of K potential keys, choose one randomly l ¡ l Equivalent to selecting a random number between 0 and K– 1 inclusive Why is this hard: generating random numbers ¡ Actually, numbers are usually pseudo-random, that is, generated by an algorithm INFSCI 2935: Introduction to Computer Security 72

What is “Random”? l Sequence of cryptographically ransom numbers: a sequence of numbers n 1, n 2, … such that for any integer k > 0, an observer cannot predict nk even if all of n 1, …, nk– 1 are known ¡ Best: physical source of randomness Electromagnetic phenomena l Characteristics of computing environment such as disk latency l Ambient background noise l INFSCI 2935: Introduction to Computer Security 73

What is “Pseudorandom”? l Sequence of cryptographically pseudorandom numbers: sequence of numbers intended to simulate a sequence of cryptographically random numbers but generated by an algorithm ¡ Very difficult to do this well l Linear congruential generators [nk = (ank– 1 + b) mod n] broken (a, b and n are relatively prime) Polynomial congruential generators [nk = (ajnk– 1 j + … + a 1 nk– 1 a 0) mod n] broken too Here, “broken” means next number in sequence can be determined INFSCI 2935: Introduction to Computer Security 74

Best Pseudorandom Numbers l Strong mixing function: function of 2 or more inputs with each bit of output depending on some nonlinear function of all input bits ¡ Examples: DES, MD 5, SHA-1 ¡ Use on UNIX-based systems: (date; ps gaux) | md 5 where “ps gaux” lists all information about all processes on system INFSCI 2935: Introduction to Computer Security 75

Digital Signature Construct that authenticates origin, contents of message in a manner provable to a disinterested third party (“judge”) l Sender cannot deny having sent message (service is “nonrepudiation”) l ¡ Limited to technical proofs l ¡ Inability to deny one’s cryptographic key was used to sign One could claim the cryptographic key was stolen or compromised l Legal proofs, etc. , probably required; INFSCI 2935: Introduction to Computer Security 76

Common Error l Classical: Alice, Bob share key ¡ Alice sends m || { m }k to Bob k This is a digital signature WRONG l This is not a digital signature ¡ Why? Third party cannot determine whether Alice or Bob generated message INFSCI 2935: Introduction to Computer Security 77

Classical Digital Signatures l Require trusted third party ¡ l Alice, Bob each share keys with trusted party Cathy To resolve dispute, judge gets { m }k. Alice, { m }k. Bob, and has Cathy decipher them; if messages matched, contract was signed Alice { m }k. Alice Bob { m }k. Alice Cathy { m }k. Bob INFSCI 2935: Introduction to Computer Security 78

Public Key Digital Signatures l Alice’s keys are d. Alice, e. Alice l Alice sends Bob m || { m }d. Alice l In case of dispute, judge computes { { m }d. Alice }e. Alice l and if it is m, Alice signed message ¡ She’s the only one who knows d. Alice! INFSCI 2935: Introduction to Computer Security 79
8b5b1668153d74836c23e59eec13ac16.ppt