Introduction to Choice-Based Conjoint CBC Copyright Sawtooth Software

Introduction to Choice-Based Conjoint (CBC) Copyright Sawtooth Software, Inc.

Conjoint Methods: Card-Sort Method (CVA) Using a 100 -pt scale where 0 means definitely would NOT and 100 means definitely WOULD… How likely are you to purchase… Coke 6 -pack $1. 89 Your Answer: ______

Conjoint Methods: Pairwise Method (ACA or CVA) Which would you prefer? Coke 6 -pack $1. 89 Strongly Prefer Left 1 2 3 4 Pepsi 8 -pack $2. 29 5 Strongly Prefer Right 6 7 8 9

Choice-Based Conjoint Question

Comparing the Methods (cont. ): Traditional Card Sort: – Respondent task is not as realistic as CBC – Ranking or ratings typically provide enough information to compute utilities (preferences) for each individual – Usually only compute Main Effects (no interactions)

Comparing the Methods (cont. ): Pairwise Presentation: – Respondent task is often not as realistic as CBC – Ratings typically provide enough information to compute utilities (preferences) for each individual – Usually only compute Main Effects (no interactions)

Comparing the Methods (cont. ): Choice-Based Conjoint Pros: – Making choices in CBC questions is similar to what buyers do in the marketplace – CBC can include a “None” option, so respondents who have no interest in purchasing can opt out of the question – Because we can analyze results by pooling respondent data, CBC permits measurement of Main Effects AND Interactions. More overall parameters can be estimated.

Comparing the Methods (cont. ): Choice-Based Conjoint Pros (cont. ): – Because we can pool respondent data, each respondent can answer as few as just 1 question – Respondents can answer at least up to 20 choice questions with high reliability – Randomized designs permit showing respondents all combinations of levels and are quite efficient – Particularly well suited to pricing studies

Comparing the Methods (cont. ): Choice-Based Conjoint Cons: – Choices are inefficient: they indicate only which product is preferred, but not by how much – Aggregate models assume respondent homogeneity, which may be inaccurate representation for a market (but Latent Class analysis and new developments in Bayesian estimation techniques help resolve this issue) – Usually requires larger sample sizes than with CVA or ACA

Comparing the Methods (cont. ): Choice-Based Conjoint Cons (cont. ): – Tasks are more complex, so respondents can process fewer attributes (early academics recommended six or fewer, but in practice it seems respondents can evaluate a few more than that if the text is concise and the tasks are laid out well) – Complex tasks may encourage response simplification strategies – Usually requires larger sample sizes than with CVA or ACA

Comparing the Methods (cont. ): Analyzing the Data: – ACA: Ordinary Least Squares regression (OLS) or Hierarchical Bayes (HB) – CVA: OLS (ratings), Monotone regression (rankings) or Hierarchical Bayes (HB) – CBC: Counting analysis, Multinomial Logit, Latent Class, or Hierarchical Bayes (HB) – Adaptive CBC (ACBC): Hierarchical Bayes (HB), Monotone regression

Main Effects Versus Interactions Main Effects: - Isolating the effect (impact) of each attribute, holding everything else constant Assume two attributes: – BRAND: Coke, Pepsi, Store Brand – PRICE: $1. 50, $2. 00, $2. 50

Main Effects Versus Interactions (cont. ): Hypothetical Main Effects Utilities: Interpretation: Across all brands (holding brand constant), $1. 50 is worth 80 points, etc.

Main Effects Versus Interactions (cont. ): We can add the main effect utilities together and infer the preference for each brand at each price. But this assumes the same price function for each brand.

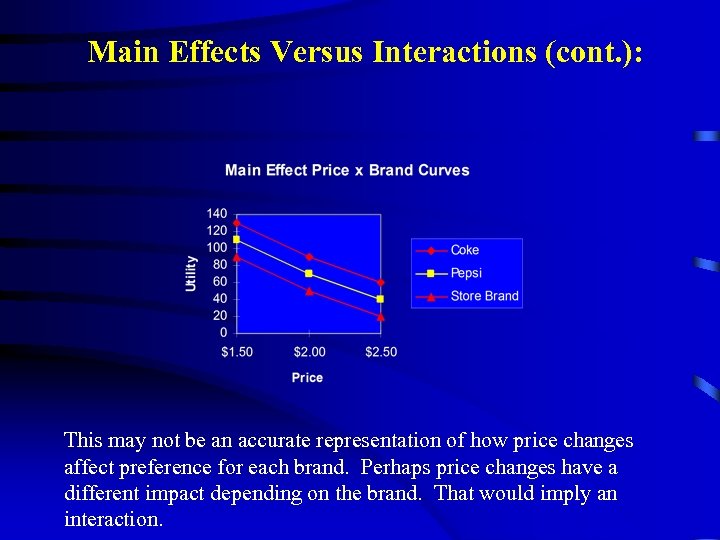
Main Effects Versus Interactions (cont. ): This may not be an accurate representation of how price changes affect preference for each brand. Perhaps price changes have a different impact depending on the brand. That would imply an interaction.

Main Effects Versus Interactions (cont. ): CBC counts the percent of times each brand/price combination is chosen. Each cell in the grid above is directly and independently measured (two-way interaction).

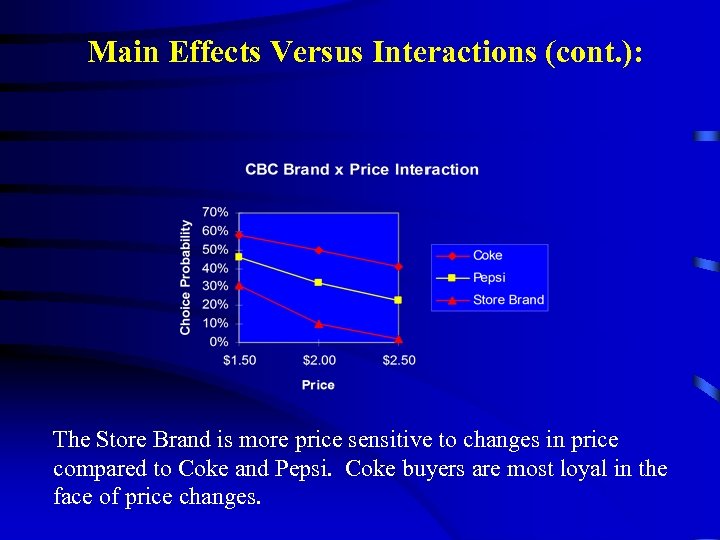
Main Effects Versus Interactions (cont. ): The Store Brand is more price sensitive to changes in price compared to Coke and Pepsi. Coke buyers are most loyal in the face of price changes.

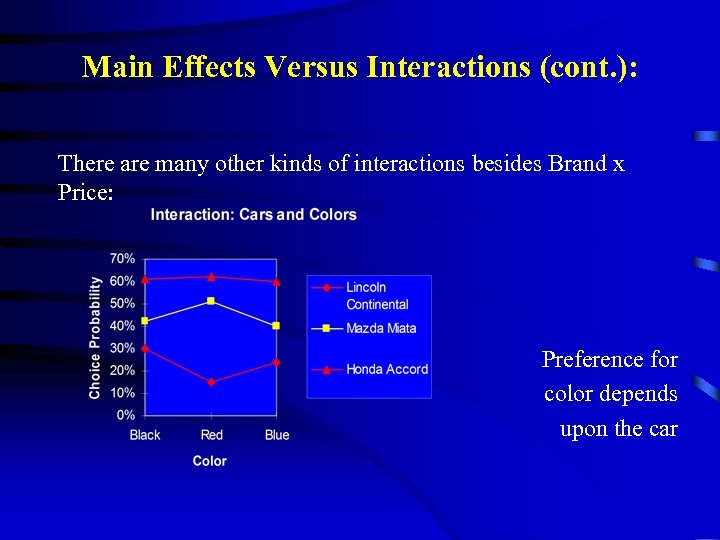
Main Effects Versus Interactions (cont. ): There are many other kinds of interactions besides Brand x Price: Preference for color depends upon the car

Sawtooth Software’s CBC Systems • Windows- or Web-based computer-administered interviews or paper surveys • Capacity: 30 attributes with up to 250 levels each (with Advanced Design Module) • Experimental design produced automatically • Prohibitions between attribute levels can be specified • Fixed designs can be specified • Choice sets can include a “none” or “constant” option • Data analyzed automatically by counting or multinomial logit, optional modules for Latent Class and HB • Market simulator included

The CBC System: Advanced Modules • Paper and Pencil Module – Assists in creating and analyzing data for paper and pencil interviews • Latent Class Segmentation Module – Detects and models market segments – Helps relax the assumption of homogeneity, but still does not achieve individual-level data – Permits specification of linear terms, and respondent weighting • Hierarchical Bayes Analysis CBC/HB

Advanced Design Module • Advanced Design Module: – Support “brand-specific attribute” designs and estimation (some researchers refer to these as “true” discrete choice designs) – More than one “Constant Alternative” (None) option – Expanded number of attributes to accommodate brand-specific attribute designs (up to 30 attributes) – Ability to conduct/analyze partial-profile experiments

Why Latent Class and HB? • To reduce the Red Bus/Blue Bus (IIA) Problem, one must account for: – Substitution effects – Differential cross-elasticities – Differential self-elasticities

Aggregate Logit • Assume an aggregate logit solution where: – Utility (Train) = Utility (Red Bus) On any given day, difficult to predict which way any one respondent will travel to work. Resulting in the following aggregate shares: – Train 50%; Red Bus 50%

Aggregate Logit: • Assume we add another alternative where: – Utility (Train) = Utility (Red Bus) = Utility (Blue Bus) Again, difficult to predict which way any one respondent will travel to work. • Train 33. 3%; Red Bus 33. 3%; Blue Bus 33. 3% • Net Bus ridership increased from 50% to 66. 7% by offering a bus of a different color

Two-Group Latent Class Solution: • Left Half of Room – Strongly Prefer Buses • Right Half of Room – Strongly Prefer Trains In aggregate, it still appears that Utility (Bus) = Utility (Train)

Two-Group Latent Class Simulation: • Now offer both Red and Blue buses • Net Bus ridership still 50% (no Share Inflation) Capturing heterogeneity has resulted in differential substitution effects

Differential Cross-Elasticity under Latent Class • Now raise price of Blue Bus – Many Blue Bus riders shift to Red Buses – Train ridership unaffected Capturing heterogeneity has revealed differential cross-elasticity

Differential Elasticity under Latent Class • Assume: – Train riders = Not price sensitive – Bus riders = Very price sensitive

Differential Elasticity under Latent Class • If raise Train price – Few train riders shift to buses • If raise Red and Blue bus prices – Many bus riders shift to trains Capturing heterogeneity has captured differential elasticities

Conclusions • Capturing heterogeneity under Latent Class or HB – Reduces Red Bus/Blue Bus problem – Automatically accounts for differential substitution, elasticities and cross effects with simple main-effects models • If those effects are due to differences in preferences between people

Advanced CBC Designs • Outline: – Conditional Pricing – Alternative-Specific Plans – Partial-Profile Designs

Common Issue: Brands with Different Price Ranges • Clients often produce a set of attributes and levels as following: Brand 1: $10, $15, $20 Brand 2: $20, $25, $30 Brand 3: $15, $20, $25 • Seems like a reasonable request: more realistic price ranges, increased utility balance within sets • How to handle?

Set up Prohibitions? • You could specify prohibitions between brand price: • But, design efficiency for main effects would be compromised • And CBC software doesn’t let you estimate interaction terms for two attributes including prohibitions

CBC with Conditional Pricing • If the brands differ quite widely in their price ranges, you can include a conditional pricing “look-up” table: • When the survey runs, CBC inserts the appropriate price depending on the brand • The internal design matrix still reflects just 3 levels of price!

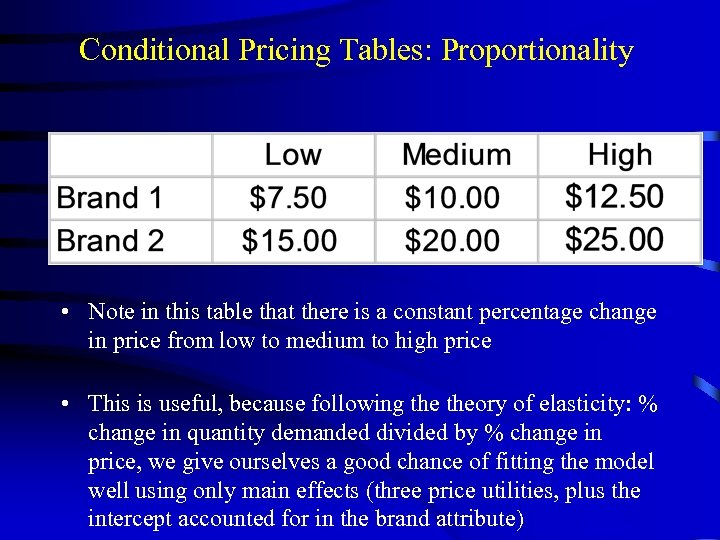
Conditional Pricing Tables: Proportionality • Note in this table that there is a constant percentage change in price from low to medium to high price • This is useful, because following theory of elasticity: % change in quantity demanded divided by % change in price, we give ourselves a good chance of fitting the model well using only main effects (three price utilities, plus the intercept accounted for in the brand attribute)

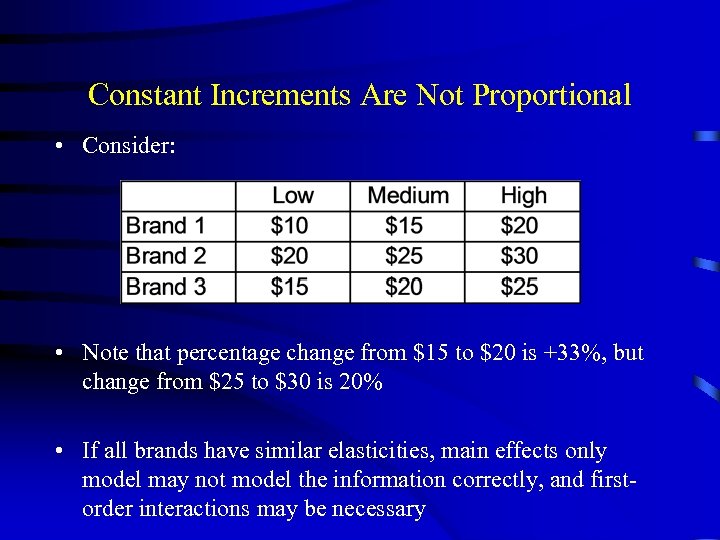
Constant Increments Are Not Proportional • Consider: • Note that percentage change from $15 to $20 is +33%, but change from $25 to $30 is 20% • If all brands have similar elasticities, main effects only model may not model the information correctly, and firstorder interactions may be necessary

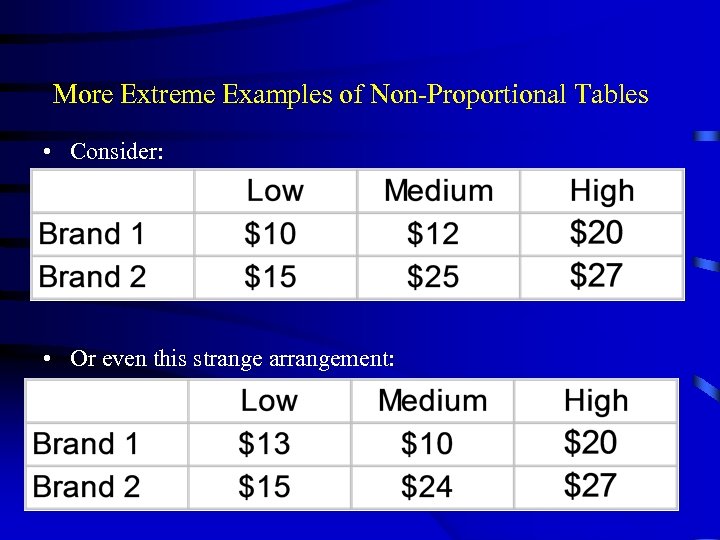
More Extreme Examples of Non-Proportional Tables • Consider: • Or even this strange arrangement:

Non-Proportional Conditional Pricing Tables • As long as price is conditional on just ONE other attribute (such as brand), you can always model the data correctly using first-order interactions, no matter what the pattern of prices within the table • But beware making price conditional on two or more attributes (e. g. brand package size) and not using proportional tables! • If price is conditional on two or more attributes, and the pricing table is not proportional, then you may not be able to model effects correctly with CBC software

Conditional Pricing--Brand Intercept • If using conditional pricing, remember that the utility of brand is no longer interpreted as “the preference for this brand, everything else held constant. ” • It is the preference for this brand, given its average price

Using the Market Simulator • To specify $20 for Brand 1, we use a price level “ 3” in the simulator; but to specify $20 for Brand 2, we use a price level “ 1” • Why does this work? : brand utilities account for average shift in price, and additional interaction terms (if specified) account for the differing impact of price

Recommendations • Specify price changes as near-constant percentage changes from an average price, for example: • Give yourself the best chance of fitting a good model using just main effects – If interaction effects aren’t significant, then you can save degrees of freedom and model properly with main effects only – If you don’t use a near-proportional table, it increases the likelihood that you have to estimate interactions

Research Questions • Does including conditional pricing improve design efficiency relative to designs where all brands share the same prices? – Probably yes, because of increased utility balance among alternatives in a set • Can including conditional pricing change the measured elasticity by brand? – Yes, but in predictable ways? Needs to be researched!

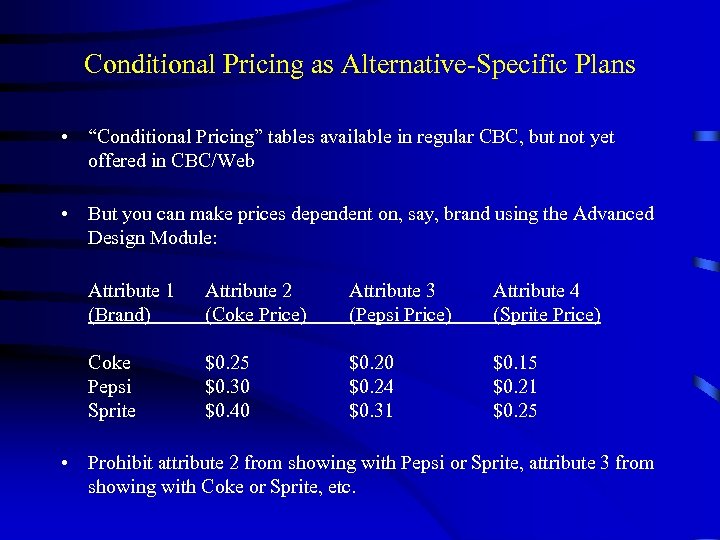
Conditional Pricing as Alternative-Specific Plans • “Conditional Pricing” tables available in regular CBC, but not yet offered in CBC/Web • But you can make prices dependent on, say, brand using the Advanced Design Module: Attribute 1 (Brand) Attribute 2 (Coke Price) Attribute 3 (Pepsi Price) Attribute 4 (Sprite Price) Coke Pepsi Sprite $0. 25 $0. 30 $0. 40 $0. 24 $0. 31 $0. 15 $0. 21 $0. 25 • Prohibit attribute 2 from showing with Pepsi or Sprite, attribute 3 from showing with Coke or Sprite, etc.

Alternative-Specific Plans--The “Real” Discrete Choice • Some researchers like to distinguish DCM (Discrete Choice Modeling) from CBC (Choice. Based Conjoint) based on the flexibility of the plans they support • Until a few years ago, Sawtooth Software’s CBC only supported designs in which all attributes were common to all product alternatives • “Real” DCM plans have some attributes conditional on the product alternative

Alternative-Specific Choice Design Example • Car and Bus travel have their own unique set of attributes (Car: parking fee), (Bus: frequency, fare). “Walk, ” “Bike, ” and “I’d choose another way to get to work” are constant alternatives

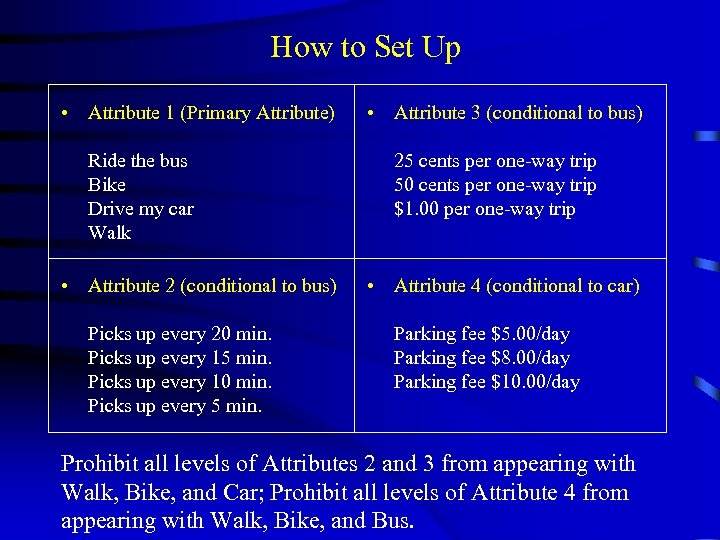
How to Set Up • Attribute 1 (Primary Attribute) Ride the bus Bike Drive my car Walk • Attribute 2 (conditional to bus) Picks up every 20 min. Picks up every 15 min. Picks up every 10 min. Picks up every 5 min. • Attribute 3 (conditional to bus) 25 cents per one-way trip 50 cents per one-way trip $1. 00 per one-way trip • Attribute 4 (conditional to car) Parking fee $5. 00/day Parking fee $8. 00/day Parking fee $10. 00/day Prohibit all levels of Attributes 2 and 3 from appearing with Walk, Bike, and Car; Prohibit all levels of Attribute 4 from appearing with Walk, Bike, and Bus.

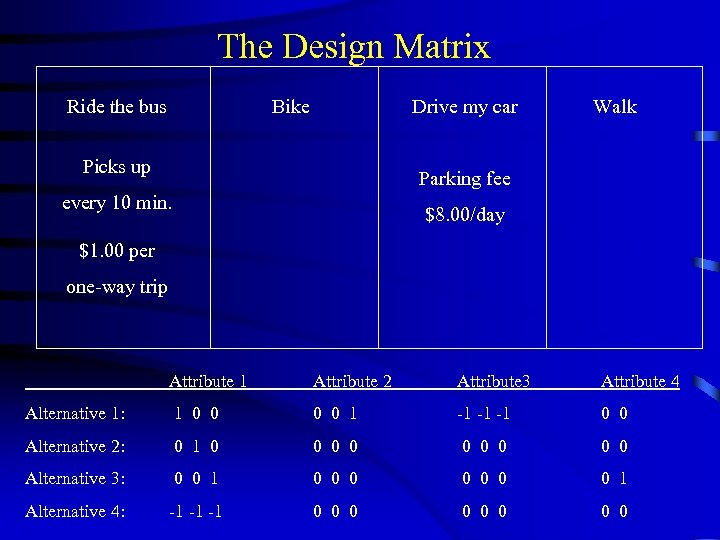
The Design Matrix Ride the bus Bike Drive my car Picks up Walk Parking fee every 10 min. $8. 00/day $1. 00 per one-way trip Attribute 1 Attribute 2 Attribute 3 Attribute 4 Alternative 1: 1 0 0 1 -1 -1 -1 0 0 Alternative 2: 0 1 0 0 0 0 0 Alternative 3: 0 0 1 0 0 0 0 1 Alternative 4: -1 -1 -1 0 0 0 0

Estimation for Alternative-Specific Plans • In terms of software usage, part worth estimation feels no different than for regular CBC, latent class, or HB – the alternative-specific (conditional) effects are not generic “main effects, ” but are conditional upon the levels of the primary attribute they were displayed with – standard errors of conditional effects much larger than those for “common” attributes

Simulations with Alternative-Specific Designs • Special Considerations for “Alternative-Specific” Designs (some alternatives have more/fewer applicable attributes than others): – Corrections for product similarity by RFC and “Model 3” require number of attributes used for each alternative be the same – Therefore, RFC and “Model 3” cannot be used within Sawtooth Software simulator for alternative-specific designs • What to do when using alternative-specific designs? – Use HB! And use Share of Preference method or First Choice-whichever fits holdouts best

How Many Attributes Are Reasonable? • CBC questions involve a lot of reading (multiple attributes across multiple alternatives) and little information gained (choices) • Many researchers feel that more than about six attributes will induce respondents to adopt simplification strategies--leading to more noise and potentially biased part worths • Some researchers believe CBC questionnaires with 10 or even 20 attributes are realistic and lead to valid data

ACA or CBC? • Many researchers favor ACA when the number of attributes is greater than they feel comfortable using in CBC – ACA uses self-explicated priors and partial-profile pairs • Other researchers prefer choices to ratings/hybrid conjoint, and would rather figure out a way to have their cake and eat it too • Hence, Partial Profile CBC

What is Partial Profile? • Assume we have 10 attributes in a study: rather than show all 10 attributes in each task, we randomly choose a subset of attributes (often 4 to 6) to include • Each task presents a new subset of attributes – Given enough tasks, respondents see all attributes and levels • It is possible to fix some attributes such that they are always included in the task

Assumptions and Implications • Assumption is that respondents can evaluate just the attributes that are shown while completely ignoring the attributes not shown (ceteris paribus assumption) • Partial-profile results in lower design efficiency (fewer non -zero entries in the independent variable matrix) • But, if the loss in statistical efficiency is off-set by gains in respondents’ ability to consider the differences in the attributes being shown and answer with lower error, then we may be better off

Sample Results: Partial Profile vs. Full-Profile Choice • Keith Chrzan has probably done the most research comparing partial-profile and full-profile CBC – He generally finds close congruence in the estimated parameters, most (but not all) studies find no difference – He has reported that the amount of noise in the parameters is reduced when using partial-profile choice (scale parameter increases) – For one data set, he found that individual-level estimation using HB or ICE performed worse than aggregate logit for predicting shares of holdouts (see Chrzan in Sawtooth Software Conference 1999)

More Findings • Jon Pinnell presented more evidence in the 2001 Sawtooth Software Conference Proceedings – He found that HB estimation may not work as well as aggregate logit in predicting individual’s choices for some (but not all) partial -profile data sets – He suggested that the increased scale factor for partial-profile parameters may be due to overfitting rather than a reduction in noise – He warned against using only two alternatives per task

What to Make of Partial-Profile Choice? • For dealing with many attributes, it often satisfies choice “purists” • May offer good results in terms of share predictions for projects involving independent attributes and fairly large sample sizes • Analysts should use holdout choices in every study to determine how best to model the parameters • Beware of attributes that have overlap in meaning (doublecounting) – this may bias the importance of price (but no research we are aware of has yet shown bias for price in partial profile choice)

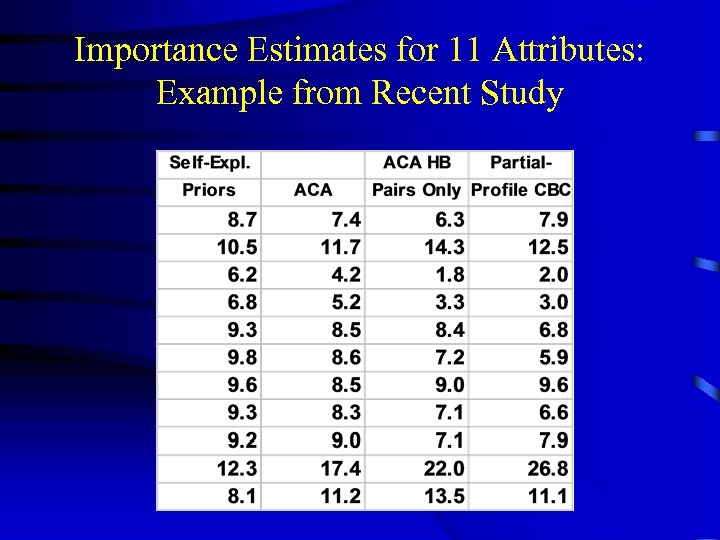
Importance Estimates for 11 Attributes: Example from Recent Study

Suggested Methods of Analysis • Logit, latent class or HB may be used – Choose the method that best predicts holdouts! – Stable estimation of interaction effects is usually not possible with partial-profile choice, unless truly huge sample sizes • Individual-level results from HB will usually have much greater degree of noise in the parameters than a parallel ACA would

Adaptive Extension of CBC • In 2008, Sawtooth Software released an adaptive form of CBC called ACBC. It is quickly gaining acceptance. • Shares the strengths of CBC, but provides a more engaging respondent experience. • Can extend CBC’s ability to study more attributes and levels.