af357a110c75bf9f7dabcf457ec5c1b4.ppt
- Количество слайдов: 67

Introduction to Business Statistics, 6 e Kvanli, Pavur, Keeling Chapter 12 – Quality Improvement Slides prepared by Jeff Heyl, Lincoln University © 2003 Thomson/South-Western Learning™ South-Western/Thomson 1

The Quality Gurus q W. Edwards Deming 14 Points for Management q Joseph M. Juran’s Trilogy q Philip B. Crosby Quality is Free © 2003 Thomson/South-Western 2

Definitions q Quality product or service: A product or service that meets or exceeds the expectations of the customer q Process: Any combination of people, machinery, material, and methods that is intended to produce a product or service q Quality Characteristics: Features of a product that describe its fitness for use © 2003 Thomson/South-Western 3

Definitions q Statistical Process Control (SPC): The application of statistical quality-control methods to measure and analyze the variation found in a process q Control Chart: A statistical chart used to monitor various aspects of a process and to determine if the process is in control or out of control © 2003 Thomson/South-Western 4

Malcolm Baldrige National Quality Award Criteria q Leadership System q Strategic Planning q Customer and Market Focus q Information and Analysis q Human Resource Focus q Process Management q Business Results © 2003 Thomson/South-Western 5

ISO 9000 Registration Basic approach is to reduce process variation throughout the organization ISO 9000: 2000 - Quality Management Systems - Fundamentals and Vocabulary ISO 9001: 2000 - Quality Management Systems - Requirements ISO 9001: 2000 - Quality Management Systems - Guidelines for Performance Improvement © 2003 Thomson/South-Western 6

Quality Improvement Tools q Flowcharts q Cause-and-Effect Diagrams © 2003 Thomson/South-Western 7
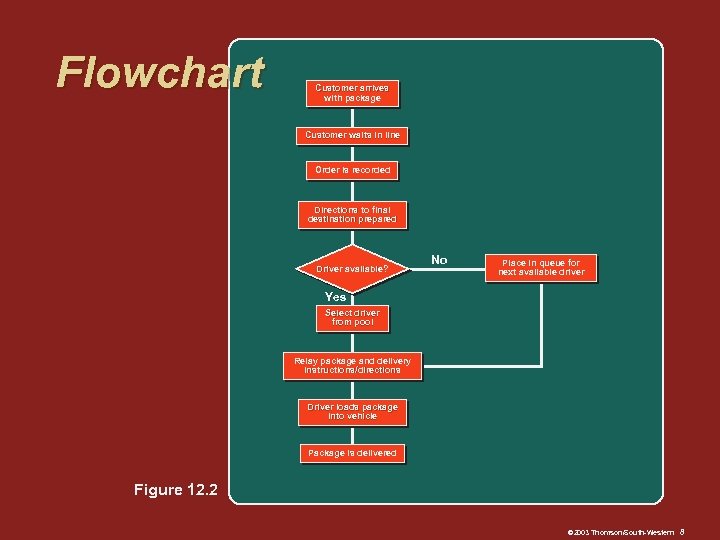
Flowchart Customer arrives with package Customer waits in line Order is recorded Directions to final destination prepared Driver available? No Place in queue for next available driver Yes Select driver from pool Relay package and delivery instructions/directions Driver loads package into vehicle Package is delivered Figure 12. 2 © 2003 Thomson/South-Western 8
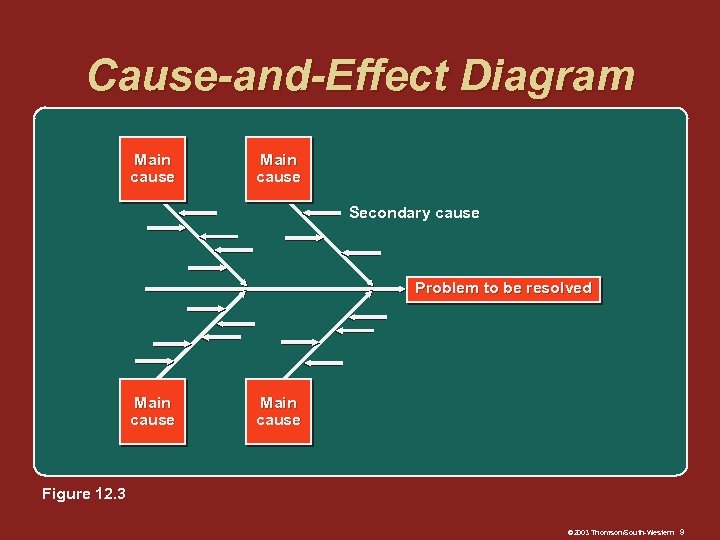
Cause-and-Effect Diagram Main cause Secondary cause Problem to be resolved Main cause Figure 12. 3 © 2003 Thomson/South-Western 9
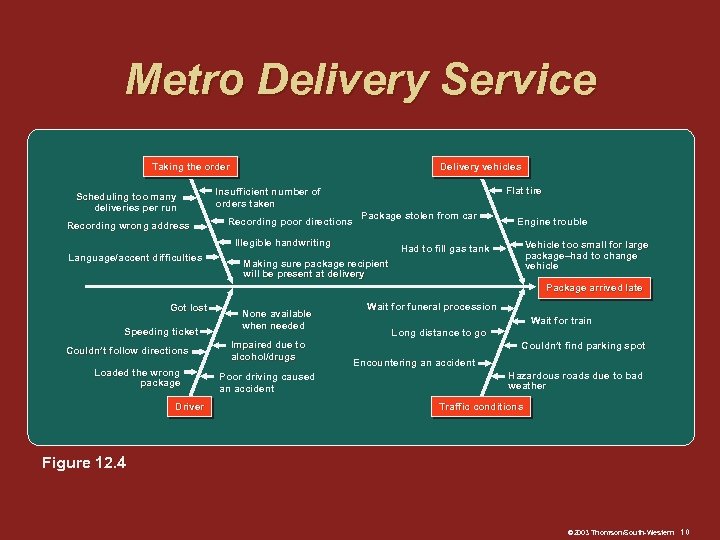
Metro Delivery Service Taking the order Scheduling too many deliveries per run Recording wrong address Delivery vehicles Flat tire Insufficient number of orders taken Recording poor directions Package stolen from car Illegible handwriting Language/accent difficulties Engine trouble Vehicle too small for large package–had to change vehicle Had to fill gas tank Making sure package recipient will be present at delivery Package arrived late Got lost Speeding ticket Couldn’t follow directions Loaded the wrong package Driver None available when needed Impaired due to alcohol/drugs Poor driving caused an accident Wait for funeral procession Wait for train Long distance to go Couldn’t find parking spot Encountering an accident Hazardous roads due to bad weather Traffic conditions Figure 12. 4 © 2003 Thomson/South-Western 10

Statistical Process Control, Process Variation and Control Charts q Machinery q People q Materials q Production Methods q The Environment © 2003 Thomson/South-Western 11

Statistical Process Control, Process Variation and Control Charts q A stable system exhibits chance causes of variation q Variations outside this stable pattern are called assignable causes of variation © 2003 Thomson/South-Western 12

Deming Funnel Experiment: Strategies q Strategy 1: Do not react to this random variation and do not move the funnel q Strategy 2: Measure the distance from the marble’s resting place to the bull’s-eye Move the funnel and equal distance, but in the opposite direction © 2003 Thomson/South-Western 13

Deming Funnel Experiment: Strategies q Strategy 3: Measure the distance from the marble’s resting place to the bull’s-eye Move the funnel this distance, in the opposite direction, starting at the bull’s-eye © 2003 Thomson/South-Western 14
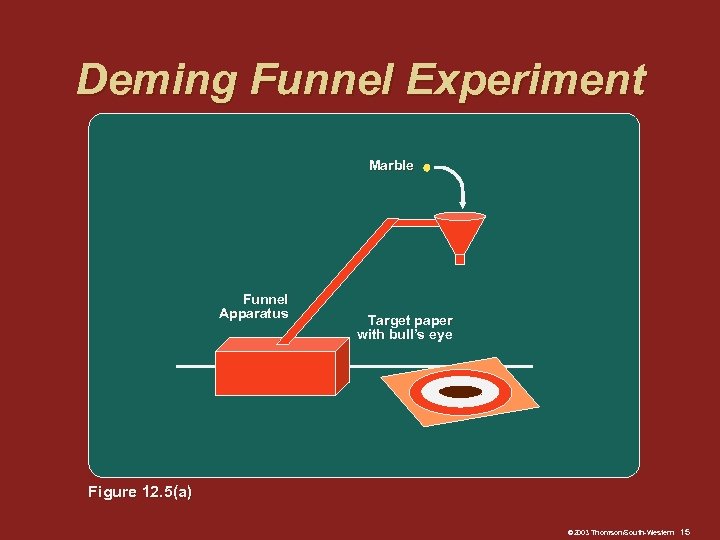
Deming Funnel Experiment Marble Funnel Apparatus Target paper with bull’s eye Figure 12. 5(a) © 2003 Thomson/South-Western 15
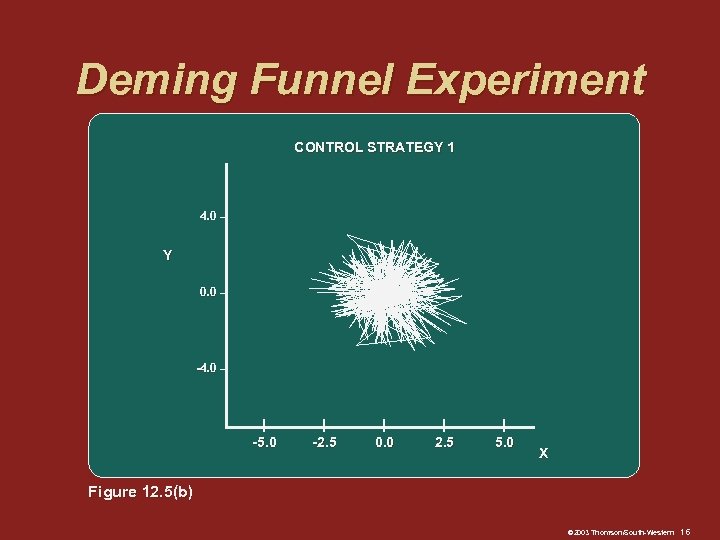
Deming Funnel Experiment CONTROL STRATEGY 1 4. 0 – Y 0. 0 – -4. 0 – | -5. 0 | -2. 5 | 0. 0 | 2. 5 | 5. 0 X Figure 12. 5(b) © 2003 Thomson/South-Western 16
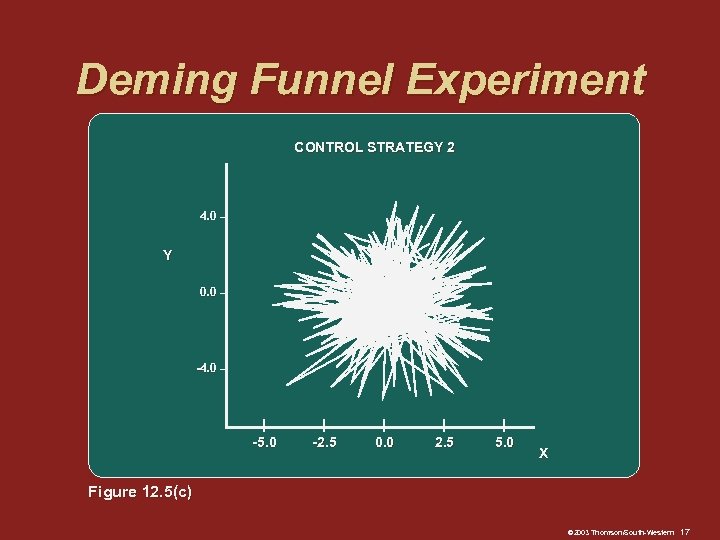
Deming Funnel Experiment CONTROL STRATEGY 2 4. 0 – Y 0. 0 – -4. 0 – | -5. 0 | -2. 5 | 0. 0 | 2. 5 | 5. 0 X Figure 12. 5(c) © 2003 Thomson/South-Western 17
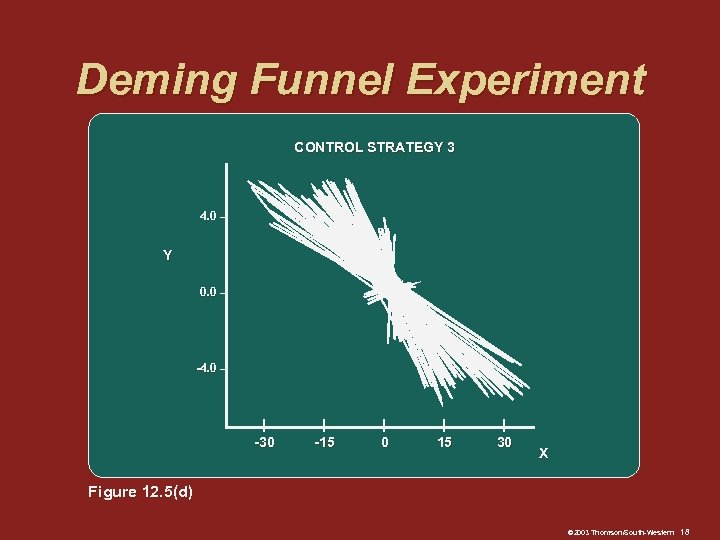
Deming Funnel Experiment CONTROL STRATEGY 3 4. 0 – Y 0. 0 – -4. 0 – | -30 | -15 | 0 | 15 | 30 X Figure 12. 5(d) © 2003 Thomson/South-Western 18

Control Charts q A process is in control if the observed variation is due to inherent or natural variation This variability is the cumulative effect of many small, essentially uncontrollable, causes q A process in out of control if a relatively large variation is introduced that can be traced to an assignable cause © 2003 Thomson/South-Western 19
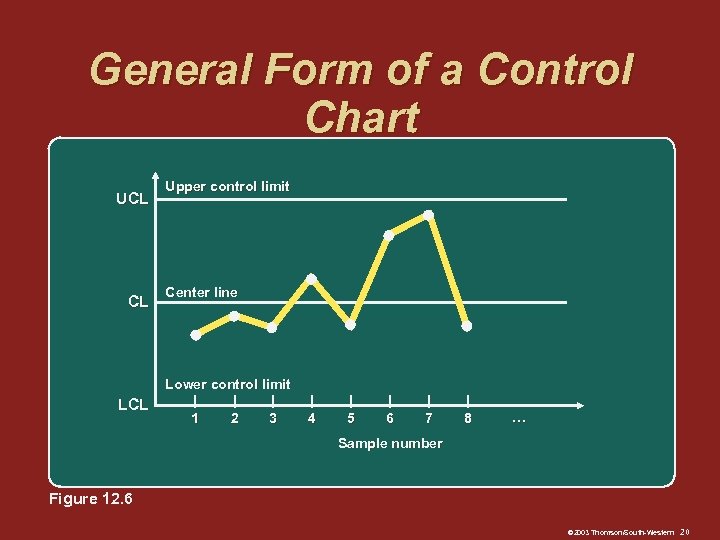
General Form of a Control Chart UCL CL LCL Upper control limit Center line Lower control limit | | | 1 2 3 | 4 | 5 | 6 | 7 | 8 . . . Sample number Figure 12. 6 © 2003 Thomson/South-Western 20
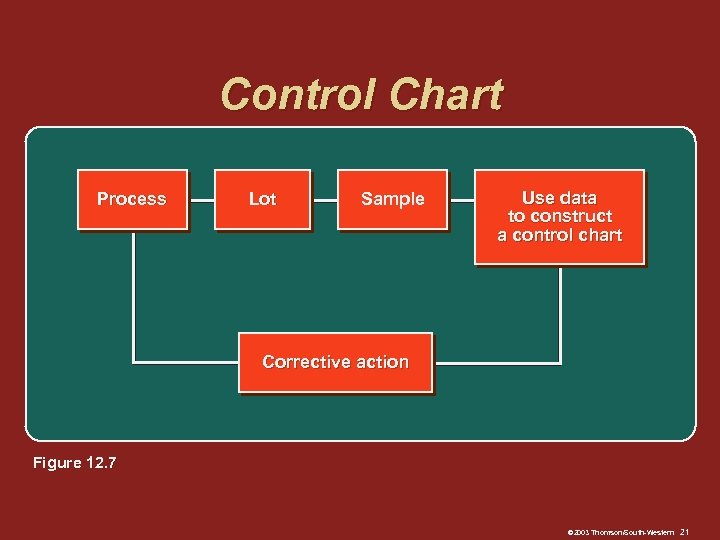
Control Chart Process Lot Sample Use data to construct a control chart Corrective action Figure 12. 7 © 2003 Thomson/South-Western 21

X and R Charts X 1 + X 2 +. . . + Xm X= m R = d 2 ^ © 2003 Thomson/South-Western 22
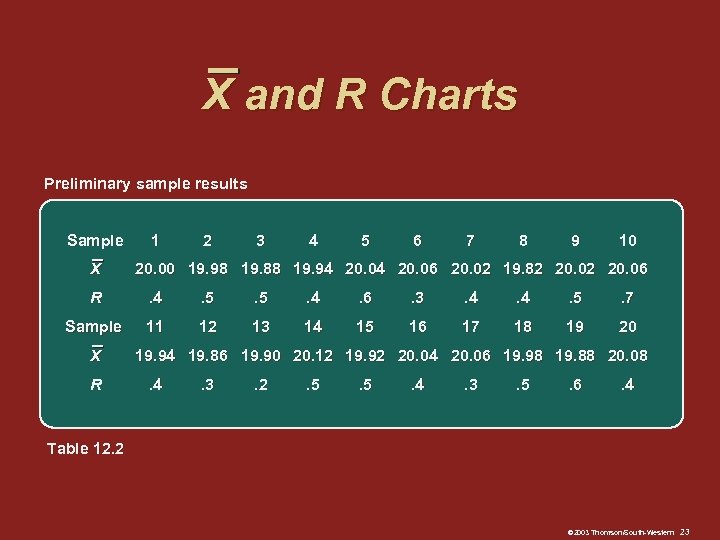
X and R Charts Preliminary sample results Sample X 1 2 3 4 5 6 7 8 9 10 20. 00 19. 98 19. 88 19. 94 20. 06 20. 02 19. 82 20. 06 R . 4 . 5 . 4 . 6 . 3 . 4 . 5 . 7 Sample 11 12 13 14 15 16 17 18 19 20 X R 19. 94 19. 86 19. 90 20. 12 19. 92 20. 04 20. 06 19. 98 19. 88 20. 08. 4 . 3 . 2 . 5 . 4 . 3 . 5 . 6 . 4 Table 12. 2 © 2003 Thomson/South-Western 23

X and R Charts Factors for constructing an R chart n d 2 d 3 2 3 4 5 6 7 8 9 10 1. 128 1. 693 2. 059 2. 326 2. 534 2. 704 2. 847 2. 970 3. 078 . 853. 888. 880. 864. 848. 833. 820. 808. 797 D 3 0 0 0. 076. 136. 184. 223 D 4 3. 267 2. 574 2. 282 2. 114 2. 004 1. 924 1. 864 1. 816 1. 777 Table 12. 3 © 2003 Thomson/South-Western 24
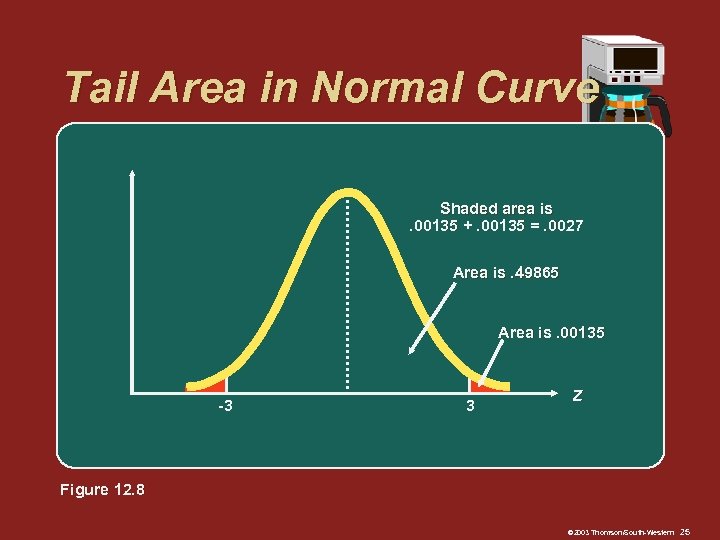
Tail Area in Normal Curve Shaded area is. 00135 +. 00135 =. 0027 Area is. 49865 Area is. 00135 -3 3 Z Figure 12. 8 © 2003 Thomson/South-Western 25

X and R Charts Process for Estimating 1. Determine the average of the m values of R 2. Select the values of d 2 from Table 12. 3 using the corresponding sample size, n 3. Estimate using: R = d 2 ^ © 2003 Thomson/South-Western 26

X and R Charts Control Limits ^ (R / d 2 ) UCL = X + 3 =X+3 n n Center Line = X ^ (R / d 2 ) LCL = X - 3 =X-3 n n © 2003 Thomson/South-Western 27
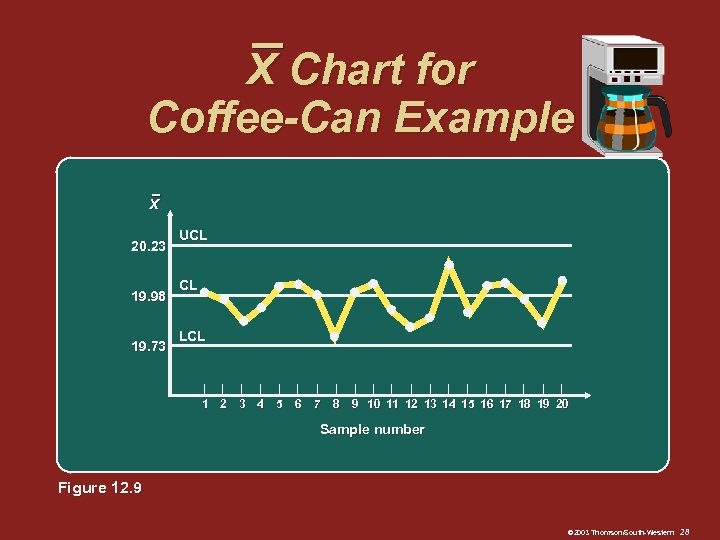
X Chart for Coffee-Can Example X 20. 23 19. 98 19. 73 UCL CL LCL | | | 1 2 3 4 5 6 | | | | 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Sample number Figure 12. 9 © 2003 Thomson/South-Western 28
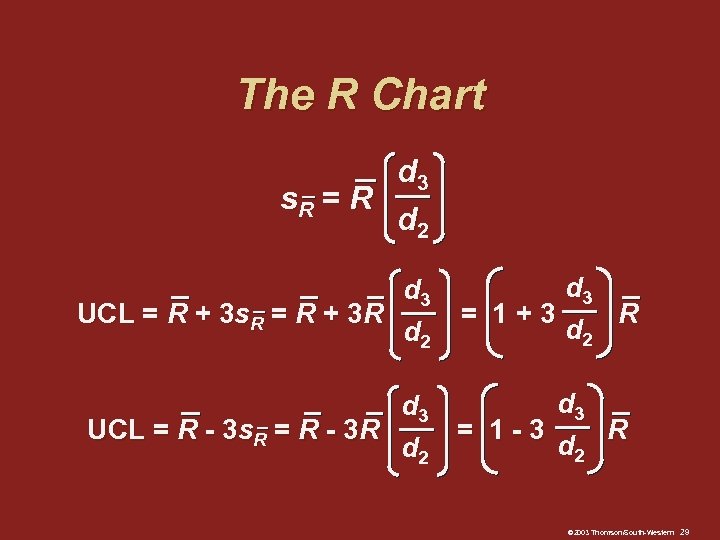
The R Chart d 3 s. R = R d 2 d 3 UCL = R + 3 s. R = R + 3 R d 2 d 3 = 1+3 R d 2 d 3 UCL = R - 3 s. R = R - 3 R = 1 -3 R d 2 © 2003 Thomson/South-Western 29
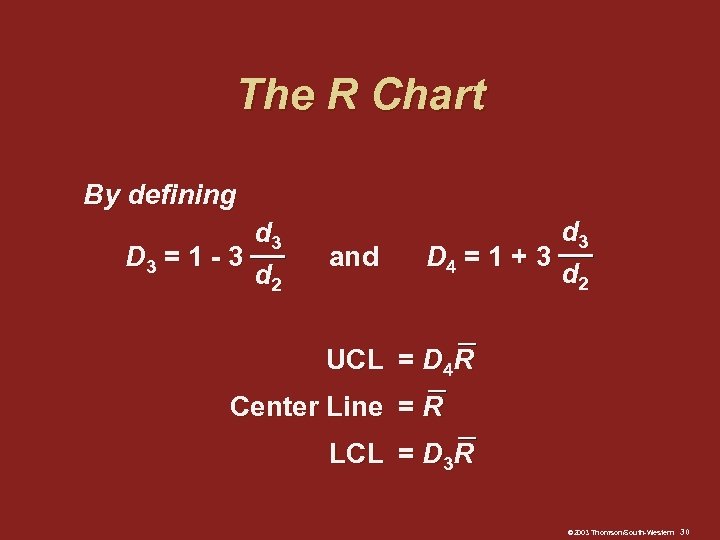
The R Chart By defining d 3 D 3 = 1 - 3 d 2 and d 3 D 4 = 1 + 3 d 2 UCL = D 4 R Center Line = R LCL = D 3 R © 2003 Thomson/South-Western 30
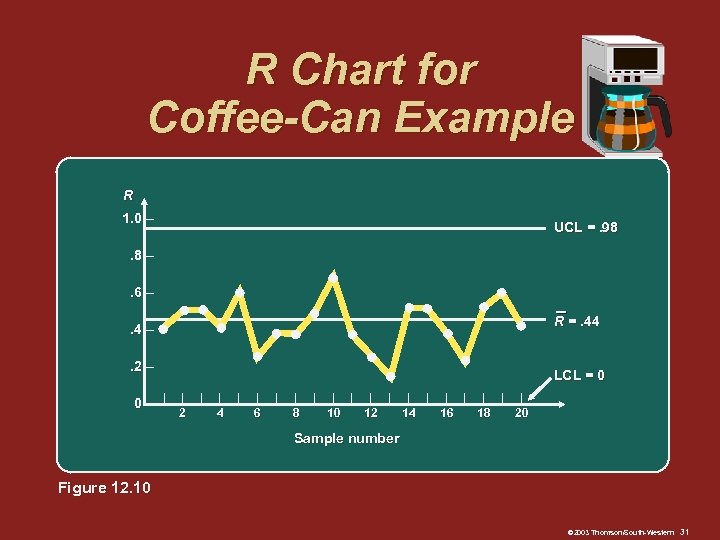
R Chart for Coffee-Can Example R 1. 0 – UCL =. 98 . 8 –. 6 – R =. 44 . 4 –. 2 – 0– | LCL = 0 | 2 | | 4 | | 6 | | 8 | | | 10 12 14 16 18 20 Sample number Figure 12. 10 © 2003 Thomson/South-Western 31
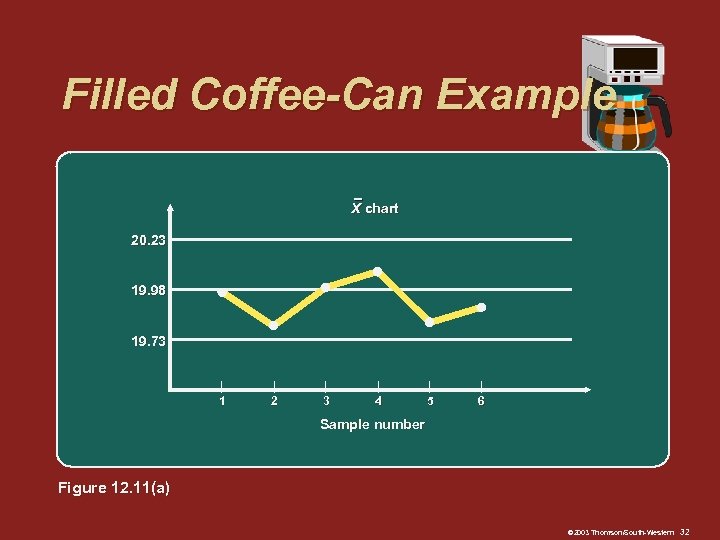
Filled Coffee-Can Example X chart 20. 23 19. 98 19. 73 | 1 | 2 | 3 | 4 | 5 | 6 Sample number Figure 12. 11(a) © 2003 Thomson/South-Western 32
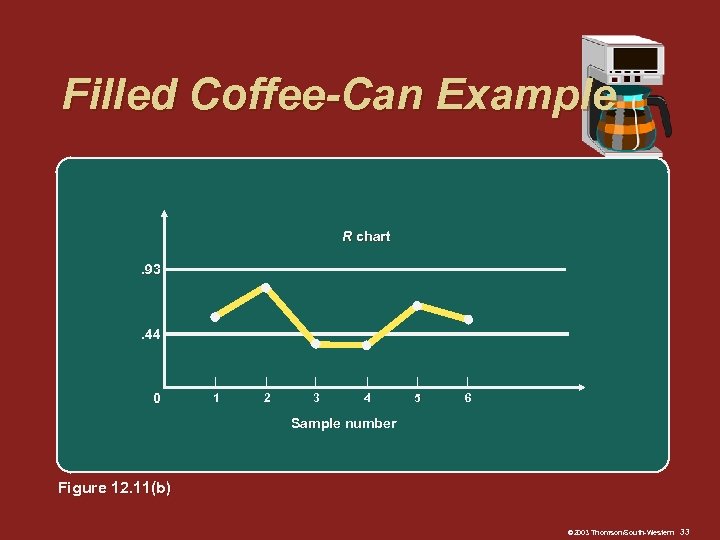
Filled Coffee-Can Example R chart. 93 – . 44 – 0 | 1 | 2 | 3 | 4 | 5 | 6 Sample number Figure 12. 11(b) © 2003 Thomson/South-Western 33

Steps for Making X and R Charts 1. 2. 3. 4. 5. 6. Collect m samples of data, each of size n Compute the average of each subgroup Compute the range for each subgroup Find the overall mean Find the average range Estimate © 2003 Thomson/South-Western 34

Steps for Making X and R Charts 7. 8. 9. Compute the 3 -sigma control limits for X Compute the 3 -sigma control limits for R Construct the control charts by plotting X and R points for each subgroup on the same vertical line © 2003 Thomson/South-Western 35

Pattern Analysis for X Charts Pattern analysis is concerned with recognizing systematic or nonrandom patterns in an X control chart and identifying the source of such process variation Each chart is divided into zones Zone A Zone B Zone C © 2003 Thomson/South-Western 36

Pattern Analysis for X Charts Pattern 1 2 3 4 5 6 7 8 Description One point beyond zone A Nine points in a row in zone C or beyond, all on one side of the center line Six points in a row, all increasing or decreasing Fourteen points in a row, alternating up and down Two out of three points in a row in zone A or beyond Four out of five points in zone B or beyond (on one side of center line) Fifteen points in a row in zones C (above or below center line) Eight points in a row beyond zones C (above or below center line) © 2003 Thomson/South-Western 37
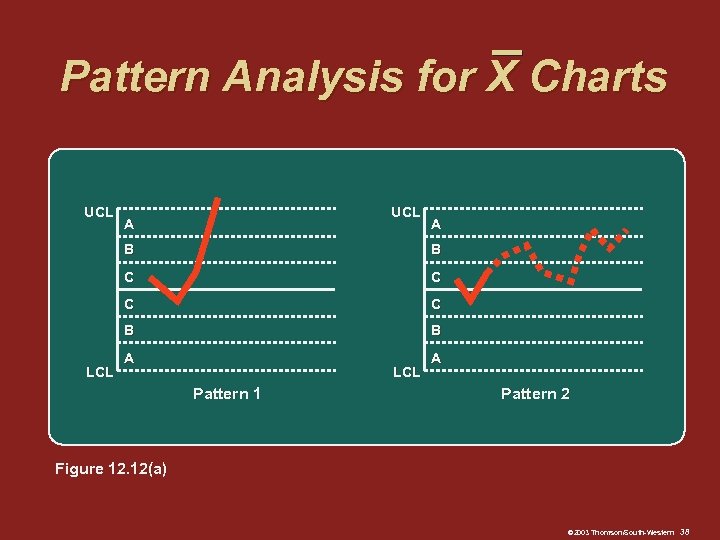
Pattern Analysis for X Charts UCL A A B C C B LCL B B A A LCL Pattern 1 Pattern 2 Figure 12. 12(a) © 2003 Thomson/South-Western 38
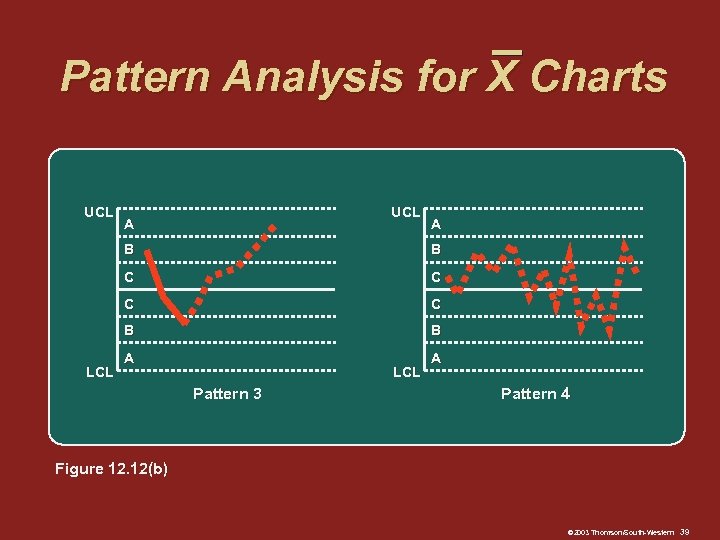
Pattern Analysis for X Charts UCL A A B C C B LCL B B A A LCL Pattern 3 Pattern 4 Figure 12. 12(b) © 2003 Thomson/South-Western 39
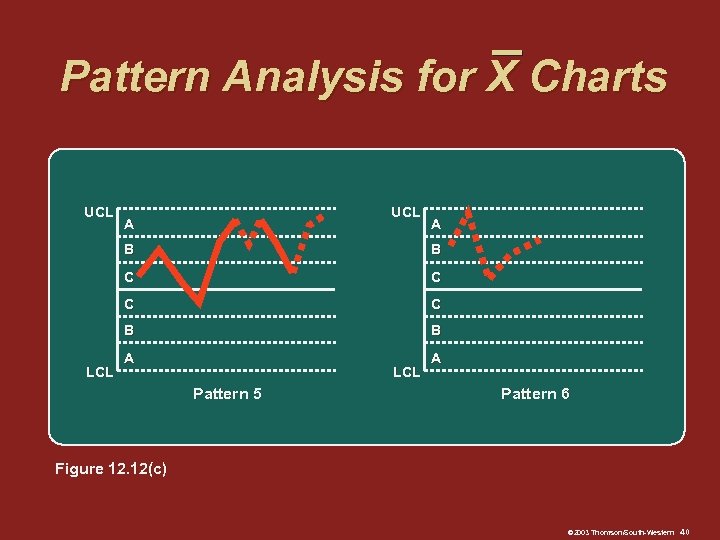
Pattern Analysis for X Charts UCL A A B C C B LCL B B A A LCL Pattern 5 Pattern 6 Figure 12. 12(c) © 2003 Thomson/South-Western 40
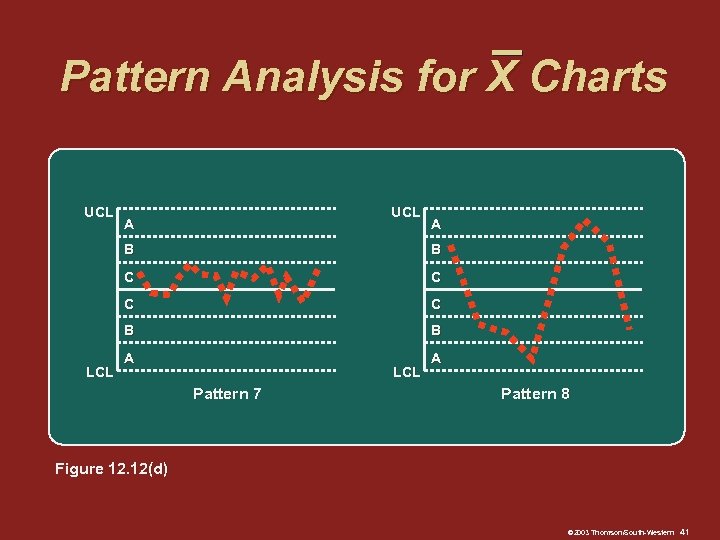
Pattern Analysis for X Charts UCL A A B C C B LCL B B A A LCL Pattern 7 Pattern 8 Figure 12. 12(d) © 2003 Thomson/South-Western 41
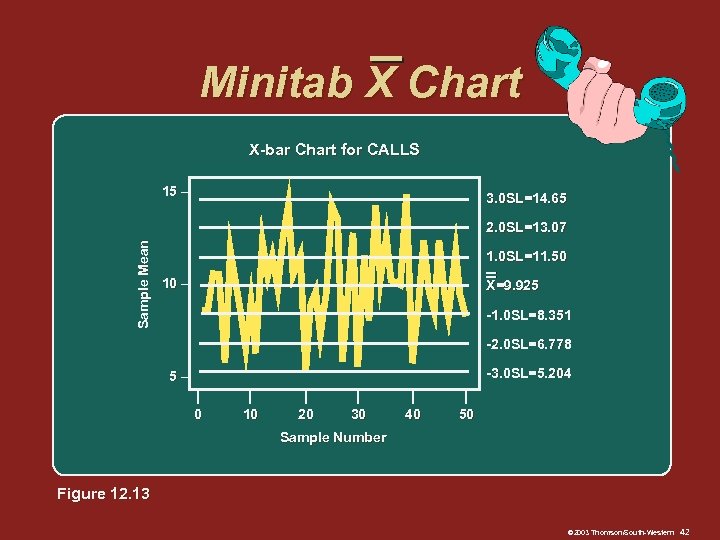
Minitab X Chart X-bar Chart for CALLS 15 – 3. 0 SL=14. 65 Sample Mean 2. 0 SL=13. 07 1. 0 SL=11. 50 10 – X=9. 925 -1. 0 SL=8. 351 -2. 0 SL=6. 778 -3. 0 SL=5. 204 5– | 0 | 10 | 20 | 30 | 40 | 50 Sample Number Figure 12. 13 © 2003 Thomson/South-Western 42
Cans of Ground Coffee Figure 12. 14 © 2003 Thomson/South-Western 43
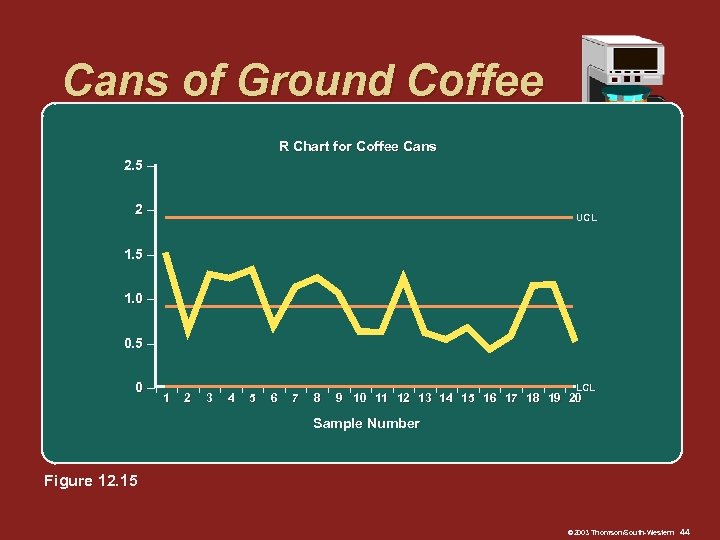
Cans of Ground Coffee R Chart for Coffee Cans 2. 5 – 2– UCL 1. 5 – 1. 0 – 0. 5 – 0 –I 1 I 2 I 3 I 4 I 5 I 6 I 7 I 8 I I I LCL 9 10 11 12 13 14 15 16 17 18 19 20 Sample Number Figure 12. 15 © 2003 Thomson/South-Western 44
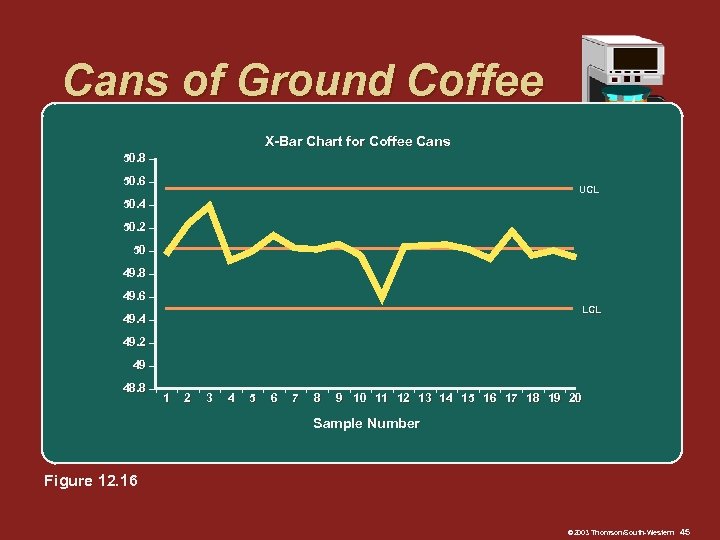
Cans of Ground Coffee X-Bar Chart for Coffee Cans 50. 8 – 50. 6 – UCL 50. 4 – 50. 2 – 50 – 49. 8 – 49. 6 – LCL 49. 4 – 49. 2 – 49 – 48. 8 –I 1 I 2 I 3 I 4 I 5 I 6 I 7 I 8 I I I 9 10 11 12 13 14 15 16 17 18 19 20 Sample Number Figure 12. 16 © 2003 Thomson/South-Western 45

Control Charts for Attribute Data Proportion Nonconforming: p Chart Reasons for Using a p Chart 1. Quality measurements are not possible 2. Quality measurements are not practical 3. Many characteristics on each part are being judged during inspection 4. The main question of interest is: “Will the process be able to produce conforming products over time? ” © 2003 Thomson/South-Western 46

Steps for Making p Charts 1. Collect m samples of data, each of size n 2. Determine the proportion nonconforming for each sample 3. Find p, the overall proportion nonconforming 4. Compute the 3 -sigma control limits 5. Draw the control lines and plot the values of pi © 2003 Thomson/South-Western 47

p Chart Equations Ti pi = n ∑Ti p= mn total number of nonconforming units p= total sample size UCL = p + 3 p(1 - p) n CL = p p(1 - p) LCL = p - 3 n © 2003 Thomson/South-Western 48
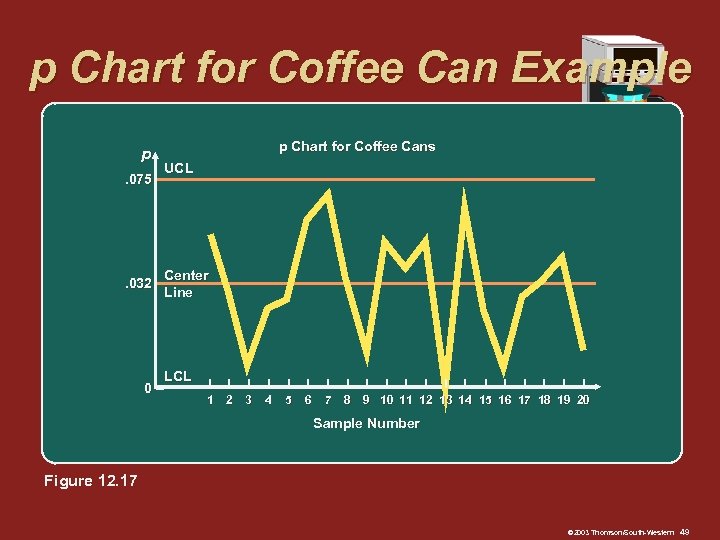
p Chart for Coffee Can Example p. 075 – . 032 – 0– p Chart for Coffee Cans UCL Center Line LCL I I 1 2 I 3 I 4 I I 5 6 I 7 I I I I 8 9 10 11 12 13 14 15 16 17 18 19 20 Sample Number Figure 12. 17 © 2003 Thomson/South-Western 49
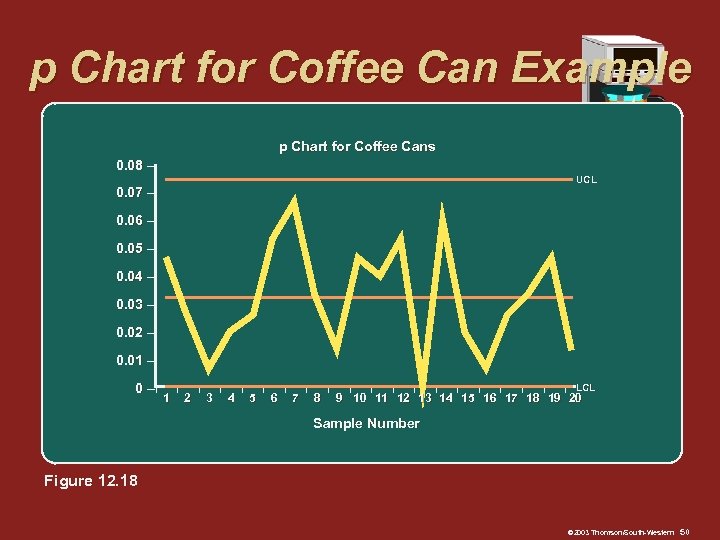
p Chart for Coffee Can Example p Chart for Coffee Cans 0. 08 – UCL 0. 07 – 0. 06 – 0. 05 – 0. 04 – 0. 03 – 0. 02 – 0. 01 – 0 –I 1 I 2 I 3 I 4 I 5 I 6 I 7 I 8 I I I LCL 9 10 11 12 13 14 15 16 17 18 19 20 Sample Number Figure 12. 18 © 2003 Thomson/South-Western 50

Control Charts for Attribute Data Number Nonconforming per Unit: c Chart Reasons for Using a c Chart 1. One or more types of nonconformities 2. Poisson distribution © 2003 Thomson/South-Western 51

The c Chart Construction 1. Collect m samples of data, each of size n 2. Determine the number of nonconformities for the ith unit. Call this value ci 3. Find the average number of nonconformities per unit, c 4. Compute the 3 -sigma control limits 5. Construct the chart © 2003 Thomson/South-Western 52

c Chart Equations ∑ ci c= m UCL = c + 3 c Center Line = c LCL = c - 3 c © 2003 Thomson/South-Western 53
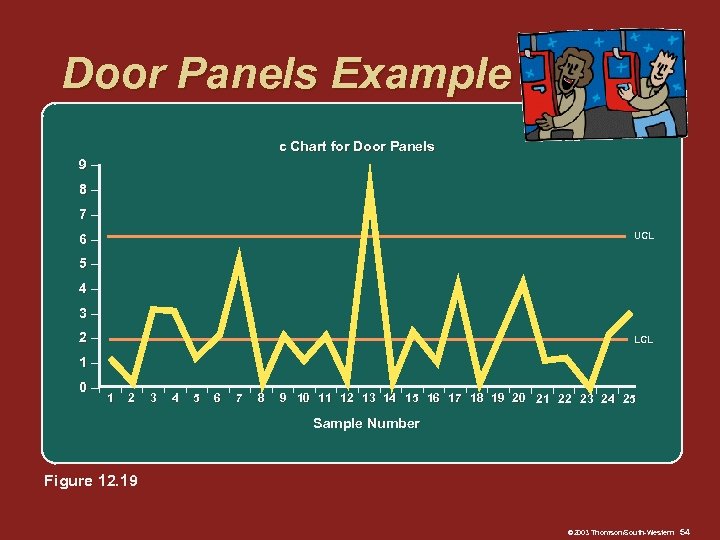
Door Panels Example c Chart for Door Panels 9– 8– 7– UCL 6– 5– 4– 3– 2– LCL 1– 0 –I 1 I 2 I 3 I 4 I 5 I 6 I 7 I 8 I I I I I 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Sample Number Figure 12. 19 © 2003 Thomson/South-Western 54

Process Capability q Specification Limits: process requirements q Lower spec limit (LSL): the lower limit of the process output that meets the process requirements q Upper spec limit (USL): the upper limit of the process output that meets the process requirements © 2003 Thomson/South-Western 55
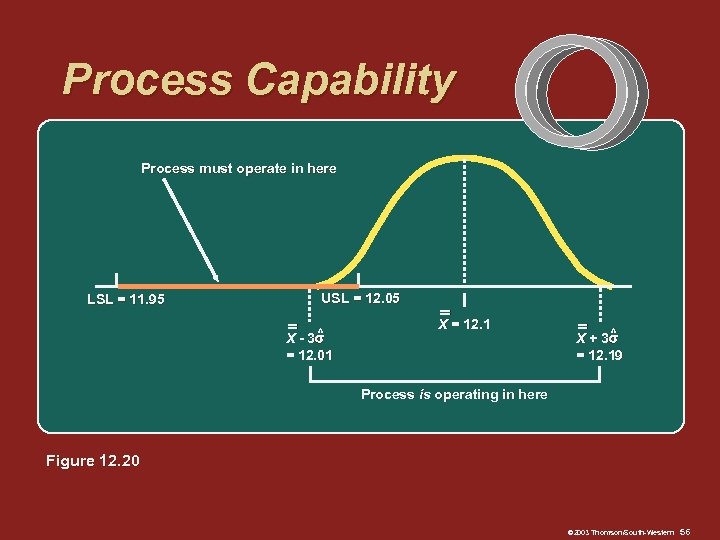
Process Capability Process must operate in here LSL = 11. 95 USL = 12. 05 ^ X - 3 = 12. 01 X = 12. 1 ^ X + 3 = 12. 19 Process is operating in here Figure 12. 20 © 2003 Thomson/South-Western 56
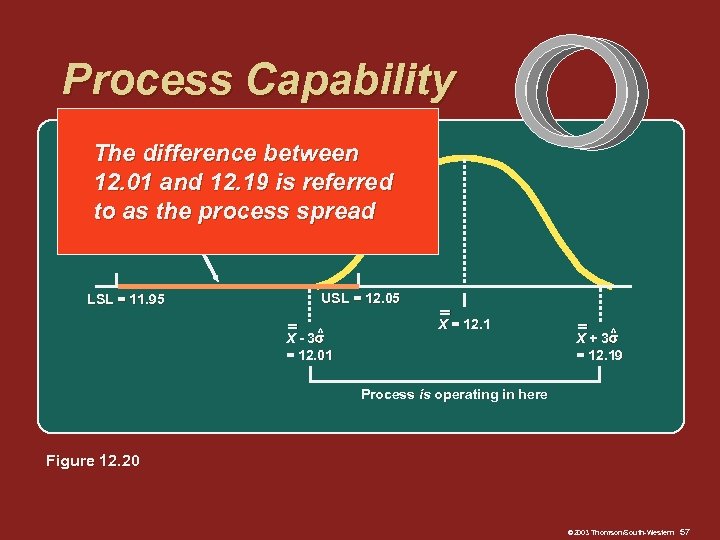
Process Capability The Process must operate in here difference between 12. 01 and 12. 19 is referred to as the process spread LSL = 11. 95 USL = 12. 05 ^ X - 3 = 12. 01 X = 12. 1 ^ X + 3 = 12. 19 Process is operating in here Figure 12. 20 © 2003 Thomson/South-Western 57
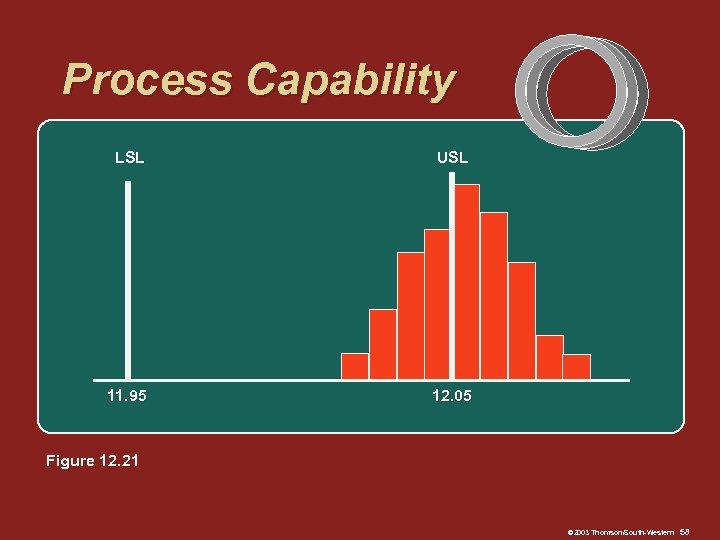
Process Capability LSL USL 11. 95 12. 05 Figure 12. 21 © 2003 Thomson/South-Western 58

Process Capability Ratio Cp Assumptions: 1. The process is centered within specifications 2. The process is normally distributed 3. The process is stable (in control) © 2003 Thomson/South-Western 59

Formulas for Cp USL - LSL Cp = ^ 6 USL - X Cp = ^ 3 (upper spec limit only) X - LSL Cp = ^ 3 (lower spec limit only) © 2003 Thomson/South-Western 60
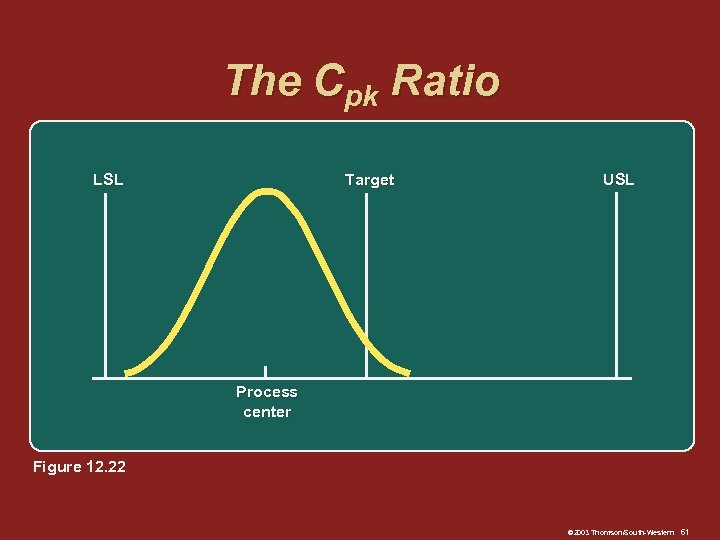
The Cpk Ratio LSL Target USL Process center Figure 12. 22 © 2003 Thomson/South-Western 61

Process Capability Ratio Cpk Assumptions: 1. The process may or may not be centered in spec 2. The process is normally distributed 3. The process is stable 4. Control charts will be used to monitor the process over time © 2003 Thomson/South-Western 62

Procedure for Finding Cpk X - LSL 1. Determine RL = ^ 3 USL - X 2. Determine RU = ^ 3 3. Cpk = Minimum of RL and RU © 2003 Thomson/South-Western 63

Taking Cpk One Step Further If the process is capable (Cpk > 1) q Monitor the process q Pursue continual imporvement If the process is not capable (Cpk ≤ 1) Monitor the process Pursue continual imporvement Invest time, money, and resources to reduce process variation q Consider removing this product from production q q q © 2003 Thomson/South-Western 64
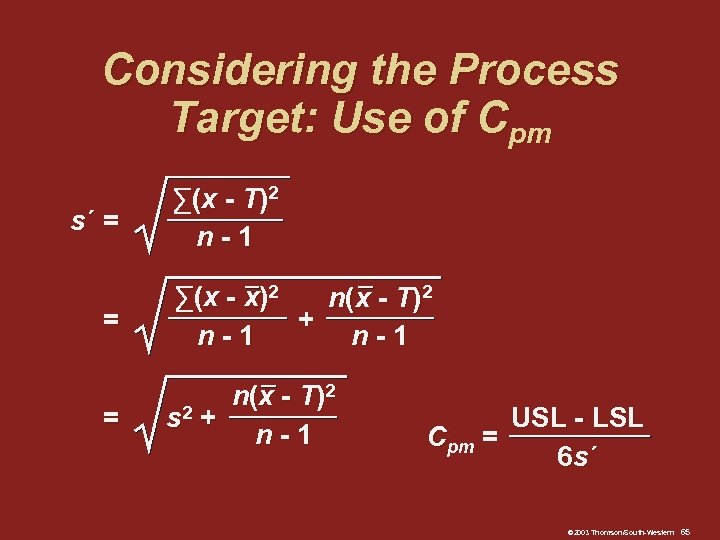
Considering the Process Target: Use of Cpm s´ = ∑(x - T)2 n-1 = ∑(x - x)2 n (x - T )2 + n-1 = n (x - T )2 s 2 + n-1 USL - LSL Cpm = 6 s´ © 2003 Thomson/South-Western 65
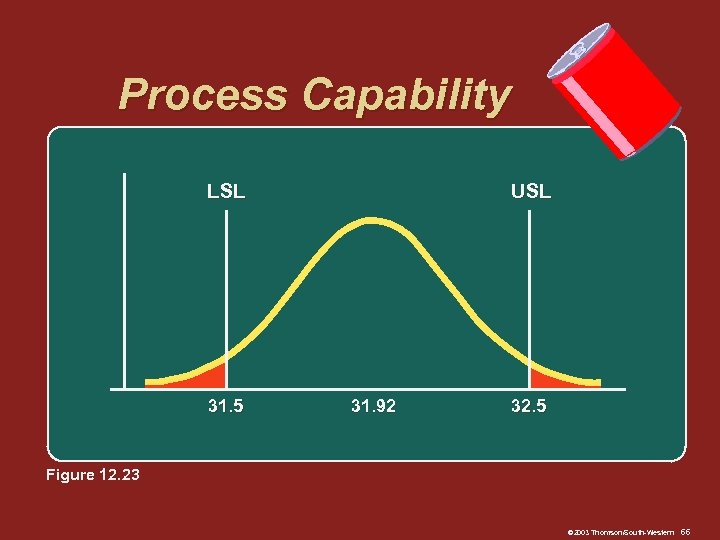
Process Capability LSL 31. 5 USL 31. 92 32. 5 Figure 12. 23 © 2003 Thomson/South-Western 66

Process Capability Cpk Number of Noncomforming Units per Million Produced . 5. 75 1. 00 1. 30 1. 50 2. 00 133, 614 24, 448 2, 700 96 6. 8. 002 Table 12. 4 © 2003 Thomson/South-Western 67
af357a110c75bf9f7dabcf457ec5c1b4.ppt