Introduction to Business Management Statistics Class 2 Topic

Introduction to Business Management: Statistics Class 2 Topic 3. Data visualization using tables, charts and diagrams

In this topic you learn l To develop tables and charts for numerical data l To develop tables and charts for categorical data The principles of properly presenting graphs l

Planned 3. 1 Organizing qualitative data. Summary tables and contingency tables. 3. 2 Organizing quantitative data. Frequency distributions. 3. 3 The concept of array data. Static, dynamic and panel arrays and methods of presentation.

Types of Variables Categorical (qualitative) variables have values that can only be placed into categories, such as “yes” and “no. ” Numerical (quantitative) variables have values that represent quantities. § § Discrete variables arise from a counting process Continuous variables arise from a measuring process

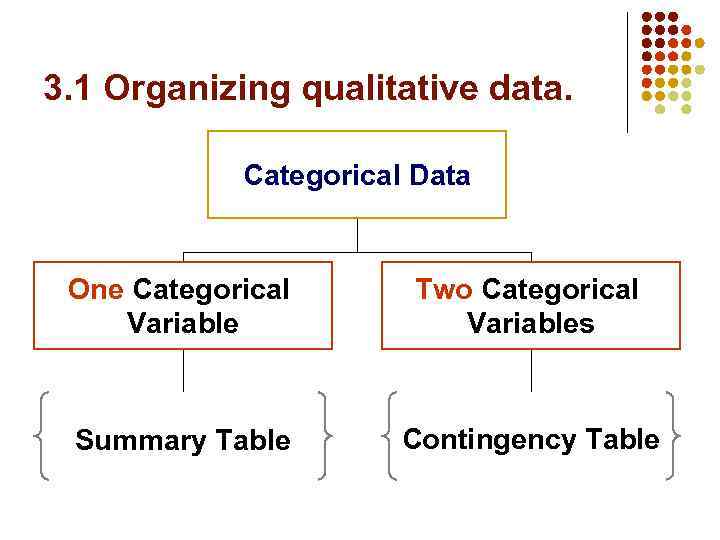
3. 1 Organizing qualitative data. Categorical Data One Categorical Variable Two Categorical Variables Summary Table Contingency Table

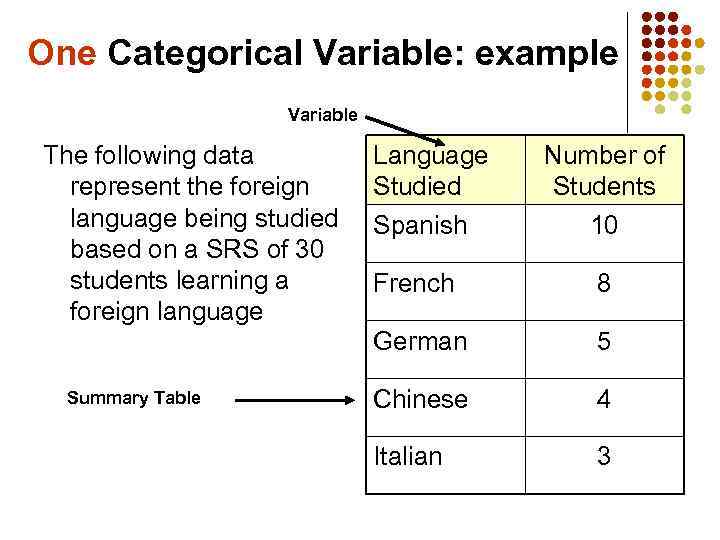
One Categorical Variable: example Variable The following data represent the foreign language being studied based on a SRS of 30 students learning a foreign language Language Studied Spanish Number of Students 10 8 German Summary Table French 5 Chinese 4 Italian 3

One Categorical Variable A summary table indicates the frequency, amount, or percentage of items in a set of categories so that you can see differences between categories.

Two Categorical Variables: example Variables The following data represent the foreign language being studied based on a SRS of 30 students learning a foreign language, by gender. Language Studied Gender Males Females Spanish 6 4 French 2 6 German 3 2 Chinese 3 1 Italian 1 2 Contingency Table

Two Categorical Variables A contingency table (cross-classification, cross-tabulation) display the frequencies for each combination of two or more variables. The term was first used by Karl Pearson in 1904. Each location in a table is called cell, and the corresponding number of items is the cell frequency.

Frequency and relative frequency A frequency distribution lists each category of data and the number of occurrences for each category of data. The relative frequency is the portion of observations within a category: A relative frequency distribution lists each category of data together with the relative frequency.

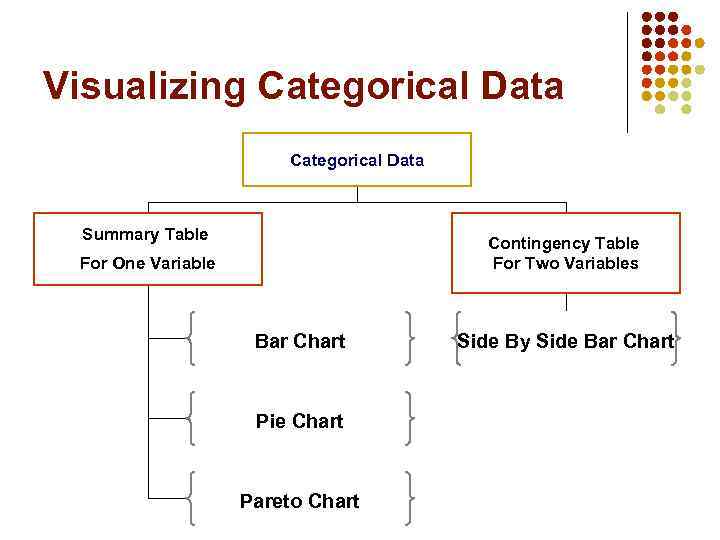
Visualizing Categorical Data Summary Table Contingency Table For Two Variables For One Variable Bar Chart Pie Chart Pareto Chart Side By Side Bar Chart

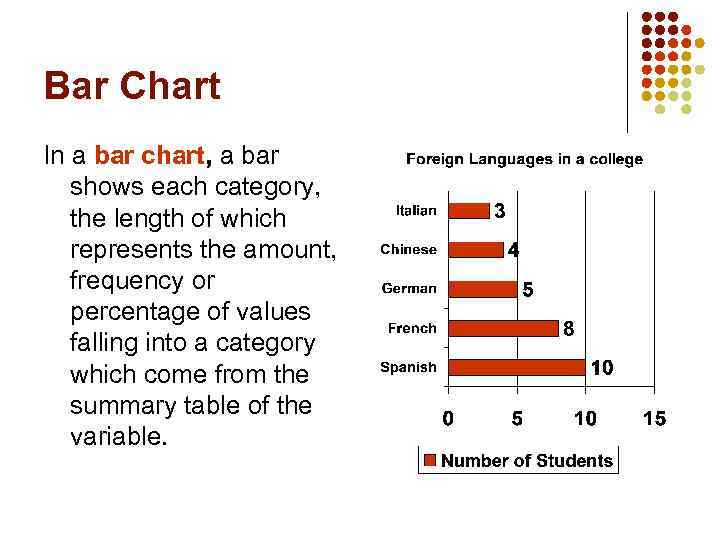
Bar Chart In a bar chart, a bar shows each category, the length of which represents the amount, frequency or percentage of values falling into a category which come from the summary table of the variable.

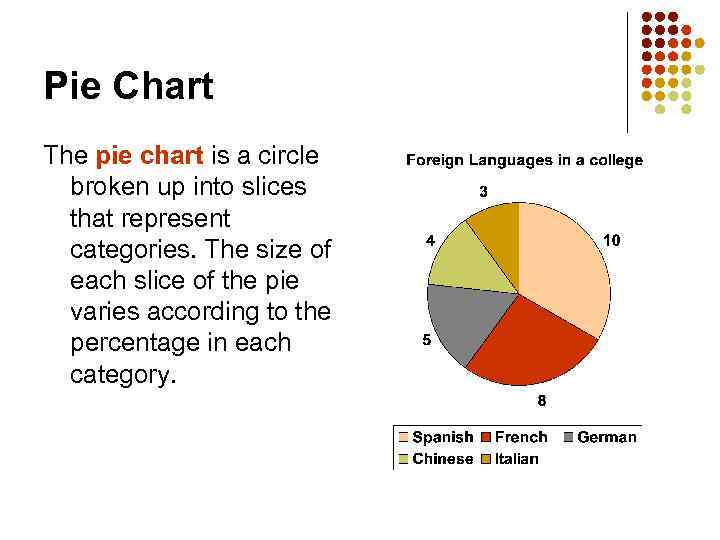
Pie Chart The pie chart is a circle broken up into slices that represent categories. The size of each slice of the pie varies according to the percentage in each category.

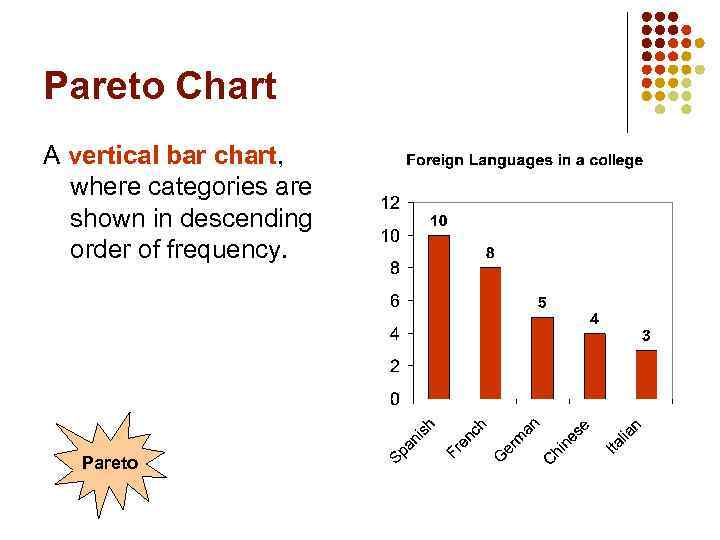
Pareto Chart A vertical bar chart, where categories are shown in descending order of frequency. Pareto

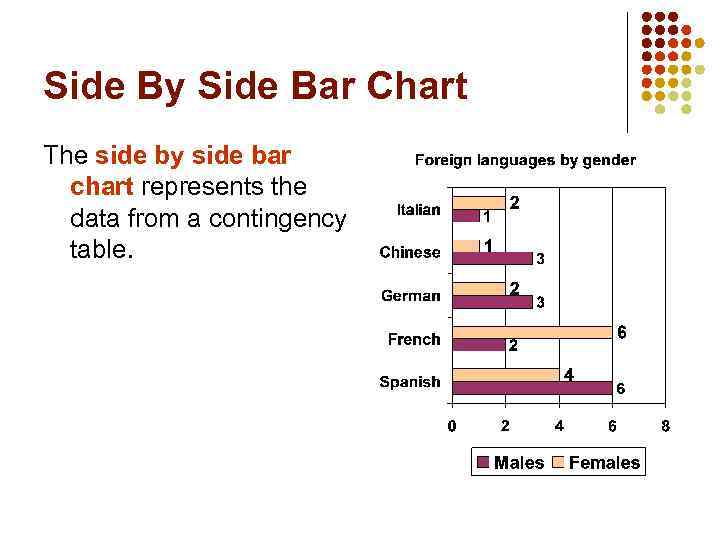
Side By Side Bar Chart The side by side bar chart represents the data from a contingency table.

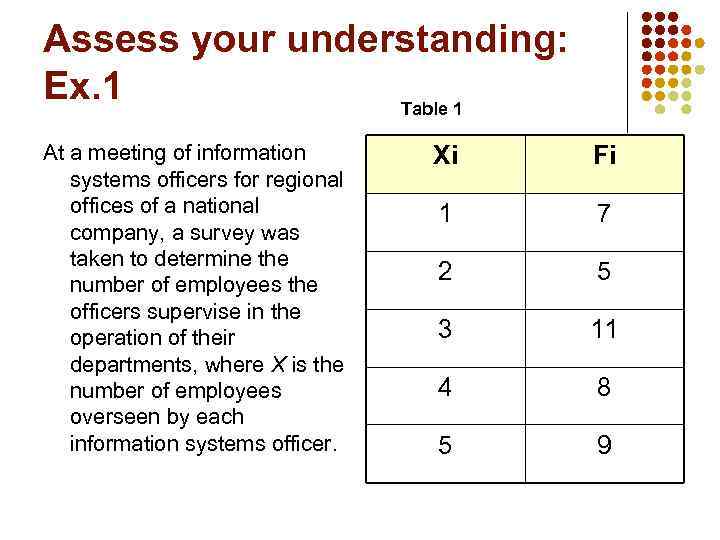
Assess your understanding: Ex. 1 Table 1 At a meeting of information systems officers for regional offices of a national company, a survey was taken to determine the number of employees the officers supervise in the operation of their departments, where X is the number of employees overseen by each information systems officer. Xi Fi 1 7 2 5 3 11 4 8 5 9

Ex. 1 (continued) Survey information is represented using: A) Summary table B) Contingency table How many total employees were supervised by those surveyed? A) 15 B) 40 C) 127 D) 200 How many regional offices are represented in the survey results? A) 5 B) 11 C) 15 D) 40 Answer: Summary Table Answer: C) 127 Answer: D) 40

Ex. 1 (continued) Explain, why Pareto chart might be preferred over bar chart? Is it possible to draw a side-by-side bar chart for the data, represented in Table 1? Why? Construct a pie chart, using data from Table 1. Construct a relative frequency distribution using data from Table 1.

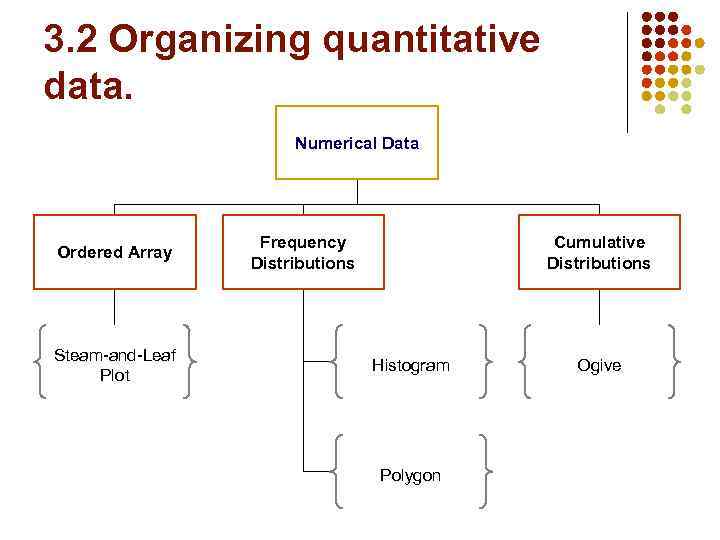
3. 2 Organizing quantitative data. Numerical Data Ordered Array Steam-and-Leaf Plot Frequency Distributions Cumulative Distributions Histogram Polygon Ogive

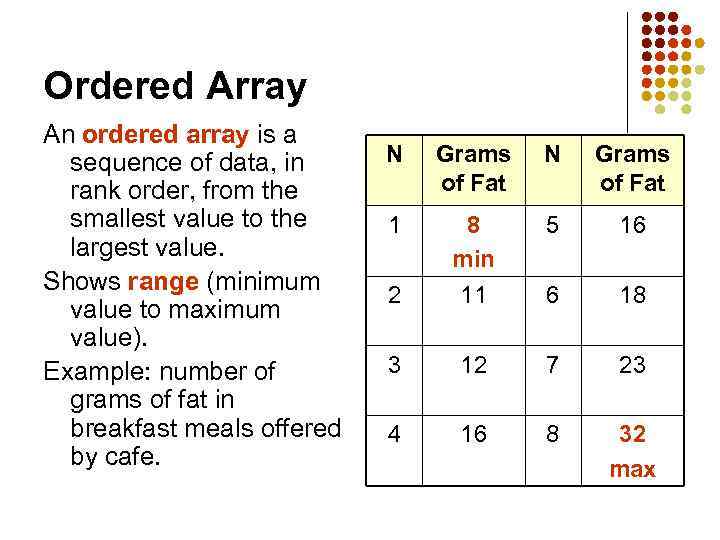
Ordered Array An ordered array is a sequence of data, in rank order, from the smallest value to the largest value. Shows range (minimum value to maximum value). Example: number of grams of fat in breakfast meals offered by cafe. N Grams of Fat 1 8 min 5 16 2 11 6 18 3 12 7 23 4 16 8 32 max

Ordered Array The Steam-and-Leaf plot is a simple way to see how the data are distributed and where concentrations of data exist. Advantage of the steam-and-leaf plot: the raw data can be retrieved from S-a-L! The best for small data sets.

The Steam-and-Leaf plot Separate the sorted data series into leading digits (the stems) and the trailing digits (the leaves). Steam Leaves 0 1 8 1 2 3 3 2 2 6 6 8

Frequency distributions The frequency distribution is a summary table in which the data are arranged into numerically ordered classes. You must give attention to selecting the appropriate number of class groupings for the table, determining a suitable width of a class grouping, and establishing the boundaries of each class grouping to avoid overlapping.

Frequency distributions: example 1. 2. 3. Calculate Range: Select number of classes (k) Compute class interval (width): N Grams of Frequency Fat 1 8 -16 5 2 16 -24 2 3 24 -32 1

Frequency distributions l l Convert the raw data into a more useful form Allows for a quick visual interpretation of the data It enables the determination of the major characteristics of the data set including where the data are concentrated / clustered When comparing two or more groups with different sample sizes, you must use either a relative frequency or a percentage distribution

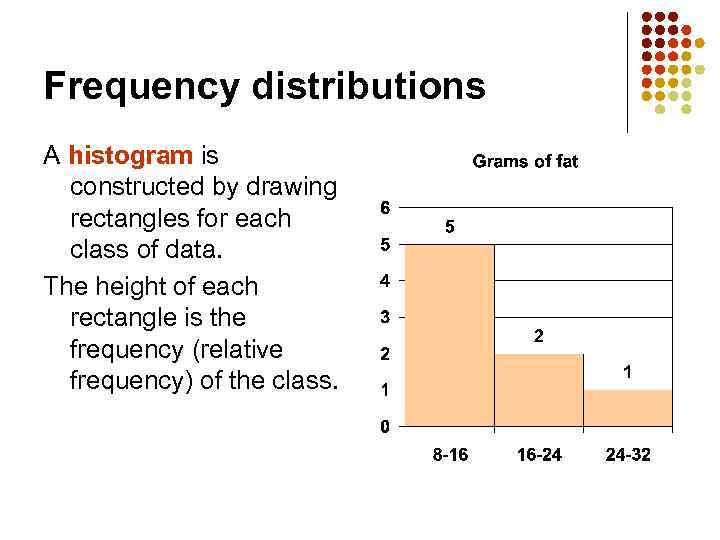
Frequency distributions A histogram is constructed by drawing rectangles for each class of data. The height of each rectangle is the frequency (relative frequency) of the class.

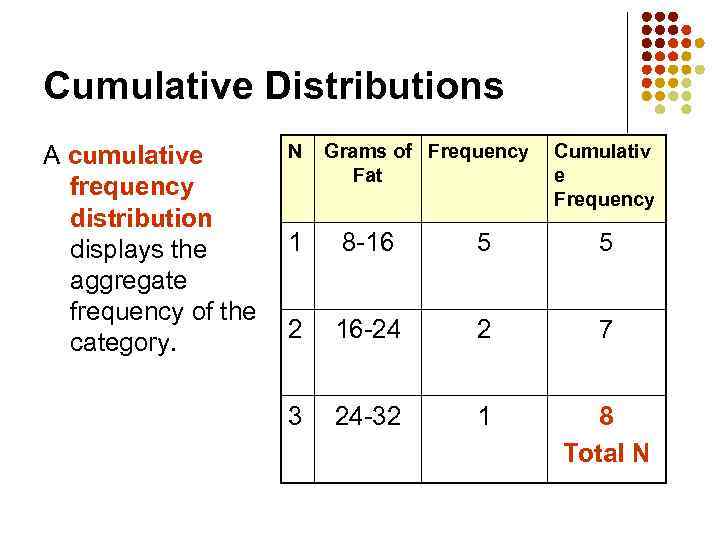
Cumulative Distributions N A cumulative frequency distribution 1 displays the aggregate frequency of the 2 category. 3 Grams of Frequency Fat Cumulativ e Frequency 8 -16 5 5 16 -24 2 7 24 -32 1 8 Total N

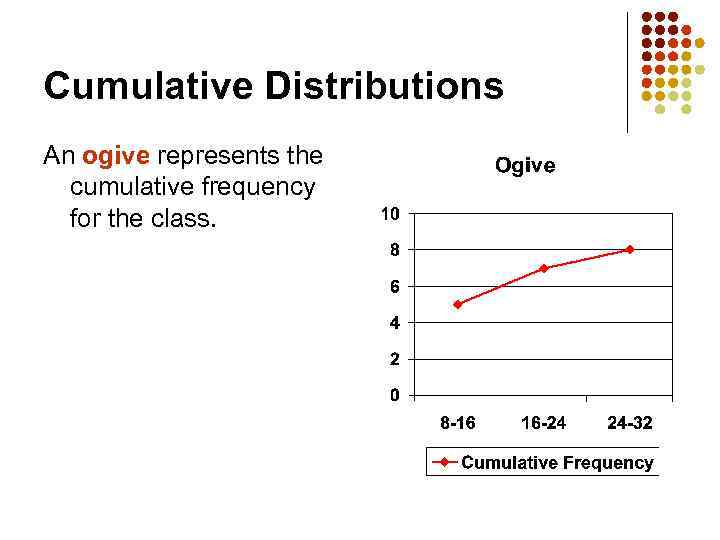
Cumulative Distributions An ogive represents the cumulative frequency for the class.

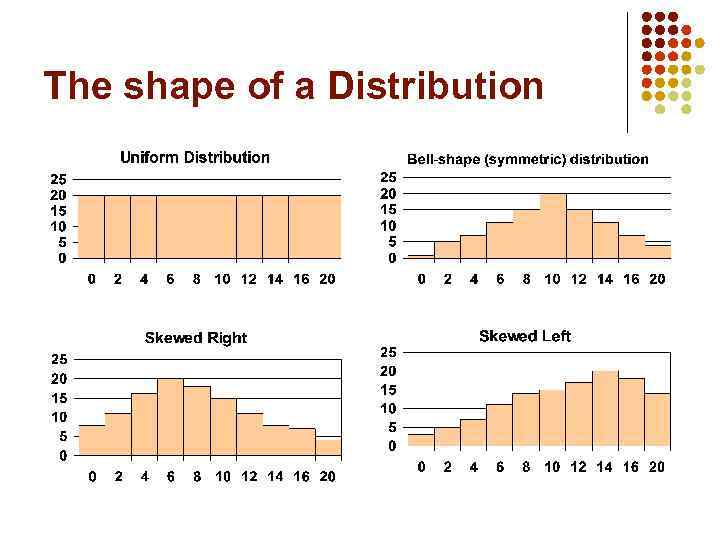
The shape of a Distribution

3. 3 The concept of array data Array is the collection of similar data types. An array is a particular method of storing elements of indexed data. Elements of data are stored sequentially in blocks within the array. Arrays can also be multidimensional - instead of accessing an element of a onedimensional list, elements are accessed by two or more indices, as from a matrix or tensor.

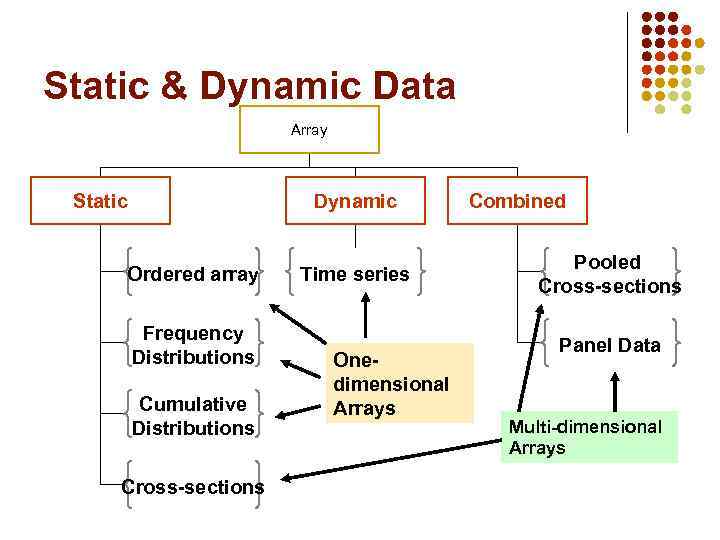
Static & Dynamic Data Array Static Dynamic Ordered array Frequency Distributions Cumulative Distributions Cross-sections Time series Onedimensional Arrays Combined Pooled Cross-sections Panel Data Multi-dimensional Arrays

Assess your understanding l l l State the advantages and disadvantages of histograms versus steam-and-leaf plots. Contrast the difference between histograms and bar charts. The cumulative frequency for the last class must always be N (total number of items). Why?

How to Lie with Charts Misinforming people by the use of statistical material might be called statistical manipulation. How it might be done?

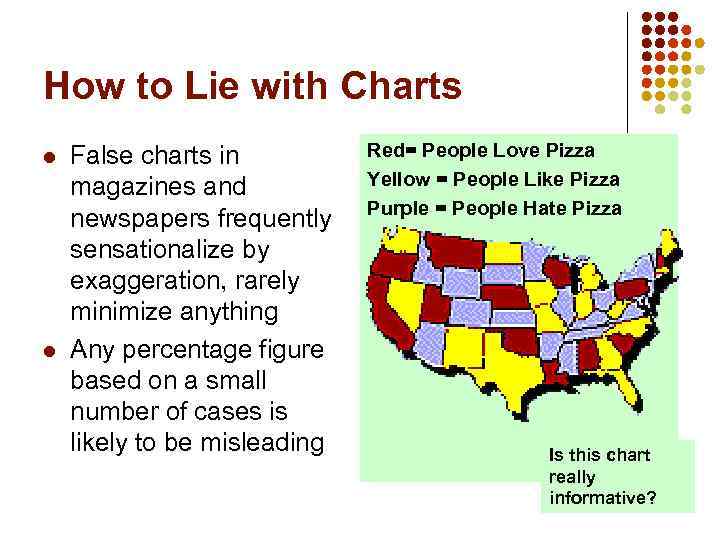
How to Lie with Charts l l False charts in magazines and newspapers frequently sensationalize by exaggeration, rarely minimize anything Any percentage figure based on a small number of cases is likely to be misleading Red= People Love Pizza Yellow = People Like Pizza Purple = People Hate Pizza Is this chart really informative?

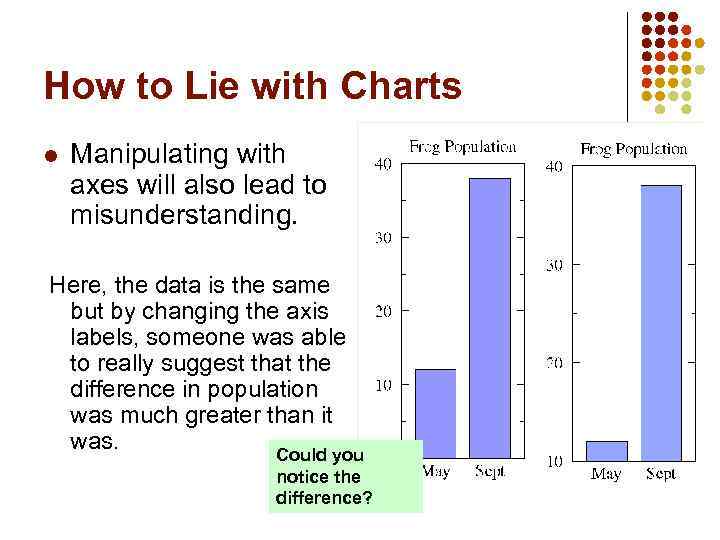
How to Lie with Charts l Manipulating with axes will also lead to misunderstanding. Here, the data is the same but by changing the axis labels, someone was able to really suggest that the difference in population was much greater than it was. Could you notice the difference?

How to Lie with Charts l l l The “shifting base” -- percentages taken off different totals to imply different amounts Percentages added together, or mathematically used in other ways (Ex. “I mix ‘em fifty-fifty: one horse, one rabbit. ”) To give statistical material, the facts and figures in newspapers and books, magazines and advertising, a very sharp second look before accepting any of them

So, while you are reading… l l Do NOT believe everything you are shown just because it is “Science” and “Data”. Look at the sources. If none are given, do NOT trust the information. Look very closely at the data axis and legend. Try to figure out if the source has some ulterior motive to manipulate your opinion. Based on Edward Tufte, Graphics Press, February 1997

The Art of Presenting Data l Graphs should (Tufte, 2001): l l l l Show the data. Induce the reader to think about the data being presented (rather than some other aspect of the graph). Avoid distorting the data. Present many numbers with minimum ink. Make large data sets (assuming you have one) coherent. Encourage the reader to compare different pieces of data. Reveal data.

In the Topic 3 we have § § Organized categorical using a summary table or a contingency table. Organized numerical data using an ordered array, a frequency distribution, a relative frequency distribution, and a cumulative percentage distribution. Visualized categorical data using the bar chart, pie chart, and Pareto chart. Visualized numerical data using the stem-and-leaf display, histogram, and ogive.

In QMBR course we would add Scatterplots l Matrix scatterplots l Residual plots l Time series plots l Correllograms … and other statistical charts l

Course content 2. Sampling methods 1. Data Collection 5. Sampling distributions 4. Variation 3. Data Visualization 7. Inferential 6. Hypothesis statistics- 1 testing basic Final Test

Home Reading LSKB pages 44 -76, Ex. 2. 47 -2. 51 (page 73) Andy Field 1. 5. 5. 2 -1. 5. 6 (pages 16 -17), Tasks 1 -3