Алгоритмы-2.1.pptx
- Количество слайдов: 49
 Introduction to Algorithms 6. 046 J/18. 401 J Analysis of Algorithms • Insertion sort • Asymptotic analysis • Merge sort • Recurrences Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson
Introduction to Algorithms 6. 046 J/18. 401 J Analysis of Algorithms • Insertion sort • Asymptotic analysis • Merge sort • Recurrences Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson
 Задача сортировки Input: последовательность чисел 〈a 1, a 2, …, an〉 Output: перестановка 〈a'1, a'2, …, a'n〉 такая, что a'1 ≤ a'2 ≤… ≤ a'n. Example: Input: 8 2 4 9 3 6 Output: 2 3 4 6 8 9 September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 5
Задача сортировки Input: последовательность чисел 〈a 1, a 2, …, an〉 Output: перестановка 〈a'1, a'2, …, a'n〉 такая, что a'1 ≤ a'2 ≤… ≤ a'n. Example: Input: 8 2 4 9 3 6 Output: 2 3 4 6 8 9 September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 5
![Insertion sort “псевдокод” September 7, 2005 INSERTION-SORT (A, n) ⊳ A[1. . n] for Insertion sort “псевдокод” September 7, 2005 INSERTION-SORT (A, n) ⊳ A[1. . n] for](https://present5.com/presentation/-59266218_234276299/image-3.jpg) Insertion sort “псевдокод” September 7, 2005 INSERTION-SORT (A, n) ⊳ A[1. . n] for j ĸ 2 to n do key ← A[ j] i←j-1 while i > 0 and A[i] > key do A[i+1] ← A[i] i←i-1 A[i+1] = key Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 6
Insertion sort “псевдокод” September 7, 2005 INSERTION-SORT (A, n) ⊳ A[1. . n] for j ĸ 2 to n do key ← A[ j] i←j-1 while i > 0 and A[i] > key do A[i+1] ← A[i] i←i-1 A[i+1] = key Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 6
![Insertion sort INSERTION-SORT (A, n) ⊳ A[1. . n] for j ĸ 2 to Insertion sort INSERTION-SORT (A, n) ⊳ A[1. . n] for j ĸ 2 to](https://present5.com/presentation/-59266218_234276299/image-4.jpg) Insertion sort INSERTION-SORT (A, n) ⊳ A[1. . n] for j ĸ 2 to n do key ← A[ j] i←j-1 while i > 0 and A[i] > key do A[i+1] ← A[i] i←i-1 A[i+1] = key “псевдокод” 1 i j n A: sorted September 7, 2005 key Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 7
Insertion sort INSERTION-SORT (A, n) ⊳ A[1. . n] for j ĸ 2 to n do key ← A[ j] i←j-1 while i > 0 and A[i] > key do A[i+1] ← A[i] i←i-1 A[i+1] = key “псевдокод” 1 i j n A: sorted September 7, 2005 key Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 7
 Пример 8 September 7, 2005 2 4 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 8
Пример 8 September 7, 2005 2 4 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 8
 Пример 8 September 7, 2005 2 4 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 9
Пример 8 September 7, 2005 2 4 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 9
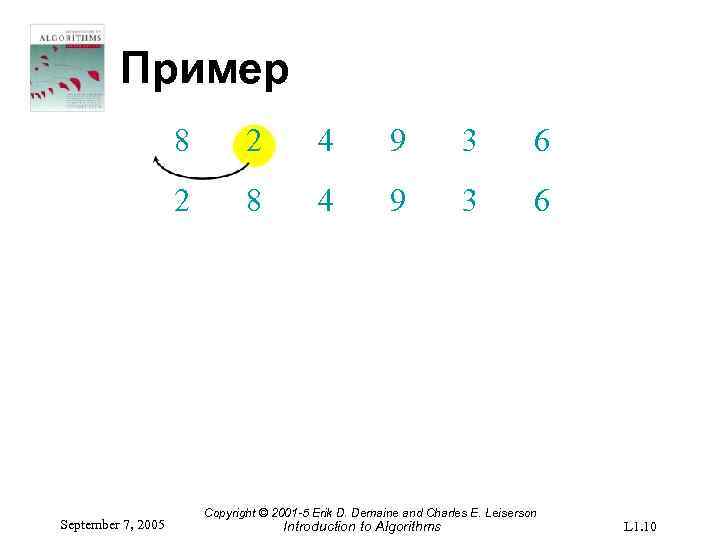 Пример 8 4 9 3 6 2 September 7, 2005 2 8 4 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 10
Пример 8 4 9 3 6 2 September 7, 2005 2 8 4 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 10
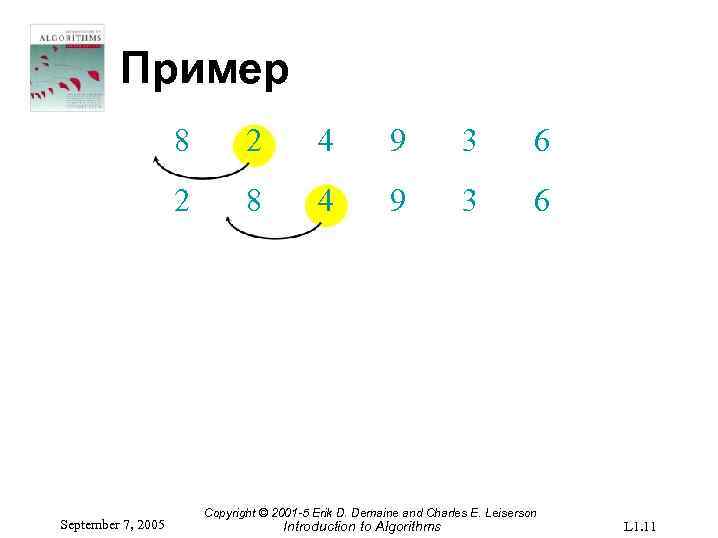 Пример 8 4 9 3 6 2 September 7, 2005 2 8 4 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 11
Пример 8 4 9 3 6 2 September 7, 2005 2 8 4 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 11
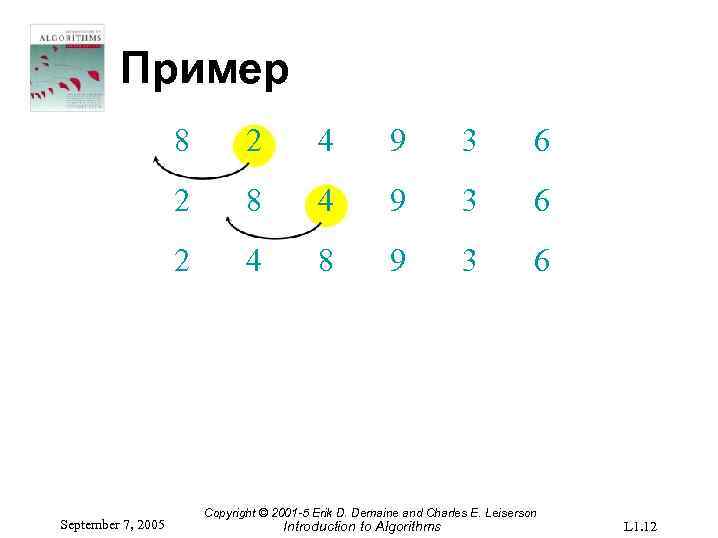 Пример 8 4 9 3 6 2 September 7, 2005 2 4 8 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 12
Пример 8 4 9 3 6 2 September 7, 2005 2 4 8 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 12
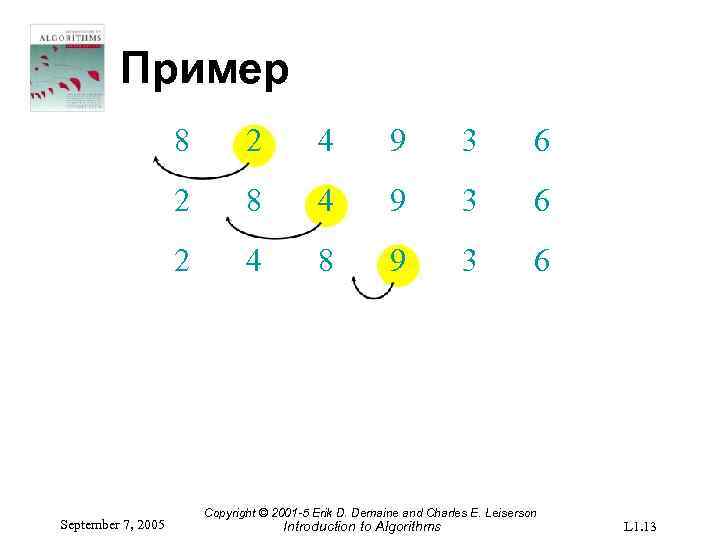 Пример 8 4 9 3 6 2 September 7, 2005 2 4 8 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 13
Пример 8 4 9 3 6 2 September 7, 2005 2 4 8 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 13
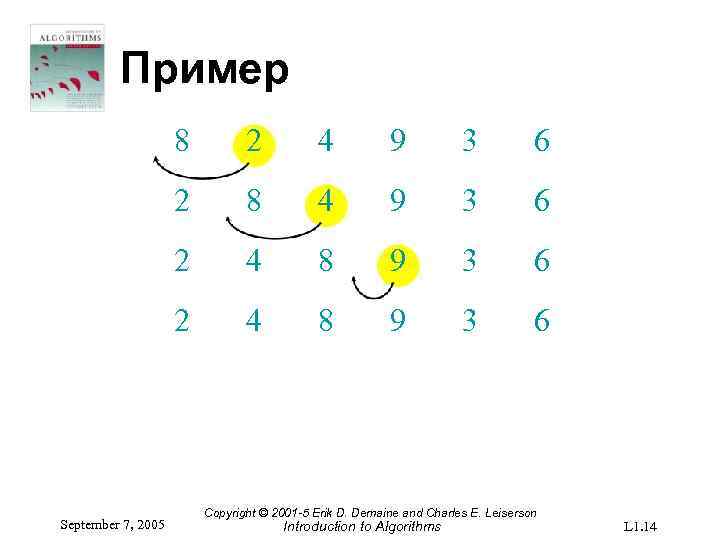 Пример 8 4 9 3 6 2 4 8 9 3 6 2 September 7, 2005 2 4 8 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 14
Пример 8 4 9 3 6 2 4 8 9 3 6 2 September 7, 2005 2 4 8 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 14
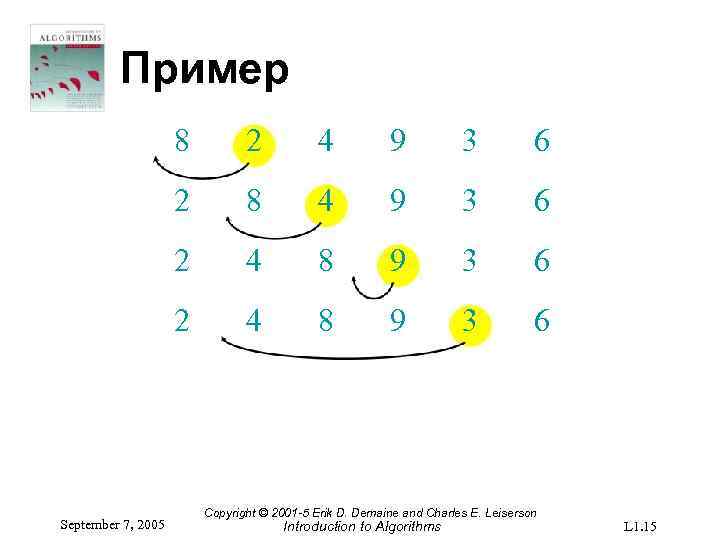 Пример 8 4 9 3 6 2 4 8 9 3 6 2 September 7, 2005 2 4 8 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 15
Пример 8 4 9 3 6 2 4 8 9 3 6 2 September 7, 2005 2 4 8 9 3 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 15
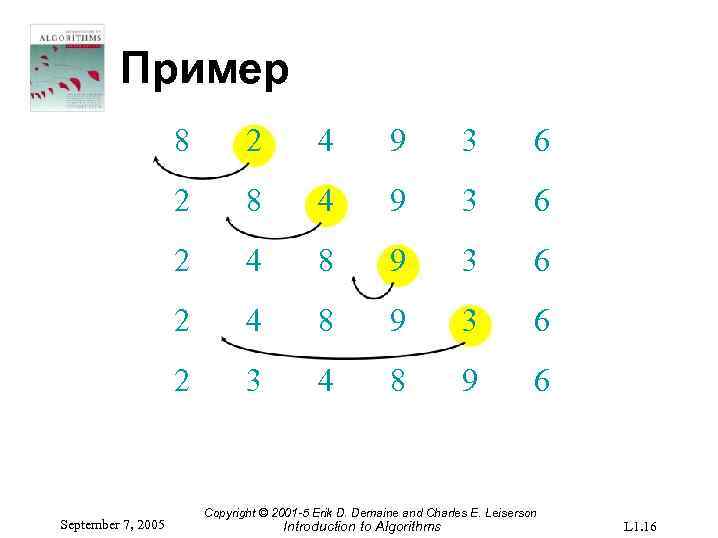 Пример 8 4 9 3 6 2 4 8 9 3 6 2 September 7, 2005 2 3 4 8 9 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 16
Пример 8 4 9 3 6 2 4 8 9 3 6 2 September 7, 2005 2 3 4 8 9 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 16
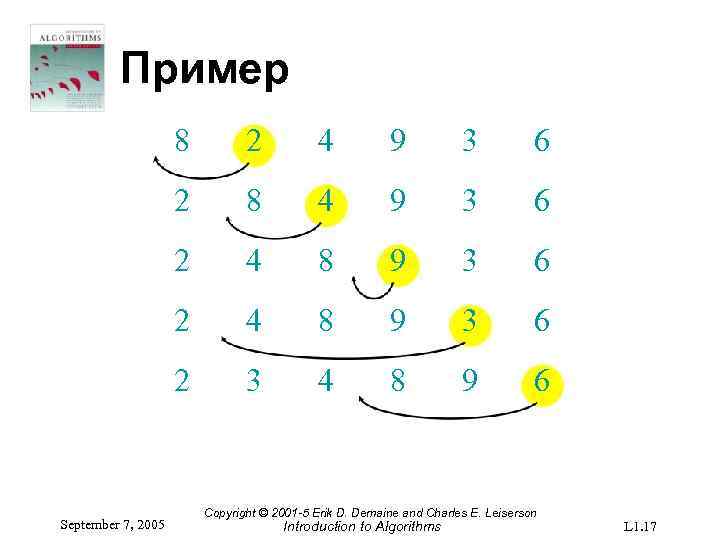 Пример 8 4 9 3 6 2 4 8 9 3 6 2 September 7, 2005 2 3 4 8 9 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 17
Пример 8 4 9 3 6 2 4 8 9 3 6 2 September 7, 2005 2 3 4 8 9 6 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 17
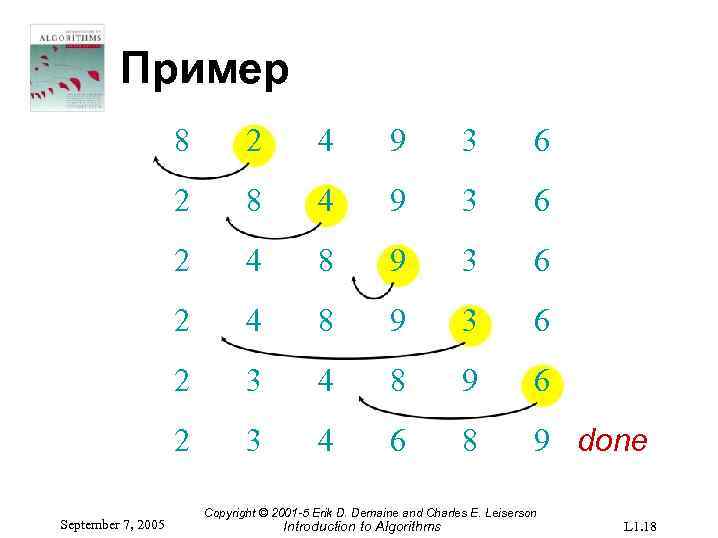 Пример 8 4 9 3 6 2 4 8 9 3 6 2 3 4 8 9 6 2 September 7, 2005 2 3 4 6 8 9 done Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 18
Пример 8 4 9 3 6 2 4 8 9 3 6 2 3 4 8 9 6 2 September 7, 2005 2 3 4 6 8 9 done Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 18
 Время работы • Зависит от начальных данных: сортированный массив быстрее. • Строим зависимость времени работы от размера входного массива, т. к. короткие сортировать быстрее. • Обычно, мы изучаем верхнюю границу времени работы, т. к. нужны гарантии. September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 19
Время работы • Зависит от начальных данных: сортированный массив быстрее. • Строим зависимость времени работы от размера входного массива, т. к. короткие сортировать быстрее. • Обычно, мы изучаем верхнюю границу времени работы, т. к. нужны гарантии. September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 19
 Виды анализа В худшем случае: (обычно) • T(n) = максимальное время работы на любых входных данных размера n. В среднем: (иногда) • T(n) = ожидаемое время работы на входных данных размера n. • Необходимо предположение о статистическом распределении. В лучшем случае: (бессмысленно) • Медленный алгоритм, работающий быстро на некоторых данных. September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 20
Виды анализа В худшем случае: (обычно) • T(n) = максимальное время работы на любых входных данных размера n. В среднем: (иногда) • T(n) = ожидаемое время работы на входных данных размера n. • Необходимо предположение о статистическом распределении. В лучшем случае: (бессмысленно) • Медленный алгоритм, работающий быстро на некоторых данных. September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 20
 Независимость от машины Каково худшее время insertion sort? • Зависит от скорости машины • относительная скорость (на той же), • абсолютная скорость (на разных). ИДЕЯ!: • Игнорируем машинно-зависимые константы. • Смотрим на рост T(n) при n →∞. “Асимптотический анализ” September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 21
Независимость от машины Каково худшее время insertion sort? • Зависит от скорости машины • относительная скорость (на той же), • абсолютная скорость (на разных). ИДЕЯ!: • Игнорируем машинно-зависимые константы. • Смотрим на рост T(n) при n →∞. “Асимптотический анализ” September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 21
 Θ-нотация Математически: Θ(g(n)) = { f (n) : существуют c 1, c 2, и n 0 такие, что 0 ≤ c 1 g(n) ≤ f (n) ≤ c 2 g(n) для всех n ≥ n 0 } Инженерно: • Выбросить низший порядок; и константы. • Пример: 3 n 3 + 90 n 2 - 5 n + 6046 = Θ(n 3) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 22
Θ-нотация Математически: Θ(g(n)) = { f (n) : существуют c 1, c 2, и n 0 такие, что 0 ≤ c 1 g(n) ≤ f (n) ≤ c 2 g(n) для всех n ≥ n 0 } Инженерно: • Выбросить низший порядок; и константы. • Пример: 3 n 3 + 90 n 2 - 5 n + 6046 = Θ(n 3) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 22
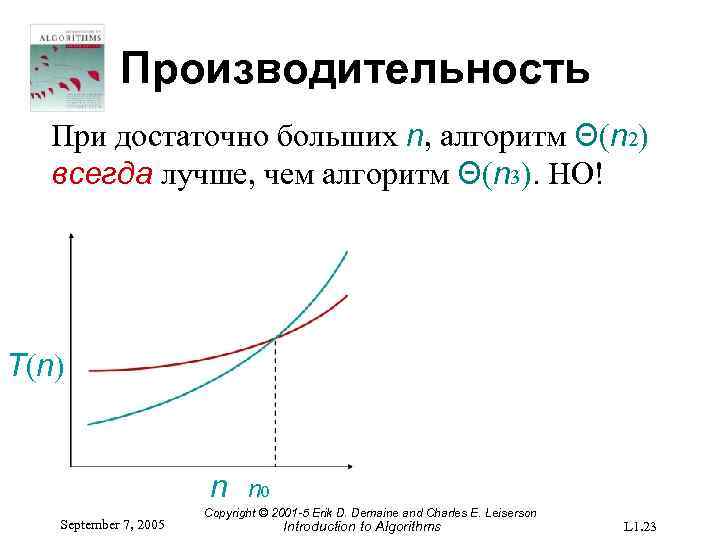 Производительность При достаточно больших n, алгоритм Θ(n 2) всегда лучше, чем алгоритм Θ(n 3). НО! T(n) n September 7, 2005 n 0 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 23
Производительность При достаточно больших n, алгоритм Θ(n 2) всегда лучше, чем алгоритм Θ(n 3). НО! T(n) n September 7, 2005 n 0 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 23
 Insertion sort В худшем случае: Обратная сортировка. T(n)= n ∑ Θ(j) =Θ(n 2 ) j= 2 [арифм. послед. ] В среднем: Все перестановки равновероятны. T(n)= n Θ(j / 2)=Θ(n 2 ) ∑ j= 2 Быстрый ли это алгоритм? • Вполне, для малых n. • Вовсе нет, для больших n. September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 24
Insertion sort В худшем случае: Обратная сортировка. T(n)= n ∑ Θ(j) =Θ(n 2 ) j= 2 [арифм. послед. ] В среднем: Все перестановки равновероятны. T(n)= n Θ(j / 2)=Θ(n 2 ) ∑ j= 2 Быстрый ли это алгоритм? • Вполне, для малых n. • Вовсе нет, для больших n. September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 24
![Merge sort (слиянием) MERGE-SORT A[1. . n] 1. Если n = 1, готово. 2. Merge sort (слиянием) MERGE-SORT A[1. . n] 1. Если n = 1, готово. 2.](https://present5.com/presentation/-59266218_234276299/image-22.jpg) Merge sort (слиянием) MERGE-SORT A[1. . n] 1. Если n = 1, готово. 2. Сортируем A[ 1. . n/2 ] и A[ n/2 +1. . n ]. 3. “Сливаем” 2 сортированных рез-та. Основная процедура: MERGE September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 25
Merge sort (слиянием) MERGE-SORT A[1. . n] 1. Если n = 1, готово. 2. Сортируем A[ 1. . n/2 ] и A[ n/2 +1. . n ]. 3. “Сливаем” 2 сортированных рез-та. Основная процедура: MERGE September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 25
 Merge 20 12 13 11 7 9 2 1 September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 26
Merge 20 12 13 11 7 9 2 1 September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 26
 Merge 20 12 13 11 7 9 2 1 1 September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 27
Merge 20 12 13 11 7 9 2 1 1 September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 27
 Merge 20 12 13 11 7 9 7 2 1 2 9 1 September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 28
Merge 20 12 13 11 7 9 7 2 1 2 9 1 September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 28
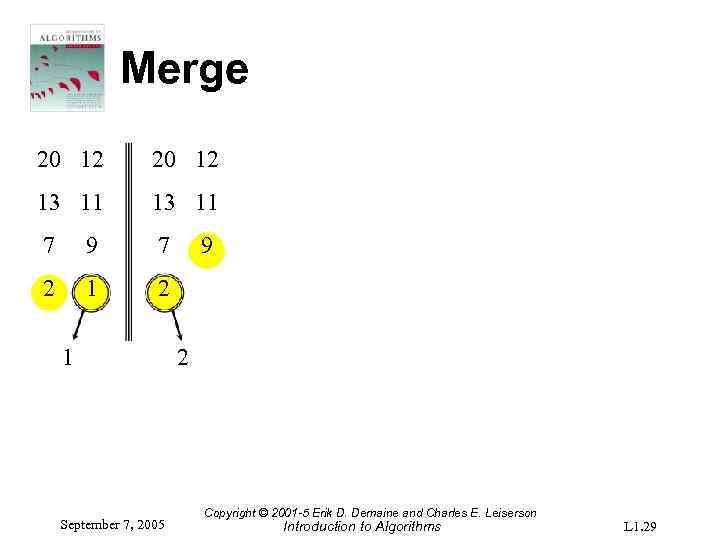 Merge 20 12 13 11 7 9 7 2 1 September 7, 2005 9 2 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 29
Merge 20 12 13 11 7 9 7 2 1 September 7, 2005 9 2 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 29
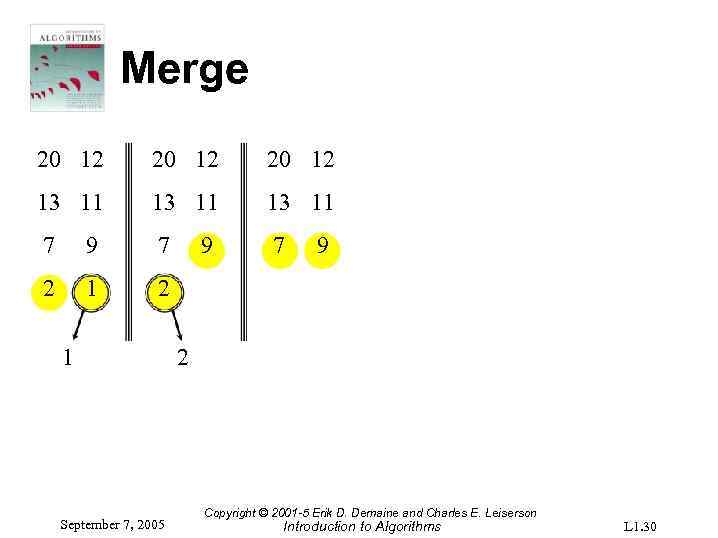 Merge 20 12 13 11 7 9 7 7 2 1 September 7, 2005 9 9 2 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 30
Merge 20 12 13 11 7 9 7 7 2 1 September 7, 2005 9 9 2 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 30
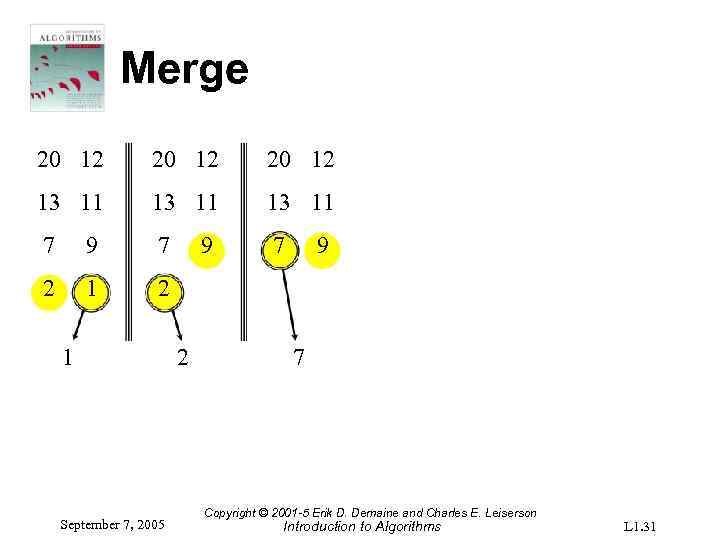 Merge 20 12 13 11 7 9 7 7 2 1 September 7, 2005 9 2 9 7 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 31
Merge 20 12 13 11 7 9 7 7 2 1 September 7, 2005 9 2 9 7 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 31
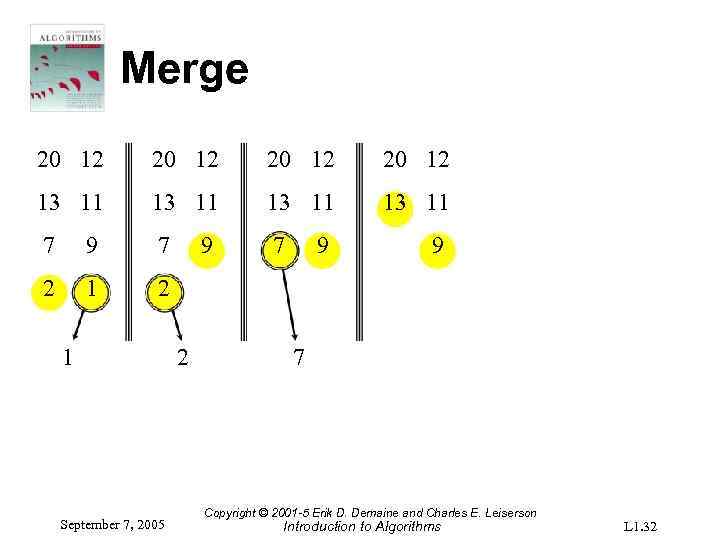 Merge 20 12 13 11 7 9 7 7 2 1 September 7, 2005 9 2 9 9 7 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 32
Merge 20 12 13 11 7 9 7 7 2 1 September 7, 2005 9 2 9 9 7 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 32
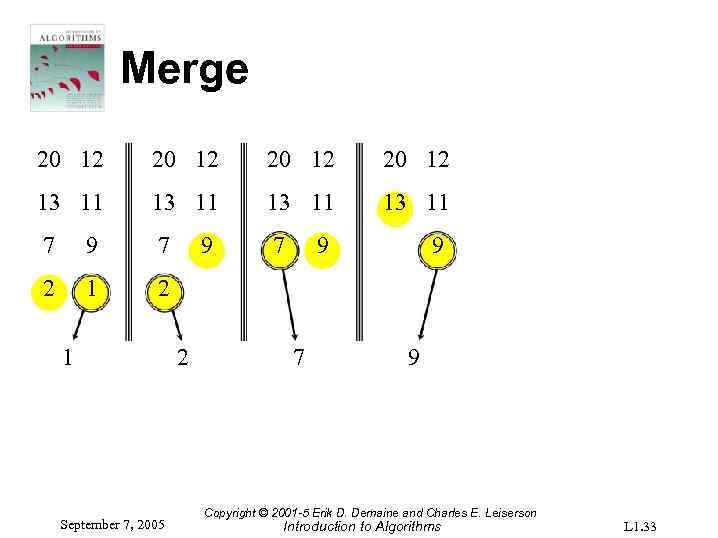 Merge 20 12 13 11 7 9 7 7 2 1 September 7, 2005 9 2 9 7 9 9 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 33
Merge 20 12 13 11 7 9 7 7 2 1 September 7, 2005 9 2 9 7 9 9 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 33
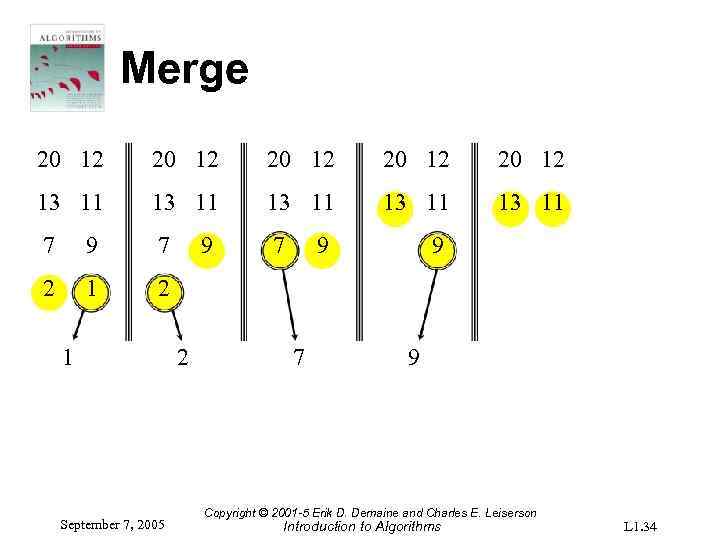 Merge 20 12 20 12 13 11 13 11 7 9 7 7 2 1 September 7, 2005 9 2 9 7 9 9 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 34
Merge 20 12 20 12 13 11 13 11 7 9 7 7 2 1 September 7, 2005 9 2 9 7 9 9 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 34
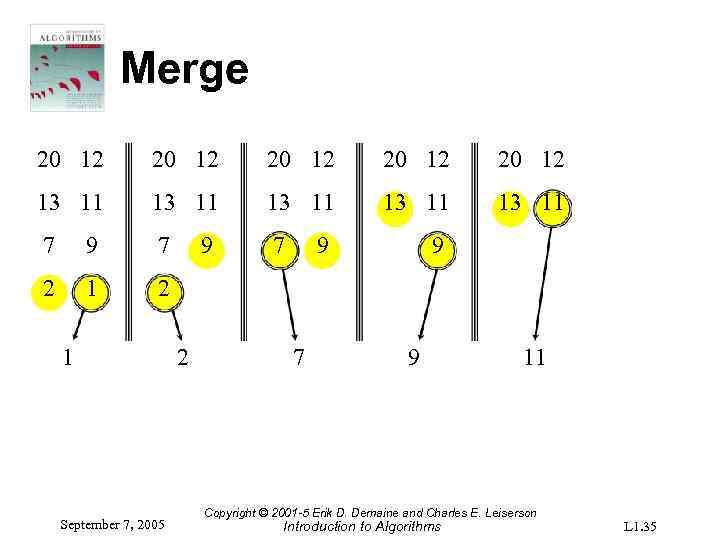 Merge 20 12 20 12 13 11 13 11 7 9 7 7 2 1 September 7, 2005 9 2 9 7 9 9 11 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 35
Merge 20 12 20 12 13 11 13 11 7 9 7 7 2 1 September 7, 2005 9 2 9 7 9 9 11 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 35
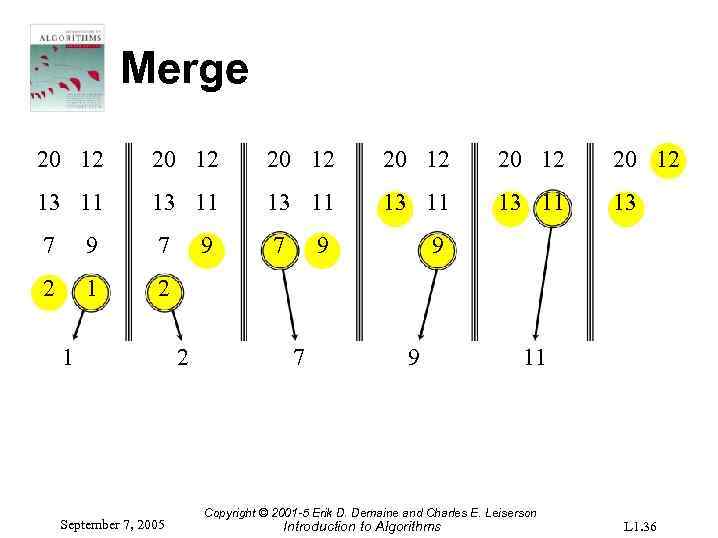 Merge 20 12 20 12 13 11 13 11 13 7 9 7 7 2 1 September 7, 2005 9 2 9 7 9 9 11 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 36
Merge 20 12 20 12 13 11 13 11 13 7 9 7 7 2 1 September 7, 2005 9 2 9 7 9 9 11 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 36
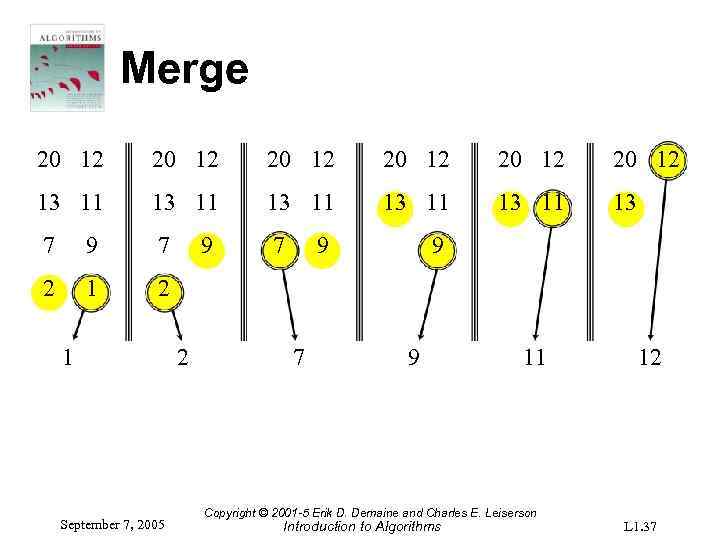 Merge 20 12 20 12 13 11 13 11 13 7 9 7 7 2 1 September 7, 2005 9 2 9 7 9 9 11 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms 12 L 1. 37
Merge 20 12 20 12 13 11 13 11 13 7 9 7 7 2 1 September 7, 2005 9 2 9 7 9 9 11 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms 12 L 1. 37
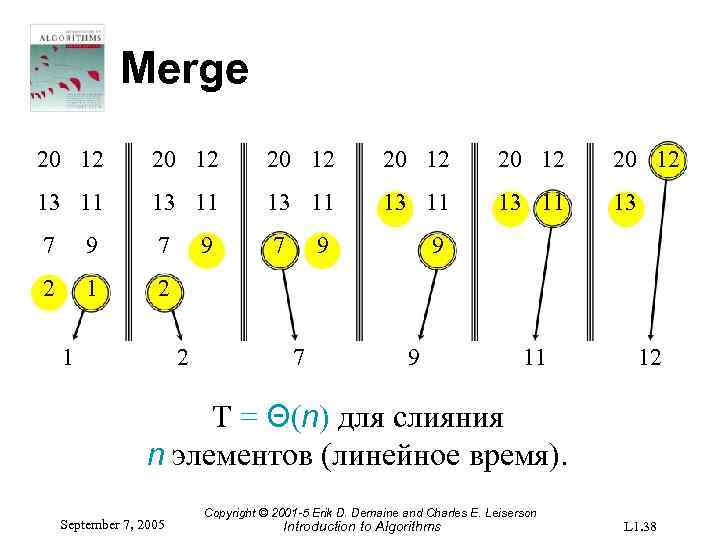 Merge 20 12 20 12 13 11 13 11 13 7 9 7 7 2 1 9 2 9 7 9 9 11 12 T = Θ(n) для слияния n элементов (линейное время). September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 38
Merge 20 12 20 12 13 11 13 11 13 7 9 7 7 2 1 9 2 9 7 9 9 11 12 T = Θ(n) для слияния n элементов (линейное время). September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 38
![Анализ T(n) Θ(1) 2 T(n/2) Несовсем Θ(n) MERGE-SORT A[1. . n] 1. Если n Анализ T(n) Θ(1) 2 T(n/2) Несовсем Θ(n) MERGE-SORT A[1. . n] 1. Если n](https://present5.com/presentation/-59266218_234276299/image-36.jpg) Анализ T(n) Θ(1) 2 T(n/2) Несовсем Θ(n) MERGE-SORT A[1. . n] 1. Если n = 1, готово. 2. Сортируем A[ 1. . n/2 ] и A[ n/2 +1. . n ]. 3. “Merge” результатов Небрежность: T( n/2 ) + T( n/2 ) , но асимптотически не важно. September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 39
Анализ T(n) Θ(1) 2 T(n/2) Несовсем Θ(n) MERGE-SORT A[1. . n] 1. Если n = 1, готово. 2. Сортируем A[ 1. . n/2 ] и A[ n/2 +1. . n ]. 3. “Merge” результатов Небрежность: T( n/2 ) + T( n/2 ) , но асимптотически не важно. September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 39
 Рекуррентное соотношение T(n) = September 7, 2005 Θ(1) if n = 1; 2 T(n/2) + Θ(n) if n > 1. Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 40
Рекуррентное соотношение T(n) = September 7, 2005 Θ(1) if n = 1; 2 T(n/2) + Θ(n) if n > 1. Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 40
 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 41
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 41
 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. T(n) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 42
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. T(n) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 42
 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn T(n/2) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 43
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn T(n/2) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 43
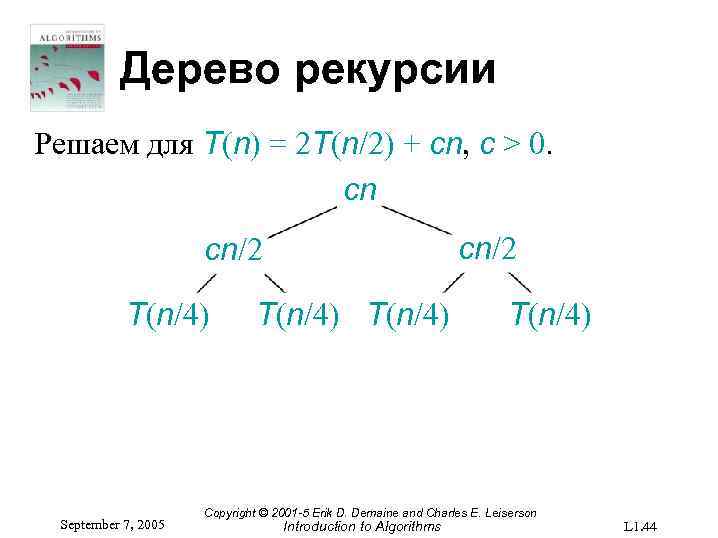 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 T(n/4) September 7, 2005 T(n/4) Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 44
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 T(n/4) September 7, 2005 T(n/4) Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 44
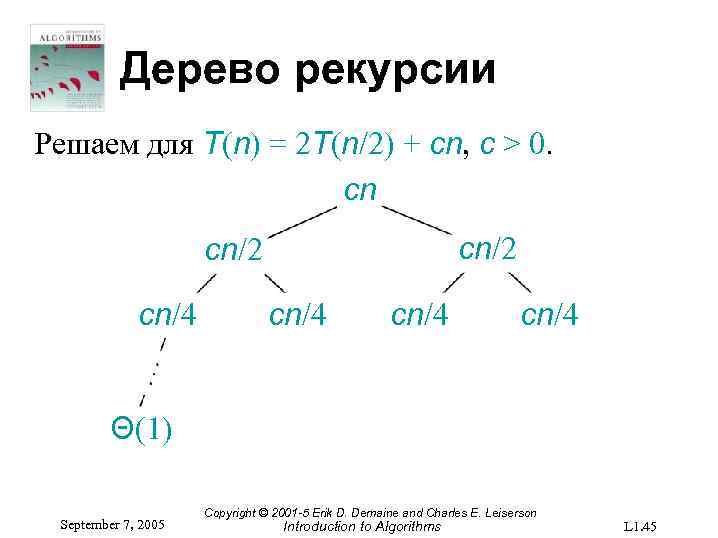 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 cn/4 Θ(1) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 45
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 cn/4 Θ(1) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 45
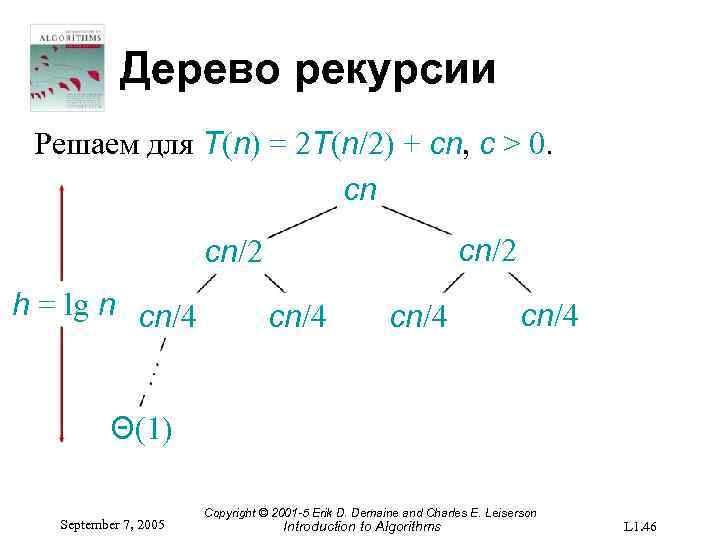 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 Θ(1) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 46
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 Θ(1) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 46
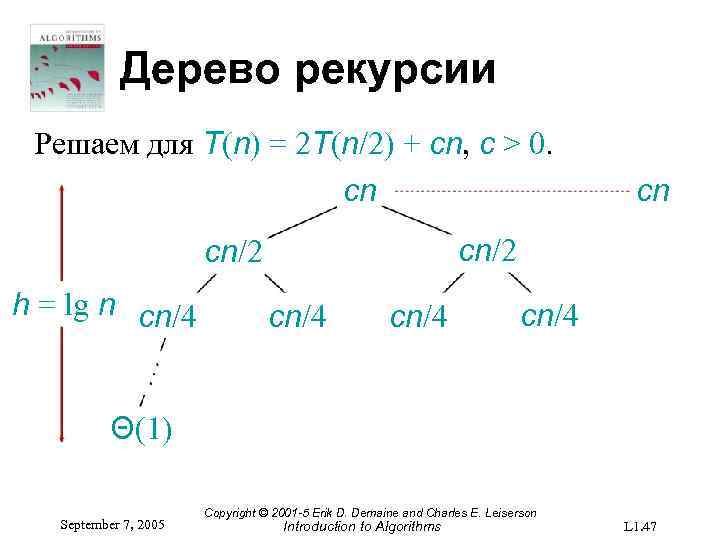 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 cn/4 Θ(1) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 47
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 cn/4 Θ(1) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 47
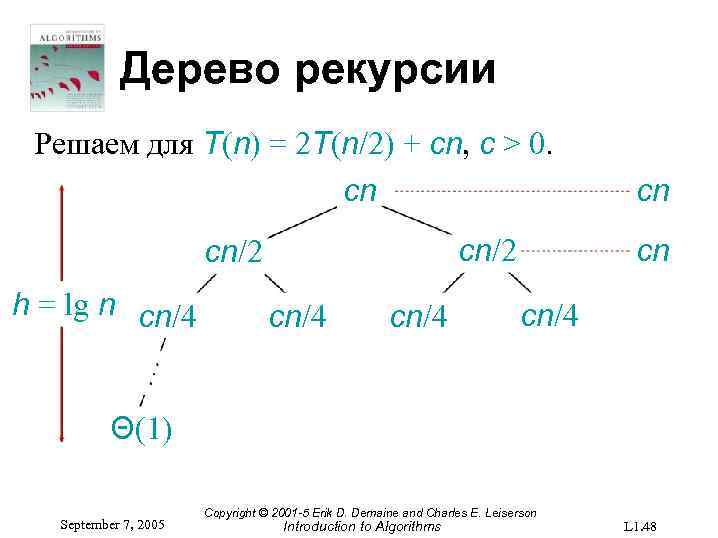 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 cn cn cn/4 Θ(1) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 48
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 cn cn cn/4 Θ(1) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 48
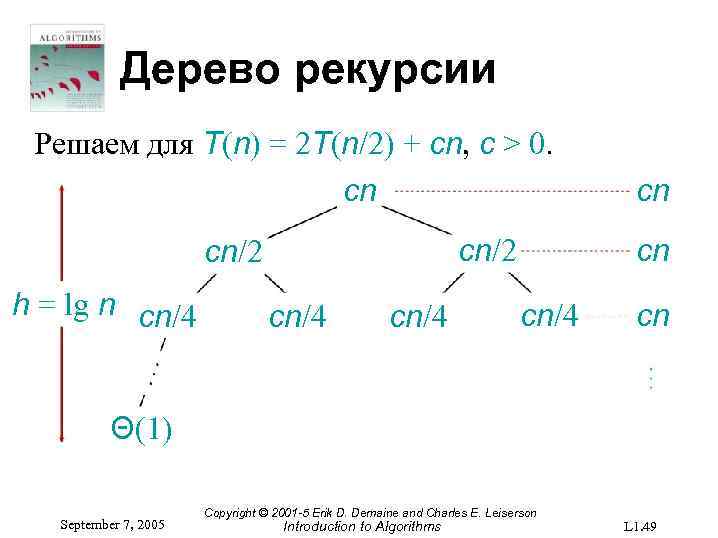 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 cn cn cn/4 cn Θ(1) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 49
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 cn cn cn/4 cn Θ(1) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 49
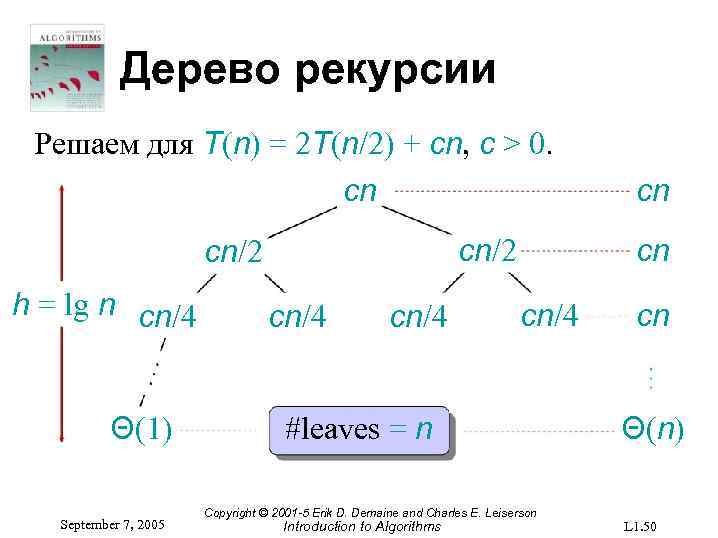 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 Θ(1) September 7, 2005 cn/4 cn cn/4 #leaves = n Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms cn cn Θ(n) L 1. 50
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 Θ(1) September 7, 2005 cn/4 cn cn/4 #leaves = n Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms cn cn Θ(n) L 1. 50
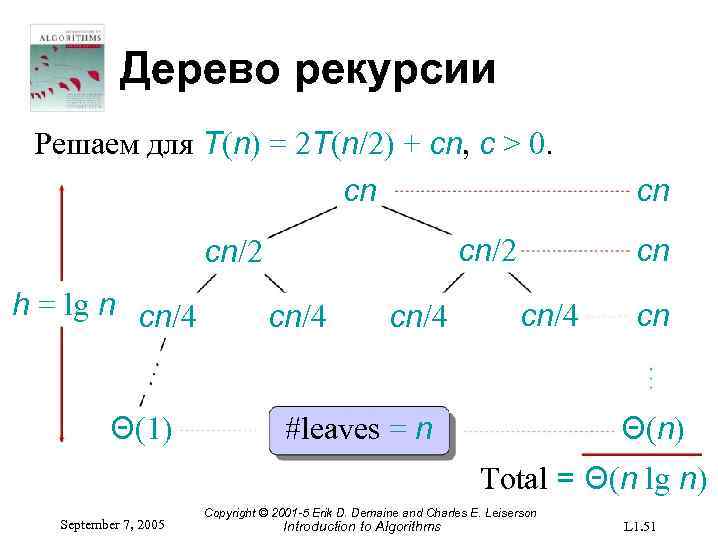 Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 Θ(1) cn/4 cn cn cn/4 cn Θ(n) #leaves = n Total = Θ(n lg n) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 51
Дерево рекурсии Решаем для T(n) = 2 T(n/2) + cn, c > 0. cn cn/2 h = lg n cn/4 Θ(1) cn/4 cn cn cn/4 cn Θ(n) #leaves = n Total = Θ(n lg n) September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 51
 Выводы • Θ(n lg n) растет медленнее, чем Θ(n 2). • Следовательно, merge sort асимптотически лучше, чем insertion sort. • Практически, лучше при n > 30 (зависит!). • Проверяйте! September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 52
Выводы • Θ(n lg n) растет медленнее, чем Θ(n 2). • Следовательно, merge sort асимптотически лучше, чем insertion sort. • Практически, лучше при n > 30 (зависит!). • Проверяйте! September 7, 2005 Copyright © 2001 -5 Erik D. Demaine and Charles E. Leiserson Introduction to Algorithms L 1. 52


