Introduction Prof Sivarama Dandamudi School of Computer Science

Introduction Prof. Sivarama Dandamudi School of Computer Science Carleton University

Why Parallel Systems? v Increased v Main execution speed motivation for many applications v Improved v Multiple fault-tolerance and reliability resources provide improved FT and reliability v Expandability v Problem scaleup v New applications Carleton University © S. Dandamudi 2

Three Metrics v Speedup v Problem size is fixed v Adding more processors should reduce time v Speedup on n processors S(n) is Time on 1 processor system Time on n-processor system v Linear speedup if S(n) = a n for 0 < a 1 v Perfectly Carleton University linear speedup if a = 1 © S. Dandamudi 3

Three Metrics (cont’d) v Scaleup v Problem size increases with system size v Scaleup on n processors C(n) is Small problem time on 1 -processor system Larger problem time on n-processor system v Linear scaleup = b for 0 < b 1 v Perfectly linear scaleup if b = 1 v C(n) Carleton University © S. Dandamudi 4

Three Metrics (cont’d) v Efficiency v Defined as the average utilization of n processors v Efficiency of n processors E(n) is related to speedup S(n) E(n) = n v If efficiency remains 1 as we add more processors v We can get perfectly linear speedups Carleton University © S. Dandamudi 5

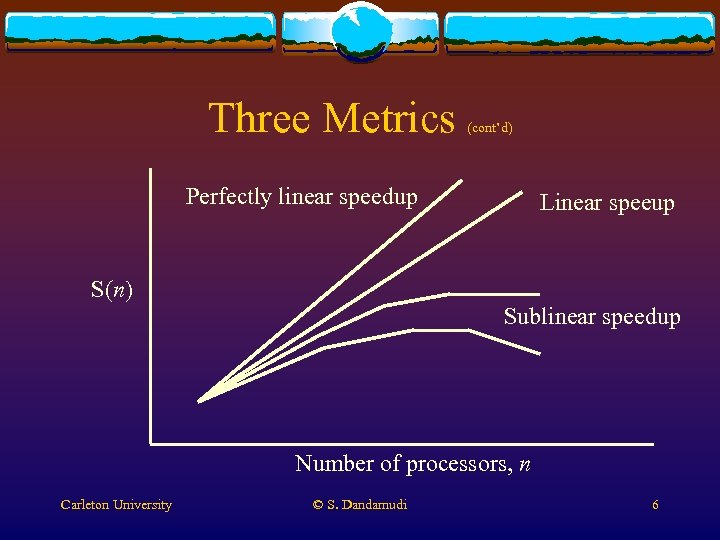Three Metrics (cont’d) Perfectly linear speedup Linear speeup S(n) Sublinear speedup Number of processors, n Carleton University © S. Dandamudi 6

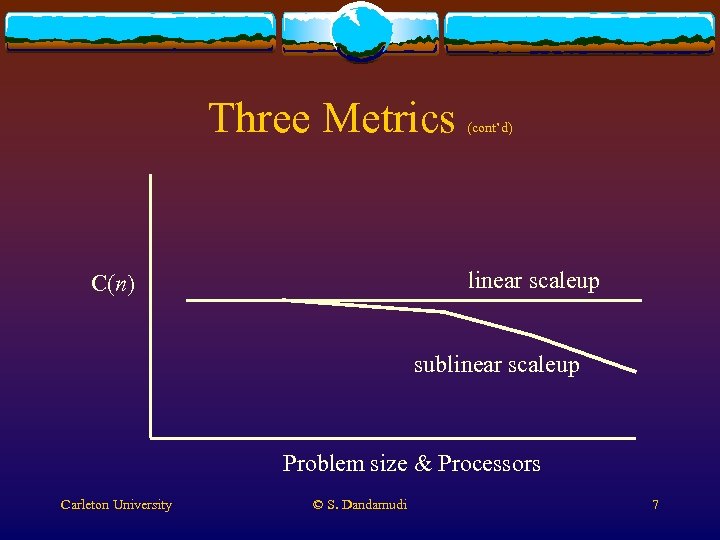Three Metrics (cont’d) linear scaleup C(n) sublinear scaleup Problem size & Processors Carleton University © S. Dandamudi 7

Example 1: QCD Problem v Quantum v Predicts chromodynamics (QCD) the mass of proton… v Requires v On approximately 3*1017 operations Cray-1 like system with 100 Mflops v Takes about 100 years v Still takes 10 years on a Pentium that is 10 times faster v IBM built a special system (GF-11) v Provides about 11 Gflops (peak—sustained about 7 Gflops) v QCD problem takes only a year or so! Carleton University © S. Dandamudi 8

Example 2: Factoring of RSA-129 v Factoring of a 129 -digit number (RSA-129) into two primes v RSA stands for v Ronald Rivest of MIT v Adi Shamir of the Weizmann Institute of Science, Israel, v Leonard Adleman of USC v v In 1977 they announced a new cryptographic scheme Known as the RSA public-key system ``Cryptography is a never-ending struggle between code makers and code breakers. '' Adi Shamir Carleton University © S. Dandamudi 9

Example 2: Factoring of RSA-129 v (cont’d) RSA-129 = 1143816257578888676692357799761466120102182 9672124236256256184293570693524573389783059 7123563958705058989075147599290026879543541 v The two primes are 34905295108476509491478496199038 98133417764638493387843990820577 x 32769132993266709549961988190834 461413177642967992942539798288533 v Solved in April 1994 (challenge posted in September 1993) v Needs over 1017 operations v 0. 1% of Internet was used v 100% of Internet would have solved the problem in 3 hours Carleton University © S. Dandamudi 10

Example 3: Toy Story v The production of the Toy Story v 140, 000 frames to render for the movie v Requires about 1017 operations v Same v Used as the RSA-129 problem dozens of SUN workstations v Each SUN about 10 MIPS Carleton University © S. Dandamudi 11

Example 4: N-Body Problem v Simulates the motion of N particles under the influence of mutual force fields based on an inverse square law v Material science, astrophysics, etc. all require a variant of the N-body problem v To double the physical accuracy seems require four times the computation v Implications Carleton University for scaleup © S. Dandamudi 12

Peak Speeds Machine Cray-1 Cray C 90 Cray T 90 Pentium 4 (3070 MHz) Athelon XP 1900+ Itanium Sony Playstation 2 Carleton University © S. Dandamudi Mflops 160 1000 2200 3070 3200 6400 6300 13

Applications of Parallel Systems v. A wide variety v Scientific applications v Engineering applications v Database applications v Artificial intelligence v Real-time applications v Speech recognition v Image processing Carleton University © S. Dandamudi 14

Applications of Parallel Systems v (cont’d) Scientific applications v Weather forecasting v QCD v Blood flow in the heart v Molecular dynamics v Evolution of galaxies v Most problems rely on basic operations of linear algebra v Solving linear equations v Finding Eigen values Carleton University © S. Dandamudi 15

Applications of Parallel Systems v Weather (cont’d) forecasting v Needs to solve general circulation model equations v Computation is carried out in v 3 -dimensional grid that partitions the atmosphere v A fourth dimension is added: time v Number v With of time steps in the simulation a grid with 270 miles, 24 -hour forecast needs v 100 billion data operations Carleton University © S. Dandamudi 16

Applications of Parallel Systems v Weather v On forecasting (cont’d) a 100 -Mflops processor v. A 24 -hour forecast takes about 1. 5 hours v Want more accuracy? v Use half the grid size, halve the time step v Involves 24 v On v To (cont’d) = 16 times more processing a 100 Mflops processor, 24 -hour forecast takes 24 hours! complete in 1. 5 hours v We need 16 times faster system Carleton University © S. Dandamudi 17

Applications of Parallel Systems v Engineering v Circuit (cont’d) applications (VLSI design) simulation v Detailed simulation of electrical characteristics v Placement v Automatic positioning of blocks on a chip v Wiring v Automated v Done Carleton University placement of wires to form desired connection after the previous placement step © S. Dandamudi 18

Applications of Parallel Systems v Artificial (cont’d) Intelligence v Production v Working systems have three components memory v Stores global database v About various facts or data about the modeling world v Production memory v Stores knowledge base v A set of production rules v Control system v Chooses Carleton University which rule should be applied © S. Dandamudi 19

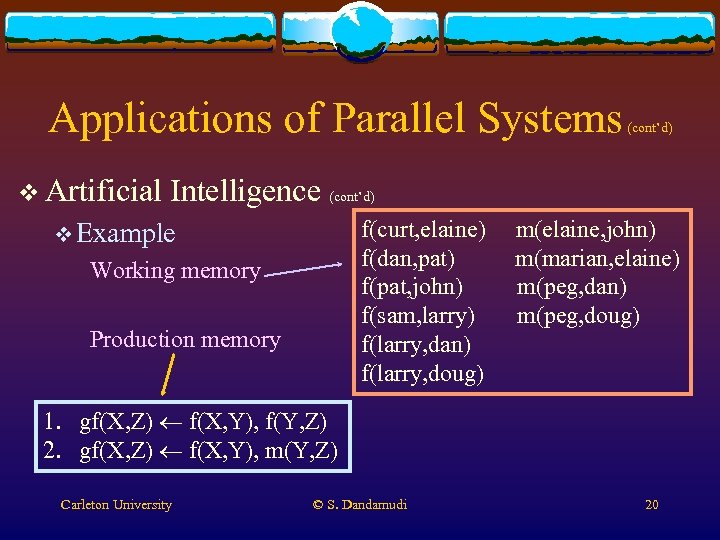Applications of Parallel Systems v Artificial (cont’d) Intelligence (cont’d) f(curt, elaine) f(dan, pat) f(pat, john) f(sam, larry) f(larry, dan) f(larry, doug) v Example Working memory Production memory m(elaine, john) m(marian, elaine) m(peg, dan) m(peg, doug) 1. gf(X, Z) f(X, Y), f(Y, Z) 2. gf(X, Z) f(X, Y), m(Y, Z) Carleton University © S. Dandamudi 20

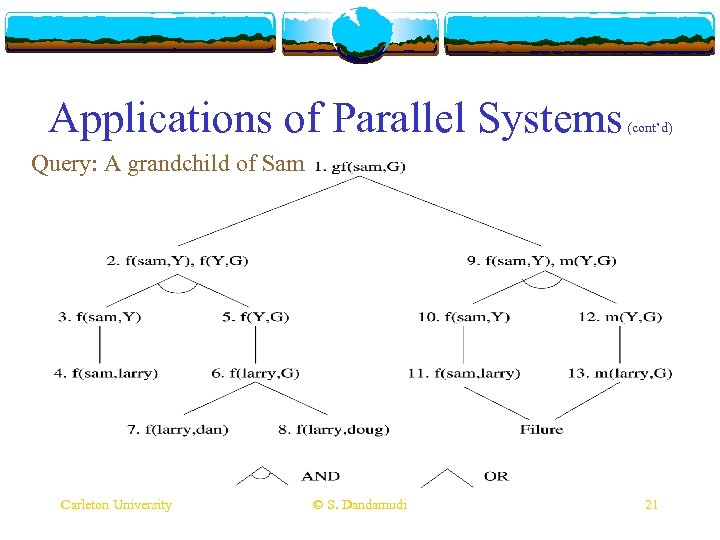Applications of Parallel Systems (cont’d) Query: A grandchild of Sam Carleton University © S. Dandamudi 21

Applications of Parallel Systems v Artificial (cont’d) Intelligence (cont’d) v Sources of parallelism v Assign each production rule its own processor v Each can search the working memory for pertinent facts in parallel with all the other processors v AND-parallelism v Synchronization is involved v OR-parallelism v Abort Carleton University other searches if one is successful © S. Dandamudi 22

Applications of Parallel Systems v Database (cont’d) applications v Relational model v Uses tables to store data v Three basic operations v Selection v Selects tuples that satisfy a specified condition v Projection v Selects certain specified columns v Join v Combines Carleton University data from two tables © S. Dandamudi 23

Applications of Parallel Systems v Database (cont’d) applications (cont’d) v Sources of parallelism v Within a single query (intra-query parallelism) v Horizontally partition relations into P fragments v Each processor independently works on each segment v Among queries (inter-query parallelism) v Execute several queries concurrently v Exploit common subqueries v Improves query throughput Carleton University © S. Dandamudi 24

Flynn’s Taxonomy v Based on number of instruction and data streams v Single-Instruction, v Uniprocessor systems v Single-Instruction, v Array Single-Data stream (SISD) Multiple-Data stream (SIMD) processors v Multiple-Instruction, v Not Single-Data stream (MISD) really useful v Multiple-Instruction, Carleton University Multiple-Data stream (MIMD) © S. Dandamudi 25

Flynn’s Taxonomy v MIMD systems v Most popular category v Shared-memory v Also systems called multiprocessors v Sometimes called tightly-coupled systems v Distributed-memory v Also systems called multicomputers v Sometimes Carleton University called loosely-coupled systems © S. Dandamudi 26

Another Taxonomy v Parallel systems v Synchronous v Vector v Array v SIMD v Systolic v Asynchronous v MIMD v Dataflow Carleton University © S. Dandamudi 27

SIMD Architecture Multiple actors, single script v SIMD comes in two flavours v v Array processors v Large v Operate on small amount of data (bits, bytes, words, …) v Illiac v number of simple processors IV, Burroughs BSP, Connection Machine CM-1 Vector processors v Small v number (< 32) of powerful, pipelined processors Operate on large amount of data (vectors) v Cray 1 (1976), Cray X/MP (mid 1980 s, 4 processors), Cray Y/MP (1988, 8 processors), Cray 3 (1989, 16 processors) Carleton University © S. Dandamudi 28

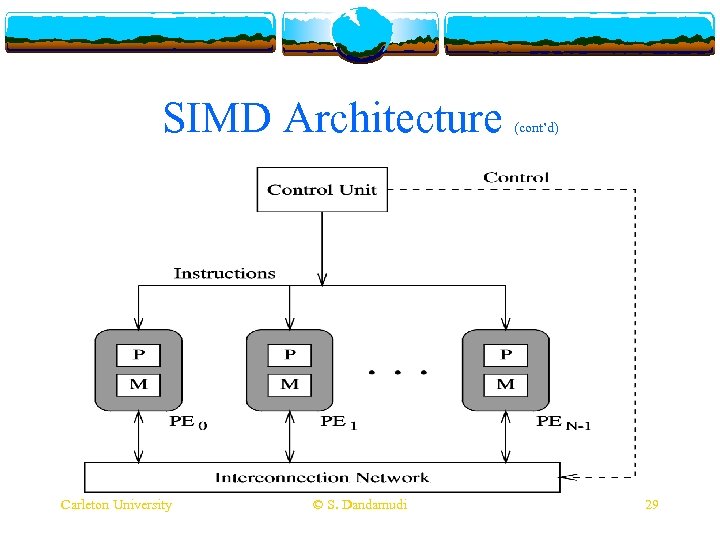SIMD Architecture Carleton University © S. Dandamudi (cont’d) 29

Shared-Memory MIMD v Two major classes v UMA v Uniform memory access v Typically bus-based v Limited to small size systems v NUMA v Non-uniform memory access v Use a MIN-based interconnection v Expandable to medium system sizes Carleton University © S. Dandamudi 30

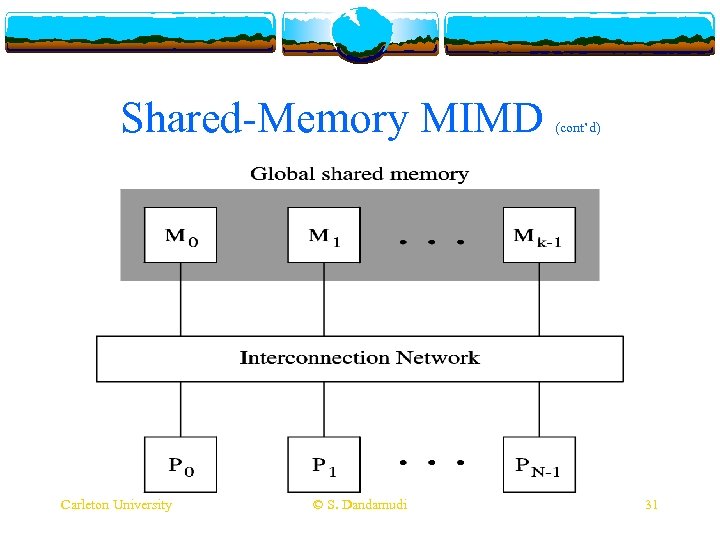Shared-Memory MIMD Carleton University © S. Dandamudi (cont’d) 31

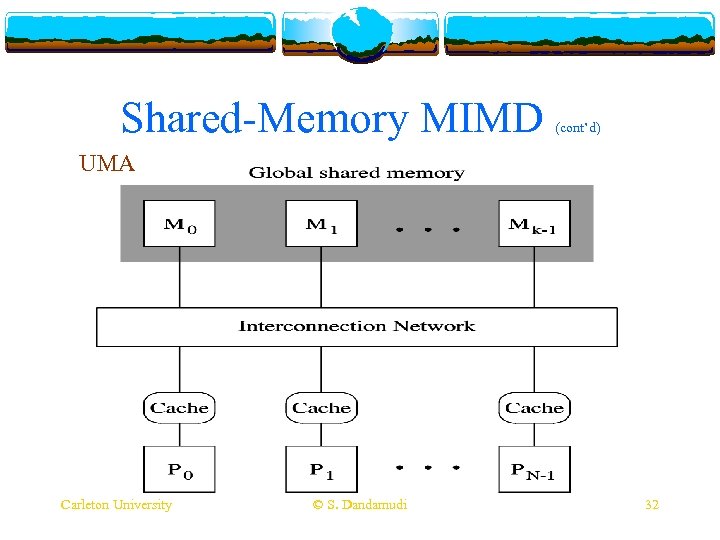Shared-Memory MIMD (cont’d) UMA Carleton University © S. Dandamudi 32

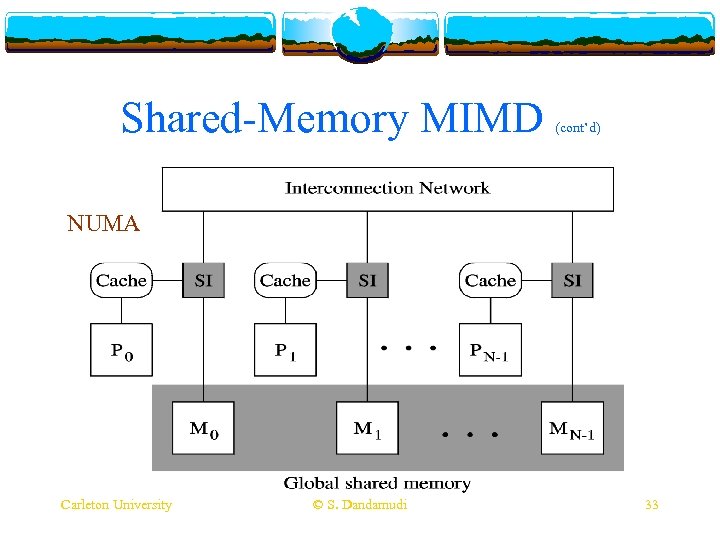Shared-Memory MIMD (cont’d) NUMA Carleton University © S. Dandamudi 33

Shared-Memory MIMD (cont’d) v Examples v SGI Power Onyx v Cray C 90 v IBM SP 2 Node v Symmetric Multi-Processing (SMP) v Special case of shared-memory MIMD v Identical processors share the memory Carleton University © S. Dandamudi 34

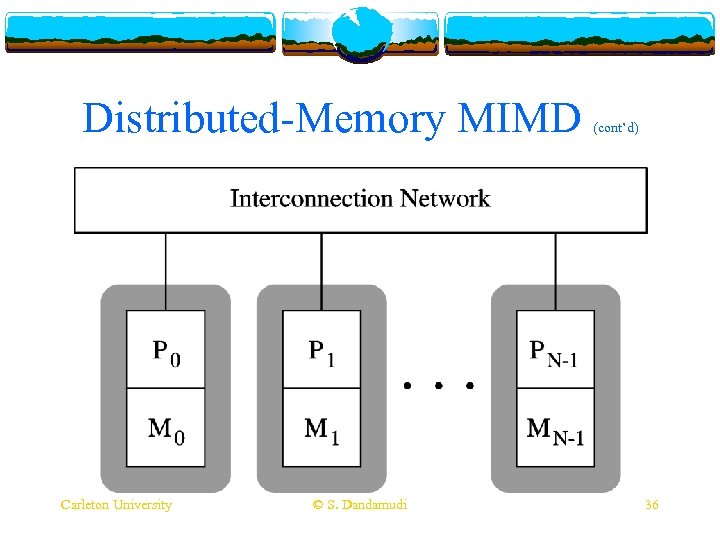
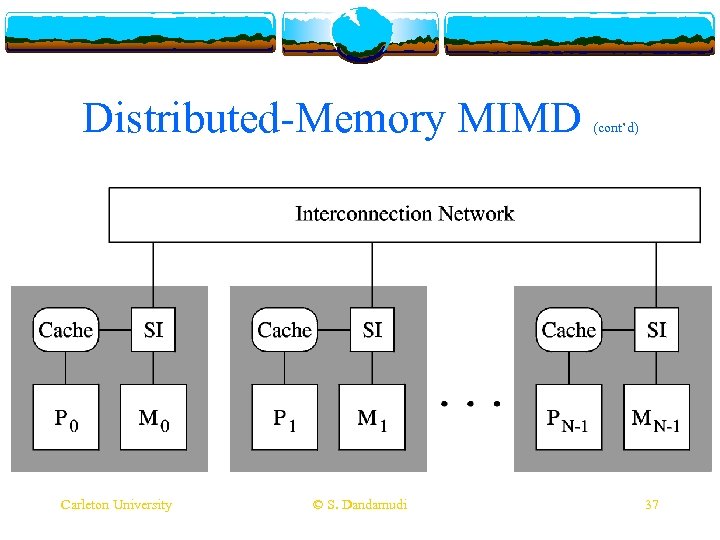
Distributed-Memory MIMD v Typically use message-passing v Interconnection v Point-to-point v System v Intel network is static network scales up to thousands of nodes TFLOPS system consists of 9000+ processors v Similar to cluster systems v Popular architecture for large parallel systems Carleton University © S. Dandamudi 35

Distributed-Memory MIMD Carleton University © S. Dandamudi (cont’d) 36

Distributed-Memory MIMD Carleton University © S. Dandamudi (cont’d) 37

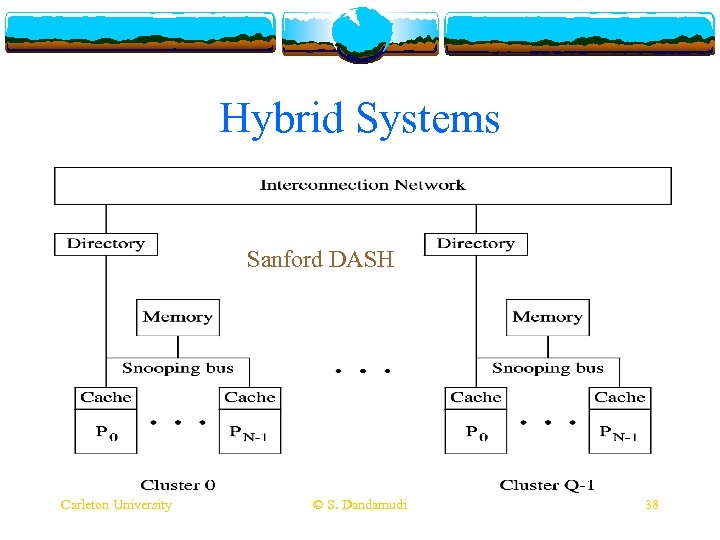Hybrid Systems Sanford DASH Carleton University © S. Dandamudi 38

Distributed Shared Memory v Advantages v Relatively v Global v Fast of shared-memory MIMD easy to program shared memory view communication & data sharing v Via the shared memory v No physical copying of data v Load distribution is not a problem Carleton University © S. Dandamudi 39

Distributed Shared Memory v Disadvantages v Limited (cont’d) of shared-memory MIMD scalability v UMA can scale to 10 s of processors v NUMA can scale to 100 s of processors v Expensive Carleton University network © S. Dandamudi 40

Distributed Shared Memory v Advantages v Good (cont’d) of distributed-memory MIMD scalability v Can scale to 1000 s of processors v Inexpensive v Uses static interconnection v Cheaper v Can network (relatively speaking) to build use off-the-shelf components Carleton University © S. Dandamudi 41

Distributed Shared Memory v Disadvantages v Not (cont’d) of distributed-memory MIMD easy to program v Deal with explicit message-passing v Slow network v Expensive data copying v Done v Load by message passing distribution is an issue Carleton University © S. Dandamudi 42

Distributed Shared Memory (cont’d) v DSM is proposed to take advantage of these two types of systems v Uses distributed-memory MIMD hardware v A software layer gives the appearance of sharedmemory to the programmer v. A memory read, for example, is transparently converted to a message send and reply v Example: Carleton University Treadmarks from Rice © S. Dandamudi 43

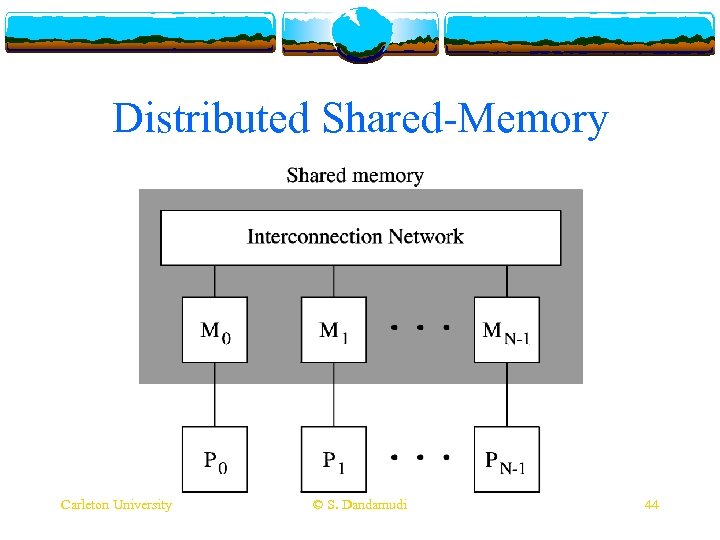
Distributed Shared-Memory Carleton University © S. Dandamudi 44

Cluster Systems v Built with commodity processors v Cost-effective v Often use the existing resources v Take advantage of the technological advances in commodity processors v Not tied to a single vendor v Generic components means v Competitive price v Multiple sources of supply Carleton University © S. Dandamudi 45

Cluster Systems v Several (cont’d) types v Dedicated set of workstations (Do. W) v Specifically built as a parallel system v Represents one extreme v Dedicated to parallel workload v No serial workload v Closely related to the distributed-memory MIMD v Communication network latency tends to be high v Example: Fast Ethernet Carleton University © S. Dandamudi 46

Cluster Systems v Several (cont’d) types (cont’d) v Privately-owned workstations (Po. W) v Represents the other extreme v All workstations are privately owned v Idea is to harness unused processor cycles for parallel workload v Receives v Local local jobs from owners jobs must receive higher priority v Workstations v Owner Carleton University might be dynamically removed from the pool shutting down/resetting the system, keyboard/mouse activity © S. Dandamudi 47

Cluster Systems v Several types (cont’d) v Community-owned v All workstations (Co. W) workstations are community-owned v Example: v In (cont’d) Workstations in a graduate lab the middle of Do. W and Po. W v In Po. W, a workstation could be removed when there is owner activity v Not so in Co. W systems v Parallel workload continues to run v Resource management should take these differences into account Carleton University © S. Dandamudi 48

Cluster Systems (cont’d) v Beowulf v Use PCs for parallel processing v Closely resembles a Do. W v Dedicated PCs (no scavenging of processor cycles) v A private system network (not a shared one) v Open design using public domain software and tools v Also known as v Po. PC (Pile of PCs) Carleton University © S. Dandamudi 49

Cluster Systems v Beowulf (cont’d) v Advantages v Systems not tied to a single manufacturer v Multiple vendors supply interchangeable components v Leads to better pricing v Technology tracking is straightforward v Incremental expandability v Configure the system to match user needs v Not limited to fixed, vendor-configured system Carleton University © S. Dandamudi 50

Cluster Systems v Beowulf (cont’d) v Example system v Linux Networ. X designed the largest and most powerful Linux cluster v Delivered to Lawrence Livermore National Lab (LLNL) in 2002 v Uses 2, 304 Intel 2. 4 GHz Xeon processors v Peak rating: 11. 2 Tflops v Aggregate memory: 4. 6 TB v Aggregate disk space: 138. 2 TB v Ranked 5 th fastest supercomputer in the world Carleton University © S. Dandamudi 51

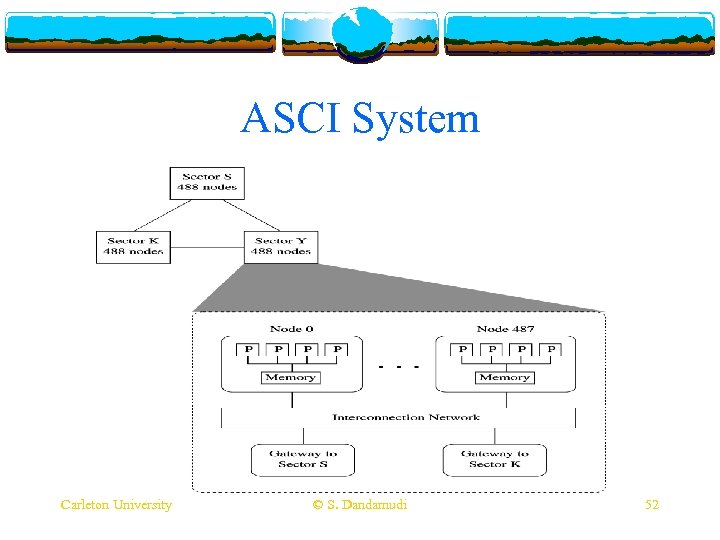ASCI System Carleton University © S. Dandamudi 52

Dataflow Systems v Different from control flow v Availability of data determines which instructin should executed v Example: v On A = (B + C) * (D – E) von Neumann machine v Takes 6 instructions v Sequential Carleton University dependency © S. Dandamudi add store sub store mult store B, C T 1 D, E T 2 T 1, T 2 A 53

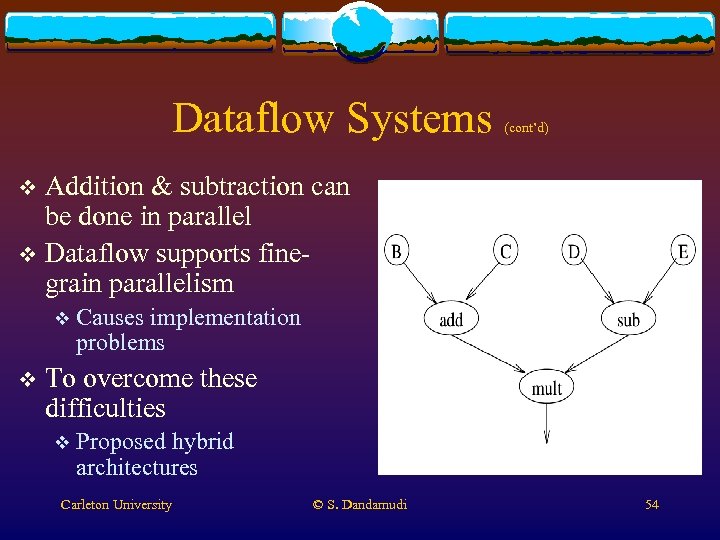Dataflow Systems (cont’d) Addition & subtraction can be done in parallel v Dataflow supports finegrain parallelism v v v Causes implementation problems To overcome these difficulties v Proposed hybrid architectures Carleton University © S. Dandamudi 54

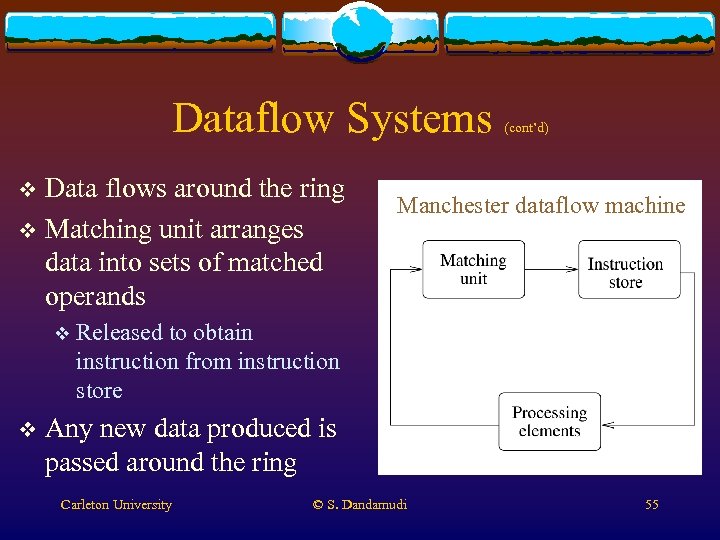Dataflow Systems Data flows around the ring v Matching unit arranges data into sets of matched operands v v v (cont’d) Manchester dataflow machine Released to obtain instruction from instruction store Any new data produced is passed around the ring Carleton University © S. Dandamudi 55

Interconnection Networks v. A critical component in many parallel systems v Four design issues v Mode of operation v Control strategy v Switching method v Topology Carleton University © S. Dandamudi 56

Interconnection Networks v Mode (cont’d) of operation v Refers to the type of communication used v Asynchronous v Typically used in MIMD v Synchronous v Typically used in SIMD v Mixed Carleton University © S. Dandamudi 57

Interconnection Networks v Control v Refers (cont’d) strategy to how routing is achieved v Centralized control v Can cause scalability problem v Reliability is an issue v Non-uniform node structure v Distributed control v Uniform node structure v Improved reliability v Improved scalability Carleton University © S. Dandamudi 58

Interconnection Networks v Switching v Two (cont’d) method basic types v Circuit switching v. A complete path is established v Good for large data transmission v Causes problems at high loads v Packet switching v Uses store-and-forward method v Good for short messages v High latency Carleton University © S. Dandamudi 59

Interconnection Networks v Switching method (cont’d) v Wormhole v Uses (cont’d) routing pipelined transmission v Avoids v Complete the buffer problem in packet switching (virtual) circuit is established as in circuit switching v Avoids some of the problems associated with circuit switching v Extensively Carleton University used in current systems © S. Dandamudi 60

Interconnection Networks v Network v Static (cont’d) topology v Links are passive and static v Cannot be reconfigured to provide direct connection v Used in distributed-memory MIMD systems v Dynamic v Links topology can be reconfigured dynamically v Provides v Used direct connection in SIMD and shared-memory MIMD systems Carleton University © S. Dandamudi 61

Interconnection Networks v Dynamic (cont’d) networks v Crossbar v Very expensive v Limited to small sizes v Shuffle-exchange v Single-stage v Multistage v Also Carleton University called MIN (Multistage interconnection network) © S. Dandamudi 62

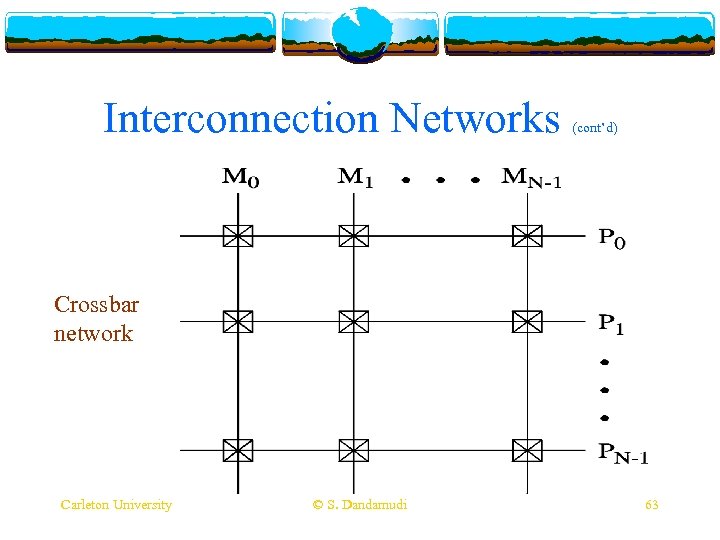Interconnection Networks (cont’d) Crossbar network Carleton University © S. Dandamudi 63

Interconnection Networks v Shuffle-exchange v Use (cont’d) networks a switching box v Gives the capability to dynamically reconfigure the network v Different types of switches v 2 -function v 4 -function v Connections v Perfect shuffle v Think Carleton University between stages follow the shuffle pattern of how you mix a deck of cards © S. Dandamudi 64

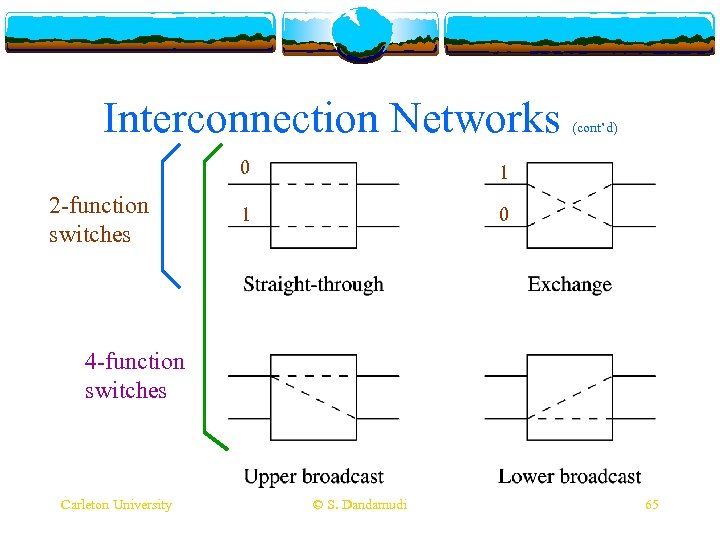Interconnection Networks 0 2 -function switches 1 1 (cont’d) 0 4 -function switches Carleton University © S. Dandamudi 65

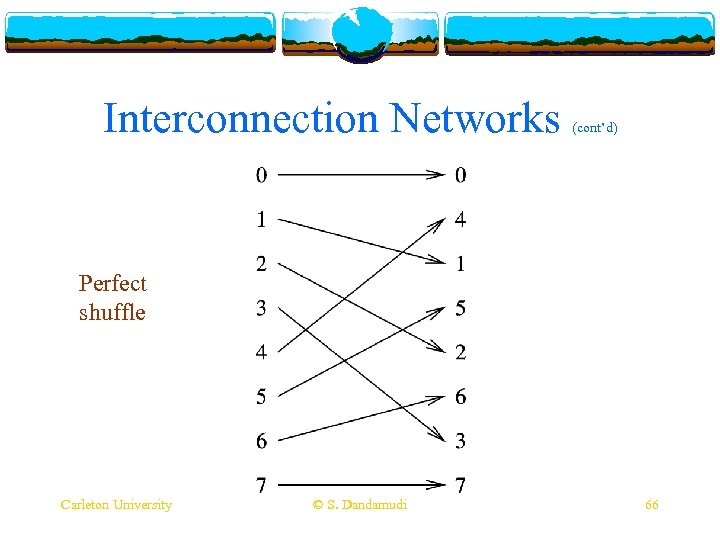Interconnection Networks (cont’d) Perfect shuffle Carleton University © S. Dandamudi 66

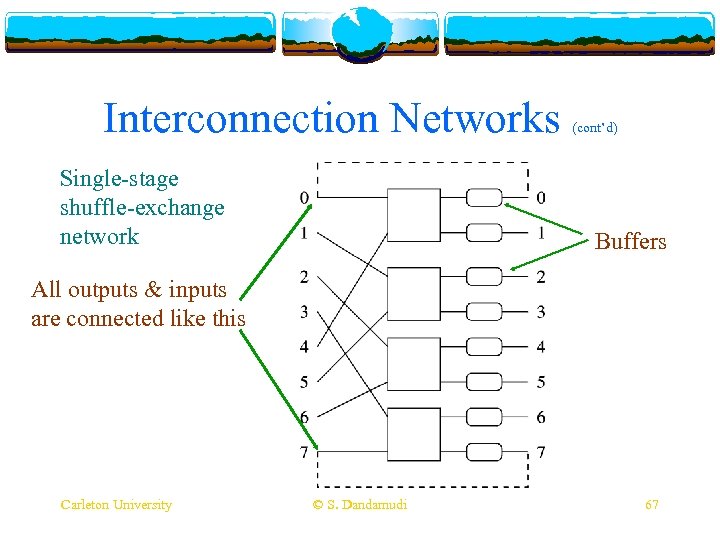Interconnection Networks Single-stage shuffle-exchange network (cont’d) Buffers All outputs & inputs are connected like this Carleton University © S. Dandamudi 67

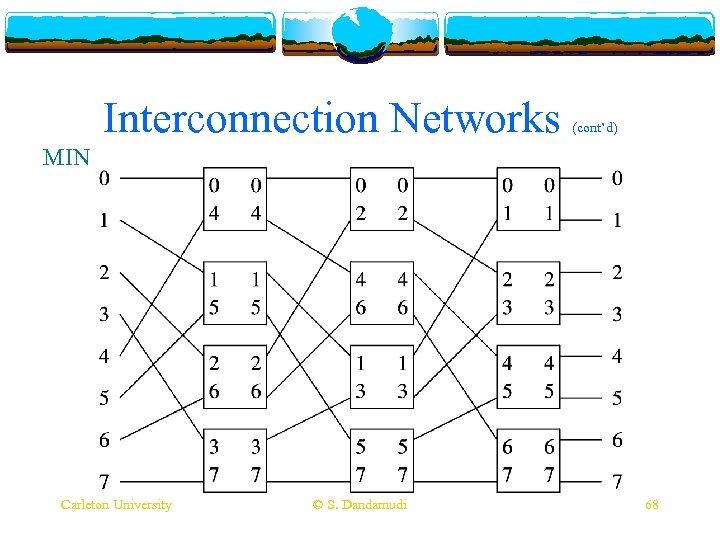Interconnection Networks (cont’d) MIN Carleton University © S. Dandamudi 68

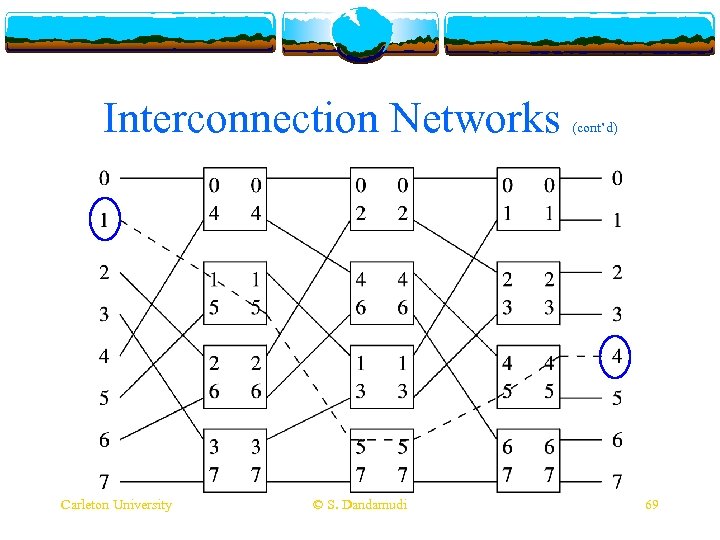Interconnection Networks Carleton University © S. Dandamudi (cont’d) 69

Interconnection Networks (cont’d) IBM SP 2 switch Carleton University © S. Dandamudi 70

Interconnection Networks v Static (cont’d) interconnection networks v Complete connection v One extreme v High cost, low latency v Ring network v Other extreme v Low cost, high latency v. A variety of networks between these two extremes Carleton University © S. Dandamudi 71

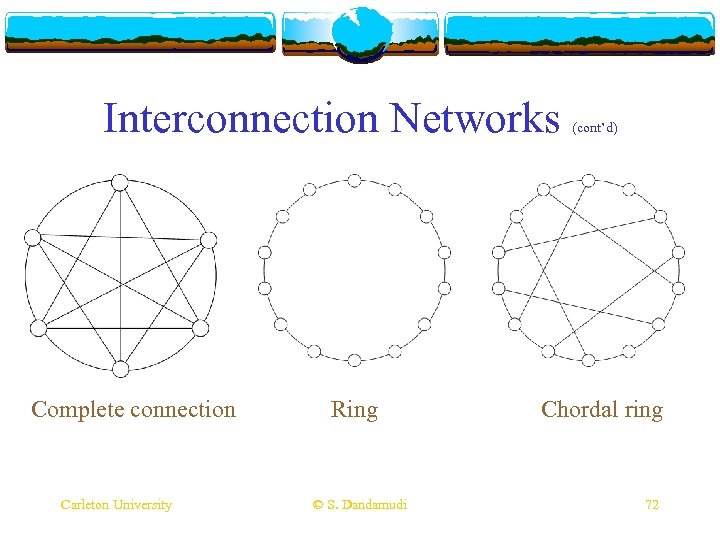Interconnection Networks Complete connection Carleton University Ring © S. Dandamudi (cont’d) Chordal ring 72

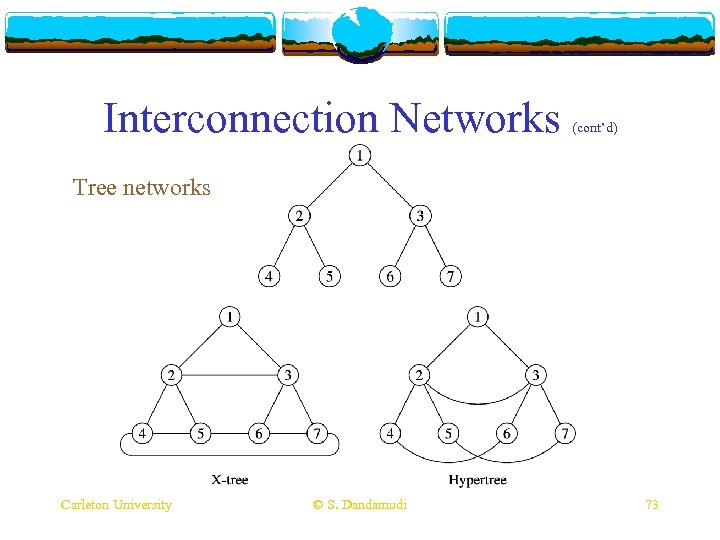Interconnection Networks (cont’d) Tree networks Carleton University © S. Dandamudi 73

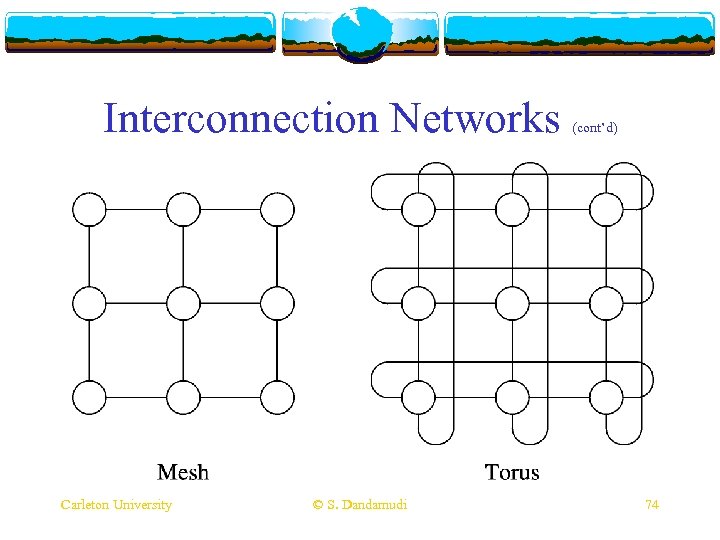Interconnection Networks Carleton University © S. Dandamudi (cont’d) 74

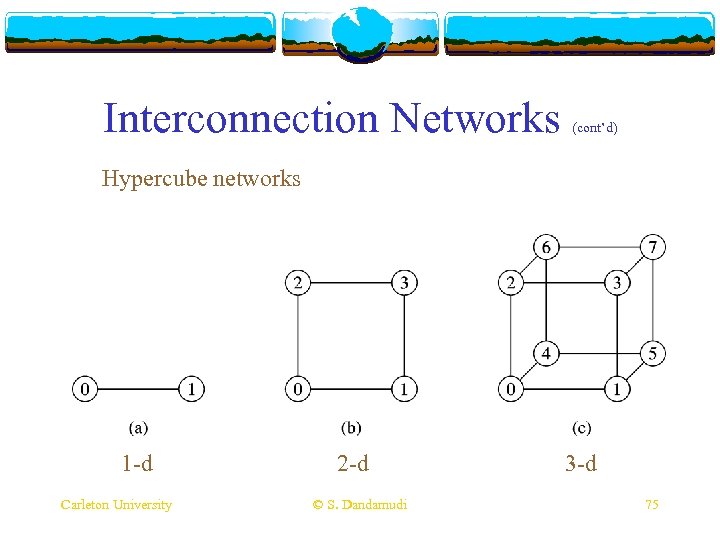Interconnection Networks (cont’d) Hypercube networks 1 -d Carleton University 2 -d © S. Dandamudi 3 -d 75

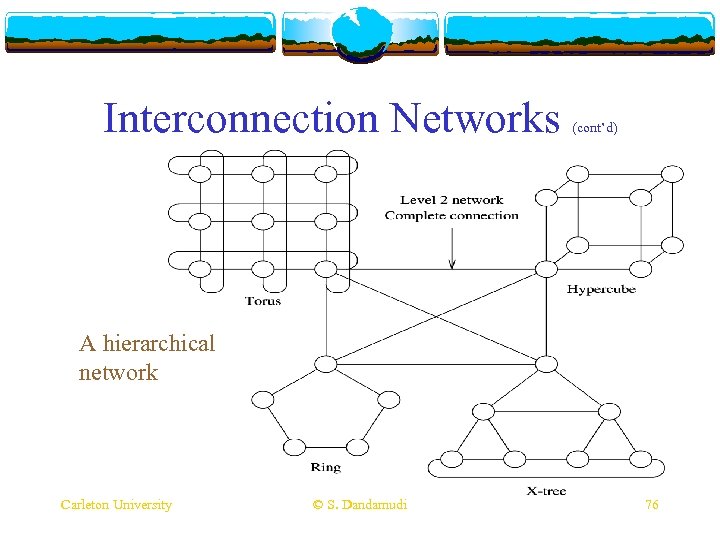Interconnection Networks (cont’d) A hierarchical network Carleton University © S. Dandamudi 76

Future Parallel Systems v Special-purpose systems + Very efficient + Relatively simple - Narrow domain of applications May be cost-effective v Depends Carleton University on the application © S. Dandamudi 77

Future Parallel Systems v General-purpose (cont’d) systems + Cost-effective + Wide range of applications - Decreased speed - Decreased hardware utilization - Increased software requirements Carleton University © S. Dandamudi 78

Future Parallel Systems v In (cont’d) favour of special-purpose systems v Harold Stone argues v Major advantage of general-purpose systems is that they are economical due to their wide area of applicability v Economics of computer systems is changing rapidly because of VLSI v Makes Carleton University the special-purpose systems economically viable © S. Dandamudi 79

Future Parallel Systems v In (cont’d) favour of both types of systems v Gajski argues v Problem space is constantly expanding v Special-purpose systems can only be designed to solve “mature” problems v Always new applications for which no “standardized” solution exists v For these applications, general-purpose systems are useful Carleton University © S. Dandamudi 80

Performance v Amdahl’s law fraction of a program: a v Parallel fraction: 1 - a v Execution time on n processors v Serial T(n) = T(1) a + T(1) (1 – a) n n v Speedup S(n) = a n + (1 – a) Carleton University © S. Dandamudi Amdahl’s law 81

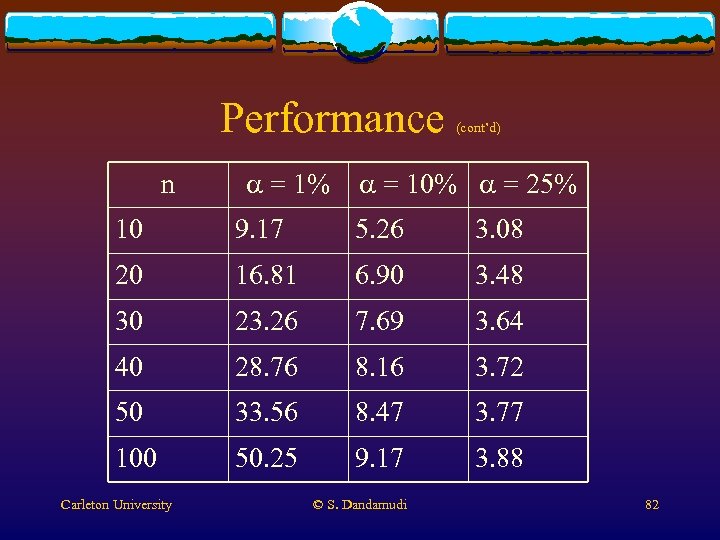Performance n a = 1% (cont’d) a = 10% a = 25% 10 9. 17 5. 26 3. 08 20 16. 81 6. 90 3. 48 30 23. 26 7. 69 3. 64 40 28. 76 8. 16 3. 72 50 33. 56 8. 47 3. 77 100 50. 25 9. 17 3. 88 Carleton University © S. Dandamudi 82

Performance v Gustafson-Barsis v Obtained v For (cont’d) law a speedup of 1000 on a 1024 -node n. CUBE/10 the problem, a values ranged from 0. 4% to 0. 8% v Won Gordon Bell prize in 1988 v Amdahl’s law predicts a speedup of 201 to 112! v Assumes v Problem that (1 - a) is independent of n scales up with system T(1) = a + (1 - a) n v Speedup Carleton University T(n) = a + (1 - a) = 1 S(n) = n – (n – 1) a © S. Dandamudi 83

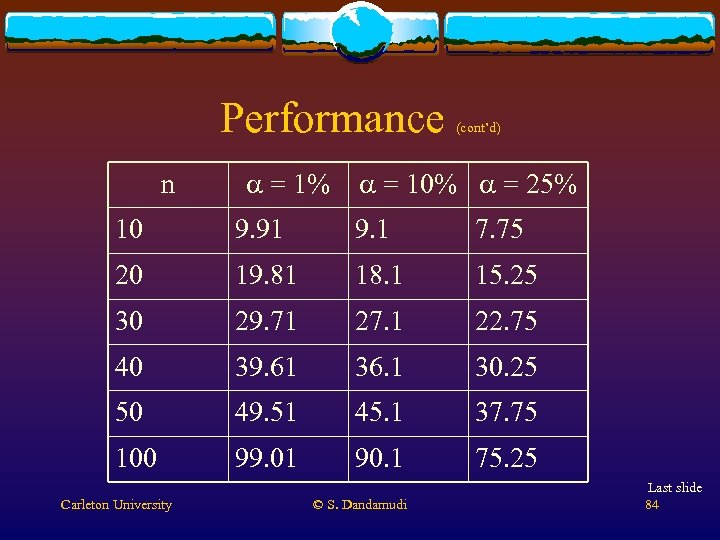Performance n a = 1% (cont’d) a = 10% a = 25% 10 9. 91 9. 1 7. 75 20 19. 81 18. 1 15. 25 30 29. 71 27. 1 22. 75 40 39. 61 36. 1 30. 25 50 49. 51 45. 1 37. 75 100 99. 01 90. 1 75. 25 Carleton University © S. Dandamudi Last slide 84