Introduction of Nuclear Reactions Kiyoshi Kato Hokkaido University

Introduction of Nuclear Reactions Kiyoshi Kato Hokkaido University 2014. 10. 8

Brief history of nuclear reactions 1909 -1911 E. Rutherford: Au + α (from Po) E. Fermi 9 Be + α (from Po) n+2α 　　　　n+ 36 nuclei (from H to U) (1) large (n, γ) cross sections (2) zero-energy cross sections depend on targets strongly -> long life time states (resonances) 10 -16 sec N. Bohr, G. Breit and E. P. Wigner Compound nucleus model

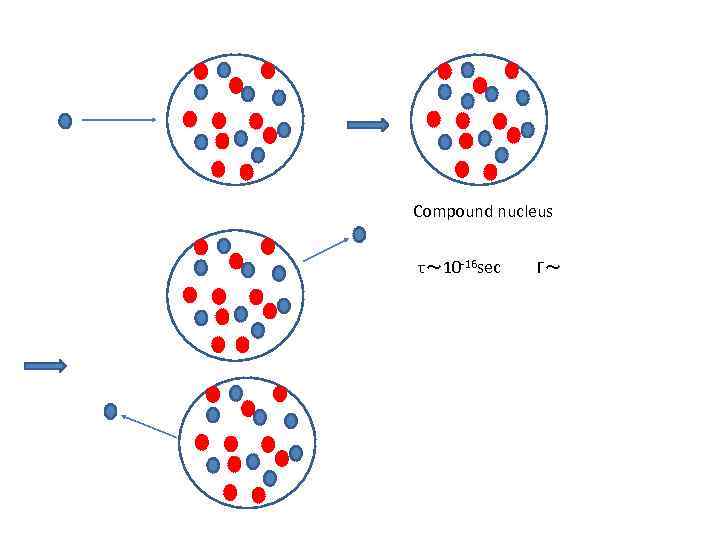Compound nucleus τ～ 10 -16 sec　　　Γ～

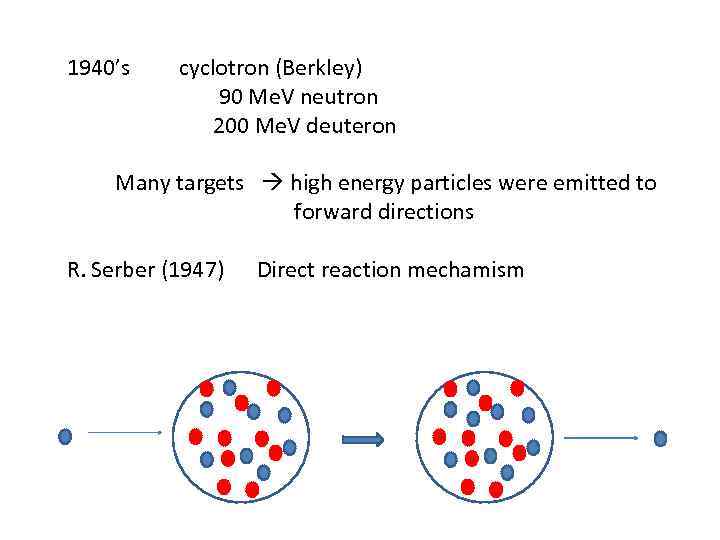1940’s　　　cyclotron (Berkley) 90 Me. V neutron 200 Me. V deuteron Many targets high energy particles were emitted to forward directions R. Serber (1947) Direct reaction mechamism

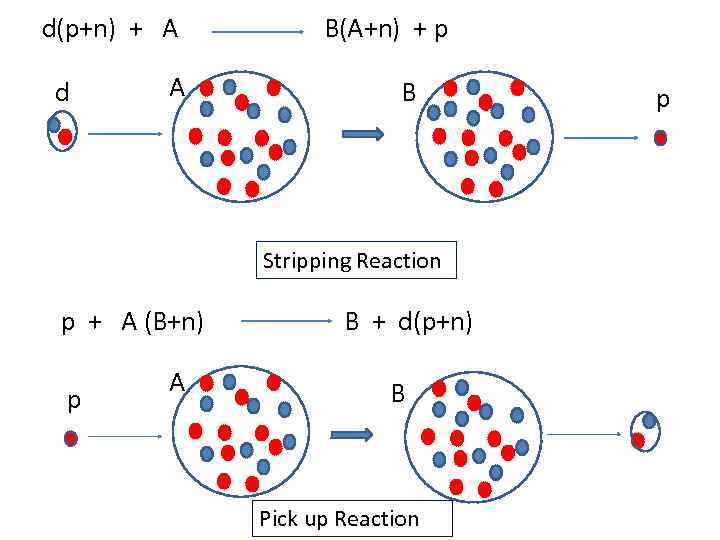d(p+n) + A d A B(A+n) + p B Stripping Reaction p + A (B+n) p A B + d(p+n) B Pick up Reaction p

1952 Barschall n (3 Me. V) + A total reaction <σt> low energy resolution ΔEn <σt(En, A)> Gross structure 　　　　　　　 Feshbach, Porter, Weisskopf (1954) Optical Potential Model: U=V+i. W 1969 for n-A 12 C+12 C (Resonances: Intermediate width) 1970’s Heavy Ion Reactions Nuclear Cluster Structures 1980’s p+A π-on production (Second beam experiments) π―A scattering 1990’s I. Tanihata (Berkeley) 11 Li halo structure Radioactive beam experiments

2000’s Second beam experiments K-on Physics (Hypernuclear Physics) High-energy Heavy Ion Reactions U+U Quark-Gluon Plasma 　　　　　　At RHIC (Berkeley) and LHC (CERN)

Basic Knowledge of Nuclear Reactions Various Nucleus Reactions: Incident particle + Target nucleus (Two-body collision) Emitted particles + Residual nuclei or A + a B + b 1 + b 2 + ……… + bn A(a, b 1 b 2・・・・・・ bn)B A(a, a)A: elastic scattering A(a, a’)A*, A(a, a*)A* : inelastic scattering Transmutation, rearrangement

channels A +a A* + a’ B+b C + c 1+ c 2+ ・・・・・・+ c. M ・・・・・・ Incident channel α＝｛A, a} Exit channel α‘＝｛A*, a’} β＝{B, b} γ＝{C + c 1+ c 2+ ・・・・・・+ c. M} ・・・・・・

Threshold value of reaction ε：　internal energy of particle Exothermic reaction Endothermic reaction Einc > channel β　is an open channel Cross sections of reaction 1 b =10 -24 cm 2 mb, μb, nb, pb total cross section, total elastic cross section, total reaction cross section

Angular distribution of an emitted particle differential cross section (b/sr) energy spectrum double differential cross section For a polarized beam, cross sections is called as polarization or analyzing power Laboratory frame, center-of-mass- frame

Outline of nuclear reaction mechanism Low energy nuclear reactions of a + A internal excitations of a and A are neglidgeble Coulomb barrier between a and A: distance of closest approach tunneling effect neutron has no Coulomb barrier After entering in the nuclear interaction region, the incident particle can be described by the optical potential. During the interaction incident and target particles by the optical potential, various degrees of freedom in incident and target particles become active. This process is described by