Introducing Students to Classic Problems in Probability Allan

Introducing Students to Classic Problems in Probability Allan Rossman Department of Statistics Cal Poly – San Luis Obispo arossman@calpoly. edu Rossman NZAMT 2013 1

What’s my point? n Classic problems in probability q q q q Rossman Provide great opportunities for exploring, understanding concepts of randomness Lend themselves to interactive investigations Can be presented at various mathematical levels Illustrate mathematical as well as statistical ideas Create pedagogical alternatives to rolling dice and flipping coins for their own sake Are intellectually stimulating Can be fun! NZAMT 2013 2

What are my goals for this workshop? n n Acquaint you with some classic problems in probability Demonstrate solutions to these problems q q n Using simulation Using enumeration Provide ideas for activities that you can use with your students q Rossman In variety of courses, levels NZAMT 2013 3

What concepts will be introduced? n n n n Randomness Probability Simulation Relative frequency Permutations Expected value Decision making under uncertainty Rossman NZAMT 2013 4

What are these classic problems? n n Problem of the points Matching problem Collector problem Secretary problem Rossman NZAMT 2013 5

Problem of the points n n Helped to motive the study of probability Discussed in correspondence between Pascal and Fermat Rossman NZAMT 2013 6

Problem of the points n n n A simplified version: Suppose that Heather and Tom each put in $5 to play a game They flip a fair coin repeatedly q q Rossman If 4 Heads occur before 4 Tails, Heather wins If 4 Tails occur before 4 Heads, Tom wins NZAMT 2013 7

Problem of the points n n Outcome: H H T (3 Heads, 2 Tails) Then game is interrupted, cannot be completed! How should the prize ($10) be divided? What might you propose? Rossman NZAMT 2013 8

Problem of the points n My students’ answers q q n Game was not finished, so each takes $5 back Heather won 3/5 of the flips, so she gets $6, Tom gets $4 More mathematical approach q Rossman Divide prize proportionally to each player’s probability of winning if the game were continued NZAMT 2013 9

Problem of the points n How to calculate these probabilities? q q n I’ll ask everyone to use a coin to simulate 5 repetitions of this random process q n Simulation Enumeration Remember that Heather wins with one more Head, but Tom needs two Tails to win Estimate Heather’s probability of winning by proportion of times that she wins Rossman NZAMT 2013 10

Problem of the points n n n Enumeration analysis H: Heather wins TT: Tom wins Are these equally likely, so Heather has 2/3 probability of winning? No: H (prob. 5), TH (prob. 25), TT (prob. 25) Heather’s probability of winning: ¾ =. 75 So, Heather should take $7. 50, Tom $2. 50 Rossman NZAMT 2013 11

Problem of the points n Variation: What if they were playing to get 10 heads or tails and were interrupted after 9 heads and 8 tails? q q Rossman Heather needs 1 more Head, Tom needs 2 more Tails Same analysis, same answer! NZAMT 2013 12

Problem of the points n New variation: What if they were playing to 5 and had stopped after H H T? q More complicated enumeration: Heather wins with n n n q Heather has. 6875 probability of winning n Rossman H H (prob. 25) H T H (. 125) H T T H (. 0625) T H H (. 125) T H (. 0625) T T H H (. 0625) Heather should take $6. 875 NZAMT 2013 13

Matching problem n n Four mothers give birth to baby boys on the same night at the same hospital As a very, VERY sick joke (do not try this at home!), the hospital staff returns the babies to the mothers at random How likely is it that everyone will get the right baby? Or nobody will? Or at least one will? What is the average number that would get the right baby in the long run? Rossman NZAMT 2013 14

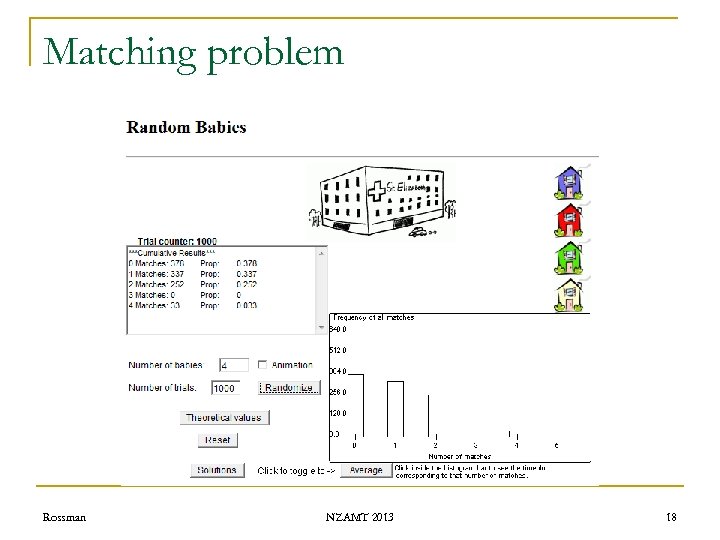
Matching problem n Simulate q q q q Rossman Put baby’s name on each of four index cards Shuffle cards thoroughly Random distribute cards to four “mothers” Repeat … Approximate probabilities by proportions NZAMT 2013 15

Matching problem n Simulate q q q Rossman Turn to technology: Random Babies applet (www. rossmanchance. com/applets/) Which is the most likely outcome? How unlikely is getting 4 matches? Is 3 very unlikely or impossible? What’s the long-run average number of correct matches? What happens as you conduct more repetitions? NZAMT 2013 16

Matching problem Rossman NZAMT 2013 17

Matching problem Rossman NZAMT 2013 18

Matching problem Rossman NZAMT 2013 19

Matching problem Rossman NZAMT 2013 20

Matching problem n Enumeration 1234 1243 1324 1342 1423 1432 2134 2143 2314 2341 2413 2431 3124 3142 3214 3241 3412 3421 4123 4132 4213 4231 4312 4321 n Count # of matches for each outcome Rossman NZAMT 2013 21

Matching problem n Enumeration 1234 4 2134 2 3124 1 4123 0 Rossman 1243 2 2143 0 3142 0 4132 1 1324 2 2314 1 3214 2 4213 1 1342 1 2341 0 3241 1 4231 2 NZAMT 2013 1423 1 2413 0 3412 0 4312 0 1432 2 2431 1 3421 0 4321 0 22

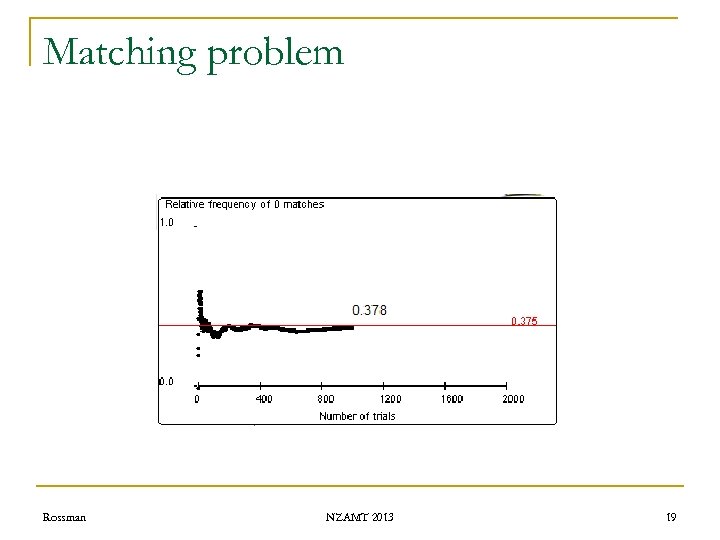
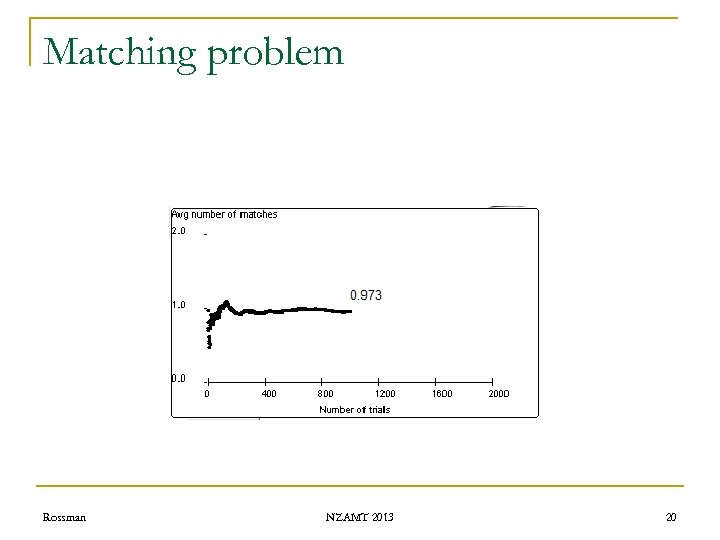
Matching problem n Exact probabilities q q q n 0 matches: 9/24 =. 375 1 match: 8/24 ≈. 333 2 matches: 6/24 =. 250 3 matches: 0 4 matches: 1/24 ≈. 042 Expected value q q Rossman 0(9/24) + 1(8/24) + 2(6/24) + 4(1/24) = 24/24 = 1 Long-run average value NZAMT 2013 23

Collector problem n n n Each cereal box is equally likely to contain any one of 3 prizes You want to collect the entire series of 3 prizes Suppose that you buy boxes one at a time q q Rossman What is the fewest that you might need to buy? What is the most that you might need to buy? How many boxes should you buy to have a 95% chance of success? How many boxes do you “expect” to need (on average)? NZAMT 2013 24

Collector problem n What if there are k prizes? q q Rossman Same questions as above How likely are you to succeed if your strategy is to buy twice as many boxes as prizes? NZAMT 2013 25

Collector problem n Simulate! q q q q Rossman Write each prize on an index card Shuffle cards thoroughly Select one card at random, note which prize Repeat, until all prizes have been obtained Note the number of selections needed Repeat … Estimate probability distribution (of number of boxes needed) by distribution of results NZAMT 2013 26

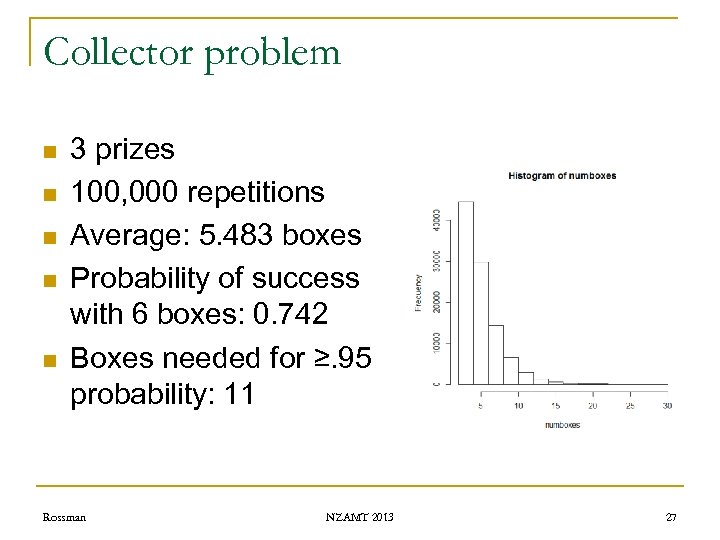
Collector problem n n n 3 prizes 100, 000 repetitions Average: 5. 483 boxes Probability of success with 6 boxes: 0. 742 Boxes needed for ≥. 95 probability: 11 Rossman NZAMT 2013 27

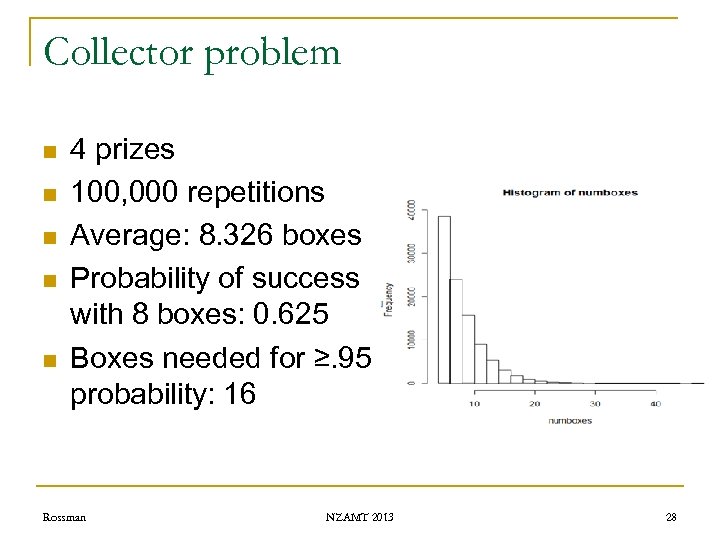
Collector problem n n n 4 prizes 100, 000 repetitions Average: 8. 326 boxes Probability of success with 8 boxes: 0. 625 Boxes needed for ≥. 95 probability: 16 Rossman NZAMT 2013 28

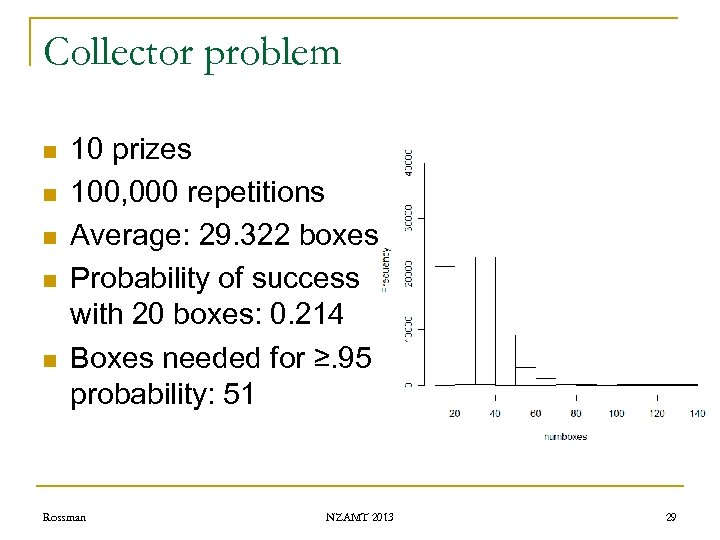
Collector problem n n n 10 prizes 100, 000 repetitions Average: 29. 322 boxes Probability of success with 20 boxes: 0. 214 Boxes needed for ≥. 95 probability: 51 Rossman NZAMT 2013 29

Secretary problem My all-time favorite probability/math problem! Your task is to hire a new employee, subject to these constraints: n You know how many candidates have applied (n) n The candidates arrive in random order n You interview candidates one at a time n You can rank candidates after interviewing them q But you have no prior sense of quality Rossman NZAMT 2013 30

Secretary problem More constraints: n After you have interviewed a candidate, you must decide immediately whether to hire No follow-up interviews No going back later q q Your task is to choose the best! n q Rossman Any other result: you’ve failed! NZAMT 2013 31

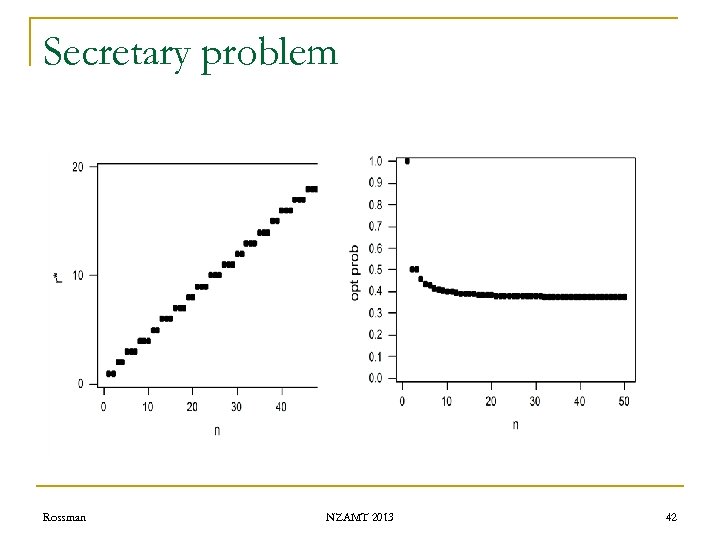
Secretary problem Predict the optimal probability of success when: n n=3 n n = 12 n n = 500 n n = 4, 484, 451 (population of NZ) n n = 7, 182, 483, 662 (world population) Rossman NZAMT 2013 32

Secretary problem n Enumeration for n = 1: A: 1 Probability of success = 1! Rossman NZAMT 2013 33

Secretary problem Enumeration for n = 2: n A: 12 B: 21 Two strategies n q q Hire first candidate Hire second candidate Probability of success =. 5 Rossman NZAMT 2013 34

Secretary problem Enumeration for n = 3: n A: 123 D: 231 B: 132 E: 312 C: 213 F: 321 Seems like probability of success = 1/3 n q Rossman Can we do better? NZAMT 2013 35

Secretary problem Key insight n We can learn from the first candidate q Optimal strategy n q q Let one go by Then hire first candidate who is the best so far A: 123 D: 231 Rossman B: 132 E: 312 NZAMT 2013 C: 213 F: 321 36

Secretary problem n Enumeration for n = 4: A: 1234 E: 1423 I: 2314 M: 3124 Q: 3412 U: 4213 n B: 1243 F: 1432 J: 2341 N: 3142 R: 3421 V: 4231 C: 1324 G: 2134 K: 2413 O: 3214 S: 4123 W: 4312 D: 1342 H: 2143 L: 2431 P: 3241 T: 4132 X: 4321 Same form for optimal strategy q But should we let 1 go by or let 2 go by? Rossman NZAMT 2013 37

Secretary problem Let 1 go by A: 1234 E: 1423 I: 2314 M: 3124 Q: 3412 U: 4213 n B: 1243 F: 1432 J: 2341 N: 3142 R: 3421 V: 4231 C: 1324 G: 2134 K: 2413 O: 3214 S: 4123 W: 4312 D: 1342 H: 2143 L: 2431 P: 3241 T: 4132 X: 4321 Probability of success = 11/24 ≈. 4583 Rossman NZAMT 2013 38

Secretary problem Let 2 go by A: 1234 E: 1423 I: 2314 M: 3124 Q: 3412 U: 4213 n B: 1243 F: 1432 J: 2341 N: 3142 R: 3421 V: 4231 C: 1324 G: 2134 K: 2413 O: 3214 S: 4123 W: 4312 D: 1342 H: 2143 L: 2431 P: 3241 T: 4132 X: 4321 Probability of success = 10/24 ≈. 4167 Rossman NZAMT 2013 39

Secretary problem n n n = 4: Optimal strategy q Let 1 go by, then hire first one who is best so far q Probability of success = 11/24 ≈. 4583 n Decreasing, but not as quickly as most expect Rossman NZAMT 2013 40

Secretary problem Rossman NZAMT 2013 41

Secretary problem Rossman NZAMT 2013 42

Secretary problem n Recall: n For large values of n: n And so: Rossman NZAMT 2013 43

Secretary problem n Recall: n n Goal: choose r to maximize f(r) Elementary calculus gives: n Optimal probability of success becomes: Rossman NZAMT 2013 44

Secretary problem Remarkable result: n As n gets infinitely large q q q Rossman Optimal strategy is to let ≈ first 1/e (about 37%) go by Then hire first who is best so far Optimal probability of success 1/e, about 37% NZAMT 2013 45

Secretary problem n Extensions q q Rossman Hidden number game Finding your soul-mate in life NZAMT 2013 46

Thanks! n arossman@calpoly. edu Rossman NZAMT 2013 47