Into the 4 th Dimension Edgewise Roger House

Into the 4 th Dimension Edgewise Roger House Scientific Buzz Café French Garden Sebastopol, CA 2016 February 10 Copyright © 2016 Roger House

What we're going to talk about What is a graph? What is the dimension of a graph? What is the least number of edges a fourdimensional graph must have?

What's a graph?

Remember these graphs?

And these?

And graphs you can eat

None of these graphs are the kinds of graphs we're interested in at the moment

A different kind of graph We're going to deal with much different kinds of graphs, namely, mathematical graphs.

Definition of a graph Definition: A graph G consists of a finite nonempty set V of vertices together with a set E of unordered pairs of distinct vertices of V. The pair e = {u, v} of vertices in E is called an edge of G.

There will be a quiz on the definition But not on the one above On the one below

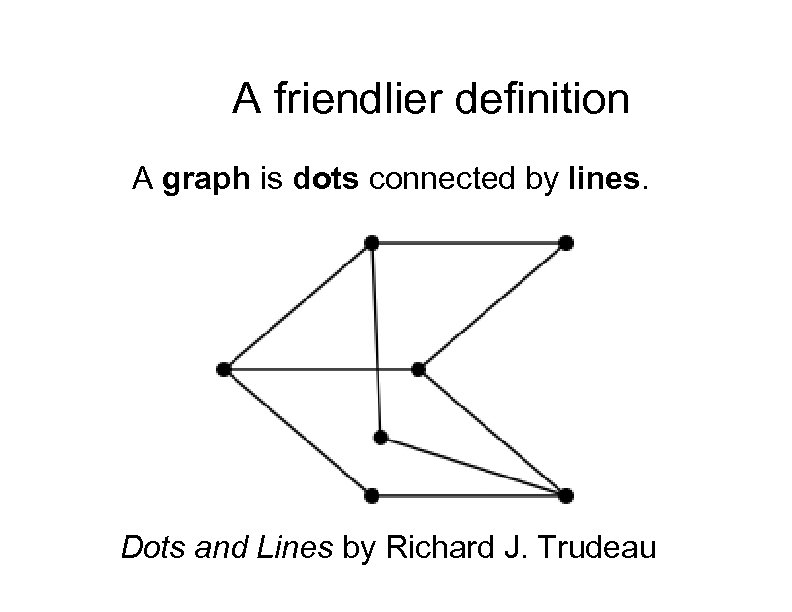A friendlier definition A graph is dots connected by lines. Dots and Lines by Richard J. Trudeau

Fancy terminology The dots are called vertices. The lines are called edges. (Or points, or nodes, or. . . ) (The graph above has 7 vertices and 9 edges. ) Two vertices connected by an edge are adjacent. An edge is incident with its two vertices. The degree of a vertex is the number of edges incident with the vertex.

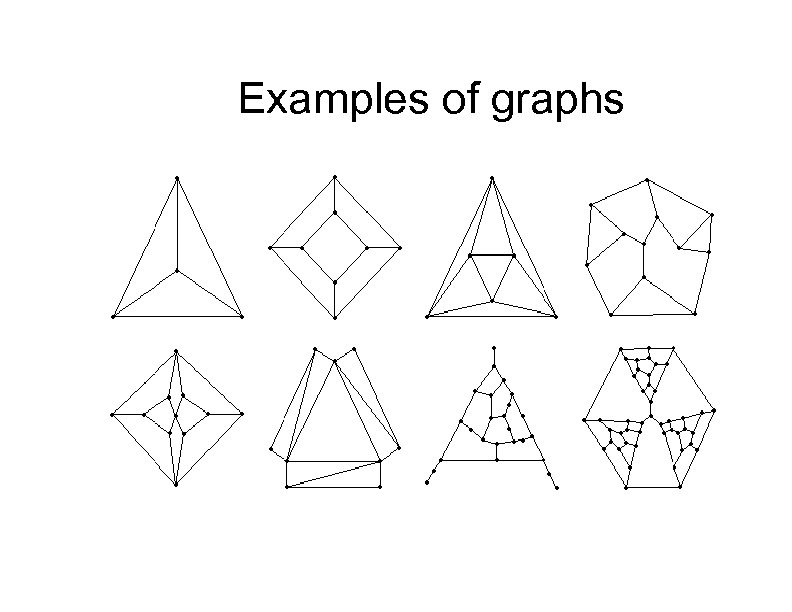Examples of graphs

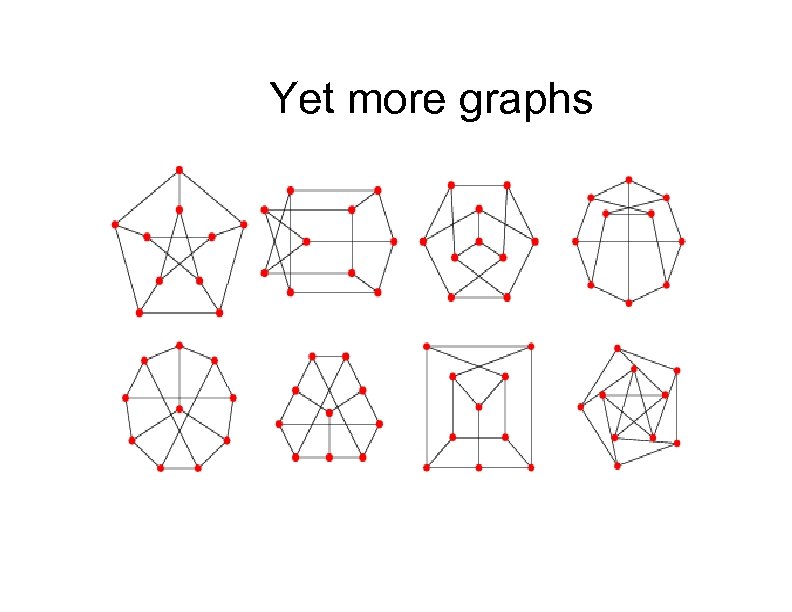Yet more graphs

Let's start at the beginning What is the simplest, most basic graph? The empty set? No. The definition says the set of vertices must be nonempty So this is it:

What is the next simplest graph? How many vertices? Seems like 2 must be the answer So this is the next simplest graph:

What is the third simplest graph? Three vertices? Are there any more graphs with 2 vertices? How about this one: Are there any more graphs with 2 vertices?

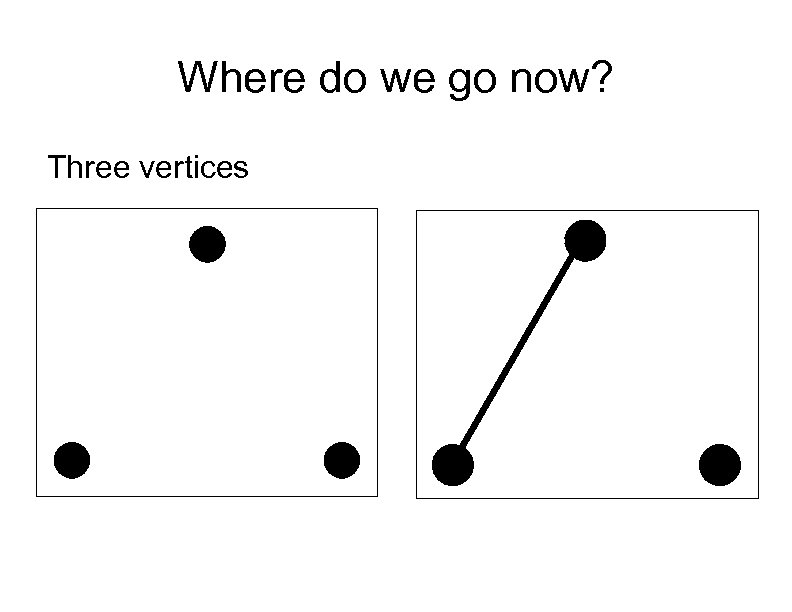Where do we go now? Three vertices

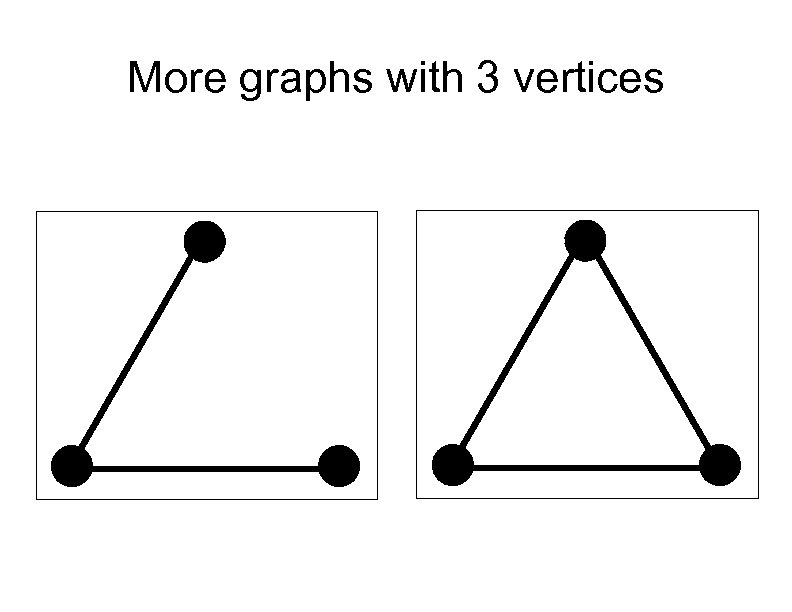More graphs with 3 vertices

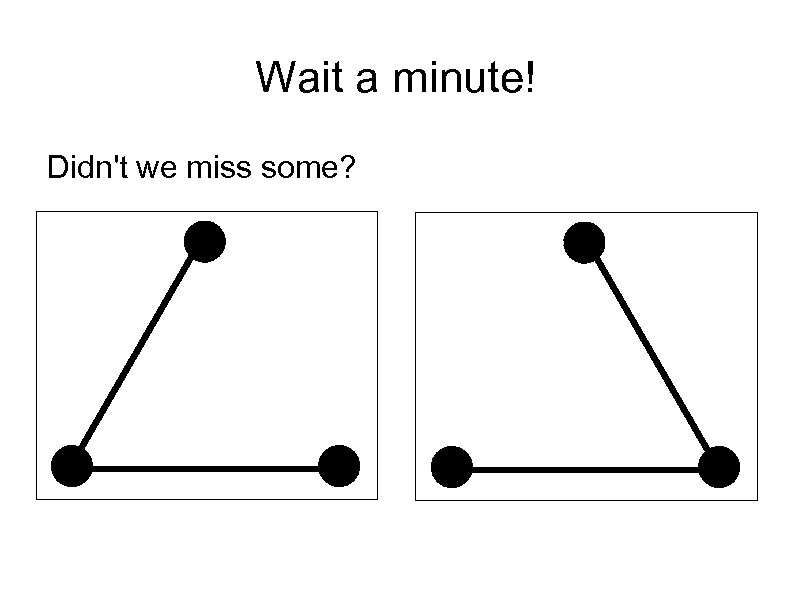Wait a minute! Didn't we miss some?

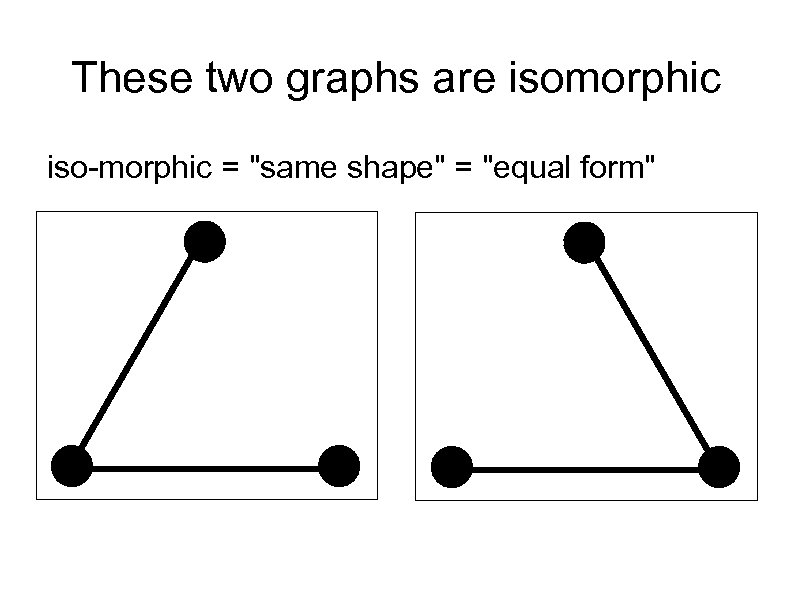These two graphs are isomorphic iso-morphic = "same shape" = "equal form"

The Graph Isomorphism Problem Is there an efficient algorithm for determining if two finite graphs are isomorphic? None is known But there is no proof that one does not exist NEWS BULLITEN 2015 Nov. 6: Laszlo Babai has reported that he has a quasipolynomial time algorithm for the graph isomorphism problem This is not an "efficient" algorithm, but it is a significant advance

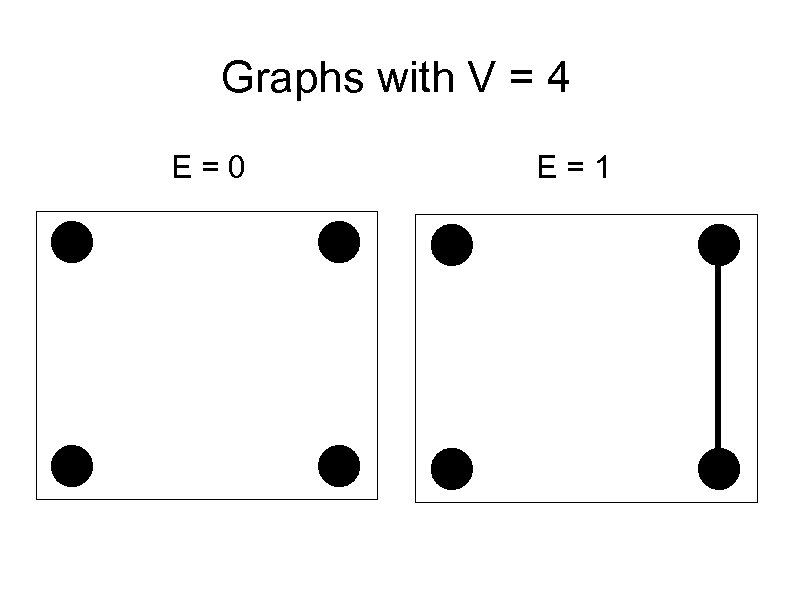Graphs with V = 4 E=0 E=1

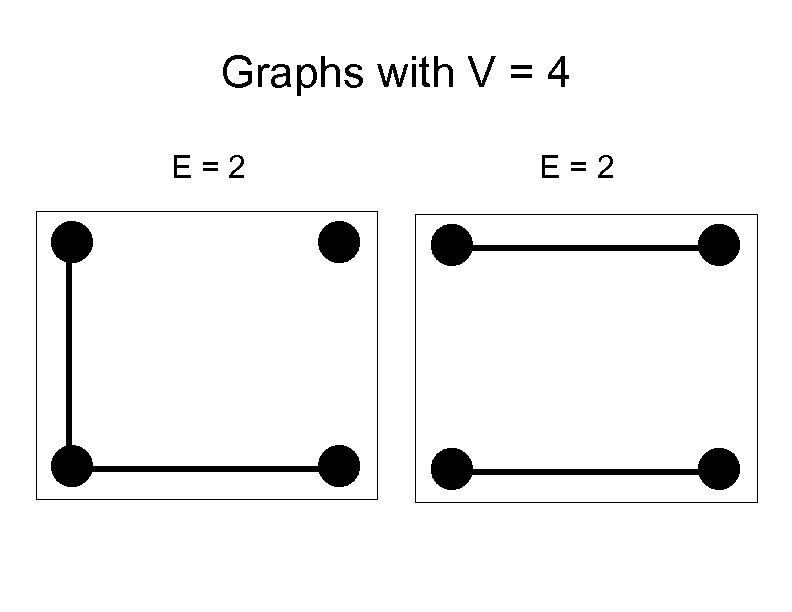Graphs with V = 4 E=2

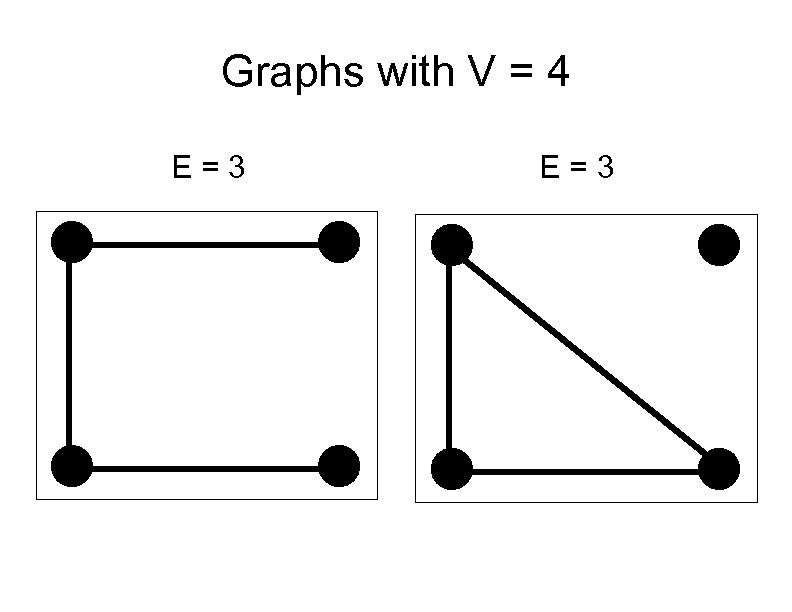Graphs with V = 4 E=3

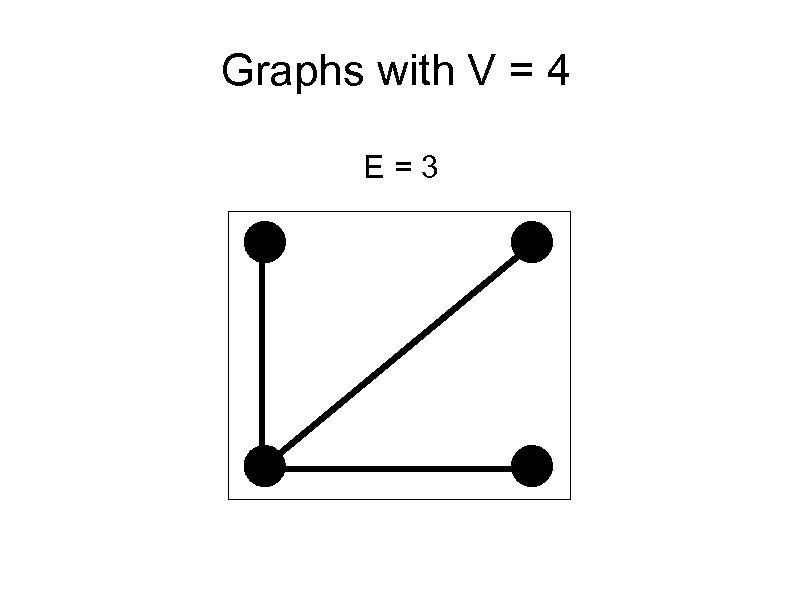Graphs with V = 4 E=3

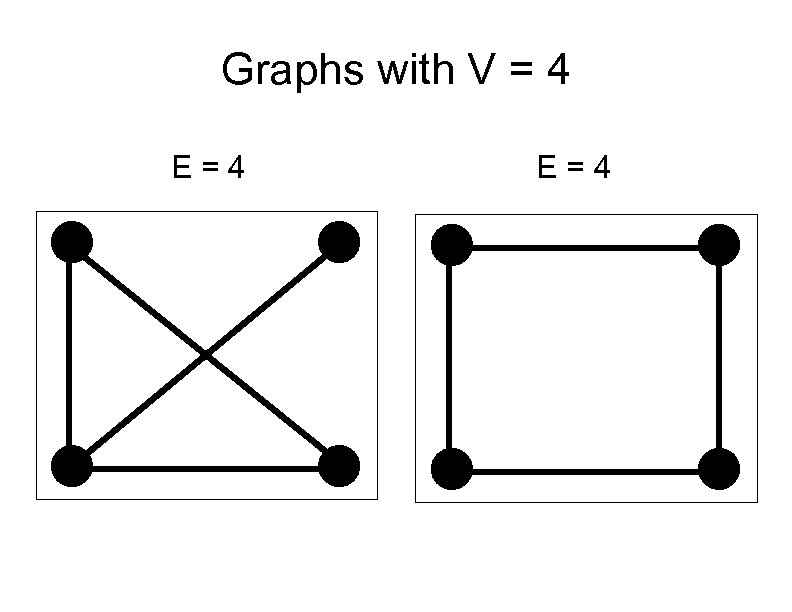Graphs with V = 4 E=4

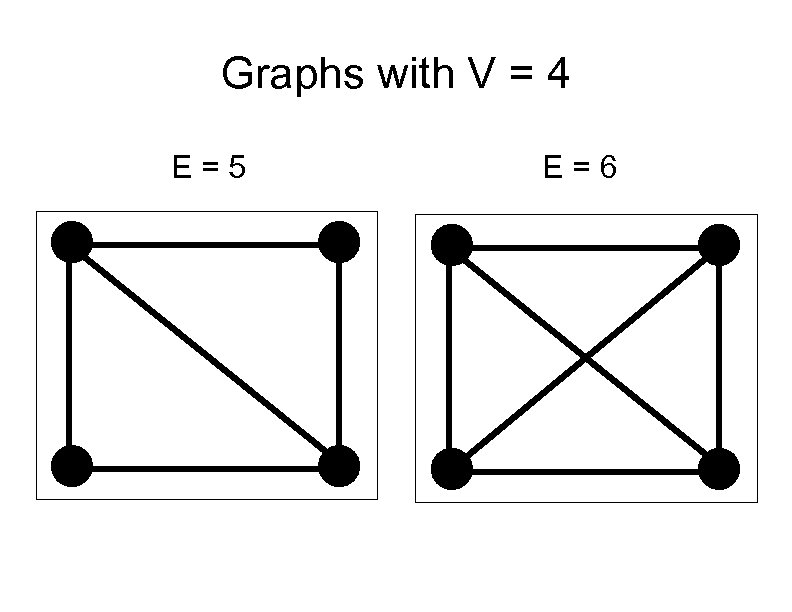Graphs with V = 4 E=5 E=6

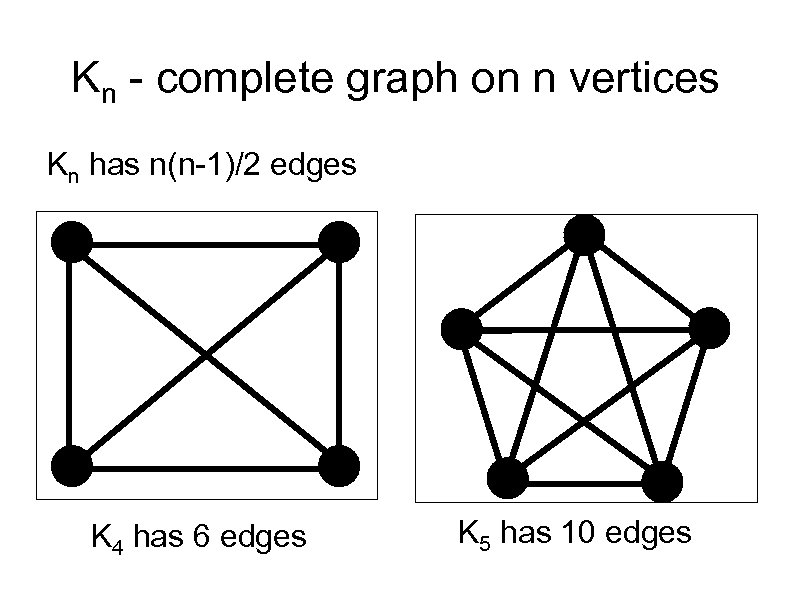Kn - complete graph on n vertices Kn has n(n-1)/2 edges K 4 has 6 edges K 5 has 10 edges

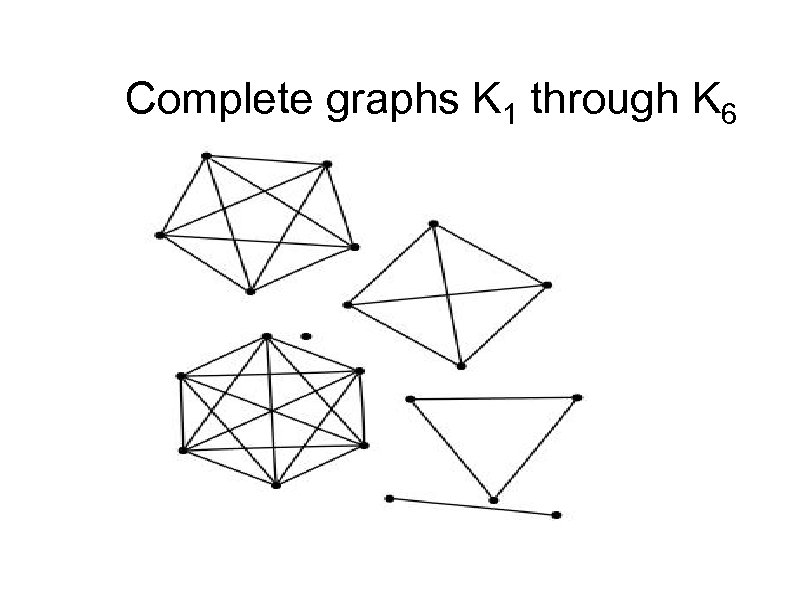Complete graphs K 1 through K 6

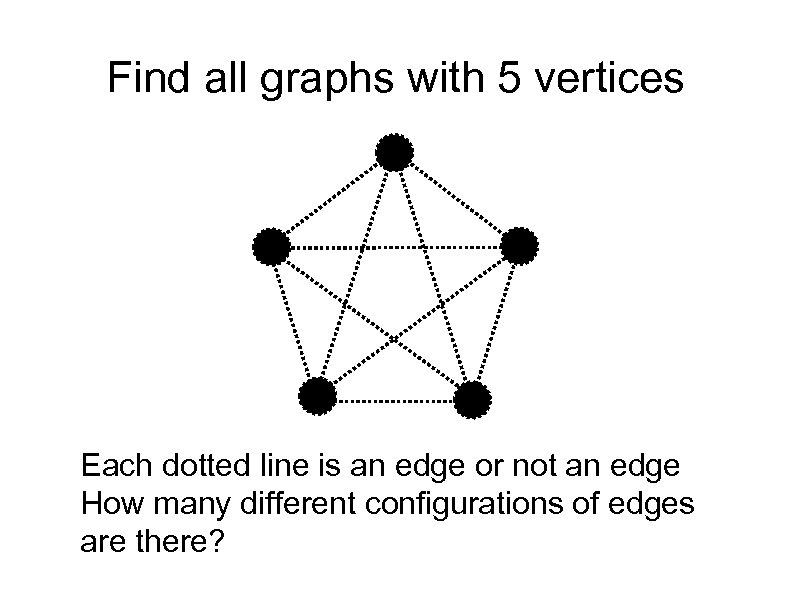Find all graphs with 5 vertices Each dotted line is an edge or not an edge How many different configurations of edges are there?

Find all graphs with 5 vertices K 5 has 5(5 -1)/2 = 10 edges So there are 10 dotted lines, each one either an edge or not an edge So there are 210 = 1024 possible configurations So there are 1024 graphs with 5 vertices, right? No! Remember isomorphic graphs? There are 10 configurations with only one edge They're all isomorphic, so only 1 graph results

Are there enough graphs? V 1 2 3 4 5 6 7 8 9 10 max E 2 E 0 1 1 2 3 8 6 64 10 1, 024 15 32, 768 21 2, 097, 152 28 268, 435, 456 36 68, 719, 476, 736 45 35, 184, 372, 088, 832 #graphs 1 2 4 11 34 156 1, 044 12, 346 274, 668 12, 005, 168

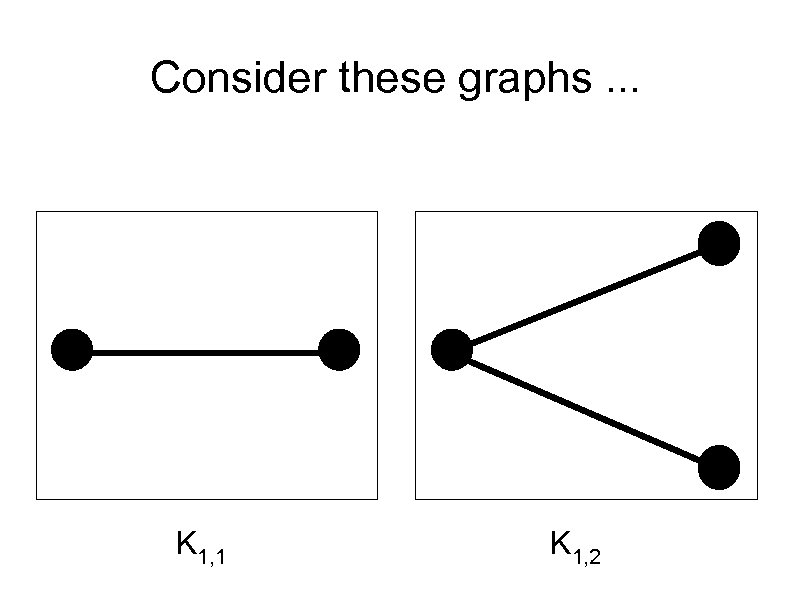Consider these graphs. . . K 1, 1 K 1, 2

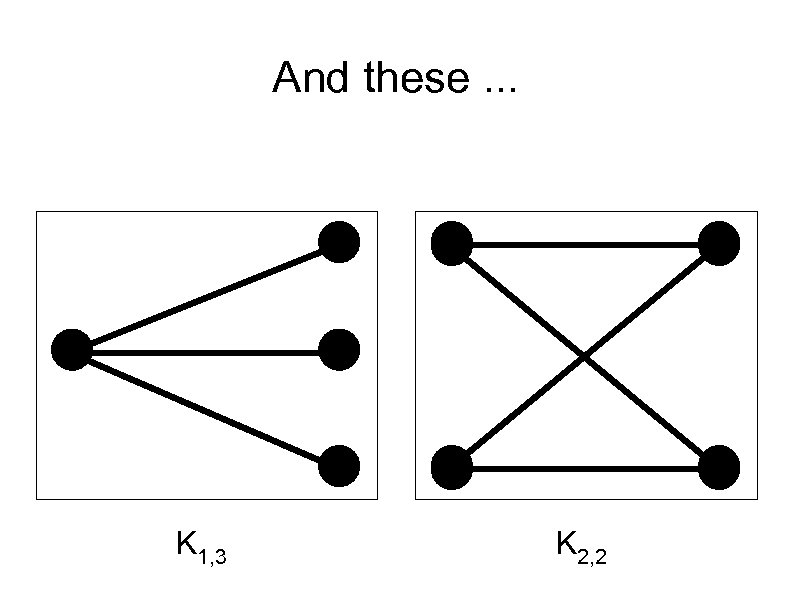And these. . . K 1, 3 K 2, 2

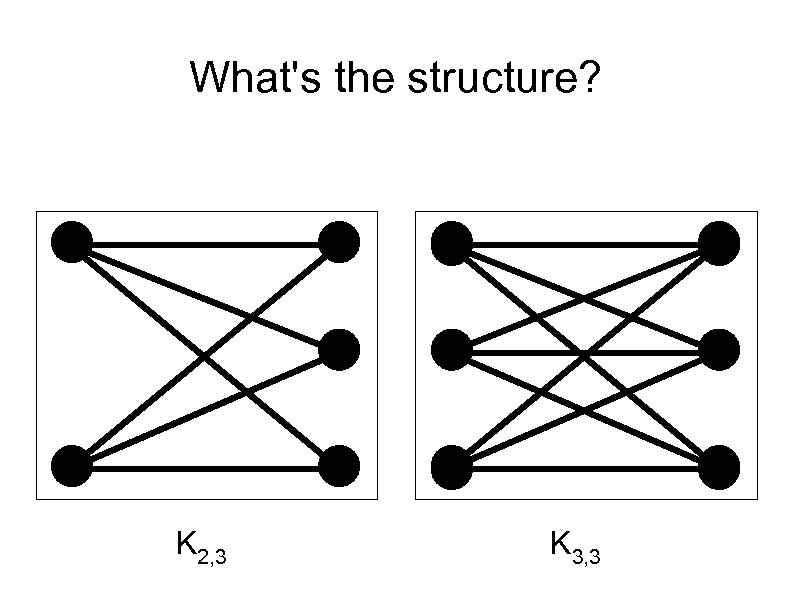What's the structure? K 2, 3 K 3, 3

Complete bipartite graphs If the set of all vertices can be partitioned into sets V and W such that every edge connects a vertex in V to a vertex in W, then the graph is called bipartite If a bipartite graph has as many edges as possible, then it is called a complete bipartite graph Notation: Km, n, where m = |V| and n = |W| How many edges in Km, n? |Km, n| = mn

Not all bipartite graphs are complete

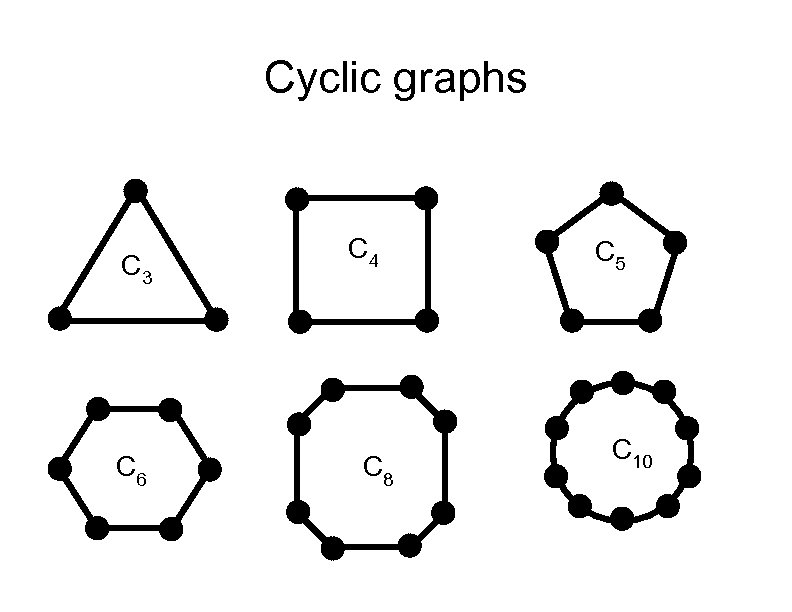Cyclic graphs C 3 C 6 C 4 C 8 C 5 C 10

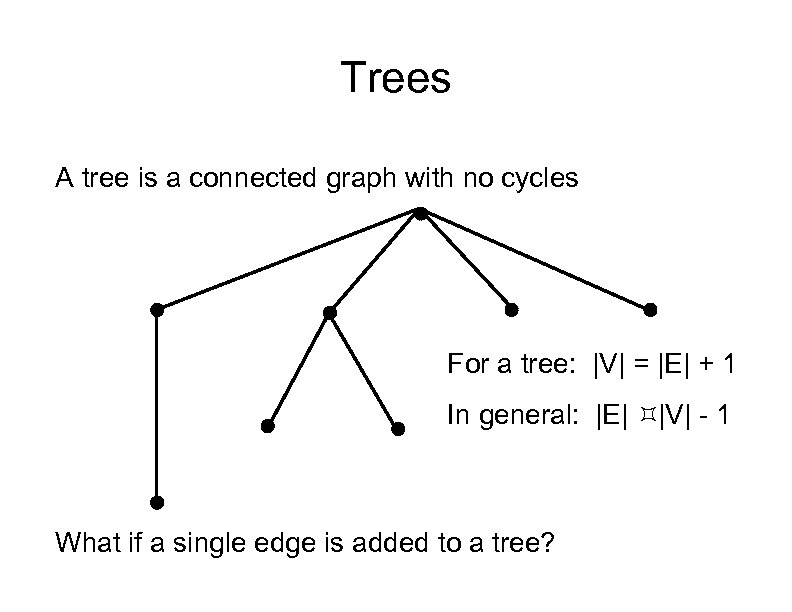Trees A tree is a connected graph with no cycles For a tree: |V| = |E| + 1 In general: |E| |V| - 1 What if a single edge is added to a tree?

What now? This concludes a crash introduction to graph theory We move on to our next main question:

What is the dimension of a graph?

But first: What do we mean by dimension?

A one-dimensional world Consider a straight line with an origin and a unit distance marked on it: 0 1 We can specify any point on the line with one number, the distance from the point to the origin, where points to the left are negative

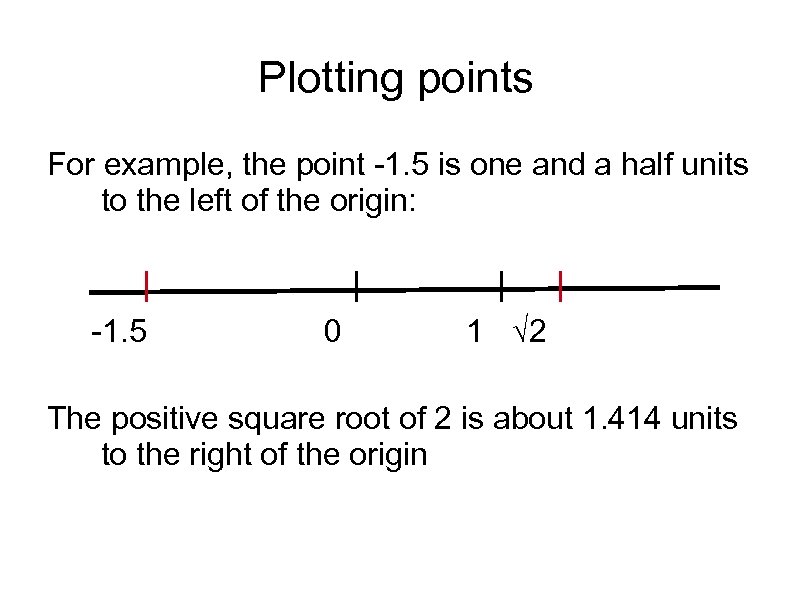Plotting points For example, the point -1. 5 is one and a half units to the left of the origin: -1. 5 0 1 √ 2 The positive square root of 2 is about 1. 414 units to the right of the origin

One-dimension - one number So, once an origin and a unit distance are specified, every point in a one-dimensional space can be specified by exactly one real number Conversely, for every real number, there is exactly one point in one-dimensional space Terminology: 1 -space

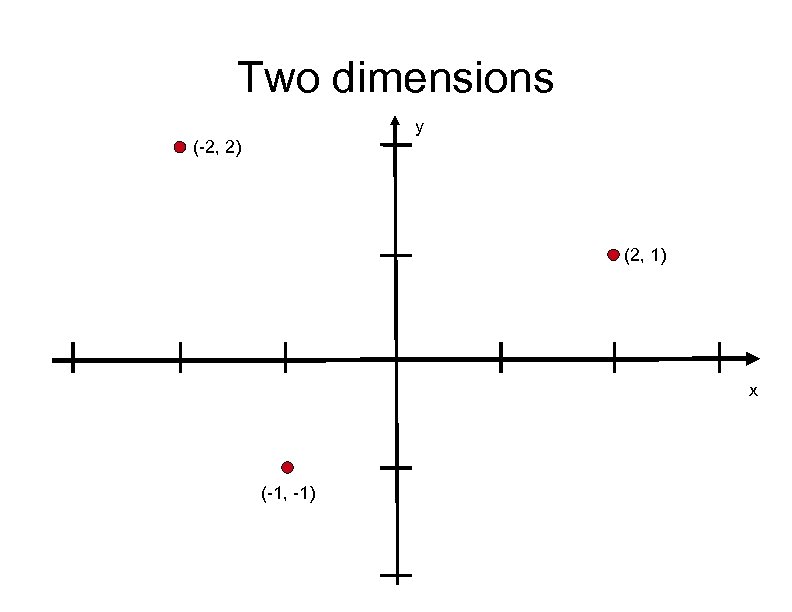Two dimensions y (-2, 2) (2, 1) x (-1, -1)

Two-dimensions - two numbers So, given two orthogonal axes (i. e. , perpendicular to each other), and a unit distance, every point in a two-dimensional space can be specified by exactly two real numbers Conversely, for every ordered pair of real numbers, there is exactly one point in twodimensional space Terminology: 2 -space, the plane 2

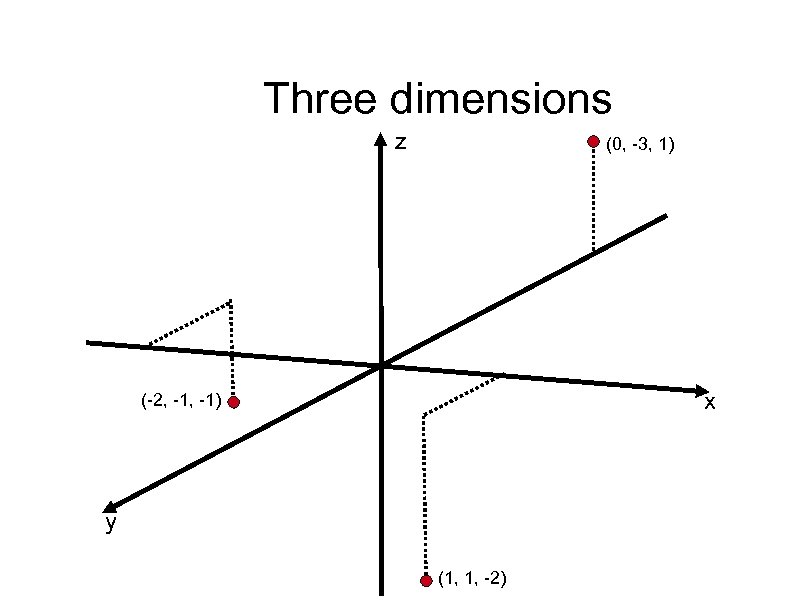Three dimensions z (0, -3, 1) x (-2, -1) y (1, 1, -2)

Three-dimensions - three numbers So, given three orthogonal axes (i. e. , each pair of axes are perpendicular), and a unit distance, every point in a three-dimensional space can be specified by exactly three real numbers Conversely, for every ordered triple of real numbers, there is exactly one point in threedimensional space Terminology: 3 -space 3

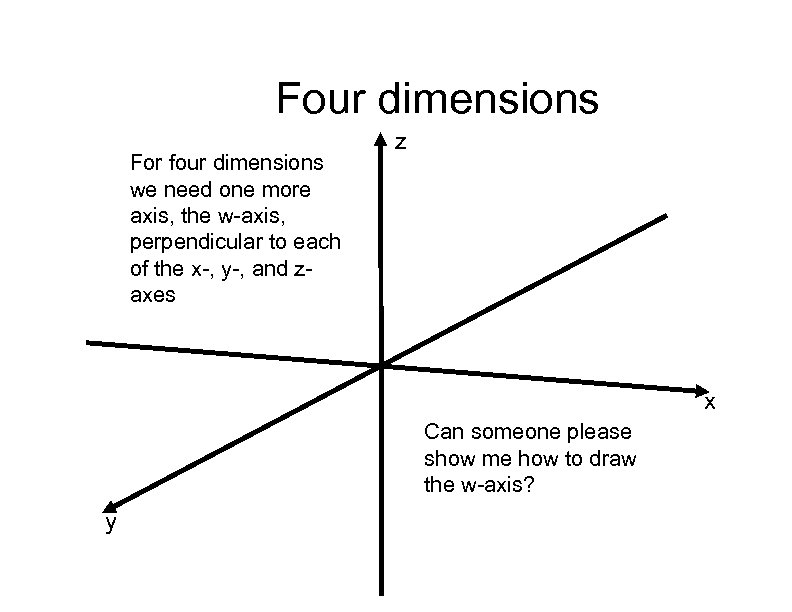Four dimensions For four dimensions we need one more axis, the w-axis, perpendicular to each of the x-, y-, and zaxes z x Can someone please show me how to draw the w-axis? y

Four-dimensions - four numbers We cannot draw the w-axis; we live in 3 -space, and anything in n-space for n > 3 is very difficult for us to visualize But 4 -dimensional space exists, nevertheless Given four orthogonal axes (i. e. , each pair of axes are perpendicular), and a unit distance, every point in a four-dimensional space can be specified by exactly four real numbers Conversely, for every ordered 4 -tuple of real numbers, there is exactly one point in fourdimensional space (4 -space, 4)

n-dimensions - n numbers Given n > 4 orthogonal axes (i. e. , each pair of axes are perpendicular), and a unit distance, every point in an n-dimensional space can be specified by exactly n real numbers Conversely, for every ordered n-tuple of real numbers, there is exactly one point in ndimensional space Terminology n-space n

Other dimensions What about ∞, an infinite-dimensional space? Yep, we got'em But they are not of interest for this talk However, there is one other space we don't want to forget: The 0 -dimensional space Pick any point It's dimension is 0

The dimension of a graph In 1965, the illustrious trio P. Erdős, F. Harary, and W. T. Tutte published a paper entitled On the dimenion of a graph The first thing they did in this paper was to define the dimension of a graph

The dimension of a graph G, denoted dim(G), is the minimum n such that G has a unitdistance representation in n, i. e. , every edge is of length 1. The vertices of G are mapped to distinct points of n, but edges may cross Intuitively: Given a graph, construct a model where every edge is of length 1, and then figure out whether it can live in 1 -space, 2 space, 3 -space, 4 -space, . . . , n-space

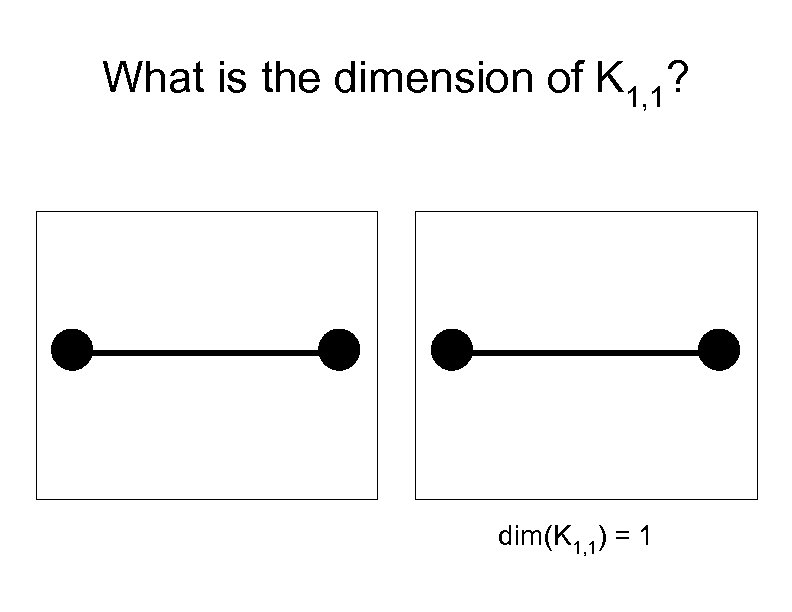What is the dimension of K 1, 1? dim(K 1, 1) = 1

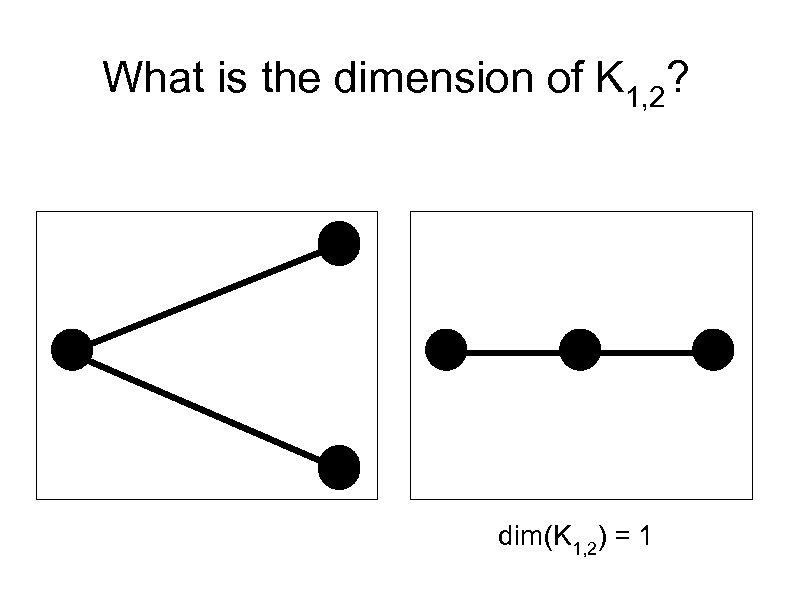What is the dimension of K 1, 2? dim(K 1, 2) = 1

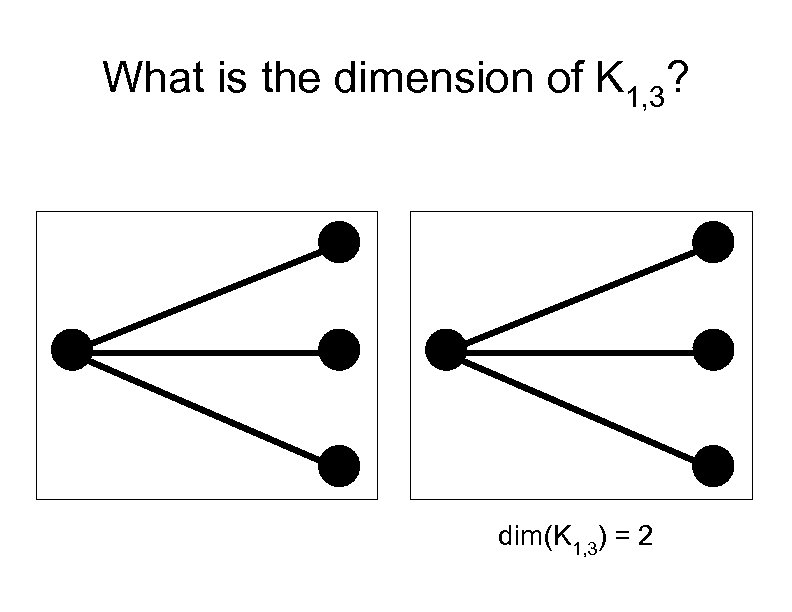What is the dimension of K 1, 3? dim(K 1, 3) = 2

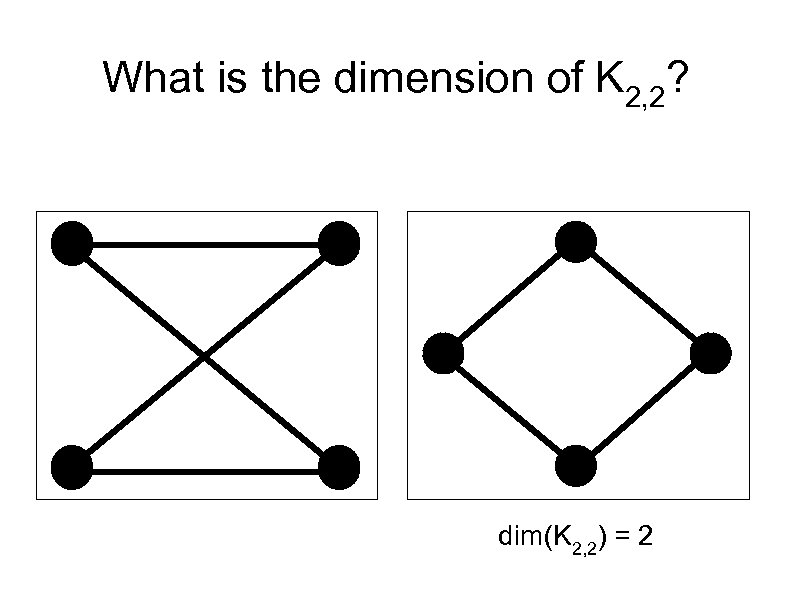What is the dimension of K 2, 2? dim(K 2, 2) = 2

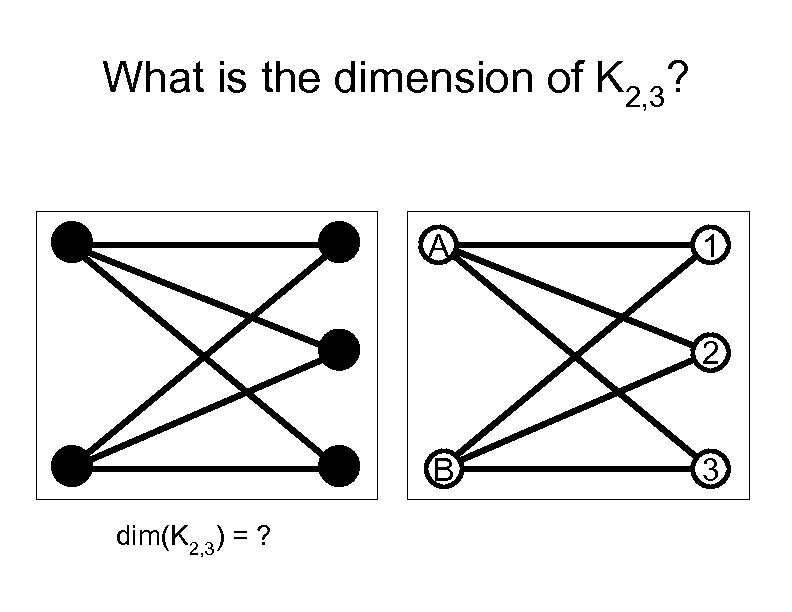What is the dimension of K 2, 3? A 1 2 B dim(K 2, 3) = ? 3

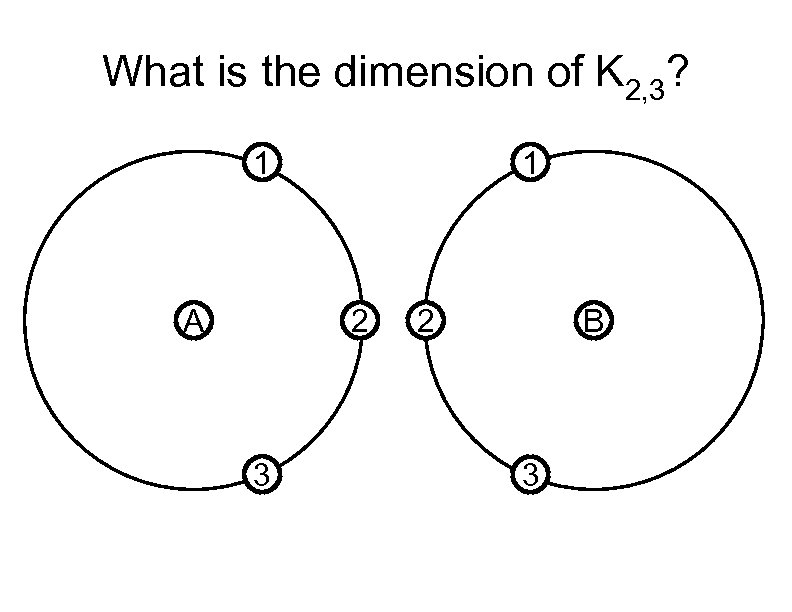What is the dimension of K 2, 3? 1 A 1 2 3 2 B 3

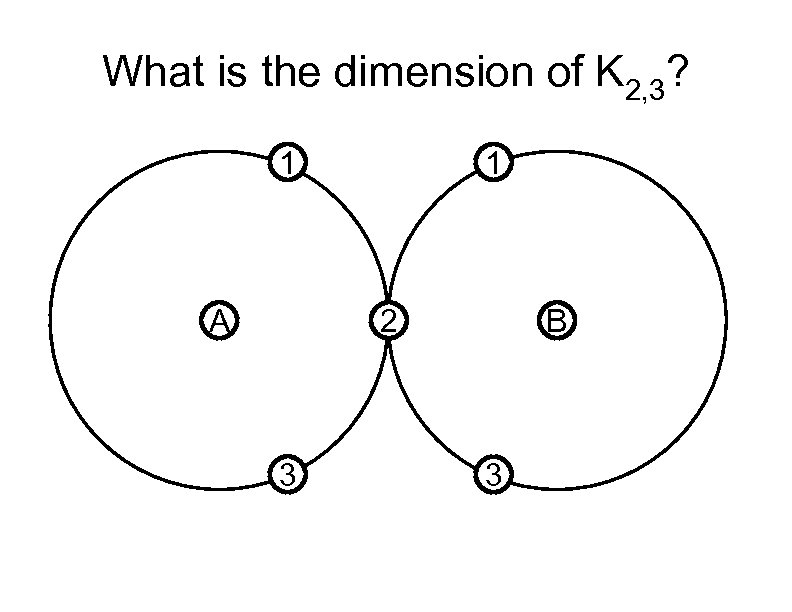What is the dimension of K 2, 3? 1 A 1 2 3 B 3

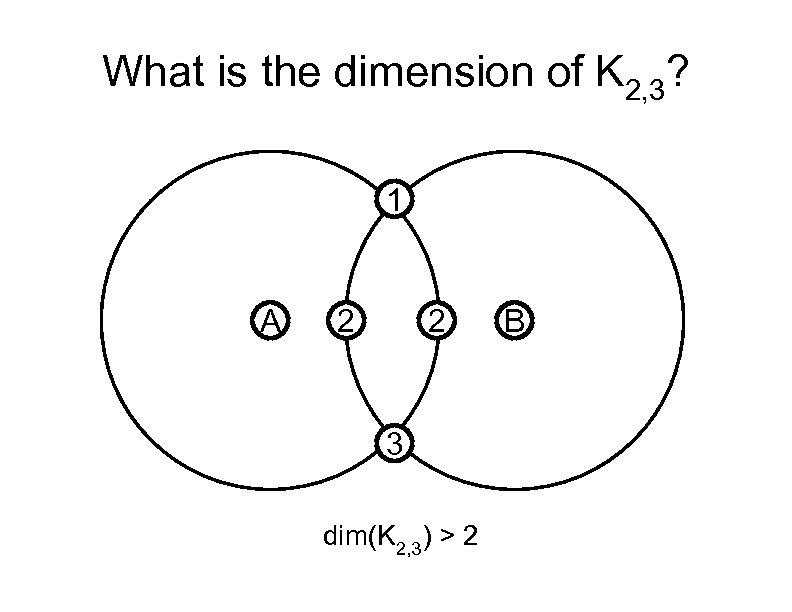What is the dimension of K 2, 3? 1 A 2 2 3 dim(K 2, 3) > 2 B

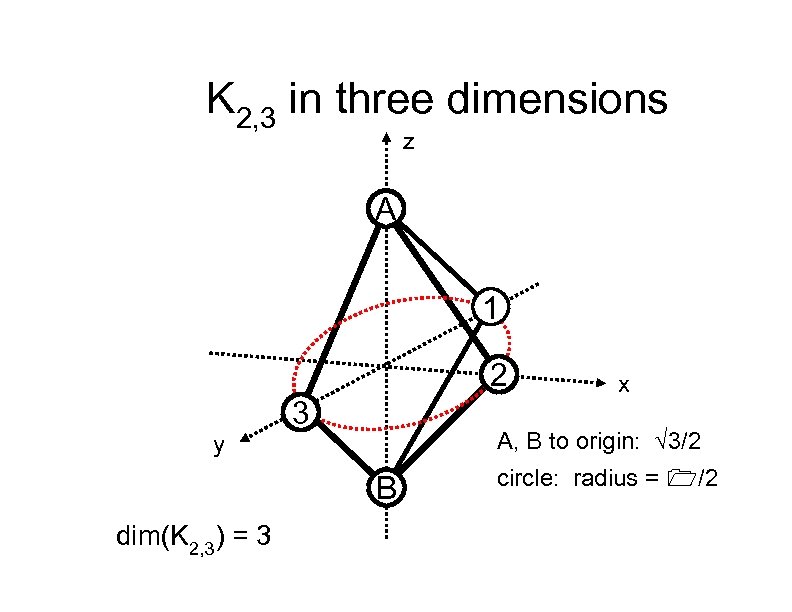K 2, 3 in three dimensions z A 1 2 y 3 A, B to origin: √ 3/2 B dim(K 2, 3) = 3 x circle: radius = 1/2

What about Kn, m for n, m ≥ 3? There a lot of points on that circle dim(K 2, m) = 3 for m > 3 What is dim(K 3, 3)? What's a lower bound on dim(K 3, 3)? Since K 2, 3 is a subgraph of K 3, 3 dim(K 2, 3) £dim(K 3, 3) So dim(K 3, 3) ≥ 3

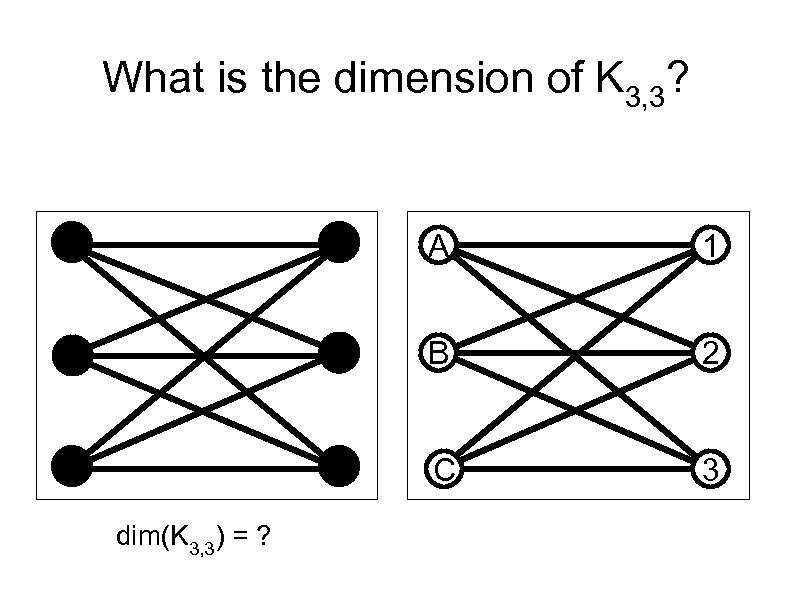What is the dimension of K 3, 3? A B 2 C dim(K 3, 3) = ? 1 3

What is the dimension of K 3, 3? We know dim(K 3, 3) 3 Might dim(K 3, 3) = 3? Using an argument like that for K 3, 2 but with three spheres instead of two circles, we can show that K 3, 3 cannot be embedded in 3 -space with edges of length 1 So dim(K 3, 3) > 3

What is the dimension of K 3, 3? So dim(K 3, 3) 4 In fact, dim(K 3, 3) = 4 To show this, we consider two circles of radius 1/Ö in 4: 2 C 1: x 2 + y 2 = ½ C 2: z 2 + w 2 = ½

What is the dimension of K 3, 3? Pick any point P = (x, y, 0, 0) on circle C 1 Pick any point Q = (0, 0, z, w) on circle C 2 The distance between P and Q is the square root of (x-0)2 + (y-0)2 + (0 -z)2 + (0 -w)2 = x 2 + y 2 + z 2 + w 2 = (x 2 + y 2) + (z 2 + w 2) =½+½ =1

What is the dimension of K 3, 3? So every point P on circle C 1 is at a distance 1 from every point Q on circle C 2 Pick any three distinct points on C 1 and call them A, B, and C Pick any three distinct points on C 2 and call them 1, 2, and 3 Insert an edge of length 1 from each letter to each digit We have an embedding of K 3, 3 in 4

What is the dimension of Km, n? What about dim(Km, n) for m, n ≥ 3? There a lot of points on those two circles dim(Km, n) = 4 for m, n ≥ 3

What is the dimension of Kn? K 3 can be represented as an equilateral triangle: dim(K 3) = 2 K 4 can be represented as a regular tetrahedron dim(K 4) = 3 K 5 can be represented as. . . ? dim(K 5) = ? An exercise for the perspicacious student: Show that dim(Kn) = n - 1

Basic results about dimension dim(Kn) = n - 1 dim(Kn - e) = n - 2 dim(K 1, 1) = dim(K 1, 2) = 1, dim(K 1, m) = 2 for m 3 dim(K 2, 2) = 2, dim(K 2, m) = 3 for m 3 dim(Km, n) = 4 for m, n 3 dim(Cn) = 2 for Cn a cyclic graph of order n 3 dim(tree) £ 2 if H is a subgraph of G then dim(H) £dim(G)

Questions Now we have answered our first two questions: What is a graph? What is the dimension of a graph? Only one question is left:

What is the least number of edges a four-dimensional graph must have?

Exactly what is the question? In 2009 The Mathematical Coloring Book by Alexander Soifer was published In this book a question posed by Paul Erdős in 1991 appears What is the smallest number of edges in a graph G if dim(G) = 4? In the rest of this talk we will answer this question, but first, who was Paul Erdős?

Paul Erdős (1913 -1996)

Paul Erdős was one of the most prolific mathematicians of the 20 th century He wrote at least 1, 475 papers Some years during his 70's he wrote over 50 papers He was an incredible collaborator: 511 coauthors There is a website devoted to keeping track of his collaborators: The Erdős Number Project (wwwp. oakland. edu/enp)

What's your Erdős Number? The Collabortion Graph has about 401, 000 vertices, each one an author An edge from author A to author B means that they have co-authored at least one paper There about 676, 000 edges in the graph If there is an edge from Erdős to author A, then author A has Erdős Number 1 If author B co-authored with A (and A has number 1), then B has Erdős Number 2 And so on. . . Most of us have Erdős Number ∞

Paul Erdős (1913 -1996)

How did he do it? No wife No children No hobbies No home No job And, BTW, he was a mathematical genius

No home? Erdős was born in Budapest in 1913 and grew up there, the child of two math teachers At 21 he went to Manchester, England At 25 he was at Princeton University In 1952 the U. S. denied a re-entry visa Reason? One story is that when asked what he thought of Karl Marx, he said: "I'm not competent to judge. But no doubt he was a great man. "

"Another roof, another proof" Eventually he was able to travel freely, and travel he did He showed up at colleagues front doors, all his possessions in a small suitcase, and announced, "My brain is open!" After a couple of days (or weeks), busy collaborating, proving new results, he got on a plane and moved on Some friends, Fan Chung and Ronald Graham among them, kept a room in readiness for him

Fan Chung & Ronald Graham

No job? Erdős lived on prizes for his work, and stipends from lectures He gave most of his money away Some of his money was posted as rewards for proving conjectures $25 for results just out of reach of current math Thousands for difficult, significant problems There is still money to be claimed Payment by check signed by Erdős (can't cash) Cashable check paid by Ronald Graham

Some sayings of Erdős "Some French socialist said that private property is theft … I say that private property is a nuisance. " "If numbers aren't beautiful, I don't know what is. " Erdős' suggestion for his own epitaph: "Finally I am becoming stupider no more. "

Sayings by others "Want to meet Erdős? Just stay here and wait. He'll show up. " Often attributed to Erdős but actually said by another Hungarian: Alfréd Rényi: "A mathematician is a machine for turning coffee into theorems. "

Literature inspired by Erdős A conjecture thought to be sound Was that every circle was round In a paper of Erdős Written in Kurdish A counterexample is found!

A film and books Film: N is a Number Books: The Man Who Loved Only Numbers by Paul Hoffman My Brain is Open by Bruce Schechter

A parting word

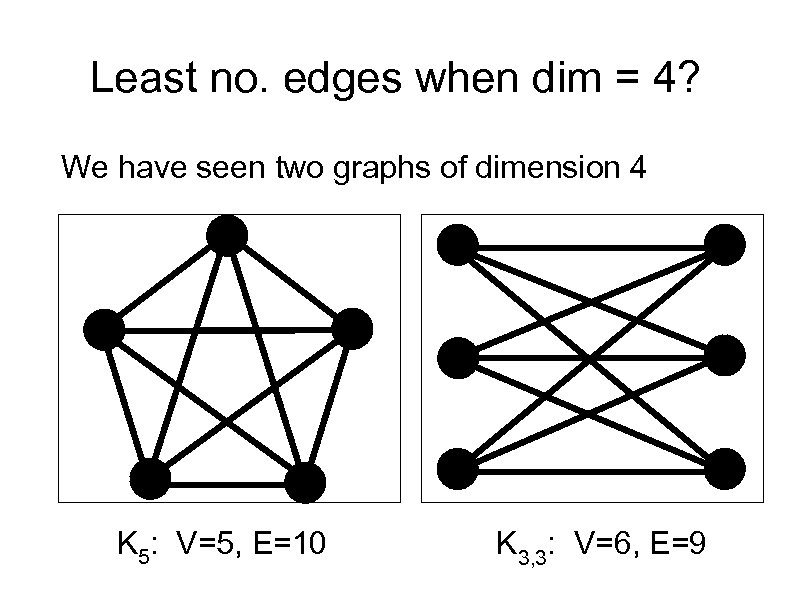Least no. edges when dim = 4? We have seen two graphs of dimension 4 K 5: V=5, E=10 K 3, 3: V=6, E=9

Minimum number of vertices? Since dim(Kn) = n-1, we know dim(K 5) = 4 Since dim(Kn - e) = n-2, we know dim(K 5 - e) = 3, so every proper subgraph of K 5 has dimension at most 3 So a four dimensional graph with a minimum number of edges must have more than 5 vertices Therefore we need to look at graphs with 6 or more vertices

Number of edges? Remember that a connected graph must have at least one more vertex than it has edges, i. e. , |E| |V| - 1 So, if |V| = 6, it must be that |E| 6 - 1 = 5 Therefore we need to look at graphs with 5 or more edges We already have a four-dimensional graph with 9 edges (K 3, 3), so we need not consider graphs with more than 9 edges

Maximum number of vertices? Using |E| |V| - 1 again with |E| = 9, we have 9 |V| - 1, so |V| £ 10 Therefore we need to look at graphs with 10 or fewer vertices To sum up: Find a four-dimensional graph with 6 £|V| £ 10 5 £|E| £ 9

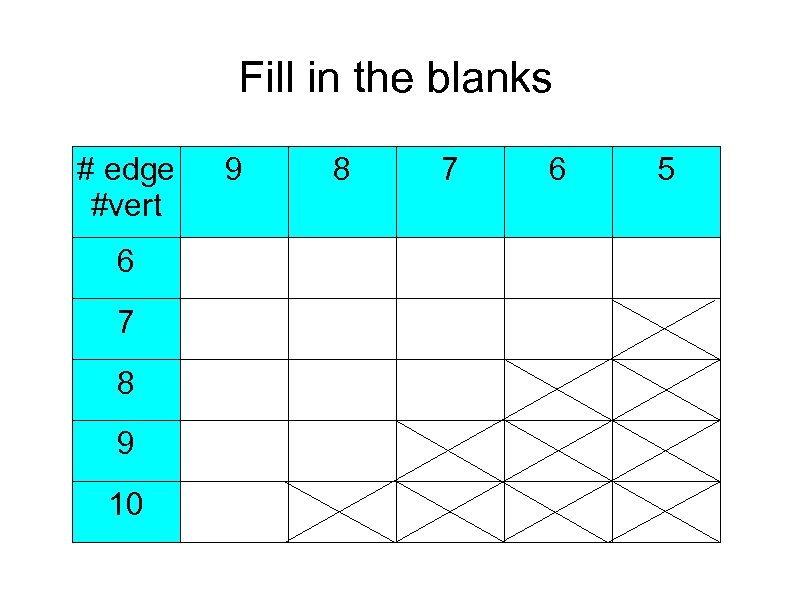Fill in the blanks # edge #vert 6 7 8 9 10 9 8 7 6 5

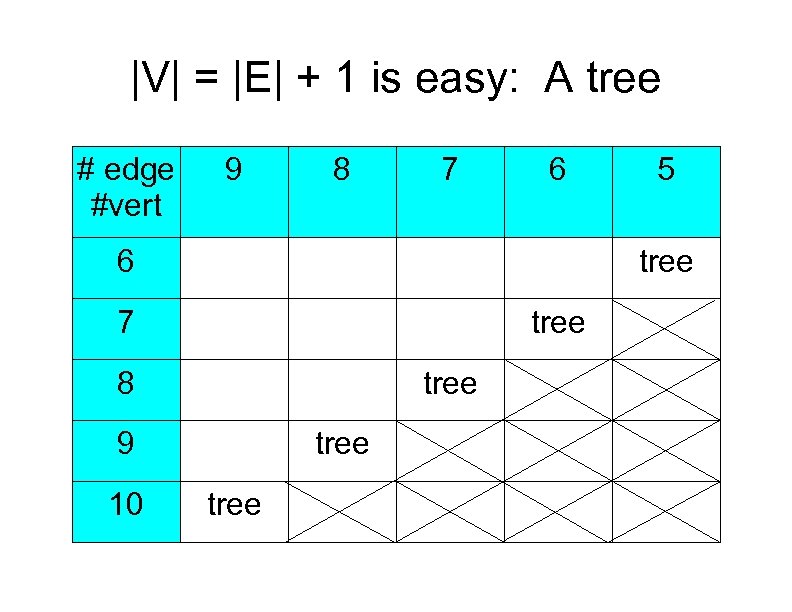|V| = |E| + 1 is easy: A tree # edge #vert 9 8 7 6 6 tree 7 tree 8 tree 9 10 5 tree

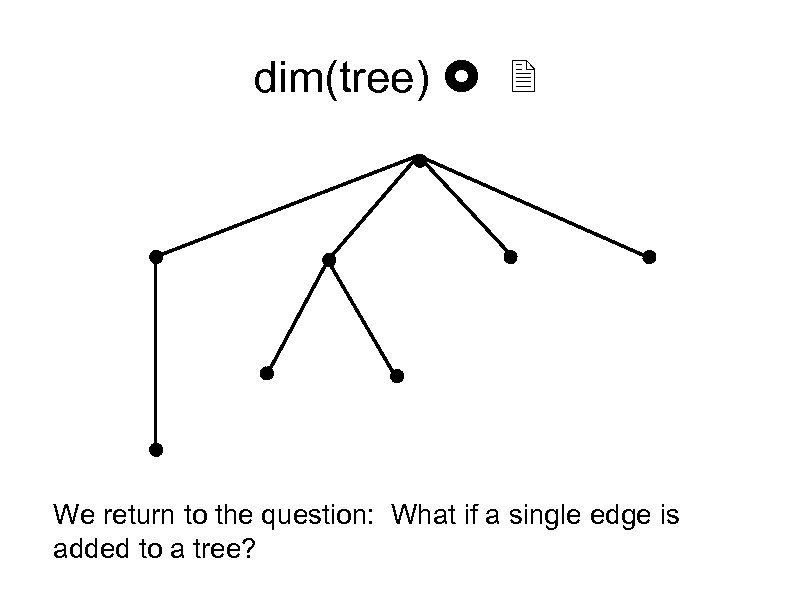dim(tree) £ 2 We return to the question: What if a single edge is added to a tree?

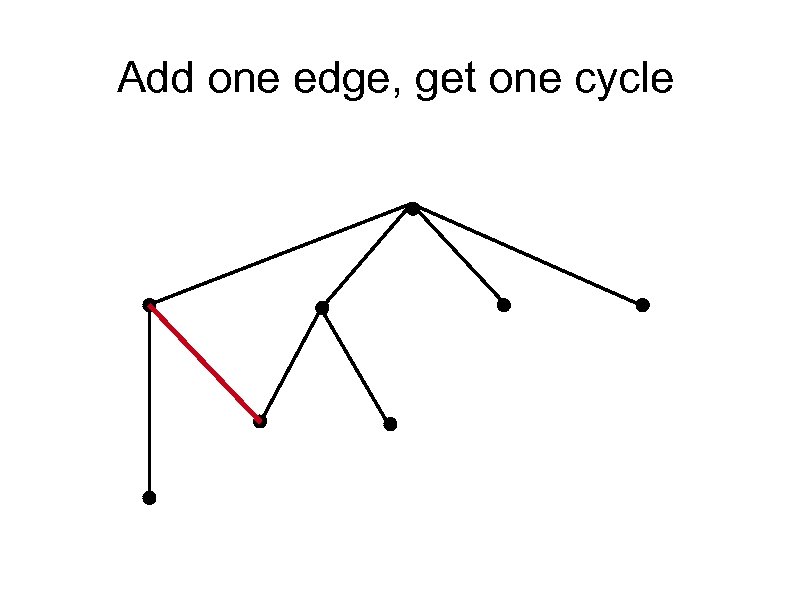Add one edge, get one cycle

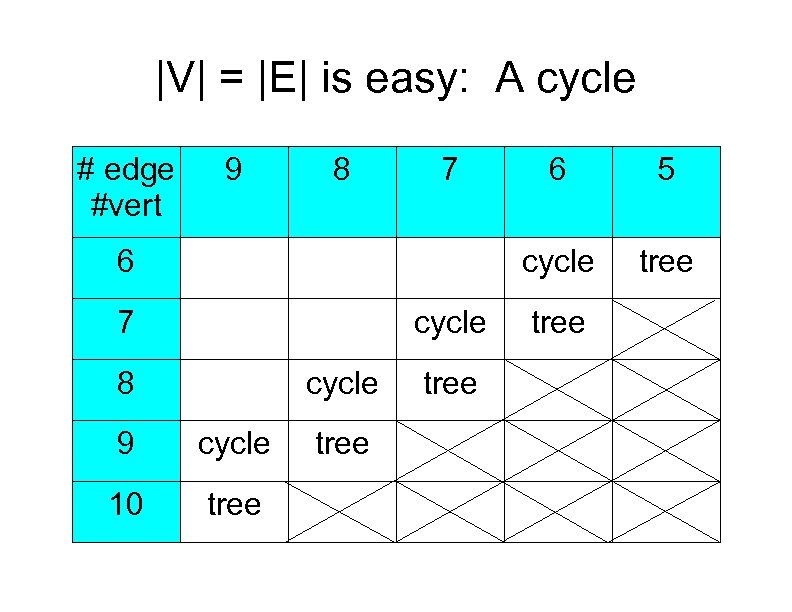|V| = |E| is easy: A cycle # edge #vert 9 8 7 7 cycle 8 cycle 9 cycle 10 tree 5 cycle 6 6 tree

Add two edges and get what?

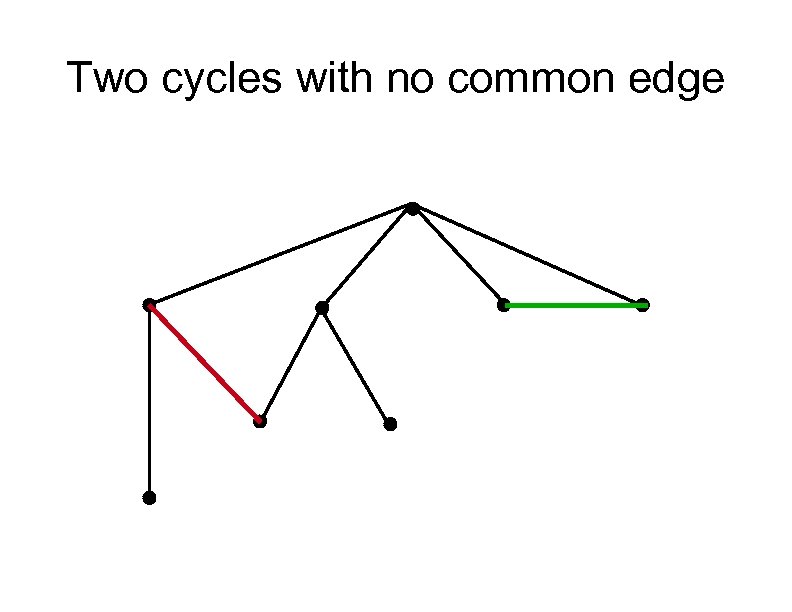Two cycles with no common edge

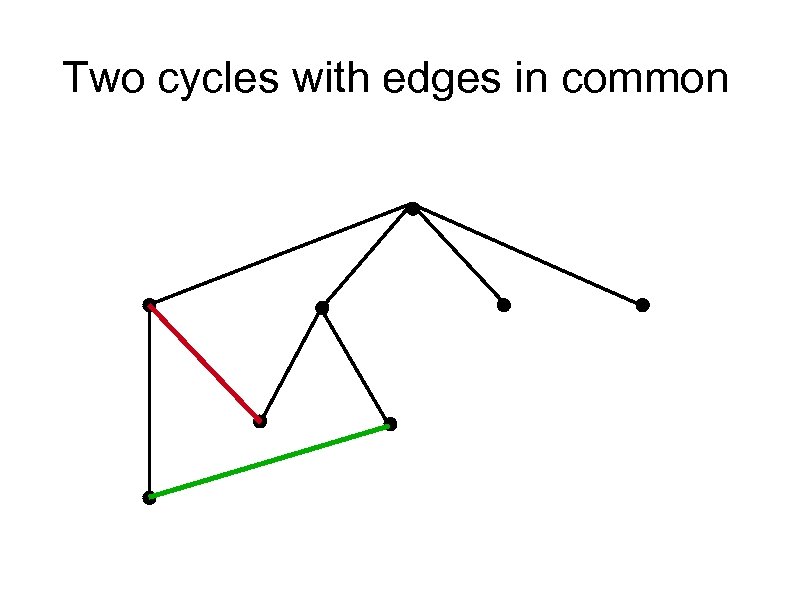Two cycles with edges in common

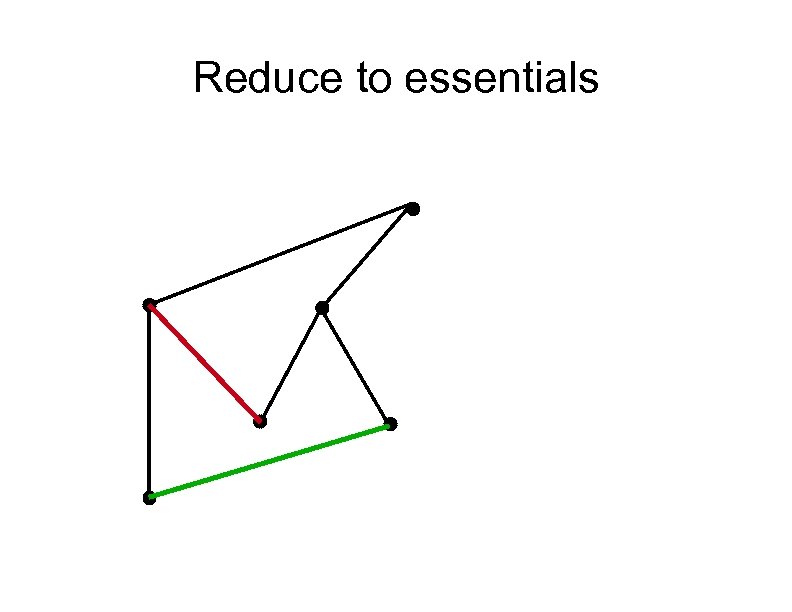Reduce to essentials

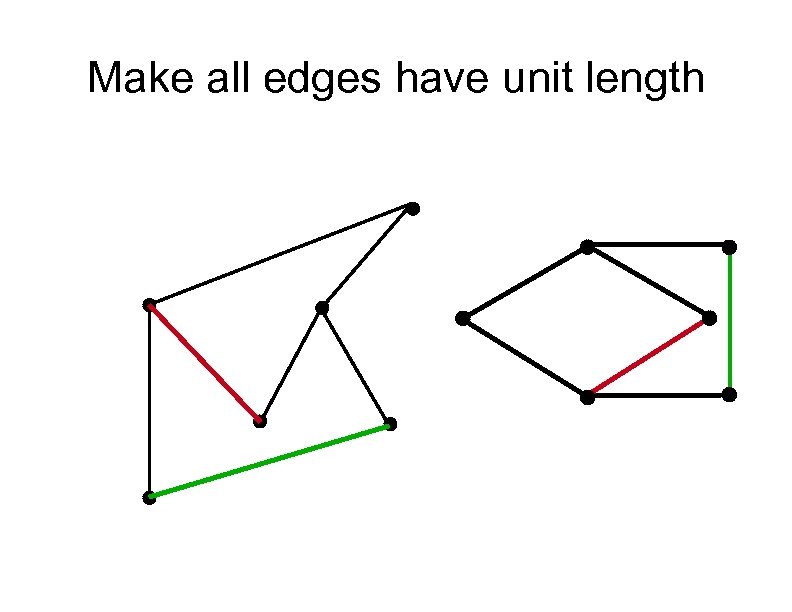Make all edges have unit length

3 -routes When two edges are added to a tree so that the result is two cycles sharing at least one common edge, the resulting graph is called a 3 -route A 3 -route consists of three paths which have nothing in common except their end vertices So there is a left path, a middle path, and a right path from one end vertex to the other end vertex

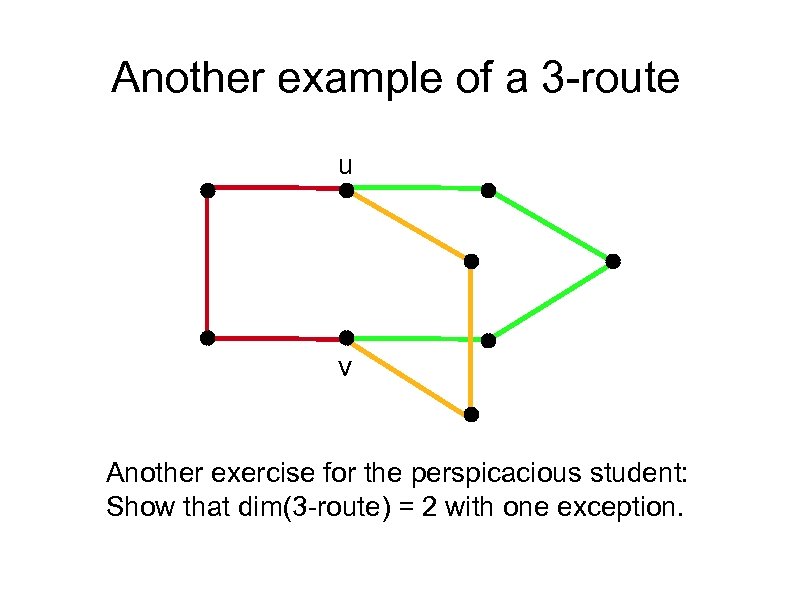Another example of a 3 -route u v Another exercise for the perspicacious student: Show that dim(3 -route) = 2 with one exception.

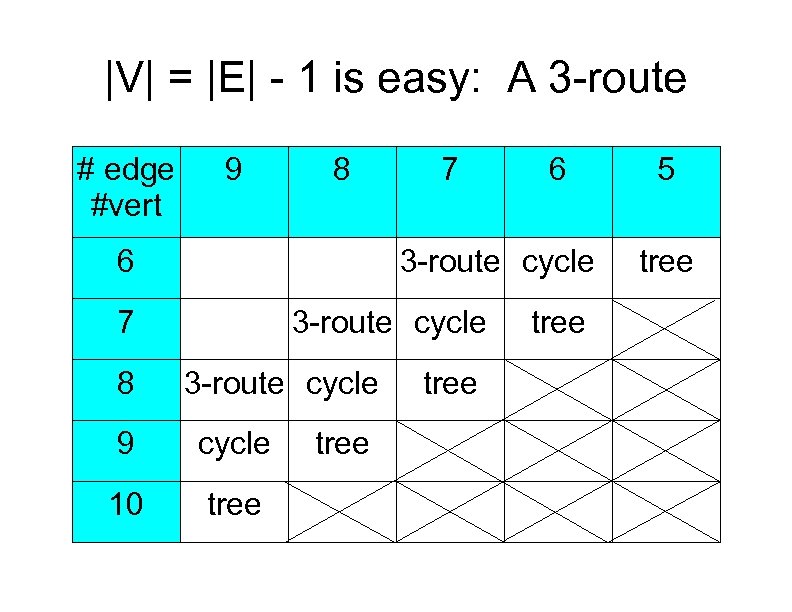|V| = |E| - 1 is easy: A 3 -route # edge #vert 9 8 6 6 3 -route cycle 7 8 7 3 -route cycle 9 cycle 10 tree 5 tree

We're getting closer and closer Now only these three cases are left: 6 vertices, 8 edges 6 vertices, 9 edges 7 vertices, 9 edges There are 156 graphs with 6 vertices and 1044 graphs with 7 vertices Way too many To the rescue: An Atlas of Graphs by R. C. Read and R. J. Wilson

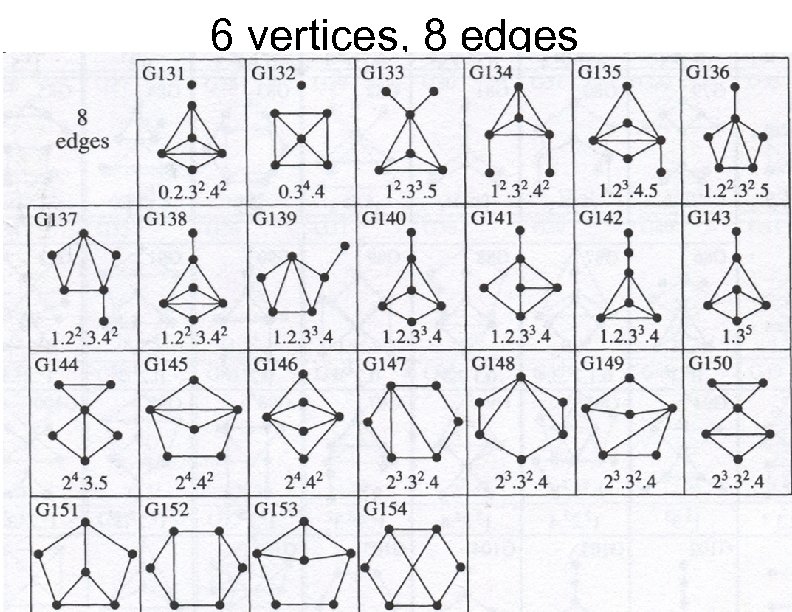6 vertices, 8 edges

Narrowing down The Atlas lets us pare down to fewer graphs: 6 vertices, 8 edges: 24 graphs 6 vertices, 9 edges: 21 graphs 7 vertices, 9 edges: 131 graphs Total: 176 graphs It's still too many But let's take a look at that Atlas page again

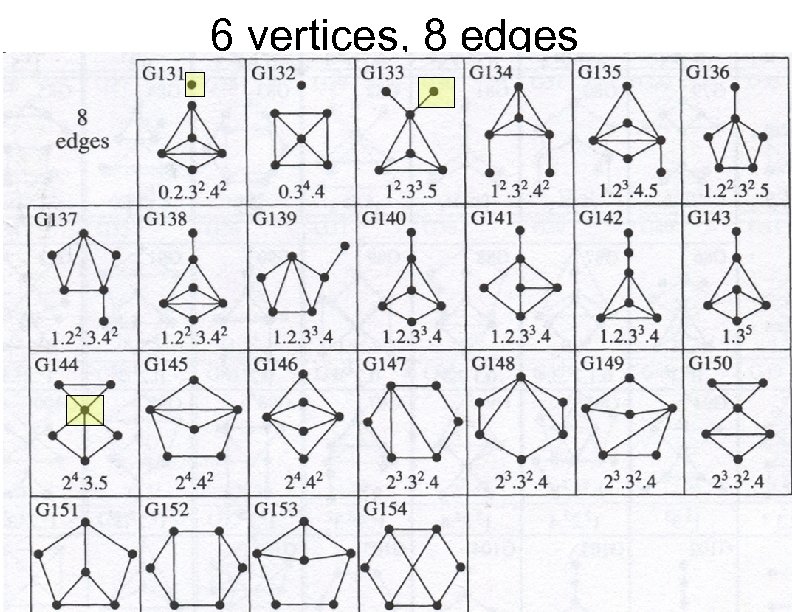6 vertices, 8 edges

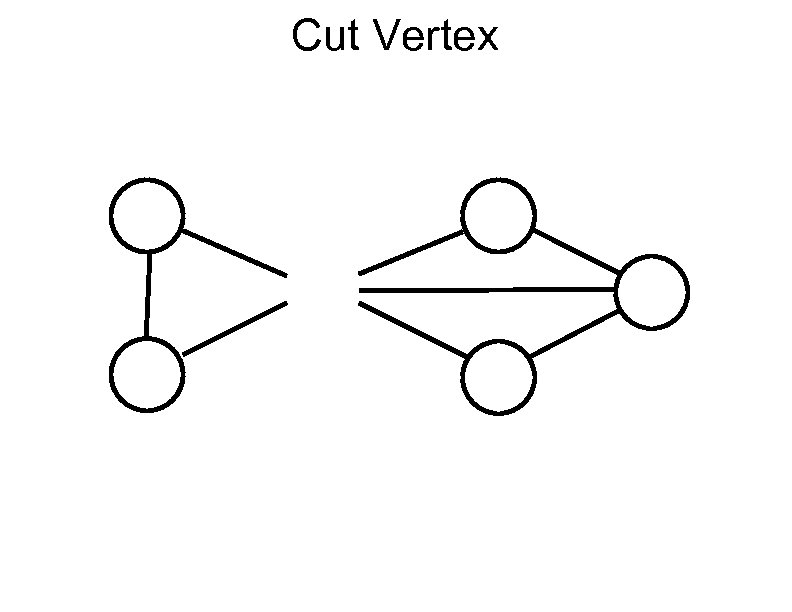
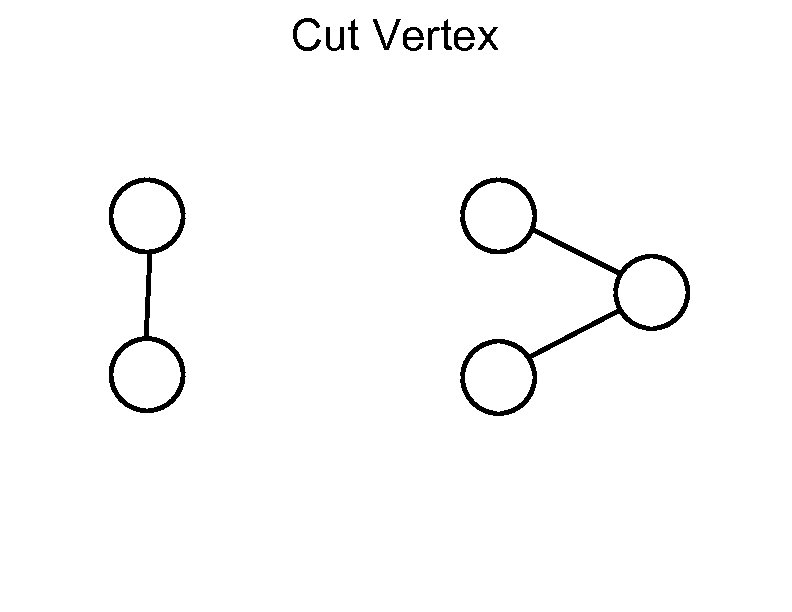
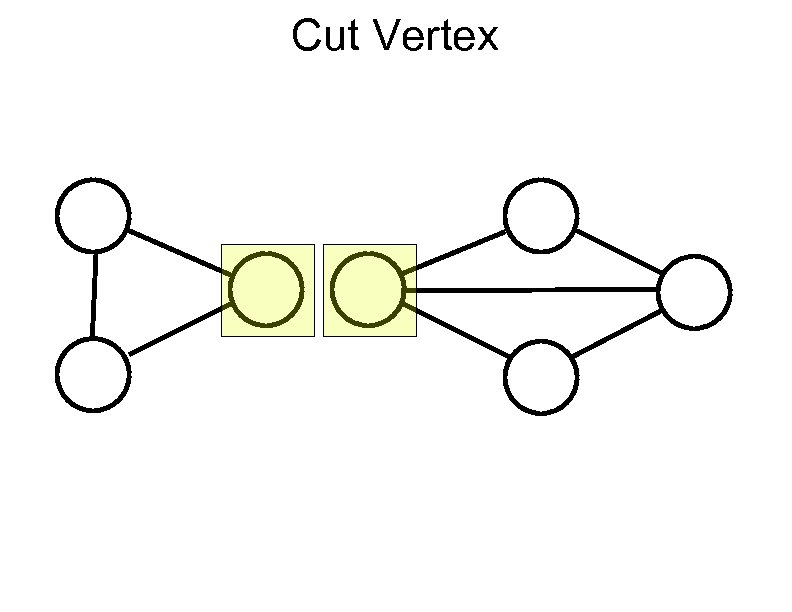
Cut Vertex

Cut Vertex

Cut Vertex

Cut Vertex

Narrowing down yet more These graphs are not of interest: A graph with vertices of degree 0 or 1 A graph which is not connected A graph which has a cut vertex Yet another exercise for the perspicacious student: If G is a four-dimensional graph with a minimum number of edges, then G cannot contain a cut vertex Terminology: A graph with no cut vertex is said to have vertex connectivity 2

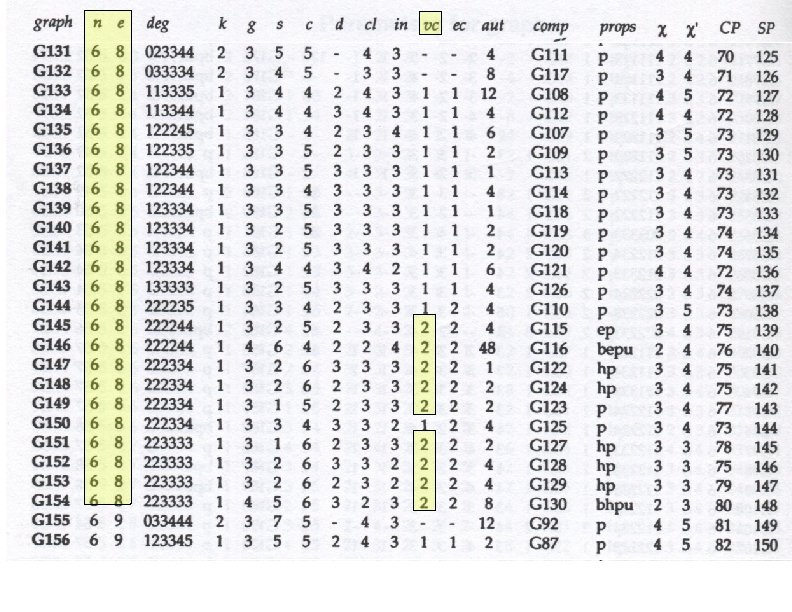
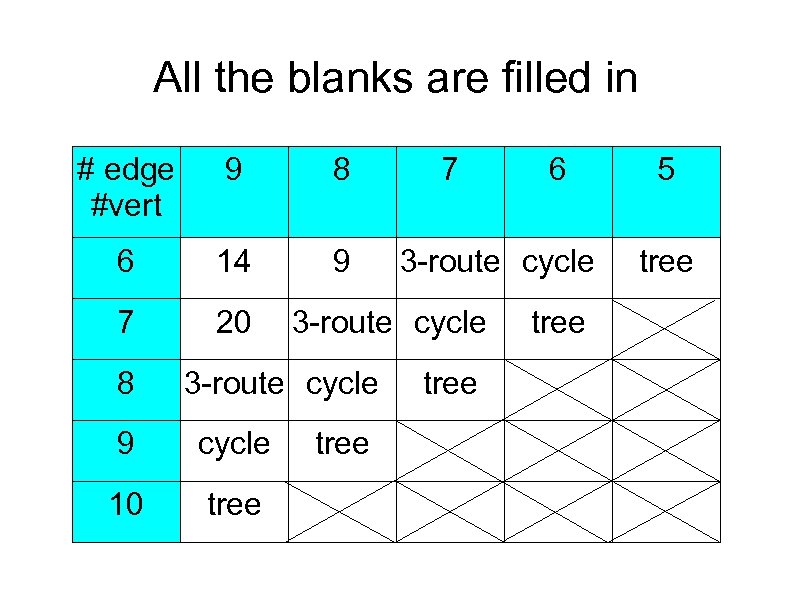All the blanks are filled in # edge #vert 9 8 6 14 9 7 20 8 cycle 10 tree 6 3 -route cycle 9 7 tree 5 tree

Narrowed down enough? So we are now down to this many graphs: 6 vertices, 8 edges: 9 graphs 6 vertices, 9 edges: 14 graphs 7 vertices, 9 edges: 20 graphs Total: 43 graphs Lacking a brilliant flash of insight, we look at all of the 43 graphs and see if we can embed them in 2 -, 3 -, or 4 -dimensions

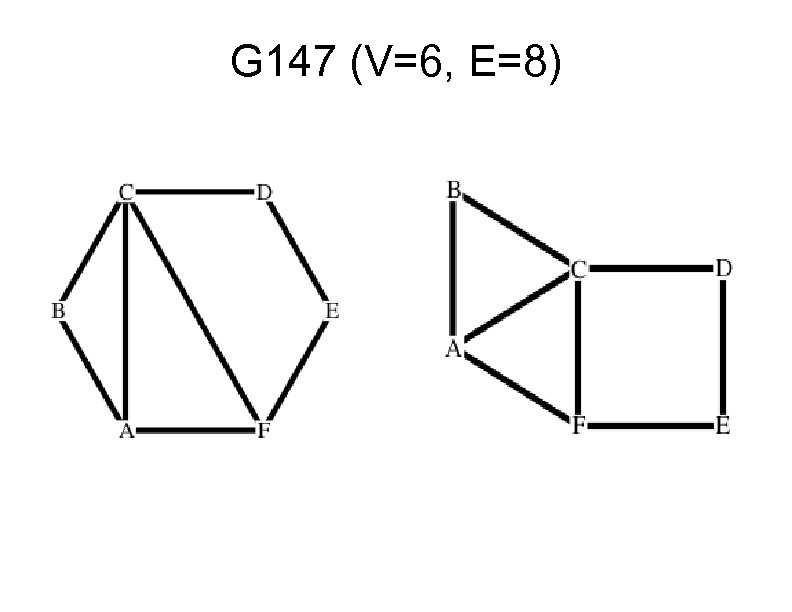G 147 (V=6, E=8)

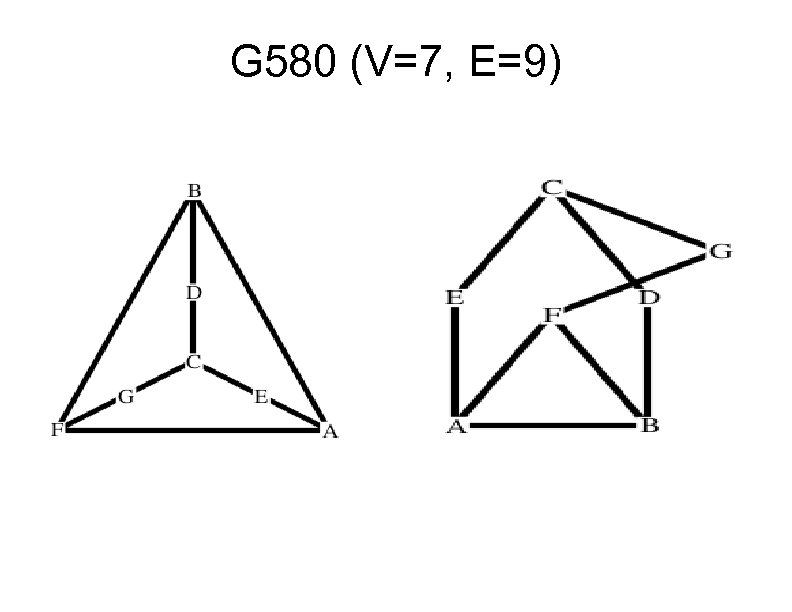G 580 (V=7, E=9)

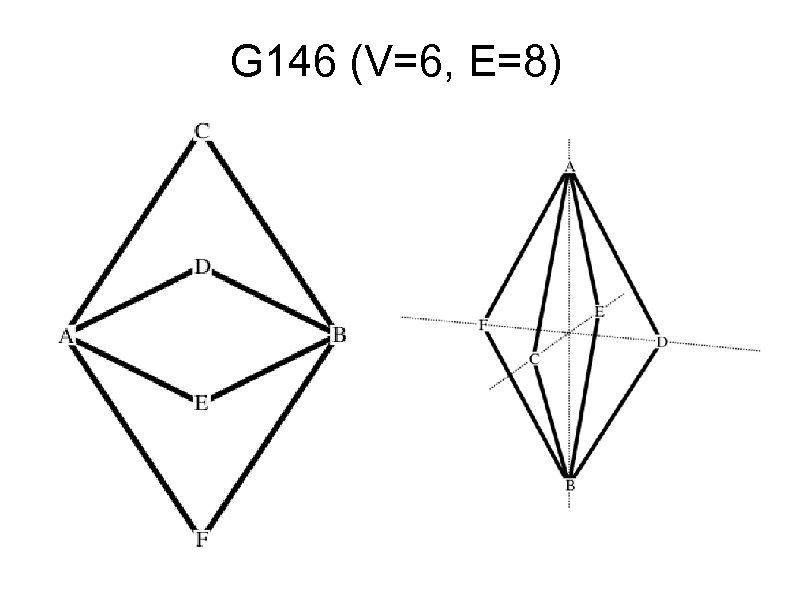G 146 (V=6, E=8)

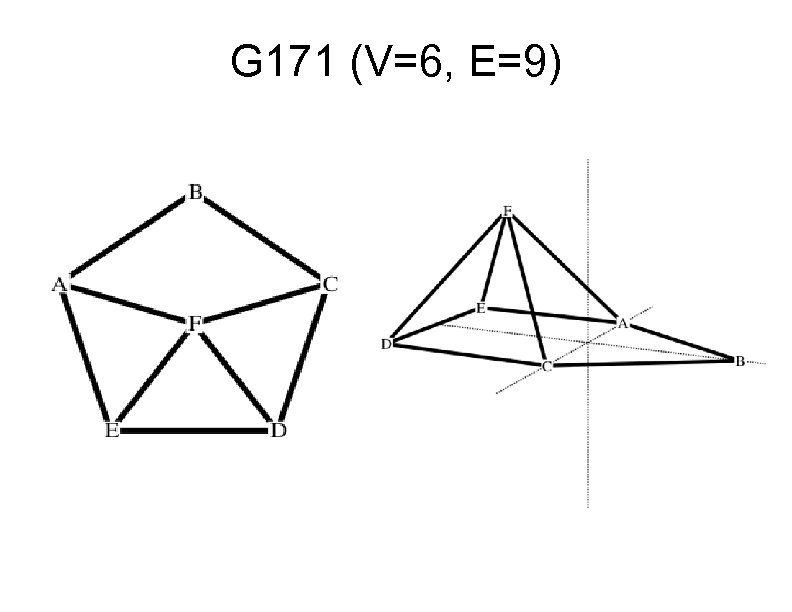G 171 (V=6, E=9)

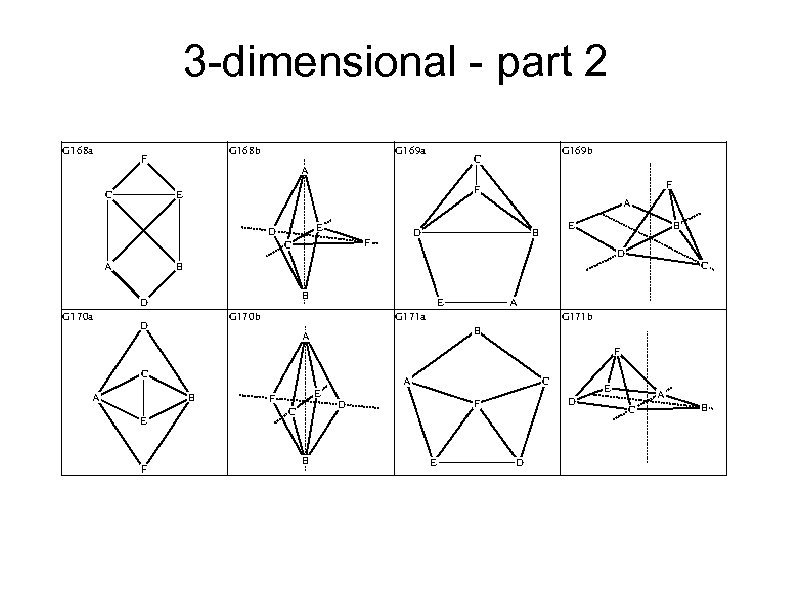
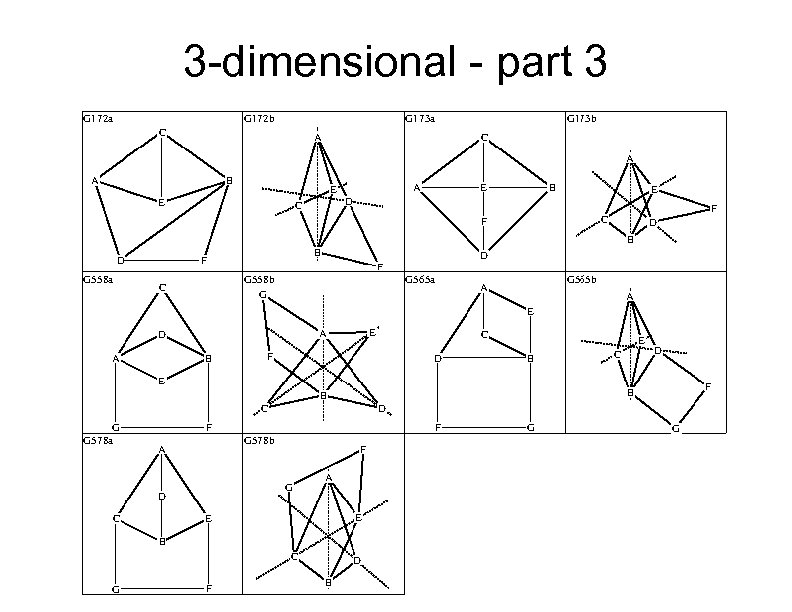
Only 39 more to go Fortunately, we are running out of time, so you won't have to look at the details of the 39 remaining embeddings Here is the breakdown by dimension: 2 -dimensional: 27 graphs 3 -dimensional: 15 graphs 4 -dimensional: 1 graph Total: 43 graphs Here all 43 embeddings:

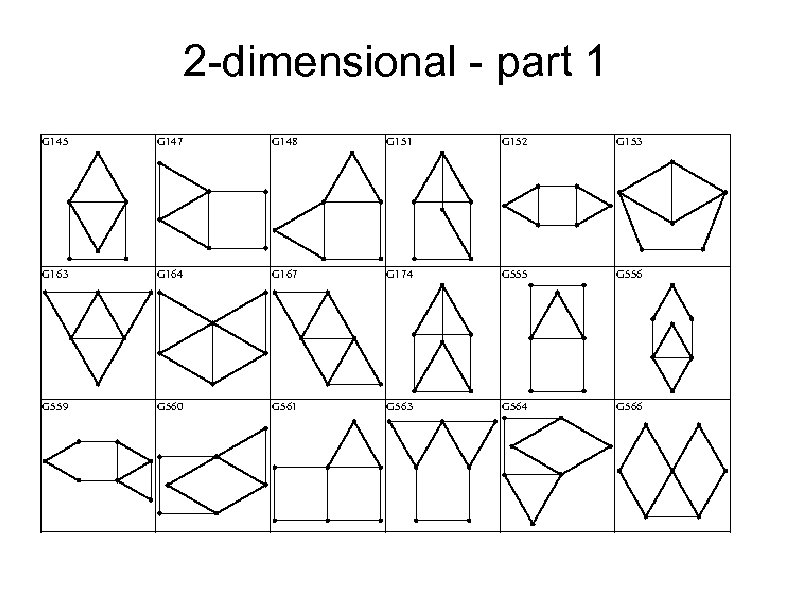2 -dimensional - part 1

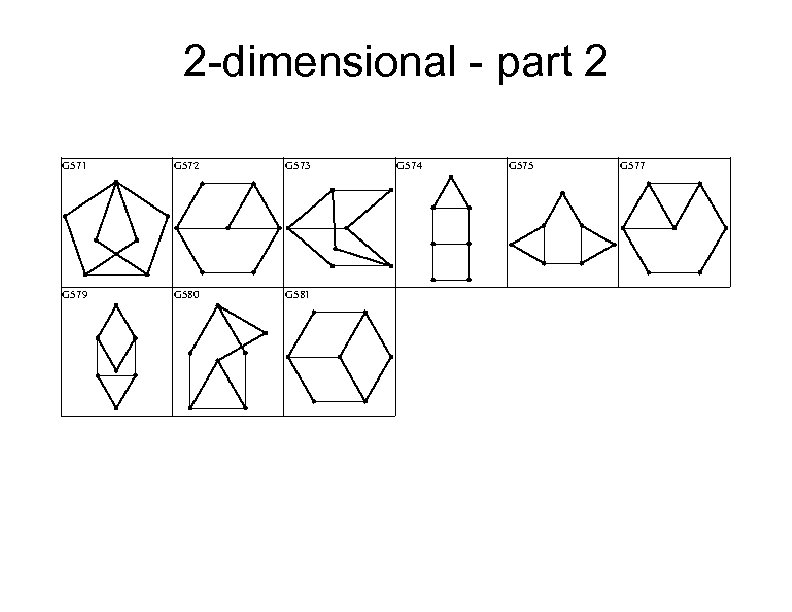2 -dimensional - part 2

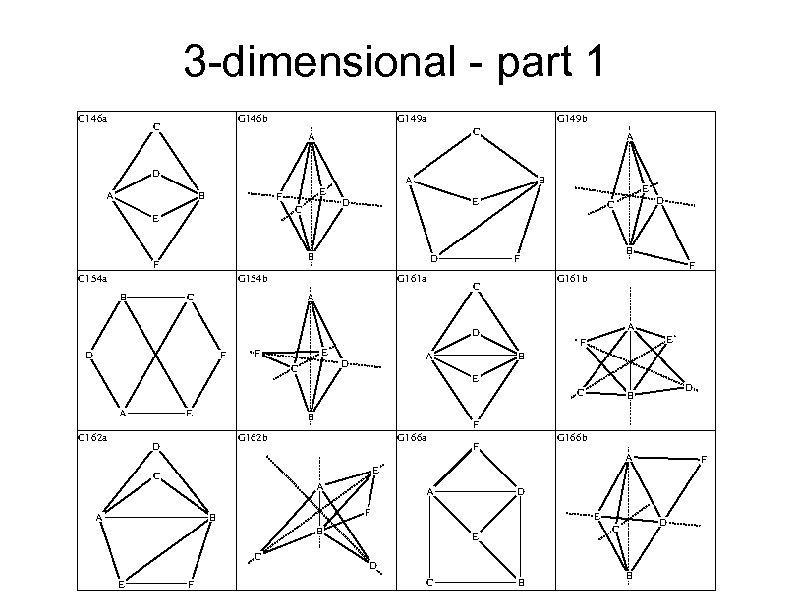3 -dimensional - part 1

3 -dimensional - part 2

3 -dimensional - part 3

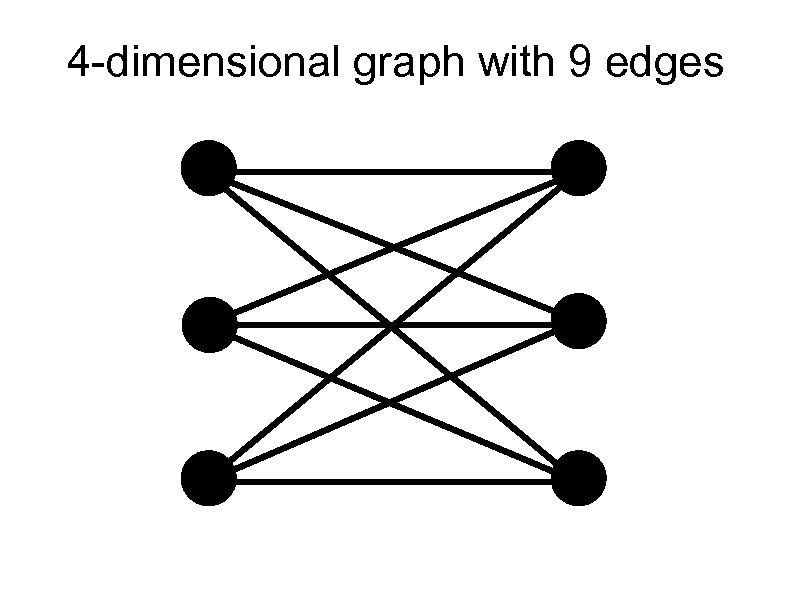
There's only one left Of the 43 candidate graphs, 42 are 2 - or 3 dimensional, leaving just one graph, which answers the original question A 4 -dimensional graph must have at least 9 edges, and there is only one 4 dimensional graph with 9 edges: K 3, 3 I had a lovely unit-distance drawing of K 3, 3 in 4 dimensions, but I lost it. This will have to do:

4 -dimensional graph with 9 edges

That's all, folks For all the details see: rogerfhouse. com Thank you