Интервальные оценки коэффициентов теоретического уравнения регрессии По аналогии

Интервальные оценки коэффициентов теоретического уравнения регрессии По аналогии с парной регрессией после определения точечных оценок bj коэффициентов j могут быть рассчитаны интервальные оценки указанных коэффициентов: 1

доверительный интервал, который с надежностью (1 - ) накрывает определяемый параметр j: 2

Анализ качества эмпирического уравнения множественной регрессии Проверка статистического качества оцененного уравнения регрессии проводится по следующим направлениям: 3

ü проверка статистической значимости коэффициентов уравнения регрессии; ü проверка общего качества уравнения регрессии; ü проверка выполнимости предпосылок МНК. 4

Проверка статистической значимости коэффициентов уравнения регрессии Статистическая значимость коэффициентов множественной линейной регрессии с m объясняющими переменными проверяется на основе t-статистики: 5

. имеющей распределение Стьюдента с числом степеней свободы v =n-m-1, где n - число наблюдений. При требуемом уровне значимости наблюдаемое значение t-статистики сравнивается с критической точкой. распределения Стьюдента. 6

Если , то коэффициент bj считается статистически значимым. В противном случае коэффициент считается статистически незначимым (статистически близким к нулю), то есть фактор Xj линейно не связан с зависимой переменной Y и его можно исключить из набора объясняющих переменных. 7

Проверка общего качества уравнения регрессии После проверки значимости каждого коэффициента регрессии проверяется общее качество уравнения регрессии. Для этого используется коэффициент детерминации R 2: 8

Иногда при расчете коэффициента детерминации для получения несмещенных оценок вводится так называемый скорректированный (исправленный) коэффициент детерминации: 9

Очевидно, что для m>1. С ростом значений m скорректированный коэффициент детерминации растет медленнее обычного и увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t-статистика этой переменной по модулю больше единицы. 10

После оценки статистической значимости каждого коэффициента анализируется совокупная значимость коэффициентов, то есть проверяется гипотеза об общей значимости: H 0: 1= 2=…= m=0. 11

Проверка данной гипотезы осуществляется на основе дисперсионного анализа сравнения объясненной и остаточной дисперсий. H 0: (объясненная дисперсия) =(остаточная дисперсия), H 1: (объясненная дисперсия) >(остаточная дисперсия). 12

Строится F-статистика: При выполнении предпосылок МНК построенная F-статистика имеет распределение Фишера с числами степеней свободы v 1=m, v 2=n-m-1. 13

Если при требуемом уровне значимости Fнабл>F ; m; n-m, то H 0 отклоняется в пользу H 1, то есть объясненная дисперсия существенно больше остаточной, а значит уравнение регрессии качественно отражает динамику изменения зависимой переменной Y. 14

Если Fнабл

На практике часто вместо указанной гипотезы проверяют гипотезу о статистической значимости коэффициента детерминации R 2: H 0: 2=0, R H 1: R 2>0. 16

Для проверки данной гипотезы используется следующая F-статистика: Нулевая гипотеза отклоняется, если F>Fкр. Это равносильно тому, что R 2>0, то есть R 2 статистически значим. 17

Проверка выполнимости предпосылок МНК. Статистика Дарбина—Уотсона Статистическая значимость коэффициентов регрессии и близкое к единице значение 2 не коэффициента детерминации R гарантируют высокое качество уравнения регрессии. 18

Причиной этого может являться невыполнимость необходимых предпосылок МНК. Оценивая линейное уравнение регрессии, мы предполагаем, что реальная взаимосвязь переменных линейна, а отклонения от регрессионной прямой являются случайными, независимыми друг от друга величинами с нулевым математическим ожиданием и постоянной дисперсией. 19

Если эти предположения не выполняются, то оценки коэффициентов регрессии не обладают свойствами несмещенности, эффективности и состоятельности, и анализ их значимости будет неточным. 20

При статистическом анализе уравнения регрессии на начальном этапе проверяют выполнимость предпосылки о статистической независимости отклонений между собой. 21

Для этого рассчитывается коэффициент корреляции, называемый в этом случае коэффициентом автокорреляции первого порядка: 22

На практике для анализа коррелированности отклонений вместо коэффициента корреляции используют тесно с ним связанную статистику Дарбина—Уотсона DW, рассчитываемую по формуле: 23

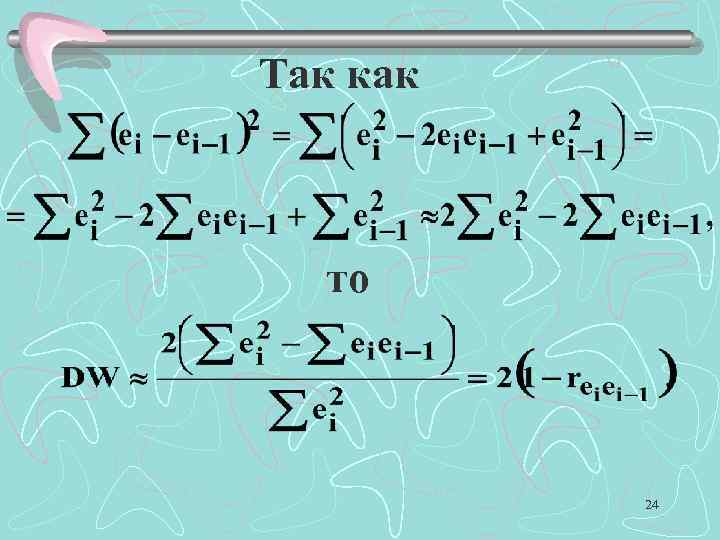Так как то 24

Таким образом, необходимым условием независимости случайных отклонений является близость к двойке значения статистики Дарбина—Уотсона. Тогда, если DW 2, мы считаем отклонения от регрессии случайными. 25

Это означает, что ü построенная линейная регрессия, вероятно, отражает реальную зависимость; ü скорее всего, не осталось неучтенных существенных факторов, влияющих на зависимую переменную; 26

ü какая-либо другая нелинейная формула не превосходит по статистическим характеристикам предложенную линейную. 27

В этом случае, даже когда R 2 невелико, вполне вероятно, что необъясненная дисперсия вызвана влиянием на зависимую переменную большого числа различных факторов, индивидуально слабо влияющих на исследуемую переменную. 28

Для ответа на вопрос, какие значения DW можно считать статистически близкими к двум, разработаны специальные таблицы, позволяющие при данном числе наблюдений n, количестве объясняющих переменных m и заданном уровне значимости определять границы приемлемости (критические точки) наблюдаемой статистики DW. 29

Не обращаясь к таблице, можно пользоваться «грубым» правилом и считать, что автокорреляция остатков отсутствует, если 1, 5 < DW < 2, 5. Для более надёжного вывода целесообразно обращаться к табличным значениям. При наличии автокорреляции остатков полученное уравнение регрессии обычно считается неудовлетворительным. 30