ИНТЕРПОЛЯЦИЯ Способы задания математической функции аналитический y f x

ИНТЕРПОЛЯЦИЯ Способы задания математической функции • аналитический y=f(x) Например: y=x 2, y=sin(x) и т. п. • табличный (дискретные значения функции заданы только в узлах): Например: X 0 2 F – 1 0. 2 3 3. 5 0. 8

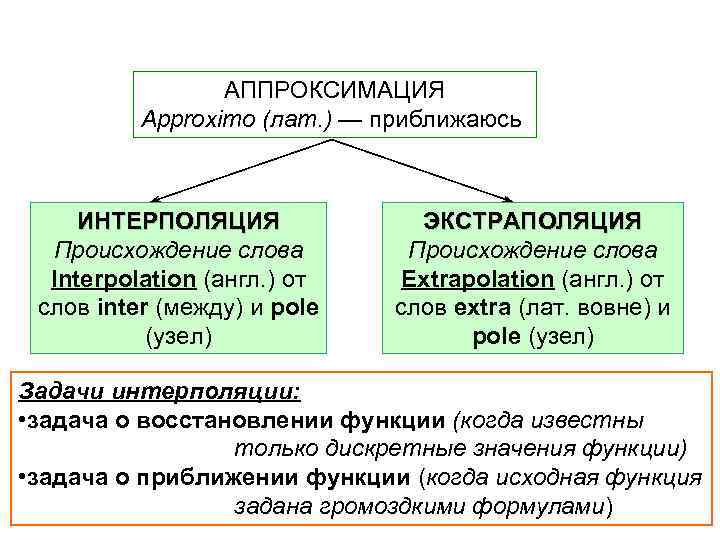
АППРОКСИМАЦИЯ Approximo (лат. ) — приближаюсь ИНТЕРПОЛЯЦИЯ Происхождение слова Interpolation (англ. ) от слов inter (между) и pole (узел) ЭКСТРАПОЛЯЦИЯ Происхождение слова Extrapolation (англ. ) от слов extra (лат. вовне) и pole (узел) Задачи интерполяции: • задача о восстановлении функции (когда известны только дискретные значения функции) • задача о приближении функции (когда исходная функция задана громоздкими формулами)

ПОСТАНОВКА ЗАДАЧИ ИНТЕРПОЛЯЦИИ Дано: xi fi Функция fi задана табличным способом x 0 f 0 x 1 f 1 x 2. . f 2. . x. N f. N На интервале [a, b] заданы точки xi, i=0, 1, . . . , N; a x i b, и значения неизвестной функции в этих точках fi, i=0, 1, . . , N Задача: найти промежуточные значения функции в точках, не совпадающих с узлами интерполяции 3

ПОСТАНОВКА ЗАДАЧИ ИНТЕРПОЛЯЦИИ Дано: xi fi Функция fi задана табличным способом x 0 f 0 x 1 f 1 x 2. . f 2. . x. N f. N 1. Найти функцию F(x), принимающую в точках xi те же значения fi, i=0, 1, . . , N (xi - узлы интерполяции, интерполяции условия F(xi)= fi – условия интерполяции) интерполяции 2. Найти значение F(z) для заданного значения z [a, b] z ≠ xi 3. Найти значение F’(z) для заданного значения z [a, b] Если известна исходная функция g(x), то можно оценить погрешность метода интерполяции в произвольной точке z [a, b]: 4 r(z)=|g(z)–F(z)|.

МЕТОДЫ ИНТЕРПОЛЯЦИИ глобальные локальные строим одну (глобальную) функцию на каждом интервале [xi– 1, xi] на всем интервале [a, b] строим свою (локальную) функцию Если известна исходная функция g(x), то можно оценить погрешность метода интерполяции в произвольной точке z [a, b]: r(z)=|g(z)–F(z)|. 5

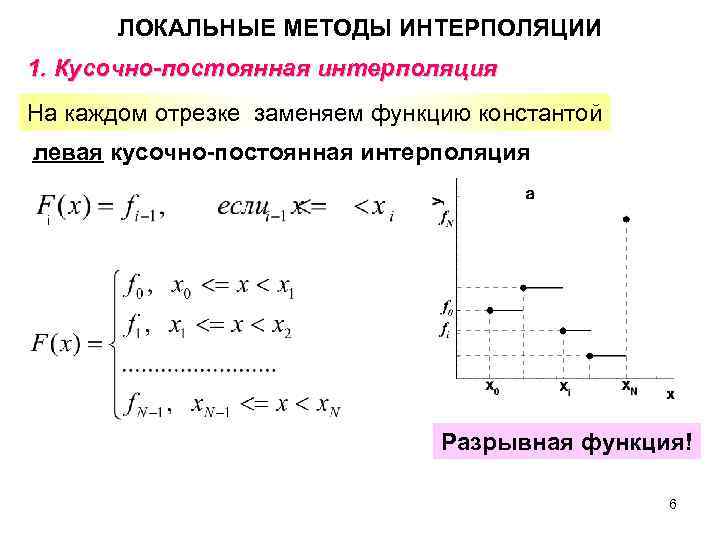
ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 1. Кусочно-постоянная интерполяция На каждом отрезке заменяем функцию константой левая кусочно-постоянная интерполяция i Разрывная функция! 6

ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 1. Кусочно-постоянная интерполяция На каждом отрезке заменяем функцию константой правая кусочно-постоянная интерполяция Разрывная функция! 7

ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 1. Кусочно–постоянная интерполяция ДОСТОИНСТВА: НЕДОСТАТКИ: 1. ПРОСТОЙ МЕТОД 1. БОЛЬШАЯ ПОГРЕШНОСТЬ ДЛЯ МАЛЫХ N 2. СХОДИТСЯ , 3. МОЖНО ИСПОЛЬЗОВАТЬ ДЛЯ НАХОЖДЕНИЯ ИНТЕГРАЛОВ (формула прямоугольников) 2. ФУНКЦИЯ РАЗРЫВНАЯ 3. НЕЛЬЗЯ ДИФФЕРЕНЦИРОВАТЬ 8

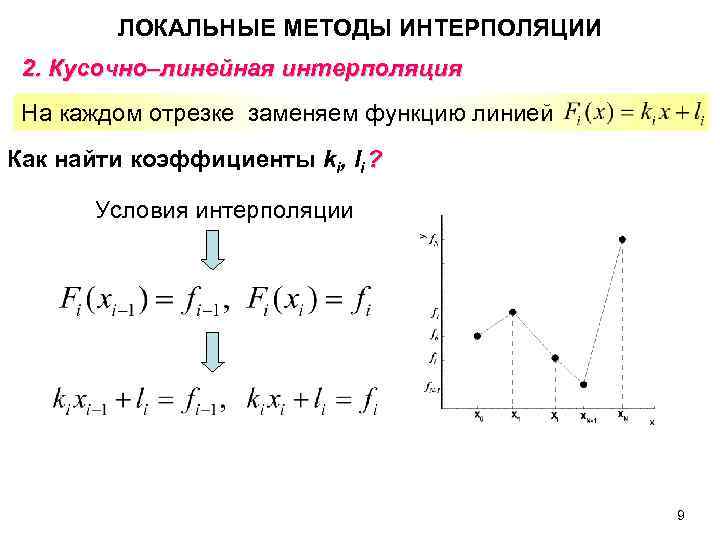
ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 2. Кусочно–линейная интерполяция На каждом отрезке заменяем функцию линией Как найти коэффициенты ki, li ? Условия интерполяции 9

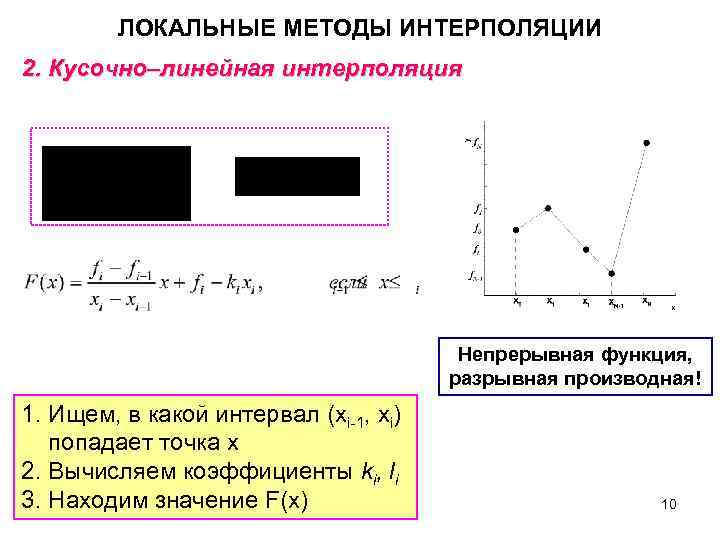
ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 2. Кусочно–линейная интерполяция Непрерывная функция, разрывная производная! 1. Ищем, в какой интервал (xi-1, xi) попадает точка x 2. Вычисляем коэффициенты ki, li 3. Находим значение F(x) 10

ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 2. Кусочно–линейная интерполяция ДОСТОИНСТВА: НЕДОСТАТКИ: 1. ПРОСТОЙ МЕТОД 1. БОЛЬШАЯ ПОГРЕШНОСТЬ ДЛЯ МАЛЫХ N 2. СХОДИТСЯ 3. ФУНКЦИЯ НЕПРЕРЫВНА 2. ФУНКЦИЯ 4. МОЖНО ИСПОЛЬЗОВАТЬ НЕГЛАДКАЯ ДЛЯ НАХОЖДЕНИЯ 3. НЕЛЬЗЯ ИНТЕГРАЛОВ (формула ДИФФЕРЕНЦИРОВАТЬ трапеций) 11

РЕШИТЬ ПРИМЕР Задана таблица значений функций: x 0 2 3 3. 5 f -1 0. 2 0. 5 0. 8 Найти значение функции при z=1 Кусочно-постоянная левая интерполяция f(z)=-1 Кусочно-постоянная правая интерполяция f(z)=0. 2 Кусочно-линейная интерполяция f(z)=-0. 4 12

ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 3. Кусочно–параболическая интерполяция На каждом отрезке заменяем функцию параболой Fi(z)=ai+bi(z–xi)+ci (z–xi)2/ 2 Для поиска неизвестных коэффициентов ai, bi, ci используем: 1. Условия интерполяции Fi(xi)=fi 2. Условия непрерывности функции Fi(xi)=Fi-1(xi) 3. Условия непрерывности первой производной функции Fi’(xi)=Fi-1’(xi) 13

ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 4. Кусочно–кубическая интерполяция = кубический сплайн На каждом отрезке заменяем функцию кубической параболой , i=1, …, N Для поиска 4 N неизвестных коэффициентов ai, bi, ci, di используем: 1. Условия интерполяции Si(xi)=fi, i=1, …, N 2. Условия непрерывности функции Si(xi)=Si-1(xi) 3. Условия непрерывности первой производной функции Si’(xi)=Si-1’(xi) 4. Условия непрерывности второй производной функции Si’’(xi)=Si-1’’(xi) S 1’’(x 0)=0, SN’’(x. N)=0 14

ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 4. Кусочно–кубическая интерполяция = кубический сплайн Учитывая, что получим где

ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 4. Кусочно–кубическая интерполяция = кубический сплайн Исключая из системы коэффициенты ai, bi, di, получим СЛАУ Данная СЛАУ с трехдиагональной матрицей решается методом прогонки

ЛОКАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ 3. Кусочно–параболическая интерполяция 4. Кубический интерполяционный сплайн ДОСТОИНСТВА: 1. ПРОСТЫЕ МЕТОДЫ 2. ДЛЯ НАХОЖДЕНИЯ КОЭФФИЦИЕНТОВ ИСПОЛЬЗУЕТСЯ ТОЧНЫЙ ЭКОНОМИЧНЫЙ МЕТОД ПРОГОНКИ 3. СХОДЯТСЯ, МАЛЕНЬКАЯ ПОГРЕШНОСТЬ 4. ФУНКЦИЯ, ПРОИЗВОДНАЯ НЕПРЕРЫВНЫ 5. МОЖНО ИСПОЛЬЗОВАТЬ ДЛЯ НАХОЖДЕНИЯ ИНТЕГРАЛОВ И ПРОИЗВОДНЫХ 6. ИСПОЛЬЗУЮТ В КОМПЬЮТЕРНОЙ ГРАФИКЕ 17

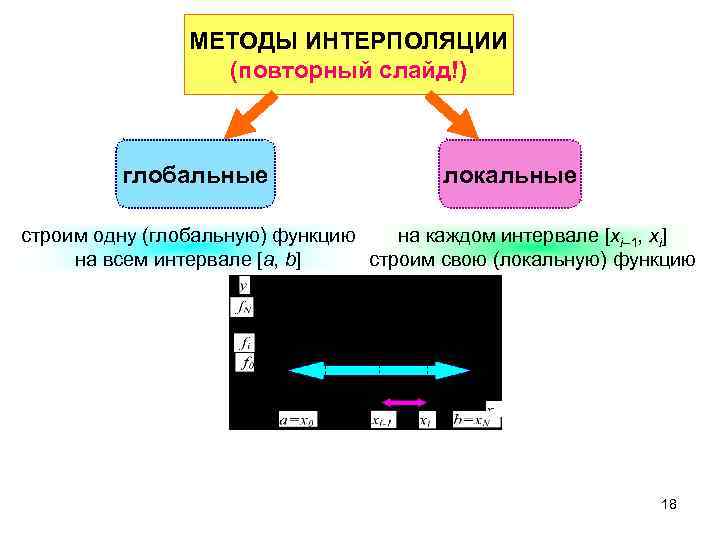
МЕТОДЫ ИНТЕРПОЛЯЦИИ (повторный слайд!) глобальные локальные строим одну (глобальную) функцию на каждом интервале [xi– 1, xi] на всем интервале [a, b] строим свою (локальную) функцию 18

ГЛОБАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ На интервале [a, b] строим полином Pm(x)=a 0+a 1 x+a 2 x 2+a 3 x 3+…+am xm m=? Если у нас 2 точки (x 0, f 0) и (x 1, f 1), тогда m=1 и мы можем построить полином 1 ой степени P 1(x)=a 0+a 1 x Если у нас 3 точки (x 0, f 0), (x 1, f 1) и (x 2, f 2), тогда m=2 и мы можем построить полином 2 ой степени P 2(x)=a 0+a 1 x+a 2 x 2 Тогда для N+1 точек PN(x)=a 0+a 1 x+a 2 x 2+a 3 x 3+…+a. N x. N 19

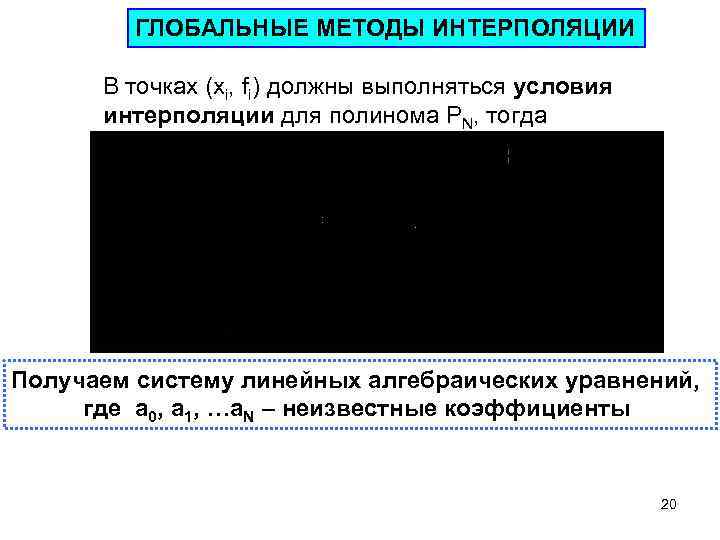
ГЛОБАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ В точках (xi, fi) должны выполняться условия интерполяции для полинома PN, тогда Получаем систему линейных алгебраических уравнений, где a 0, a 1, …a. N – неизвестные коэффициенты 20

Известно, что СЛАУ имеет решение, если ее определитель отличен от нуля Определитель системы Определитель отличен от нуля, если xk xm (т. е. все узлы интерполяции различные). Таким образом, доказано, что система имеет решение и для N узлов можно построить интерполяционный полином степени N 21

Чтобы построить полином PN , необходимо найти коэффициенты a 0, a 1, a 2, …, a. N , а для этого надо решить СЛАУ степени N, что является сложной задачей Рассмотрим более простой способ построения полинома степени N 22

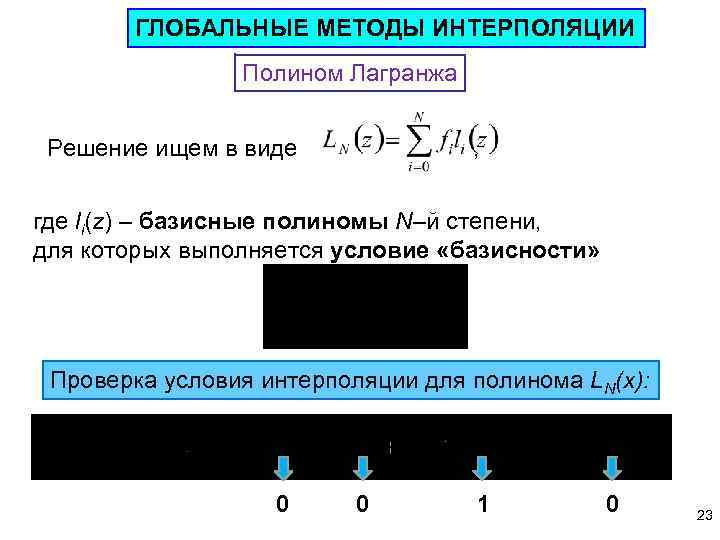
ГЛОБАЛЬНЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ Полином Лагранжа Решение ищем в виде , где li(z) – базисные полиномы N–й степени, для которых выполняется условие «базисности» Проверка условия интерполяции для полинома LN(x): 0 0 1 0 23

Построение базисных полиномов: i=0, 1, . . . , N Например: 24

Построение базисных полиномов: Проверка условий «базисности» : =0, i k т. к. k принимает одно из значений 1, …, i-1, i+1, …, N 25

Компактная запись формулы для полинома Лагранжа Полином Лагранжа имеет малую погрешность при небольших значениях N<20 26

ПРИМЕРЫ Для N=1 Формула совпадает с формулой кусочно-линейной интерполяции ! Для N=2 27

Решить пример Задана таблица значений функций: x 0 2 3 3. 5 f -1 0. 2 0. 5 0. 8 Найти значение функции при z=1 28

Решить пример Задана таблица значений функций: x 0 2 3 3. 5 f -1 0. 2 0. 5 0. 8 Найти значение функции при z=1 29

РЕШИТЬ ПРИМЕР Задана таблица значений функций: x 0 2 3 3. 5 f -1 0. 2 0. 5 0. 8 Найти значение функции при z=1 30

ПОДБОР ЭМПИРИЧЕСКИХ ФУНКЦИЙ • Применяется для приближённого представления заданной функции другими (более простыми) функциями, а также оказывается полезным при обработке результатов наблюдений (экспериментов)

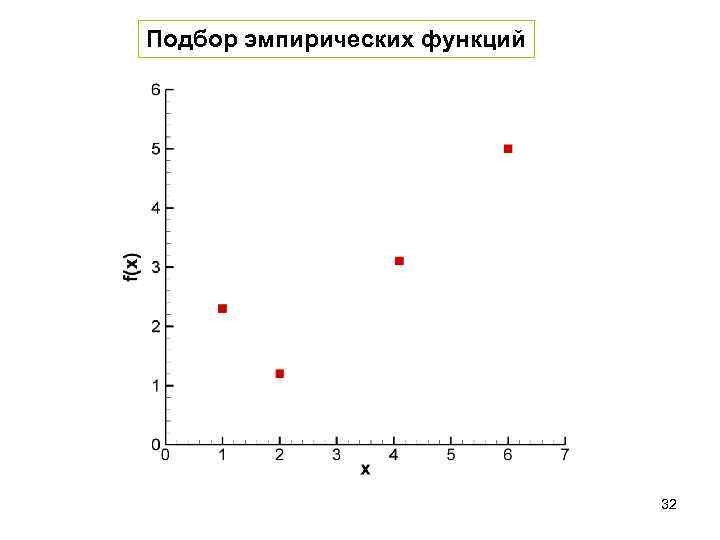
Подбор эмпирических функций 32

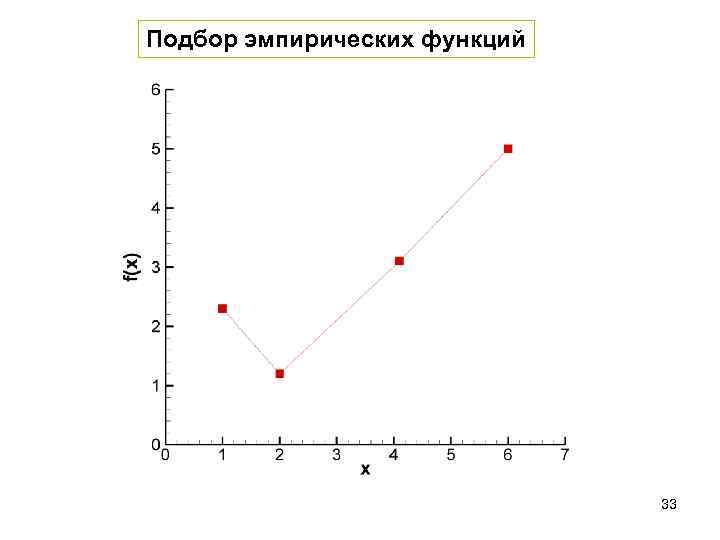
Подбор эмпирических функций 33

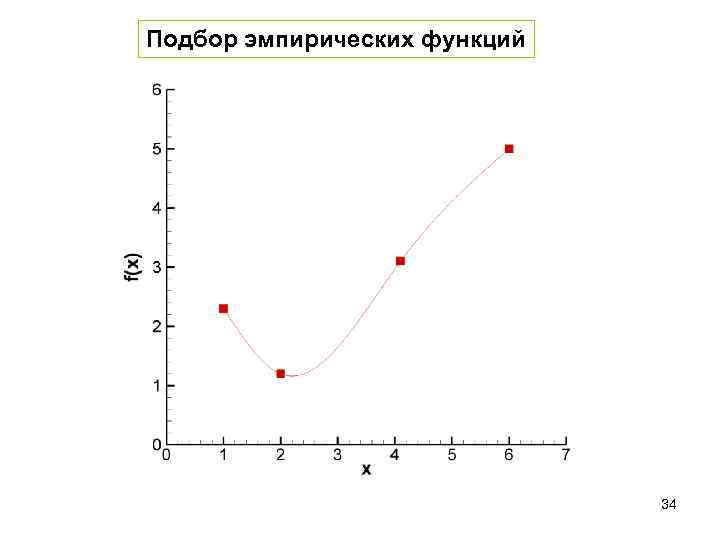
Подбор эмпирических функций 34

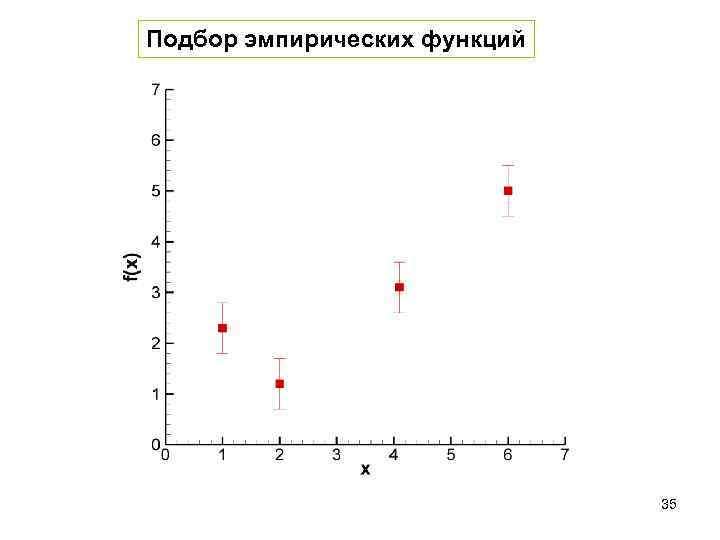
Подбор эмпирических функций 35

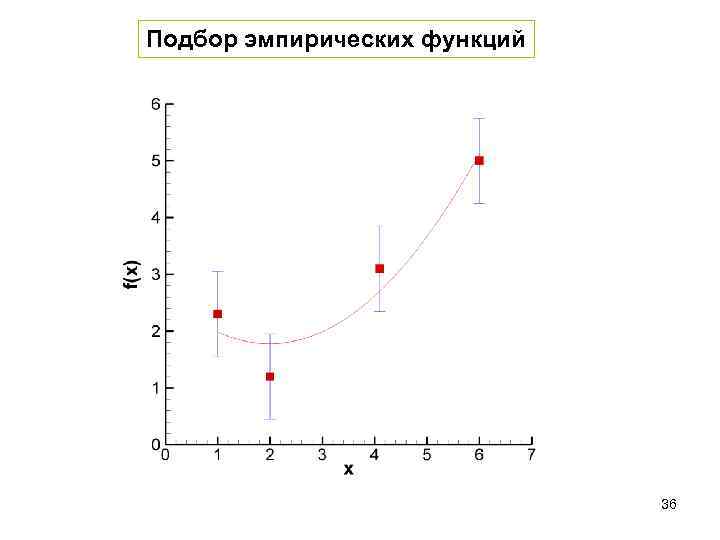
Подбор эмпирических функций 36

Подбор эмпирических функций 1. Подбор вида функции , содержащей неизвестные параметры 2. Определение этих параметров, наилучших в некотором смысле На практике важен случай функции вида: 37

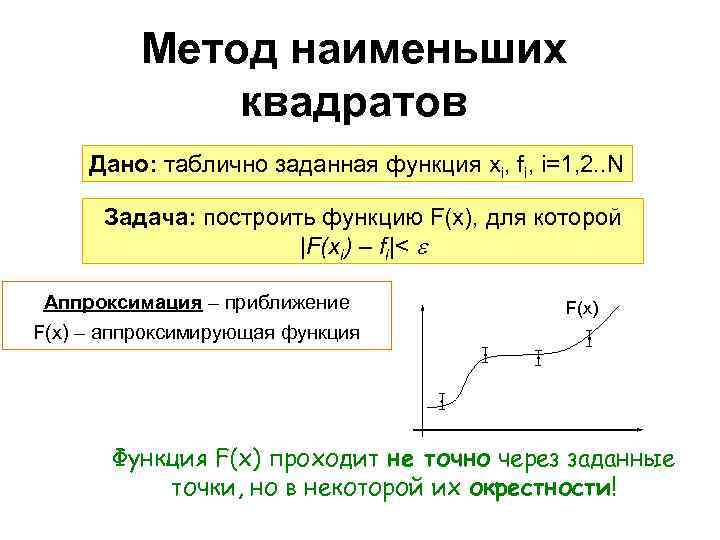
Метод наименьших квадратов Дано: таблично заданная функция xi, fi, i=1, 2. . N Задача: построить функцию F(x), для которой |F(xi) – fi|< Аппроксимация – приближение F(x) – аппроксимирующая функция F(x) Функция F(x) проходит не точно через заданные точки, но в некоторой их окрестности!

Метод наименьших квадратов СТЕПЕНЬ БЛИЗОСТИ К ЭМПИРИЧЕСКИМ ДАННЫМ ОПРЕДЕЛЯЕТСЯ ИЗ УСЛОВИЯ МИНИМУМА СУММЫ КВАДРАТОВ ОТКЛОНЕНИЙ ВЫЧИСЛЕННЫХ (АППРОКСИМИРУЮЩИХ) И ЭКСПЕРИМЕНТАЛЬНЫХ (ЗАДАННЫХ) ДАННЫХ Σ(F(xi)-fi)2→min 39

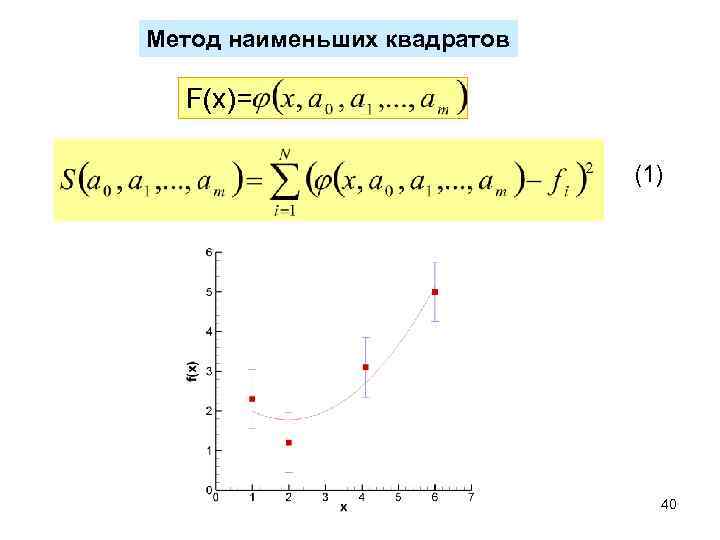
Метод наименьших квадратов F(x)= (1) 40

Метод наименьших квадратов Условие минимума функции S (1) предполагает равенство нулю всех частных производных функции по коэффициентам ai 41

Метод наименьших квадратов Выберем в качестве аппроксимирующей функции полином степени m Тогда формула (1) примет вид 42

Метод наименьших квадратов Вычислим производные 43

Метод наименьших квадратов Приравнивая производные нулю и собирая коэффициенты при неизвестных, получаем систему . 44

Допустим, будем искать решение в виде полинома 3 й степени F(x) P 3(x)=a 1+a 2 x+a 3 x 2+a 4 x 3 В i–й точке полином P 3(x) отклоняется от значения fi на величину (P 3(xi) – fi) Суммируем квадраты отклонений полинома по всем точкам i=1, 2, …, N, получим функционал квадратов отклонений:

Чтобы найти минимум этого функционала, надо приравнять к нулю его частные производные по переменным a 1, a 2, a 3, a 4

Нормальная система Получили СЛАУ относительно неизвестных а 1, а 2, а 3, а 4

Пример xi -5 -3. 5 -2 1. 5 3. 25 5 fi Заданы координаты точек: 0. 5 1. 2 1. 4 1. 6 1. 7 1. 5 Построить функцию, аппроксимирующую данные, в виде P 1(x)=a 0+a 1 x

Пример xi -5 -3. 5 -2 1. 5 3. 25 5 fi Заданы координаты точек: 0. 5 1. 2 1. 4 1. 6 1. 7 1. 5 Построить функцию, аппроксимирующую данные, в виде P 1(x)=a 0+a 1 x N=6, для линейной зависимости нормальная система имеет вид:

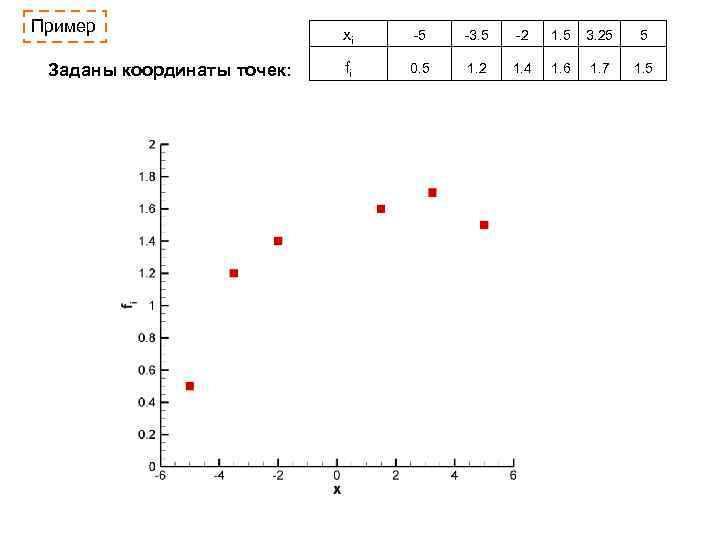
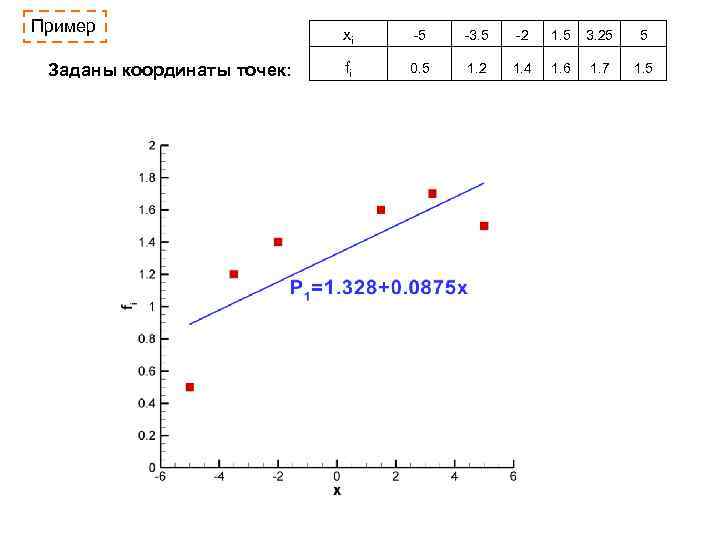
Пример Заданы координаты точек: xi -5 -3. 5 -2 1. 5 3. 25 5 fi 0. 5 1. 2 1. 4 1. 6 1. 7 1. 5

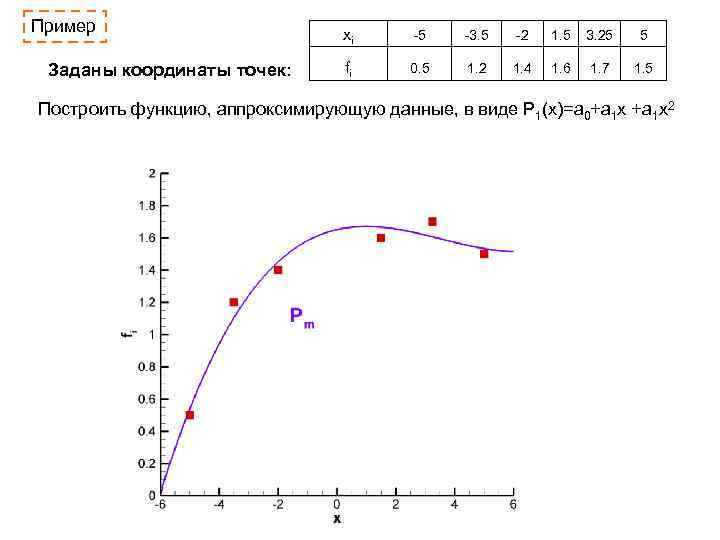
Пример Заданы координаты точек: xi -5 -3. 5 -2 1. 5 3. 25 5 fi 0. 5 1. 2 1. 4 1. 6 1. 7 1. 5 Построить функцию, аппроксимирующую данные, в виде P 1(x)=a 0+a 1 x 2