57c92adda43a72c6c17e4c07eaecaec7.ppt
- Количество слайдов: 43

International Capital Budgeting Chapter Eighteen Copyright © 2012 by the Mc. Graw-Hill Companies, Inc. All rights reserved.

Chapter Outline § Review of Domestic Capital Budgeting § The Adjusted Present Value Model § Capital Budgeting from the Parent Firm’s Perspective § Risk Adjustment in the Capital Budgeting Process § Sensitivity Analysis § Real Options 18 -2

Review of Domestic Capital Budgeting § Identify the size and timing of all relevant cash flows on a time line. § Identify the riskiness of the cash flows to determine the appropriate discount rate. § Find NPV by discounting the cash flows at the appropriate discount rate. § Compare the value of competing cash flow streams at the same point in time. 18 -3

Review of Domestic Capital Budgeting The basic net present value equation is Where: CFt = expected incremental after-tax cash flow in year t TVT = expected after-tax terminal value including return of net working capital C 0 = initial investment at inception K = weighted average cost of capital T = economic life of the project in years The NPV rule is to accept a project if NPV 0 18 -4

Review of Domestic Capital Budgeting For our purposes it is necessary to expand the NPV equation. CFt = (Rt – OCt – Dt – It)(1 – t) + Dt + It (1 – t) Rt is incremental revenue OCt is incremental operating cash flow It is incremental interest expense is the marginal tax rate Dt is incremental depreciation 18 -5

Review of Domestic Capital Budgeting We can use CFt = (OCFt)(1 – t) + t Dt to restate the NPV equation, T NPV = S (1 + K) + t=1 CFt t TVT (1 + K)T – C 0 as: T NPV = S t=1 (OCFt)(1 – t) + t Dt (1 + K)t + TVT (1 + K)T – C 0 18 -6

The Adjusted Present Value Model T NPV = S t=1 (OCFt)(1 – t) (1 + K)t T + t Dt S (1 + K) t=1 t + TVT (1 + K)T – C 0 can be converted to adjusted present value (APV) T S APV = t=1 (OCFt)(1 – t) (1 + Ku)t + t Dt (1 + i)t + t It (1 + i)t + TVT (1 + Ku) – C 0 T by appealing to Modigliani and Miller’s results. 18 -7

The Adjusted Present Value Model T S APV = t=1 (OCFt)(1 – t) (1 + Ku)t + t Dt (1 + i)t + t It (1 + i)t + TVT (1 + Ku) – C 0 T § The APV model is a value additivity approach to capital budgeting. Each cash flow that is a source of value to the firm is considered individually. § Note that with the APV model, each cash flow is discounted at a rate that is appropriate to the riskiness of the cash flow. 18 -8

Domestic APV Example Consider a project where the timing and size of the incremental after-tax cash flows for an all-equity firm are: –$1, 000 0 $125 1 $250 2 $375 3 $500 4 CF 0 = –$1000 The unlevered cost of equity is r 0 = 10%: The project would be rejected by CF 1 = $125 an all-equity firm: CF 2 = $250 I = 10 CF 3 = $375 NPV = –$56. 50 CF 4 = $500 18 -9

Domestic APV Example (continued) § Now, imagine that the firm finances the project with $600 of debt at r = 8%. § The tax rate is 40%, so each year they have an interest tax shield worth $19. 20: × I =. 40 × ($600 ×. 08) =. 40 × $48 = $19. 20 18 -10

-$1, 000 $125 $250 $375 $500 0 1 2 3 The APV of the project under leverage is: T S APV = t=1 APV = (OCFt)(1 – t) (1 + Ku $125 1. 10 + + $19. 20 )t + $250 (1. 10)2 + t Dt (1 + + $19. 20 (1. 08)2 i)t $375 (1. 10)3 + + t It (1 + + $19. 20 (1. 08)3 i)t 4 + TVT (1 + Ku)T – C 0 $500 (1. 10)4 + $19. 20 (1. 08)4 – $1, 000 1. 08 APV = $7. 09 The firm should accept the project if it finances with debt. 18 -11

International Capital Budgeting from the Parent Firm’s Perspective T S APV = t=1 (OCFt)(1 – t) (1 + Ku )t + t Dt (1 + i)t + t It (1 + i)t + TVT (1 + Ku)T – C 0 § The APV model is useful for a domestic firm analyzing a domestic capital expenditure or for a foreign subsidiary of an MNC analyzing a proposed capital expenditure from the subsidiary’s viewpoint. § The APV model is NOT useful for an MNC in analyzing foreign capital expenditure from the parent firm’s perspective. 18 -12

International Capital Budgeting from the Parent Firm’s Perspective § Donald Lessard developed an APV model for MNCs analyzing a foreign capital expenditure. The model recognizes many of the particulars peculiar to foreign direct investment. 18 -13

APV Model of Capital Budgeting from the Parent Firm’s Perspective T APV = S t=1 + St. OCFt(1 – t) (1 + Kud)t St TVT T + T St t Dt St t It S (1 + i ) +S (1 + i ) t=1 d t t=1 – S 0 C 0 + S 0 RF 0 + S 0 CL 0 + d T t S St LPt t (1 + Kud)T t = 1 (1 + id) The marginal corporate tax OCFt represents only the S 0 RF 0 The operatingthe cash of be The operating cash flows must represents cash flows must Denotes the larger of the rate, , is present value (in portion of operating value translated back into the parent’s currency) of any be discounted at the parent’s or domestic rate foreign accumulated restricted fundsrate flows available for remittance firm’s currency at the spot unlevered concessionary (in theexpected to prevail in each period. subsidiary’s. loans, CL 0, amount of remitted to that can be legally. RF 0) that are and loan payments, LPt , freed up by the project. the parent firm. discounted at i. d 18 -14

Capital Budgeting from the Parent Firm’s Perspective § One recipe for international decision makers: – – Estimate future cash flows in foreign currency. Convert to the home currency at the predicted exchange rate. • Use PPP, IRP, et cetera for the predictions. – Calculate NPV using the home currency cost of capital. 18 -15

Capital Budgeting from the Parent Firm’s Perspective: Example § A U. S. -based MNC is considering a European opportunity. § It’s a simple example: – There is no incremental debt. – There is no incremental depreciation. – There are no concessionary loans. – There are no restricted funds. 18 -16

Capital Budgeting from the Parent Firm’s Perspective: Example § We can use a simplified APV: T APV = S St. OCFt(1 – t) t=1 + (1 + St TVT (1 + T APV = Kud)t S t=1 Kud)T T + T St t Dt St t It S (1 + i ) +S (1 + i ) t=1 d t t=1 d – S 0 C 0 + S 0 RF 0 + S 0 CL 0 + St. OCFt(1 – t) (1 + Kud)t t T S (1 + i ) t=1 – S 0 C 0 St LPt d t no incremental debt no incremental depreciation no concessionary loans no restricted funds 18 -17
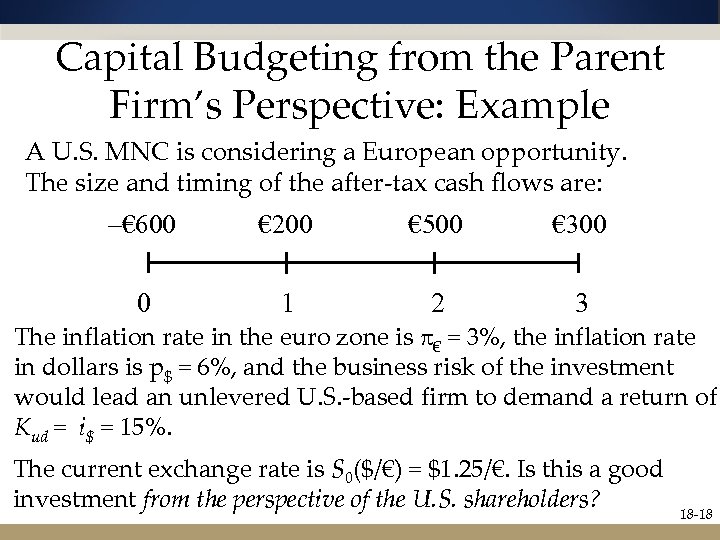
Capital Budgeting from the Parent Firm’s Perspective: Example A U. S. MNC is considering a European opportunity. The size and timing of the after-tax cash flows are: –€ 600 € 200 € 500 € 300 0 1 2 3 The inflation rate in the euro zone is € = 3%, the inflation rate in dollars is p$ = 6%, and the business risk of the investment would lead an unlevered U. S. -based firm to demand a return of Kud = i$ = 15%. The current exchange rate is S 0($/€) = $1. 25/€. Is this a good investment from the perspective of the U. S. shareholders? 18 -18
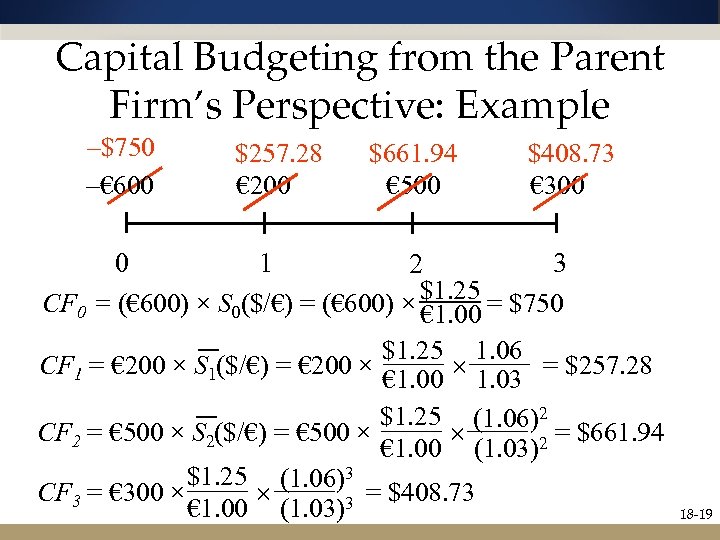
Capital Budgeting from the Parent Firm’s Perspective: Example –$750 –€ 600 $257. 28 € 200 $661. 94 € 500 $408. 73 € 300 0 1 3 2 CF 0 = (€ 600) × S 0($/€) = (€ 600) × $1. 25 = $750 € 1. 00 $1. 25 1. 06 CF 1 = € 200 × S 1($/€) = € 200 × = $257. 28 € 1. 00 1. 03 $1. 25 (1. 06)2 CF 2 = € 500 × S 2($/€) = € 500 × 2 = $661. 94 € 1. 00 (1. 03) $1. 25 (1. 06)3 CF 3 = € 300 × 3 = $408. 73 € 1. 00 (1. 03) 18 -19

Capital Budgeting from the Parent Firm’s Perspective: Example –$750 $257. 28 $661. 94 0 1 2 $408. 73 3 Find the NPV using the cash flow menu of your financial calculator and an interest rate of i$ = 15%: CF 0 = –$750 CF 1 = $257. 28 CF 2 = $661. 94 CF 3 = $408. 73 I = 15 NPV = $242. 99 18 -20

Capital Budgeting from the Parent Firm’s Perspective: Alternative § Another recipe for international decisionmakers: – Estimate future cash flows in the foreign currency. – Estimate the foreign currency discount rate. – Calculate the foreign currency NPV using the foreign cost of capital. – Translate the foreign currency NPV into dollars using the spot exchange rate. 18 -21

Foreign Currency Cost of Capital Method – € 600 € 200 € 500 € 300 0 1 2 3 € = 3% i$ = 15% p$ = 6% Let’s find i€ and use that on the euro cash flows to find the NPV in euros. Then translate the NPV into dollars at the spot rate. $1. 25 The current exchange rate is S 0($/€) = € 18 -22

Finding the Foreign Currency Cost of Capital: i€ Recall that the Fisher Effect holds that: (1 + e) × (1 + $) = (1 + i$) real rate inflation rate nominal rate So, for example, the real rate in the U. S. must be 8. 49%: (1 + e) = (1 + i$) (1 + $) e= 1. 15 1. 06 – 1 = 0. 0849 18 -23

Finding the Foreign Currency Cost of Capital: i€ If the Fisher Effect holds here and abroad, then: (1 + e$) = (1 + i$) (1 + $) and (1 + e€) = (1 + i€) (1 + €) If the real rates are the same in dollars and euros (e€ = e$) we have a very useful parity condition: (1 + i$) (1 + $) = (1 + i€) (1 + €) 18 -24

Finding the Foreign Currency Cost of Capital: i€ If we have any three of these variables, we can find the fourth: (1 + i$) (1 + i€) = (1 + $) (1 + €) In our example, we want to find i€: (1 + i€) = i€ = (1 + i$) × (1 + €) (1 + $) (1. 15) × (1. 03) (1. 06) – 1 i€ = 0. 1175 18 -25

International Capital Budgeting: Example – € 600 € 200 € 500 € 300 0 1 2 3 Find the NPV using the cash flow menu and i€ = 11. 75%: CF 0 = –€ 600 CF 1 = € 200 CF 2 = € 500 CF 3 = € 300 I = 11. 75 NPV = € 194. 39 $1. 25 = $242. 99 € 194. 39 × € 18 -26

– € 600 € 200 0 1 NPV = –€ 600 + € 500 € 200 1. 1175 + € 300 2 € 500 (1. 1175)2 + 3 € 300 (1. 1175)3 = € 194. 39 $1. 25 = $242. 99 € 194. 39 × € –$750 $257. 28 0 NPV = –$750 + 1 $257. 28 1. 15 $661. 94 + 2 $661. 94 (1. 15)2 $408. 73 + 3 $408. 73 (1. 15)3 = $242. 99 18 -27

International Capital Budgeting § You have two equally valid approaches: – Change the foreign cash flows into dollars at the exchange rates expected to prevail. Find the $NPV using the dollar cost of capital. – Find the foreign currency NPV using the foreign currency cost of capital. Translate that into dollars at the spot exchange rate. § If you watch your rounding, you will get exactly the same answer either way. § Which method you prefer is your choice. 18 -28

Computing IRR Recall that a project’s Internal Rate of Return (IRR) is the discount rate that gives a project a zero NPV = –€ 600 + € 200 1+IRR€ + € 500 (1+IRR€)2 + € 300 (1+IRR€)3 = € 0 IRR€ = 28. 48% NPV = –$750 + $257. 28 1+IRR$ = 32. 23% + $661. 94 (1+IRR$) + 2 $408. 73 (1+IRR$) = $0 3 18 -29

Directly Computing IRR$ and IRR€ NPV = –€ 600 + € 200 1+IRR€ + € 500 (1+IRR€)2 CF 0 = –€ 600 CF 2 = € 500 CF 1 = € 200 + € 300 (1+IRR€)3 = € 0 CF 3 = € 300 NPV = –$750 + CF 0 = –$750 $257. 28 1+IRR$ + $661. 94 (1+IRR$)2 IRR€ = 28. 48% + $408. 73 (1+IRR$)3 = $0 CF 2 = $661. 94 CF 1 = $257. 28 CF 3 = $408. 73 IRR$ = 32. 23% 18 -30

Converting from IRR$ to IRR€ § Use the same IRP and PPP conditions that we used to convert from one discount rate to another. 1+IRR$ 1+IRR€ In our example, it was easy to find = IRR€. Finding IRR$ without converting (1 + $) (1 + €) all cash flows into dollars is straightforward: (1+IRR$) = (1+IRR€)(1 + $) (1 + €) € = 3%, $ = 6% i€ = (1. 2848)(1. 06) (1. 03) IRR$ = 32. 23% – 1 18 -31

Back to the Full APV § Using the intuition just developed, we can modify Lessard’s APV model as shown, if we find it convenient. S 0 T APV = S St. OCFt(1 – t) (1 + t=1 S 0 + Kud)t f St TVT (1 + Kud)T f T + S 0 T St t Dt St t It S (1 + i ) +S (1 + i ) t=1 d t t=1 d f – S 0 C 0 + S 0 RF 0 + S 0 CL 0 + t f T S (1 + i ) t=1 S 0 St LPt d t f 18 -32

Risk Adjustment in the Capital Budgeting Process § Clearly risk and return are correlated. § Political risk may exist along side of business risk, necessitating an adjustment in the discount rate. § We can measure this risk with sensitivity analysis, where different estimates are used for expected inflation rates, cost and pricing estimates, and other inputs to give the manager a more complete picture of the planned capital investment. § Lends itself to computer simulation. 18 -33

Real Options § The application of options pricing theory to the evaluation of investment options in real projects is known as real options. – A timing option is an option on when to make the investment. – A growth option is an option to increase the scale of the investment. – A suspension option is an option to temporarily cease production. – An abandonment option is an option to quit the investment early. 18 -34

Value of the Option to Delay A French firm is considering a 1 -year investment in the United Kingdom with a pound-denominated rate of return of i£ = 15%. The firm’s local cost of capital is i€ = 10%. –£ 1, 000 £ 1, 150 The current exchange rate is S 0(€|£) = € 2. 00 £ project cash flows 0 1 Complicating matters, the Bank of England is considering either tightening or loosening its monetary policy. It is believed that in one year there are only two possibilities: S 1(€|£) = € 2. 20/£ or S 1(€|£) = € 1. 80/£ Following revaluation, the exchange rate is expected to remain steady for at least another year. 18 -35
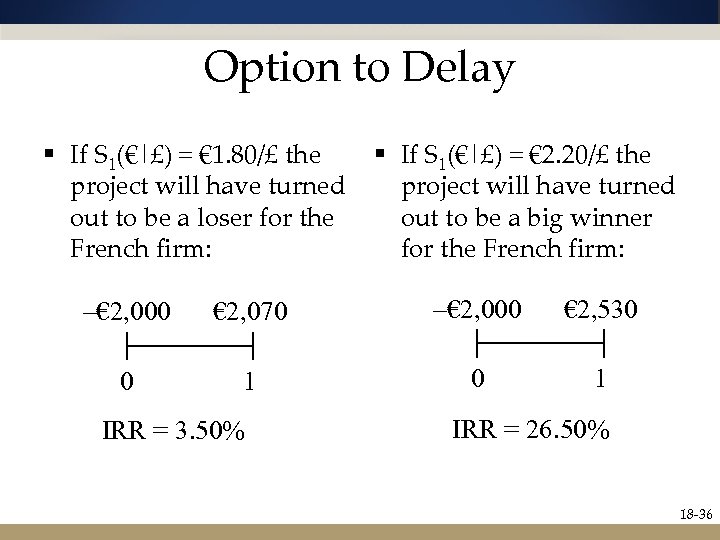
Option to Delay § If S 1(€|£) = € 1. 80/£ the project will have turned out to be a loser for the French firm: § If S 1(€|£) = € 2. 20/£ the project will have turned out to be a big winner for the French firm: –€ 2, 000 € 2, 070 –€ 2, 000 € 2, 530 0 1 IRR = 3. 50% IRR = 26. 50% 18 -36

Option to Delay: Example § An important thing to notice is that there is an important source of risk (exchange rate risk) that isn’t incorporated into the French firm’s local cost of capital of i€ = 10%. – That’s why there are no NPV estimates on the last slide. § Even with that, we can see that taking the project on today entails a “win big—lose big” gamble on exchange rates. § Analogous to buying an at-the-money call option on British pounds with a maturity of one year. 18 -37

Option to Delay: Example § The remaining slides assume a knowledge of the material contained in Chapter 7, especially the notion of a replicating portfolio. § But, also basic things like a call option give the holder the right to buy a specific asset at a specific price for a specific amount of time. 18 -38
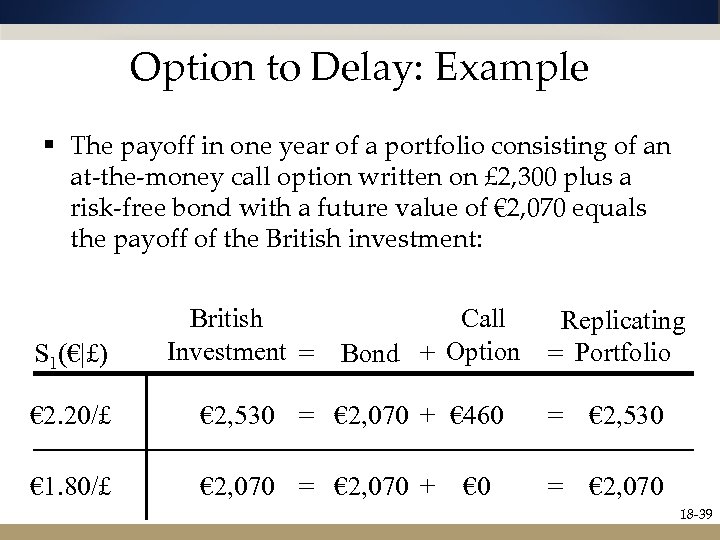
Option to Delay: Example § The payoff in one year of a portfolio consisting of an at-the-money call option written on £ 2, 300 plus a risk-free bond with a future value of € 2, 070 equals the payoff of the British investment: S 1(€|£) British Call Investment = Bond + Option Replicating = Portfolio € 2. 20/£ € 2, 530 = € 2, 070 + € 460 = € 2, 530 € 1. 80/£ € 2, 070 = € 2, 070 + = € 2, 070 € 0 18 -39

Option to Delay: Example § So the present value of the project at time zero can be found by getting a quote from an option dealer on an at-the-money call on £ 2, 300 and adding to that the present value of € 2, 070 at the euro-zone risk-free rate. § The NPV of the project is that sum less the cost of the project, –€ 2, 000: € 2, 070 NPV = –€ 2, 000 + value of option + 1+ i€ 18 -40

Option to Delay: Example § Suppose that our option dealer quotes an option premium of € 0. 05 per pound and our banker quotes the euro-zone risk-free rate at i€ = 6%. § The NPV of the project at time zero to the French firm is: € 2, 070 NPV 0 = –€ 2, 000 + € 115 + 1. 06 = € 67. 83 § Before we accept a positive NPV project, we should make sure that we are not bypassing alternative projects with higher NPVs. − Waiting a year to start the same project is an alternative. 18 -41

Option to Delay: Example § If the firm can wait a year to start the project, the cash flows look like: If S 1(€|£) = € 1. 80 per £ If S 1(€|£) = € 2. 20 per £ –€ 1, 800 € 2, 070 –€ 2, 200 € 2, 530 0 1 IRR = 15% NPV 1 = € 81. 82 = –€ 1, 800 + € 2, 070 1. 10 IRR = 15% NPV 1 = € 100 18 -42

Option to Delay: Example § We have a choice: invest in the project today or wait a year. § If we jump in today, the NPV 0 is € 67. 83 and the FV of today’s NPV 0 in one year from now is NPV 1 = € 74. 61 = 1. 10 × € 67. 83. § Clearly, it’s better to wait a year. – Worst case, NPV 1 = € 81. 82, but there is a chance that the NPV at time one is € 100. – Both of these outcomes beat € 74. 61. 18 -43
57c92adda43a72c6c17e4c07eaecaec7.ppt