db766b757353282abd9ebf38db9b85de.ppt
- Количество слайдов: 82

Internal Model Concepts at SCOR Presented by Ulrich Müller, SCOR SE Tel Aviv, November 23, 2010

Initial remarks The emerging European supervisory framework Solvency II not only has a Standard Model (successor of QIS 5) but offers the possibility of employing an Internal Model. Motivation: an Internal Model assesses the risks of large insurers and reinsurers more accurately than the Standard Model. The internal modeling methods presented here reflect the requirements of the reinsurer SCOR. They are based on the work of the Fin. Mod team and other departments at SCOR developed its Internal Model for internal use, before Solvency II, in the sense of Own Risk and Solvency Assessment (ORSA). Now the enhanced model is in the Solvency II pre-approval process As a large reinsurer, SCOR has a more diversified business portfolio than most primary insurance companies of similar size Therefore the scope of modeling challenges is huge: modeling of P&C and Life business, dependencies, retrocession, asset and credit risk etc Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 2

Agenda 1 Internal Models and regulation: SST and Solvency II 2 Economic profit distribution, risk-adjusted capital, market risk, credit risk 3 Risks in life (re)insurance 4 P&C liabilities: underwriting, reserving, dependencies, retrocession 5 Integrated company model: aggregation, additional dependencies 6 Conclusions Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 3

The Internal Model as a stochastic simulation engine The Internal Model is comprehensive: All risks of the company are stochastically simulated (Monte-Carlo simulation) Stress scenarios are fully contained in the normal stochastic simulation: the simulation scenarios with the most extreme outcomes behave like stress scenarios Then there is no need to add some artificial extra stress scenarios The main result is required Risk-Adjusted (or Risk-Based) Capital (RAC) for the whole company and for individual parts and risk types Capital is required to cover extreme outcomes. These arise from extreme events (heavy tails of distributions) and dependencies between risks. Therefore the modeling of distributions including realistic (often heavy) tails and dependencies is key Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 4
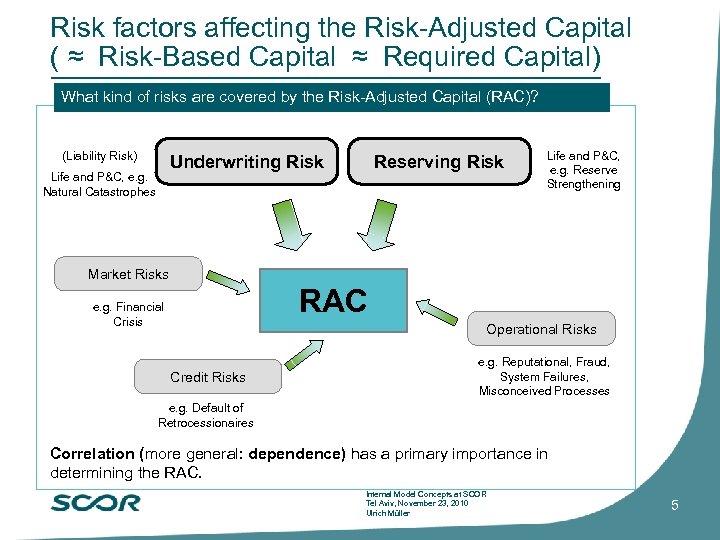
Risk factors affecting the Risk-Adjusted Capital ( ≈ Risk-Based Capital ≈ Required Capital) What kind of risks are covered by the Risk-Adjusted Capital (RAC)? (Liability Risk) Underwriting Risk Life and P&C, e. g. Natural Catastrophes Reserving Risk Life and P&C, e. g. Reserve Strengthening Market Risks RAC e. g. Financial Crisis Operational Risks Credit Risks e. g. Reputational, Fraud, System Failures, Misconceived Processes e. g. Default of Retrocessionaires Correlation (more general: dependence) has a primary importance in determining the RAC. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 5
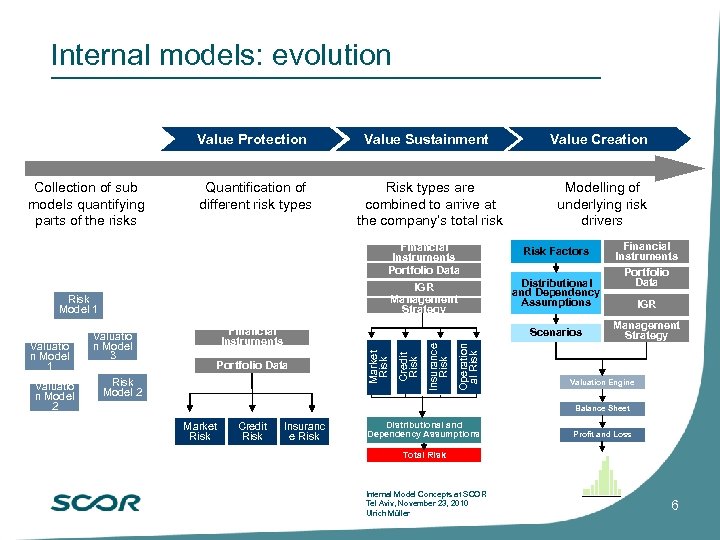
Internal models: evolution Value Protection Collection of sub models quantifying parts of the risks Value Sustainment Quantification of different risk types Risk types are combined to arrive at the company’s total risk Value Creation Modelling of underlying risk drivers Financial Instruments Portfolio Data Risk Factors IGR Management Strategy Distributional and Dependency Assumptions Risk Model 1 Risk Model 2 Operation al Risk Portfolio Data Insurance Risk Scenarios Credit Risk Valuatio n Model 2 Financial Instruments Market Risk Valuatio n Model 1 Valuatio n Model 3 Financial Instruments Portfolio Data IGR Management Strategy Valuation Engine Balance Sheet Market Risk Credit Risk Insuranc e Risk Distributional and Dependency Assumptions Profit and Loss Total Risk Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 6

Applications of the Internal Model: internal use, Swiss Solvency Test (SST), Solvency II Internal use of the Group Internal Model: l Risk assessment, capital allocation, planning, basis for new business pricing, asset allocation, retrocession optimization etc. l Report on results to the Executive Committee and the Risk Committee of the Board of Directors l European regulators encourage the internal use under the heading “Own Risk and Solvency Assessment” (ORSA) Swiss Solvency Test (SST): l SCOR Switzerland (a legal entity of the SCOR Group) produces SST reports based on the Internal Model since 3 years. l The Swiss regulator (FINMA) has reviewed the Internal Model, with a focus on some parts of special interest Solvency II: The Internal Model (with some adaptations to Solvency II guidelines) is in the pre-approval process Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 7

Methodology: Solvency II and Swiss Solvency Test (SST) Both use the same underlying mathematical methodology: Solvency Capital Requirement should buffer risks emanating during a 1 -year time horizon Risk is defined on the basis of the change in economic value (available capital) over a 1 -year time horizon A risk margin is assessed to cover the cost of the capital necessary to buffer non-hedgeable risks during the entire runoff of the liabilities. There are differences between Solvency II and SST: Treatment of group solvency, standard model vs standard formula, Va. R at 0. 5% vs t. Va. R at 1% as a risk measure, treatment of operational risk, … Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 8

Dependency modeling in the Internal Model and the Solvency II Standard Model (or QIS 5) Comparing two approaches: l QIS 5 / possible Solvency II Standard Model: Loss distributions with thin tails (normal or log-normal) low capital requirement per single risk or line of business flat, uniform correlation of risk factors also in the tail. This is compensated by of high, prescribed correlation coefficients between risks low diversification benefit. l Internal Model of SCOR: Loss distributions with heavy tails wherever appropriate in realistic modeling; increased correlation of risk factors in the tails (case of stress, extreme behavior) higher capital requirement. But: The correlation of average events / risks factors is often quite moderate larger diversification effect between risks for a well-diversified company. Main problem: QIS 5 tends to underestimating risks of single risk factors, single lines of business and “monoliners” and to overestimating risks of strongly diversified companies Approval process: pre-approval of the Internal Model and its dependence model by national regulator(s). Essential for a globally well-diversified reinsurer such as SCOR and for any insurance business based on strong diversification between different risks. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 9

Agenda 1 Internal Models and regulation: SST and Solvency II 2 Economic profit distribution, risk-adjusted capital, market risk, credit risk 3 Risks in life (re)insurance 4 P&C liabilities: underwriting, reserving, dependencies, retrocession 5 Integrated company model: aggregation, additional dependencies 6 Conclusions Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 10

Measuring risk: Risk-Based Capital and economic profit distribution A (re)insurance company is assessing the risk of existing or new business for several purposes: regulatory solvency tests, rating agency models, capital allocation in planning and pricing, … The risk of a certain business is usually measured in terms of the capital required to carry it: Risk-Adjusted Capital (RAC) = Risk. Based Capital ≈ Required Capital The RAC has to be compared to the available capital of a company in order to assess its solvency. Both capital measures rely on the economic valuation of business Here we focus on risk-adjusted capital and its computation Risk implies uncertainty. The economic profit (= change in economic value) is not certain; we model its distribution as a basis for RAC calculations. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 11
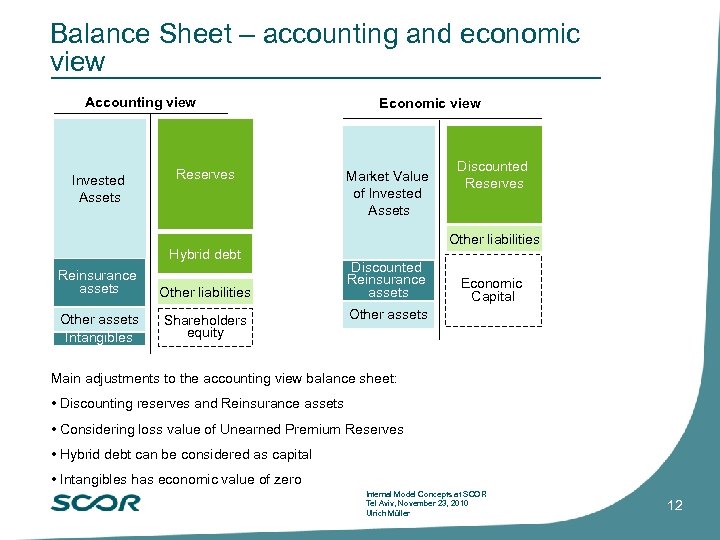
Balance Sheet – accounting and economic view Accounting view Invested Assets Reserves Hybrid debt Reinsurance assets Other liabilities Other assets Intangibles Shareholders equity Economic view Market Value of Invested Assets Discounted Reserves Other liabilities Discounted Reinsurance assets Economic Capital Other assets Main adjustments to the accounting view balance sheet: • Discounting reserves and Reinsurance assets • Considering loss value of Unearned Premium Reserves • Hybrid debt can be considered as capital • Intangibles has economic value of zero Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 12

Profit distribution as a centerpiece of risk modeling There are different definitions of risk and risk-based capital (Internal Model, Solvency II, Swiss Solvency Test, rating agency models, models for capital allocation in pricing and planning, …) Some (traditional) models are simple factor models: short-cuts that directly aim at results using fixed parameters and formulas. For large multi-line companies, factor models are of little use as they are too coarse and underestimate diversification For state-of-the-art models, we need full profit distributions of all parts of the business Profit distributions can be used for the stochastic simulation of the future behavior (Monte-Carlo simulation) A set of simulated scenarios can serve as a substitute of profit distributions (e. g. in Property Cat modeling) Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 13

Economic profit distributions and model granularity Economic profit distribution = distribution of the future change in economic value. This profit is uncertain, stochastic Time horizon: usually one year. What will be the value of the business at the end of this period? We take economic values as best estimates at the end of the stochastically simulated period. This implies discounting of all projected cash flows, for all simulated scenarios We want to know profit distributions not only for the whole company but also for its many parts high granularity Granularity: different legal entities, segments and lines of business, types of risks, …. The lowest level of granularity is a modeling unit. We model profit distributions by modeling unit. A large model has hundreds of units! Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 14
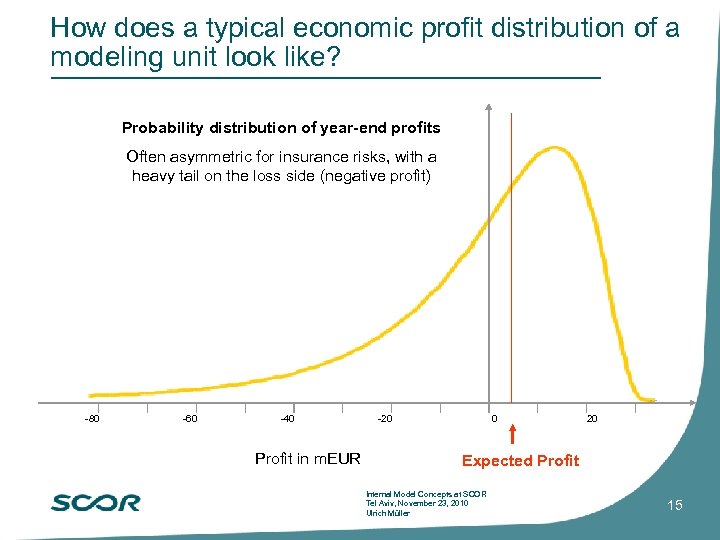
How does a typical economic profit distribution of a modeling unit look like? Probability distribution of year-end profits Often asymmetric for insurance risks, with a heavy tail on the loss side (negative profit) -80 -60 -40 Profit in m. EUR -20 0 20 Expected Profit Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 15

Measuring risk and capital adequacy Different stakeholders have different views on the risk measure Different perceptions on capital adequacy: SCOR’s Group internal model, Swiss Solvency Test, Solvency II l The Group Internal model interprets required capital as deviation of the economic t. Va. R(1%) result from the economic expected profit (= xt. Va. R(1%)). Consequently, available capital includes the economic expected profit l The Swiss Solvency Test defines required capital as t. Va. R(1%) Result of the one-year change + market value margin l Solvency II is based on x. Va. R(0. 5%) The internal model should make it possible to satisfy all the requirements but should not depend on them. Different results are consistently derived from the same, common core model. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 16

Economic value and profit: variations in definition Different stakeholders and users need different definitions of economic value and profit. Model developers have to be ready to support different definitions in their stochastic simulations Ultimate view vs one-year (or year-by-year) view: l Ultimate view: Economic value of all future cash flows until the business is totally over l Year-by-year view: Given the known starting condition at the end of a future year, the economic value at the end of the following year (relevant for computing the Market Value Margin in solvency tests) l One-year view: Economic value at the end of the first future year (relevant for required capital in solvency tests) Value before tax or after tax (also: before or after dividend payment) Using different interest rates for discounting future cash flows. We prefer using the risk-free yield curve at valuation time. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 17

Aggregating profit distributions We model economic profit distributions for small pieces of business, but we often need results for larger segments – and the whole company Many aggregate views are of interest. Example: Aggregating from the modeling unit “New Business Motor proportional, underwriting risk, Legal Entity A”. l l First aggregation: – Total new business Motor, underwriting risk, Legal Entity A; or – Total new proportional P&C business, underwriting risk, Legal Entity A; or – Total risk new business Motor, Legal Entity A (including interest rate risk) Second aggregation: – Total new business Motor, Legal Entity A; or – Total new proportional P&C business, underwriting risk, all legal entities consolidated Third aggregation: – Total new P&C business; or – Total Legal Entity A Last aggregation: – Total consolidated company, all risks Different user want to see different aggregate results, based on aggregated profit distributions For aggregating profit distributions, we need dependency models Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 18

Risk measures The following risk measures at level α, ξα, are commonly used: • Value-at-Risk • Expected Shortfall (= t. Va. R) Recall that, unlike ES, Va. R is generally not coherent due to lack of subadditivity. i. e. : Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 19

Risk-based capital: t. Va. R and xt. Va. R n For any stochastic economic value change ΔEV, ultimate or not, the required capital per liability (or asset) segment can be measured in terms of the Tail Value at Risk (t. Va. R): t. Va. Rstand-alone = - E[ ΔEV | case of the 1% shortfall of the EV of the stand-alone segment ] t. Va. Rdiversified = - E[ ΔEV | case of the 1% shortfall of the EV of the whole entity ] Euler principle n While t. Va. R is “Swiss-Solvency-Test-compatible”, our method of choice in the Group Internal Model is xt. Va. R, its difference from the unconditional expectation: xt. Va. Rstand-alone = E[ ΔEV] - t. Va. Rstand-alone xt. Va. Rdiversified = E[ ΔEV] - t. Va. Rdiversified This is our standard definition of risk-based capital n We do not use Va. R (but for Solvency II, we are adding this). Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 20

Allocation of diversified Risk-Based Capital (RAC) to Partial Risks Xi Euler principle (our preferred choice) Haircut principle - Contribution of Xi to Z (whole portfolio) - Risk Adjusted Capital (RAC) allocated to Xi - Percentage of RAC allocated to Xi Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 21

The Economic Scenario Generator (ESG) of SCOR Consistent scenarios for the future of the economy, needed for: Modeling assets and liabilities affected by the economy Expected returns, risks, full distributions Business decisions (incl. asset allocation, hedging of risks) Many economic variables: yield curves, asset classes, inflation, GDP … Credit cycle level, supporting the credit risk model 6 currency zones (EUR, USD, GBP, CHF, JPY, AUD; flexible) and FX rates Correlations, dependencies between all economic variables Heavy tails of distributions Realistic behavior of autoregressive volatility clusters Realistic, arbitrage-free yield-curve behavior Short-term and long-term scenarios (month/quarter … 40 years) Typical application: Monte-Carlo simulation of risks driven by the economy. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 22
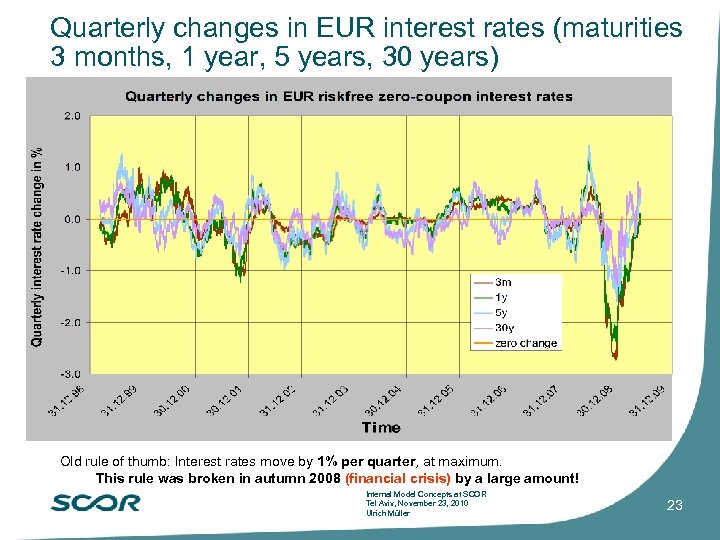
Quarterly changes in EUR interest rates (maturities 3 months, 1 year, 5 years, 30 years) Old rule of thumb: Interest rates move by 1% per quarter, at maximum. This rule was broken in autumn 2008 (financial crisis) by a large amount! Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 23

ESG based on bootstrapping Our implementation: Economic Scenario Generator (ESG) based on bootstrapping. This is a semi-parametric method. Reviewed by FINMA Bootstrapping historical behaviors for simulating the future Bootstrapping is a method that automatically fulfills many requirements, e. g. realistic dependencies between variables Some variables need additional modeling (“filtered bootstrap”): l Tail correction for modeling heavy tails (beyond the quantiles of historical data) l GARCH models for autoregressive clustering of volatility l Yield curve preprocessing (using forward interest rates) in order to obtain arbitrage-free, realistic behavior l Weak mean reversion of some variables (interest rates, inflation, …) in order to obtain realistic long-term behavior Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 24

Innovation vectors Last known vector Future simulated data vectors economic variables Historic data vectors USD equity economic variables The bootstrapping method: data sample, innovations, simulation EUR FX rate GBP 5 year IR time scenarios Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 25

Volatility modeling in the ESG: GARCH The volatility of most variables in finance exhibits autoregressive clusters: long periods of low volatility / long periods of high volatility. The bootstrapping method (random sampling) disrupts those clusters. Solution: GARCH model to re-introduce volatility clusters: • GARCH model for the volatility σi of the time series of innovations xi , for each variable, where • Iterative GARCH(1, 1) equation: • Robust calibration of the GARCH parameters on historical samples: The bootstrapping method uses normalized innovations: xi / σi. At each simulation step, the resampled innovation xi / σi is rescaled by the current, updated GARCH volatility σj new innovation xi σj / σi Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 26

Heavy tails in the ESG Market shocks and extreme price moves matter in economic risk assessment. Look at the tails of distributions! Bootstrapping covers some shocks: those contained in historical data. The size of historical samples (for many variables) is limited. Extreme shocks (such as a “ 1 in 200 years” event) are probably missing in the recorded history. Solution in the ESG: use “tail-corrected” innovations. Corrected innovation = Historical innovation * , where is a positive random variable with a mean square of 1 and a Paretoshaped upper tail (with a realistic tail index). Due to this tail correction, some occasional simulation scenarios will behave like “stress scenarios”: larger shocks than in the samples. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 27
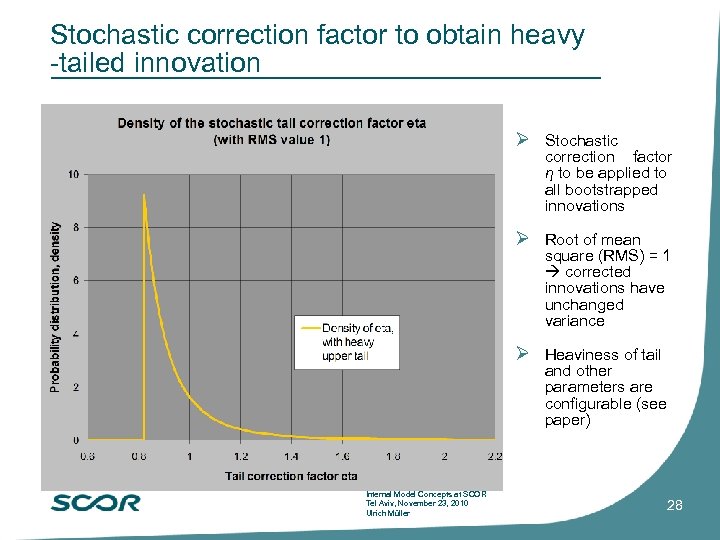
Stochastic correction factor to obtain heavy -tailed innovation Stochastic correction factor η to be applied to all bootstrapped innovations Root of mean square (RMS) = 1 corrected innovations have unchanged variance Heaviness of tail and other parameters are configurable (see paper) Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 28
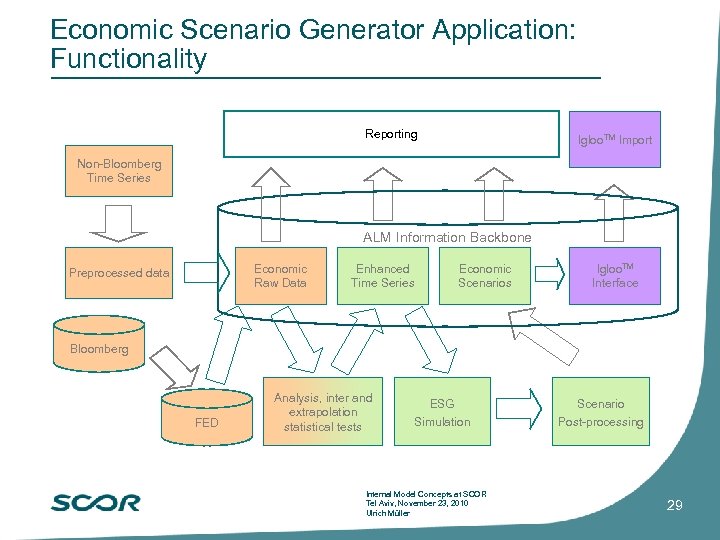
Economic Scenario Generator Application: Functionality Reporting Igloo. TM Import Non-Bloomberg Time Series ALM Information Backbone Economic Raw Data Preprocessed data Enhanced Time Series Economic Scenarios Igloo. TM Interface Bloomberg FED Analysis, inter and extrapolation statistical tests ESG Simulation Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller Scenario Post-processing 29
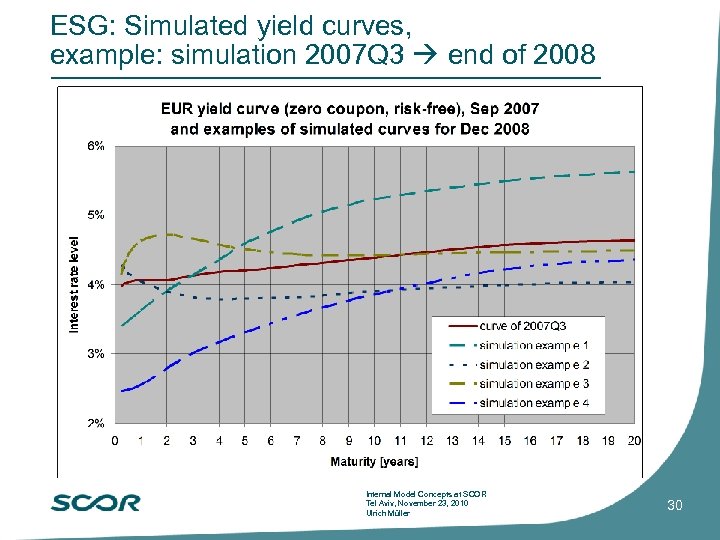
ESG: Simulated yield curves, example: simulation 2007 Q 3 end of 2008 Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 30
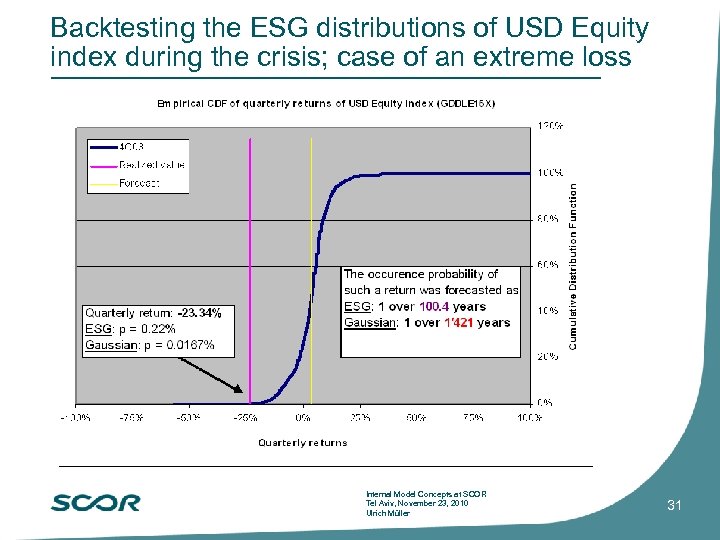
Backtesting the ESG distributions of USD Equity index during the crisis; case of an extreme loss Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 31

SCOR ESG withstands extreme scenarios Extreme scenarios are an integral part of our ESG Extreme rates of 0% or below Extreme rates of around 40% The ESG calculates scenarios with interest rates of 0% or slightly below (not below -1%) The national banking institutions have raised the amount of money in circulation on levels not seen for decades Historic data shows examples of such occasions Expected inflation can only be fought by high interest rates Yen – rates fell slightly below Zero in the early 1990’s Historic examples show that extreme rates can become reality: Mexico, Argentine, Turkey or other EMEA-countries, 26% US Fed rate in the 1980’s, hyperinflation of the 1920’s in Germany Swiss national bank in the 1980’s used negative interest rates as a tool to make investments in Swiss Francs unattractive to fight the strength of the currency Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 32
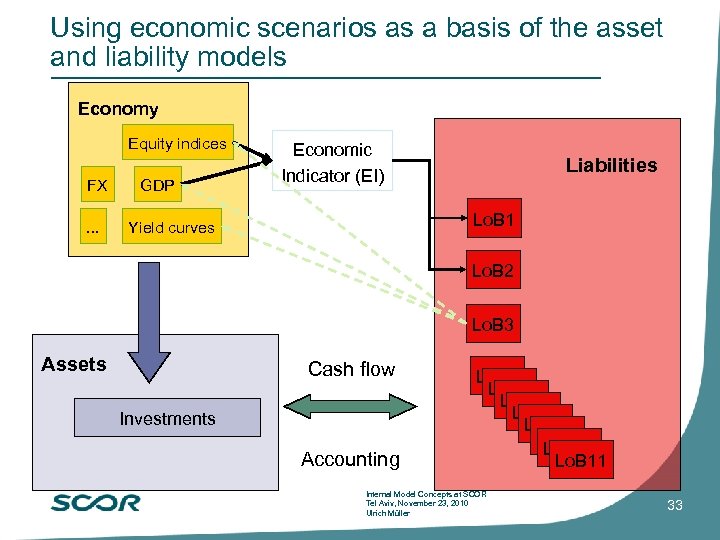
Using economic scenarios as a basis of the asset and liability models Economy Equity indices FX. . . GDP Economic Indicator (EI) Liabilities Lo. B 1 Yield curves Lo. B 2 Lo. B 3 Assets Cash flow Investments Accounting Lo. B 4 Lo. B 5 Lo. B 6 Lo. B 7 Lo. B 8 Lo. B 9 Lo. B 10 Lo. B 11 Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 33

Simulation of invested assets All invested assets are modeled based on the ESG scenarios Example: bond portfolios are valuated based on interest rate scenarios, with roll-overs Asset allocation as important input to the asset model Cash flows from liabilities are invested as well Credit risk of corporate bonds is applied Resulting asset positions after 1 year are simulated taking into consideration ESG returns, asset allocation, cash flows from liabilities and credit risk Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 34

Credit risk model based on credit spreads of corporate bonds We are able to explain most of the credit spread seen in the market by the probability of default given by structural credit risk models. Denzler et al. : From default probabilities to credit spreads: credit risk models do explain market prices. Finance Research Letters, 3: 79 -95 This is possible by assuming a non-Gaussian credit migration rate for the default probability. Simulation results show that a Pareto-like log-gamma type of distribution for the migration rate describes the process reasonably well. The model is powerful enough to explain credit spreads from general parameters obtained from the market. Thus the model can be used to compute the price of credit risk for a corporate bond from a default probability – and the other way around. The model reproduces default statistics (e. g. S&P) and has been calibrated with Moody’s KMV default probabilities Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 35
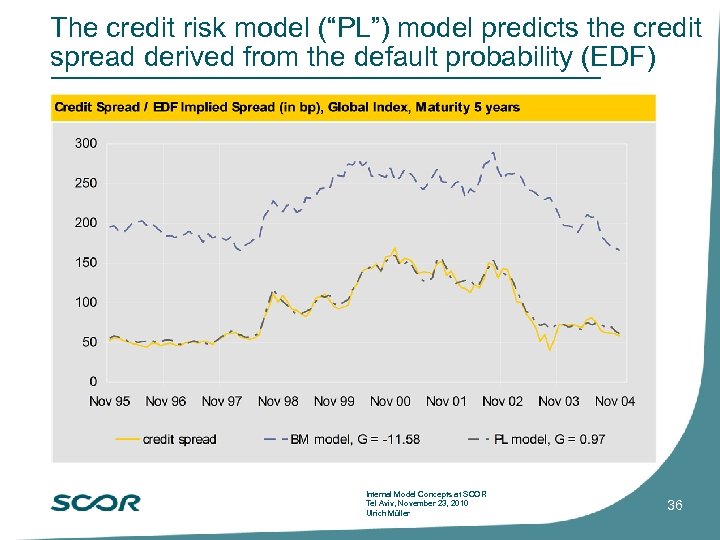
The credit risk model (“PL”) model predicts the credit spread derived from the default probability (EDF) Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 36
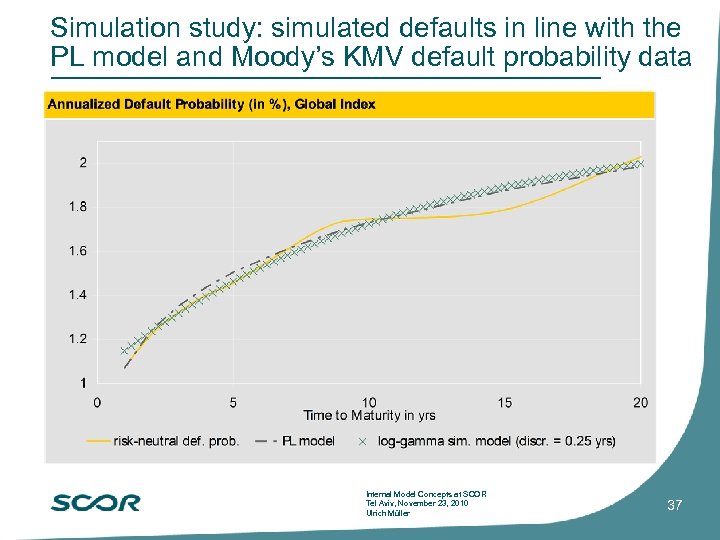
Simulation study: simulated defaults in line with the PL model and Moody’s KMV default probability data Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 37

Agenda 1 Internal Models and regulation: SST and Solvency II 2 Economic profit distribution, risk-adjusted capital, market risk, credit risk 3 Risks in life (re)insurance 4 P&C liabilities: underwriting, reserving, dependencies, retrocession 5 Integrated company model: aggregation, additional dependencies 6 Conclusions Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 38

Modeling of Life liabilities There are differences between P&C and Life business, such as … l Life is often long-term business: cash flow projections over decades l Old life business continues to generate premium, so the underwriting year and the difference between new and old business is not as relevant as for P&C l Risk factors such as mortality or morbidity are a better basis for modeling life risks than the lines of business For economic life business risks, market-consistent valuation has become important: Some life business behaves like a replicating asset portfolio, typically including financial derivatives However, life reinsurers have a lot of biometric risks: mortality trends, mortality shock (pandemic), lapse risk, …. More important than economic risks! Embedded Value is a dominant valuation concept for life business. Our capital model largely relies on (side) results of the official Embedded Value computations at SCOR Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 39
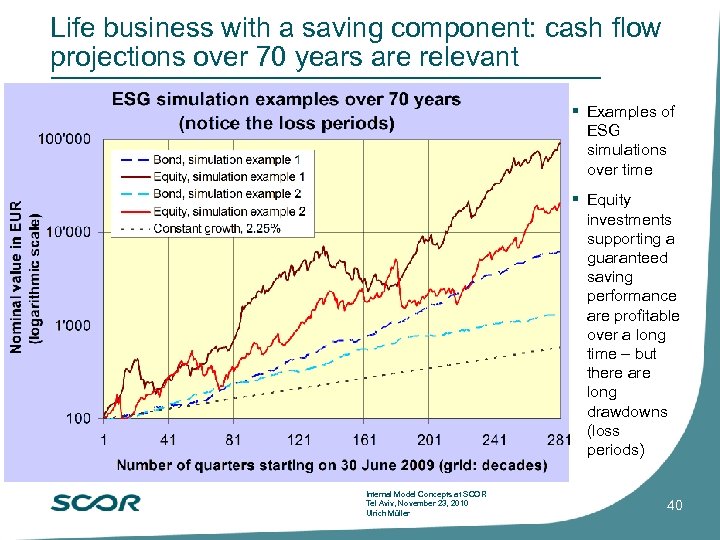
Life business with a saving component: cash flow projections over 70 years are relevant Examples of ESG simulations over time Equity investments supporting a guaranteed saving performance are profitable over a long time – but there are long drawdowns (loss periods) Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 40

Risk factors and lines of business (Lo. B) in the life model Risk factors Random fluctuations (mixed factors) Mortality trend (EU, America, Asia, …) Longevity trend Disability trend Long term care (LTC) trend Critical illness (CI) trend Lapse Local catastrophy Pandemic (Europe, America, Asia, …) Financial risks (inflation, deflation, …) … more … The risk factors affect the one-year change in our view of the business, including projected future long-term cash flows Lo. B Life (EU, America, Asia, …) Annuity Health Disability Long Term Care (LTC) Critical Illness (CI) Personal Accident Financing with deficit accounting Financing without deficit accounting Investment Treaties Guaranteed Minimum Death Benefit … more … The list of Lo. B corresponds to the list of Lo. B used in the Embedded Value process Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 41

Profit distributions of life business based on risk factors Simulation of changes of Present Values of Future Profit (PVFP), similar to Embedded Value By risk factor. Some risk factors have dependencies on other risk factors Pandemic as a main risk factor has a truncated Pareto model for excess mortality By line of business (Lo. B). Each Lo. B has an exposure function against each risk factor (matrix) By legal entity By currency Thus the modeling units have a 4 -dimensional granularity Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 42

Dependencies between Life risks: excess mortalities in two different regions, due to pandemic risk Two regions: America, Europe The same pandemic model for both regions: Pareto with lower and upper cut-off, 3 pandemics expected per 200 years. The cumulative probabilities (CDFs) follow an upper-tail Clayton copula with parameter theta (θ); 2500 simulations Exploring the following theta values: 0 (independent), 1, 3, 8 Scattergrams for resulting excess mortalities in America and Europe (not for the CDFs here) What is the right degree of dependency, in your opinion? Which theta? Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 43

Example: Hierarchical dependency of regions and sub-regions, due to the same risk type Hierarchical tree of regions and sub-regions. Sub-regions within the same main region have stronger dependency for a certain risk factor (e. g. pandemic) Modeling all regions cumulative probability distributions (CDFs) for all of them At each node of the tree, there is an upper-tail Clayton copula with parameter theta (θ); 400 simulations here Theta between sub-regions (West. Asia and East. Asia): θ = 7; theta between main regions: θ = 2 It is numerically possible to apply hierarchical dependency between risk factors without any exposure information Resulting scattergrams for the CDFs show the desired dependency behavior Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 44

Example: Complete dependency tree for all risk factors of Life insurance Hierarchical tree of all risk factors (a simple, schematic proposal) Different copula types (including independence) are possible at each node of the tree The risk factors “Mortality Trend” and “Longevity” refer to changes in long-term trend expectations within one simulation year (e. g. change in underlying mortality tables) The preferred copula for “Mortality Trend” and “Longevity” is the Gauss copula (= rank correlation) because these factors are correlated throughout the distribution, not only in the tails The preferred copula for “Pandemic” (= “Mortality Shock”) is the Clayton copula. Severe pandemics are more likely to spread over the whole world than small ones (tail dependence) Economic risks covered by Economic Scenario Generator (ESG, also affecting P&C business and invested assets). Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 45

Agenda 1 Internal Models and regulation: SST and Solvency II 2 Economic profit distribution, risk-adjusted capital, market risk, credit risk 3 Risks in life (re)insurance 4 P&C liabilities: underwriting, reserving, dependencies, retrocession 5 Integrated company model: aggregation, additional dependencies 6 Conclusions Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 46

Overview: P&C liability modeling Property and Casualty (P&C) reinsurance is the dominant business of SCOR. We distinguish between the following business maturities: l Reserve business (insured period over, just development risk) l Unearned prior-year business (still under direct insurance risk) l New business to be written in the simulation year We distinguish between further categories (high granularity): l Many lines of business (Lo. B), grouped in categories l Proportional / non-proportional treaty and facultative reinsurance business l Business in different legal entities We model the effect of retrocession gross and net profit distributions Hierarchical dependency tree between the many modeling units Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 47

Granularity of P&C Scenarios Legal Entities: e. g. SCOR_PC, SCOR Switzerland… Items: Premiums, Losses, Expenses Perspective: Gross, Retro Maturity: New Business, Reserves, Prior-Year Business Lines of Business: e. g. Property, Motor, Aviation, Credit & Surety… Reinsurance Type: Treaty Business, Facultative Business Cover: Proportional, Non-Proportional Programme: Retro programme names… Currencies of Programmes: e. g. EUR, USD, GBP Patterns The input granularity is important to support output reporting flexibility!. . . but with this, increasing performance issues have to be carefully considered…. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 48

Modeling P&C reserve risk based on the historical development of insurance losses Loss reserves of a (re)insurance company: Amount of reserves = Expected size all of claims to be paid in the future, given all the existing “earned” (≈ old) contracts Reserves are best estimates. Estimates may need correction based on new claim information Upward correction of reserves loss, balance sheet hit Reserve risk = risk of correction of loss reserves Reserve risk is a dominant risk type, often exceeding the risks due to new business (e. g. future catastrophes) and invested asset risk Reserve risks can be assessed quantitatively. For assessing reserve risks, we use historical claim data Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 49
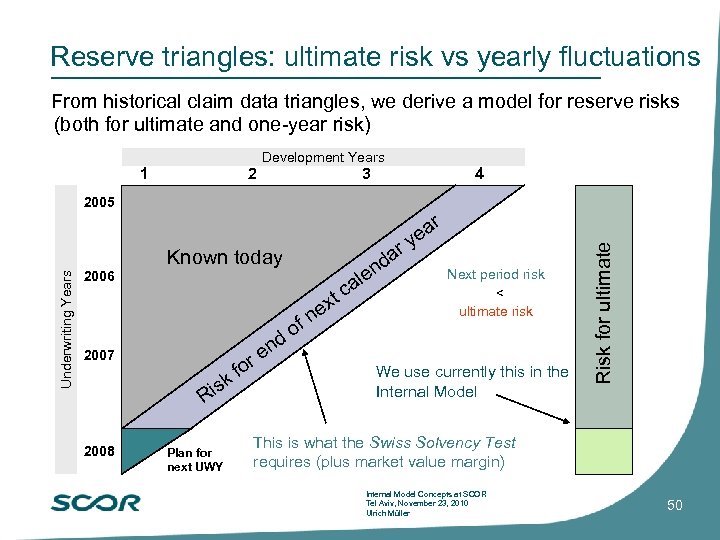
Reserve triangles: ultimate risk vs yearly fluctuations From historical claim data triangles, we derive a model for reserve risks (both for ultimate and one-year risk) 1 2 Development Years 3 4 2005 2006 ar d Known today x len ca t e 2007 r fo k s Ri 2008 nd Plan for next UWY o e f n Next period risk < ultimate risk We use currently this in the Internal Model Risk for ultimate Underwriting Years r a ye This is what the Swiss Solvency Test requires (plus market value margin) Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 50

Triangle analysis of cumulative insurance claims Development year (years since the underwriting of contracts) Underwriting year (when contracts were written) ↓ This triangle is the basis of further analysis. Here: cumulative reported claims. There are other types (claims paid, …). Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 51

Measuring the stochastic behavior of historical claim reserves: Mack’s method Chain-ladder method: computing the average development of claims over the years Result: Typical year-to-year development factors for claims ( patterns) Method by Mack (1993): computing local deviations from these average development factors Variance of those local deviations estimate of reserve risk Very sensitive to local data errors overestimation of risk Correctness of data is very important, data cleaning needed We developed a robust variation of the Mack method (published in the Astin Bulletin) Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 52
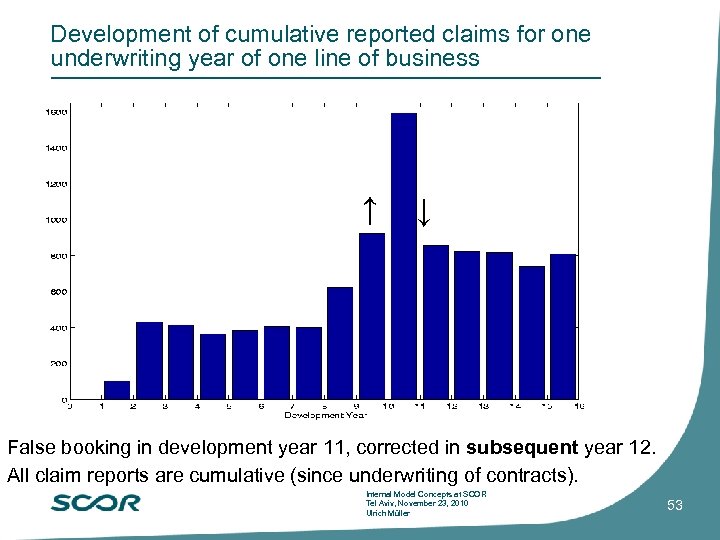
Development of cumulative reported claims for one underwriting year of one line of business ↑ ↓ False booking in development year 11, corrected in subsequent year 12. All claim reports are cumulative (since underwriting of contracts). Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 53

Modeling the profit distributions of new and unearned prior-year P&C business New business is subject to technical pricing at SCOR has a sophisticated pricing tool profit distributions per treaty The tool NORMA aggregates treaties with proper dependency assumptions between treaties profit distributions per modeling unit Our risk-based capital calculation uses the resulting gross profit distributions, for new and unearned business NORMA models dependencies between the modeling units of P&C business NORMA also models retrocession treaties (for new, unearned and reserve business stochastically simulated scenarios for retrocession recoveries and net losses per modeling unit Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 54

Dependency between risks is key Risk Diversification reduces a company’s need for risk-based capital. This is key to both insurance and investments. However, risks are rarely completely independent: l Stock market crashes are usually not limited to one market. The financial crisis again shows that local markets depend on each other. l Certain lines of business are affected by economic cycles, such as liability, credit & surety or life insurance. l Motor insurance is correlated to motor liability insurance and both will vary during economic cycles. l Big catastrophes can produce claims in various lines of business. Dependency between risks reduces the benefits of diversification. The influence of dependency on the aggregated risk-based capital is thus crucial and needs to be carefully analyzed. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 55

Extreme events and dependencies Extreme events are major risk drivers for insurers. Examples: l Natural catastrophes (Non-Life insurance) l Pandemic (Life insurance) Dependencies between different risks are also major risk drivers. l Risk diversification between different lines of business is limited by dependencies. Large or extreme events are often the cause of dependencies. l A large windstorm may affect different countries whose risk exposures are independent in case of smaller events. l September 11, 2001, caused large losses in different lines of business (Life, Property, Aviation, Business Interruption) that are usually less dependent. The coincidence of extreme events and increase dependence is called tail dependence. Tail dependence > “everyday dependence”. Large events should be explicitly modeled as common causes, if possible. If not possible, we need a dependence model (e. g. copula-based). Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 56
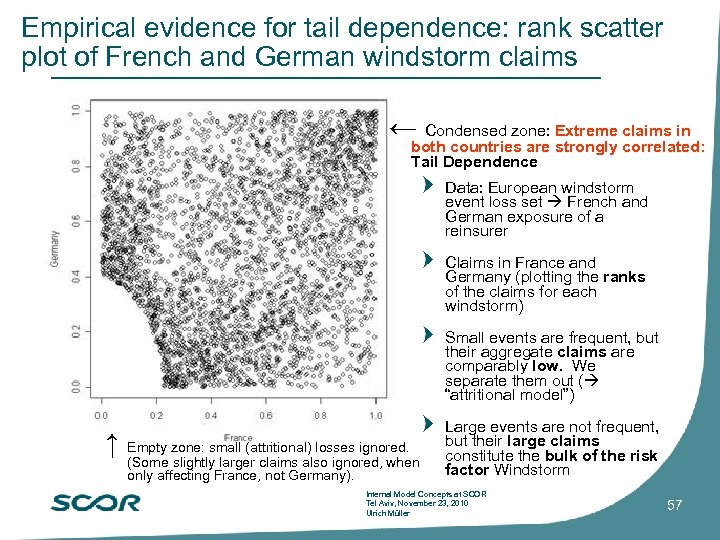
Empirical evidence for tail dependence: rank scatter plot of French and German windstorm claims ← Condensed zone: Extreme claims in both countries are strongly correlated: Tail Dependence Data: European windstorm event loss set French and German exposure of a reinsurer Claims in France and Germany (plotting the ranks of the claims for each windstorm) Small events are frequent, but their aggregate claims are comparably low. We separate them out ( “attritional model”) ↑ Empty zone: small (attritional) losses ignored. (Some slightly larger claims also ignored, when only affecting France, not Germany). Large events are not frequent, but their large claims constitute the bulk of the risk factor Windstorm Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 57

Empirical evidence from French and German windstorms We observe a concentration of correlation in the upper tail: large windstorms in France are often large windstorms in Germany as well. If we assume a uniform correlation everywhere, l we underestimate the (value at) risk due to large, common events in both countries; l and/or we overestimate the correlation of averagesized events. In the example of windstorms, we do not have to model the dependency explicitly as long as we have event sets. For other perils and lines of business, we have no event set We need an explicit dependency model with upper tail dependence. Our choice: copulas rather than uniform linear correlation. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 58

Why is correlation in the upper tail often higher? The basic reason for increased correlation in the upper tail of loss distributions: Large events often have a wide range of impact and high severity at the same time Examples for large events with wide impact and high severity: l A large European windstorm causes simultaneous, large losses in different countries (e. g. Lothar) l September 11, 2001, had simultaneous, large losses in several lines of business: Life, Property, Aviation, Business Interruption, … l A change in law simultaneously affects the settlement of different Liablility and Professional Liability treaties of certain types (in markets that were initially thought to be independent) Examples for small (but frequent) events and lower severity: l A smaller windstorm causes notable losses only within a limited area of one market l A fire in a factory causes local damage, in only one market and line of business: Property l A specific court decision leads to a moderately higher individual loss in Motor Liability, with no consequences for other treaties or lines of business The opposite can also happen: large localized losses and small losses with a wide range of impact. But these types of events are less typical. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 59
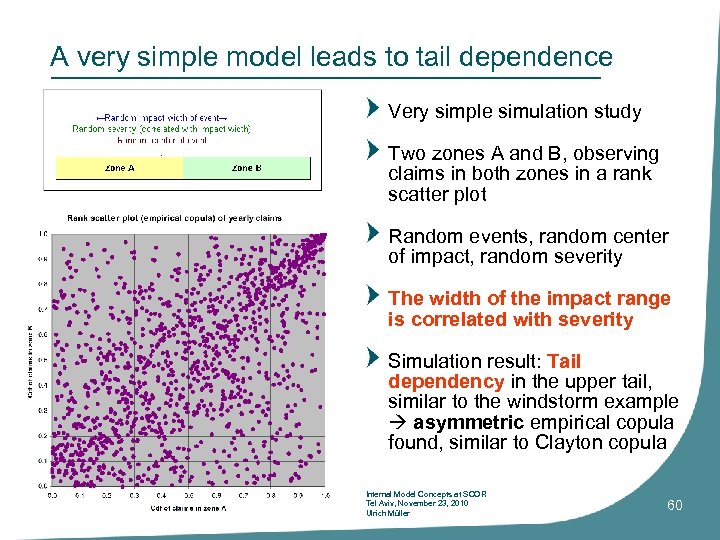
A very simple model leads to tail dependence Very simple simulation study Two zones A and B, observing claims in both zones in a rank scatter plot Random events, random center of impact, random severity The width of the impact range is correlated with severity Simulation result: Tail dependency in the upper tail, similar to the windstorm example asymmetric empirical copula found, similar to Clayton copula Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 60

Dependence modeling: Conventional correlation vs. copulas with tail dependence Linear correlation as well as rank correlation are models for a unified dependency behavior, regardless of the size of losses or events. Therefore correlation-based models tend to underestimating the tail dependence ( underestimation of capital requirement!) and overestimating dependence in case of average behavior. We need a dependency model that supports increased tail dependency. Our choice is copulas. Which copulas? The tail dependency is related to large losses (often due to extreme events) rather than small losses Tail dependency affects only one of the two tails asymmetric copula needed Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 61

Clayton Copula θ = 0. 1 θ = 0. 5 θ = 1. 0 θ = 2. 0 Asymmetric Copula The Clayton Copula CDF is defined by: With a Generator of the Copula: The Clayton copula is Archimedean Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 62
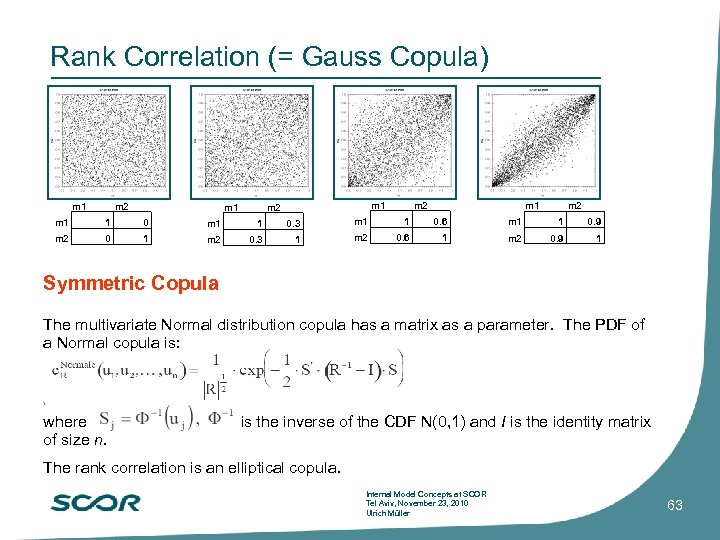
Rank Correlation (= Gauss Copula) m 1 m 2 m 1 m 2 m 1 1 0. 3 m 1 1 0. 6 m 1 1 0. 9 m 2 0 1 m 2 0. 3 1 m 2 0. 6 1 m 2 0. 9 1 Symmetric Copula The multivariate Normal distribution copula has a matrix as a parameter. The PDF of a Normal copula is: where of size n. is the inverse of the CDF N(0, 1) and I is the identity matrix The rank correlation is an elliptical copula. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 63

Many different dependencies are modeled, some with copulas We model the marked dependencies with copulas. Dependencies between risk factors (e. g. trends in mortality and longevity in Life modeling) Dependencies between different treaties within the same line of business (Lo. B) Dependencies between loss developments in new and old business (reserves) within the same line of business Dependencies between events in neighbouring regions (e. g. windstorms in France and Germany). Dependencies between related Lo. B (e. g. Fire and Engineering) Dependencies between less related Lo. B (e. g. Fire and Professional Liability) Dependencies between Life and Non-Life (through Cat, terrorism etc) Dependencies between economy and insurance liabilities (through discount rate etc) Dependencies between economy and credit risk (credit cycle modeled in the ESG) Dependencies between invested assets and the economy (rather obvious) Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 64
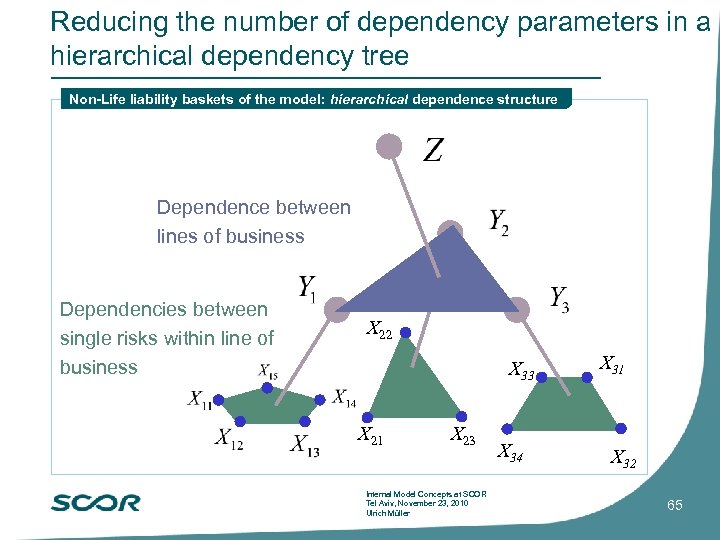
Reducing the number of dependency parameters in a hierarchical dependency tree Non-Life liability baskets of the model: hierarchical dependence structure Dependence between lines of business Dependencies between single risks within line of business X 22 X 33 X 21 X 23 Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller X 34 X 31 X 32 65
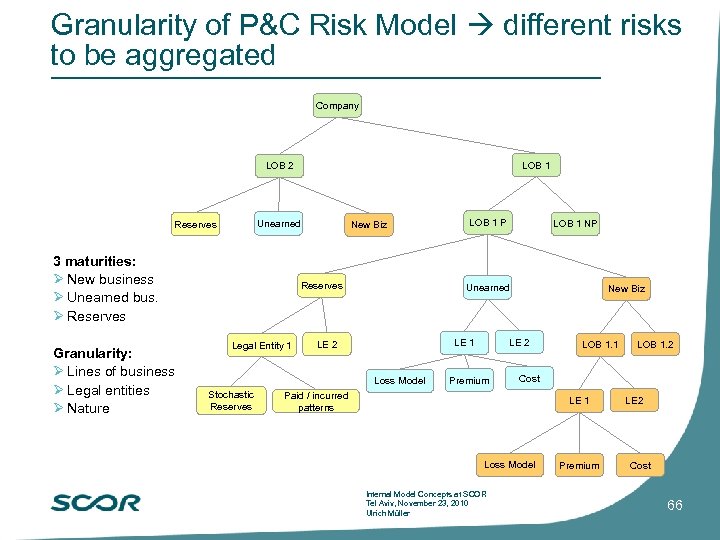
Granularity of P&C Risk Model different risks to be aggregated Company LOB 1 LOB 2 Reserves Unearned 3 maturities: New business Unearned bus. Reserves Granularity: Lines of business Legal entities Nature New Biz Reserves Legal Entity 1 LOB 1 NP Unearned New Biz LE 2 LE 1 LE 2 Loss Model Stochastic Reserves LOB 1 P Premium LOB 1. 1 Cost Paid / incurred patterns LE 1 Loss Model Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller LOB 1. 2 Premium LE 2 Cost 66

Comparing the number of dependency parameters: correlation matrix vs. copula tree Task: Modeling all P&C liabilities of a large company in 500 modeling baskets (different risk factors, lines of business, legal entities, markets, business maturities (reserves vs. new business), business types (proportional, non-proportional, facultative). Alternative 1: Using a correlation matrix between all the 500 modeling baskets We need 500 * 499 / 2 = 124759 correlation coefficients. This is not a parsimonious parameter set. Alternative 2: Using a hierarchical copula tree with (typically) 350 nodes on 7 hierarchical layers, each node with one parameter (e. g. a Clayton copula theta). We need 350 parameters. This is parsimonious and manageable in comparison. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 67

Strategy for modeling dependencies Using the knowledge of the underlying business, develop a hierarchical model for dependencies in order to reduce the parameter space and describe more accurately the main sources of dependent behavior Wherever we know a causal dependency, we model it explicitly Otherwise we systematically use non-symmetric copulas: Clayton copula Wherever there is enough data, we statistically calibrate the parameters SCOR has a launched a new project to improve the calibration of copula parameters Prob. Ex In absence of data, we use stress scenarios to estimate conditional probabilities Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 68

Dependencies between Property & Casualty Risks: Pr. Ob. Ex Combining three sources of information SCOR developed a new method to calibrate P&C dependence parameters Through a Bayesian model, three sources of information are combined: • Prior information (regulators) • Observations (data) • Expert judgements We invite experts to a Workshop where they are asked to assess dependencies within their Lo. B. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 69

The importance of the P&C dependency calibration project Some figures on the P&C calibration process Dependence within 19 P&C Lines of Business are calibrated via Pr. Ob. Ex The meetings take place between April and September, 2010 A final meeting will assess dependence between Lines of Business Around 120 experts, in 12 different locations, are taking part in the calibration process Results will have an important impact for SCOR The P&C model calibration directly aims at dependencies between concrete parts of the SCOR P&C business portfolio. Unlike the Life model, the P&C model does not separate risk factor models from exposure models. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 70

Dependence Measure – What are we asking the experts? X+Y How to measure dependence? X Y We ask the experts: “Suppose Y exceeds the 1 -in-100 year threshold. What is the probability that also X exceeds its 1 -in -100 year threshold? ” Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 71

Pr. Ob. Ex, combined view Final distribution via the three sources of information Prior Information Observation Expert judgements Pr. Ob. Ex combines the three sources to provide SCOR with the finest estimate for dependence parameters Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 72

Agenda 1 Internal Models and regulation: SST and Solvency II 2 Economic profit distribution, risk-adjusted capital, market risk, credit risk 3 Risks in life (re)insurance 4 P&C liabilities: underwriting, reserving, dependencies, retrocession 5 Integrated company model: aggregation, additional dependencies 6 Conclusions Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 73
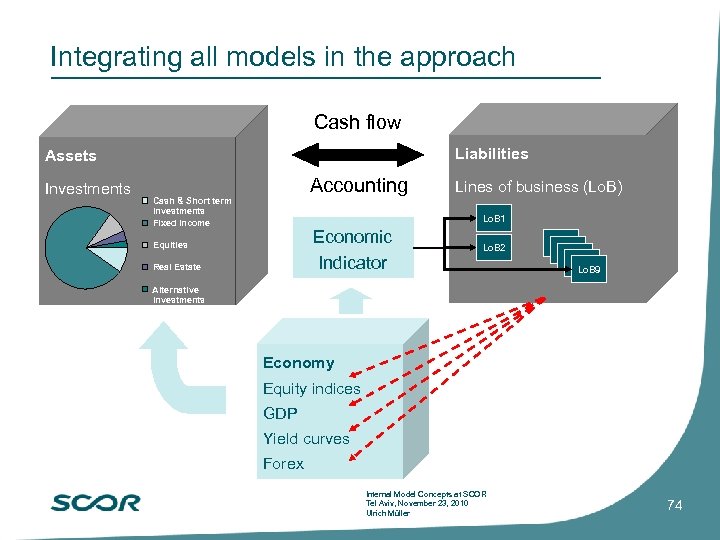
Integrating all models in the approach Cash flow Liabilities Assets Investments Accounting Cash & Short term investments Fixed Income Lines of business (Lo. B) Lo. B 1 Economic Indicator Equities Real Estate Lo. B 2 Lo. B 4 Lo. B 9 Alternative Investments Economy Equity indices GDP Yield curves Forex Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 74
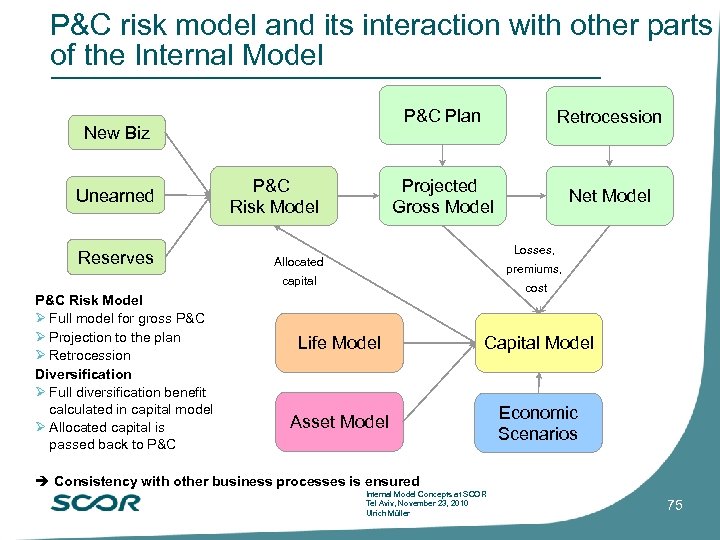
P&C risk model and its interaction with other parts of the Internal Model P&C Plan Projected Gross Model New Biz Unearned Reserves P&C Risk Model Retrocession Net Model Losses, Allocated premiums, capital P&C Risk Model Full model for gross P&C Projection to the plan Retrocession Diversification Full diversification benefit calculated in capital model Allocated capital is passed back to P&C cost Life Model Capital Model Asset Model Economic Scenarios Consistency with other business processes is ensured Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 75

Which dependencies are modeled between the main modeling blocks? The two marked dependencies are between main model blocks and have to be modeled in the main aggregate risk calculation rather than within a partial block. Dependencies between risk factors (e. g. trends in mortality and longevity) in Life modeling Dependencies between different treaties within the same lines of business (Lo. B) Dependencies between loss developments in new and old business (reserves) within the same line of business Dependencies between events in neighbouring regions (e. g. windstorms in France and Germany). Dependencies between related Lo. B (e. g. Fire and Engineering) Dependencies between less related Lo. B (e. g. Fire and Professional Liability) Dependencies between Life and Non-Life (through Cat, terrorism etc) Dependencies between economy and insurance liabilities (through discount rate, claims inflation, etc) Dependencies between economy and credit risk (credit cycle modeled in the ESG) Dependencies between invested assets and the economy (rather obvious) Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 76

Results are per Legal Entity / Consolidated Group All results are simulated per legal entity Internal reinsurance, legal entity relationships, taxes etc. are considered It is essential to have modeling flexibility regarding legal entities (but of course also for other dimensions) as those structures can change… Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 77
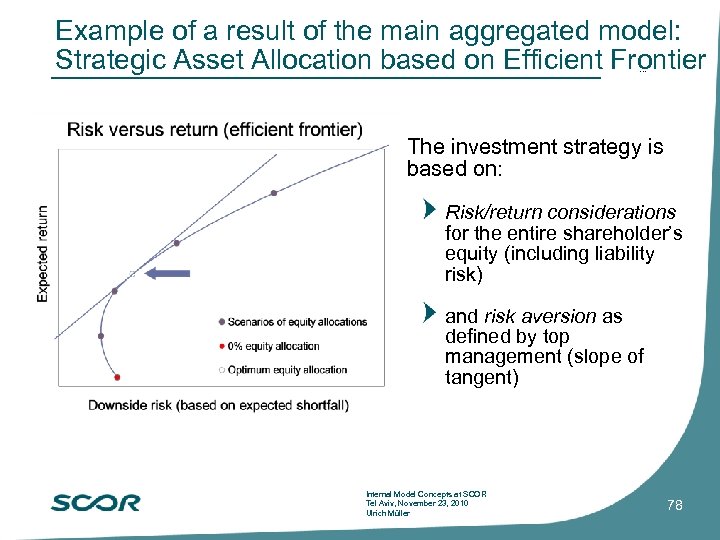
Example of a result of the main aggregated model: Strategic Asset Allocation based on Efficient Frontier … The investment strategy is based on: Risk/return considerations for the entire shareholder’s equity (including liability risk) and risk aversion as defined by top management (slope of tangent) Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 78

Agenda 1 Internal Models and regulation: SST and Solvency II 2 Economic profit distribution, risk-adjusted capital, market risk, credit risk 3 Risks in life (re)insurance 4 P&C liabilities: underwriting, reserving, dependencies, retrocession 5 Integrated company model: aggregation, additional dependencies 6 Conclusions Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 79

Conclusions (I) The Internal Model … is used internally for capital allocation, planning etc. (ORSA) l … is a part of regulatory solvency tests (SST, Solvency II) l … captures the risks of a large, highly diversified company better than a standard model or standard formula Modeling many partial risks: economy, market and credit risk, invested assets, Life liabilities, P&C liabilities, … As a basis of the risk-adjusted capital calculation, we use economic profit distributions per modeling unit A central Economic Scenario Generator (ESG) determines the stochastic simulation of all assets and liabilities as far as they depend on the economy Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 80

Conclusions (II) For aggregating profit distributions, the modeling of the dependence between partial risks and units plays a key role The dependence between large losses (strongly negative profits) is often stronger than for average profits tail dependence We model tail dependence with copulas, often the Clayton copula, sometimes in hierarchical dependency trees The life model distinguishes between primary risk factors (such as pandemic) and lines of business depending on these factors through exposure functions Our preferred choice of the overall risk-based capital is the xt. Va. R at 1%, where the Euler Principle is used to allocate the total amount to the different risks and segments of the company Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 81

Thank you … … for your attention. Your comments and questions are welcome. Internal Model Concepts at SCOR Tel Aviv, November 23, 2010 Ulrich Müller 82
db766b757353282abd9ebf38db9b85de.ppt