Intergenerational mobility Cheti Nicoletti ISER University of Essex

Intergenerational mobility Cheti Nicoletti ISER, University of Essex 2009

Motivation • Studies on intergenerational (im)mobility try to examine the association between children’s and parents’ socio-economic outcome (usually income, earnings, occupational class or prestige). • It is believed that low intergenerational mobility is indicative of unequal opportunities between people born in advantaged and disadvantaged families and that policy should improve opportunities for those from disadvantaged backgrounds.

Motivation • Notice that two societies could have the same level of inequality in earnings within a generation but a completely different level of intergenerational transmission of earnings. • A society where the relative position of a person in the earnings distribution is exactly inherited from the parents’ one is considered unfair.

Previous studies • • • A first study of intergenerational transmission can be dated back to Galton (1886) who regress children’s height on parents’ one. More recently sociologists have studied intergenerational mobility and have especially focused on the association between class positions of parents and children (see Erikson and Goldthorpe 1992). Economists have begun to be extensively interested in this topic after Becker and Tomes (1979, 1986) developed a model of the transmission of earnings, assets and consumptions from parents to children. Atkinson (1981) and Atkinson, Maynard and Trinder (1983) are the first papers to study intergenerational earnings mobility in the UK (men born in York in 1950 and traced to the late 1970 s). Review article: Solon, G. (1999) Intergenerational mobility in the labor market, In O. Ashenfelter and D. Card (eds. ) Handbook of Labor Economics, Volume 3, Chapter 29, 1761 -1800. Amsterdam: Elsevier. Look forthcoming chapter “Intergenerational income mobility and the role of family background” in Handbook of Economic Inequality Markus Jäntti and Anders Björklund

Intergenerational mobility equation

Data requirement • • 1. 2. 3. We need to observe a long run permanent measure (income, earnings, occupational prestige) for both fathers and their children Possible data sources: Panel data which follow individual across time (for example the Panel Study of Income dynamic in US, the British Household Panel Survey) Cohort studies which follow people born in a specific cohort from when born or other longitudinal studies (for example the British Cohort Studies 1958 and 1970, National Longitudinal Survey in the US) Cross-sectional data with retrospective questions asked to children about their fathers (for example Oxford Mobility Study, which provides data on occupational class for children and their fathers when they, the sons, were 14 years old. )

Measurement error on father’s earnings • We observe current earnings xit instead of a permanent measure of earnings xi xit=xi +εit where εit iid (0, σε 2 ) and independent of xi and yi • This implies that we underestimate β ( for β>0) • Notice that a similar error for yit would not bias β, but it would bias the intergenerational correlation

Solution suggested by Solon (1992) and Zimmerman (1992) • If xit is observable for t=1, …T, we can consider

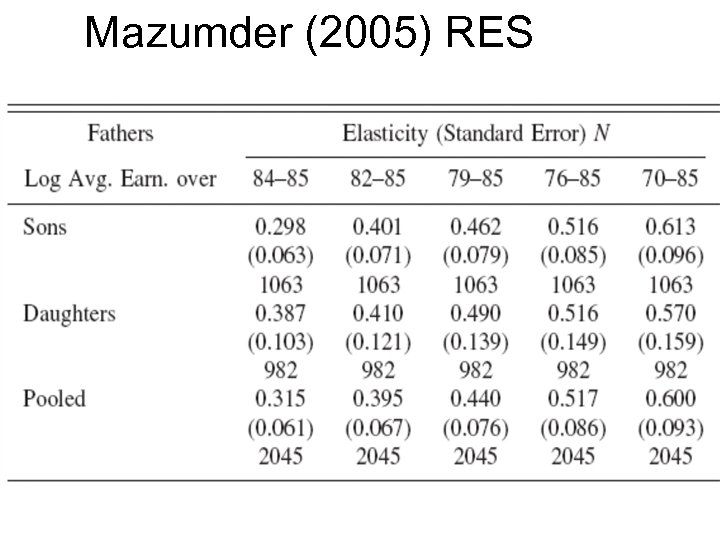
Mazumder (2005) RES

Life cycle bias • Earnings (even if averaged) can be a bad proxy for permanent earnings if measured when people are too old or too young (Life cycle bias). • Solution: Control with a polynomial in age or age dummies in the intergenerational equation

Life cycle bias 1. 2. 3. Controlling for sons and fathers age in the intergenerational mobility equation can help in reducing the measurement error bias. But this correction is not enough if the earnings growth is heterogeneous across individuals. Imposing and upper and a lower bound for sons and fathers age can be a solution (ex. Blanden et al 2004 and 2007, 30 -33; Gershuny 2002, 34 -36; Ermsich and Nicoletti 2007, 31 -45). Lee and Solon (2005) suggest to estimate an intergenerational mobility equation using sons observed at any age but allowing the elasticity to vary across cohort and son’s age. (See for example Ermsich and Nicoletti 2007)

Comparing Intergenerational across cohorts in Britain • • • Comparing measure of intergenerational mobility across children (sons) born in different cohorts is very difficult because of data comparability and data availability issues. It is for example difficult to observe earnings for both children and their parents for very long cohort period Blanden, Gregg, Mac. Millan (2007, The Economic Journal) compared NCDS 1958 and BC 1970 (but the two datasets have a lot comparability issues) and found a negative trend in mobility Nicoletti, Ermisch (2007, The B. E. Journal of Economic Analysis & Policy) compared children born from 1950 to 1972 using the BHPS (but they use a two sample two stage procedure which usually provide an overestimation of the intergenerational mobility) and found no trend for the period 1950 -72 and a slight negative but not significant trend for the 1960 -1972 period Breene and Goldthorpe (2001, European Sociological Review) and Goldthrope and Jackson (2007, British Journal of Sociology) studied class mobility and found little change across the two generations when considering measures of exchange mobility, in contrast to the negative trend in mobility found in Blanden et al. (2004, 2007)) using the same two cohorts.

Advantages and disadvantages of panel data Ø Advantages • • Repeated observations are available so that it is easier to measure the long run economic status. Panel surveys are usually based on representative samples of the full population. Ø Disadvantages • Coresidence selection: Son must be living together with his father in at least one wave of the panel.

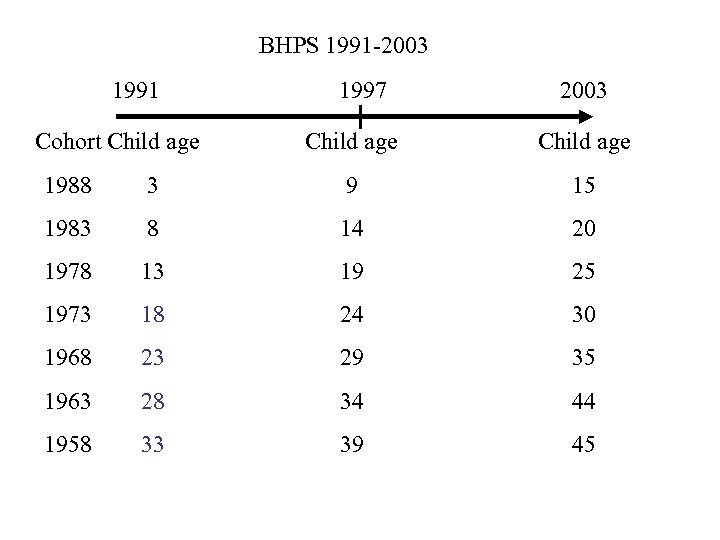
BHPS 1991 -2003 1991 Cohort Child age 1997 2003 Child age 1988 3 9 15 1983 8 14 20 1978 13 19 25 1973 18 24 30 1968 23 29 35 1963 28 34 44 1958 33 39 45

How can the BHPS help us? • • All BHPS respondents are asked to report occupational characteristics of their parents when they were 14 THEREFORE We know the occupational prestige, say HG, even for sons and fathers living apart during the panel. We can estimate the correlation of HG without any coresidence selection. We can consider the subsample of sons coresident with the fathers at least once during the panel and assess the relevance of the coresidence selection. We can then compare different methods to correct for the coresidence selection.

Taking account of coresidence selection Francesconi and Nicoletti (Journal of Applied Econometrics, 2006) find that the intergenerational mobility in occupational prestige is underestimated when using the subsample of sons born between 1966 and 1985. They try different estimation methods to correct for sample selection and find that only the inverse propensity score is able to attenuate the selection problem This sample selection evaluation is possible because all BHPS respondents are asked to report occupational characteristics of their parents when they were 14

Coresidence • If we select only children coresident with their parents in at least one wave of the panel, we can have a problem of sample selection. The subsample is probably not a random sample. • This can cause a bias in the estimation of β

Selection model (coresidence model) Z=dummies for education, age, regions, ethnicity, religiosity and two house price indexes

Selection problem • Y=log son earnings X= log father earnings • Z=dummies for education, age, regions, ethnicity, religiosity and two house price indexes • If ε depends of u Selection due to unobservables • Ex. unobserved work abilities which are related to y and to the probability to leave parental home earlier • If ε depends of Z Selection due to observables • Ex: Y|X depends on Z (education and age) then ε depends on Z and we have selection due to observables

Selection due to observables: Propensity score weighting estimation • Y=log son earnings X= log father earnings • Z=dummies for education, age, regions, ethnicity, religiosity and two house price indexes • If ε and u are independent but ε depends on some of the Z (for education, age, etc. ) Weighted least square estimation of β with weights given by

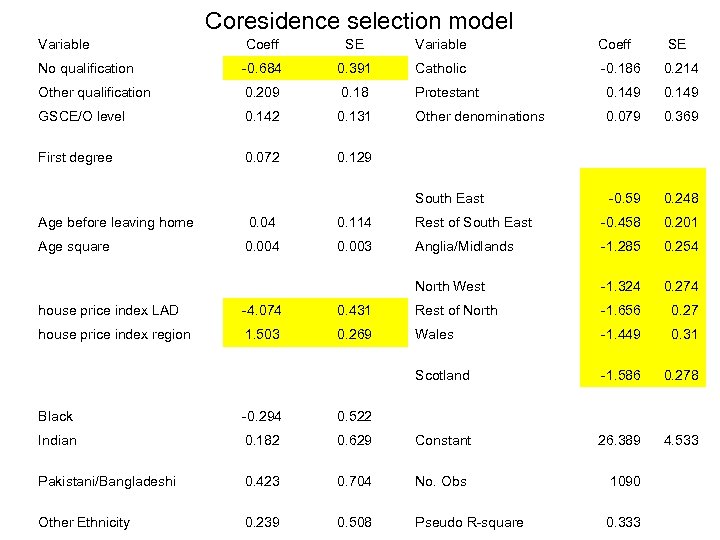
Coresidence selection model Variable Coeff SE No qualification -0. 684 0. 391 Catholic -0. 186 0. 214 Other qualification 0. 209 0. 18 Protestant 0. 149 GSCE/O level 0. 142 0. 131 Other denominations 0. 079 0. 369 First degree 0. 072 0. 129 South East -0. 59 0. 248 Age before leaving home 0. 04 0. 114 Rest of South East -0. 458 0. 201 Age square 0. 004 0. 003 Anglia/Midlands -1. 285 0. 254 North West -1. 324 0. 274 house price index LAD -4. 074 0. 431 Rest of North -1. 656 0. 27 house price index region 1. 503 0. 269 Wales -1. 449 0. 31 Scotland -1. 586 0. 278 26. 389 4. 533 Black -0. 294 0. 522 Indian 0. 182 0. 629 Constant Pakistani/Bangladeshi 0. 423 0. 704 No. Obs 1090 Other Ethnicity 0. 239 0. 508 Pseudo R-square 0. 333

Intergenerational mobility mediated by education • • • y=α+xβ+ε If ε and u are independent but ε depends on education Then to take account that ε is not independent of education (omitted variable) we can consider y=αN+xβN+edu δ +ω Regression adjustment βN is consistently estimated (because ω is independent of u and of education) β=Cov(x, y)/Var(x)=βN+Cov(x, edu)Var(x)-1δ βN is the intergenerational association (elasticity) in earnings net of the effect (or not mediated by) the education. (β-βN) is the intergenerational mobility in earnings mediated by the education

Another solution for the coresidence selection problem using the BHPS • PROBLEM: We can observe both sons’ and their fathers’ earnings only if they have been living together in at least 1 wave during the panel. This is possible in 12% of the cases in our sample (cohort period 1950 -1972). • SOLUTION: we use a TS 2 SLS estimator which combines two separate samples from the BHPS

The two-sample two-stage least squares (plim TS 2 SLS = plim TS 2 SIV) The TS 2 SLS estimator combines two separate samples from the BHPS: • 1 st dataset (Full sample) containing information on sons’ earnings, and fathers’ education and occupational characteristics when sons were 14 years (collected through retrospective questions to sons); • 2 nd dataset (Supplemental sample) containing information on earnings and occupational characteristics of potential fathers (Hope-Goldthorpe index; the Cambridge scale; dummies to distinguish occupations in professional, managerial and technical, skilled nonmanual, skilled manual and unskilled; 19 dummies for socio–economic groups). References 2 SIV: Angrist and Krueger (1992), Arellano and Meghir (1992), Ridder and Moffitt (2005), Inoue and Solon (2005)

Two-sample two-stage least squares estimator (TS 2 SLS) Combining the two samples 1. Estimation of the log earnings equation for fathers using the supplemental sample (imputation regression) x=Z +v 2. Estimation of the main equation using the full sample and replacing (imputing) x

Previous studies on intergenerational mobility using TS 2 SLS estimator The choice of instruments in previous studies is quite often dictated by the few variables available: • Bjorklund and Jantti (1997) use education level and occupation in Sweden, • Fortin and Lefebvre (1998) use 16 occupational groups in Canada • Grawe (2004) uses education levels for Ecuador, Nepal, Pakistan and Peru. Our potential IV are instead given by: • Hope-Goldthorpe index; the Cambridge scale; dummies to distinguish occupations in professional, managerial and technical, skilled non-manual, skilled manual and unskilled; 19 dummies for socio–economic groups, education level and age. (similarly to Lefranc A, Trannoy A. 2005)

Intergenerational earnings mobility (sons 31 -45 and fathers 31 -55) First step: We estimate the imputation regression We regress x on the following IV • • • the log Hope-Goldthorpe index, 4 dummies for managerial duties (self-employed, 1 manager, 2 foreman/supervisor, 3 not foreman/supervisor) 3 education level dummies (no qualification or some qualification, 1 further education qualification, 2 first degree or higher) age and age square 2 cohort groups (1930 -1938, 1939 -1946)

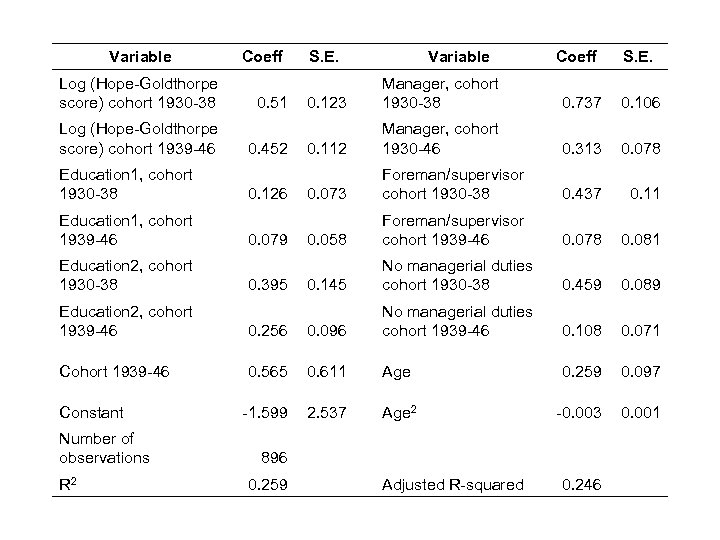
Variable Log (Hope-Goldthorpe score) cohort 1930 -38 Log (Hope-Goldthorpe score) cohort 1939 -46 Education 1, cohort 1930 -38 Education 1, cohort 1939 -46 Education 2, cohort 1930 -38 Coeff 0. 51 0. 452 0. 126 0. 079 0. 395 S. E. Variable Coeff S. E. 0. 123 Manager, cohort 1930 -38 0. 737 0. 106 0. 112 Manager, cohort 1930 -46 0. 313 0. 078 0. 073 Foreman/supervisor cohort 1930 -38 0. 437 0. 11 0. 058 Foreman/supervisor cohort 1939 -46 0. 078 0. 081 0. 145 No managerial duties cohort 1930 -38 0. 459 0. 089 0. 108 0. 071 Education 2, cohort 1939 -46 0. 256 0. 096 No managerial duties cohort 1939 -46 Cohort 1939 -46 0. 565 0. 611 Age 0. 259 0. 097 -1. 599 2. 537 Age 2 -0. 003 0. 001 Constant Number of observations R 2 896 0. 259 Adjusted R-squared 0. 246

Intergenerational earnings mobility (sons 31 -45 and fathers 31 -55) Second step: y= + x + u y = son’s log earnings; x = father’s log earnings; , and are coefficients; u is i. i. d (0, σ2) We estimate separately for rolling cohort groups 1950 -55, 1951 -56, 1952 -57, …, 1967 -1972

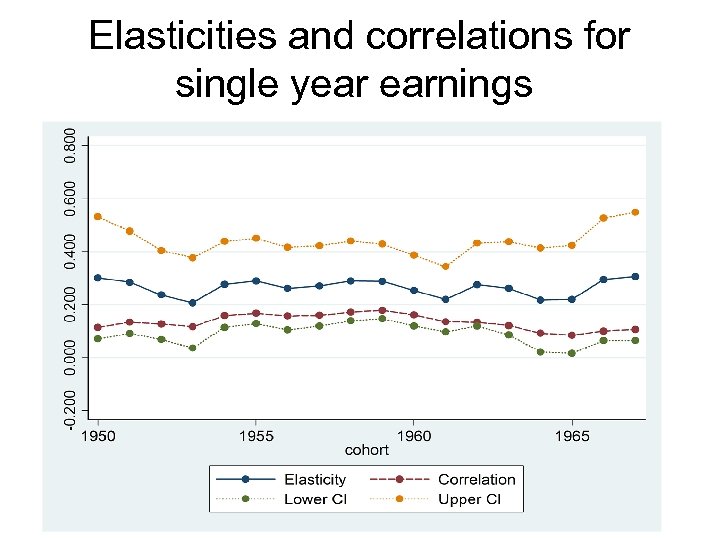
Elasticities and correlations for single year earnings

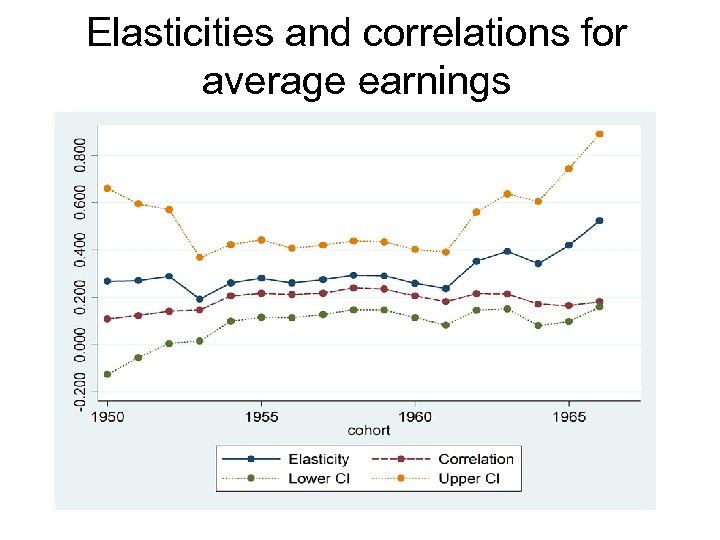
Elasticities and correlations for average earnings

Another sample selection problem: Labour market selection • The intergenerational occupational mobility can be estimated only for people who are employed. • This means the we can use only the subsample of people who are employed and this can cause a selection bias. • This selection can be especially relevant when estimating the association between earnings of daughters and fathers because women have usually more work interruptions.

Employment selection model y=α+xβ+ε d*=Z γ+u d=l(d*>0) where y is the daughter’s occupational prestige (log Hope. Goldthorpe score) x is her father’s occupational prestige d=1 for daughters are employed at least in at least one wave and 0 otherwise Z=occupational prestige father, dummies for education, age, regions, ethnicity, religiosity, marital status and number of children aged between 0 -2, 3 -4.

Intergenerational mobility and employment selection Ø If εi and ui are not independent then we have selection due to unobservables (For example unobserved work skills or cognitive skills which affect both the probability of employment and earnings for daughters) Ø If εi depends on Zi then we have selection due to observables (for example education, age and work experience which can affect both the probability of employment and the daughters’ earnings)

Intergenerational mobility and employment selection • Since εi (yi) depends on some of the variables Zi (for example education, age, etc. ) • We have first of all control for selection due to observables • This is possible using for example propensity score weighting or regression adjustment.

Propensity score weighting • First step: Estimation of the binary model for the employment probability • Second step: Weighted least square estimation (notice that the weights are estimated, so a proper estimation should be adopted to estimate the standard errors)

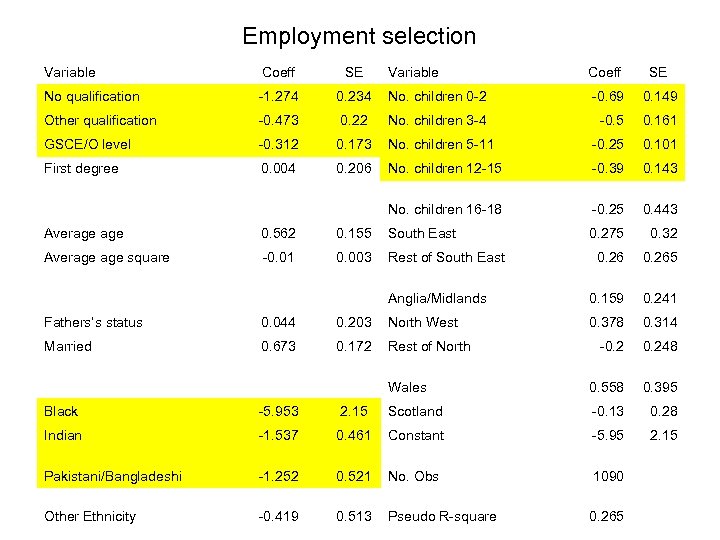
Employment selection Variable Coeff SE No qualification -1. 274 0. 234 Other qualification -0. 473 GSCE/O level First degree Variable Coeff SE No. children 0 -2 -0. 69 0. 149 0. 22 No. children 3 -4 -0. 5 0. 161 -0. 312 0. 173 No. children 5 -11 -0. 25 0. 101 0. 004 0. 206 No. children 12 -15 -0. 39 0. 143 No. children 16 -18 -0. 25 0. 443 0. 275 0. 32 0. 265 Anglia/Midlands 0. 159 0. 241 0. 378 0. 314 -0. 248 Wales 0. 558 0. 395 Average 0. 562 0. 155 South East Average square -0. 01 0. 003 Rest of South East Fathers’s status 0. 044 0. 203 North West Married 0. 673 0. 172 Rest of North Black -5. 953 2. 15 Scotland -0. 13 0. 28 Indian -1. 537 0. 461 Constant -5. 95 2. 15 Pakistani/Bangladeshi -1. 252 0. 521 No. Obs 1090 Other Ethnicity -0. 419 0. 513 Pseudo R-square 0. 265

Selection due to unobservables Ø If εi and ui are not independent then we have selection due to unobservables (For example unobserved work skills or cognitive skills which affect both the probability of employment and earnings for daughters) Ø Usually Heckman procedures are adopted, but these procedure are not very adequate in the case of intergenerational models because εi depends also on Z (omitted variables problems) Ø We need to control for selection on observables and unobservables too by for example combining Heckman and propensity score methods

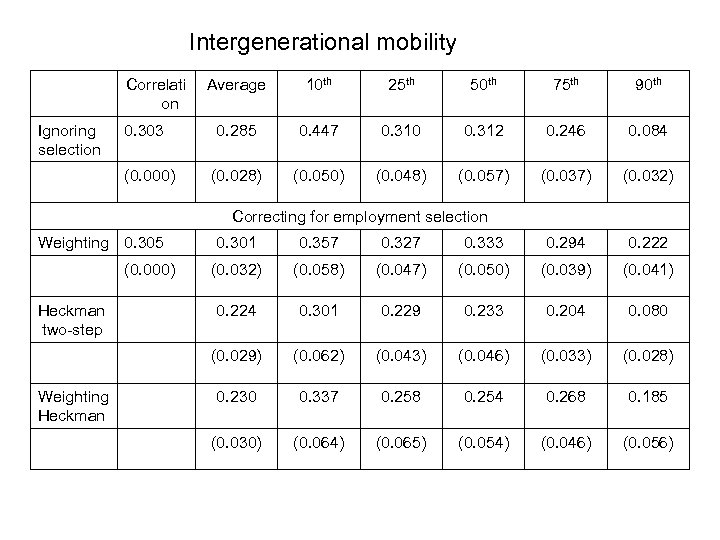
Intergenerational mobility Correlati on Ignoring selection 0. 303 (0. 000) Average 10 th 25 th 50 th 75 th 90 th 0. 285 0. 447 0. 310 0. 312 0. 246 0. 084 (0. 028) (0. 050) (0. 048) (0. 057) (0. 032) Correcting for employment selection Weighting 0. 305 Heckman two-step Weighting Heckman 0. 357 0. 327 0. 333 0. 294 0. 222 (0. 032) (0. 058) (0. 047) (0. 050) (0. 039) (0. 041) 0. 224 0. 301 0. 229 0. 233 0. 204 0. 080 (0. 029) (0. 000) 0. 301 (0. 062) (0. 043) (0. 046) (0. 033) (0. 028) 0. 230 0. 337 0. 258 0. 254 0. 268 0. 185 (0. 030) (0. 064) (0. 065) (0. 054) (0. 046) (0. 056)

Some references for regressions with sample selection • • Buchinski, M. (2001) Quantile regression with sample selection: Estimation women return to education in the U. S. , Empirical Economics, 26, 86 -113. Ibrahim, J. G. , Chen, M. -H. , Lipsitz, S. R. , Herring, A. H. (2005) Missing-data methods for generalized linear models: A comparative review, Journal of the American Statistical Association, 100, 469, 332 -346. Lipsitz, S. R. , Fitzmaurice, G. M. , Molenberghs, G. , Zhao, L. P. (1997), Quantile regression methods for longitudinal data with drop-outs, Applied Statistics, 463476. Robins, J. M. , Rotnitzky, A. (1995), Semiparametric Effciency in Multivariate Regression Models With Missing Data, Journal of the American Statistical Association, 90, 122 -129. Vella F. (1998), Estimating models with sample selection bias: a survey', The Journal of Human Resources, vol. 3, 127 -169. Wooldridge, J. M. (2007) Inverse probability weighted M-Estimation for General missing data problems, Journal of Econometrics, 141, 2, 12811301. Wooldridge, J. M. (2007) Inverse probability weighted M-Estimation for General missing data problems, Journal of Econometrics, 141, 2, 1281 -1301.