Interferometric Synthetic-Aperture Radar In SAR and Applications Chris

Interferometric Synthetic-Aperture Radar (In. SAR) and Applications Chris Allen (callen@eecs. ku. edu) Course website URL people. eecs. ku. edu/~callen/826/EECS 826. htm 1

Outline Syllabus Instructor information, course description, prerequisites Textbook, reference books, grading, course outline Preliminary schedule Introductions What to expect First assignment Radar fundamentals Active RF/microwave remote sensing Electromagnetic issues Antennas Resolution (spatial, range) 2

Syllabus Prof. Chris Allen Ph. D. in Electrical Engineering from KU 1984 10 years industry experience Sandia National Labs, Albuquerque, NM Allied. Signal, Kansas City Plant, Kansas City, MO Phone: 785 -864 -8801 Email: callen@eecs. ku. edu Office: 3024 Eaton Hall Office hours: Mondays and Wednesdays 2: 30 to 3: 30 p. m. Course description Description and analysis of processing data from synthetic-aperture radars and interferometric synthetic-aperture radars. Topics covered include SAR basics and signal properties, range and azimuth compression, signal processing algorithms, interferometry and coregistration. 3

Syllabus Prerequisites Introductory course on radar systems (e. g. , EECS 725) Introductory course on radar signal processing (e. g. , EECS 744) Textbook Processing of SAR Data by A. Hein Springer, 2004, ISBN 3540050434 4

Syllabus Reference books Synthetic Aperture Radar Processing by G. Franschetti and R. Lanari CRC Press, 1999, ISBN 0849378990 Digital Processing of Synthetic Aperture Radar Data by I. Cumming and F. Wong Artech House, 2005, ISBN 1580530583 Spotlight-Mode Synthetic Aperture Radar C. Jakowatz, et al, Springer, 1996, ISBN 0792396774 Synthetic Aperture Radar: Systems and Signal Processing J. Curlander and R. Mc. Donough Wiley, 1991, ISBN 047185770 X 5

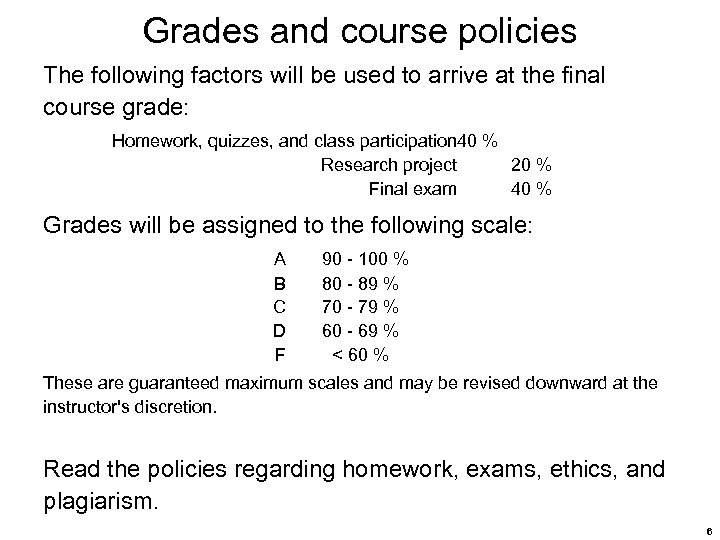Grades and course policies The following factors will be used to arrive at the final course grade: Homework, quizzes, and class participation 40 % Research project 20 % Final exam 40 % Grades will be assigned to the following scale: A B C D F 90 - 100 % 80 - 89 % 70 - 79 % 60 - 69 % < 60 % These are guaranteed maximum scales and may be revised downward at the instructor's discretion. Read the policies regarding homework, exams, ethics, and plagiarism. 6

Preliminary schedule Course Outline (subject to change) Intro – SAR system overview and signal properties 1 weeks SAR basics – radar range equation and associated geometries 2 weeks SAR signal processing 3 weeks SAR signal processing algorithms 2 weeks Interferometry basics and processing 6 weeks (data recording, nonideal motion, layover and shadowing, moving targets) (side-looking, squint, and spotlight modes) (range and azimuth compression, range migration, autofocus) (range-Doppler, scaling, omega-k) (registration, decorrelation, phase unwrapping, implementation, terrain mapping, surface velocity mapping, change detection, single-pass vs. multi-pass) Class Meeting Schedule August: 24, 26, 28, 31 September: 2, 4, (7 th Labor Day), 9, 11, 14, 16, 18, 21, 23, 25, 28, 30 October: 2, 5, 7, 9, (12 th Fall Break), 14, 16, 19, 21, 23, 26, 28, 30 November: 2, 4, 6, 9, 11, 13, 16, 18, 20, 21, 23, (26 th Thanksgiving), 30 December: 2, 4, 7, 9 Final exam scheduled for Monday, Dec 14, 10: 30 AM to 1: 00 PM 7

Introductions Name Major Specialty What you hope to get from of this experience (Not asking what grade you are aiming for ) 8

What to expect Most presentation material will be in Power. Point format Student interaction is encouraged Homework assignments will be posted on website We may have guest lecturers later in the semester To break the monotony, we’ll try to take a 2 -minute break during each session (roughly every 15 to 20 min) 9

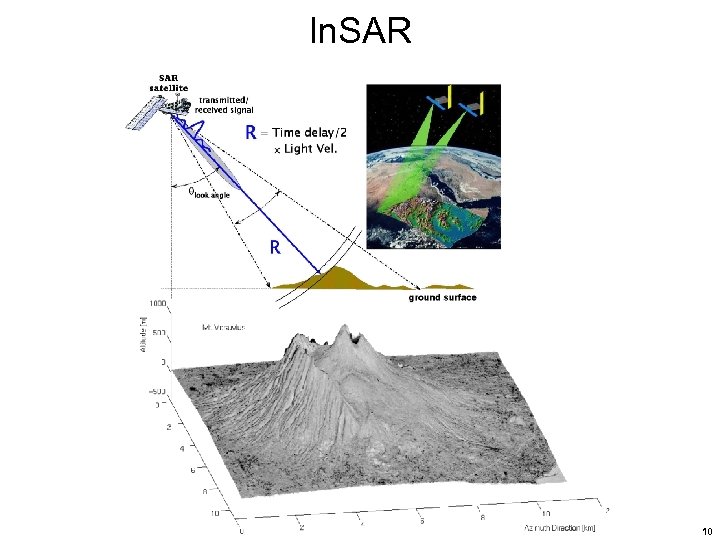In. SAR 10

Your first assignment Send me an email (from the account you check most often) To: callen@eecs. ku. edu Subject line: Your name – EECS 800 Tell me a little about yourself Attach your ARTS form (or equivalent) ARTS: Academic Requirements Tracking System Its basically an unofficial academic record I use this to get a sense of what academic experiences you’ve had 11

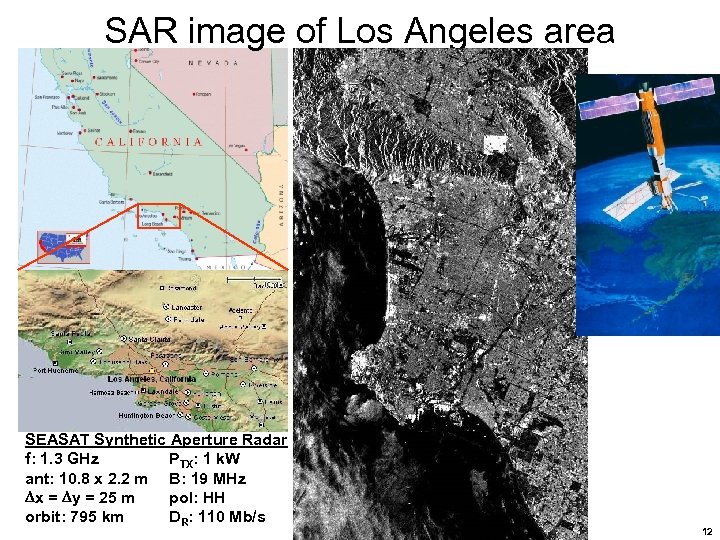SAR image of Los Angeles area SEASAT Synthetic Aperture Radar f: 1. 3 GHz PTX: 1 k. W ant: 10. 8 x 2. 2 m B: 19 MHz x = y = 25 m pol: HH orbit: 795 km DR: 110 Mb/s 12

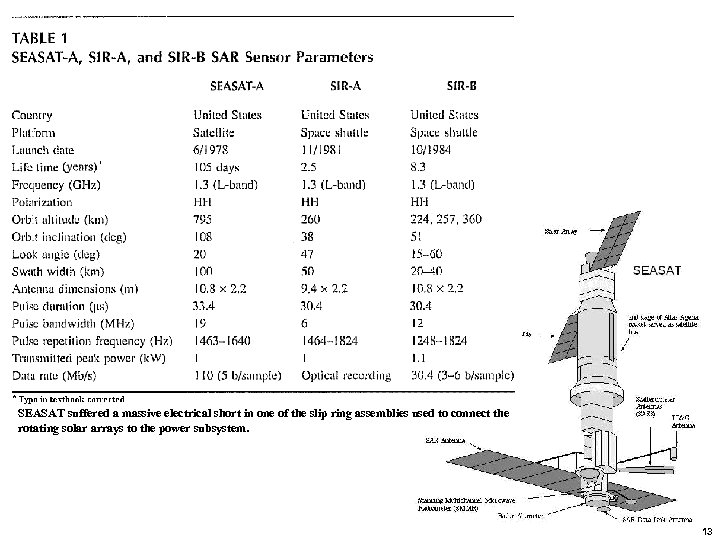SEASAT suffered a massive electrical short in one of the slip ring assemblies used to connect the rotating solar arrays to the power subsystem. 13

SAR image of Gibraltar ERS-1 Synthetic Aperture Radar f: 5. 3 GHz PTX: 4. 8 k. W ant: 10 m x 1 m B: 15. 5 MHz x = y = 30 m fs: 19 MSa/s orbit: 780 km DR: 105 Mb/s Nonlinear internal waves propagating eastwards and oil slicks can be seen. 14

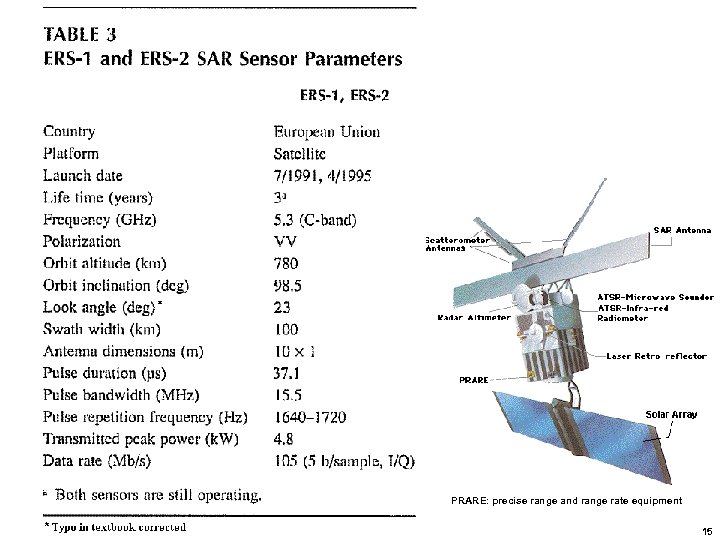PRARE: precise range and range rate equipment 15

Radar fundamentals (review) ERS-1 Synthetic Aperture Radar center frequency, f: 5. 3 GHz • C-band, = c/f = 5. 7 cm c = 3 x 108 m/s Antenna dimensions, ant: 10 m x 1 m (width x height) • • Approx. beamwidth, /antenna dimension az 0. 057 m/10 m = 5. 7 mrad or 0. 32° el 0. 057 m/1 m = 57 mrad or 3. 2° Antenna gain, G 4 /( az el) G(d. Bi) = 10 log 10(G) G = 4 /(0. 057 x 0. 0057) = 38700 or 46 d. Bi Minimum along-track resolution, ymin = ℓ/2 ℓ = 10 m, ymin = 5 m, y = 30 m > ymin d. Bi is d. B relative to isotropic antenna ℓ is antenna’s along-track dimension Bandwidth, B: 15. 5 MHz • Range resolution (slant range, cross-track), r = c/2 B • r = c/(2 x 15. 5 MHz) = 9. 7 m • Ground resolution (cross-track), x = r /sin is the incidence angle Pulse duration, : 37. 1 s • Pulse compression ratio, B = 575 (28 d. B) • Blind range c /2 = 5. 6 km B (d. B) = 10 log 10(B ) 16

Radar fundamentals (review) ERS-1 Synthetic Aperture Radar Sampling frequency, fs: 19 MSa/s, 5 b/sample, I/Q • Nyquist requires fs ≥ 15. 5 MSa/s • fs = 1. 23 Nyquist rate (23% oversampling) Orbit altitude, h: 780 km • Orbital velocity, v, • Ground velocity, vg, for Earth, = 398, 600 km 3/s 2 Re = 6378. 145 km • v = 7. 46 km/s, vg = 6. 65 km/s • Minimum pulse-repetition frequency, PRFmin = 2 v/ℓ • PRFmin = 2(7460)/10 = 1490 Hz • 1720 Hz ≥ PRF ≥ 1640 Hz (from ERS specs) Look angle, : 23° • • sin = (1 + h/Re) sin = 26° Ground resolution, x = r /sin x = 22 m 17

Radar fundamentals (review) ERS-1 Synthetic Aperture Radar Ground swath width, Wgr: 100 km • • Slant swath width, Wr = Wgr sin Wr = 43. 8 km Echo duration from swath, s = + 2 Wr/c s = 37. 1 s + 292 s = 329. 1 s Data rate, DR: 105 Mb/s • • Samples/echo = 329. 1 s x 19 MSa/s = 6250 Samples/echo Sample rate = PRF x Samples/echo Sample rate = 1640 x 6300 = 10. 3 MSa/s Data rate = Sample rate x bits/sample = 10. 3 MSa/s x 10 bits/Sa = 103 Mb/s 18

Ka-band, 4″ resolution Helicopter and plane static display f: 35 GHz 19

Sandia’s real-time SAR 20

Radar fundamentals (review) Radar range equation, received signal power, and signal-to -noise ratio For a monostatic radar system and a point target Where Pt is the transmitted signal power, W Pr is the power intercepted by the receiver, W G is the gain of the antenna in the direction of the target R is the range from the antenna to the scatterer, m is the target’s radar scattering cross section (RCS), m 2 is the wavelength of the radar signal, m 21

Radar fundamentals (review) Receiver noise power, PN k is Boltzmann’s constant (1. 38 10 -23 J K-1) T 0 is the absolute temperature (290 K) B is receiver bandwidth, Hz F is receiver noise figure Signal-to-noise ratio (SNR) is may be expressed in decibels 22

Radar fundamentals (review) Example: Sandia Lynx SAR Radar center frequency, f = 16 GHz Transmit power, PT = 320 W (55. 1 d. Bm) d. Bm: d. B relative to 1 m. W Slant range resolution, r = 0. 3 m (1 ft) Receiver noise figure, FREC = 2. 8 (F = 4. 5 d. B) Antenna beamwidths, 3. 2° x 7° Range to target, R = 30 km (18. 6 miles) Target RCS, = 0. 001 m 2 (-30 d. Bsm) = ° x y Find the Pr , PN , and the SNR First derive some related radar parameters Wavelength, = c/f = 0. 01875 m Antenna gain, G 4 /( az el) G = 1840 or 32. 6 d. Bi Bandwidth, B = c/2 r B = 500 MHz 23

Radar range equation example Find Pr Solve in d. B Pr(d. Bm) = Pt(d. Bm) + 2 G(d. Bi) + 2 (d. B) + (d. Bsm) – 3 4 (d. B) – 4 R(d. B) Pt(d. Bm) = 55. 1 G(d. Bi) = 32. 6 4 (d. B) = 11 (d. B) = -17. 3 (d. Bsm) = -30 R(d. B) = 44. 8 Pr(d. Bm) = -156. 3 d. Bm or 2. 3 10 -19 W (0. 23 a. W) Find PN Solve in d. B PN(d. Bm) = k. T 0(d. Bm) + B(d. B) + F(d. B) k. T 0(d. Bm) = -174 B(d. B) = 87 F(d. B) = 4. 5 PN(d. Bm) = -82. 5 d. Bm or 5. 6 p. W Find SNR = – 156. 3 – (– 82. 5) = -73. 7 d. B or 4. 3 10 -8 24

Radar fundamentals (review) Signal processing improves SNR Pulse compression gain, B Assuming = 20 s yields a 40 -d. B pulse compression gain Coherent integration improves SNR by N N is the number of integrations N = synthetic-aperture length * PRF / velocity Synthetic-aperture length, L = az R, L = 1675 m Assume velocity = 36 m/s (Predator UAV cruise speed is 130 km/h ) Assuming a 1 -k. Hz PRF N = 46500 or 46 -d. B improvement Therefore the SNR from a -30 -d. Bsm target is 12. 3 d. B Many measurements require SNR > 10 d. B 25

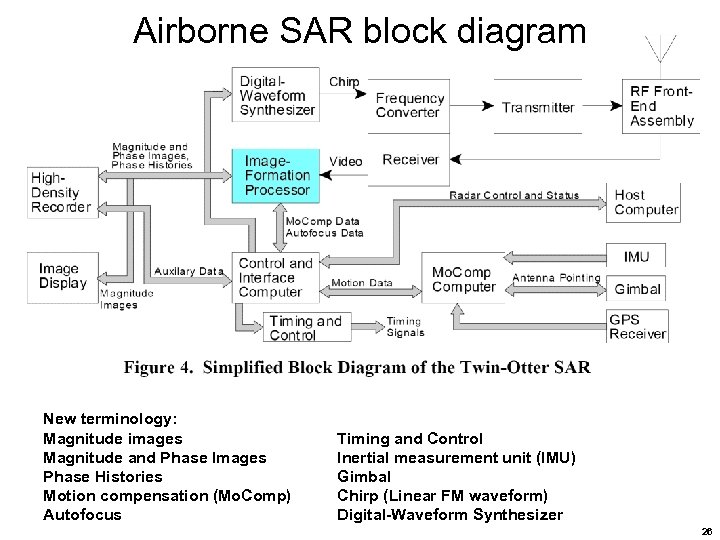Airborne SAR block diagram New terminology: Magnitude images Magnitude and Phase Images Phase Histories Motion compensation (Mo. Comp) Autofocus Timing and Control Inertial measurement unit (IMU) Gimbal Chirp (Linear FM waveform) Digital-Waveform Synthesizer 26

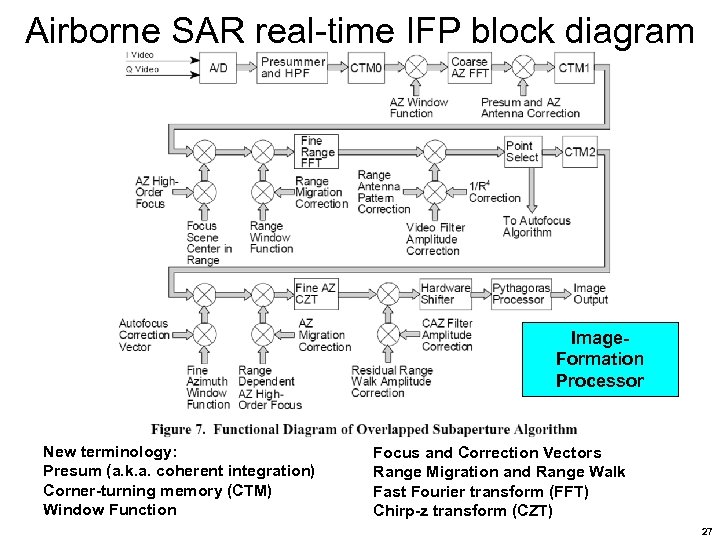Airborne SAR real-time IFP block diagram Image. Formation Processor New terminology: Presum (a. k. a. coherent integration) Corner-turning memory (CTM) Window Function Focus and Correction Vectors Range Migration and Range Walk Fast Fourier transform (FFT) Chirp-z transform (CZT) 27

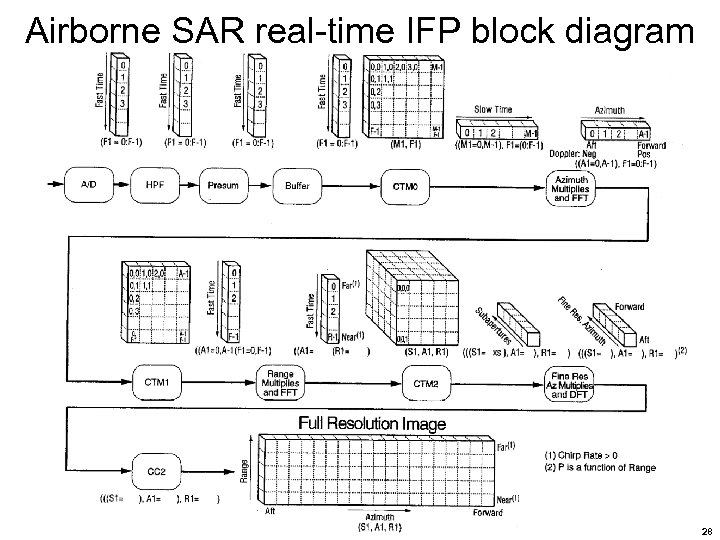Airborne SAR real-time IFP block diagram 28

29

In. SAR Coherent Change Detection 30

Backscattering 31

Radar response to extended targets The preceding development considered point target with a simple RCS, . The point-target case enables simplifying assumptions in the development. Gain and range are treated as constants Consider the case of extended targets including surfaces and volumes. The backscattering characteristics of a surface are represented by the scattering coefficient, , where A is the illuminated area. 32

Factors affecting backscatter The backscattering characteristics of a surface are represented by the scattering coefficient, For surface scattering, several factors affect Dielectric contrast Large contrast at boundary produces large reflection coefficient Air ( r = 1), Ice ( r ~ 3. 2), (Rock (4 r 9), Soil (3 r 10), Vegetation (2 r 15), Water (~ 80), Metal ( r ) Surface roughness (measured relative to ) RMS height and correlation length used to characterize roughness Incidence angle, ( ) Surface slope Skews the ( ) relationship Polarization VV HH » HV VH 33

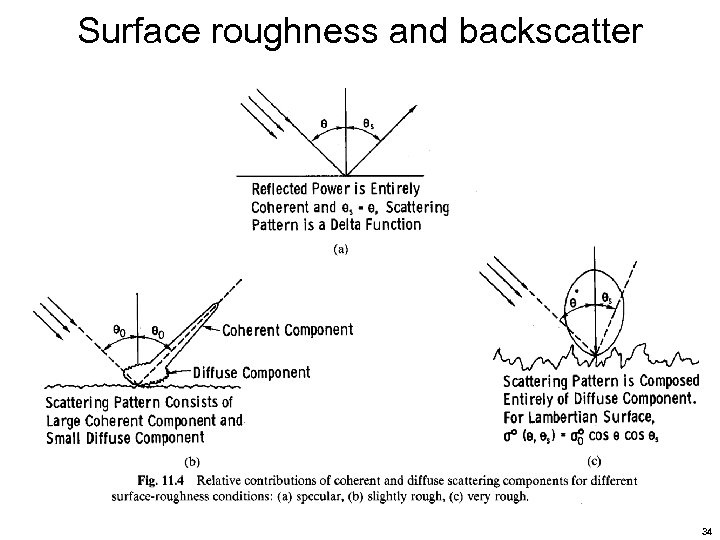Surface roughness and backscatter 34

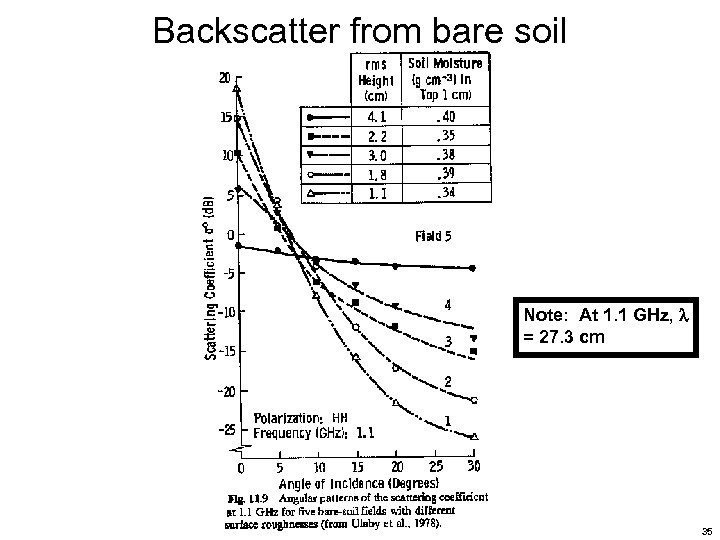Backscatter from bare soil Note: At 1. 1 GHz, = 27. 3 cm 35

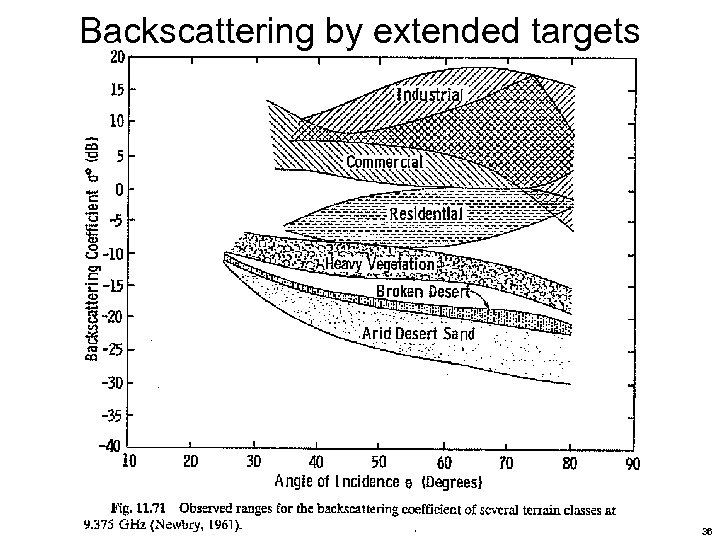Backscattering by extended targets 36

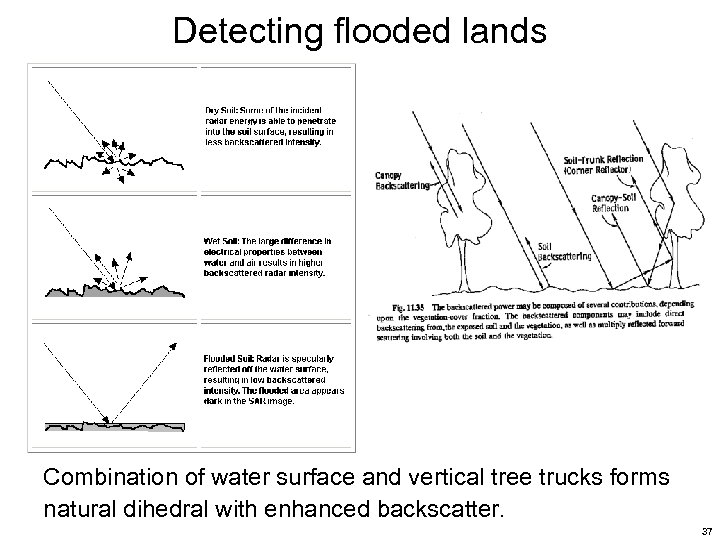Detecting flooded lands Combination of water surface and vertical tree trucks forms natural dihedral with enhanced backscatter. 37

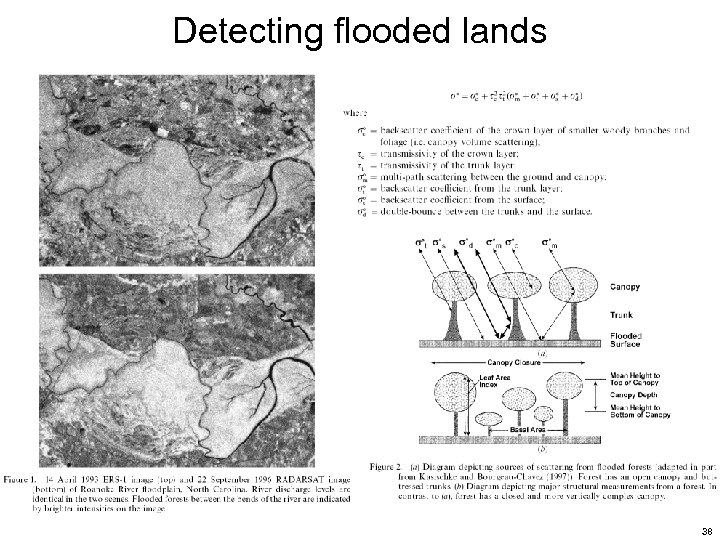Detecting flooded lands 38

Doppler shifts and PRF 39

Doppler shifts and radial velocity The signal from a target may be written as c = 2 fc and the relative phase of the received signal, A target moving relative to the radar produces a changing phase (i. e. , a frequency shift) known as the Doppler frequency, f. D where vr is the radial component of the relative velocity. The Doppler frequency can be positive or negative with a positive shift corresponding to target moving toward the radar. 40

Doppler shifts and radial velocity The received signal frequency will be Example Consider a police radar with a operating frequency, fo, of 10 GHz. ( = 0. 03 m) It observes an approaching car traveling at 70 mph (31. 3 m/s) down the highway. (v = -31. 3 m/s) The frequency of the received signal will be fo – 2 v/ = fo + 2. 086 k. Hz or 10, 002, 086 Hz Another car is moving away down the highway traveling at 55 mph (+24. 6 m/s). The frequency of the received signal will be fo – 2 v/ = fo – 1. 64 k. Hz or 9, 998, 360 Hz 41

Doppler shifts and radial velocity Given the position, P, and velocity, u, both the radar and the target, the resulting Doppler frequency can be determined Instantaneous position and velocity Relative velocity, u ^ u R = u cos(q) f. D = 2 u cos(q) / Radial velocity component The ability to resolve targets based on their Doppler shifts depends on the processed bandwidth, B, that is inversely related to the observation (or integration) time, T 42

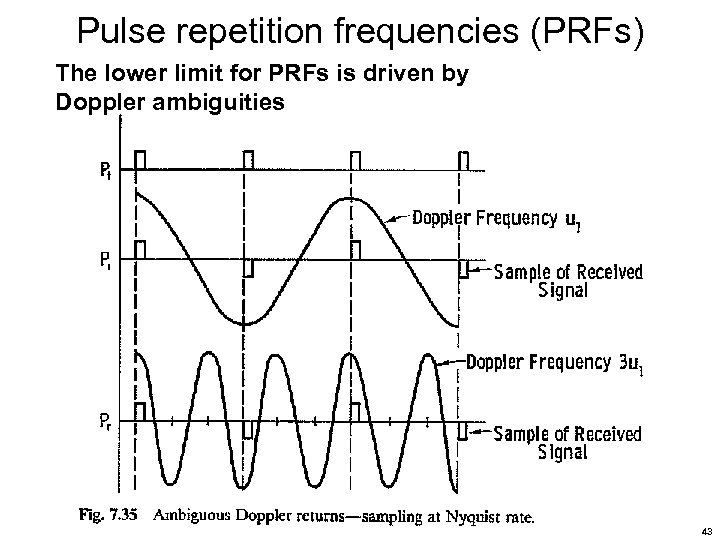Pulse repetition frequencies (PRFs) The lower limit for PRFs is driven by Doppler ambiguities 43

Doppler ambiguities To unambiguously reconstruct a waveform, the Nyquist. Shannon sampling theorem (developed and refined from the 1920 s to 1950 s at Bell Labs) states that exact reconstruction of a continuous -time baseband signal from its samples is possible if the signal is bandlimited and the sampling frequency is greater than twice the signal bandwidth. Application to radar means that the pulse-repetition frequency (PRF) must be at least twice the Doppler bandwidth. For sidelooking SAR (centered about 0 Doppler), the PRF must be twice the highest Doppler shift. For the case where the Doppler frequency shift will be 250 Hz (a 500 -Hz Doppler bandwidth), the PRF must be at least 500 Hz. [The Nyquist-Shannon theorem also has application to signal digitization in the analog-to-digital converter (ADC) requiring that the ADC sampling frequency be at least twice the waveform bandwidth. ] 44

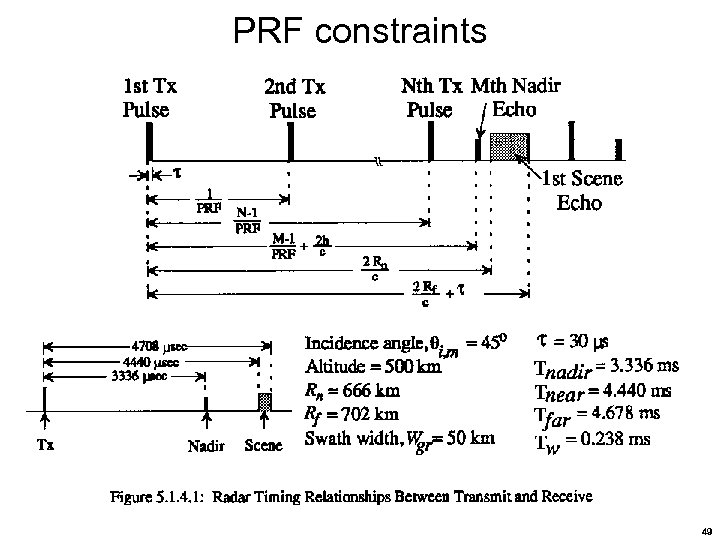
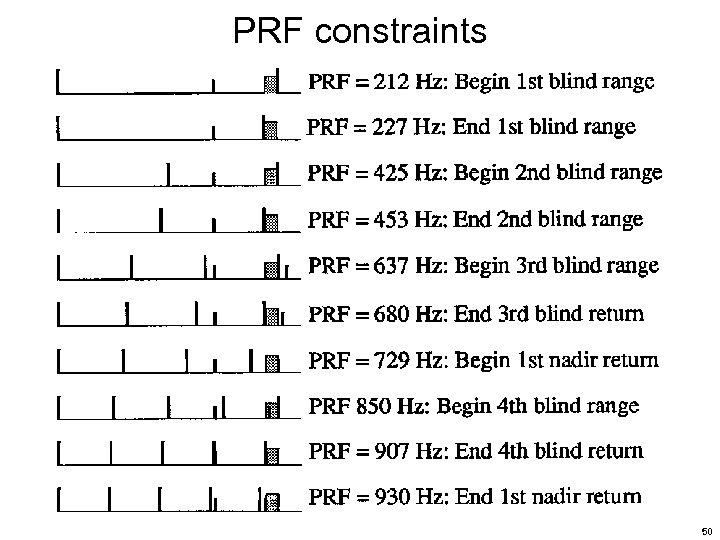
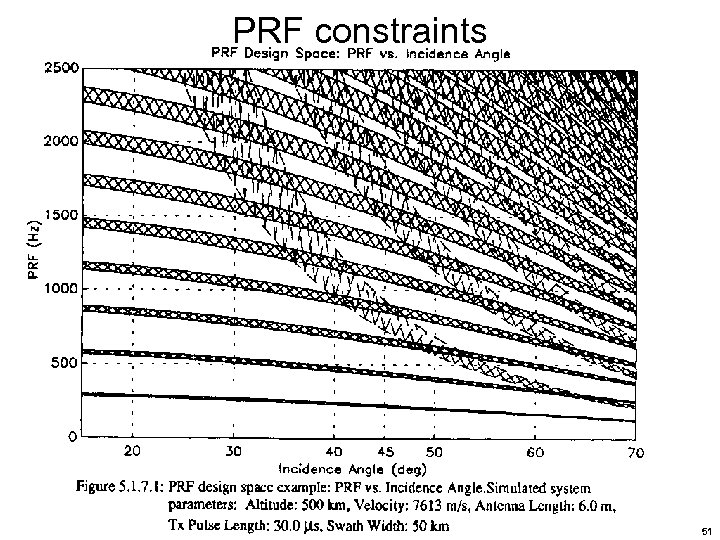
PRF constraints Recapping what we’ve seen— The lower PRF limit is determined by Doppler ambiguities The upper PRF limit is determined by the range ambiguities Eclipsing Furthermore, for systems that do not support receiving while transmitting, various forbidden PRFs will exist that will eclipse the receive intervals with transmission pulses, which leads to where Tnear and Tfar refer to signal arrival times for near and far targets, is the transmit pulse duration, and N represents whole numbers (1, 2, 3, …) corresponding to pulses 45

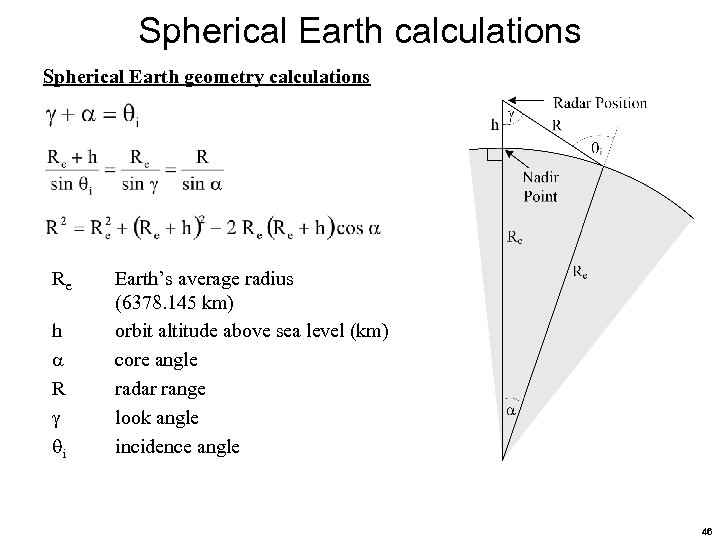Spherical Earth calculations Spherical Earth geometry calculations Re h R i Earth’s average radius (6378. 145 km) orbit altitude above sea level (km) core angle radar range look angle incidence angle 46

Spherical Earth calculations Satellite orbital velocity calculations (for circular orbits) Re h v vg Earth’s average radius (6378. 145 km) orbit altitude above sea level (km) satellite velocity satellite ground velocity standard gravitational parameter (398, 600 km 3/s 2 for Earth) 47

Spherical Earth calculations Swath width geometry calculations Re Rn Rf Wgr Wr n f i, m Earth’s average radius (6378. 145 km) range to swath’s near edge range to swath’s far edge swath width on ground slant range swath width core angle to swath’s near edge core angle to swath’s far edge incidence angle at mid-swath 48

PRF constraints 49

PRF constraints 50

PRF constraints 51

Antenna length, velocity, and PRF Given an antenna length, ℓ wavelength, velocity, v We know (small angle approximation) The Doppler bandwidth, f. D, is Therefore PRFmin is Aircraft case v = 200 m/s, ℓ = 1 m PRFmin = 400 Hz Spacecraft case v = 7000 m/s, ℓ = 10 m PRFmin = 1. 4 k. Hz Note that PRFmin is independent of 52

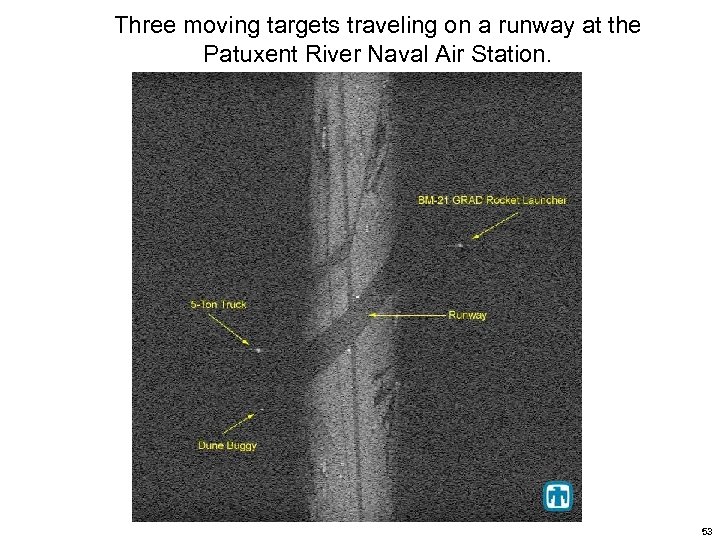Three moving targets traveling on a runway at the Patuxent River Naval Air Station. 53

Real-aperture side-looking airborne radar (SLAR) 54

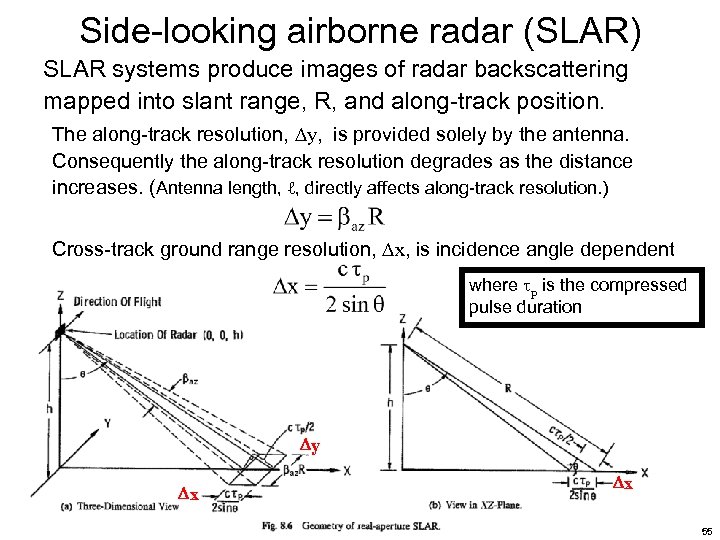Side-looking airborne radar (SLAR) SLAR systems produce images of radar backscattering mapped into slant range, R, and along-track position. The along-track resolution, y, is provided solely by the antenna. Consequently the along-track resolution degrades as the distance increases. (Antenna length, ℓ, directly affects along-track resolution. ) Cross-track ground range resolution, x, is incidence angle dependent where p is the compressed pulse duration y x x 55

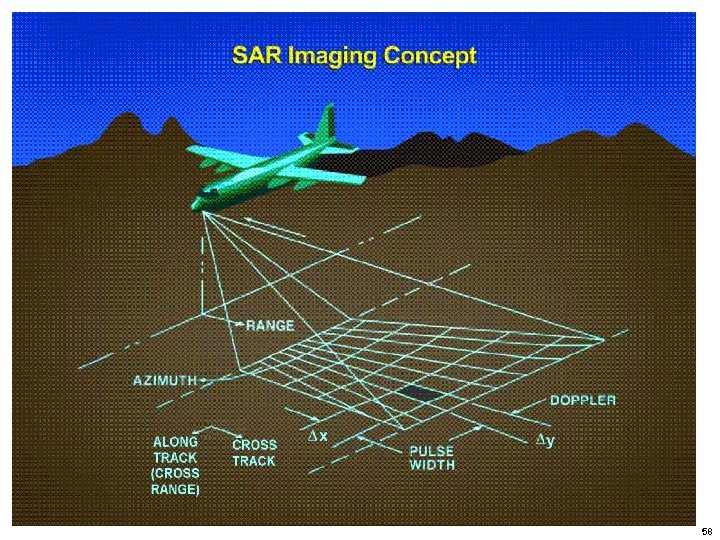
Side-looking synthetic-aperture radar (SAR) 56

Synthetic-aperture radar (SAR) Synthetic-aperture radar is an imaging radar concept that was developed in the early 1950 s by Goodyear Aircraft Company. It is remarkable in that when fully processed, SAR images have very fine resolution that are range independent. Numerous variations of SAR have been derived from the basic concept and these include inverse SAR (ISAR), interferometric SAR (In. SAR), and Scan. SAR. The basis concept for SAR appears fairly simple though upon inspection it is more complex. The core concept may be thought of in at least five different ways: Synthesized antenna aperture Doppler beam sharpening Correlation with reference point-target response Matched filter for received point-target signal De-chirping of Doppler frequency shift Optical focusing equivalent 57

58

Synthetic-aperture radar (SAR) In SAR systems a very long antenna aperture is synthesized resulting in fine along-track resolution. For a synthesized aperture length, L, the along-track resolution, y, is As with SLAR, the cross-track resolution, x, is incidence angle dependent L, is determined by the system configuration. For a fully focused stripmap system, Lm = az R (m), where az is the azimuthal or along-track beamwidth of the real antenna ( az /ℓ) R is the range to the target For L = Lm, y = ℓ/2 (independent of range and wavelength) For unfocused SAR, the maximum synthetic aperture length, Lum, is For L = Lum, 59

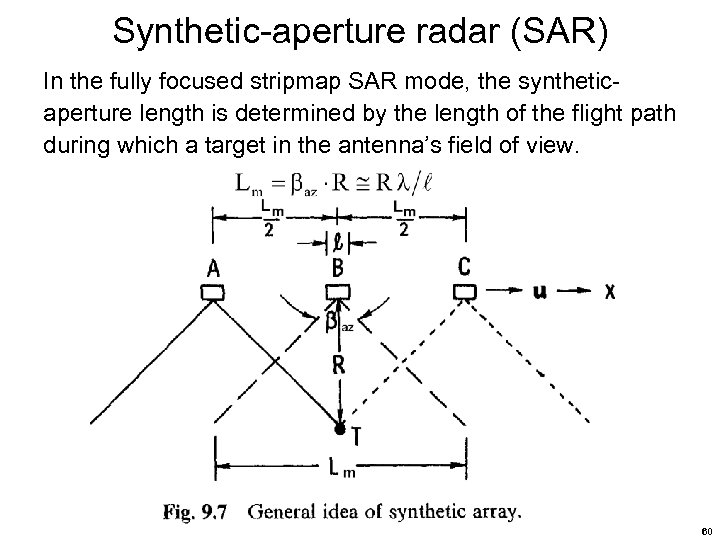Synthetic-aperture radar (SAR) In the fully focused stripmap SAR mode, the syntheticaperture length is determined by the length of the flight path during which a target in the antenna’s field of view. 60

Synthetic-aperture radar (SAR) In spotlight mode, the synthetic aperture length L may exceed Lm because the antenna is steered to illuminate the region of interest as the system passes by, and where (radians) is the change in aspect angle over which the target is viewed. For small , y /(2 ) 61

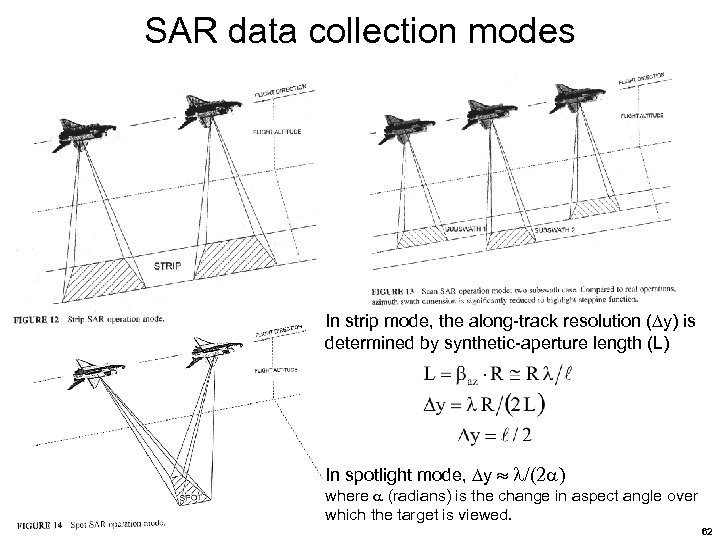SAR data collection modes In strip mode, the along-track resolution ( y) is determined by synthetic-aperture length (L) In spotlight mode, y /(2 ) where (radians) is the change in aspect angle over which the target is viewed. 62

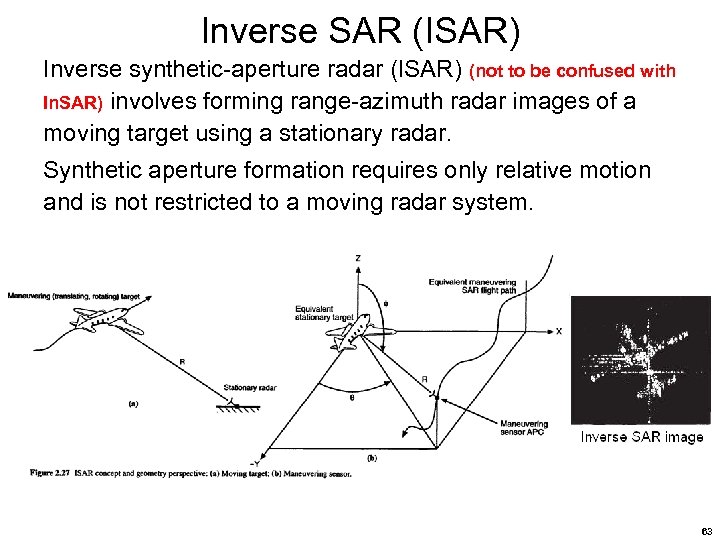Inverse SAR (ISAR) Inverse synthetic-aperture radar (ISAR) (not to be confused with In. SAR) involves forming range-azimuth radar images of a moving target using a stationary radar. Synthetic aperture formation requires only relative motion and is not restricted to a moving radar system. 63

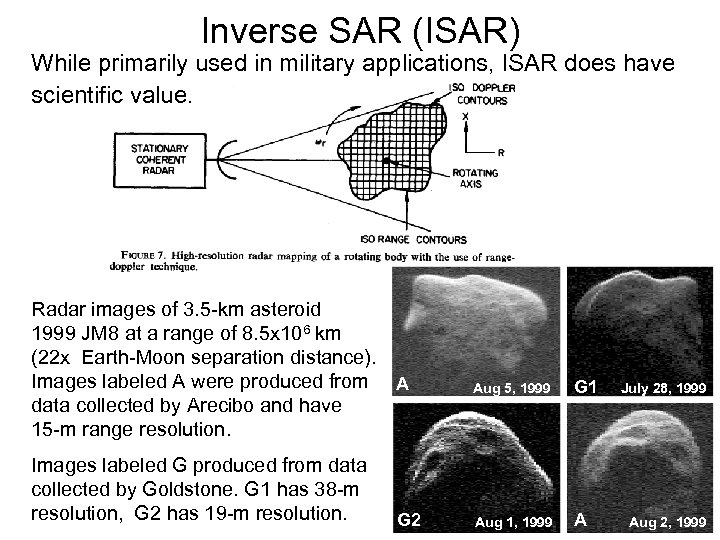Inverse SAR (ISAR) While primarily used in military applications, ISAR does have scientific value. Radar images of 3. 5 -km asteroid 1999 JM 8 at a range of 8. 5 x 106 km (22 x Earth-Moon separation distance). Images labeled A were produced from A data collected by Arecibo and have 15 -m range resolution. Images labeled G produced from data collected by Goldstone. G 1 has 38 -m resolution, G 2 has 19 -m resolution. G 2 Aug 5, 1999 G 1 Aug 1, 1999 A July 28, 1999 Aug 2, 1999 64

Arecibo Observatory Funded by National Science Foundation Operated by Cornell University Located in Puerto Rico 1 -MW transmitter f: 2. 38 GHz, : 12. 6 cm 305 -m diameter, non-steerable reflector (Earth’s largest curved focusing dish) Collects data for: radio astronomy (passive), terrestrial aeronomy (study of Earth’s upper atmosphere), planetary radar studies 65

Goldstone Solar System Radar Part of NASA/JPL Deep Space Network (DSN) Located in California Fully-steerable 70 -m parabolic reflector 500 -k. W transmitter f: 8. 560 GHz : 3. 5 cm Operates in both monostatic and bistatic modes with New Mexico’s twenty-seven 25 -m antennas Very Large Array or Arecibo 66