Интерференция света при отражении от плоскопараллельной пластинки полосы

Интерференция света при отражении от плоскопараллельной пластинки (полосы равного наклона)

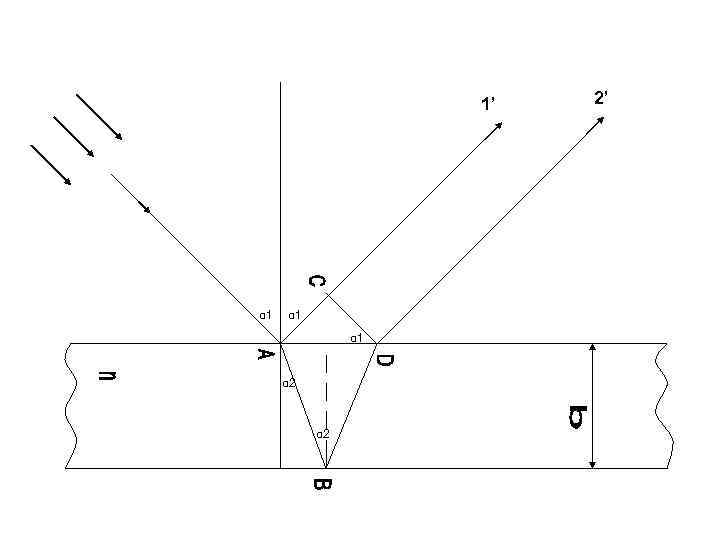1’ α 1 α 1 α 2 2’

n-показатель преломления Δ 12 = n. S 2 –S 1 Δ 12 -оптическая разность хода S 2 =AB+BD S 1 =AC 1)cosα 2=b/AB; AB=b/cosα 2 2)AB=BD 3)sinα 1/sinα 2=n; sinα 1 =n* sinα 2 -закон преломления 4)sinα 1 =AC/AD; AC=AD* sinα 1 5)tgα 2=AD/2 b; AD=2 b*tgα 2 Δ=n*2 b/cosα 2 -2 b*tgα 2 sinα 1 =2 b*n/cosα 22 b*n*sinα 2 sinα 1/n*cosα 2=2 b/n*cosα 2(n 2 -sin 2α 1)= │ncosα 2=√n 2 cos 2α 2=√n 2(1 -sin 2α 2)=√n 2 -n 2 sin 2α 2=√n 2 sin 2α 1│=2 b/√n 2 -sin 2α 1(n 2 -sin 2α 1)=2 b*√n 2 -sin 2α 1 Δ 12=2 b*√n 2 -sin 2α 1 -λ 0/2 –оптическая разность хода

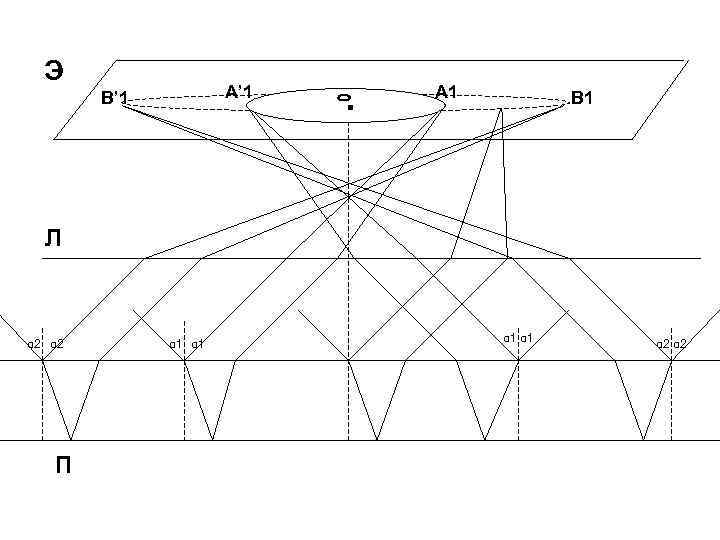Э A’ 1 B’ 1 . A 1 B 1 Л α 2 П α 1 α 1 α 2

В результате при отражении от тонкой пластинки на экране мы наблюдаем возникновение системы чередующихся светлых и темных круговых полос с общим центром в точке О. Каждая полоса образована лучами падающими на пластинку под одинаковым углом. Полученные интерференционные полосы носят название полосы равного наклона