Интерференция света Интерференция света 1 Монохроматичность и

Интерференция света

Интерференция света 1. Монохроматичность и когерентность волн •

•

2. Интерференция волн • Пусть первая волна проходит от точки разделения до точки наложения в среде с показателем преломления n 1 путь r 1, а вторая волна в среде с показателем преломления n 2 путь r 2. Разность фаз двух накладывающихся волн будет равна: или

• Главным условием интерференции волн является когерентность волн. Следовательно, интерференция света – это сложение когерентных волн, в результате которого происходит пространственное перераспределение светового потока, в результате чего в одних местах появляются максимумы, а в других минимумы интенсивности.

3. Методы наблюдения интерференции света • Для получения когерентных световых волн с помощью обычных (не лазерных) источников света применяют метод разделения света от одного источника на две или несколько систем световых лучей. В каждой из них представлено излучение одних и тех же атомов, поэтому они могут быть когерентны. Практически это можно осуществить с помощью экранов, щелей, зеркал и преломляющих тел. Рассмотрим два примера.

1. Метод Юнга. • Источником света служит ярко освещенная щель S, от которой свет падает на экран Э 1, в котором имеются две узкие равноудаленные щели S 1 и S 2, параллельные S. Щели S 1 и S 2 можно рассматривать как источники света. • Интерференционная картина наблюдается на экране Э 2 в области наложения волн от этих источников.

2. Бипризма Френеля. • Бипризма Френеля состоит из двух одинаковых призм с малыми преломляющими углами, сложенных основаниями. • Свет от источника S преломляется в обеих призмах и распространяется за ними в виде двух систем волн, как бы исходящих от двух мнимых источников S 1 и S 2. Интерференция этих волн наблюдается в области их пересечения на экране.

4. Расчет интерференционной картины от двух когерентных источников света • • Рассмотрим два когерентных источника света S 1 и S 2, которые находятся на расстоянии d. Экран Э, на котором наблюдается интерференционная картина, расположен параллельно обеим щелям на расстоянии L от них, причем L >> d. Откуда Или При условии L >> d, можно считать l 1 + l 2 2 L, откуда следует, что ширина интерференционной полосы равна

5. Интерференция света в тонких пленках Пусть на плоскопараллельную пластинку с показателем преломления n и толщиной d под углом падает плоская монохроматическая волна (пучок параллельных лучей). На поверхности пленки в точке О луч 1 разделится на два луча: частично отразится (луч 1) и частично преломится 2. Преломленный луч в точке С также частично отразится от нижней поверхности пленки, и частично преломится в воздух. Отраженный в точке С луч, дойдя до точки В, опять частично отразится и преломится (луч 2), выходя в воздух под углом . Луч, отраженный в точке В, опять отразится от нижней поверхности пленки но он будет иметь меньшую интенсивность, и мы его рассматривать в дальнейшем не будем. Лучи 1 и 2, отраженные от верхней и нижней поверхностей пленки, испущены одним и тем же источником и поэтому когерентны. Они параллельны, и поэтому если на их пути поставить собирающую линзу, то они сойдутся в одной из точек фокальной плоскости линзы, и на экране в этой плоскости будет наблюдаться интерференционная картина.

Разность хода лучей 2 и 1, возникающая при прохождении их от точки О до точки наложения Р, равна = n. S 2 – S 1= n(OC+CB) - OA, Подставим Учитывая закон преломления или получим

На экране в точке Р будет максимум, если Минимум можно наблюдать, если выполняется условие

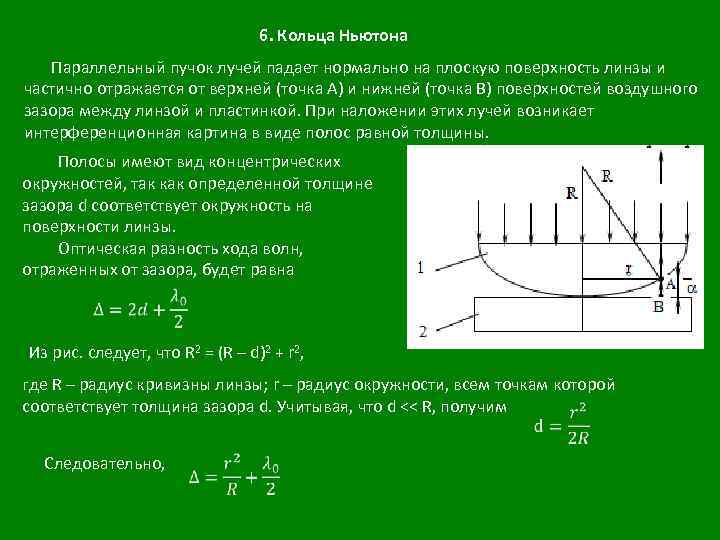6. Кольца Ньютона Параллельный пучок лучей падает нормально на плоскую поверхность линзы и частично отражается от верхней (точка А) и нижней (точка В) поверхностей воздушного зазора между линзой и пластинкой. При наложении этих лучей возникает интерференционная картина в виде полос равной толщины. Полосы имеют вид концентрических окружностей, так как определенной толщине зазора d соответствует окружность на поверхности линзы. Оптическая разность хода волн, отраженных от зазора, будет равна Из рис. следует, что R 2 = (R – d)2 + r 2, где R – радиус кривизны линзы; r – радиус окружности, всем точкам которой соответствует толщина зазора d. Учитывая, что d << R, получим Следовательно,

Применяя выражения для условий максимума и минимума, получим выражение для радиуса m-го светлого кольца: В центре линзы будет наблюдаться темное пятно, которое соответствует m = 0