ИНТЕРФЕРЕНЦИЯ СВЕТА ИНТЕРФЕРЕНЦИЯ СВЕТА






























лекция 10 - интерференция.pptx
- Количество слайдов: 42
 ИНТЕРФЕРЕНЦИЯ СВЕТА
ИНТЕРФЕРЕНЦИЯ СВЕТА
 ИНТЕРФЕРЕНЦИЯ СВЕТА 2
ИНТЕРФЕРЕНЦИЯ СВЕТА 2
 Пусть в некоторую точку пространства приходят две световые волны одинакового направления. Амплитуда суммарного колебания определяется по правилу сложения двух колебаний одинакового направления. В результате получим:
Пусть в некоторую точку пространства приходят две световые волны одинакового направления. Амплитуда суммарного колебания определяется по правилу сложения двух колебаний одинакового направления. В результате получим:
 Если разность фаз =( 1 - 2) возбуждаемых волнами колебаний остается постоянной во времени, то волны называются когерентными. В этом случае говорят о сложении колебаний в фазе или синфазном сложении, для которого следует, что амплитуда суммарных колебаний равна сумме амплитуд каждого из колебаний 4
Если разность фаз =( 1 - 2) возбуждаемых волнами колебаний остается постоянной во времени, то волны называются когерентными. В этом случае говорят о сложении колебаний в фазе или синфазном сложении, для которого следует, что амплитуда суммарных колебаний равна сумме амплитуд каждого из колебаний 4
 Если рассмотреть сложение колебаний с противоположными фазами или противофазном сложении, то амплитуда суммарных колебаний равна модулю разности амплитуд каждого из колебаний:
Если рассмотреть сложение колебаний с противоположными фазами или противофазном сложении, то амплитуда суммарных колебаний равна модулю разности амплитуд каждого из колебаний:
 Квадрат амплитуды напряженности электрического поля пропорционален интенсивности I электромагнитного поля. С учётом этого следует выражение для интенсивности суммы колебаний электромагнитных волн: 6
Квадрат амплитуды напряженности электрического поля пропорционален интенсивности I электромагнитного поля. С учётом этого следует выражение для интенсивности суммы колебаний электромагнитных волн: 6
 Явление перераспределения в пространстве интенсивности электромагнитного поля, представляющего собой сумму двух монохроматических волн одной частоты, в зависимости от их разности фаз называется интерференцией. 7
Явление перераспределения в пространстве интенсивности электромагнитного поля, представляющего собой сумму двух монохроматических волн одной частоты, в зависимости от их разности фаз называется интерференцией. 7
 При суперпозиции когерентных волн в одних точках пространства возникают максимумы, а в других – минимумы интенсивности, т. е. нет нарушения закона сохранения энергии. 8
При суперпозиции когерентных волн в одних точках пространства возникают максимумы, а в других – минимумы интенсивности, т. е. нет нарушения закона сохранения энергии. 8
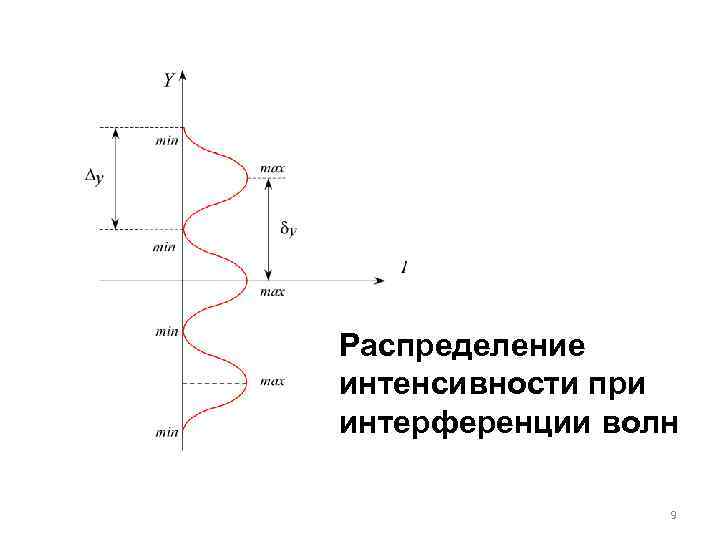
 Распределение интенсивности при интерференции волн 9
Распределение интенсивности при интерференции волн 9
 Ширина интерференционного максимума: . . Расстояние между интерференционными максимумами (полосами): Следовател ьно 10
Ширина интерференционного максимума: . . Расстояние между интерференционными максимумами (полосами): Следовател ьно 10
 11
11
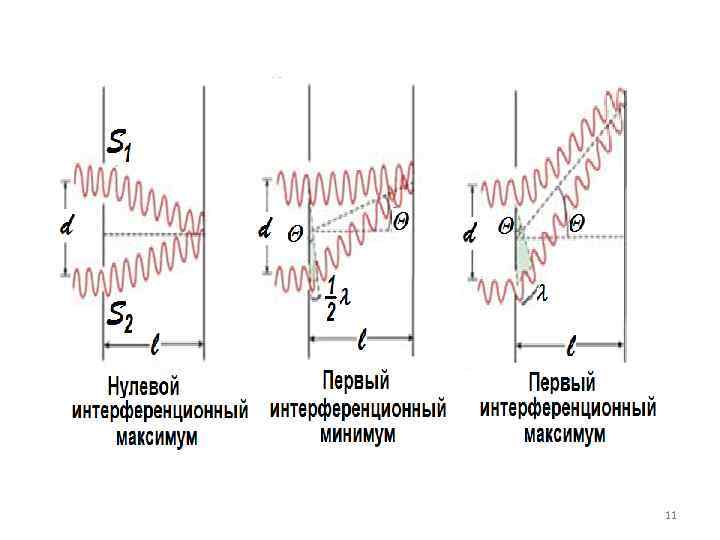
 Явление интерференции можно наблюдать, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником, на две части. В результате получим две когерентные волны. Затем необходимо сложить их, предварительно заставив пройти различные оптические пути.
Явление интерференции можно наблюдать, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником, на две части. В результате получим две когерентные волны. Затем необходимо сложить их, предварительно заставив пройти различные оптические пути.
 13
13
 В общем случае полученные таким образом две световые волны пройдут до точки сложения пути s 1 и s 2. Первая волна возбудит в точке сложения колебание А вторая волна – колебание 14
В общем случае полученные таким образом две световые волны пройдут до точки сложения пути s 1 и s 2. Первая волна возбудит в точке сложения колебание А вторая волна – колебание 14
 скорость распространения первой и второй волны Таким образом, разность фаз колебаний, возбуждаемых в точке сложения, будет равна
скорость распространения первой и второй волны Таким образом, разность фаз колебаний, возбуждаемых в точке сложения, будет равна
 оптическая разность хода 16
оптическая разность хода 16
 Если оптическая разность хода равна целому числу длин волн, то волны в точке сложения колеблются синфазно, так как разность фаз равна числу кратному 2π. =2 kl/2 (k=0, 1, 2, …) Условие интерференционного максимума: max
Если оптическая разность хода равна целому числу длин волн, то волны в точке сложения колеблются синфазно, так как разность фаз равна числу кратному 2π. =2 kl/2 (k=0, 1, 2, …) Условие интерференционного максимума: max
 Если же оптическая разность хода равна полуцелому числу длин волн в вакууме то волны в точке сложения колеблются в противофазе, так, как разность фаз равна получаем условие интерференционного минимума: 18
Если же оптическая разность хода равна полуцелому числу длин волн в вакууме то волны в точке сложения колеблются в противофазе, так, как разность фаз равна получаем условие интерференционного минимума: 18
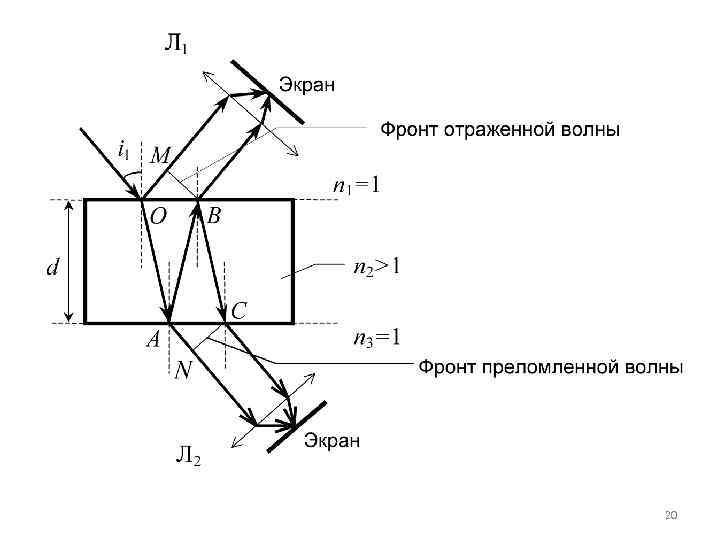
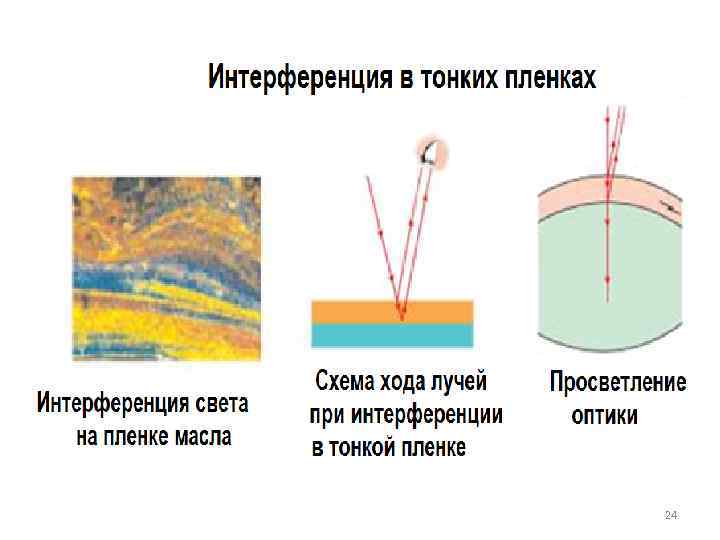
 Интерференция света в тонких пластинках (пленках) 1) монохроматическая падающая 2) пленка в воздухе (показатели волна (длина волны ) преломления среды над пленкой n 1 и под пленкой n 3 равны единице). Волна падает под углом i 1 на тонкую плоскопараллельную пластину (пленку), показатель преломления которой равен n 2. В точке О волна разделяется на преломленную (луч ОА ) и отраженную 19
Интерференция света в тонких пластинках (пленках) 1) монохроматическая падающая 2) пленка в воздухе (показатели волна (длина волны ) преломления среды над пленкой n 1 и под пленкой n 3 равны единице). Волна падает под углом i 1 на тонкую плоскопараллельную пластину (пленку), показатель преломления которой равен n 2. В точке О волна разделяется на преломленную (луч ОА ) и отраженную 19
 20
20
 Оптическая разность хода равна: . в отраженном свете – в проходящем свете – 21
Оптическая разность хода равна: . в отраженном свете – в проходящем свете – 21
 . ; При отражении от оптически более плотной среды (среды с бóльшим показателем преломления) фаза волны меняется на , что соответствует изменению оптической длины пути на в отраженном свете (в точке О) – 22
. ; При отражении от оптически более плотной среды (среды с бóльшим показателем преломления) фаза волны меняется на , что соответствует изменению оптической длины пути на в отраженном свете (в точке О) – 22
 , в проходящем свете (в точке А) – 23
, в проходящем свете (в точке А) – 23
 24
24
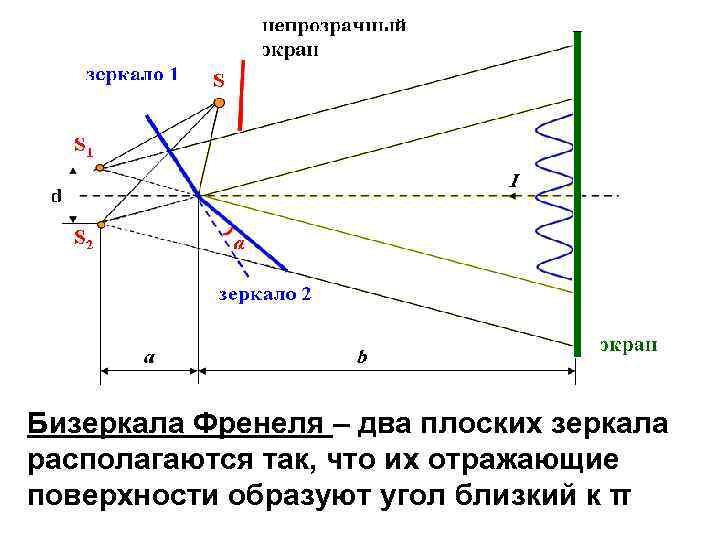
 Бизеркала Френеля – два плоских зеркала располагаются так, что их отражающие поверхности образуют угол близкий к π
Бизеркала Френеля – два плоских зеркала располагаются так, что их отражающие поверхности образуют угол близкий к π
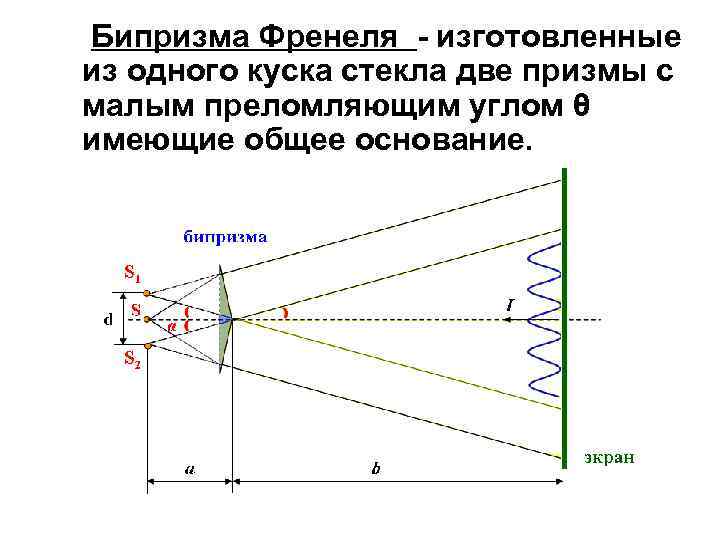
 Бипризма Френеля - изготовленные из одного куска стекла две призмы с малым преломляющим углом θ имеющие общее основание.
Бипризма Френеля - изготовленные из одного куска стекла две призмы с малым преломляющим углом θ имеющие общее основание.
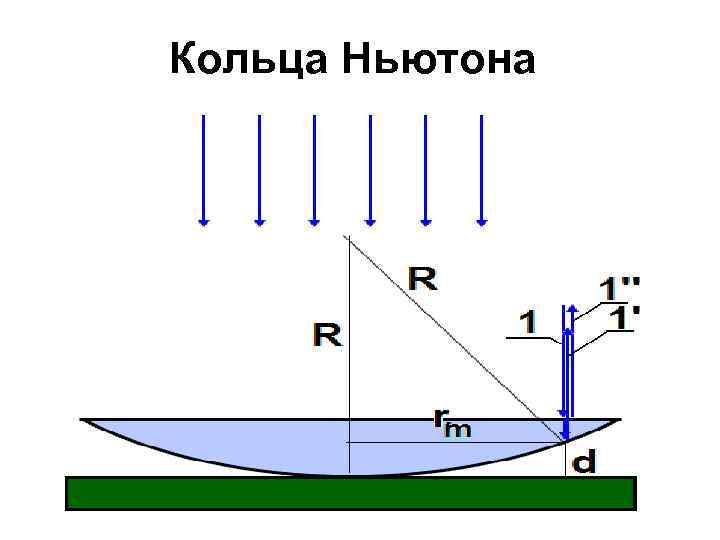
 Кольца Ньютона
Кольца Ньютона
 где R – радиус плосковыпуклой линзы. Четным m соответствуют радиусы светлых колец, нечетным радиусы темных колец (наблюдение в отраженном свете). В проходящем свете – наоборот.
где R – радиус плосковыпуклой линзы. Четным m соответствуют радиусы светлых колец, нечетным радиусы темных колец (наблюдение в отраженном свете). В проходящем свете – наоборот.
 Полосы равной толщины Полосы на поверхности клина с углом наклона меньшим или равным нескольким Кольца Ньютона угловым минутам
Полосы равной толщины Полосы на поверхности клина с углом наклона меньшим или равным нескольким Кольца Ньютона угловым минутам
 Контрольные вопросы 1. Что называется интерференцией? 2. Условие максимума и минимума интерференции 3. Оптическая разность хода – формула 4. Ширина интерференционной полосы и расстояние между интерференционными максимумами 5. Интерференция в тонких пленках 6. Кольца Ньютона 30
Контрольные вопросы 1. Что называется интерференцией? 2. Условие максимума и минимума интерференции 3. Оптическая разность хода – формула 4. Ширина интерференционной полосы и расстояние между интерференционными максимумами 5. Интерференция в тонких пленках 6. Кольца Ньютона 30
 . Стоячие волны образуются в результате интерференции двух встречных плоских волн (например, бегущей и отраженной волны). 31
. Стоячие волны образуются в результате интерференции двух встречных плоских волн (например, бегущей и отраженной волны). 31
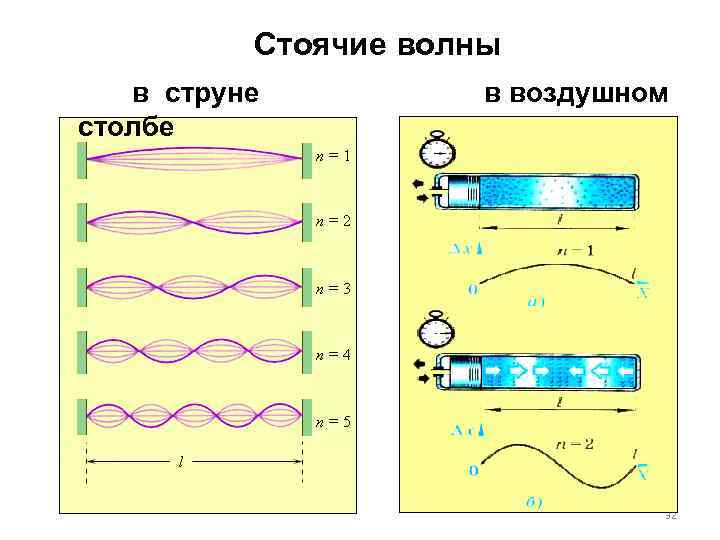
 Стоячие волны в струне в воздушном столбе 32
Стоячие волны в струне в воздушном столбе 32
 . . При интерференции встречных волн 1 и 2 образуется результирующая волна: Если разность фаз = 0, то Если разность фаз = , то 33
. . При интерференции встречных волн 1 и 2 образуется результирующая волна: Если разность фаз = 0, то Если разность фаз = , то 33
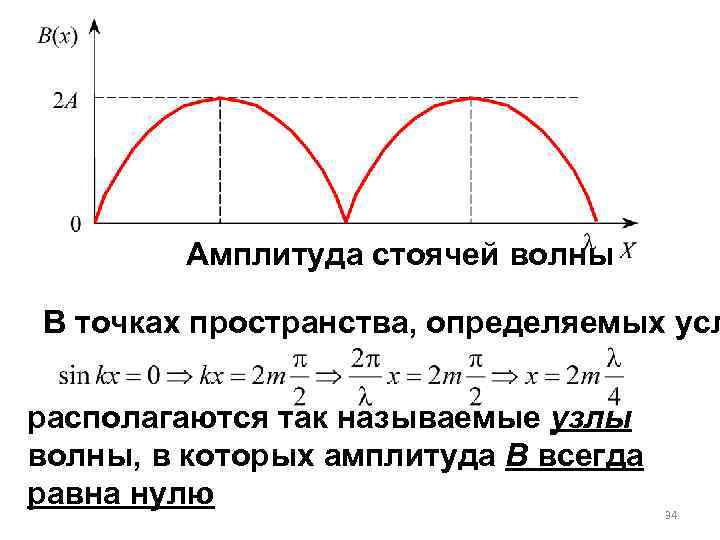
 Амплитуда стоячей волны В точках пространства, определяемых усл располагаются так называемые узлы волны, в которых амплитуда В всегда равна нулю 34
Амплитуда стоячей волны В точках пространства, определяемых усл располагаются так называемые узлы волны, в которых амплитуда В всегда равна нулю 34
 В точках пространства, определяемых ус . располагаются так называемые пучности волны, в которых амплитуда В может быть максимальной, то есть В = 2 А , в моменты времени, определяемые условием 35
В точках пространства, определяемых ус . располагаются так называемые пучности волны, в которых амплитуда В может быть максимальной, то есть В = 2 А , в моменты времени, определяемые условием 35
 В остальных точках пространства амплитуда волны может изменяться в пределах: 0 < B < 2 A. Образовавшаяся в результате интерференции волна является стоячей – через узлы энергия не переносится. 36
В остальных точках пространства амплитуда волны может изменяться в пределах: 0 < B < 2 A. Образовавшаяся в результате интерференции волна является стоячей – через узлы энергия не переносится. 36
 Стоячие волны в ограниченных ср Краевые условия: • в точках закрепления струны или стержня, а также на заглушках труб, всегда возникают узлы стоячей волны (в этих местах волна отражается от более плотной среды); • на свободных концах стержня и на открытых концах труб всегда возникают пучности стоячей волны (в этих местах волна отражается от менее плотной среды). 37
Стоячие волны в ограниченных ср Краевые условия: • в точках закрепления струны или стержня, а также на заглушках труб, всегда возникают узлы стоячей волны (в этих местах волна отражается от более плотной среды); • на свободных концах стержня и на открытых концах труб всегда возникают пучности стоячей волны (в этих местах волна отражается от менее плотной среды). 37
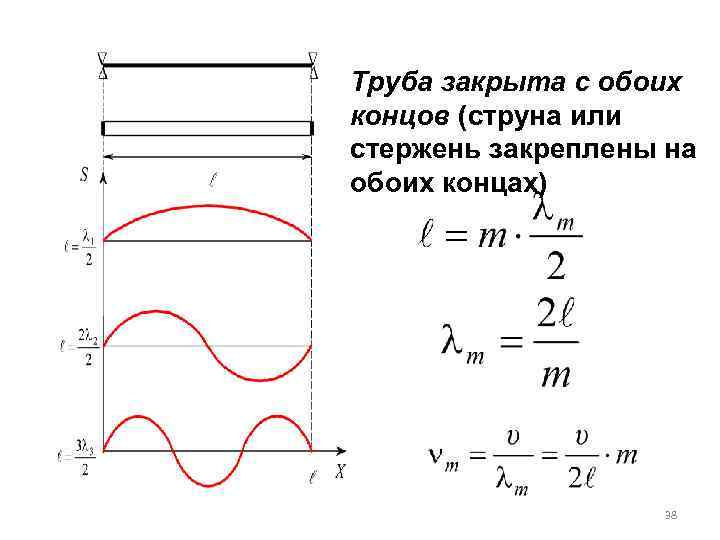
 Труба закрыта с обоих концов (струна или стержень закреплены на обоих концах) 38
Труба закрыта с обоих концов (струна или стержень закреплены на обоих концах) 38
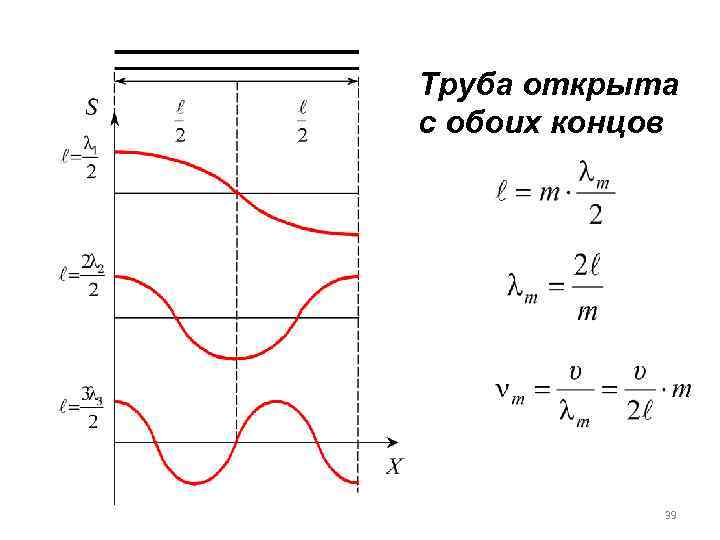
 Труба открыта с обоих концов 39
Труба открыта с обоих концов 39
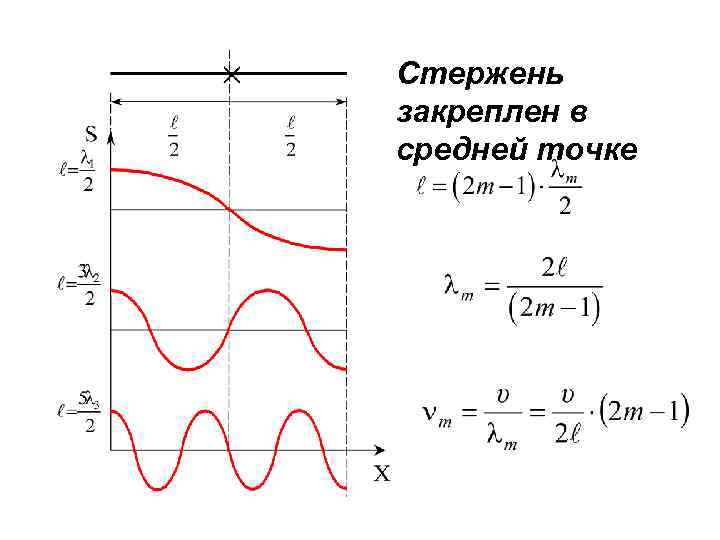
 Стержень закреплен в средней точке
Стержень закреплен в средней точке
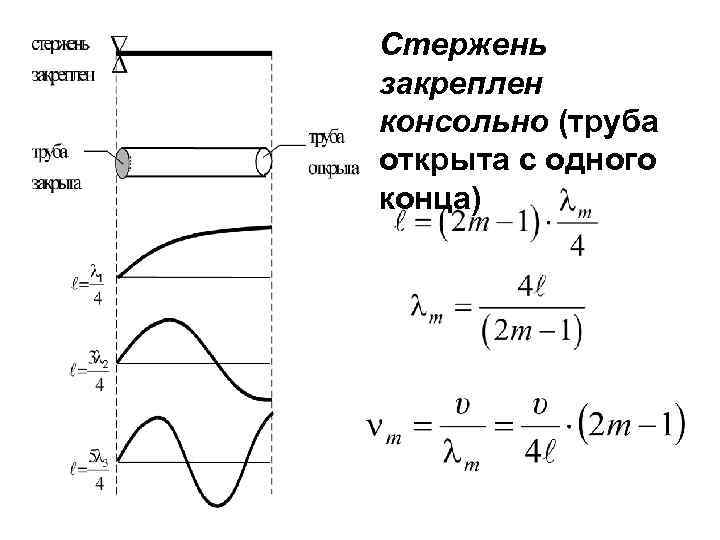
 Стержень закреплен консольно (труба открыта с одного конца)
Стержень закреплен консольно (труба открыта с одного конца)
 Наименьшие возможные частоты стоячих волн (при m = 1) называются основными , более высокие частоты называются обертонами.
Наименьшие возможные частоты стоячих волн (при m = 1) называются основными , более высокие частоты называются обертонами.

