d9fa60eee76aacde5db7143791289518.ppt
- Количество слайдов: 31

Interesting Examples of Capture-Recapture from Biology, Public Health, & Epidemiology H. James Norton & George W. Divine Website: www. jimnortonphd. com

How many fish are in the lake?

• Student: “Throw many sticks of dynamite into lake and then count the dead fish!” • Instead use capture-recapture method. • Dictionary of Epidemiology defines capture -recapture as a method of estimating the size of a target population (or a subset of the population) using overlapping and presumably incomplete but intersecting sets of data about the population.

Level of Statistical Sophistication • Assumptions are fairly easy to understand. • The derivation of the Lincoln-Peterson equation is not difficult. • For children, proportions and basic algebra. • For undergraduates, 95% CI’s. • For graduate students, log-linear models.

Brief History of Capture-Recapture Method • 1662 – Used to estimate population of London. • 1802 – Pierre Laplace explains formulas he used to estimate the population of France. • 1896 – Peterson used this method to estimate populations of Danish fish. • 1930 – Lincoln used it to estimate waterfowl in the U. S. • 1949 – Sekar & Deming use these principles to estimate birth and death rates in India. • 1954 – Chapman modifies Lincoln-Peterson formula. • 1963 – Wittes & Sidel publish the first use of capture-recapture in epidemiology by estimating the number of hospital patients using methicillin. • 1972 – Feinberg publishes paper on the use of log-linear models to analyze data from a multiple-list capture-recapture.
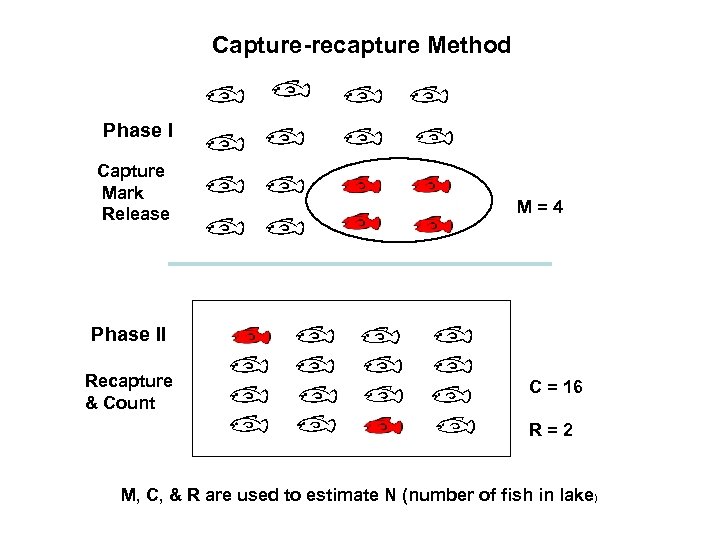
Capture-recapture Method Phase I Capture Mark Release M = 4 Phase II Recapture & Count C = 16 R = 2 M, C, & R are used to estimate N (number of fish in lake)

Assumptions for Capture-Recapture Method 1. All the individuals (animals) have an equal chance of being caught in Phase I. 2. The population is closed. No emigration or immigration. (No animals can leave the area and no new animals can enter the area. ) 3. There are no births or deaths during the time-period between Phase I and Phase II. 4. After the animals are marked they must be randomly redistributed into the population. (They must completely mix into the population. ) 5. The probability that a marked animal can be caught in Phase II must remain the same as in Phase I. This means the marking cannot cause an injury and slow the animal. The marked animals cannot “learn” from Phase I and therefore are more likely be able to avoid capture in Phase II.

Violation of Assumption #2 & Possibly #3

50 king penguins with bands were compared to 50 penguins with implanted microchips. The banded birds had 40% fewer chicks and a 16% lower survival rate. Violation of Assumption #5 Nature, 469 (13 January 2011), 203 -206 Claire Saraux &Yvon Le Maho

• Capture and tag(mark) M fish and release. • At later date C fish are caught. • R of these fish were previously tagged (recaptured). • Let N = estimated # of fish in lake. • Lincoln-Peterson method: N = (M x C) / R

Example Using Lincoln-Peterson Equation 80(M) fish are captured, marked (tagged) and released. 60(C) fish are later captured, of which 12(R) were recaptured (previously tagged). N = (60 x 80) /12 = 400

Derivation of Lincoln-Peterson Formula Let M = # marked in Phase I C = # captured during Phase II R = # recaptured in Phase II N = # animals in target population What is the proportion of animals in population that are marked? M/N What is the proportion in Phase II that were marked? R/C (which is an estimate of M/N) Set M/N = R/C , Cross multiply , M x C = R x N Solve for N N = (M x C) / R

More Advanced Topics for Undergraduates: Unbiased estimators & 95% Confidence Interval The Lincoln-Peterson equation: N = (M x C) / R is a biased estimator for N. It slightly overestimates N and what should you do if R = 0? N = [(M+1)(C+1) ÷ (R+1)] – 1 is an unbiased estimator with standard error SE = SQRT [(M+1)(C+1)(M-R)(C-R) ÷ (R+1)(R+2)] As usual, the 95% CI for N is N± 1. 96(SE) Redoing the last example where M = 80, C = 60, R = 12, & N = 400 yields an unbiased estimate of N = 379 with SE = 82. 6 and a 95% CI for N of (217, 541) SQRT = square root

Demonstrations of Capture-Recapture : • Grasshoppers or Crickets (mark with white out – not PETA approved) • White beans (mark with a black pen) • Marbles I use marbles and when I capture a fish (marble) I replace it with a red marble.
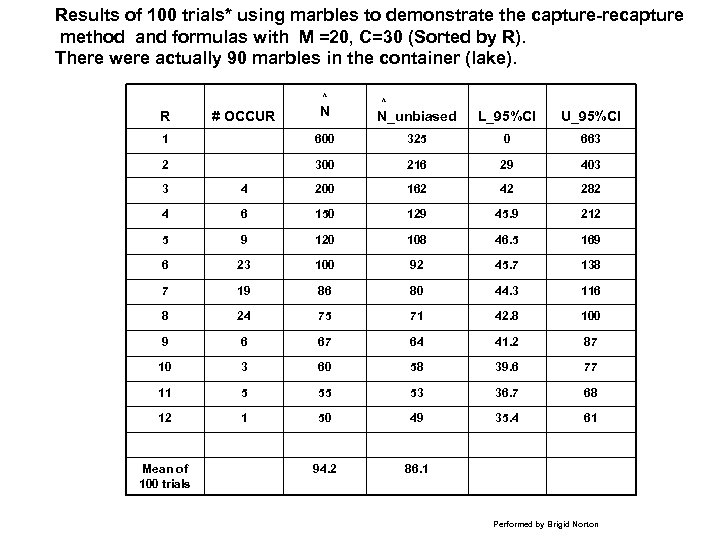
Results of 100 trials* using marbles to demonstrate the capture-recapture method and formulas with M =20, C=30 (Sorted by R). There were actually 90 marbles in the container (lake). N ^ N_unbiased L_95%CI U_95%CI 1 600 325 0 663 2 300 216 29 403 ^ . R # OCCUR 3 4 200 162 42 282 4 6 150 129 45. 9 212 5 9 120 108 46. 5 169 6 23 100 92 45. 7 138 7 19 86 80 44. 3 116 8 24 75 71 42. 8 100 9 6 67 64 41. 2 87 10 3 60 58 39. 6 77 11 5 55 53 36. 7 68 12 1 50 49 35. 4 61 94. 2 86. 1 Mean of 100 trials Performed by Brigid Norton
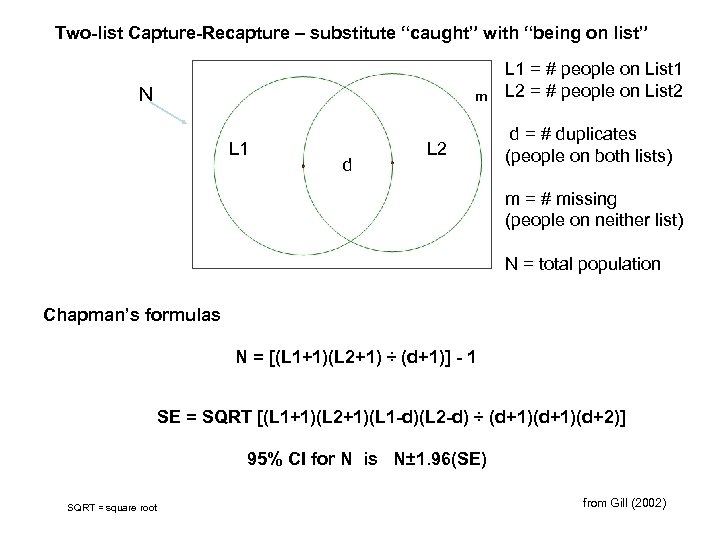
Two-list Capture-Recapture – substitute “caught” with “being on list” N m L 1 d L 2 L 1 = # people on List 1 L 2 = # people on List 2 d = # duplicates (people on both lists) m = # missing (people on neither list) N = total population Chapman’s formulas N = [(L 1+1)(L 2+1) ÷ (d+1)] - 1 SE = SQRT [(L 1+1)(L 2+1)(L 1 -d)(L 2 -d) ÷ (d+1)(d+2)] 95% CI for N is N± 1. 96(SE) SQRT = square root from Gill (2002)

Assumptions for simple two-list capture-recapture • UNAIDS/WHO Guidelines on Estimating the Size of Populations Most at Risk for HIV lists 5 Assumptions: • The population is closed. • Identifying information is collected in both samples. Individuals captured in both samples can be matched. • Capture in the second sample is independent of the first sample. • Each person has the same probability of being included (simple random samples). • Sufficient sample sizes. Estimates based on small samples or too few matched individuals can be misleading.

Example of two-list capture-recapture • Flaccid paralysis is an abnormal condition characterized by the weakening or loss of muscle tone. It may be caused by disease or by trauma affecting the nerves associated with the muscles. • Whitfield & Kelly (2002) estimate the incidence of acute flaccid paralysis (AFP) in Victoria, Australia. • List 1 is a national register for AFP. • List 2 was made using hospital case records by discharge diagnosis consistent with AFP-compatible conditions as defined by WHO. • L 1 = 14 cases. L 2 = 29 cases. Number cases on both lists, d = 10. • Using the Chapman formulas they estimate the number of cases: N = 40 with 95% CI (29, 51)

HOMEWORK • Refer to the example concerning AFP. • Suppose 5 years later the authors used the same sources for the lists and analyzed the results in a similar manner for the new data. At the back of your handout are the new lists. List 1 is from the national registry and list 2 is gathered from medical records. • Use the lists to determine L 1(# names on list 1), L 2 (# names on list 2), and d (duplicates – names on both lists). Use Chapman’s formulas to calculate an unbiased estimate of N and its 95% CI. • Did you encounter any potential problems with the lists? • List 1 has George Divine while list 2 has George Devine. • List 1 has Brigid Norton while list 2 has Bridgette Norton. Are these the same people or different people? List 1* Last Name Adler Baird Bieber Bowles Carey Channing Chung Divine Earp Gifford Grable Herrera Houdini Howard Jones Kayser Kelterman King Kuralt Norton Grace Cornelia Justin Crandall Drew Carol Connie George Wyatt Kathy Lee Betty Carolina Harry Ron James Earl Raymond Daniel Larry Charles Brigid List 2 First Name *partial list – complete list last slide of presentation Last Name Adams Bieber Devine Grable Houdini Jones Klein Lee Mac. Arthur Messing Michaels Nelson Norton Picasso Ringwald Ross Sanchez Taylor Turner Williams First Name John Justin George Betty Harry Bobby Calvin Spike Douglas Debra Loren Ricky Bridgette Pablo Molly Diana Mark Liz Tina Conrad

k-list(k>2) capture-recapture • What if the researcher has access to more than 2 lists? • What if there is a positive dependence between 2 of the lists? Then N underestimates the true number in the population. Example, a list from family practitioners and a list from a clinic that takes referrals from the family practitioners. • What if there is a negative dependence between 2 lists? Then N overestimates the true number in the population. Example, a list from family practitioners that treat mostly patients with private insurance and a list from a clinic that treats mostly patients without insurance. • Answer – use log-linear models. Can handle > 2 lists and can model dependencies among the lists.

Example of 3 -list capture-recapture • Hook , Albright & Cross (1980) supply data from 3 lists of persons with spina bifida in New York State between 1969 -1974. • Spina bifida is a serious birth defect in which the spinal cord is malformed and lacks its usual protective skeletal and soft tissue covering. • The sources of the 3 lists are medical records, birth certificates, and death certificates. • Zelterman in Advanced Log-Linear Models Using SAS® describes how to analyze this data set using Poisson regression in PROC GENMOD. • By using interaction terms in the model one is able to estimate the co-dependencies among the lists and take them into account in the final prediction model.
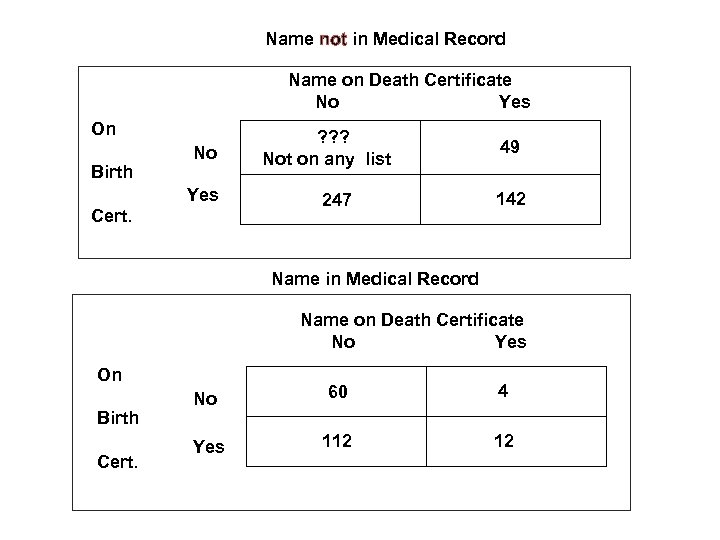
Name not in Medical Record Name on Death Certificate No Yes On Birth No Yes Cert. ? ? ? Not on any list 49 247 142 Name in Medical Record Name on Death Certificate No Yes On Birth Cert. No Yes 60 4 112 12

Analyze Data using Poisson regression in PROC GENMOD Input data Data crlists; input count birth death medical @@; cards; 49 010 247 100 142 110 60 001 40 011 4 011 112 101 12 111 ; run; First Run model with only main effects Proc genmod data=crlists; Model count= birth death medical / dist=Poisson link=log; Run;

Add interaction terms to model until best fitting model is determined ( or use backwards selection). Proc genmod data=crlists; Model count= birth death medical birth*death / dist=Poisson link=log; Run; Best model count= birth death medical death*medical Parameter Estimate p-value Intercept 4. 653 p < 0. 0001 Birth 0. 856 p < 0. 0001 Death -0. 611 p < 0. 0001 Medical -0. 764 p < 0. 0001 Death*Medical -1. 764 p < 0. 0001 To estimate missing cell(persons on none of the lists) set all variables = 0 leaving only the intercept. Take the anti-log (4. 653) = 105 to estimate for # persons not on any of 3 lists (use base e). Estimate of # persons with spina bifida in New York State =

More Examples of k-lists capture-recapture in Public Health & Epidemiology • • Zavreh, 2 -lists, estimating road traffic mortality. Chao, 3 -lists, number of cases of hepatitis A. Gurgel, 3 -lists, number of street children. Corraro, 4 -lists, number of alcohol related problems. Bruno, 4 -lists, number of diabetic cases. Ball, 4 -lists, number of killings in Kosovo. Abeni, 4 -lists, prevalence of HIV-1 infections. Fisher, 6 -lists, number of homeless and homeless mentally ill people.

“Not everything that can be counted counts, and not everything that counts can be counted. ”

There are 3 kinds of statisticians: Those who can count, & those who can't.

References Abeni DD, Porta D, Perucci CA. Deliveries, abortion and HIV-1 Infection in Rome, 1989 -1994. The Lazio AIDS Collaborative Group. Eur J Epidemiol. 1997 Jun; (13)4 373 -8. Ball P, Betts W, Scheuren F, Dudukovich J, Asher J. Killings and Refugee Flow in Kosovo March –June 1999. A Report to the International Criminal Tribunal for the Former Yugoslavia. American Academy for the Advancement of Science; 2002 Jan 3. Bruno G, La. Porte R, Merletti F, Biggeri A, Mc. Carty D, Pagano G: National diabetes programmes: application of capture-recapture to “count” diabetes? Diabetes Care. 1994; 17: 548 -556. Chao A, Tsay PK, Lin S-H, Shau W-Y, Chao Day-Yu. The applications of capture-recapture models to epidemiological data. Statist. Med 2001; 20: 3123 -3157. Corral G, Bagnardi V, Vittadini G, Favilli S. Capture-recapture methods to size alcohol related problems in a population. J Epidemiol Community Health 2000; 54: 603 -610. Cressey D. Band of Brothers. Researchers’ flipper bands can seriously dent penguin survival, and also skew the results of research. Nature 2011 Jan 12; 10, 1038. Fisher N, Turner SW, Pugh R, Taylor C. Estimating numbers of homeless and homeless mentally ill people in north east Westminster by using capture-recapture analysis. BMJ 1994 Jan 1; 308: 27 -30. Gill GV, Ismail AA, Beeching NJ. The use of capture-recapture techniques in determining the prevalence of type 2 diabetes. QJ Med 2001; 94: 341 -346. Gurgel R, de Fonseca JDC, Neyra-Castaneda D, Gill G, Cuevas L. Capture-recapture to estimate the number of street children in a city in Brazil. Arch Dis Child 2004 March; 89(3): 222 -224. Herzog T. Applications of Capture-Recapture Methods. FHA/HUD Khorasani-Zavareh et al. Post crash management of road traffic injury victims in Iran. Stakeholders’ views on current barriers and potential facilitators. BMC Emerg Med 2009; 9: 8.

References Continued Mahr A, Guillevin L, Poissonnet M, Segolene A. Prevalences of Polyarteritis Nodosa, Microscopic Polyangiitis, Wegener’s Granulomatosis and Churg-Strauss Syndrome in a French Urban Multiethnic Population in 2000: A Capture-Recapture Estimate. Arthritis and Rheumatism 2004 Feb 15; 51: 92 -99. Pollock K. Modeling Capture, recapture and removal statistics for estimation of demographic parameters for fish and wildlife populations: Past, Present and Future. Journal of the American Statistical Association 1991 March; 86: 225 -238. UNAIDS/WHO Working Group on Global HIV/AIDS and STI Surveillance. Guidelines on Estimating the Size of Populations Most at Risk to HIV. World Health Organization. 2010. Verlatto G, Muggeo M. Capture-Recapture Method in the Epidemiology of Type 2 Diabetes Care, 2000 June. (23) 6: 759. Whitfield K, Kelly H. Using the two-source capture-recapture method to estimate the incidence of acute flaccid paralysis in Victoria, Australia. Bulletin of the World Health Organization 2002, 80 (11): 846 -851. Wittes J, Sidel V. A Generalization of the simple capture-recapture model with applications to epidemiological research. J Chron Dis. 1968, (21) 287 -301.

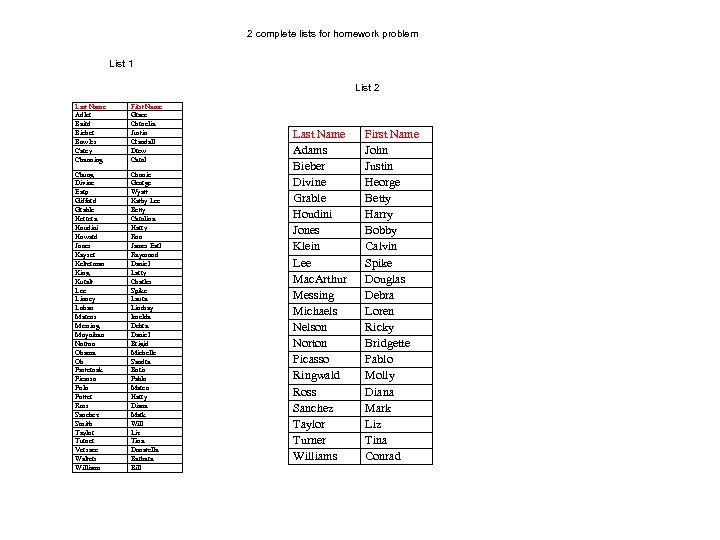
2 complete lists for homework problem List 1 List 2 Last Name Adler Baird Bieber Bowles Carey Channing First Name Grace Cornelia Justin Crandall Drew Carol Chung Divine Earp Gifford Grable Herrera Houdini Howard Jones Kayser Kelterman King Kuralt Lee Linney Lohan Marcos Messing Moynihan Norton Obama Oh Pasternak Picasso Polo Potter Ross Sanchez Smith Taylor Turner Versace Walters Williams Connie George Wyatt Kathy Lee Betty Carolina Harry Ron James Earl Raymond Daniel Larry Charles Spike Laura Lindsay Imelda Debra Daniel Brigid Michelle Sandra Boris Pablo Marco Harry Diana Mark Will Liz Tina Donatella Barbara Bill Last Name Adams Bieber Divine Grable Houdini Jones Klein Lee Mac. Arthur Messing Michaels Nelson Norton Picasso Ringwald Ross Sanchez Taylor Turner Williams First Name John Justin Heorge Betty Harry Bobby Calvin Spike Douglas Debra Loren Ricky Bridgette Pablo Molly Diana Mark Liz Tina Conrad
d9fa60eee76aacde5db7143791289518.ppt