Interest Rates and Present Value Chapter 7

Interest Rates and Present Value Chapter 7

Interest rates • We have thought about people trading fish and hamburgers lets think about a different type of trade • Joe would like to trade coconuts that will be ripe tomorrow in order to get ripe coconuts today • Bill is willing to trade some of the coconuts he has today in order to get coconuts tomorrow. • At what rate will they trade in a competitive market? • For quite a few reasons we think if Bill is going to give up 10 coconuts today he is going to want more than 10 coconuts back tomorrow • This is called interest 2

Why Do we want more tomorrow? • People are impatient-all else equal I would rather have a candy bar today than wait for it until tommorow • There is some risk that Joe will die or renege on his promise (the larger the risk of this the more interest we will want) • I might be able to do something useful with the coconuts (or money) in the meantime • Use the coconuts to build a shelter that I can live in (and if this is money I could buy a house today, live in it, and then sell the house tomorrow) • Use it to buy an ice cream truck, make money selling ice cream, and then sell the ice cream truck at the end of the day • Or if some emergency comes up and I need the money right away, I don’t have it and need to wait until I get paid back 3

Interest Rate • The interest rate is the percentage, usually expressed in annual terms, of a balance that is paid by a borrower to a lender that is in addition to the original amount borrowed or lent. • If I trade 100 coconuts today for 108 coconuts next year, the interest rate is 8% • As a practical matter it doesn’t usually work this way: Banks act as intermediaries • Joe borrows coconuts from the bank • Bill saves his coconuts in the bank • While they never actually meet each other-Joe is essentially borrowing from Bill 4

Nominal vs. Real Interest Rates • Nominal Interest Rate: the advertised rate of interest • Real Interest Rate: the rate of interest after inflation expectations are accounted for; the compensation for waiting on consumption • As an example suppose the inflation rate is 10% and the nominal interest rate is 10% • I put $100 into my account this year (2011) • I get $110 next year (2012) • However, that $110 in 2012 is worth the same amount as $100 in 2011, so I didn’t really earn any interest • In that case the real interest rate would be 0 • I would probably want to spend that $100 now before inflation erodes its value • In economics we usually care about the real interest rate 5

Present Value • Present Value is the interest adjusted value of future payment streams. • To think of this consider two different scenarios: 1. I pay you $300 this year 2. I pay you $100 this year, $100 in 2012, and $100 in 2013 • The interest rate is 5% • Are these the same? • Think about it this way: 1. I get my $300 now, spend $100 and save $200 • Next year I have $210 in the bank, I spend $110 and save $100 • In 2013 I now have $105 to spend 6

• Obviously I prefer the $300 today. • This is because the present value of a stream of $100 for three years is less than $300. • Well how much is it exactly? • The present value of the first $100 today is $100 • The present value of $100 next year must solve the following equation (r is the interest rate) That is, if I put PV in the bank today, I will have $100 in the bank tomorrow 7

So Now what about the present value of $100 in 2012? To see where this comes from suppose • I put $Y into the bank in 2011. • This would be give me $Y(1+r) in 2012 • If I just kept it in the bank I would get $Y(1+r) in 2013 Thus the present value of $100 in 2013 is: 8

And the value of the stream of $100 for 3 years is worth: More generally the present value of a payment $Y n years from now is worth today Rather than doing more calculations lets look at what this means 9

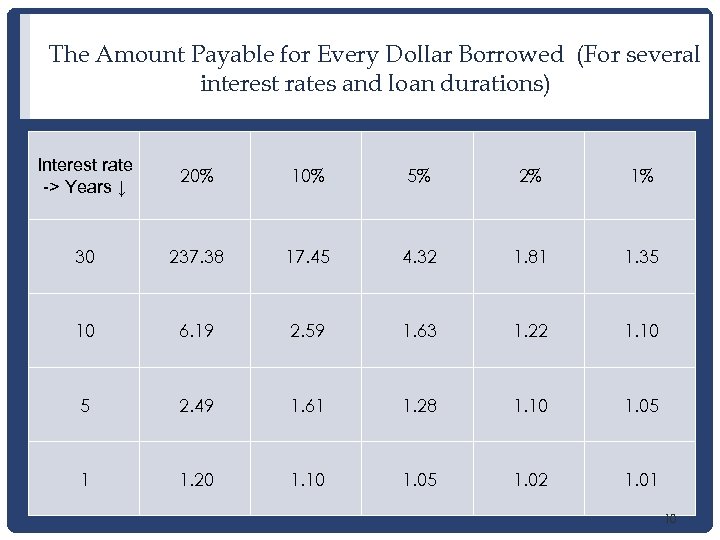The Amount Payable for Every Dollar Borrowed (For several interest rates and loan durations) Interest rate -> Years ↓ 20% 10% 5% 2% 1% 30 237. 38 17. 45 4. 32 1. 81 1. 35 10 6. 19 2. 59 1. 63 1. 22 1. 10 5 2. 49 1. 61 1. 28 1. 10 1. 05 1 1. 20 1. 10 1. 05 1. 02 1. 01 10

Examples From This Table • If you borrow $1 and promise to pay it back in 5 years at 5% interest you will owe $1. 28 which is the original $1 plus 28 cents in interest. • If you borrow $1 and promise to pay it back in 30 years at 20% interest you will owe $237. 38 which is the original $1 plus $236. 38 in interest. 11

Business Venture • Suppose you have the following business venture: • Invest $100 into the venture for 5 years • receive $100 in proceeds starting in year 6 and lasting for 7 years • Is this a good investment? • It depends on the interest rate 12

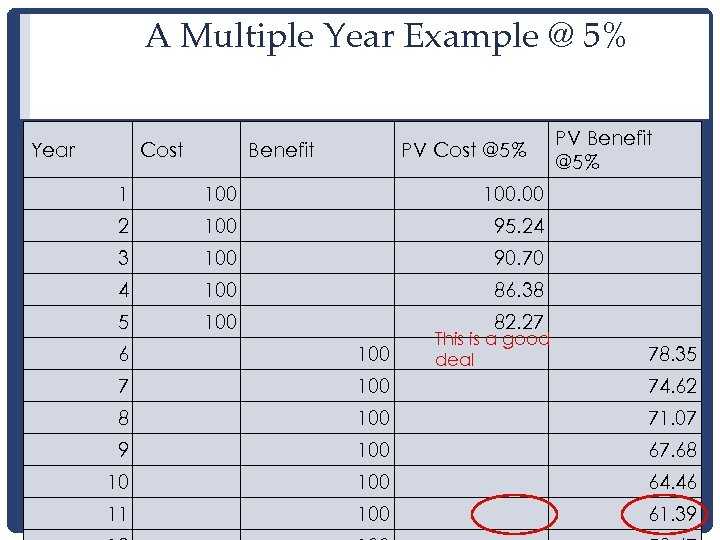A Multiple Year Example @ 5% Year Cost Benefit PV Cost @5% 1 100. 00 2 100 95. 24 3 100 90. 70 4 100 86. 38 5 100 PV Benefit @5% 82. 27 This is a good deal 6 100 78. 35 7 100 74. 62 8 100 71. 07 9 100 67. 68 10 100 64. 46 11 100 61. 39

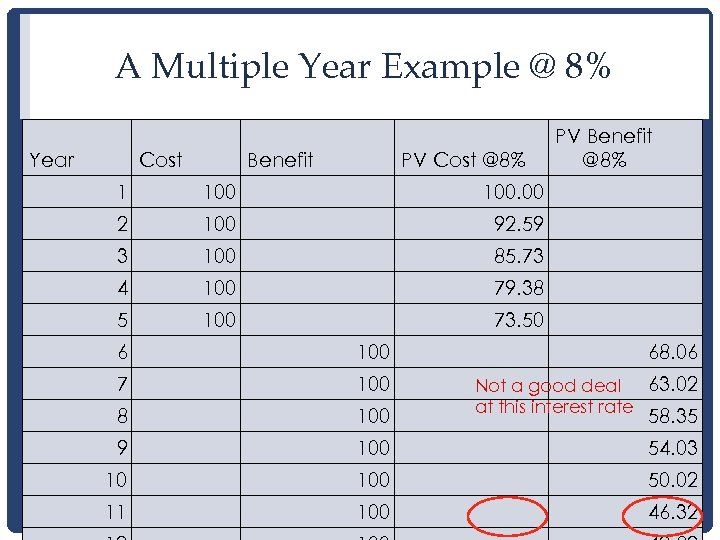A Multiple Year Example @ 8% Year Cost Benefit PV Cost @8% 1 100. 00 2 100 92. 59 3 100 85. 73 4 100 79. 38 5 100 PV Benefit @8% 73. 50 6 100 68. 06 7 100 8 100 Not a good deal 63. 02 at this interest rate 9 100 54. 03 10 100 50. 02 11 100 46. 32 58. 35

Internal rate of return • At 5% (or less) this was a good investment • At 8% (or more) this is a bad investment • Internal rate of return : The interest rate where the present value of costs and benefits are equal. • If my interest rate is lower than the internal rate, I should do it • If it is higher than the internal rate, I should not do it 15

Mortgages, Car Payments, Etc. • Mortgages are loans taken out to buy homes. Typically you borrow a large sum of money and promise to pay it back in even amounts each month for 10, 15, or 30 years. • Car loans are similar to mortgages in that you borrow a large sum but the loan duration is usually two to six years. • How does the financing department figure out the monthly payment at a 2. 9% interest for a $32, 000 car? • Given the interest they choose it to be the constant payment such that the present value of my car payments at a 2. 9% rate is $32, 000 16

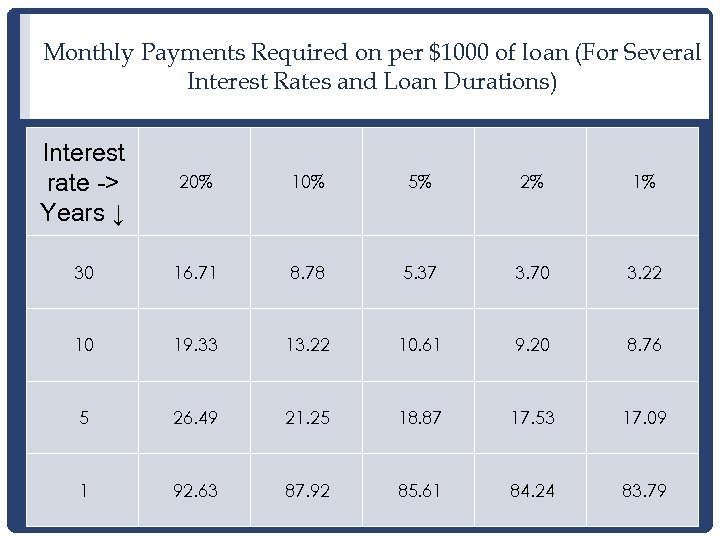Monthly Payments Required on per $1000 of loan (For Several Interest Rates and Loan Durations) Interest rate -> Years ↓ 20% 10% 5% 2% 1% 30 16. 71 8. 78 5. 37 3. 70 3. 22 10 19. 33 13. 22 10. 61 9. 20 8. 76 5 26. 49 21. 25 18. 87 17. 53 17. 09 1 92. 63 87. 92 85. 61 84. 24 83. 79

Examples From This Table • If you borrow $1000 and promise to pay it back monthly over 5 years at 5% interest you will owe $18. 87 per month. • If you borrow $1000 and promise to pay it back monthly over 10 years at 20% interest you will owe $19. 33 per month. 18

Future Value • Future value: the interest-adjusted value of past payments. • That is if I put $Y in the bank today and take it out n years from now I get dollars when I take it out 19

Risk and Reward • Risk: the possibility that the investor will not get those anticipated payoffs – Default Risk: the risk to the investor that the borrower will not pay – Market Risk: the risk that the market value of an asset will change in an unanticipated manner • Reward – Risk Premium the reward investors receive for taking greater risk 20

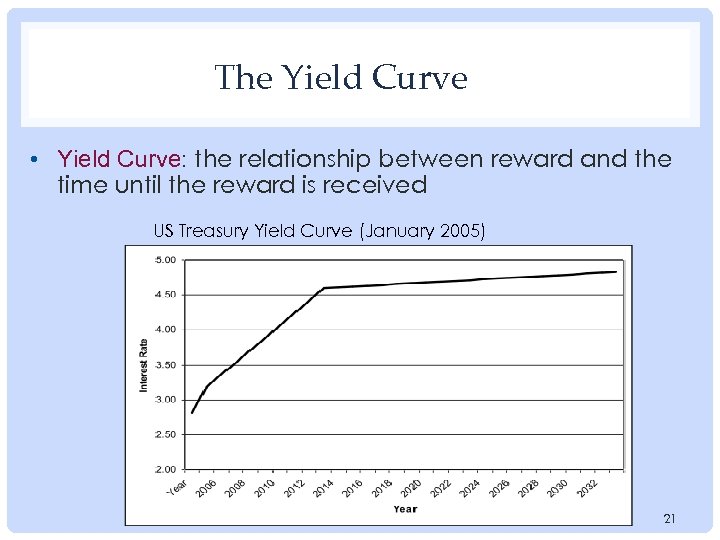The Yield Curve • Yield Curve: the relationship between reward and the time until the reward is received US Treasury Yield Curve (January 2005) 21