Interest Rate Factor in Financing Objectives

Interest Rate Factor in Financing Objectives • • • Present value of a single sum Future value of a single sum Present value of an annuity Future value of an annuity Calculate the effective annual yield for a series of cash flows Define what is meant by the internal rate of return

Compound Interest • PV= present value • i=interest rate, discount rate, rate of return • I=dollar amount of interest earned • FV= future values • Other terms: • Compounding • Discounting

Compound Interest FV=PV (1 + i)n • When using a financial calculator: • n= number of periods i= interest rate PV= present value or deposit PMT= payment FV= future value n, i, and PMT must correspond to the same period: • Monthly, quarterly, semi annual or yearly. • • •

The Financial Calculator • • • n= number of periods i=interest rate PV= present value, deposit, or mortgage amount PMT= payment FV= future value When using the financial calculator three variables must be present in order to compute the fourth unknown. • PV or PMT must be entered as a negative

Future Value of a Lump Sum FV=PV(1+i)n • This formula demonstrates the principle of compounding, or interest on interest if we know: • • 1. An initial deposit • 2. An interest rate • 3. Time period • We can compute the values at some specified time period.

Present Value of a Future Sum • PV=FV 1/(1+i)n The discounting process is the opposite of compounding • The same rules must be applied when discounting • • n, i and PMT must correspond to the same period • Monthly, quarterly, semi-annually, and annually

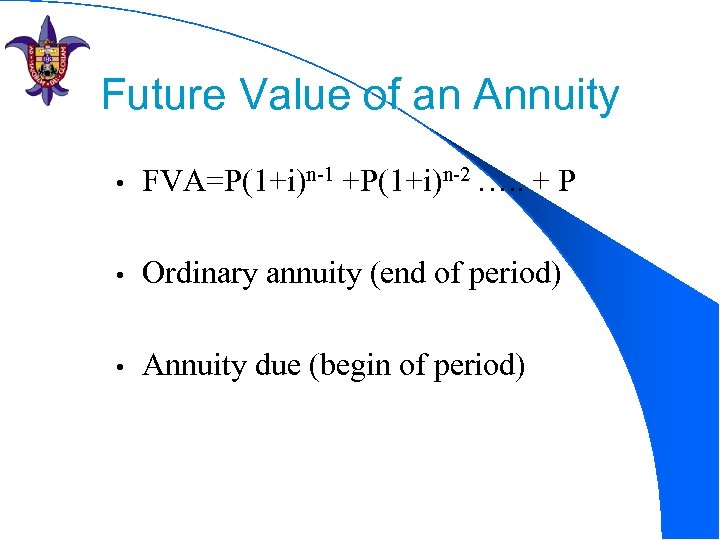
Future Value of an Annuity • FVA=P(1+i)n-1 +P(1+i)n-2 …. . + P • Ordinary annuity (end of period) • Annuity due (begin of period)

Present Value of an Annuity • PVA= R 1/(1+i)1 + R 1/(1+i)2…. . R 1/(1+i)n

Future Value of a Single Lump Sum • Example: assume Astute investor invests $1, 000 today which pays 10 percent, compounded annually. What is the expected future value of that deposit in five years? • Solution= $1, 610. 51

Future Value of an Annuity • Example: assume Astute investor invests $1, 000 at the end of each year in an investment which pays 10 percent, compounded annually. What is the expected future value of that investment in five years? • Solution= $6, 105. 10

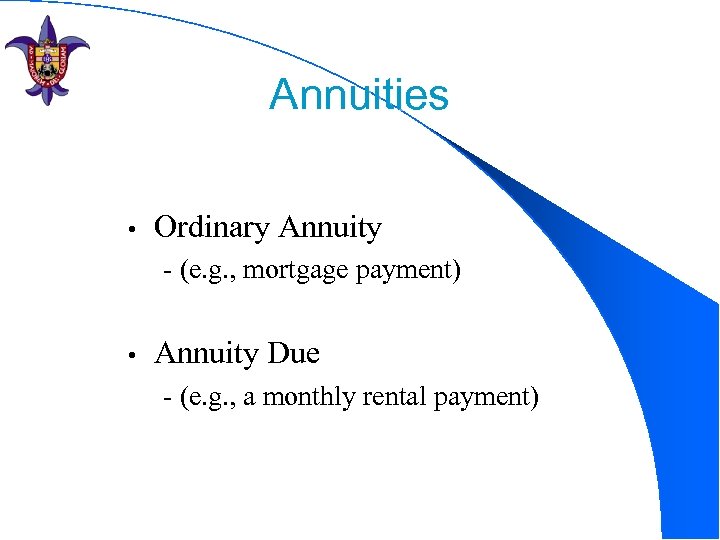
Annuities • Ordinary Annuity - (e. g. , mortgage payment) • Annuity Due - (e. g. , a monthly rental payment)

Sinking Fund Payment • Example: assume Astute investor wants to accumulate $6, 105. 10 in five years. Assume Ms. Investor can earn 10 percent, compounded annually. How much must be invested each year to obtain the goal? • Solution= $1, 000. 00

Present Value of a Single Lump Sum • Example: assume Astute investor has an opportunity that provides $1, 610. 51 at the end of five years. If Ms. Investor requires a 10 percent annual return, how much can astute pay today for this future sum? • Solution = $1, 000

Payment to Amortize Mortgage Loan • Example: assume Astute investor would like a mortgage loan of $100, 000 at 10 percent annual interest, paid monthly, amortized over 30 years. What is the required monthly payment of principal and interest? • Solution= $877. 57

Yield & IRR • IRR (Internal Rate of Return) is the most Important alternative to NPV. The IRR is closely related to NPV. With the IRR, we try to find a single rate of return that summarizes the merits of a project. Furthermore we want this rate to be an "internal" rate in the sense that it depends only on the cash flows of a particular investment, not on rates offered elsewhere. • If future value and present value are known then you can play a guessing game. • For example if you have a $5, 639 investment that will be worth $15, 000 after 7 years. If you guess that the IRR will be 10% you get a PV of $7, 697. Is our next guess greater than 10% or less? Why? • Solve on calculator

Remaining Loan Balance Calculation • Example: determine the remaining balance of a mortgage loan of $100, 000 at 10 percent annual interest, paid monthly, amortized over 30 years at the end of year four. • The balance is the PV of the remaining payments discounted at the contract interest rate. • Solution= $97, 402. 31

Conventional Mortgage Objectives Characteristics of constant payment (CPM), constant amortization (CAM), and graduated payment mortgages (GPM) • Effective cost of borrowing v. s. lenders effective yield • Calculate discount points or loan origination fees •

Determinants of Mortgage Interest Rates Real rate of interest- the required rate at which economic units save rather than consume • Rate of inflation • Nominal rate or constant rate i= r+f • Nominal rate= real rate plus a premium for inflation •

Determinants of Mortgage Interest Rates • • • Default risk- creditworthiness of borrowers Interest rate risk- rate change due to market conditions and economic conditions Prepayment risk- falling interest rates Liquidity risk i=r+ f+ P…

Exhibit 4 -1 to be inserted by Mc. Graw-Hill

Development of Mortgage Payment Patterns • • • Constant amortization mortgage (CAM) Constant payment Interest computed on the monthly loan balance Constant amortization amount Total payment= constant amortization amount plus monthly interest

Development of Mortgage Payment Patterns • • • Constant payment mortgage (CPM) Constant monthly payment on original loan Fixed rate of interest for a given term Amount of amortization varies each month Completely repaid over the term of the loan

Development of Mortgage Payment Patterns Graduated payment mortgage (GPM) • Mortgage payments are lower in the initial years of the loan • GPM payments are gradually increased at predetermined rates •

Loan Closing Costs and Effective Borrowing Costs • Statutory costs • Third party charges • Additional finance charges i. e. loan discount fees, points

Effective Interest Cost Examples • • • Contractual loan amount $60, 000 Less origination fee(3%) $ 1, 800 Net cash disbursed by lender $58, 200 Interest rate= 12% Term 30 years

Effective Interest Cost Examples Continued • Calculator solution – n=360 – PMT= -617. 17 – PV= 58, 200 – FV= 0 – i=1. 034324 (12. 41% annualized)

Other Fixed Rate Mortgages • • • Characteristics and Requirements: Regulation Z- truth in lending (APR) RESPA- Real Estate Settlement Procedures Act Prepayment penalties and other fees Reverse annuity mortgages (RAMs)

Reverse Annuity Mortgage Example Residential property value $500, 000 • Loan amount $250, 000 • (to be disbursed in monthly installments) Term 10 years • Interest Rate • 120 months 10%

Reverse Annuity Mortgage Example Continued • Calculator solution: – FV=-250, 000 – i=10%/ 12 – PMT= ? – n=120 – Solve for payment $1220. 44