Interatomic Potentials for Ionic Systems Byeong-Joo Lee POSTECH-CMSE

Зарегистрируйтесь, чтобы просмотреть полный документ!

Interatomic Potentials for Ionic Systems Byeong-Joo Lee POSTECH-CMSE Byeong-Joo Lee www. postech. ac. kr/~calphad

Background • Importance of Ionic Materials ü Sensor, Battery, Devices, Metal Surfaces, etc. • Need to handle “ionic + covalent + metallic” materials ü Interfacial Reaction between metals and Si. O 2 substrate ü Diffusion of metallic atoms in amorphous Si. O 2 • Atomistic simulation on “ionic + covalent + metallic” materials ü ? ? ? Byeong-Joo Lee www. postech. ac. kr/~calphad

Purpose and Scope • Development of Interatomic Potential Model that covers “ionic + covalent + metallic” materials, simultaneously. ü Review interatomic potentials for ionic and hybrid materials ü Propose possible form of an interatomic potential formalism Byeong-Joo Lee www. postech. ac. kr/~calphad

Outline • Interatomic Potential for Ionic Materials ü Point Charge Model ü Polarization (Shell Model) • Many-Body Potentials ü Tersoff ü EAM – MEAM – 2 NN MEAM ü Many-body potentials used for ionic systems • Many-Body Potentials for Ionic Materials ü Charge Equilibration Model ü EAM + Qeq ü Tersoff + Qeq • Proposal of New Interatomic Potential Form Byeong-Joo Lee www. postech. ac. kr/~calphad

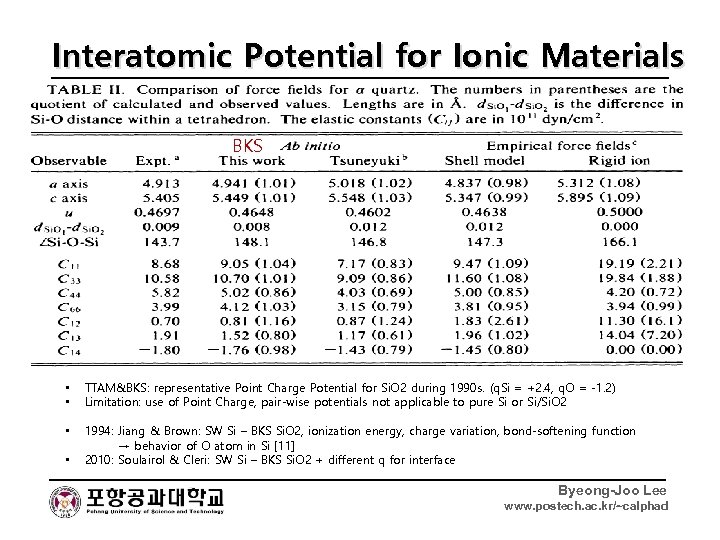
Interatomic Potential for Ionic Materials Fixed Point Charge TTAM Born-Mayer-Huggins. BKS • • Initially applied to liquid or glass, not crystals : probably, unable to reproduce crystal structures 1 st MD on Si. O 2 glass Woodcock [5], 1976 • More information available with upgraded measuring techniques for crystal structures and dynamics • 1988: BMH + many-body interaction to reproduce O-Si-O bonding angle: (cosθjik - cosθojik)2 [6] • 1988: BMH + modified Coulomb interaction considering excess charge distribution in oxygen + Ab Initio on Si. O 2 model clusters → α-quartz, α-cristobalite, Coesite, Stishovite, for the first time → TTAM [7] 1990: BMH + Ab Initio + Experimental Information on α-quartz → better description than TTAM → BKS [8] • • • TTAM&BKS: representative Point Charge Potential for Si. O 2 during 1990 s. (q. Si = +2. 4, q. O = -1. 2) Limitation: use of Point Charge, pair-wise potentials not applicable to pure Si or Si/Si. O 2 • 1994: Jiang & Brown: SW Si – BKS Si. O 2, ionization energy, charge variation, bond-softening function → behavior of O atom in Si [11] 2010: Soulairol & Cleri: SW Si – BKS Si. O 2 + different q for interface • Byeong-Joo Lee www. postech. ac. kr/~calphad

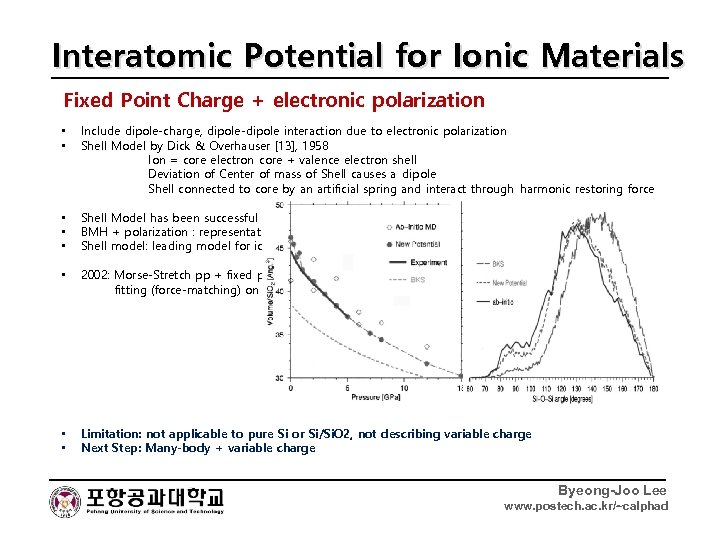
Interatomic Potential for Ionic Materials Fixed Point Charge + electronic polarization • • Include dipole-charge, dipole-dipole interaction due to electronic polarization Shell Model by Dick & Overhauser [13], 1958 Ion = core electron core + valence electron shell Deviation of Center of mass of Shell causes a dipole Shell connected to core by an artificial spring and interact through harmonic restoring force • • • Shell Model has been successful for diatomic molecule, alkali halides and also for Al 2 O 3 [14] BMH + polarization : representative approach during 1980 s for alkali halides, binary, mixed oxides [15] Shell model: leading model for ionic materials in GULP [19] • 2002: Morse-Stretch pp + fixed point charge Coulomb + dipole polarization for Oxygen ions [17] fitting (force-matching) on liquid Si. O 2 → better description for polymorphs than BKS • • Limitation: not applicable to pure Si or Si/Si. O 2, not describing variable charge Next Step: Many-body + variable charge Byeong-Joo Lee www. postech. ac. kr/~calphad

Many-Body Potential : EAM – 2 NN MEAM • Embedding energy of impurity atoms is determined by the electron density of the host (from first-principles) → individual atoms are impurity atoms → EAM concept [29, 30] • • How to compute F and Ф ? No specific function form was given in initial EAM → reason for so many EAMs Rose universal equation of state [23] gives a guide [31] • EAM : linear superposition for computation of electron density of a site → mainly for fcc • Introduction of bonding directionality → Modified EAM (1 nn interaction only) → applied to Si [32], bcc [33] and hcp [34], but stability problem • Need to consider 2 NN interactions to solve critical shortcomings in MEAM → 2 NN MEAM [36, 37] → applicable to both metallic and covalent systems: metals, carbides, nitrides, Si, Ge, etc. [38 -40] Byeong-Joo Lee www. postech. ac. kr/~calphad

Many-Body Potential : Tersoff • 1985 Abell : Close relation between Morse-type pair potential and Rose universal behavior → replacement of Born-Mayer by Morse-Stretch • Tersoff potential [24 -26] bij : bond order – 1 nn interaction, bond length and angle, effect of local environments, etc. • applied to C [27] and Si. C [28] and extended to Brenner-REBO [87 -89] • for alloys : arithmetic mean to λ, μ and geometric mean to A, B, R, S Byeong-Joo Lee www. postech. ac. kr/~calphad

Many-Body Potential for Ionic Materials • Umeno [14] : using Tersoff for Si. O 2 Independent fitting to λ, μ, A, B instead of mean values applicable to β-cristobalite, β-quartz which was difficult by BKS • Kuo [15] : using MEAM for Si. O 2 applicable to α, β-quartz, α, β-cristobalite, β-tridymite Byeong-Joo Lee www. postech. ac. kr/~calphad

Charge Equilibration Model • 1991 Rappe & Goddard [48] : based on previous concepts on electronegativity, equilibration [49 -57]. - equilibrium charge in molecules considering Coulomb interaction and penalty energy for charged isolated atoms (atomic self-energy) IP & EA : ionization potential과 electron affinity χ 0 : electronegativity J 0 : atomic hardness representing Coulomb repulsion between two electrons in an orbital JAB : Coulomb interaction between A & B computed by a Coulomb integral on atomic charge density expressed for a Slater-type orbital • Basic idea in Qeq model is to equalize the atomic chemical potential of all individual atoms (χ1 = χ2 = … = χN) • First applied to Si. O 2 in 1999 [58] : Morse-Stretch pair potential + charge equilibration - Quartz-Stishovite phase transition & Silica glass • Swamy & Gale [59] in 2000 : Titanium oxide system including rutile, anatase, brookite, Ti. O 2 -II, Ti 2 O 3, monoclinic high- and low temp forms of Ti 3 O 5, Ti. O, ramsdellite-type Ti. O 2, g-Ti 3 O 5, two Magneli phases: Ti 4 O 7 and Ti 6 O 11 Byeong-Joo Lee www. postech. ac. kr/~calphad

EAM + Charge Equilibration 1994 Streitz & Mintmire [60] : first Qeq approach for crystalline materials, EAM + Qeq for Al 2 O 3 • • 2004 Zhou [70] : solving charge stability problem, - extened to multicomponent oxides, O-Al-Ni-Co-Fe system [71] • 2007 Lazic [74] : MEAM (different from Baskes) + Qeq, not much is published Oxidation of Al nano cluster [61, 62] Byeong-Joo Lee www. postech. ac. kr/~calphad

Tersoff + Charge Equilibration • 1996 Yasukawa [76] : introduce atomic energy ΣiΦi & Coulomb energy ½ΣiΣj. EIONij - effective point charge with cutoff function in Coulomb potential, not with Ewald summation - Considering changes in ionic radius and short range interaction due to charge • • • Crack propagation behavior of Si. O 2 with or without H 2 O Adhesion strength on Al, Cu/Ti. N, W, Si. O 2 thin film interface [77] Upgrade in parameter [78] & Formalism for Coulomb interaction [79] • 2007 Sinnott & Phillpot group [80] : confirm application to α, β-quartz, α, β-cristobalite, but stability problem. - atomic self-energy up to 4 th order & introduction of bond-bending energy, (cosθOSi. S - cosθo. OSi. O)2, - COMB (Optimized Many-Body Potential), but cannot generate amorphous Si. O 2 & bad results for α-quartz 2010 modified version for Si. O 2 [81] : Slater 1 s orbital type Coulomb integral & Ewald + another penalty term - applicable to α, β-quartz, α, β-cristobalite, β-tridymite, Coesite, Stishovite, generally worse than TTAM 2010 Hf/Hf. O 2, Cu/Cu 2 O [83, 84] : different bond-bending form depending on cation element • • Byeong-Joo Lee www. postech. ac. kr/~calphad

Others : Reax. FF • Bond-Order : based on correlation between bond order & bond distance or bond energy describe bond dissociation → chemical reaction - including bonding angle, torsion, charge equilibration, van der Waals interaction, etc. - mainly for hydrocarbon system [85], but also to oxides, Si/Si. O 2 system [86] • Most powerful : covering Hydrocarbon system like Brenner-REBO [87 -89] and charge equilibration like COMB • Number of parameters for Carbon, for example : 90 s - how to determine the parameter values ? → 10 ~ 15 systems during up to now - retirement of Prof. Goddard → Dr. van Duin @ Penn State Byeong-Joo Lee www. postech. ac. kr/~calphad

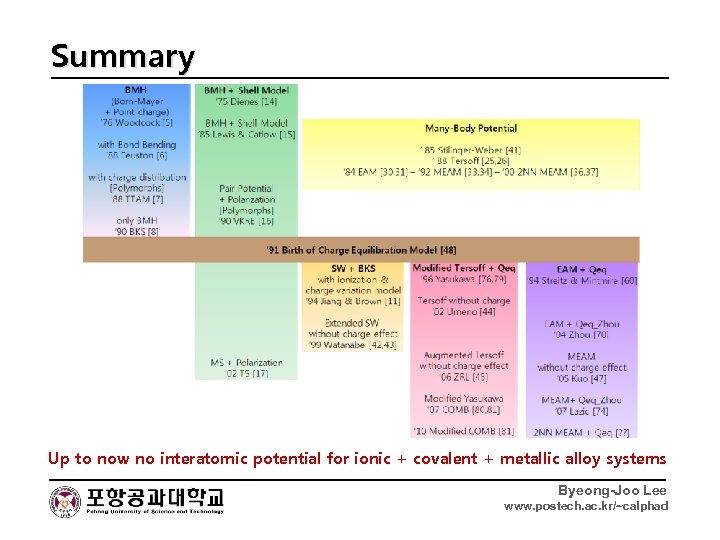
Summary Up to now no interatomic potential for ionic + covalent + metallic alloy systems Byeong-Joo Lee www. postech. ac. kr/~calphad

Potential for Ionic+Covalent+Metallic Materials • Charge Effect ? Correct physics : easy parameterization and good trasferability • Point Charge vs. Charge Distribution ? TTAM that considered charge distribution could describe the Si. O 2 polymorphs for the first time • Shell Model ? No publication for shell model + many-body potential Variable charge can be superior to fixed charge, for bond dissociation, surface, interface, and other defects • Coulomb Integral ? COMB 10 [81] is generally worse than BKS or TTAM for Si. O 2 polymorphs Coulomb intergral (COMB 10 [81]) vs. effective point charge (Yasukawa 2010 [79]) ? • Summation of Long Range Potential (1/r radial behavior) ? Ewald method [70], PPPM [75], direct summation method [82] • Charge Equilibration Method ? Inverse matrix [60], Conjugate gradient method [70], Lagrangian dynamics [80] • Manybody Potential ? - COMB had to change the functional form for bond-bending term, probably due to the limitation of Tersoff. [Tersoff potential has never been applied to metallic alloy systems] - MEAM is also a kind of bond order potential, 2 NN MEAM has been applied to both covalent and metallic alloy systems • Conclusion 2 NN MEAM + Qeq = Tersoff+Qeq + EAM+Qeq Paying attention to charge stability and extension to multicomponent systems, and searching for the best solution for Coulomb integral, long range potential and charge equilibraion Byeong-Joo Lee www. postech. ac. kr/~calphad

References 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60. 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. 71. 72. 73. 74. 75. 76. 77. 78. 79. 80. 81. 82. 83. 84. 85. 86. 87. 88. 89. B. J. Alder and T. E. Wainwright, ” Studies in Molecular Dynamics. I. General Method, ” J. Chem. Phys. 31, 459 (1959). L. V. Woodcock, “Isothermal Molecular Dynamics Calculations for Liquid Salts, ” Chem. Phys. Lett. 10, 257 (1971). A. Rahman, R. H. Fowler and A. H. Narten, ”Structure and Motion in Liquid Be. F 2, Li. Be. F 3, and Li. F from Molecular Dynamics Calculations, ” J. Chem. Phys. 57, 3010 (1972). L. V. Woodcock, Advances in Molten Salts Chemistry , Vol. 3 Chap. 1, pp. 1 -75, Plenum, New York (1975). L. V. Woodcock, C. A. Angell and P. Cheeseman, “Molecular Dynamics Studies of the Vitreous State: Simpl e Ionic Systems and Silica, ” J. Chem. Phys. 65, 1565 (1976). B. P. Feuston and S. H. Garofalini, “Empirical Three-Body Potential for Vitreous Silica, ” J. Chem. Phys. 89, 5818 (1988). S. Tsuneyuki, M. Tsukada, H. Aoki and Y. Matsui, “First-Principles Interatomic Potential of Silica Applied to Molecular Dynamics, ” Phys. Rev. Lett. 61, 869 (1988). B. W. H. van Beest, G. J. Kramer and R. A. van Santen, “Force Fields for Silicas and Aluminophosphates Based on Ab Initio Calculations, ” Phys. Rev. Lett. 64, 1955 (1990). C. R. A. Catlow and A. M. Stoneham, “Ionicity in Solids, ” J. Phys. C: Solid State Phys. 16, 4321 (1983). J. R. Tessman, A. H. Kahn and W. Shockley, “Electronic Polarizabilities of Ions in Crystals, ” Phys. Rev. 92, 890 (1953). Z. Jiang and R. A. Brown, “Modeling Oxygen Defects in Silicon Crystals using an Empirical Interatomic Potential, ” Chem. Engin. Sci. 49, 2991 (1994). R. Soulairol and F. Cleri, “Interface Structure of Silicon Nanocrystals Embedded in an Amorphous Silica Matrix, ” Solid State Sciences 12, 163 (2010). B. G. Dick and A. W. Overhauser, “Theory of the Dielectric Constants of Alkali Halide Crystals, ” Phys. Rev. 112, 90 (1958). G. J. Dienes, D. O. Welch, C. R. Fischer, R. D. Hatcher, O. Lazareth and M. Samberg, “Shell-Model Calculation of Some Point-Defect Properties in α-Al 2 O 3, ” Phys. Rev. B 11, 3060 (1975). G. V. Lewis and C. R. A. Catlow, “Potential Models for Ionic Oxides, ” J. Phys. C: Solid State Phys. 18, 1149 -1161 (1985). P. Vashishta, R. K. Kalia, J. P. Rino and I. Ebbsjö, “Interaction Potential for Si. O 2: A Molecular-Dynamics Study of Structural Correlations, ” Phys. Rev. B 41, 12197 (1990). P. Tangney and S. Scandolo, “An Ab Initio Parametrized Interatomic Force Field for Silica, ” J. Chem. Phys. 117, 8898 (2002). D. Herzbach, K. Binder and M. H. Müser, “Comparison of Model Potentials for Molecular-Dynamics Simulations of Silica, ” J. Chem. Phys. 123, 124711 (2005). J. D. Gale and A. L. Rohl, “The General Utility Lattice Program (GULP), ” Mol. Simul. 29, 291 (2003). J. H. Rose, F. Ferrante and J. R. Smith, “Universal Binding Energy Curves for Metals and Bimetallic Interfaces, ” Phys. Rev. Lett. 47, 675 (1981). J. R. Smith, F. Ferrante and J. H. Rose, “Universal Binding-Energy Relation in Chemisorptions, ” Phys. Rev. B 25, 1419 (1982). J. H. Rose, F. Ferrante and J. R. Smith, “Universal features of bonding in metals, ” Phys. Rev. B 28, 1835 (1983). J. H. Rose, J. R. Smith, F. Guinea and F. Ferrante, “Universal Features of the Equation of State of Metals, ” Phys. Rev. B 29, 2963 (1984). J. Tersoff, “New Empirical Model for the Structural Properties of Silicon, ” Phys. Rev. Lett. 56, 632 (1986) J. Tersoff, “New Empirical Approach for the Structure and Energy of Covalent Systems, ” Phys. Rev. B 37, 6991 (1988). J. Tersoff, “Empirical Interatomic Potential for silicon with improved elastic properties, ” Phys. Rev. B 38, 9902 (1988). J. Tersoff, “Empirical Interatomic Potential for Carbon with Applications to Amorphous Carbon, ” Phys. Rev. Lett. 61, 2879 (1988). J. Tersoff, ”Modeling Solid-State Chemistry: Interatomic Potentials for Multicomponent Systems, ” Phys. Rev. B 39, 5566 (1989). M. S. Daw and M. I. Baskes, “Semiempirical, Quantum Mechanical Calculation of Hydrogen Embrittlement in Metals, ” Phys. Rev. Lett. 50, 1285 (1983). M. S. Daw and M. I. Baskes, “Embedded-Atom Method: Derivation and Application to Impurities, Surfaces, and Other Defects in Metals, ” Phys. Rev. B 29, 6443 (1984). S. M. Foiles, M. I. Baskes and M. S. Daw, “Embedded-Atom Method Functions for the fcc Metals Cu, Ag, Au, Ni, Pd, Pt and Their Alloys, ” Phys. Rev. B 33, 7983 (1986). M. I. Baskes, J. S. Nelson and A. F. Wright, “Semiempirical Modified Embedded-Atom Potentials for Silicon and Germanium, ” Phys. Rev. B 40, 6085 (1989). M. I. Baskes, “Modified Embedded-Atom Method Potentials for Cubic Materials and Impurities, ” Phys. Rev. B 46, 2727 (1992). M. I. Baskes and R. A. Johnson, “Modified Embedded Atom Method Potentials for HCP Metals, ” Modelling Simul. Mater. Sci. Eng. 2, 147 (1994). M. I. Baskes, “Determination of Modified Embedded Atom Method Parameters for Nickel, ” Mater. Chem. Phys. 50, 152 (1997). B. -J. Lee, M. I. Baskes, “Second Nearest-Neighbor Modified Embedded-Atom Method Potential, ” Phys. Rev. B 62, 8564 (2000). B. -J. Lee, M. I. Baskes, H. Kim, Y. K. Cho, “Second Nearest-Neighbor Modified Embedded Atom Method Potentials for BCC Transition Metals, ” Phys. Rev. B 64, 184102 (2001). H. -K. Kim, W. -S. Jung, B. -J. Lee, “Modified Embedded-Atom Method Interatomic Potentials for the Nb-C, Nb-N, Fe-Nb-C and Fe-Nb-N systems, ” J. Mater. Res. 25, 1288 (2010). B. -J. Lee, “A Semi-Empirical Atomistic Approach in Materials Research, ” J. Phase Equilib. Diff. 30, 509 (2009). B. -J. Lee, W. -S. Ko, H. -K. Kim, E. -H. Kim, “Overview: The modified embedded-atom method Interatomic Potentials and recent progress in atomistic Simulations, ” CALPHAD 34, 510 (2010). F. H. Stillinger and A. Weber, “Computer simulation of local order in condensed phases of silicon, ” Phys. Rev. B 31, 5262 (1985). T. Watanabe, H. Fujiwara, H. Noguchi, T. Hoshino and I. Ohdomari, “Novel Interatomic Potential Energy Function for Si, O Mixed Systems, ” Jpn. J. Appl. Phys. 38, L 366 (1999). T. Watanabe, D. Yamasaki, K. Tatsumura and I. Ohdomari, “Improved Interatomic Potential for stressed Si, O mixed systems, ” Appl. Surf. Sci. 234, 207 (2004). Y. Umeno, T. Kitamura, K. Date, M. Hayashi, and T. Iwasaki, “Optimization of Interatomic Potential for Si/Si. O 2 system based on force matching, ” Comput. Mater. Sci. 25, 447 (2002). S. R. Billeter, A. Curioni, D. Fischer and W. Andreoni, “Ab Initio Derived Augmented Tersoff Potential for Silicon Oxynitride Compounds and Their Interfaces with Silicon, ” Phys. Rev. B 73, 155329 (2006). M. I. Baskes, “Modified Embedded Atom Method Calculations of Interfaces, ” Report number: SAND--96 -8484 C, Sandia National Laboratories, Livermore, 1996. C. -L. Kuo and P. Clancy, “Development of Atomistic MEAM Potentials for the Silicon–Oxygen–Gold Ternary System, ” Modelling Simul. Mater. Sci. Eng. 13, 1309 (2005). A. K. Rappe and W. A. Goddard III, “Charge Equilibration for Molecular Dynamics Simulations, ” J. Phys. Chem. 95, 3358 (1991). R. S. Mulliken, “A New Electroaffinity Scale; Together with Data on Valence States and on Valence Ionization Potentials and Electron Affinities, ” J. Chem. Phys. 2, 782 (1934). R. T. Sanderson, “Partial Charges on Atoms in Organic Compounds, ” Science 11, 207 (1955). L. Pauling, The Nature of the Chemical Bond , Cornell University Press, Ithaca, New York, (1960). R. P. Iczkowsky and J. L. Margrave, “Electronegativity, ” J. Am. Chem. Soc. 83, 3547 (1961). R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, “Electronegativity: The Density Functional Viewpoint, ” J. Chem. Phys. 68, 3801 (1978). P. Politzer and H. Weinstein, “Some Relations between Electronic Distribution and Electronegativity, ” J. Chem. Phys. 71, 4218 (1979). R. G. Parr and R. G. Pearson, “Absolute Hardness: Companion Parameter to Absolute Electronegativity, ” J. Am. Chem. Soc. 105, 7512 (1983). W. J. Mortier, K. van Genechten and J. Gasteiger, “Electronegativity Equalization: Application and Parametrization, ” J. Am. Chem. Soc. 107, 829 (1985). W. J. Mortier, S. K. Ghosh and S. Shankar, “Electronegativity-Equalization Method for the Calculation of Atomic Charges in Molecules”, J. Am. Chem. Soc. 108, 4315 (1986). E. Demiralp, T. Cagin and W. A. Goddard, “Morse Stretch Potential Charge Equilibrium Force Field for Ceramics: Application to the Quartz-Stishovite Phase Transition and to Silica Amorphous”, Phys. Rev. Lett. 82, 1708 (1999). V. Swamy, J. D. Gale, “Transferable Variable-Charge Interatomic Potential for Atomistic Simulation of Titanium Oxides”, Phys. Rev. B 62, 5406 (2000). F. H. Streitz and J. W. Mintmire, “Electrostatic Potentials for Metal-Oxide Surfaces and Interfaces, ” Phys. Rev. B 50, 11996 (1994). T. Campbell, R. K. Kalia, A. Nakano, P. Vashishta, S. Ogata and S. Rodgers, “Dynamics of Oxidation of Aluminum Nanoclusters using Variable Charge Molecular-Dynamics Simulations on Parallel Computers, ” Phys. Rev. Lett. 82, 4866 (1999). T. Campbell, G. Aral, S. Ogata, R. K. Kalia, A. Nakano and P. Vashishta, “Oxidation of aluminum Nanoclusters, ” Phys. Rev. B 71, 205413 (2005). N. Rosen, “Calculation of Interaction between Atoms with s-Electrons, ” Phys. Rev. 38, 255 (1931). C. C. J. Roothaan, “A Study of Two-Center Integrals Useful in Calculations on Molecular Structure. I, ” J. Chem. Phys. 19, 1445 (1951). S. W. de Leeuw, J. W. Perram and E. R. Smith, “ Simulation of Electrostatic Systems in Periodic Boundary Conditions. I. Lattice Sums and Dielectric Constants, ” Proc. R. Soc. London Ser. A 373, 27 (1980). E. R. Smith, “Electrostatic Energy in Ionic Crystals, ” Proc. R. Soc. London Ser. A 375, 475 (1981). D. E. Parry, “The Electrostatic Potential in the Surface Region of an Ionic Crystal, ” Surf. Sci. 49, 433 (1975). J. Hautman and M. L. Klein, “An Ewald Summation Method for Planar Surfaces and Interfaces, ” Mol. Phys. 75, 379 (1992). D. M. Heyes, “Surface Stress of Point Charge Lattices, ” Surf. Sci. Lett. 293, L 857 (1993). X. W. Zhou, H. N. G. Wadley, J. -S. Filhol, M. N. Neurock, “Modified Charge Transfer–Embedded Atom Method Potential for Metal/Metal Oxide Systems, ” Phys. Rev. B 69, 035402 (2004). X. W. Zhou, H. N. G. Wadley, “A Charge Transfer Ionic–Embedded Atom Method Potential for the O–Al–Ni–Co–Fe System, ” J. Phys. : Condens. Matter 17, 3619 (2005). J. R. Smith, H. Schlosser, W. Leaf, J. Ferrante and J. H. Rose, “Connection between Energy Relations of Solids and Molecules, ” Phys. Rev. A 39, 514 (1989). J. Ferrante, H. Schlosser and J. H. Rose, “Global expression for representing diatomic Potential-energy curves, ” Phys. Rev. A 43, 3487 (1991). I. Lazic, M. Ernst, B. Thijsse, “Atomistic Simulation Methods for Studying Self Healing Mechanisms in Al/Al 2 O 3, ” Proceedings of the First International Conference on Self Healing Materials, 18 -20 April 2007, Noordwijk aan Zee, The Netherlands R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, Mc. Graw-Hill, New York, 1981. A. Yasukawa, “Using an Extended Tersoff Interatomic Potential to Analyze the Static-Fatigue Strength of Si. O 2 under Atmospheric Influence, ” JSME Int. J. , Ser. A 39, 313 (1996). T. Iwasaki and H. Miura, “Molecular dynamics analysis of adhesion strength of interfaces between thin films, ” J. Mater. Res. 16, 1789 (2001). A. Yasukawa, in Japan Society of Mechanical Engineers , p. 71, Sept. 19, 2003, Hitachi City, Ibaraki, Japan. A. Yasukawa, “Atomistic Simulation of Environment-Assisted Crack Propagation Behavior of Si. O 2, ” J. Solid Mech. Mater. Engin. 4, 599 (2010). J. Yu, S. B. Sinnott, S. R. Phillpot, “Charge optimized many-body Potential for the Si/Si. O 2 system, ” Phys. Rev. B 75, 085311 (2007) T. -R. Shan, B. D. Devine, M. Hawkins, A. Asthagiri, S. R. Phillpot and S. B. Sinnott, “Second-Generation Charge-Optimized Many-Body Potential for Si/Si. O 2 and amorphous Silica, ” Phys. Rev. B 82, 235302 (2010). D. Wolf, P. Keblinski, S. R. Phillpot, and J. Eggebrecht, “Exact Method for the Simulation of Coulombic Systems by Spherically Truncated, Pairwise r -1 Summation, ” J. Chem. Phys. 110, 8254 (1999). T. -R. Shan, B. D. Devine, T. W. Kemper, S. B. Sinnott and S. R. Phillpot, “Charge Optimized Many-Body Potential for the Hafnium/Hafnium Oxide System, ” Phys. Rev. B 81, 125328 (2010). B. D. Devine, T. -R. Shan, S. B. Sinnott, and S. R. Phillpot, “Charge Optimized Many-Body Potential for the Copper/Copper Oxide System, ” 2011 (unpublished) A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard III, “Reax. FF: A Reactive Force Field for Hydrocarbons, ” J. Phys. Chem. A 105, 9396 (2001). A. C. T. van Duin, A. Strachan, S. Stewman, Q. Zhang, X. Xu and W. A. Goddard III, “Reax. FFSi. O Reactive Force Field for Silicon and Silicon Oxide Systems, ” J. Phys. Chem. A 107, 3803 (2003). D. W. Brenner, ”Empirical Potential for Hydrocarbons for Use in Simulating the Chemical Vapor Deposition of Diamond Films, ” Phys. Rev. B 42, 9458 (1990). S. J. Stuart, A. B. Tutein and J. A. Harrison, “A reactive Potential for Hydrocarbons with Intermolecular Interactions, ” J. Chem. Phys. 112, 6472 (2000). D. W Brenner, O. A Shenderova, J. A Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, “A second-generation reactive empirical bond order (REBO) Potential energy expression for Hydrocarbons, ” J. Phys. : Condens. Matter 14, 783 (2002). Byeong-Joo Lee www. postech. ac. kr/~calphad

Atomistic Simulations - MEAM & Applications Byeong-Joo Lee Dept. of MSE Pohang University of Science and Technology (POSTECH) calphad@postech. ac. kr Byeong-Joo Lee www. postech. ac. kr/~calphad

Semi-Empirical Atomic Potentials - Historical Background • Pair Potentials (~1980) ▷ Elastic Constants are NOT correctly reproduced • Many Body Potentials (1980's) ▷ Embedded Atom Method (EAM: 1983) ▷ Finnis and Sinclair Potential (1984) ▷ Glue Model (1986) ▷ Equilivalent-Crystal Model (1987) Byeong-Joo Lee www. postech. ac. kr/~calphad

Semi-Empirical Atomic Potentials – History of Development • EAM Potentials (1983, M. S. Daw and M. I. Baskes) ▷ Successful mainly for FCC elements - many other many-body potentials show similar performance • 1 NN MEAM Potentials (1987, 1992, M. I. Baskes) ▷ Show Possibility for description of various structures - important to be able to describe multi-component system • 2 NN MEAM Potentials (2000, B. -J. Lee & M. I. Baskes) ▷ Applicable to fcc, bcc, hcp, diamond structures and their alloys Byeong-Joo Lee www. postech. ac. kr/~calphad

EAM/MEAM – General E F : Total Potential Energy : Embedding Energy : Electron Density (Considering Bonding Directionality) : Pair Interaction Energy Byeong-Joo Lee www. postech. ac. kr/~calphad

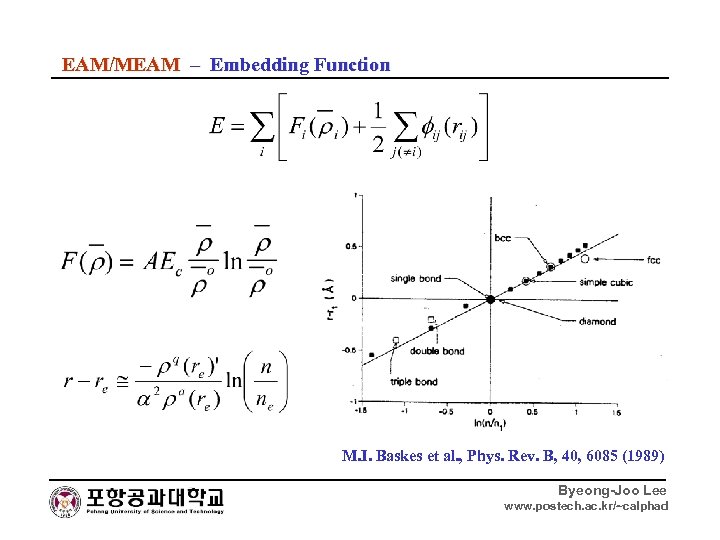
EAM/MEAM – Embedding Function M. I. Baskes et al. , Phys. Rev. B, 40, 6085 (1989) Byeong-Joo Lee www. postech. ac. kr/~calphad

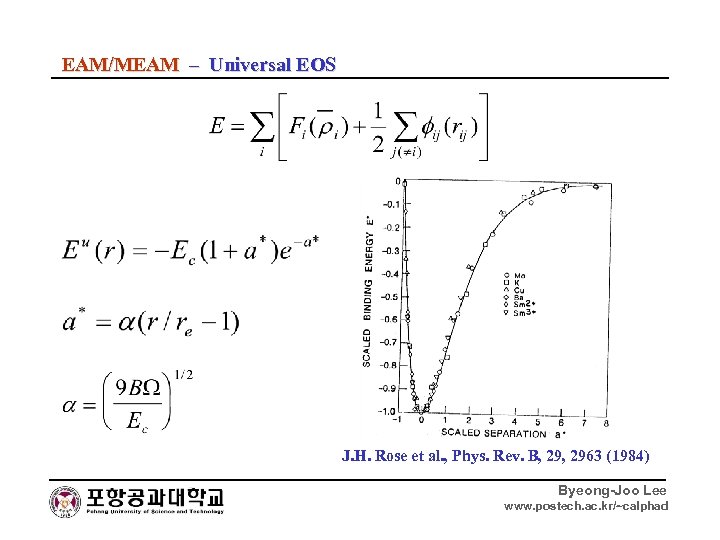
EAM/MEAM – Universal EOS J. H. Rose et al. , Phys. Rev. B, 2963 (1984) Byeong-Joo Lee www. postech. ac. kr/~calphad

EAM/MEAM – Electron Density for EAM Byeong-Joo Lee www. postech. ac. kr/~calphad

EAM/MEAM – Electron Density for MEAM + Angular contribution Byeong-Joo Lee www. postech. ac. kr/~calphad

EAM/MEAM – Electron Density for MEAM + Angular contribution with ti(0) =1 Byeong-Joo Lee www. postech. ac. kr/~calphad

EAM/MEAM – 1 st Nearest Neighbor MEAM Byeong-Joo Lee www. postech. ac. kr/~calphad

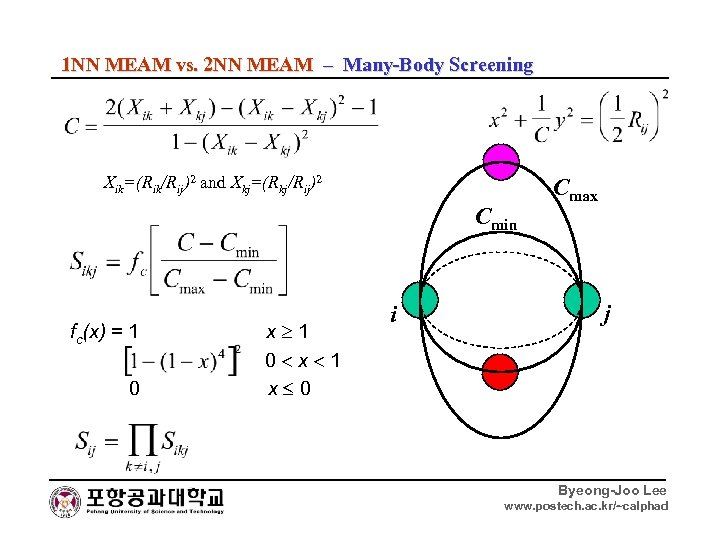
1 NN MEAM vs. 2 NN MEAM – Many-Body Screening Xik=(Rik/Rij)2 and Xkj=(Rkj/Rij)2 Cmin fc(x) = 1 x 1 0 x 0 i Cmax j Byeong-Joo Lee www. postech. ac. kr/~calphad

2 NN MEAM – Computation of pair-wise potential Byeong-Joo Lee www. postech. ac. kr/~calphad

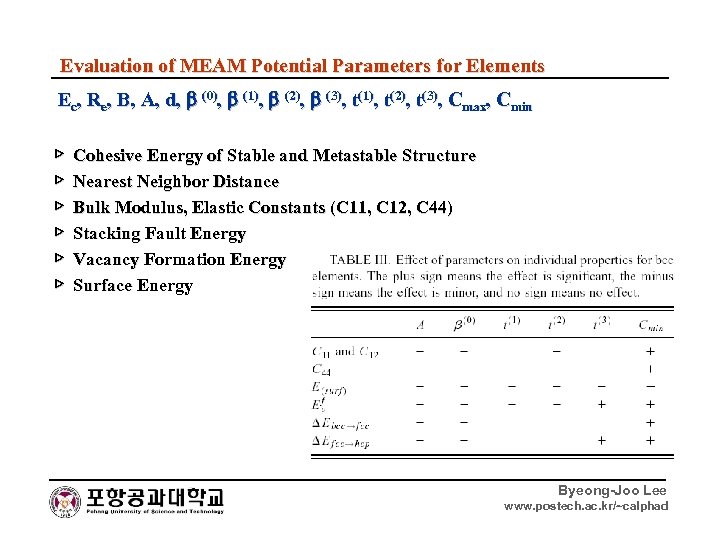
Evaluation of MEAM Potential Parameters for Elements Ec, Re, B, A, d, (0), (1), (2), (3), t(1), t(2), t(3), Cmax, Cmin ▷ Cohesive Energy of Stable and Metastable Structure ▷ Nearest Neighbor Distance ▷ Bulk Modulus, Elastic Constants (C 11, C 12, C 44) ▷ Stacking Fault Energy ▷ Vacancy Formation Energy ▷ Surface Energy Byeong-Joo Lee www. postech. ac. kr/~calphad

Semi-Empirical Atomic Potentials - Performance • Elastic Constants ▷ B, C 11, C 12, C 44, . . . • Defect Energy ▷ Surface Energy ▷ Heat of Vacancy Formation, … • Structural Energy ▷ Energy and Lattice Parameters in Different Structures • Thermal Property ▷ Specific Heat ▷ Thermal Expansion Coefficient ▷ Melting Temperature, . . . Byeong-Joo Lee www. postech. ac. kr/~calphad

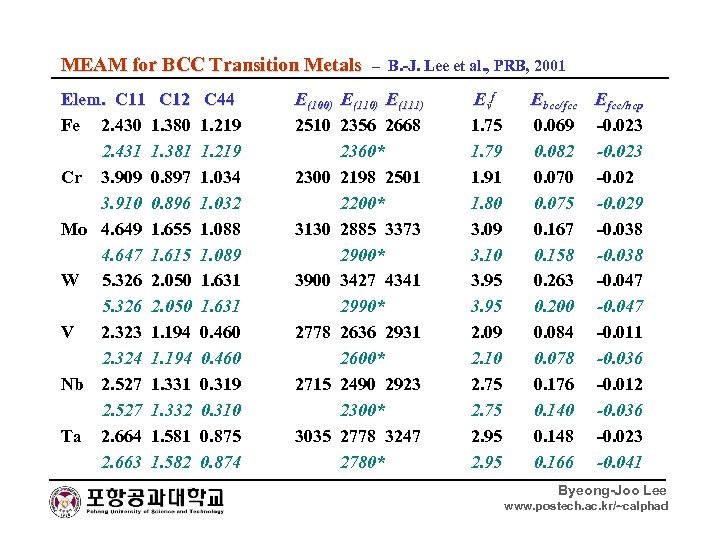
MEAM for BCC Transition Metals – B. -J. Lee et al. , PRB, 2001 Elem. C 11 C 12 C 44 E(100) E(111) Evf Ebcc/fcc Efcc/hcp Fe 2. 430 1. 380 1. 219 2510 2356 2668 1. 75 0. 069 -0. 023 2. 431 1. 381 1. 219 2360* 1. 79 0. 082 -0. 023 Cr 3. 909 0. 897 1. 034 2300 2198 2501 1. 91 0. 070 -0. 02 3. 910 0. 896 1. 032 2200* 1. 80 0. 075 -0. 029 Mo 4. 649 1. 655 1. 088 3130 2885 3373 3. 09 0. 167 -0. 038 4. 647 1. 615 1. 089 2900* 3. 10 0. 158 -0. 038 W 5. 326 2. 050 1. 631 3900 3427 4341 3. 95 0. 263 -0. 047 5. 326 2. 050 1. 631 2990* 3. 95 0. 200 -0. 047 V 2. 323 1. 194 0. 460 2778 2636 2931 2. 09 0. 084 -0. 011 2. 324 1. 194 0. 460 2600* 2. 10 0. 078 -0. 036 Nb 2. 527 1. 331 0. 319 2715 2490 2923 2. 75 0. 176 -0. 012 2. 527 1. 332 0. 310 2300* 2. 75 0. 140 -0. 036 Ta 2. 664 1. 581 0. 875 3035 2778 3247 2. 95 0. 148 -0. 023 2. 663 1. 582 0. 874 2780* 2. 95 0. 166 -0. 041 Byeong-Joo Lee www. postech. ac. kr/~calphad

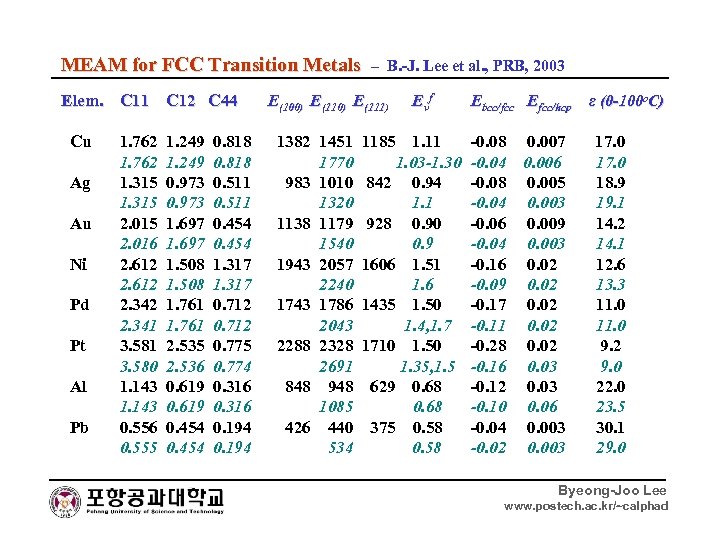
MEAM for FCC Transition Metals – B. -J. Lee et al. , PRB, 2003 Elem. C 11 C 12 C 44 E(100) E(111) Evf Ebcc/fcc Efcc/hcp ε (0 -100 o. C) Cu 1. 762 1. 249 0. 818 1382 1451 1185 1. 11 -0. 08 0. 007 17. 0 1. 762 1. 249 0. 818 1770 1. 03 -1. 30 -0. 04 0. 006 17. 0 Ag 1. 315 0. 973 0. 511 983 1010 842 0. 94 -0. 08 0. 005 18. 9 1. 315 0. 973 0. 511 1320 1. 1 -0. 04 0. 003 19. 1 Au 2. 015 1. 697 0. 454 1138 1179 928 0. 90 -0. 06 0. 009 14. 2 2. 016 1. 697 0. 454 1540 0. 9 -0. 04 0. 003 14. 1 Ni 2. 612 1. 508 1. 317 1943 2057 1606 1. 51 -0. 16 0. 02 12. 6 2. 612 1. 508 1. 317 2240 1. 6 -0. 09 0. 02 13. 3 Pd 2. 342 1. 761 0. 712 1743 1786 1435 1. 50 -0. 17 0. 02 11. 0 2. 341 1. 761 0. 712 2043 1. 4, 1. 7 -0. 11 0. 02 11. 0 Pt 3. 581 2. 535 0. 775 2288 2328 1710 1. 50 -0. 28 0. 02 9. 2 3. 580 2. 536 0. 774 2691 1. 35, 1. 5 -0. 16 0. 03 9. 0 Al 1. 143 0. 619 0. 316 848 948 629 0. 68 -0. 12 0. 03 22. 0 1. 143 0. 619 0. 316 1085 0. 68 -0. 10 0. 06 23. 5 Pb 0. 556 0. 454 0. 194 426 440 375 0. 58 -0. 04 0. 003 30. 1 0. 555 0. 454 0. 194 534 0. 58 -0. 02 0. 003 29. 0 Byeong-Joo Lee www. postech. ac. kr/~calphad

MEAM for Silicon C 11 C 12 C 44 E(100) E(111) Evf Edia/fcc Edia/hcp Edia/bcc ε (1012 dyne/cm 2) (erg/cm 2) (e. V) (0 -100 o. C) 1. 67 0. 65 0. 80 2631 1766 1442 3. 67 0. 55 0. 52 2. 65 1. 68 0. 65 0. 80 1135* 3. 3 -4. 3 0. 57 0. 55 0. 53 2. 69 Byeong-Joo Lee www. postech. ac. kr/~calphad

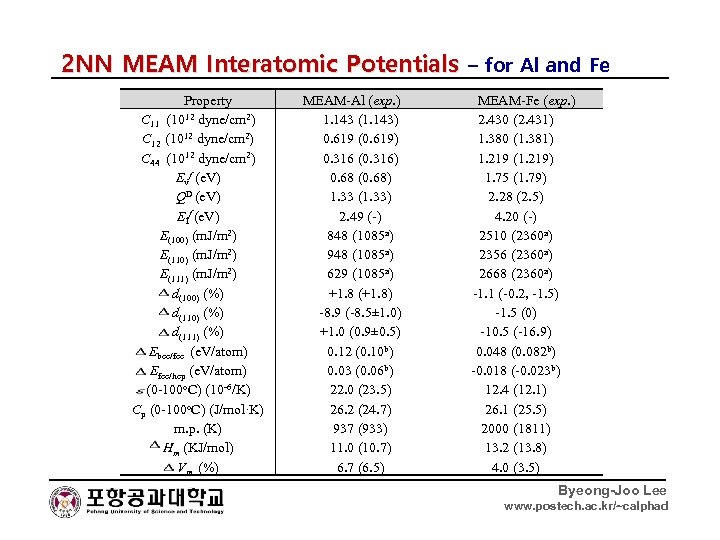
2 NN MEAM Interatomic Potentials – for Al and Fe Property C 11 (1012 dyne/cm 2) C 12 (1012 dyne/cm 2) C 44 (1012 dyne/cm 2) Evf (e. V) QD (e. V) EIf (e. V) E(100) (m. J/m 2) E(111) (m. J/m 2) d(100) (%) d(111) (%) Ebcc/fcc (e. V/atom) Efcc/hcp (e. V/atom) (0 -100 o. C) (10 -6/K) Cp (0 -100 o. C) (J/mol·K) m. p. (K) Hm (KJ/mol) Vm (%) MEAM-Al (exp. ) 1. 143 (1. 143) 0. 619 (0. 619) 0. 316 (0. 316) 0. 68 (0. 68) 1. 33 (1. 33) 2. 49 (-) 848 (1085 a) 948 (1085 a) 629 (1085 a) +1. 8 (+1. 8) -8. 9 (-8. 5± 1. 0) +1. 0 (0. 9± 0. 5) 0. 12 (0. 10 b) 0. 03 (0. 06 b) 22. 0 (23. 5) 26. 2 (24. 7) 937 (933) 11. 0 (10. 7) 6. 7 (6. 5) MEAM-Fe (exp. ) 2. 430 (2. 431) 1. 380 (1. 381) 1. 219 (1. 219) 1. 75 (1. 79) 2. 28 (2. 5) 4. 20 (-) 2510 (2360 a) 2356 (2360 a) 2668 (2360 a) -1. 1 (-0. 2, -1. 5) -1. 5 (0) -10. 5 (-16. 9) 0. 048 (0. 082 b) -0. 018 (-0. 023 b) 12. 4 (12. 1) 26. 1 (25. 5) 2000 (1811) 13. 2 (13. 8) 4. 0 (3. 5) Byeong-Joo Lee www. postech. ac. kr/~calphad

2 NN MEAM – 2 NNMEAM for Alloy Systems Byeong-Joo Lee www. postech. ac. kr/~calphad

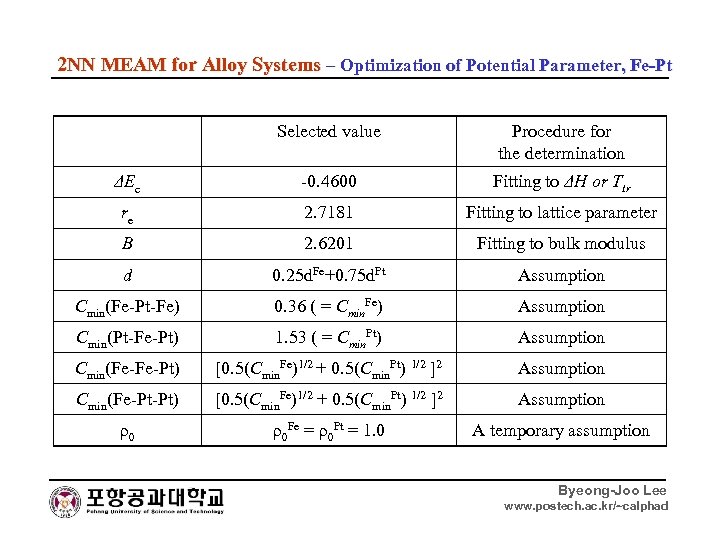
2 NN MEAM for Alloy Systems – Optimization of Potential Parameter, Fe-Pt Selected value Procedure for the determination ΔEc -0. 4600 Fitting to ΔH or Ttr re 2. 7181 Fitting to lattice parameter B 2. 6201 Fitting to bulk modulus d 0. 25 d. Fe+0. 75 d. Pt Assumption Cmin(Fe-Pt-Fe) 0. 36 ( = Cmin. Fe) Assumption Cmin(Pt-Fe-Pt) 1. 53 ( = Cmin. Pt) Assumption Cmin(Fe-Fe-Pt) [0. 5(Cmin. Fe)1/2 + 0. 5(Cmin. Pt) 1/2 ]2 Assumption Cmin(Fe-Pt-Pt) [0. 5(Cmin. Fe)1/2 + 0. 5(Cmin. Pt) 1/2 ]2 Assumption ρ0 ρ0 Fe = ρ0 Pt = 1. 0 A temporary assumption Byeong-Joo Lee www. postech. ac. kr/~calphad

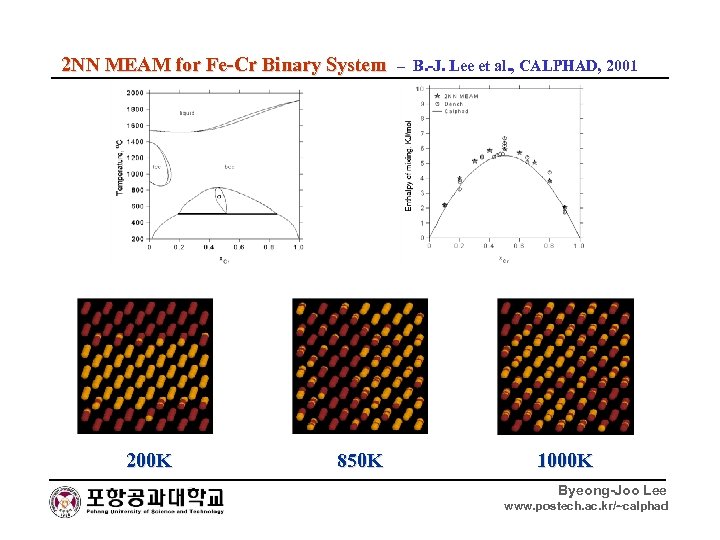
2 NN MEAM for Fe-Cr Binary System – B. -J. Lee et al. , CALPHAD, 2001 200 K 850 K 1000 K Byeong-Joo Lee www. postech. ac. kr/~calphad

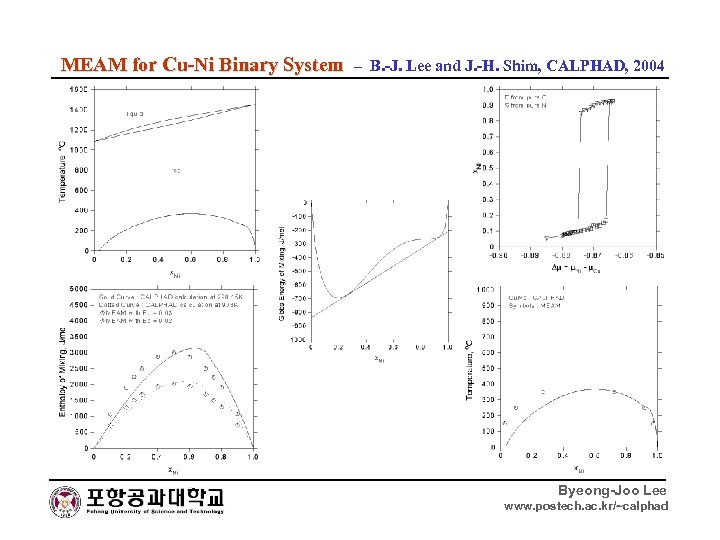
MEAM for Cu-Ni Binary System – B. -J. Lee and J. -H. Shim, CALPHAD, 2004 Byeong-Joo Lee www. postech. ac. kr/~calphad

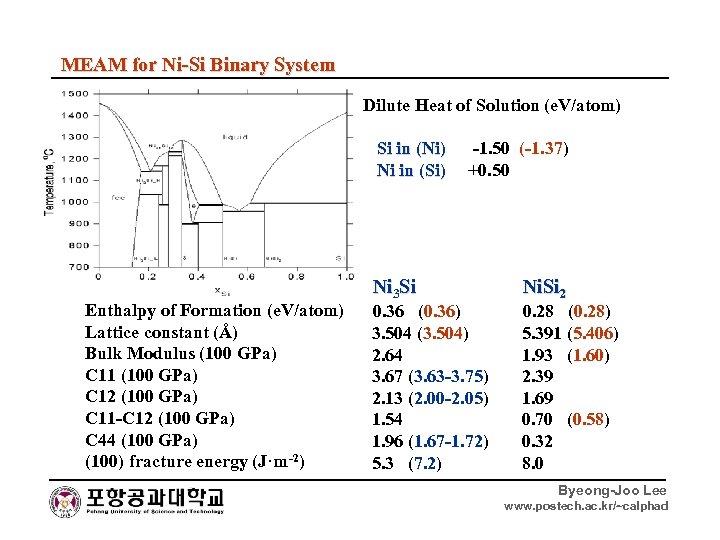
MEAM for Ni-Si Binary System Dilute Heat of Solution (e. V/atom) Si in (Ni) -1. 50 (-1. 37) Si in (Ni) Ni in (Si) +0. 50 Ni in (Si) Enthalpy of Formation (e. V/atom) Lattice constant (Å) Bulk Modulus (100 GPa) C 11 (100 GPa) C 12 (100 GPa) C 11 -C 12 (100 GPa) C 44 (100 GPa) (100) fracture energy (J·m-2) Ni 3 Si 0. 36 (0. 36) Ni. Si 2 0. 28 (0. 28) 3. 504 (3. 504) 2. 64 3. 67 (3. 63 -3. 75) 2. 13 (2. 00 -2. 05) 1. 54 1. 96 (1. 67 -1. 72) 5. 3 (7. 2) 5. 391 (5. 406) 1. 93 (1. 60) 2. 39 1. 69 0. 70 (0. 58) 0. 32 8. 0 Byeong-Joo Lee www. postech. ac. kr/~calphad

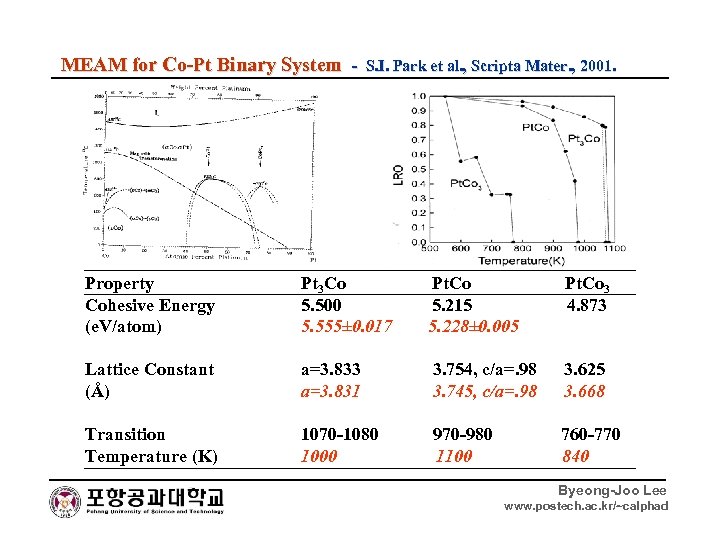
MEAM for Co-Pt Binary System - S. I. Park et al. , Scripta Mater. , 2001. Property Pt 3 Co Pt. Co 3 Cohesive Energy 5. 500 5. 215 4. 873 (e. V/atom) 5. 555± 0. 017 5. 228± 0. 005 Lattice Constant a=3. 833 3. 754, c/a=. 98 3. 625 (Å) a=3. 831 3. 745, c/a=. 98 3. 668 Transition 1070 -1080 970 -980 760 -770 Temperature (K) 1000 1100 840 Byeong-Joo Lee www. postech. ac. kr/~calphad

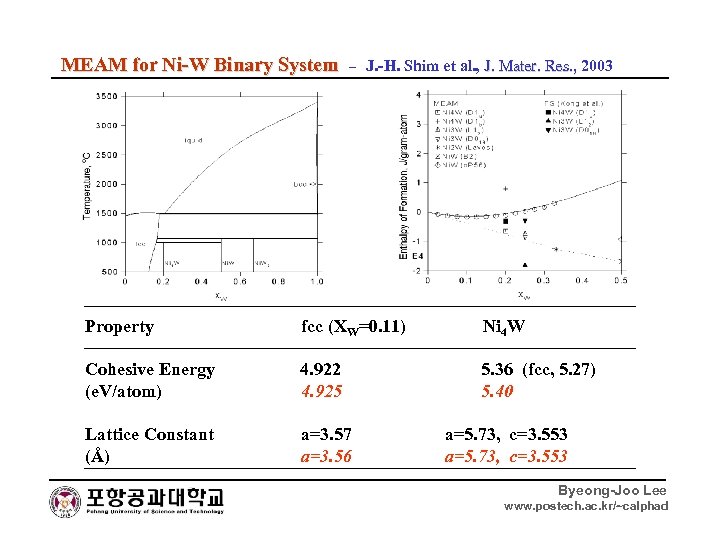
MEAM for Ni-W Binary System – J. -H. Shim et al. , J. Mater. Res. , 2003 Res. , Property fcc (XW=0. 11) Ni 4 W Cohesive Energy 4. 922 5. 36 (fcc, 5. 27) (e. V/atom) 4. 925 5. 40 Lattice Constant a=3. 57 (Å) a=3. 56 a=5. 73, c=3. 553 Byeong-Joo Lee www. postech. ac. kr/~calphad

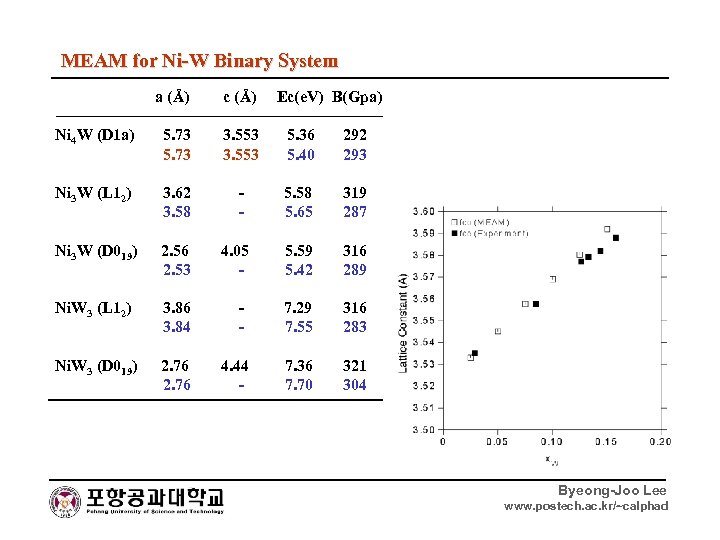
MEAM for Ni-W Binary System a (Å) c (Å) Ec(e. V) B(Gpa) Ni 4 W (D 1 a) 5. 73 3. 553 5. 36 5. 73 3. 553 5. 40 292 293 Ni 3 W (L 12) 3. 62 - 5. 58 3. 58 - 5. 65 319 287 Ni 3 W (D 019) 2. 56 4. 05 5. 59 2. 53 - 5. 42 316 289 Ni. W 3 (L 12) 3. 86 - 7. 29 3. 84 - 7. 55 316 283 Ni. W 3 (D 019) 2. 76 4. 44 7. 36 2. 76 - 7. 70 321 304 Byeong-Joo Lee www. postech. ac. kr/~calphad

Empirical Potentials for Multicomponent Systems • Fe ▷ Finnis-Sinclair – modified by Calder and Bacon (1993) • Fe-Cu ▷ Osetsky (1996) • Fe: Pair-Potential, Osetsky (1995) • Cu: Pair-Potential, Osetsky (1995) ▷ Ackland, Bacon, Calder (1997) • Fe: F-S type, Ackland et al. (1997) • Cu: F-S type, Ackland, Tichy, Vitek, Finnis (1987) ▷ Ludwig, Farkas, . . (1998) → C. S. Becquart, C. Domain, • Fe: EAM, Simonelli, Pasianot, Savino (1993) • Cu: EAM, Voter (1993) Byeong-Joo Lee www. postech. ac. kr/~calphad

History of Fe-C Alloy Potential • R. A. Johnson, G. J. Dienes, A. C. Damask, Acta Metall. 12, 1215 (1964). • metal-metal: pairwise interaction • metal-carbon: pairwise interaction • can consider only one carbon atoms, not applicable to carbides • V. Rosato, Acta Metall. 37, 2759 (1989). • metal-metal: many-body interaction • metal-carbon: pairwise interaction • can consider only one carbon atoms, not applicable to carbides • M. Ruda, D. Farkas, and J. Abriata, Scr. Mater. 46, 349 (2002). • metal-metal: many-body interaction (EAM) • metal-carbon: many-body interaction (EAM) • carbon-carbon: many-body interaction (EAM) • unacceptable results Byeong-Joo Lee www. postech. ac. kr/~calphad

History of Carbon Potential • J. Tersoff, Phys. Rev. Lett. 61 (1988) 2879. • • • structural properties (cohesive energies, bond lengths of various polytypes) elastic properties (elastic constants of diamond) point defect properties (vacancy formation and migration energies, and interstitial formation energies in diamond and graphite) applicable to monolayer of graphite applicable to only Diamond Structures (C, Si, Ge, Si. C, …) • • • D. W. Brenner, Phys. Rev. B 42 (1990) 9458; J. Phys. : Condens. Matter 14 (2002) 783. • • • modification of Tersoff formalism to better describe hydrocarbons M. I. Heggie, J. Phys. : Condens. Matter 3 (1991) 3065. E. P. Andribet et al. , Nucl. Instr. & Meth. in Phys. Res. B 115 (1996) 501. • • To better describe graphite structure than Tersoff Only for graphite Byeong-Joo Lee www. postech. ac. kr/~calphad

(2 NN) MEAM for Fe, C, N, Fe-C and Fe-N systems • Fe, Cr, Mo, W, V, Nb, Ta Second Nearest-Neighbor Modified Embedded Atom Method Potentials for BCC Transition Metals Byeong-Joo Lee, M. I. Baskes, Hanchul Kim and Yang Koo Cho, Phys. Rev. B. 64, 184102 (2001). • C A Modified Embedded Atom Method Interatomic Potential for Carbon Byeong-Joo Lee and Jin Wook Lee, CALPHAD 29, 7 -16 (2005). • Fe-C A Modified Embedded Atom Method Interatomic Potential for the Fe-C System Byeong-Joo Lee, Acta Materialia 54, 701 -711 (2006). • Fe-N A Modified Embedded-Atom Method Interatomic Potential for the Fe-N System: A Comparative Study with the Fe-C system Byeong-Joo Lee, T-H Lee and S-J Kim, Acta Materialia 4597 -4607 (2006). Byeong-Joo Lee www. postech. ac. kr/~calphad

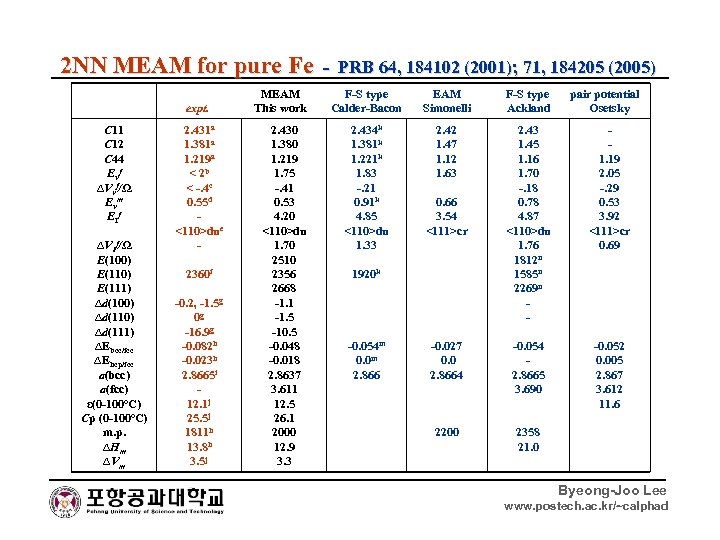
2 NN MEAM for pure Fe - PRB 64, 184102 (2001); 71, 184205 (2005) MEAM F-S type EAM F-S type pair potential expt. This work Calder-Bacon Simonelli Ackland Osetsky C 11 C 12 C 44 Ev f ∆Vvf/Ω Ev m EI f ∆VIf/Ω E(100) E(111) ∆d(100) ∆d(111) ∆Ebcc/fcc ∆Ehcp/fcc a(bcc) a(fcc) ε(0 -100 o. C) Cp (0 -100 o. C) m. p. ∆Hm ∆Vm 2. 431 a 1. 381 a 1. 219 a < 2 b < -. 4 c 0. 55 d <110>due 2360 f -0. 2, -1. 5 g 0 g -16. 9 g -0. 082 h -0. 023 h 2. 8665 i 12. 1 j 25. 5 j 1811 h 13. 8 h 3. 5 j 2. 430 1. 380 1. 219 1. 75 -. 41 0. 53 4. 20 <110>du 1. 70 2510 2356 2668 -1. 1 -1. 5 -10. 5 -0. 048 -0. 018 2. 8637 3. 611 12. 5 26. 1 2000 12. 9 3. 3 2. 434 k 1. 381 k 1. 221 k 1. 83 -. 21 0. 91 k 4. 85 <110>du 1. 33 2. 42 1. 47 1. 12 1. 63 2. 43 1. 45 1. 16 1. 70 -. 18 0. 78 4. 87 <110>du 1. 76 1812 n 1585 n 2269 n - 1. 19 2. 05 -. 29 0. 53 3. 92 <111>cr 0. 69 -0. 027 0. 0 2. 8664 -0. 054 2. 8665 3. 690 -0. 052 0. 005 2. 867 3. 612 11. 6 2200 2358 21. 0 0. 66 3. 54 <111>cr 1920 k -0. 054 m 0. 0 m 2. 866 Byeong-Joo Lee www. postech. ac. kr/~calphad

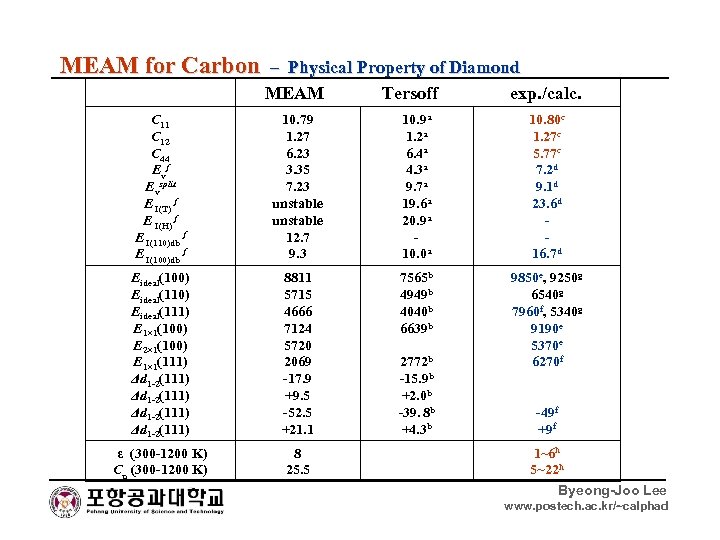
MEAM for Carbon – Physical Property of Diamond MEAM Tersoff exp. /calc. C 11 C 12 C 44 E vf Evsplit E I(T) f E I(H) f E I(110)db f E I(100)db f 10. 79 1. 27 6. 23 3. 35 7. 23 unstable 12. 7 9. 3 10. 9 a 1. 2 a 6. 4 a 4. 3 a 9. 7 a 19. 6 a 20. 9 a 10. 0 a 10. 80 c 1. 27 c 5. 77 c 7. 2 d 9. 1 d 23. 6 d 16. 7 d Eideal(100) Eideal(111) E 1× 1(100) E 2× 1(100) E 1× 1(111) Δd 1 -2(111) 8811 5715 4666 7124 5720 2069 -17. 9 +9. 5 -52. 5 +21. 1 7565 b 4949 b 4040 b 6639 b 9850 e, 9250 g 6540 g 7960 f, 5340 g 9190 e 5370 e 6270 f ε (300 -1200 K) Cp (300 -1200 K) 8 25. 5 2772 b -15. 9 b +2. 0 b -39. 8 b +4. 3 b -49 f +9 f 1~6 h 5~22 h Byeong-Joo Lee www. postech. ac. kr/~calphad

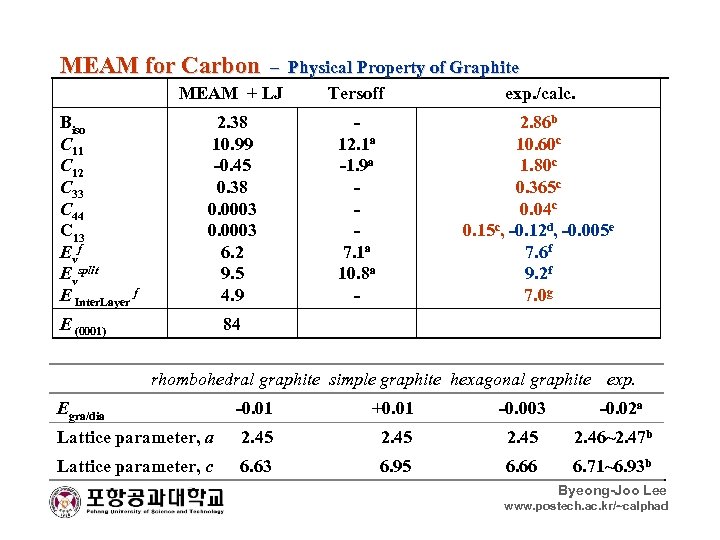
MEAM for Carbon – Physical Property of Graphite MEAM + LJ Tersoff exp. /calc. Biso C 11 C 12 C 33 C 44 C 13 Ev f Evsplit E Inter. Layer f E (0001) 2. 38 10. 99 -0. 45 0. 38 0. 0003 6. 2 9. 5 4. 9 12. 1 a -1. 9 a 7. 1 a 10. 8 a - 2. 86 b 10. 60 c 1. 80 c 0. 365 c 0. 04 c 0. 15 c, -0. 12 d, -0. 005 e 7. 6 f 9. 2 f 7. 0 g 84 rhombohedral graphite simple graphite hexagonal graphite exp. Egra/dia -0. 01 +0. 01 -0. 003 -0. 02 a Lattice parameter, a 2. 45 2. 45 2. 46~2. 47 b Lattice parameter, c 6. 63 6. 95 6. 66 6. 71~6. 93 b Byeong-Joo Lee www. postech. ac. kr/~calphad

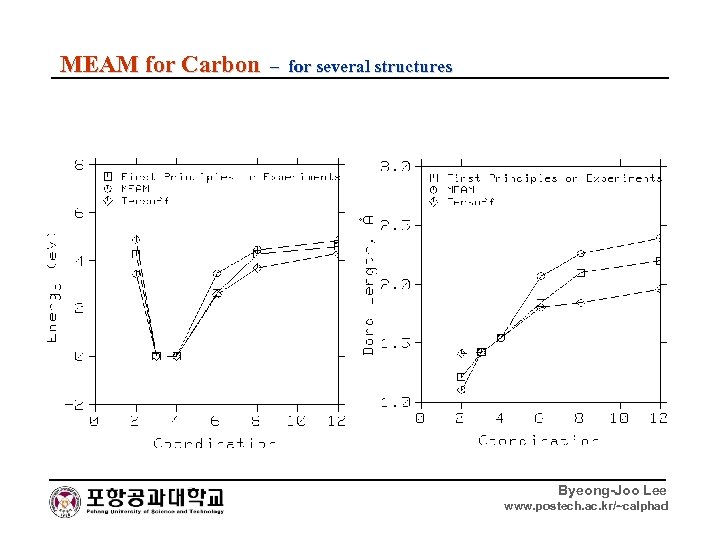
MEAM for Carbon – for several structures Byeong-Joo Lee www. postech. ac. kr/~calphad

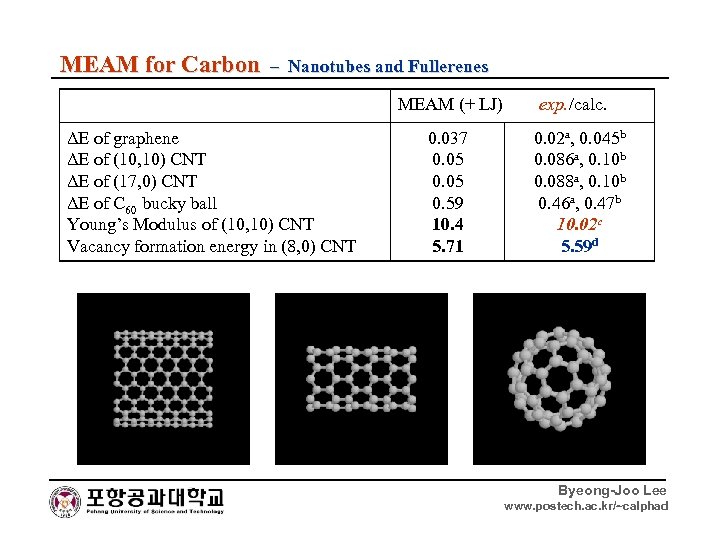
MEAM for Carbon – Nanotubes and Fullerenes MEAM (+ LJ) ΔE of graphene ΔE of (10, 10) CNT ΔE of (17, 0) CNT ΔE of C 60 bucky ball Young’s Modulus of (10, 10) CNT Vacancy formation energy in (8, 0) CNT 0. 037 0. 05 0. 59 10. 4 5. 71 exp. /calc. 0. 02 a, 0. 045 b 0. 086 a, 0. 10 b 0. 088 a, 0. 10 b 0. 46 a, 0. 47 b 10. 02 c 5. 59 d Byeong-Joo Lee www. postech. ac. kr/~calphad

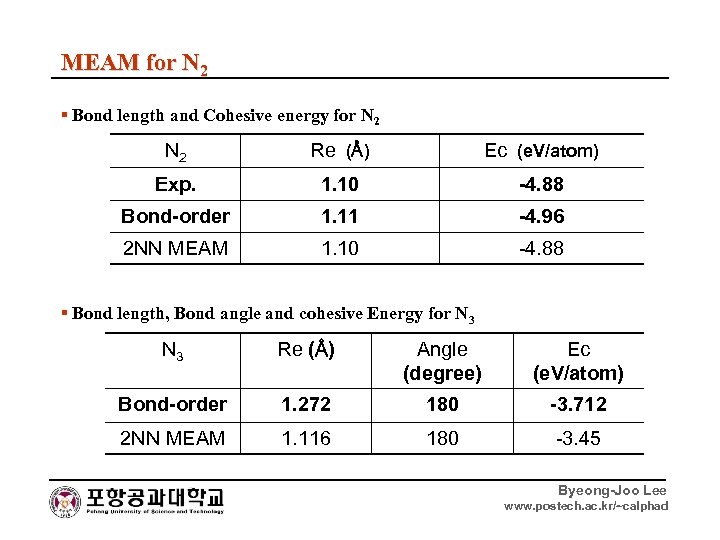
MEAM for N 2 ▪ Bond length and Cohesive energy for N 2 Re (Å) Ec (e. V/atom) Exp. 1. 10 -4. 88 Bond-order 1. 11 -4. 96 2 NN MEAM 1. 10 -4. 88 ▪ Bond length, Bond angle and cohesive Energy for N 3 Re (Å) Angle (degree) Ec (e. V/atom) Bond-order 1. 272 180 -3. 712 2 NN MEAM 1. 116 180 -3. 45 Byeong-Joo Lee www. postech. ac. kr/~calphad

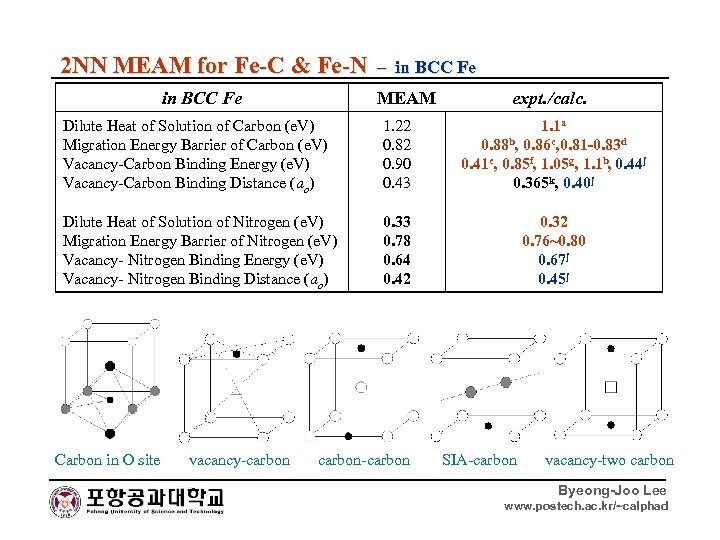
2 NN MEAM for Fe-C & Fe-N – in BCC Fe MEAM expt. /calc. Dilute Heat of Solution of Carbon (e. V) Migration Energy Barrier of Carbon (e. V) Vacancy-Carbon Binding Energy (e. V) Vacancy-Carbon Binding Distance (ao) 1. 22 0. 82 0. 90 0. 43 1. 1 a 0. 88 b, 0. 86 c, 0. 81 -0. 83 d 0. 41 e, 0. 85 f, 1. 05 g, 1. 1 b, 0. 44 j 0. 365 k, 0. 40 j Dilute Heat of Solution of Nitrogen (e. V) Migration Energy Barrier of Nitrogen (e. V) Vacancy- Nitrogen Binding Energy (e. V) Vacancy- Nitrogen Binding Distance (ao) 0. 33 0. 78 0. 64 0. 42 0. 32 0. 76~0. 80 0. 67 j 0. 45 j Carbon in O site vacancy-carbon-carbon SIA-carbon vacancy-two carbon Byeong-Joo Lee www. postech. ac. kr/~calphad

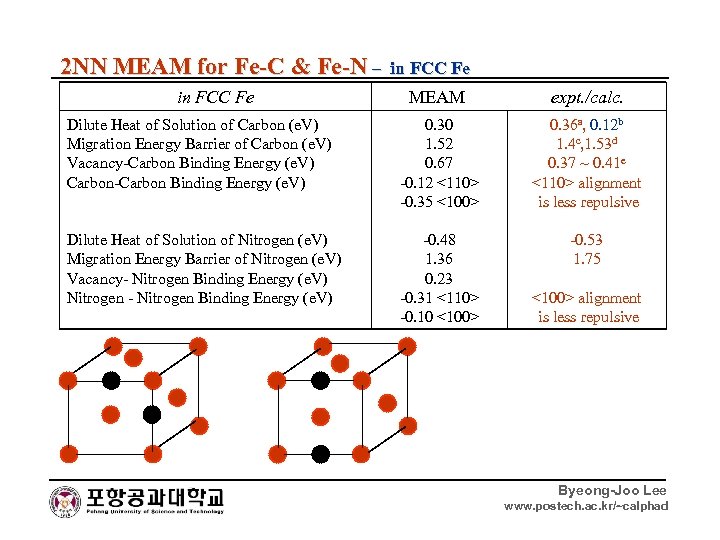
2 NN MEAM for Fe-C & Fe-N – in FCC Fe MEAM expt. /calc. Dilute Heat of Solution of Carbon (e. V) Migration Energy Barrier of Carbon (e. V) Vacancy-Carbon Binding Energy (e. V) Carbon-Carbon Binding Energy (e. V) 0. 30 1. 52 0. 67 -0. 12 <110> -0. 35 <100> 0. 36 a, 0. 12 b 1. 4 c, 1. 53 d 0. 37 ~ 0. 41 e <110> alignment is less repulsive Dilute Heat of Solution of Nitrogen (e. V) Migration Energy Barrier of Nitrogen (e. V) Vacancy- Nitrogen Binding Energy (e. V) Nitrogen - Nitrogen Binding Energy (e. V) -0. 48 1. 36 0. 23 -0. 31 <110> -0. 10 <100> -0. 53 1. 75 <100> alignment is less repulsive Byeong-Joo Lee www. postech. ac. kr/~calphad

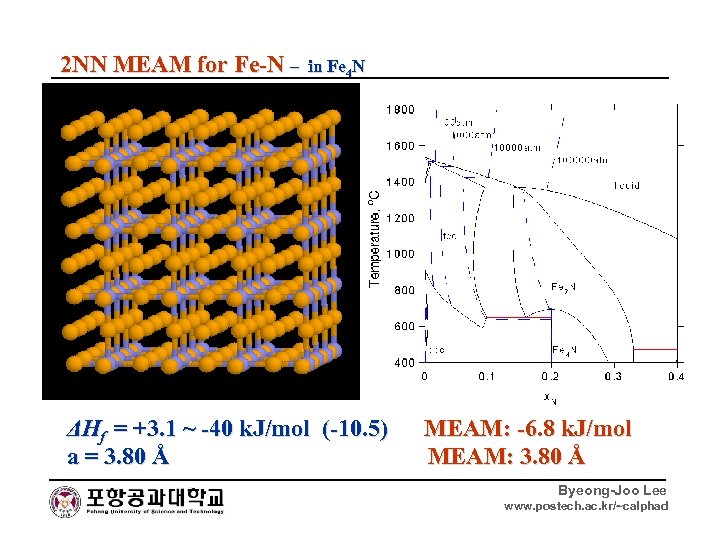
2 NN MEAM for Fe-N – in Fe 4 N ΔHf = +3. 1 ~ -40 k. J/mol (-10. 5) MEAM: -6. 8 k. J/mol a = 3. 80 Å MEAM: 3. 80 Å Byeong-Joo Lee www. postech. ac. kr/~calphad

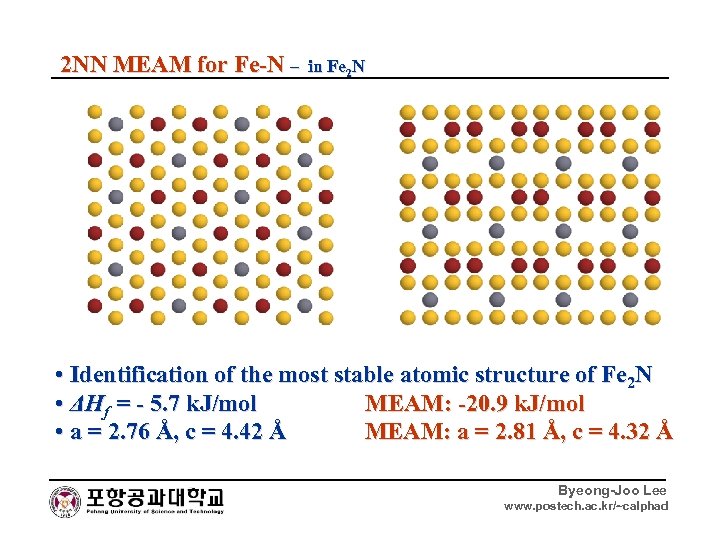
2 NN MEAM for Fe-N – in Fe 2 N • Identification of the most stable atomic structure of Fe 2 N • ΔHf = - 5. 7 k. J/mol MEAM: -20. 9 k. J/mol • a = 2. 76 Å, c = 4. 42 Å MEAM: a = 2. 81 Å, c = 4. 32 Å Byeong-Joo Lee www. postech. ac. kr/~calphad

Atomistic Simulation – Interatomic Potentials and Applications Interatomic Potential: Performance of 2 NN MEAM for Elements and Alloys • • Fundamental Properties of Structural Materials • Elastic Property • Defect (Point, Dislocation, Grain Bd. /Interface) Property • Phase Transformations • Deformation/Fracture Mechanism Fundamental Properties of Nano Materials • Thermodynamic Property • Atomic/Nano Structural Evolution Fundamental Properties of Amorphous Materials Irradiation Defects, etc. Byeong-Joo Lee www. postech. ac. kr/~calphad

Second Nearest Neighbor Modified EAM (2 NN MEAM) Pure Elements • Fe, Cr, Mo, W, V, Nb, Ta, Li • Cu, Ag, Au, Ni, Pd, Pt, Al, Pb • Ti, Zr & Mg • Mn, P • C, Si, Ge, In Phys. Rev. B. 64, 184102 (2001); MSMSE 20, 035005 (2012). Phys. Rev. B. 68, 144112 (2003). Phys. Rev. B. 74, 014101 (2006); CALPHAD 33, 650 -57 (2009). Acta Materialia 57, 474 -482 (2009). ; J. Phys. : Condensed Matters (2012), in press. CALPHAD 29, 7 -16 (2005); 31, 95 -104 (2007); 32, 34 -42 (2008); 32, 82 -88 (2008) Multicomponent Systems • Fe-C, Fe-N, Fe-H • Fe-Ti & Fe-Nb • Fe-Ti-C & Fe-Ti-N • Fe-Nb-C & Fe-Nb-N • Al-H & Ni-H, V-H • Fe-Mn • Fe-Cr • Fe-Cu • Fe-Pt • Fe-Al • Fe-P • Al-Ni • Co-Cu • Co-Pt • Cu-Ni • Ni-W • Cu-Ti • Cu-Zr-Ag • Mg-Al , Mg-Li • Ga-In-N Acta Materialia 54, 701 -711 (2006); 54, 4597 -4607 (2006); 55, 6779 -6788 (2007). Scripta Materialia 59, 595 -598 (2008). Acta Materialia 56 , 3481 -3489 (2008); Acta Materialia 57 , 3140 -3147 (2009). J. Materials Research 25, 1288 -1297 (2010). J. Materials Research 26, 1552 -1560 (2011); CALPHAD 35, 302 -307 (2011). Acta Materialia 57, 474 -482 (2009). CALPHAD 25, 527 -534 (2001). Phys. Rev. B. 71, 184205 (2005). J. Materials Research 21, 199 -208 (2006). J. Phys. : Condensed Matters 22, 175702 (2010) J. Phys. : Condensed Matters (2012), in press. CALPHAD 31, 53 (2007). J. Materials Research 17, 925 -928 (2002). Scripta Materialia 45, 495 -502 (2001). CALPHAD 28, 125 -132 (2004). J. Materials Research 18, 1863 -1867 (2003). Mater. Sci. and Eng. A 449 -451, 733 (2007). J. Materials Research 23, 1095 (2008). Scripta Materialia 61, 801 (2009). CALPHAD 33, 650 -57 (2009); MSMSE 20, 035005 (2012). J. Phys. : Condensed Matter 21, 325801 (2009). Byeong-Joo Lee www. postech. ac. kr/~calphad

Скачать презентацию Interatomic Potentials for Ionic Systems Byeong-Joo Lee POSTECH-CMSE

b36784c495e44f80da98998a0d9d1345.ppt

Количество слайдов: 58