Интерактивные таблицы по геометрии 7 класс Составитель: Широкова

Интерактивные таблицы по геометрии 7 класс Составитель: Широкова Ирина Леонидовна МОУ СОШ № 2 г. Алапаевск Свердловская область 2009

Содержание Луч и угол Сравнение отрезков Сравнение углов Измерение отрезков Измерение углов Перпендикулярные и параллельные прямые Свойство параллельности и перпендикулярности Признаки равенства треугольников Медиана, высота и биссектриса треугольника Равнобедренный треугольник и его свойства Построение циркулем и линейкой Признаки параллельности

Луч и угол Отметим на прямой l точку О. Эта точка разделит прямую на две части, каждая из которых называется лучом, исходящим из точки О. l В луч ОВ О А луч ОА

Луч и угол УГОЛ – это геометрическая фигура, состоящая из двух лучей, исходящих из одной точки. В АОВ О – вершина угла ОА и ОВ – стороны угла внешняя область угла внутренняя область угла О А

Луч и угол Угол называется развёрнутым, если обе его стороны лежат на одной прямой. В О А АОВ – развёрнутый угол

Сравнение отрезков Для сравнения двух отрезков требуется наложить один отрезок на другой. Если концы отрезков совместятся, то отрезки равны, иначе меньшим считается тот отрезок, который после наложения является частью другого. Середина отрезка - это точка отрезка, которая делит его пополам. А О АО = ОВ О – середина отрезка АВ В

Сравнение углов Для сравнения двух углов требуется наложить так один на другой угол, чтобы две стороны углов совместились, а две другие стороны разместились по одну сторону от совместившихся сторон. 1< 2 1 2

Сравнение углов БИССЕКТРИСА УГЛА – это луч, исходящий из вершины угла и делящий его пополам. В С О А ОС – биссектриса угла АОВ АОС = ВОС

Измерение отрезков ЕДИНИЦЫ ИЗМЕРЕНИЯ ОТРЕЗКОВ А В АВ = 7 см С D CD = 8 см 7 мм = 8, 7 см Измерить отрезок – значит узнать, сколько раз в данном отрезке укладывается отрезок, принятый за единицу измерения.

Измерение отрезков Если отрезки равны, то и их длины равны. Если первый отрезок меньше второго, то длина первого отрезка меньше длины второго. Длина отрезка равна сумме длин его частей. А В С АС = 12 см АВ = 4 см ВС = 8 см АС = АВ + ВС

Измерение углов ЕДИНИЦЫ ИЗМЕРЕНИЯ УГЛОВ Единица измерения углов – градус. Градус – это угол, который равен развёрнутого угла. части Градусная мера угла – это число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Измерение углов Инструмент для измерения углов – ТРАНСПОРТИР. АОВ = 40 ВОС = 80 BOD = 120 ВОК – развёрнутый ВОК = 180 D К С О А В

Измерение углов Если два угла равны, то их градусные меры равны. Если первый угол меньше второго, то градусная мера первого угла меньше градусной меры второго угла. Угол называется: 1. острым, если он меньше 90 ; 2. тупым, если он больше 90 , но меньше 180 ; 3. прямым, если он равен 90.

Перпендикулярные прямые Две пересекающиеся прямые называются перпендикулярными, если при пересечении они образуют четыре прямых угла. С АВ CD А В D АВ и CD – взаимно перпендикулярны

Параллельные прямые Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. А В С D AB CD АВ и CD – параллельны

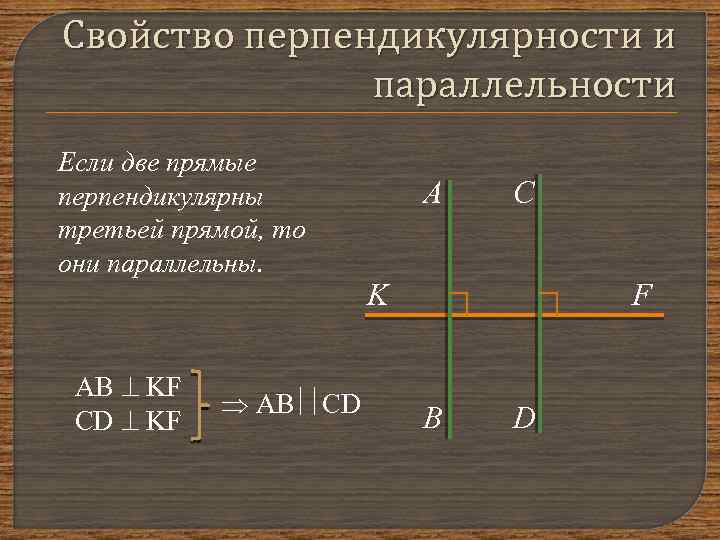
Свойство перпендикулярности и параллельности Если две прямые перпендикулярны третьей прямой, то они параллельны. AB KF CD KF AB CD А С K F В D

Перпендикулярные прямые Построение перпендикулярных прямых можно выполнить с помощью чертёжного угольника и линейки. А а АВ а В

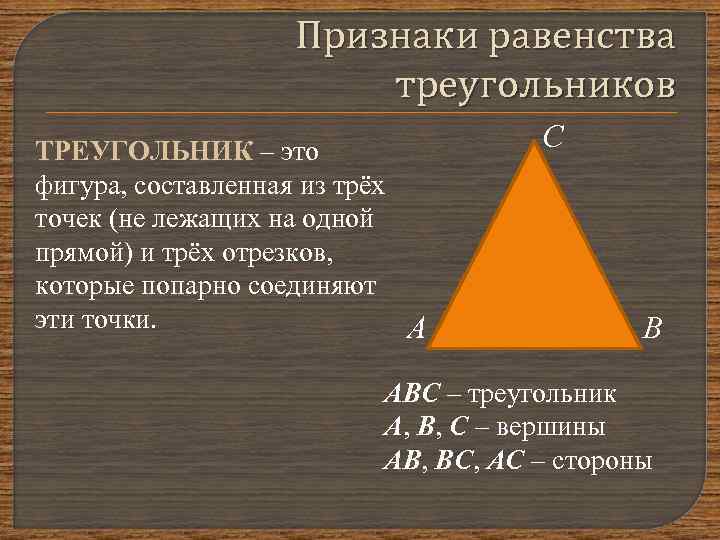
Признаки равенства треугольников ТРЕУГОЛЬНИК – это фигура, составленная из трёх точек (не лежащих на одной прямой) и трёх отрезков, которые попарно соединяют эти точки. А С В АВС – треугольник А, В, С – вершины АВ, ВС, АС – стороны

Признаки равенства треугольников Две фигуры равны, если их можно совместить наложением. Первый признак равенства треугольников А 1 Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. А = А 1 АВ = А 1 В 1 АС = А 1 С 1 АВС = А 1 В 1 С 1 С С 1 В А В 1

Признаки равенства треугольников Второй признак равенства треугольников Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней угла другого треугольника, то такие треугольники равны. А = А 1 В = В 1 АВ = А 1 В 1 С В А С 1 АВС = А 1 В 1 С 1 А 1 В 1

Признаки равенства треугольников Третий признак равенства треугольников С Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны. В А АВ = А 1 В 1 ВС = В 1 С 1 АС = А 1 С 1 АВС = А 1 В 1 С 1 В 1

Медиана треугольника МЕДИАНА ТРЕУГОЛЬНИКА – это отрезок, который соединяет вершину треугольника с серединой противоположной стороны. С А М В СМ – медиана треугольника АВС АМ = МВ

Высота треугольника ВЫСОТА ТРЕУГОЛЬНИКА – это перпендикуляр, который проведён из вершины треугольника к прямой, содержащей противоположную сторону. В В А К С К ВК – высота АВС А С С В АС и ВС – высоты АВС

Биссектриса треугольника БИССЕКТРИСА ТРЕУГОЛЬНИКА – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. С Е А В АЕ – биссектриса АВС САЕ = ВАЕ

Равнобедренный треугольник В Треугольник называется равнобедренным, если две стороны его равны. Эти равные стороны называются боковыми, а третья сторона – основанием А С равнобедренного треугольника. DАВС – равнобедренный АВ = ВС – боковые стороны АС – основание треугольника

Свойства равнобедренного треугольника Углы при основании равнобедренного треугольника равны. В В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой. BD – биссектриса, медиана и высота равнобедренного АВС А D С

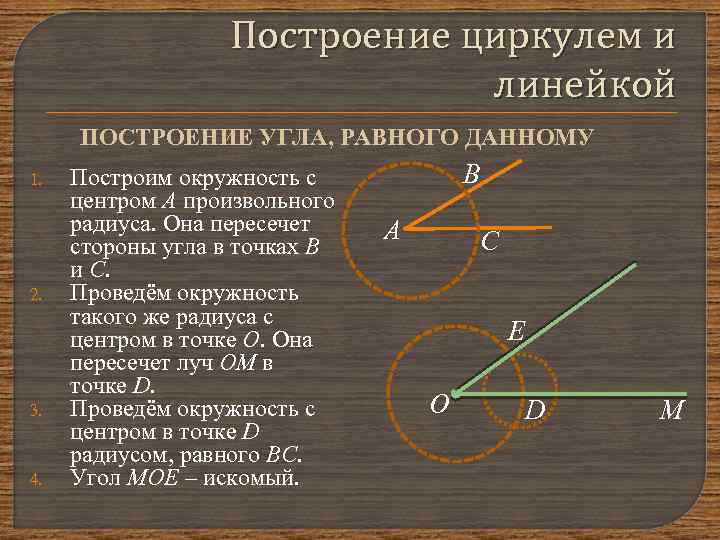
Построение циркулем и линейкой ПОСТРОЕНИЕ УГЛА, РАВНОГО ДАННОМУ 1. 2. 3. 4. Построим окружность с центром А произвольного радиуса. Она пересечет стороны угла в точках В и С. Проведём окружность такого же радиуса с центром в точке О. Она пересечет луч ОМ в точке D. Проведём окружность с центром в точке D радиусом, равного ВС. Угол МОЕ – искомый. В А С E О D М

Построение циркулем и линейкой ПОСТРОЕНИЕ БИССЕКТРИСЫ УГЛА 1. 2. 3. Проведём окружность с центром в точке О произвольного радиуса. Она пересечёт стороны угла в точках А и В. Проведём две окружности с центрами в точках А и В одинакового радиуса. Внутри угла АОВ эти окружности пересекутся в точке С. Луч ОС – искомая биссектриса угла О. А С О В

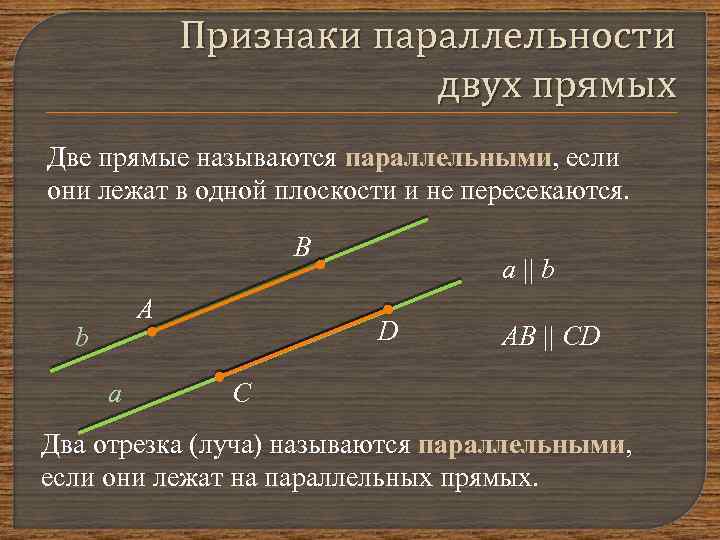
Признаки параллельности двух прямых Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. В А b a a || b D AB || CD С Два отрезка (луча) называются параллельными, если они лежат на параллельных прямых.

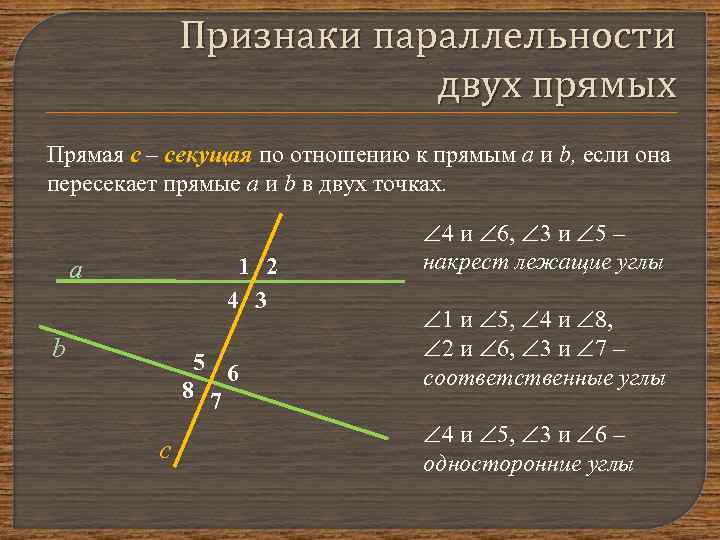
Признаки параллельности двух прямых Прямая с – секущая по отношению к прямым а и b, если она пересекает прямые а и b в двух точках. 1 2 4 3 a b 5 6 8 7 с 4 и 6, 3 и 5 – накрест лежащие углы 1 и 5, 4 и 8, 2 и 6, 3 и 7 – соответственные углы 4 и 5, 3 и 6 – односторонние углы

Признаки параллельности двух прямых 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180 , то прямые параллельны. а 1 1 b 2 c 1 a и b, b, с – секущая 1 1 = 2 + 2 = 180 a || b