Интерактивна система за технически изчисления визуализиране и програмиране

Интерактивна система за технически изчисления, визуализиране и програмиране (MATLAB) Приложение – математически изчисления; – разработка на алгоритми; – моделиране, симулиране и създаване на прототипи; – представяне, визуализиране и анализ на данни; – графика; – разработка на приложения с графичен потребителски интерфейс. Включва специални приложения (toolboxes) за обработка на сигнали, системи за управление, невронни мрежи, симулация и др.

Характеристики на системата MATLAB 1. MATLAB език – език от високо ниво за обработка на матрици; включва: оператори, функции, структури данни, вход/изход, обектно-ориентирано програмиране; 2. Работна среда на MATLAB – средства за управление на променливите в работната среда, внасяне и изнасяне на данни; разработка и управление на М-файлове, MATLAB приложения. 3. Управление на графика – двумерна и тримерна визуализация, обработка на изображения, анимация и представяне на графики; изграждане на графичен потребителски интерфейс.

4. Библиотека с математически функции – сума, тригонометрични функции, комплексна аритметика, обръщане на матрица, Беселови функции, бързи трансформации на Фурие и др. 5. Интерфейс за приложни програми – динамично свързване на модули, написани на C, C++, Java или Fortran с модули от MATLAB.

Стартиране на MATLAB Start Programs MATLAB 6. 5

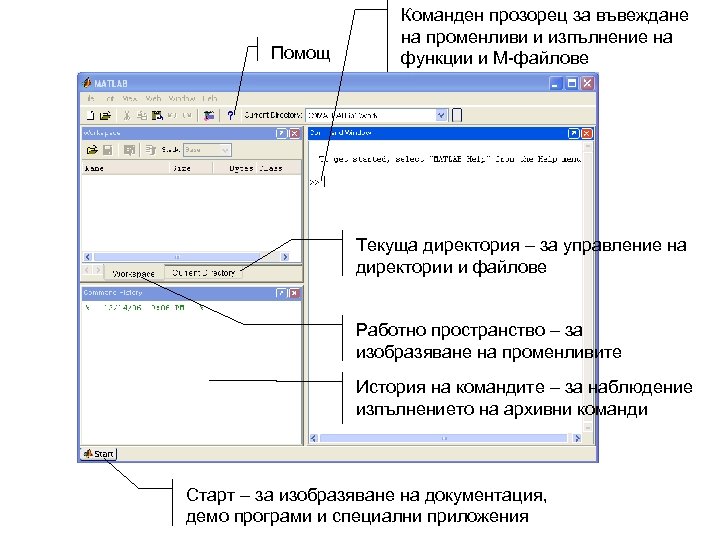Помощ Команден прозорец за въвеждане на променливи и изпълнение на функции и М-файлове Текуща директория – за управление на директории и файлове Работно пространство – за изобразяване на променливите История на командите – за наблюдение изпълнението на архивни команди Старт – за изобразяване на документация, демо програми и специални приложения

MATLAB като мощен калкулатор » указва въвеждане на команда ; блокира извеждане на резултата ans променлива със стойността на резултата = присвояване fun() вградена функция. . . пренасяне на израз на нов ред

» 2+3 ans = 5 вградена функция » x=sin(0. 5) x= 0. 4794 вектор » V=[1 2 3 4]; » sin(V) ans = 0. 8415 0. 9093 » exp(V) ans = 2. 7183 блокира извеждане на резултата 0. 1411 -0. 7568 вградена функция 7. 3891 20. 0855 54. 5982 » magic(3) ans = 8 1 6 3 5 7 4 9 2 MAGIC(N) е Nx. N матрица от целите числа 1 N 2 с еднакви суми във всеки ред, стълб и диагонали, където N>0 без N=2.

Типове данни 15 типa данни (или класове) Всеки тип данни е във формата на масив. Двумерният масив се нарича матрица. Едномерният масив се нарича вектор. Матрица 1 x 1 се нарича скалар.

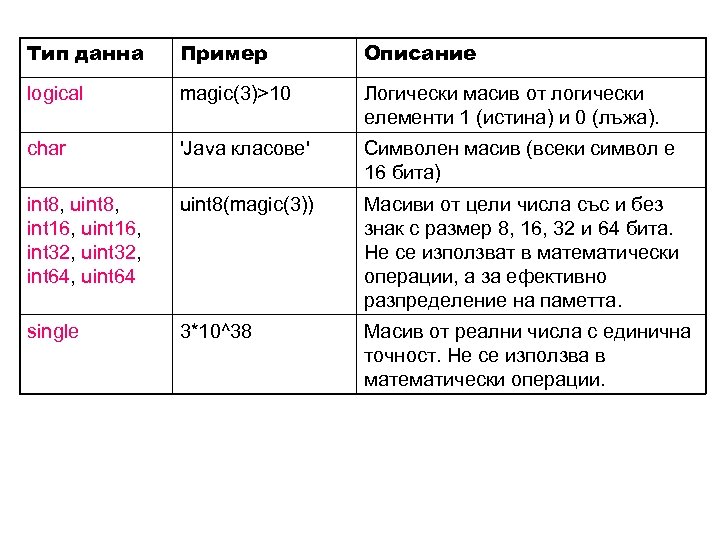Тип данна Пример Описание logical magic(3)>10 Логически масив от логически елементи 1 (истина) и 0 (лъжа). char 'Java класове' Символен масив (всеки символ е 16 бита) int 8, uint 8, int 16, uint 16, int 32, uint 32, int 64, uint 64 uint 8(magic(3)) Масиви от цели числа със и без знак с размер 8, 16, 32 и 64 бита. Не се използват в математически операции, а за ефективно разпределение на паметта. single 3*10^38 Масив от реални числа с единична точност. Не се използва в математически операции.

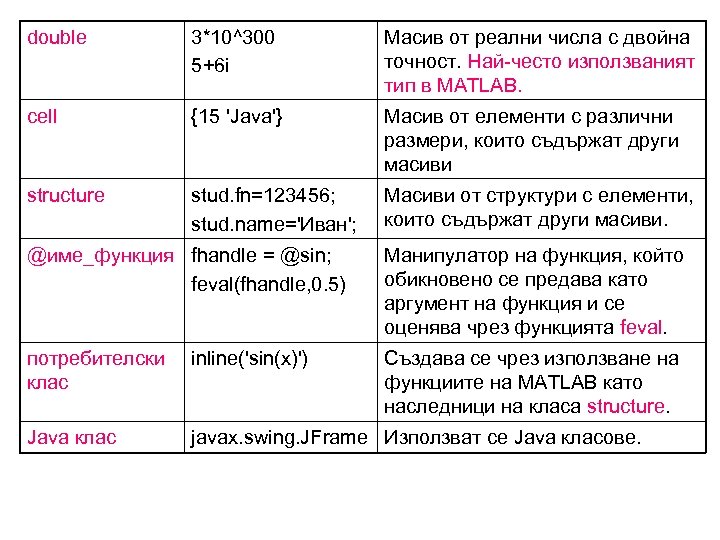double 3*10^300 5+6 i Масив от реални числа с двойна точност. Най-често използваният тип в MATLAB. cell {15 'Java'} Масив от елементи с различни размери, които съдържат други масиви structure stud. fn=123456; stud. name='Иван'; Масиви от структури с елементи, които съдържат други масиви. @име_функция fhandle = @sin; feval(fhandle, 0. 5) Манипулатор на функция, който обикновено се предава като аргумент на функция и се оценява чрез функцията feval. потребителски клас inline('sin(x)') Създава се чрез използване на функциите на MATLAB като наследници на класа structure. Java клас javax. swing. JFrame Използват се Java класове.

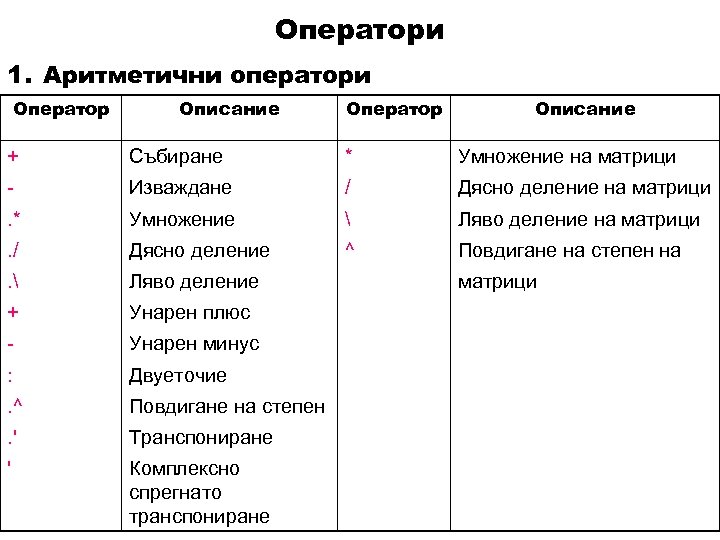Оператори 1. Аритметични оператори Оператор Описание + Събиране * Умножение на матрици - Изваждане / Дясно деление на матрици . * Умножение Ляво деление на матрици . / Дясно деление ^ Повдигане на степен на . Ляво деление + Унарен плюс - Унарен минус : Двуеточие . ^ Повдигане на степен . ' Транспониране ' Комплексно спрегнато транспониране матрици

» A=[7 2; 4 3]; » B=[1 4; 6 7]; » A+B ans = 8 6 10 10 » A*B ans = 19 42 22 37 % поелементно » A. *B ans = 7 8 24 21 » A. ^B ans = 7 4096 16 2187 % ляво деление » AB ans = -0. 6923 -0. 1538 2. 9231 2. 5385 » inv(A)*B ans = -0. 6923 -0. 1538 2. 9231 2. 5385 % дясно деление » B/A ans = -1. 0000 2. 0000 -0. 7692 2. 8462 » B*inv(A) ans = -1. 0000 2. 0000 -0. 7692 2. 8462 Функция inv(A) – обръща матрицата А.

2. Оператори за сравнение Оператор < <= > Описание Оператор По-малко >= По-малко или равно == По-голямо ~= По-голямо или равно Равно на Различно от Пример: А==B – сравнява матриците елемент-поелемент, A и B трябва да са с еднакви размери, резултантната матрица показва дали съответните елементи от A и B са равни. » A=[1 2 3; 4 5 6; 7 8 9]; » B=[1 5 10; 2 5 8; 4 7 9]; » A==B ans = 1 0 0 0 1

3. Логически оператори 3. 1. Поелементни логически оператори и функции » А=[0 1 1 0 1]; » B=[1 1 0 0 1]; Оператор Описание Пример A & B = 01001 Еквивалентна функция & Връща 1, ако елементите и в двата масива са истина ( ) и 0 за другите елементи. and(A, B) | Връща 1, ако елементите в A | B = 11101 единия масив или елементите в двата масива са истина ( 0) и 0 за другите елементи. or(A, B) ~ Допълва всеки елемент на входния масив. ~A = 10010 not(A) xor Връща 1, ако елементът само в единия масив е истина ( 0) и 0 за другите елементи. xor(A, B)=10100

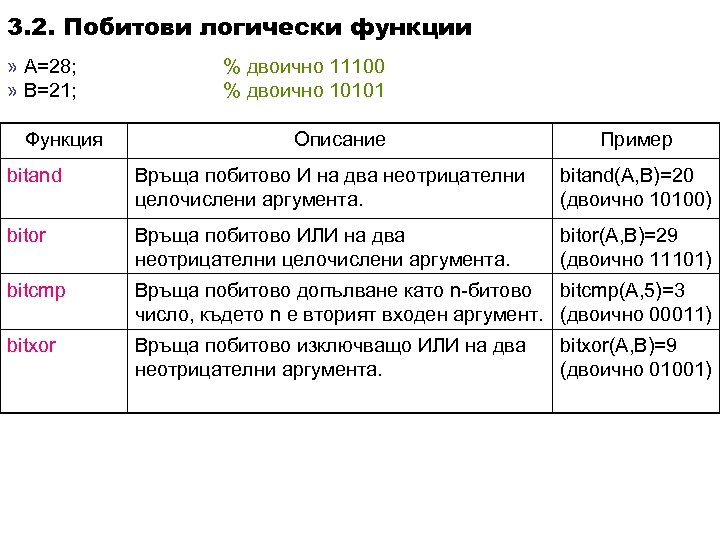3. 2. Побитови логически функции » А=28; » B=21; Функция % двоично 11100 % двоично 10101 Описание Пример bitand Връща побитово И на два неотрицателни целочислени аргумента. bitand(A, B)=20 (двоично 10100) bitor Връща побитово ИЛИ на два неотрицателни целочислени аргумента. bitor(A, B)=29 (двоично 11101) bitcmp Връща побитово допълване като n-битово bitcmp(A, 5)=3 число, където n е вторият входен аргумент. (двоично 00011) bitxor Връща побитово изключващо ИЛИ на два неотрицателни аргумента. bitxor(A, B)=9 (двоично 01001)

3. 3. Къси логически оператори (за скалари) » А=28; » B=-21; Оператор Описание Пример && Връща истина (1), ако и двата операнда са истина и лъжа (0) в противен случай. А && B =1 || Връща истина (1), ако единият или и двата операнда са истина и лъжа (0) в противен случай. А || B=1

Изрази Израз – състои се от операнди и операции; операндите могат да бъдат променливи, константи или функции. 1. Променливи – автоматично се създава променлива за всяко име и се отделя необходимата памет; – името на променливата се състои от букви, цифри, знак за подчертаване (_), като MATLAB използва първите 31 символа; – различава малки и главни букви. » A=10 % създава се 1 x 1 матрица с име А и един елемент със стойност 10 А= 10

2. Числа – съхраняват се с дълга плаваща запетая (16 значещи цифри, област 10 -308 до 10+308). Начини за представяне: – десетично представяне с незадължителна десетична точка и водещ знак плюс; – научно представяне чрез буквата е, определяща 10 на степен; – имагинерните числа използват като суфикс i или j. 10 -43 3. 4632987 1. 63 е-201. 43 i 0. 001

Комплексно число – модул (амплитуда) m=abs(z) връща модула (амплитудата) на z – фазов ъгъл theta=angle(z) връща фазовия ъгъл на z в радиани Комплексно число в полярни координати » z=3+j*4; % Конвертира z в полярни координати » A=abs(z) A= 5 » theta=angle(z) theta = 0. 9273 % Обратно конвертира до z=x+jy » z=A*exp(j*theta) z= 3. 0000 + 4. 0000 i

3. Символи и коментари Символна константа е последователност от символи, заградени в апострофи ′. Коментар започва със символа %. » A=[′София ′; ′Пловдив′] А= София Пловдив % матрица 2 x 7 4. Оператори – аритметични оператори; – оператори за сравнение; – логически оператори.

4. 1. Оператор : a: b – резултатът е вектор-ред, съдържащ числата от a до b със стъпка 1. a: c: b – резултатът е вектор-ред, съдържащ числата от a до b със стъпка c. » 1: 10 % стъпка 1 ans = 1 2 3 4 5 6 7 8 9 10 » 100: -10: 50 % стъпка -10 ans = 100 90 80 70 60 50

5. Функции аbs sqrt еxp sin clear all close all help format абсолютна стойност корен квадратен е на степен синус изчиства променливите и функциите от паметта изчиства всички променливи, глобални променливи, функции и връзки затваря фигура затваря всички прозорци с фигури получаване на помощ установява изходния формат Константи: pi i j 3. 1459265 имагинерна единица -1 » help elfun % елементарни математически функции » help specfun % специални математически функции » help elmat % матрични функции

» format short » format long » format hex » format rat % мащабиран формат с фиксирана точка с 5 цифри % мащабиран формат с фиксирана точка с 15 цифри % шестнадесетичен формат % апроксимация чрез отношение от малки цели числа

Примери: » s=(1+sqrt(10))/2 s= 2. 0811 » n=1: 5 n= 1 2 3 4 » n=n' n= 1 2 3 4 5 » x=n. ^2 x= 1 4 9 16 25 % оператор : -> вектор-ред 5 % оператор ' (транспониране) -> вектор-стълб % оператор. ^ (поелементно повдигане на степен)

Изчертаване на графики plot(y) Създава начупена линейна графика на вектора y спрямо индекса на елементите на y. plot(x, y) Създава линейна графика на вектора y спрямо вектора x. Създава много графики на векторите yi спрямо векторите xi. plot(x, y, ′цвят_маркер_линия′) Изчертава графика с определен цвят, тип маркер и тип линия; цвят_маркер_линия e 1 -, 2 - или 3 символен низ; ако се дефинира цвят_маркер без линия, изчертава се само маркерът. plot(x 1, y 1, x 2, y 2, …)

loglog(x, y) Създава логаритмична графика log 10(y) спрямо log 10(x). semilogx(x, y) Създава полулогаритмична графика на вектора y спрямо log 10(x). semilogy(x, y) Създава полулогаритмична графика на log 10(y) спрямо вектора x. polar(theta, rho) Създава графика в полярни координати на радиуса rho спрямо ъгъла theta. цвят_линия r червен b син g зелен w бял k черен c синьо зелен m пурпурен y жълт тип_линия плътна тирета и точки. от точки : двуеточия none без линия --. тип_маркер + o *. x

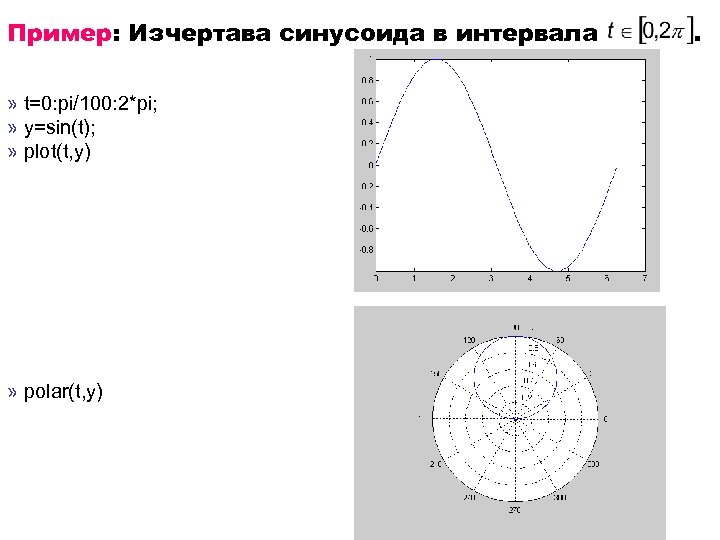Пример: Изчертава синусоида в интервала » t=0: pi/100: 2*pi; » y=sin(t); » plot(t, y) » polar(t, y) .

xlabel(′текст′) Добавя текст до x–оста. ylabel(′текст′) Добавя текст до y-оста. title(′текст′) Добавя текст като заглавие. text(x, y, ′текст′) Добавя текст, който започва от т. (x, y) на графичния екран. axis([xmin xmax ymin ymax]) Управлява мащабирането на осите. grid Променя състоянието на мрежата. grid on / grid off Добавя/премахва координатната мрежа. hold Променя състоянието на графиката. hold on / hold off Задържа текущата графика, като следващите графични команди се добавят към графиката / връща подразбиращия се режим. figure(H) Създава нова фигура с манипулоатор H или прави текущата фигура да бъде H.

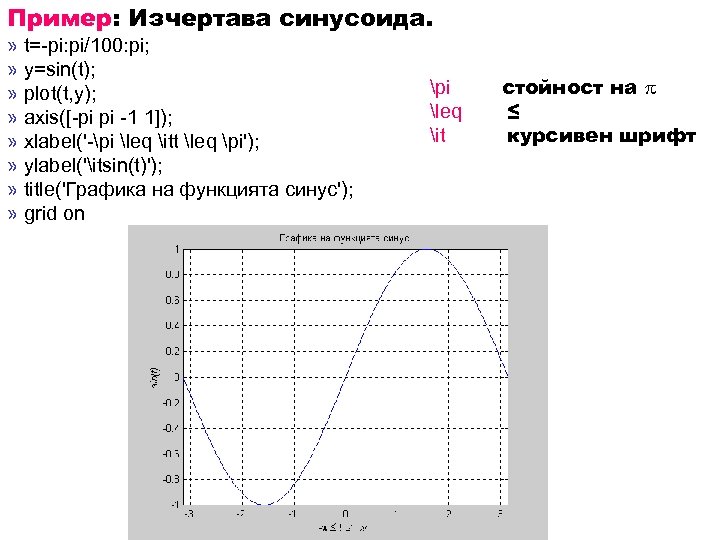Пример: Изчертава синусоида. » t=-pi: pi/100: pi; » y=sin(t); » plot(t, y); » axis([-pi pi -1 1]); » xlabel('-pi leq itt leq pi'); » ylabel('itsin(t)'); » title('Графика на функцията синус'); » grid on pi leq it стойност на ≤ курсивен шрифт

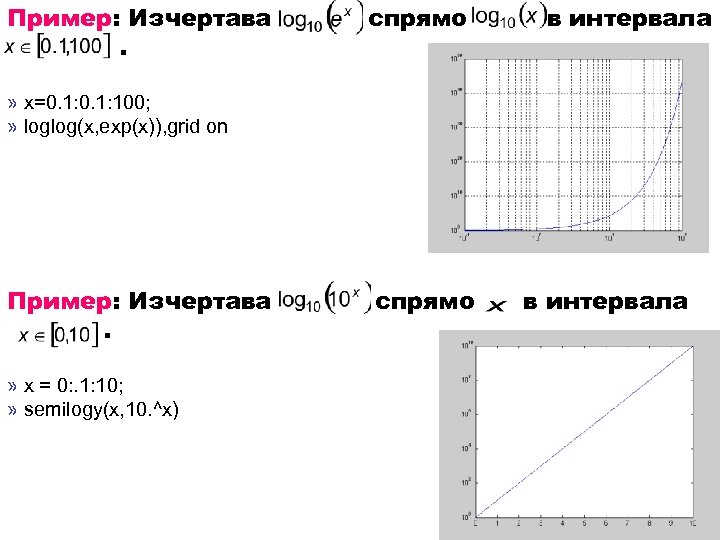Пример: Изчертава. спрямо в интервала » x=0. 1: 100; » loglog(x, exp(x)), grid on Пример: Изчертава. » x = 0: . 1: 10; » semilogy(x, 10. ^x) спрямо в интервала

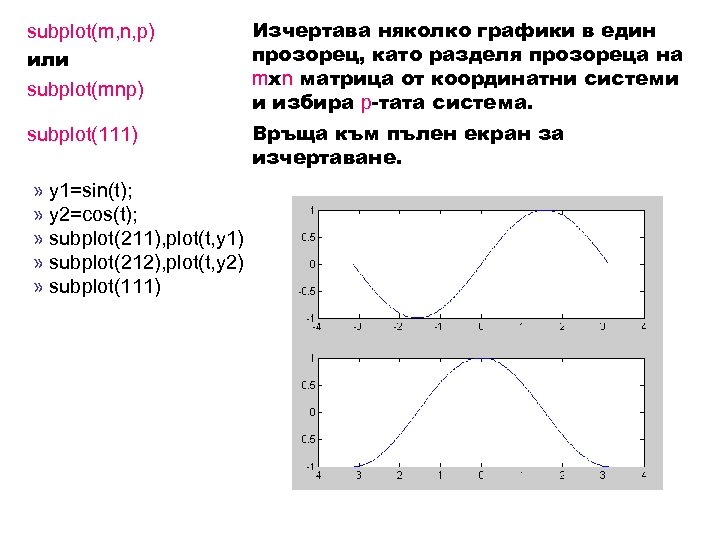subplot(m, n, p) или subplot(mnp) Изчертава няколко графики в един прозорец, като разделя прозореца на mxn матрица от координатни системи и избира p-тата система. subplot(111) Връща към пълен екран за изчертаване. » y 1=sin(t); » y 2=cos(t); » subplot(211), plot(t, y 1) » subplot(212), plot(t, y 2) » subplot(111)

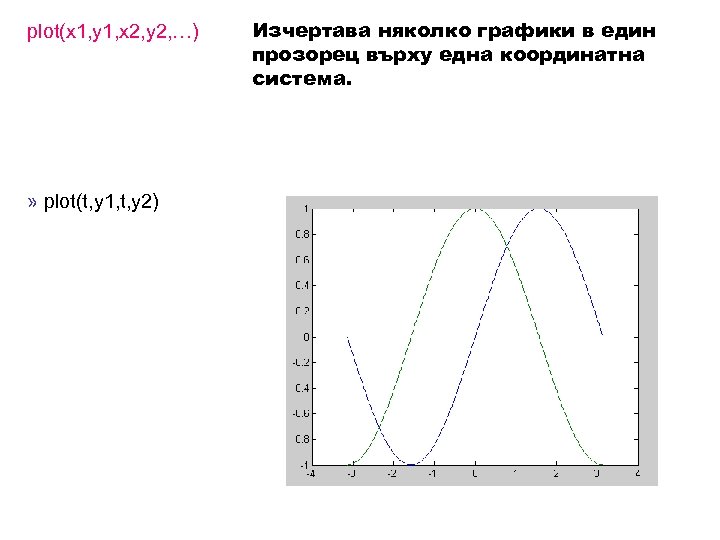plot(x 1, y 1, x 2, y 2, …) » plot(t, y 1, t, y 2) Изчертава няколко графики в един прозорец върху една координатна система.

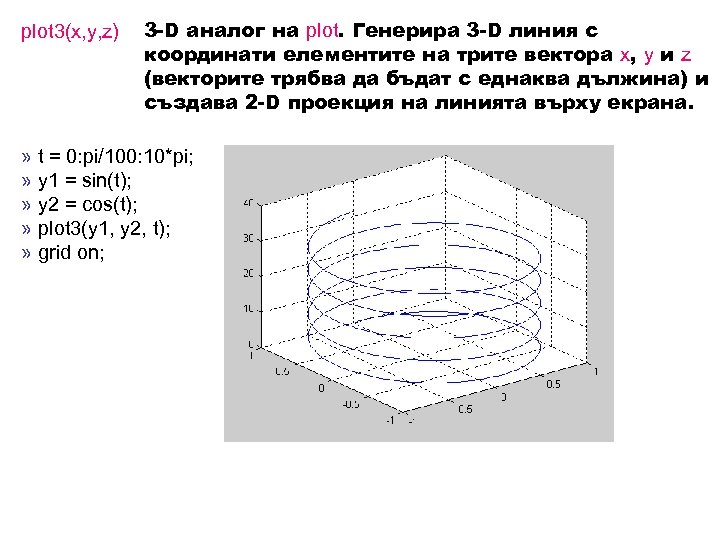plot 3(x, y, z) 3 -D аналог на plot. Генерира 3 -D линия с координати елементите на трите вектора x, y и z (векторите трябва да бъдат с еднаква дължина) и създава 2 -D проекция на линията върху екрана. » t = 0: pi/100: 10*pi; » y 1 = sin(t); » y 2 = cos(t); » plot 3(y 1, y 2, t); » grid on;

stem(y) За дискретни сигнали изчертава данните във вектора y спрямо оста x като всяка точка е малка окръжност и права линия. stem(x, y) Изчертава данните във вектора y спрямо вектора x. stem(x, y, ′filled′) Използва запълнени маркери. stem(x, y, ′тип_линия′) Използва тип_линия при изчертаването.

Пример: Изчертава дискретен сигнал y[x]. » x=1: 5; » y=[1 2 3 4 5]; » stem(x, y) » stem(x, y, 'filled') » stem(x, y, '--')

Пример: Изчертава дискретния във времето сигнал x[n], зададен чрез следните стойности: x[0]=1, x[1]=2, x[2]=1, x[3]=0, x[4]=-1, където x[n]=0 за всяко друго n. Нека векторът n да съдържа стойностите на времето в интервал от -2 до 6 s с нарастване 1 s. » n=-2: 6; » x=[0 0 1 2 1 0 -1 0 0]; » stem(n, x, 'filled') » xlabel('n') » ylabel('x[n]')

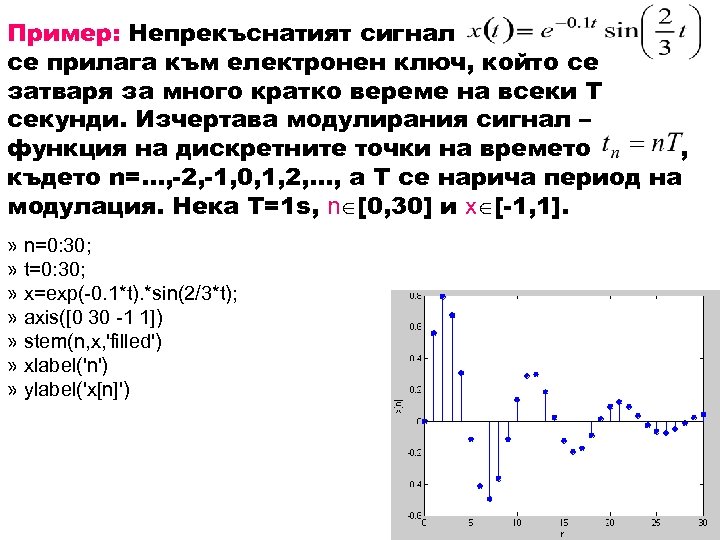Пример: Непрекъснатият сигнал се прилага към електронен ключ, който се затваря за много кратко вереме на всеки Т секунди. Изчертава модулирания сигнал – функция на дискретните точки на времето , където n=. . . , -2, -1, 0, 1, 2, . . . , а Т се нарича период на модулация. Нека Т=1 s, n [0, 30] и x [-1, 1]. » n=0: 30; » t=0: 30; » x=exp(-0. 1*t). *sin(2/3*t); » axis([0 30 -1 1]) » stem(n, x, 'filled') » xlabel('n') » ylabel('x[n]')

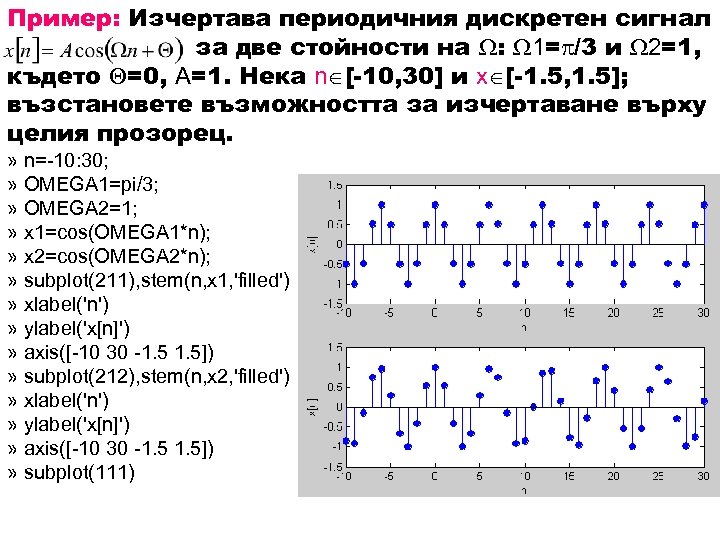Пример: Изчертава периодичния дискретен сигнал за две стойности на : 1= /3 и 2=1, където =0, А=1. Нека n [-10, 30] и x [-1. 5, 1. 5]; възстановете възможността за изчертаване върху целия прозорец. » n=-10: 30; » OMEGA 1=pi/3; » OMEGA 2=1; » x 1=cos(OMEGA 1*n); » x 2=cos(OMEGA 2*n); » subplot(211), stem(n, x 1, 'filled') » xlabel('n') » ylabel('x[n]') » axis([-10 30 -1. 5]) » subplot(212), stem(n, x 2, 'filled') » xlabel('n') » ylabel('x[n]') » axis([-10 30 -1. 5]) » subplot(111)

Матрици 1. Определения Матрица е правоъгълен масив от числа. Скалар е 1 x 1 матрица. Вектор е матрица само с един ред или стълб. 2. Въвеждане на матрици чрез явен списък от елементи – матрицата се запомня автоматично в работното пространство. » А=[16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1] A= 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1

3. Обръщение към матрица – чрез нейното име. » А A= 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 4. Сума от елементите във всеки стълб – резултатът е вектор-ред и се запазва в променливата ans. » sum(А) ans = 34 34

5. Сума от елементите на всеки ред – резултатът е вектор-стълб. Алгоритъм: 1) транспониране на матрицата (операция ′); 2) изчисляване на сумите по стълбове; 3) транспониране на резултата. » А′ ans = 16 5 9 4 3 10 6 15 2 11 7 14 13 8 12 1 » sum(А′)′ ans = 34 34

6. Сума от елементите от главния диагонал. » diag(А) ans = 16 10 7 1 » sum(diag(А)) ans = 34 7. Сума от елементите от второстепенния диагонал. » sum(diag(fliplr(А))) ans = 34 Функцията fliplr обръща матрицата отляво надясно.

8. Индекси – елементът в ред i и стълб j се означава чрез A(i, j). а) достъп до елемент на матрицата » А(4, 2) ans = 15 б) сума от елементите в 4 -тия стълб » А(1, 4)+A(2, 4)+A(3, 4)+A(4, 4) ans = 34 в) достъп до елемент на масив чрез един индекс – масивът се съхранява по стълбове като един дълъг вектор-стълб; напр. достъп до елемент A(4, 2): » А(8) ans = 15

9. Използване на оператор : » sum(A(1: 4, 4)) ans = 34 % сума от 4 -тия стълб » sum(A(: , end)) ans = 34 % сума от последния стълб

10. Обратна матрица – функция inv » A=pascal(3) A= 1 1 2 3 1 3 6 » inv(A) ans = 3 -3 1 -3 5 -2 1

11. Специални матрици zeros всички елементи са 0; ones всички елементи са 1; rand правилно разпределени случайни числа; randn нормално разпределени случайни числа; magic магически квадрат от степен N е Nx. N матрица с елементи естествени числа от 1 до N 2 така, че сумата от числата във всеки хоризонтал, вертикал или главен диагонал е една и съща, равна на N(N 2+1)/2; pascal матрица на Паскал от степен N: симетрична положително дефинирана матрица с целочислени стойности, получени от триъгълника на Паскал (първото и последното число във всеки ред е 1, а другите се получават като сума от двете числа над него).

» o=ones(2, 4) o= 1 1 1 1 » A=magic(3) A= 8 1 6 3 5 7 4 9 2 » A=pascal(3) A= 1 1 2 3 1 3 6

12. Слепване на матрици [] оператор за слепване » A=magic(3) A= 8 1 6 3 5 7 4 9 2 » B=[A A+5; A+10 A+20] B= 8 1 6 13 6 11 3 5 7 8 10 12 4 9 2 9 14 7 18 11 16 28 21 26 13 15 17 23 25 27 14 19 12 24 29 22

13. Изтриване на редове и стълбове [] двойка квадратни скоби » A=magic(3) A= 8 1 6 3 5 7 4 9 2 » A(2, : )=[] A= 8 1 6 4 9 2 % изтрива втори ред от А » A(: , 2)=[] A= 8 6 4 2 % изтрива втори стълб от А

14. Изграждане на таблици » n=(0: 9)'; » pows = [n n. ^2] pows = 0 0 1 1 2 4 3 9 4 16 5 25 6 36 7 49 8 64 9 81 % вектор-стълб % таблица от квадратите на 2

15. Вход/изход на информация – въвеждане на информация в диалогов режим – чрез функция input; X=input('низ') Като подсказка се извежда низ, потребителят въвежда MATLAB израз, който се изчислява чрез променливите от работното пространство и резултатът се запазва в X. X=input ('низ', 's') Като подсказка се извежда низ, потребителят въвежда символен низ, който се запазва в X като MATLAB низ. » A=[1 2 3 4 5]; » A(6)=input('Enter A[6]=') Enter A[6]=6 A= 1 2 3 4 5 6 » name=input('Ime=', 's') Ime=Ivan name = Ivan

– извеждане на информация – чрез функция disp; disp(X) Извежда масива X, без да отпечатва неговото име. Ако X е низ, извежда се текстът. » disp(A(6)) 6 » disp(name) Ivan

Закони в електрическите вериги 1. Първи закон на Кирхоф – сумата от токовете, излизащи от възел, е равна на нула. Уравнение на възловите напрежения [Y][U]=[I] [Y] – матрица на проводимостите, [U]=[Y]-1[I] [U] – вектор на напрежения, [I] – вектор на токове » U=YI % ляво деление или » U=inv(Y)*I 2. Втори закон на Кирхов – сумата от напрежителните падове в клоните на затворен контур е равна на сумата от електродвижещите сили на източниците в този контур. Уравнение на контурните токове [Z][I]=[U] [Z] – матрица на съпротивленията [I]=[Z]-1[U] » I=ZU % ляво деление или » I=inv(Z)*U

Пример: Изчисление на тока през резистора RB и мощността на постояннотоковия източник на напрежение по метод на контурните токове. Уравнение на контурните токове Z – матрица на съпротивленията I – вектор на контурните токове U – вектор на напреженията

» % Уравнение на контурните токове ZI=U » % Матрица на съпротивленията Z » Z=[40 -10 -30; -10 30 -5; -30 -5 65]; » % Вектор на напреженията U » U = [10; 0; 0]; » % Вектор на контурните токове I » I=ZU % или I=inv(Z)*U » IRB=I(3)-I(2) % ток през съпротивлението RB » P=I(1)*10 % мощност на захранващия източник I= 0. 4753 0. 1975 0. 2346 IRB = 0. 0370 P= 4. 7531

Файлова система MATLAB Видове файлове: 1. . mat – двоичен файл, в който се записва работната сесия на системата. Запазване съдържанието на работната сесия във файл име. mat » save име Зареждане на работната сесия от файл име. mat » load име

2. . m – текстов файл, който съдържа функции и скриптове. – файл-скрипт – съдържа команди на MATLAB: – обработва съществуващи данни в работното пространство или създава нови данни; – създадените променливи остават в работното пространство; – файл-функция – има входни аргументи и връща изходни резултати: – името на m-файла и името на функцията съвпадат; – обработва променливи в тяхното собствено работно пространство, различно от основното.

Създаване на. m файл от командния прозорец File New M-file Запазване на. m файл от командния прозорец File Save As… Промяна на директорията за съхранение на. m файловете File Set Path

Пример: Файл-скрипт my. m File New M-file A=[… 16. 0 3. 0 2. 0 13. 0 5. 0 10. 0 11. 0 8. 0 9. 0 6. 0 7. 0 12. 0 4. 0 15. 0 14. 0 1. 0]; File Save As… my Скриптът създава в работното пространство на MATLAB променлива А, която съдържа матрица. Изпълнение на. m файл – в работното пространство » my » A A= 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 Операторът my чете от файла my. m и използва създадената променлива А, която съдържа матрицата.

Пример: Файл-функция my. m File New M-file function y=my() y=[. . . 16. 0 3. 0 2. 0 13. 0 5. 0 10. 0 11. 0 8. 0 9. 0 6. 0 7. 0 12. 0 4. 0 15. 0 14. 0 1. 0]; Функцията е с име my, няма входни параметри и връща матрица. File Save As… my File Compile Изпълнение на. m файл – в работното пространство » A=my A= 16 3 5 10 9 6 4 15 2 13 11 8 7 12 14 1 Извиква се функцията my и върнатият резултат се присвоява на променливата А, която получава матрицата.

Глобални променливи global X X – глобална променлива; – ако X се дефинира в няколко функции и в работното пространство като global, тогава те споделят единствено копие на X; – инициализира се с празна матрица.

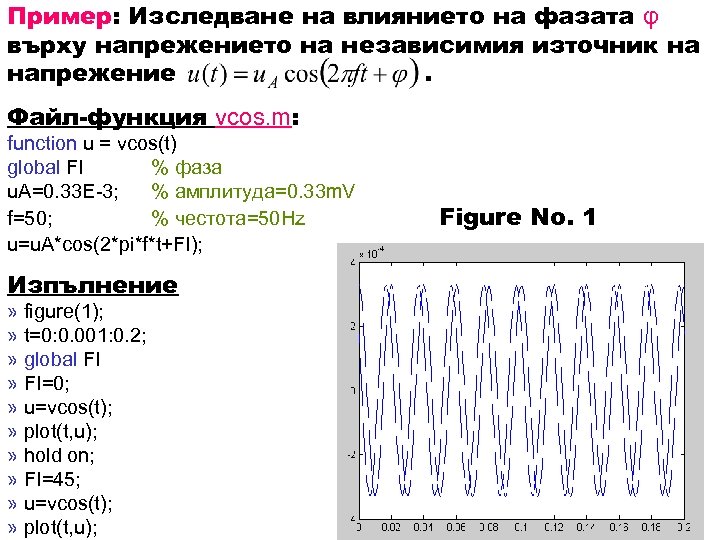Пример: Изследване на влиянието на фазата φ върху напрежението на независимия източник на напрежение. Файл-функция vcos. m: function u = vcos(t) global FI % фаза u. A=0. 33 E-3; % амплитуда=0. 33 m. V f=50; % честота=50 Hz u=u. A*cos(2*pi*f*t+FI); Изпълнение » figure(1); » t=0: 0. 001: 0. 2; » global FI » FI=0; » u=vcos(t); » plot(t, u); » hold on; » FI=45; » u=vcos(t); » plot(t, u); Figure No. 1

Управляващи структури 1. Условен оператор if if израз оператори else израз оператори end 2. Условен оператор switch_израз case_израз, оператор, …, оператор case {case_израз, . . . , case_израз} оператор, …, оператор. . . otherwise оператор, …, оператор end

3. Оператор за цикъл for променлива=старт: нарастване: край, оператори end 4. Оператор за цикъл while израз оператори end 5. Оператор за прекъсване на цикъл break – прекъсва изпълнението на while или for.

» for k=1: 10, x(k)=cos(k); еnd » x x= 0. 5403 -0. 4161 -0. 9900 -0. 6536 -0. 9111 -0. 8391 или » k=1: 10; » x=cos(k); » x » a=2; » b=5; » if(a>b) c=a; else c=b; end » c c= 5 0. 2837 0. 9602 0. 7539 -0. 1455

Пример: 3 -битов А/D конвертор Преобразува аналоговия сигнал x в цифров сигнал y съгласно уравнението: Файл-функция AD 3. m: function y=AD 3(x) if x<-2. 5 y=0; elseif x<-1. 5 y=1; elseif x<-0. 5 y=2; elseif x<0. 5 y=3; elseif x<1. 5 y=4; elseif x<2. 5 y=5; elseif x<3. 5 y=6; else y=7; end Изпълнение » y 1=AD 3(-1. 25) y 1 = 2 » y 2=AD 3(2. 57) y 2 = 6 » y 3=AD 3(6. 0) y 3 = 7

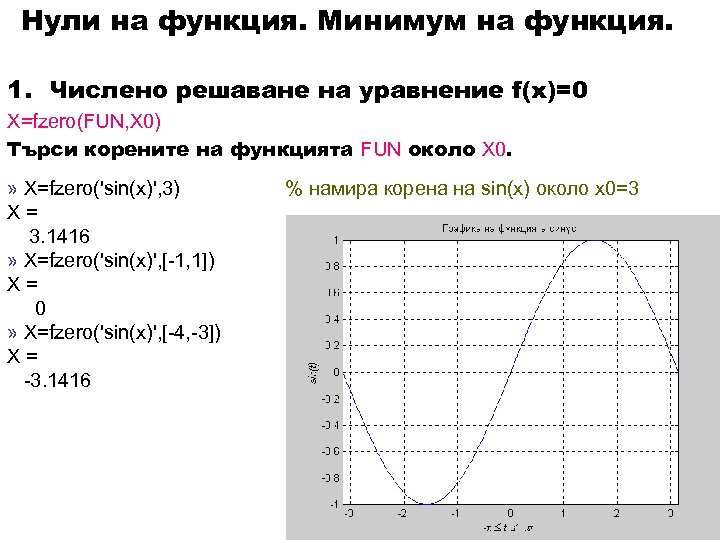Нули на функция. Минимум на функция. 1. Числено решаване на уравнение f(x)=0 X=fzero(FUN, X 0) Търси корените на функцията FUN около X 0. » X=fzero('sin(x)', 3) X= 3. 1416 » X=fzero('sin(x)', [-1, 1]) X= 0 » X=fzero('sin(x)', [-4, -3]) X= -3. 1416 % намира корена на sin(x) около x 0=3 % намира корена на sin(x) в интервала [-1, 1], % където sin(x) сменя знака си % намира корена на sin(x) в интервала [-4, -3]

2. Минимум на функция f(x) X=fminbnd(FUN, X 1, X 2) Търси минимума на функцията FUN в интервала [X 1, X 2]. » min=fminbnd('sin(x)', -2, -1) min = -1. 5708 % минимум на sin(x) в интервала -2

3. Диференциране diff(f) Връща , x е подразбиращата се символна променлива diff(f, n) Връща , x е подразбиращата се символна променлива diff(f, x, n) Връща , x е явно зададена символна променлива » syms x y; % дефинира реални символни променливи » diff(x^y) ans = x^y*y/x % първа производна спрямо x (по подразбиране) » diff(x^y, x) ans = x^y*y/x » diff(sin(y*x), x, 3) ans = -cos(y*x)*y^3 % първа производна спрямо x % трета производна спрямо x

4. Интегриране int(f) Връща , x е подразбиращата се символна променлива int(f, x) Връща , x е явно зададена символна променлива int(f, a, b) Връща , x е подразбиращата се символна променлива int(f, x, a, b) Връща , x е явно зададена символна променлива » syms x; » int(x^2, x) ans = 1/3*x^3 % неопределен интеграл » int((x^2 -2)/(x^3 -1), x, 2, 5) % определен интеграл ans = -2/3*log(2)+2/3*log(31)+2/3*3^(1/2)*atan(11/3*3^(1/2))-2/3*log(7)2/3*3^(1/2)*atan(5/3*3^(1/2))

Нелинейни числени методи I. Числено решаване на обикновени диференциални уравнения Всяко обикновено диференциално уравнение от nти ред може да се запише като система от n уравнения от първи ред така, че от лявата страна да се намират само производните, а от дясната страна производните да не участват: ode 45, ode 23, ode 113, ode 15 s, ode 23 t, ode 23 tb – всички функции решават системата от обикновени диференциални уравнения y'=f(t, y); ode 15 s, ode 23 t и ode 23 tb решават системи от вида my'=f(t, y), като от последните с изключение на ode 23 s решават уравненията m(t)y'=f(t, y).

[t, y]=ode_function('f', tspan, yo) [t, y]=ode_function('f', tspan, yo, options, p 1, p 2, . . . ) f е името на. m файла, който съдържа дясната страна на уравненията – функцията f(t, y) и връща вектор-стълб; има вида: function dydt = f(t, y) където t е скалар, dydt и y са вектор-стълбове. tspan е вектор, определящ интервала [t 0 tfinal]; yo е вектор, определя началните условия; options е незадължителен параметър, който се създава чрез функцията odeset; p 1, p 2, . . . са незадължителни параметри, които се предават на f; [t, y] е матрица на решението.

Пример: Уравнение на Ван дер Пол с начални условия: Еквивалентно е на система от диференциални уравнения от 1 ред: с начални условия:

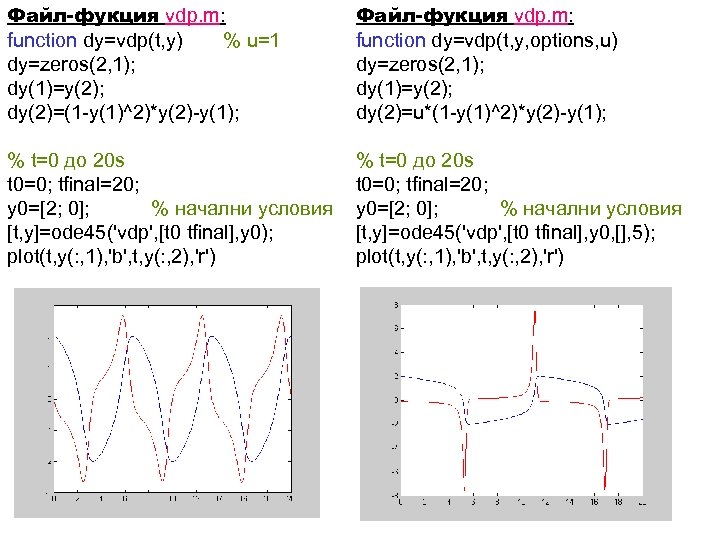Файл-фукция vdp. m: function dy=vdp(t, y) % u=1 dy=zeros(2, 1); dy(1)=y(2); dy(2)=(1 -y(1)^2)*y(2)-y(1); Файл-фукция vdp. m: function dy=vdp(t, y, options, u) dy=zeros(2, 1); dy(1)=y(2); dy(2)=u*(1 -y(1)^2)*y(2)-y(1); % t=0 до 20 s t 0=0; tfinal=20; y 0=[2; 0]; % начални условия [t, y]=ode 45('vdp', [t 0 tfinal], y 0); plot(t, y(: , 1), 'b', t, y(: , 2), 'r') % t=0 до 20 s t 0=0; tfinal=20; y 0=[2; 0]; % начални условия [t, y]=ode 45('vdp', [t 0 tfinal], y 0, [], 5); plot(t, y(: , 1), 'b', t, y(: , 2), 'r')

Анализ на преходни процеси 1. RC верига а) разреждане на кондензатор – времеконстанта Ако кондензаторът е бил зареден до напрежение , аналитичното решение е:

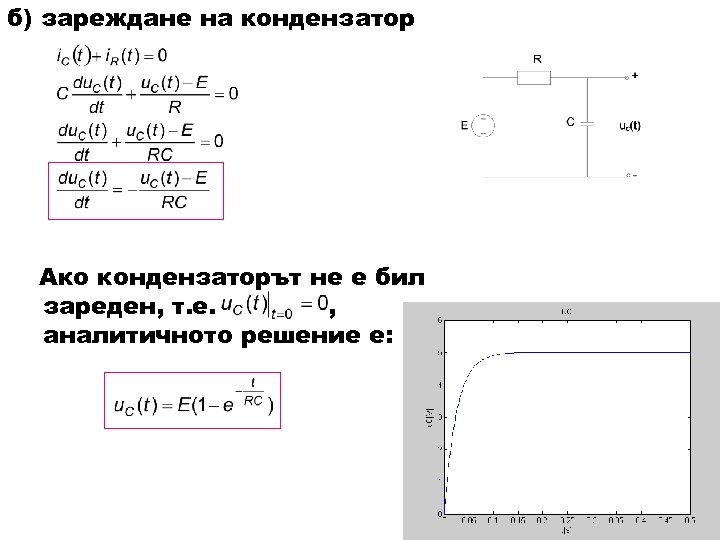б) зареждане на кондензатор Ако кондензаторът не е бил зареден, т. е. , аналитичното решение е:

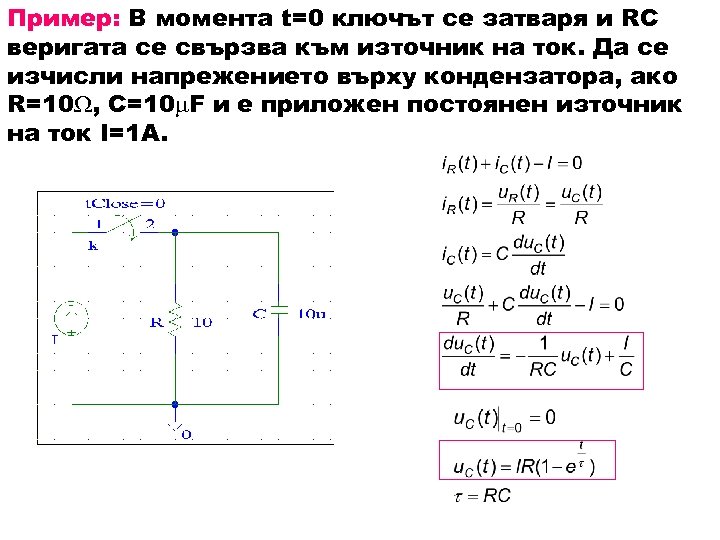Пример: В момента t=0 ключът се затваря и RC веригата се свързва към източник на ток. Да се изчисли напрежението върху кондензатора, ако R=10 , C=10 F и е приложен постоянен източник на ток I=1 A.

Файл-функции – зареждане на кондензатор 1. RC 1 diff. m – диференциално уравнение function duc=RC 1 diff(t, uc, options, I, R, C) tau=R*C; duc(1)=-uc(1)/tau+I/C; 2. RC 1. m – аналитично решение function u=RC 1(R, C, I, t) tau=R*C; u=I*R*(1 -exp(-t/tau))

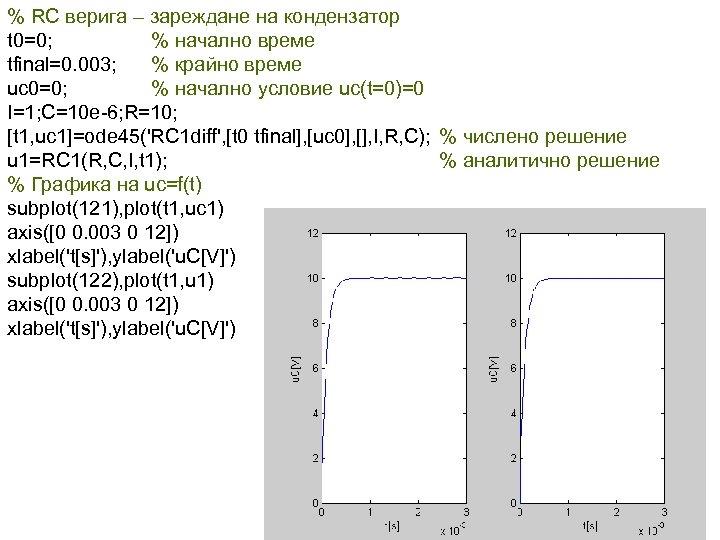% RC верига – зареждане на кондензатор t 0=0; % начално време tfinal=0. 003; % крайно време uc 0=0; % начално условие uc(t=0)=0 I=1; C=10 e-6; R=10; [t 1, uc 1]=ode 45('RC 1 diff', [t 0 tfinal], [uc 0], [], I, R, C); % числено решение u 1=RC 1(R, C, I, t 1); % аналитично решение % Графика на uc=f(t) subplot(121), plot(t 1, uc 1) axis([0 0. 003 0 12]) xlabel('t[s]'), ylabel('u. C[V]') subplot(122), plot(t 1, u 1) axis([0 0. 003 0 12]) xlabel('t[s]'), ylabel('u. C[V]')

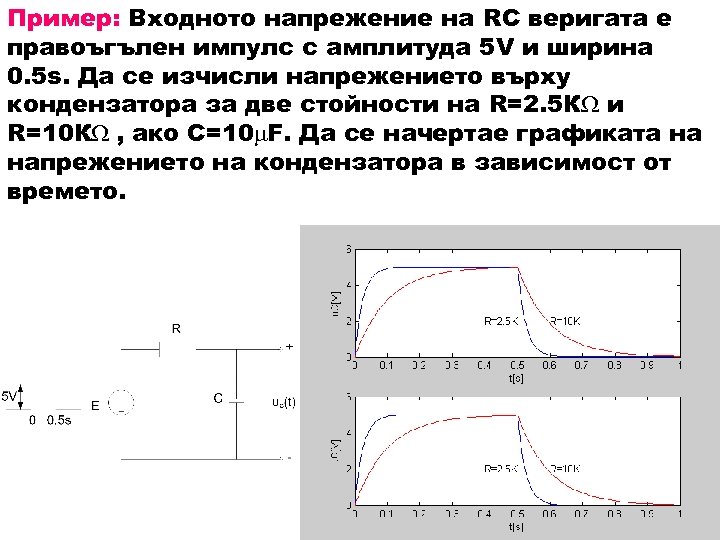Пример: Входното напрежение на RC веригата е правоъгълен импулс с амплитуда 5 V и ширина 0. 5 s. Да се изчисли напрежението върху кондензатора за две стойности на R=2. 5 К и R=10 К , ако C=10 F. Да се начертае графиката на напрежението на кондензатора в зависимост от времето.

Файл-функции 1. Разреждане на кондензатор RCDdiff. m – диференциално уравнение function duc=RCDdiff(t, uc, options, Um, R, C) tau=R*C; duc(1)=-uc(1)/tau; RCD. m – числено решение function u=RCD(R, C, Um, t) tau=R*C; u=Um*exp(-t/tau) 2. Зареждане на кондензатор RCdiff. m – диференциално уравнение function duc=RCdiff(t, uc, options, E, R, C) tau=R*C; duc(1)=-uc(1)/tau+E/tau; RC. m – числено решение function u=RC(R, C, E, t) tau=R*C; u=E*(1 -exp(-t/tau))

% RC верига t 0=0; tfinal=0. 5; uc 0=0; E=5; C=10 e-6; % начално време % крайно време % начално условие uc(t=0)=0 % амплитуда на правоъгълния импулс R=2. 5 e 3; % Числено решение [t 11, uc 11]=ode 45('RCdiff', [t 0 tfinal], [uc 0], [], E, R, C); Um=uc 11(end); [t 12, uc 12]=ode 45('RCDdiff', [t 0 tfinal], [Um], [], Um, R, C); % зареждане на C % начално условие % разреждане на C % Аналитично решение u 11=RC(R, C, E, t 11); Um=u 11(end); u 12=RCD(R, C, Um, t 12); % зареждане на C % начално условие % разреждане на C

R=10 e 3; % Числено решение [t 21, uc 21]=ode 45('RCdiff', [t 0 tfinal], [uc 0], [], E, R, C); Um=uc 21(end); [t 22, uc 22]=ode 45('RCDdiff', [t 0 tfinal], [Um], [], Um, R, C); % зареждане на C % начално условие % разреждане на C % Аналитично решение u 21=RC(R, C, E, t 21); Um=u 21(end); u 22=RCD(R, C, Um, t 22); % зареждане на C % начално условие % разреждане на C % Графика на uc=f(t) – числено решение subplot(211), plot(t 11, uc 11, 'b', t 12+0. 5, uc 12, 'b', t 21, uc 21, 'r', t 22+0. 5, uc 22, 'r') axis([0 1 0 6]), xlabel('t[s]'), ylabel('u. C[V]') text(0. 4, 2. 0, 'R=2. 5 K'), text(0. 6, 2. 0, 'R=10 K') % Графика на uc=f(t) – аналитично решение subplot(212), plot(t 11, u 11, 'b', t 12+0. 5, u 12, 'b', t 21, u 21, 'r', t 22+0. 5, u 22, 'r') axis([0 1 0 6]), xlabel('t[s]'), ylabel('u. C[V]') text(0. 4, 2. 0, 'R=2. 5 K'), text(0. 6, 2. 0, 'R=10 K')

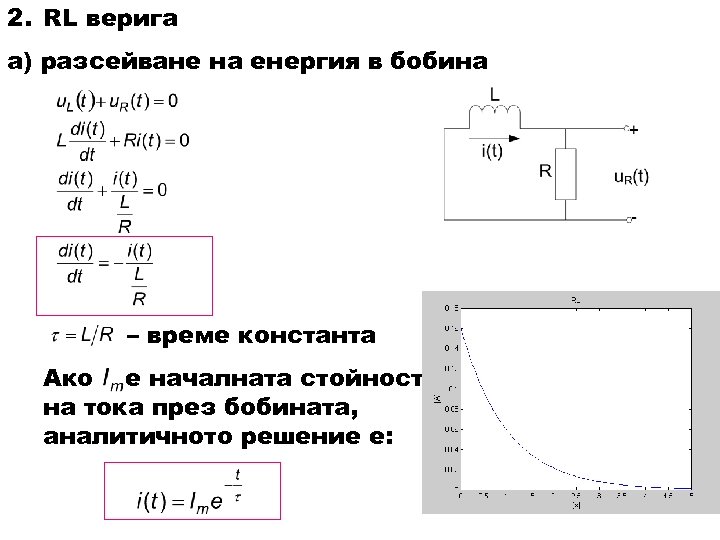2. RL верига а) разсейване на енергия в бобина – време константа Ако е началната стойност на тока през бобината, аналитичното решение е:

б) натрупване на енергия в бобина Ако началната стойност на тока през бобината е 0, , решението е:

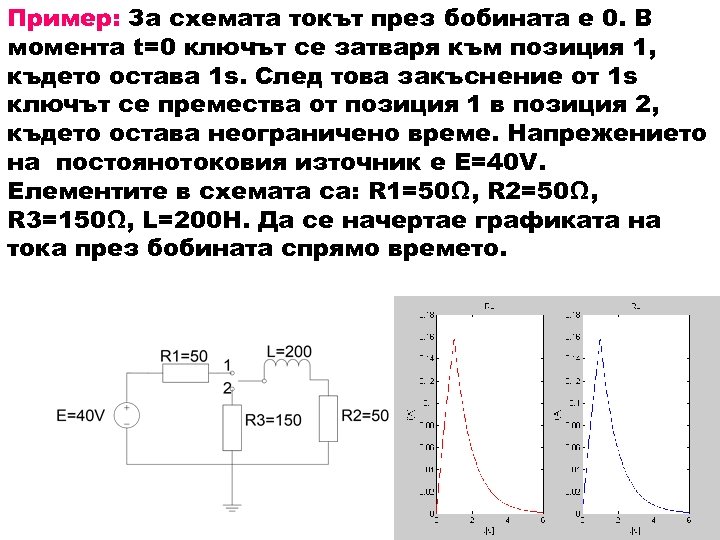Пример: За схемата токът през бобината е 0. В момента t=0 ключът се затваря към позиция 1, където остава 1 s. След това закъснение от 1 s ключът се премества от позиция 1 в позиция 2, където остава неограничено време. Напрежението на постоянотоковия източник е E=40 V. Елементите в схемата са: R 1=50Ω, R 2=50Ω, R 3=150Ω, L=200 H. Да се начертае графиката на тока през бобината спрямо времето.

Файл-функции 1. Разсейване на енергията в бобина RLDdiff. m – диференциално уравнение function di. L=RLDdiff(t, i. L, options, Im, R, L) tau=L/R; di. L(1)=-i. L(1)/tau; RLD. m – числено решение function i=RLD(R, L, Im, t) tau=L/R; i=Im*exp(-t/tau) 2. Натрупване на енергия в бобина RLdiff. m – диференциално уравнение function di. L=RLdiff(t, i. L, options, E, R, L) tau=L/R; di. L(1)=-i. L(1)/tau+E/L; RL. m – числено решение function i=RL(R, L, E, t) tau=L/R; i=E/R*(1 -exp(-t/tau))

% RL верига R 1=50; R 2=50; R 3=150; L=200; E=40; R=R 1+R 2; % ключът е в позиция 1 – натрупване на енергия в L t 0=0; % начално време tfinal=1; % крайно време i. L 0=0; % начално условие i. L(t=0)=0 [t 1, i. L 1]=ode 45('RLdiff', [t 0 tfinal], [i. L 0], [], E, R, L); % числено решение i 1=RL(R, L, E, t 1); % аналитично решение R=R 2+R 3; % ключът е в позиция 2 – разсейване на енергия в L t 0=0; % начално време tfinal=5; % крайно време Im=i. L 1(end); % начално условие [t 2, i. L 2]=ode 45('RLDdiff', [t 0 tfinal], [Im], [], Im, R, L); % числено решение Im=i 1(end); % начално условие i 2=RLD(R, L, Im, t 2); % аналитично решение % Графика на i. L=f(t) – числено решение subplot(121), plot(t 1, i. L 1, 'r', t 2+1, i. L 2, 'r') axis([0 6 0 0. 18]), xlabel('t[s]'), ylabel('i[A]'), title('RL') % Графика на i. L=f(t) – аналитично решение subplot(122), plot(t 1, i 1, 'b', t 2+1, i 2, 'b') axis([0 6 0 0. 18]), xlabel('t[s]'), ylabel('i[A]'), title('RL')

3. RLC верига

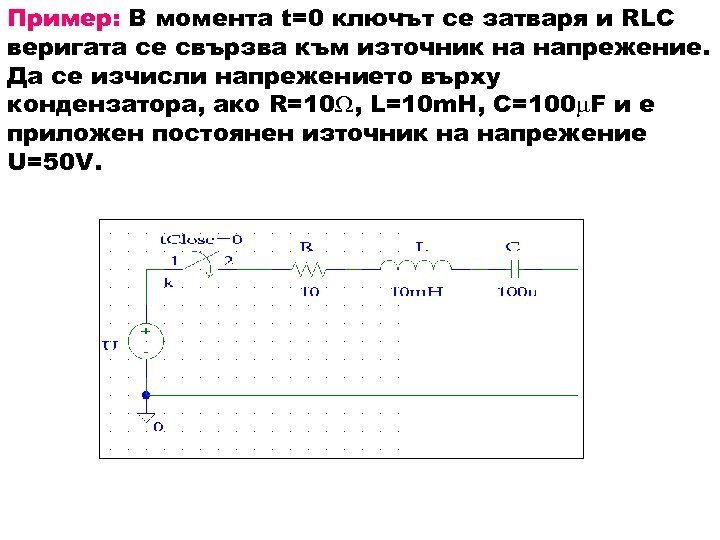Пример: В момента t=0 ключът се затваря и RLC веригата се свързва към източник на напрежение. Да се изчисли напрежението върху кондензатора, ако R=10 , L=10 m. H, C=100 F и е приложен постоянен източник на напрежение U=50 V.

Файл-функция RLC. m – RLC верига function dy=RLC(t, y, options, u, R, L, C) dy=zeros(2, 1); a=1/L; b=R/L; c=1/C; dy(1)=a*u-b*y(1)-a*y(2); dy(2)=c*y(1); % RLC верига U=50; R=10; L=10 e-3; C=100 e-6; t 0=0; % начално време tfinal=30 e-3; % крайно време i. L 0=0; % начално условие i. L(t=0)=0 u. C 0=0; % начално условие u. C(t=0)=0 [t, x]=ode 45('RLC', [t 0 tfinal], [i. L 0 u. C 0], [], U, R, L, C); plot(t, x(: , 1), 'b', t, x(: , 2), 'r') axis([0 30 e-3 -10 60]), xlabel('t[s]') text(0. 015, 2, 'i. L(t)'), text(0. 015, 52, 'u. C(t)') % числено решение

II. Числено интегриране Квадратура е числен метод за апроксимация на площта под графиката на функцията f(x), дефинирана върху интервала [a, b], т. е. определен интеграл: quad('f', a, b) – изчислява определен интеграл от f(x) от a до b с относителна грешка 1 е-3, като използва адаптивното правило на Simpson; 'f' е символен низ, съдържащ името на функцията; връща вектор от изходните стойности, ако е даден вектор с входни стойности; връща q=inf, ако е достигнато крайно ниво на рекурсия.

quad('f', a, b, tol) – интегрира, докато се достигне относителна грешка tol; за определяне на относителна и абсолютна грешка се използва tol=[относителна_грешка, абсолютна грешка]. quad('f', a, b, tol, trace) – интегрира до относителна грешка tol и при ненулева стойност на trace изчертава графика, показваща процеса на интегрирането. quad('f', a, b, tol, trace, p 1, p 2, . . . ) – позволява директно предаване на параметрите p 1, p 2, . . . към функцията f(x, p 1, p 2, . . . ); за да се използват подразбиращите се стойности за tol и trace, те се предават в празна матрица [ ]. quad работи с нелинейни функции f(x, p 1, p 2, . . . ) на скаларна променлива, т. е. една функция работи с друга функция; нелинейната функция f се представя чрез. m файл, чието име съвпада с името на функцията.

1. Интегриране на » q=quad('sin', 0, pi, [], 1) q= 2. 0000 .

2. Интегриране на » q=quad('sin', 0, 2*pi, [], 1) q= 0 .

3. Апроксимация на числото чрез Файл-функция p. m: function y=p(x) y=4. /(1. +x. ^2); » q=quad('p', 0, 1); » q q= 3. 1416

Полиноми I. Нули на полином r=roots(p) p – вектор-ред, съдържа коефициентите на полинома в намаляващ ред r – вектор-стълб, съдържа корените на полинома p Пример: » p=[1 -6 -72 -27]; » r=roots(p) r= 12. 1229 -5. 7345 -0. 3884

II. Коефициенти на полином p=poly(r) r – вектор-стълб, съдържа корените на полином p – вектор-ред, съдържа коефициентите на полинома в намаляващ ред Пример: Корените на полином са 12. 1229, -5. 7345 и -0. 3884 » r=[12. 1229 -5. 7345 -0. 3884]'; » p=poly(r) p= 1. 0000 -6. 0000 -72. 0000 -27. 0011

III. Стойност на полином y=polyval(p, s) p – вектор-ред с дължина n+1, съдържа коефициентите на полинома в намаляващ ред s – вектор-ред, съдържа стойности, за които полиномът ще се изчислява y – вектор-ред, съдържа изчислените стойности на полинома Пример: Стойности на полинома при s=1, 2 и 3 » p=[1 -6 -72 -27]; » s=[1 2 3]; » y=polyval(p, s) y= -104 -187 -270

IV. Апроксимиране с полином p=polyfit(x, y, n) x, y – данните, които се апроксимират n – степен на полинома p – вектор-ред с дължина n+1, съдържа коефициентите на полинома в намаляващ ред, който апроксимира p(x(i)) към y(i)

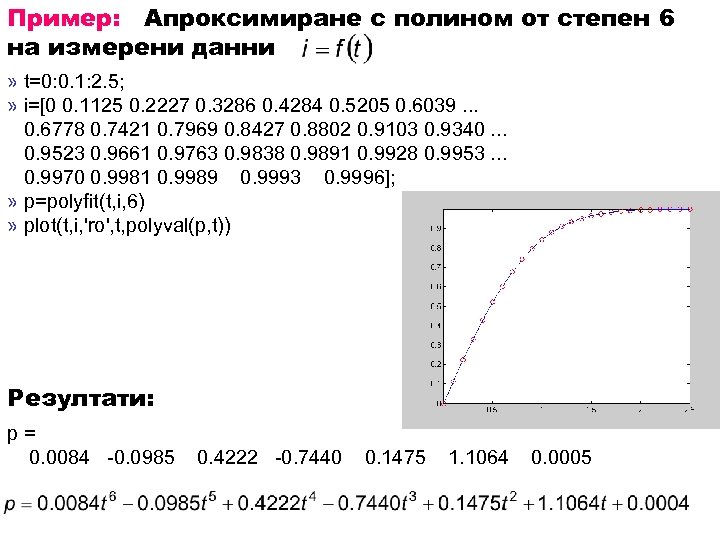Пример: Апроксимиране с полином от степен 6 на измерени данни » t=0: 0. 1: 2. 5; » i=[0 0. 1125 0. 2227 0. 3286 0. 4284 0. 5205 0. 6039. . . 0. 6778 0. 7421 0. 7969 0. 8427 0. 8802 0. 9103 0. 9340. . . 0. 9523 0. 9661 0. 9763 0. 9838 0. 9891 0. 9928 0. 9953. . . 0. 9970 0. 9981 0. 9989 0. 9993 0. 9996]; » p=polyfit(t, i, 6) » plot(t, i, 'ro', t, polyval(p, t)) Резултати: p= 0. 0084 -0. 0985 0. 4222 -0. 7440 0. 1475 1. 1064 0. 0005

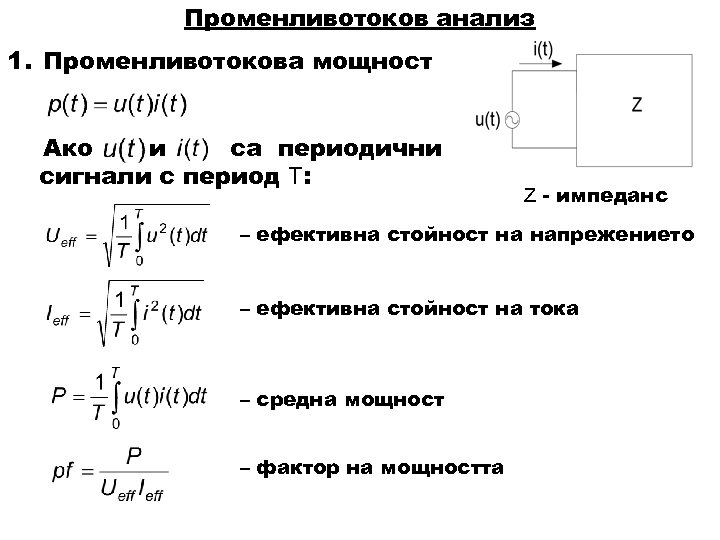Променливотоков анализ 1. Променливотокова мощност Ако и са периодични сигнали с период T: Z - импеданс – ефективна стойност на напрежението – ефективна стойност на тока – средна мощност – фактор на мощността

Ако и са синусоидални: то: – реактивна мощност – комплексна мощност – кръгова честота – преобразуване на ъгъл от градуси в радиани

Пример: Да се изчислят средната мощност, ефективните стойности на напрежението и тока, фактора на мощността (аналитично и числено), ако и. Файл-функции voltage. m function u 2=voltage(t) u 2=(10*cos(120*pi*t+60*pi/180)). ^2; current. m function i 2=current(t) i 2=(6*cos(120*pi*t+30*pi/180)). ^2; power_average. m function p=power_average(t) i=6*cos(120*pi*t+30. 0*pi/180); u=10*cos(120*pi*t+60. 0*pi/180); p=i. *u;

w=120*pi; % кръгова честота T=2*pi/w; % период на синусоидата % Числено решение a=0; % долна граница на интеграла b=T; % горна граница на интеграла u=quad('voltage', a, b); Ueff=sqrt(u/T); i=quad('current', a, b); Ieff=sqrt(i/T); p=quad('power_average', a, b); P=p/T; pf=P/(Ueff*Ieff); % Аналитично решение Ueffa=10/sqrt(2); Ieffa=6/sqrt(2); Pa=Ueffa*Ieffa*cos(30*pi/180); pfa=cos(30*pi/180); % Извеждане на резултатите disp('Ueff'), disp(Ueffa); disp('Ieff'), disp(Ieffa); disp('P'), disp(Pa); disp('pf'), disp(pfa); Резултати: Ueff 7. 0711 Ieff 4. 2426 P 25. 9808 pf 0. 8660

2. Комплексна форма на напреженията и токовете – амплитуда – начална фаза Ако , то , – комплексно напрежение. – комплексна амплитуда на напрежението – комплексна честота Ако е напълно синусоидално,

3. Предавателна функция Комплексно честотно представяне – предавателна функция – разлагане на множители – константа – нули – полюси – дробни части

[r, p, k]=residue(num, den) num – вектор-ред, съдържа коефициентите на полинома-числител в намаляващ ред den – вектор-ред, съдържа коефициентите на полинома-знаменател в намаляващ ред r – вектор-стълб, съдържа остатъците от частното на num и den p k – вектор-стълб, съдържа полюсите – вектор-ред, съдържа директните изрази

Пример: За RLC веригата намерете: – предавателната функция ; – нулите и полюсите на ; – , ако. – предавателна функция => комплексна честота – комплексна амплитуда на входното напрежение – комплексна амплитуда на изходното напрежение

R=10; L=10 e-3; C=100 e-6; % Разлагане на множители на предавателната функция num=[R/L 0]; den=[1 R/L 1/(L*C)]; z=roots(num); % нули p=roots(den); % полюси disp('z'), disp(z); % изобразява изчислените величини disp('p'), disp(p); [r, p, k]=residue(num, den); % разлагане на дроби на предавателната disp('r'), disp(r); % функция disp('p'), disp(p); disp('k'), disp(k); % Стойност на предавателната функция при дадена комплексна честота s=-3+j*2; % комплексна честота n=polyval(num, s); d=polyval(den, s); % Изходно напрежение Uout=10*exp(j*40*pi/180)*n/d; % комплексна амплитуда Um=abs(Uout); % амплитуда fi=angle(Uout)*180/pi; % начална фаза в градуси disp('Um'), disp(Um); disp('fi'), disp(fi);

Резултати: z 0 p 1. 0 e+002 * -5. 0000 + 8. 6603 i -5. 0000 - 8. 6603 i r 1. 0 e+002 * 5. 0000 + 2. 8868 i 5. 0000 - 2. 8868 i p 1. 0 e+002 * -5. 0000 + 8. 6603 i -5. 0000 - 8. 6603 i k Um 0. 0362 fi -173. 8043

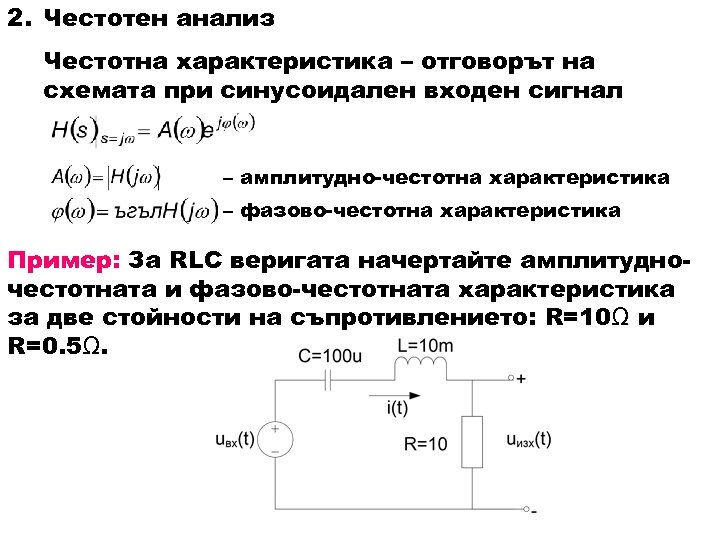2. Честотен анализ Честотна характеристика – отговорът на схемата при синусоидален входен сигнал – амплитудно-честотна характеристика – фазово-честотна характеристика Пример: За RLC веригата начертайте амплитудночестотната и фазово-честотната характеристика за две стойности на съпротивлението: R=10Ω и R=0. 5Ω.

Файл-функция transfer. m – предавателна функция function h=transfer(w, R, L, C) h=(j*w*(R/L)). /((j*w). ^2+j*w*(R/L)+1/(R*C)); L=10 e-3; C=100 e-6; w=[0. 1: 10^4]; R=10; H 1=transfer(w, R, L, C); R=0. 5; H 2=transfer(w, R, L, C); f=w/(2*pi); % Графика на амплитудно-честотните характеристики на RLC верига subplot(221), loglog(f, abs(H 1), 'b'), grid on, ylabel('|H(jomega)'), xlabel('f[Hz]'); subplot(222), loglog(f, abs(H 2), 'r'), grid on, ylabel('|H(jomega)'), xlabel('f[Hz]'); % Графика на фазово-честотните характеристики на RLC верига subplot(223), semilogx(f, angle(H 1)*180/pi, 'b'), grid on; ylabel('angle. H(jomega)(circ)'), xlabel('f[Hz]'); subplot(224), semilogx(f, angle(H 2)*180/pi, 'r'), grid on; ylabel('angle. H(jomega)(circ)'), xlabel('f[Hz]'); ,

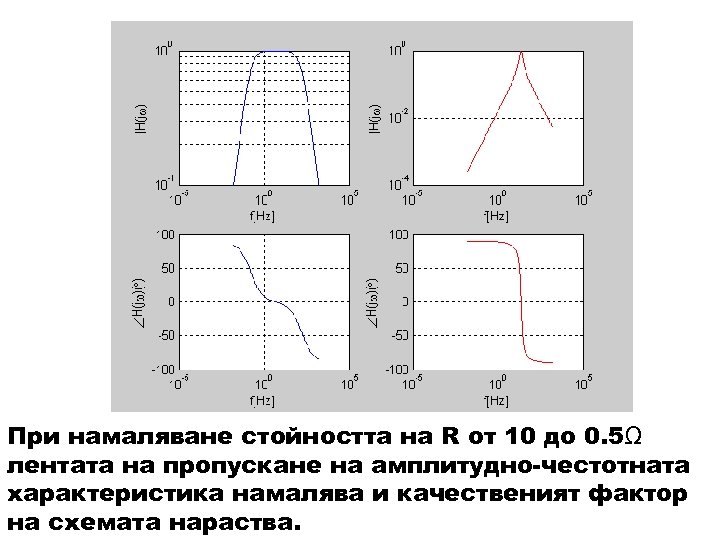При намаляване стойността на R от 10 до 0. 5Ω лентата на пропускане на амплитудно-честотната характеристика намалява и качественият фактор на схемата нараства.