Интеллектуальные информационные системы Лекция 8 Логическая модель представления

Интеллектуальные информационные системы Лекция 8 Логическая модель представления знаний.

План лекции 1. Методы доказательств в логической модели. 2. 3. доказательство на основе гипотетических допущений. доказательство «от противного» : доказательство с применением «правила резолюций» . Преимущества и недостатки логических моделей. Практические замечания. 2

Логическая модель. Основу системы доказательств в формальнологической модели ПЗ составляют методы дедуктивного вывода, применяемые к высказываниям, находящимся на более высоком уровне абстракции, чем простое суждение. В основе их лежит понятие силлогизма – правила перехода от посылки к заключению. 3

Логическая модель. Дедуктивный вывод базируется на: 1. 2. 3. 4. 5. МРР (Мodus Рonendo Ponens). МТТ (Мodus Тollendo Tollens). МРТ (Мodus Рonendo Тollens). МТР (Мodus Тollendo Рonens). ЦЕПНОЕ ПРАВИЛО (ЦП). 4

Логическая модель. Системы методов логического вывода: 1. 2. Вычислить логическое значение многоместного высказывания, аргументами которого являются простые высказывания, истинность которых доказана или известна. Доказать истинность (или ложность) некой гипотезы, выраженной многоместным высказыванием, аргументами которого являются простые высказывания, истинность которых доказана или известна. 5

Логическая модель. Силлогизм – это одно из множества правил, определяющих правильный (с позиций логического формализма) переход от посылки к заключению. Логические функции, логические переменные, пять правил дедуктивного вывода и силлогизмы составляют аксиоматику методов логики. Теоремами логики являются тавтологии правильно построенные логические формулы (составные высказывания), логические значения которых всегда равны «И» (истинны) при любых логических значениях их аргументов (атомов или простых высказываний). 6

Логическая модель. Три метода доказательств: доказательство на основе гипотетических допущений; доказательство «от противного» : доказательство с применением «правила резолюций» . 7

Доказательство на основе гипотетического допущения Доказываемое высказывание вначале приводится к виду импликации, конъюнкции или дизъюнкции (естественно, если такое приведение не противоречит исходной структуре), так чтобы один операнд был заведомо истинным или ложным. Затем применяется одно из аксиоматических правил дедуктивного вывода и на его основе делается результирующий вывод. 8

Доказательство «от противного» Вместо высказывания, которое надо доказать, формулируется противоречивое ему высказывание, которое и доказывается. Если противоречивое высказывание окажется истинным, то исходное должно быть ложным, и – наоборот. Противоречие может быть выражено либо по форме, либо по содержанию. Противоречие по форме предполагает выбор новой формулировки, но с теми же логическими значениями операндов. Противоречие по содержанию предполагает сохранение формулировки исходного предиката с заменой логических значений операндов на противоположные. 9

Доказательство с применением «правила резолюций» Метод резолюций опирается на исчисление резольвент. Существует теорема, утверждающая, что вопрос о доказуемости произвольной формулы в исчислении предикатов сводится к вопросу о доказуемости пустого списка в исчислении резольвент. Поэтому доказательство того, что список формул в исчислении резольвент пуст, эквивалентно доказательству ложности формулы в исчислении предикатов. 10

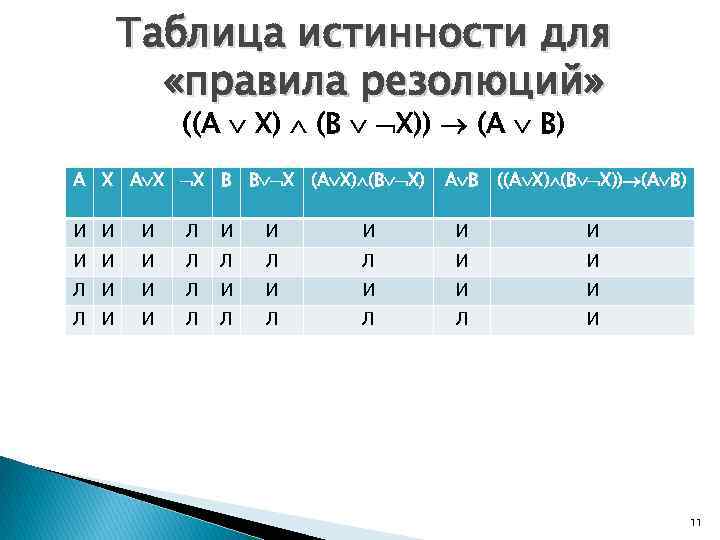Таблица истинности для «правила резолюций» ((A X) (B X)) (A B) A X X B B X (A X) (B X) A B ((A X) (B X)) (A B) И И И Л И И И И Л Л И И И Л И И Л Л Л И 11

Доказательство с применением «правила резолюций» Идея метода резолюций заключается в том, что доказательство истинности или ложности выдвинутого предположения ведется методом от противного. Для этого в исходное множество предложений включают аксиомы формальной системы и отрицание доказываемой гипотезы. Если в процессе доказательства возникает противоречие между отрицанием гипотезы и аксиомами, выражающееся в нахождении пустого списка (дизъюнкта), то выдвинутая гипотеза правильна. 12

Доказательство с применением «правила резолюций» В методе резолюций множество предложений обычно рассматривается как составной предикат, содержащий несколько предикатов, соединенных логическими функциями и кванторами существования и общности. Предложения преобразуются в клаузальную форму – разновидность (КНФ), в которой удалены кванторы существования, всеобщности, символы импликации, равнозначности и др. Клаузальную форму называют сколемовской конъюнктивной формой. 13

Доказательство с применением «правила резолюций» Клаузальное множество S=(C 1) (C 2) (C 3) … (Cn) Предложение Ci=(Pi 1) … (Pim) Атомарные предикаты или их отрицания – дизъюнкты. 14

Доказательство с применением «правила резолюций» Сущность метода резолюций состоит в проверке, содержит или не содержит S пустое предложение. Предложение является пустым, если не содержит никаких литер. Так как условием истинности S является истинность всех предложений, входящих в S, то ложность какого-либо предложения указывает на ложность исходной логической формулы. 15

Доказательство с применением «правила резолюций» Если S содержит пустое предложение Сi , то S противоречиво (невыполнимо). Иначе делается попытка вывода предложений C(i+1), C(i+2), … пока не будет получено пустое (что всегда будет иметь место для невыполнимого S). Для этого в двух предложениях, одно из которых состоит из одной литеры, а второе содержит произвольное число литер, находится контрарная пара литер, которая вычеркивается, а из оставшихся частей формируется новое предложение - резольвента. 16

Доказательство с применением «правила резолюций» Поскольку допускается наличие переменных, то для нахождения контрарных пар требуется введение операции унификации (подстановки константы вместо переменной в предикаты, имеющие одинаковые предикатные символы, но разные литеры). Чтобы унифицировать два различных выражения, отыскивается наиболее общий унификатор (подстановка, при которой выражение с большей описательной мощностью согласуется с выражением, имеющим малую описательную мощность). 17

Доказательство с применением «правила резолюций» Унификация предикатных логических формул 1. Исключение операций эквивалентности. 2. Исключение операций импликации. 3. Внесение операций отрицания внутрь формул. 4. Исключение кванторов существования. 5. Кванторы общности выносятся на первые места в формулах. 6. Раскрытие конъюнкций, попавших внутрь дизъюнкций. 18

Доказательство с применением «правила резолюций» Если задана теория Тh и предстоит сделать заключение о том, выводима ли некоторая формула Р из Тh, строится P и добавляется к Тh, при этом получают новую теорию Тh 1. После приведения P и аксиом Th к системе дизъюнктов можно построить конъюнкцию P и аксиом Тh. При этом существует возможность выводить из исходных дизъюнктов дизъюнкты следствия. Если Р выводимо из аксиом теории Тh, то в процессе вывода можно получить Q, состоящий из одной литеры, и Q. Это свидетельствует о том, что Р выводимо из Тh. 19

Доказательство с применением «правила резолюций» 1. Устранение операций эквивалентности и импликации: A<->B=(A->B) (B->A); A- >B= A B. 2. Операция отрицания продвигается внутрь формул с помощью законов де Моргана: (A B)= A B; (A B)= A B 3. Логические формулы приводятся к дизъюнктивной форме: A (B C)=(A B) (A C) 20

Доказательство с применением «правила резолюций» Правило резолюции содержит в левой части конъюнкцию дизъюнктов, поэтому приведение посылок, используемых для доказательства, к виду, представляющему собой конъюнкции дизъюнктов, является необходимым этапом практически любого алгоритма, реализующего логический вывод на базе метода резолюции. Метод резолюции легко программируется, это одно из важнейших его достоинств. 21

Доказательство с применением «правила резолюций» Дано: P->R, R Q, Q -> S. Верно ли (R S) ? 1. P R, R Q, Q S 2. (R S)= R S 3. ( P R) ( R)= P ( P Q) ( P)= Q ( Q S) ( S)= Q 22

Доказательство с применением «правила резолюций» Пример: «Если студент умеет хорошо программировать, то он может стать специалистом в области прикладной информатики» . «Если студент хорошо сдал экзамен по информационным системам, значит, он умеет хорошо программировать» . 23

Доказательство с применением «правила резолюций» X — переменная для обозначения студента; хорошо — константа, соответствующая уровню квалификации; Р(Х) — предикат, выражающий возможность субъекта X стать специалистом по прикладной информатике; Q(Х, хорошо) — предикат, обозначающий умение субъекта X программировать с оценкой хорошо; R(Х, хорошо) — предикат, задающий связь студента X с экзаменационной оценкой по информационным системам. 24

Доказательство с применением «правила резолюций» X Q(Х, хорошо)->P(X) X R(Х, хорошо)->Q(Х, хорошо). R(Иванов, хорошо). Является ли формула Р(Иванов) следствием вышеприведенной теории? 25

1. 2. 3. 4. 5. Доказательство с применением «правила резолюций» Выполним преобразование исходных формул теории в целях приведения к дизъюнктивной форме. Добавим к имеющимся аксиомам отрицание выводимого заключения. Построим конъюнкцию дизъюнктов, найдем резольвенту. Построим конъюнкцию дизъюнктов с использованием резольвенты. Запишем конъюнкцию полученной резольвенты с последним дизъюнктом теории. 26

Доказательство с применением «правила резолюций» Для определения порядка применения аксиом в процессе вывода существуют следующие эвристические правила: 1. 2. На первом шаге вывода используется отрицание выводимого заключения. В каждом последующем шаге вывода участвует резольвента, полученная на предыдущем шаге. 27

Особенности логических методов Использование логики для представления знаний дает возможность перейти от процедурного способа задания информации о предметной области к спецификации отношений между объектами, которые существуют в реальном мире. При этом программа является логической спецификацией задачи, а конкретное вычисление понимается как запрос к этой программе. База знаний представляет собой набор логических формул. Добавление или уничтожение логических формул означает модификацию базы знаний. Таким образом, логические формулы могут рассматриваться как неделимые единицы для манипулирования знаниями в таких системах. 28

Преимущества 1. 2. 3. Наличие регулярных методов вывода, в терминах которых можно определять процедуры доказательства Возможность использования семантики, которая допускает разную трактовку в зависимости от целей логических представлений. Простота , лаконичность и единообразие употребляемой нотации для представления знаний о ПО. 29

Недостатки 1. 2. Отсутствие принципов структуризации логических формул, составляющих основу базы знаний. . Применение этого типа моделей ПЗ в сферах промышленного производства или в системах управления сложными структурами не может дать приемлемого результата из-за сложности применения таких моделей, из-за жестких требований к оперативности получения новых знаний и большого объема БЗ в системах, модели которых предусматривают не только абстракции, но и реальные объекты. 30

Практические замечания. При программировании системы логических выводов необходимо реализовать все атрибутивные процедуры метода резолюции: описание свойств объектов и отношений между ними; определение правил, на основании которых могут образовываться различные типы отношений; определение правил формулирования вопросов о свойствах объектов и отношениях между ними. 31

Расширение системы Prolog • В процедуру унификации снова вводится проверка вхождения для того, чтобы эта процедура стала непротиворечивой. • Поиск в глубину заменяется поиском с итеративным углублением. Это позволяет добиться того, чтобы стратегия поиска стала полной, а увеличение продолжительности поиска измерялось лишь постоянной зависимостью от времени. 32

Расширение системы Prolog • Разрешается применение отрицаемых литералов (таких как ￢P(x)). В этой реализации имеется две отдельные процедуры; в одной из них предпринимается попытка доказать P, а в другой - доказать ￢P. 33

Расширение системы Prolog • Выражение с n атомами хранится в виде n различных правил. Например, при наличии в базе знаний выражения A<= B^ C должно быть также предусмотрено хранение в ней этого выражения, представленного как ￢B<= C ^ ￢A и как ￢C<= B ^ ￢A. Применение такого метода, известного под названием блокирование (locking), означает, что текущая цель требует унификации только с головой каждого выражения, и вместе с тем позволяет должным образом учитывать отрицание. 34

Расширение системы Prolog • Логический вывод сделан полным (даже для нехорновских выражений) путем добавления правила резолюции с линейным входным выражением: если текущая цель унифицируется с отрицанием одной из целей в стеке, то данная цель может рассматриваться как решенная. В этом состоит один из способов рассуждения от противного. Предположим, что первоначальной целью было высказывание P и что эта цель свелась в результате применения ряда этапов логического вывода к цели ￢P. Тем самым установлено, что ￢P => P, а это выражение логически эквивалентно P. 35

Расширение системы Prolog Программа PTTP сохраняет высокое быстродействие системы Prolog. Операции унификации осуществляются посредством непосредственной модификации переменных, а отмена связывания выполняется путем разгрузки контрольного стека во время возврата. Стратегия поиска основана на резолюции с применением входных выражений, а это означает, что в каждой операции резолюции участвует одно из выражений, содержащихся в первоначальной формулировке задачи. Такой подход позволяет осуществить компиляцию всех выражений из первоначальной формулировки задачи. 36

Расширение системы Prolog Основным недостатком программы PTTP является то, что пользователь должен отказаться от любых попыток взять на себя управление поиском решений. Каждое правило логического вывода в этой системе используется и в его первоначальной, и в контрапозитивной форме. Это может привести к выполнению таких операций поиска, которые противоречат здравому смыслу. 37