01 Integration.pptx
- Количество слайдов: 29

Integration 1

Today’s Objectives • Integration as the reverse of differentiation
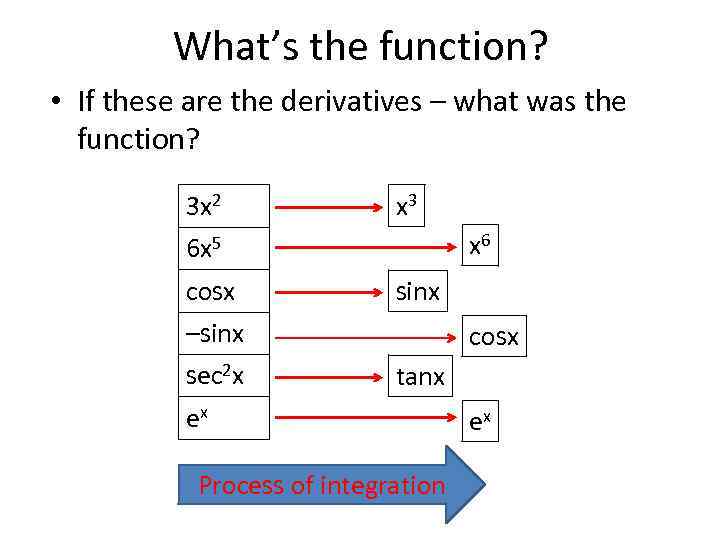
What’s the function? • If these are the derivatives – what was the function? 3 x 2 x 3 x 6 6 x 5 cosx sinx –sinx sec 2 x cosx tanx ex Process of integration ex

Integration • Integration is the reverse of differentiation but consider the following functions and their derivatives: Differentiation Function x 2 + 5 x 2 – 3 Derivative 2 x 2 x 2 x Integration - but which one?
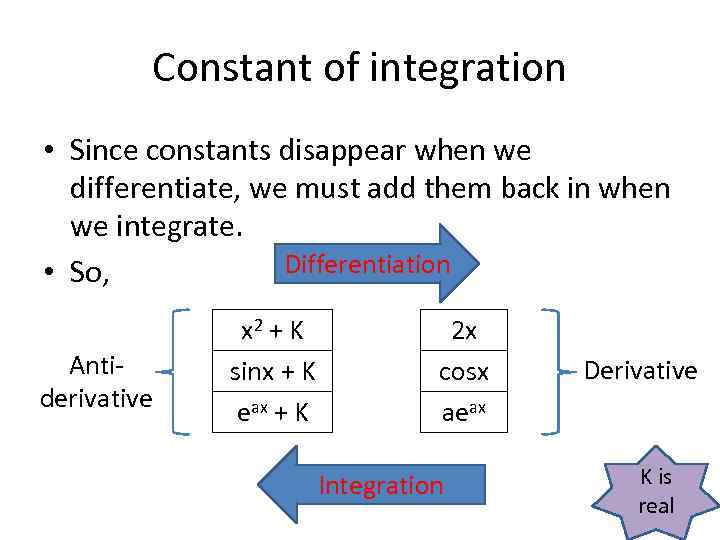
Constant of integration • Since constants disappear when we differentiate, we must add them back in when we integrate. Differentiation • So, Antiderivative x 2 + K sinx + K eax + K 2 x cosx aeax Integration Derivative K is real

Notation • We use d/dx to denote the operation of differentiation: • We use the following to denote the operation of integration: • Also,

Rules • From the above examples we can form the following rules: n is real c is real K is real

Integrating sums and differences • We found that differentiation is distributive, • And since integration is the reverse of differentiation then integration is also distributive,

Integrating (ax + b)n • We will consider differentiating (ax + b)n+1 by the chain rule: • So: • But a and n are constants and therefore:

Examples (polynomials) Integrate the following w. r. t. x: 1. 5 x 10 2. – 4/7 x 3 3. 3 x 1/2 4. 14/x 4/3 5. (2 x + 1)3 6. 1/(7 – x)2 7. 4/(6 – 5 x)1/2

Integrating trig • By the reverse of differentiation we already know:

Integrating trig • By reversing differentiation we also have:

Integrating sin(ax + b) and cos(ax + b) • Consider the derivatives of sin(ax + b) and cos(ax +b) to obtain the integrals of cos(ax + b) and sin(ax + b):

Examples (trig) Integrate the following w. r. t. x: 1. 5 sin(10 x – π/6) 2. 3 cos(π/4 – 18 x) 3. sec 2(π/3 + 5 x)

Integrating exponentials • Considering ex:

Integrating exponentials • Considering ax we must first change the base from a to e:

Integrating exponentials • Now we can integrate using the rules above for ex:

Examples (exponentials) Integrate the following w. r. t. x: 1. √(ex) 2. 3 e– 6 x + 4 3. 5 x

Integrating 1/x • Using the rule for integrating a polynomial and taking 1/x as x– 1 will result in dividing by zero and so we must use a different method. • We notice that: • And so: • But lnx is only defined for x > 0, so this result is only valid for x > 0. What about when x < 0?

Integrating 1/x • Consider the derivative of ln(–x) where –x > 0: • So: • Now if –x > 0 then x < 0. So this result is valid for x < 0.

Integrating 1/x • Combining these two results we have: • For x > 0: • For x < 0: • For all x:

Integrating c/x and 1/(ax + b) • Considering the reverse of the derivative we also have:

Examples (c/(ax + b)) Integrate the following w. r. t. x: 1. 7/x 2. 1/(15 x + 1) 3. 4/(16 x – 2)

Integrating quotients • The above is an example of integrating a quotient and we can clearly see that: • For differentiating we had the quotient rule. • Unfortunately, for integration there is not one rule for integrating all quotients. We will study more techniques next time.

Integrating products • Also for products: • For differentiating we had the product rule. • Again, unfortunately there is not one rule for integrating products and so we must study more than one technique. We will study more techniques next time.

In summary

In summary

In summary

In summary
01 Integration.pptx