06 Integration.pptx
- Количество слайдов: 36

Integration 06

Today’s Objectives • To understand that integration is the limit of summation and gives the area between a curve and the x-axis when f(x) ≥ 0. • To evaluate definite integrals, i. e. integrals between limits such as: • To establish reduction formulae between limits and then evaluate for specific values of n.
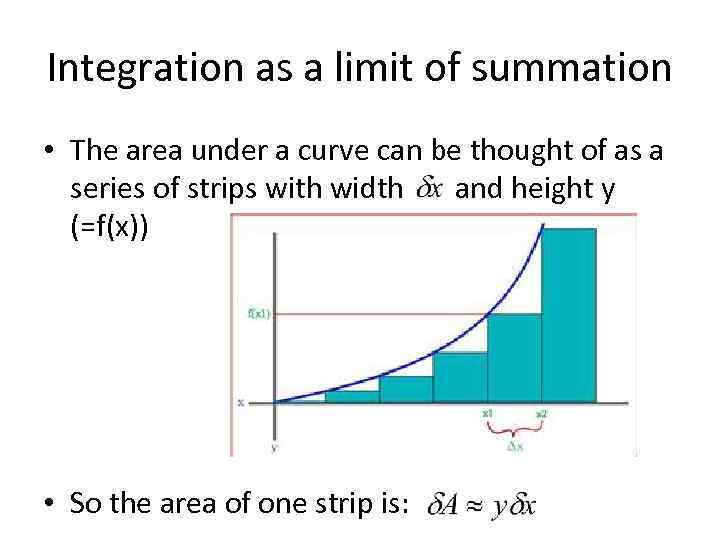
Integration as a limit of summation • The area under a curve can be thought of as a series of strips with width and height y (=f(x)) • So the area of one strip is:

Integration as a limit of summation • Now consider the graph: • Then the total area A between the boundary values of x = a and x = b is given by:

Integration as a limit of summation • Since the curve approaches the horizontal top of the rectangle as δx approaches zero, then the area of the strip approaches the area under the curve as δx approaches zero. • So,

Integration as a limit of summation • Now consider an alternative expression for A. • Considering the same starting point of the area of one strip: • Then rearranging gives: • As before, the approximation of δA becomes more accurate as δx approaches zero.

Integration as a limit of summation • So, • But, • So between x = a and x = b:

Integration as a limit of summation • Putting the two alternative equations for A together: • And therefore integration is a process of summation.
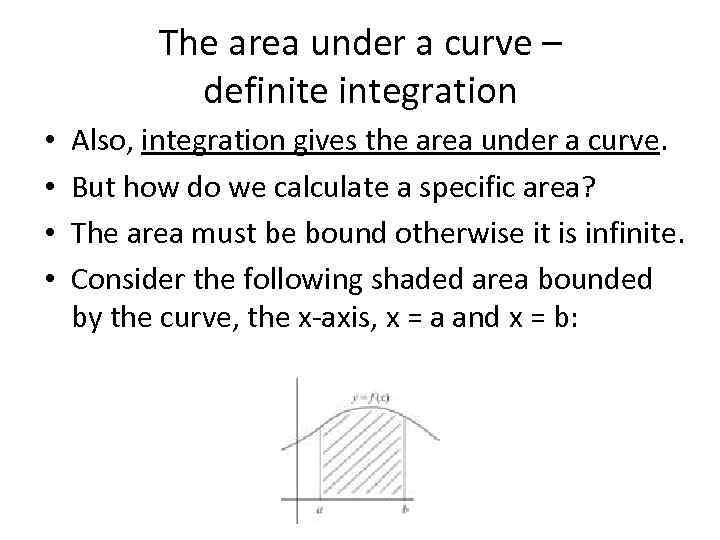
The area under a curve – definite integration • • Also, integration gives the area under a curve. But how do we calculate a specific area? The area must be bound otherwise it is infinite. Consider the following shaded area bounded by the curve, the x-axis, x = a and x = b:

The area under a curve – definite integration • We now know that the area under a curve = • If we evaluate the result of the integration, F(x), using x = a then we obtain: • However, the area under the curve at x = a is zero. • So,

The area under a curve – definite integration • Similarly, evaluating the result of the integration, F(x), at x = b gives: • However, for this curve and these boundaries, we know what C is:

The area under a curve – definite integration • Combining these results and adopting the standard notation for evaluating an integral between limits we obtain: • Integrating between limits is called definite integration.

Properties of definite integrals

Definite integration examples • We must be able to evaluate definite integrals using all the integration methods we have studied so far. • The following examples cover basic integrals, integrals by substitution, integrals by parts and reduction formulae.
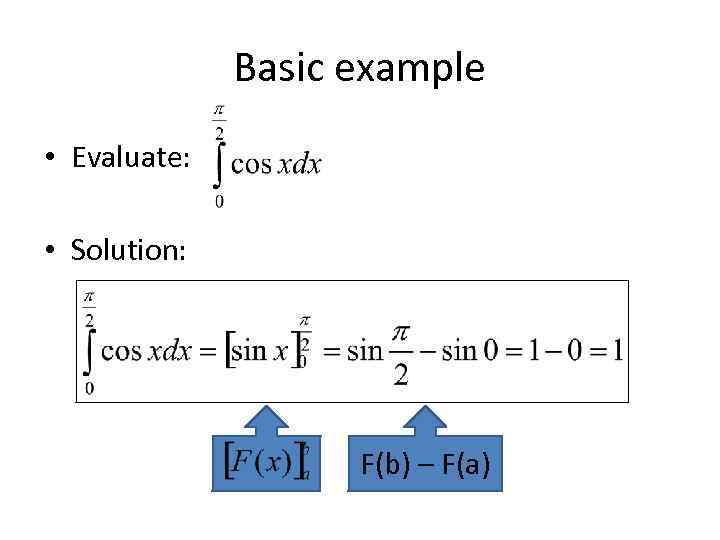
Basic example • Evaluate: • Solution: F(b) – F(a)

Substitution example • When we substitute then we have to substitute for x and ‘dx’. • When we have limits, then we will substitute for the limits too. This means that we do not have to convert back to the original variable after integration. • (Some people prefer to not substitute the limits but to convert back to the original variable after integration and then evaluate using the original limits).

Substitution example 1 • Evaluate:

Substitution example 1 Since the limits are values of u, then we don’t have to convert the function back to x. F(b) – F(a)

Substitution example 2 • Evaluate: Use principal values

Substitution example 2

Substitution example 2 F(b)- F(a)
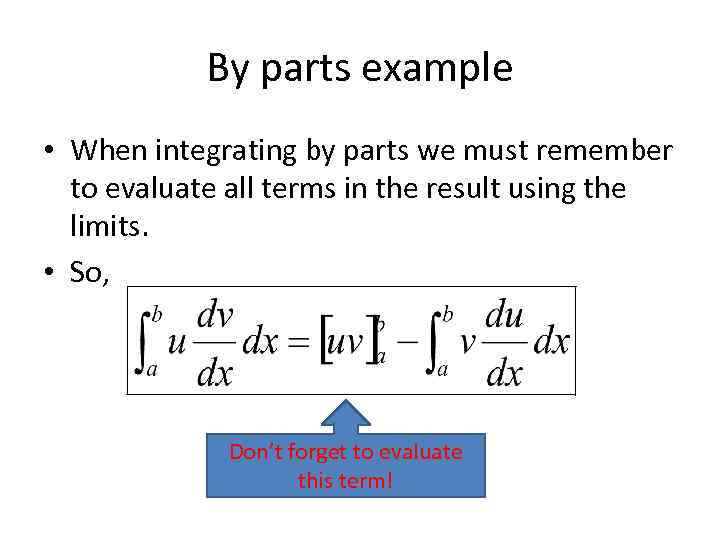
By parts example • When integrating by parts we must remember to evaluate all terms in the result using the limits. • So, Don’t forget to evaluate this term!

By parts example • Evaluate: F(b) – F(a)

Reduction formula example • Similarly for reduction formulae. • Since a reduction formula has more than one term, we must remember to evaluate all of the terms between the limits. • Consider the definite integrals for two of our previously established reduction formulae:

Previously established reduction formulae

Reduction formula example • The important thing is not to memorise specific reduction formula (definite or indefinite) but to understand the method of how to obtain the reduction formula. • As we have seen, this method will vary according to the type of function you are integrating. • Some reduction formulae simplify when limits are applied. For example, the two formulae above simplify when evaluated between 0 and π/2.

Definite reduction formulae

Definite reduction formulae • Notice that the definite integration for these limits produces the same result for both functions. • Now consider applying this result successively:

Definite reduction formulae • For specific values of n, the result will fall into two categories; when n is even and when n is odd. • Considering the formula we can see that when n is even ‘In – 2’ will reduce to ‘I 0’ and when n is odd ‘In – 2’ will reduce to ‘I 1’

Definite reduction formulae • Considering the pattern of the coefficients we can see that when n is even, the numerators are all successively odd in a decreasing order and the denominators are all successively even in a decreasing order, and when n is odd, the numerators are all even and the denominators are all odd.

Definite reduction formula • So when n is even, • And when n is odd,

Definite reduction formula • We now have to evaluate the last term for both functions cosx and sinx: Same result for both I 0’s. Same result for both I 1’s.

Definite reduction formula • Putting all of these results together we obtain, • When n is even: • When n is odd:

Reduction formula example • Using a reduction formula, evaluate: • We can use the above even formula since the limits match and n = 8. We coe stop h ffic ien ere sin tw ill b ce th e ne ega x tive t.

Reduction formula example • Using a reduction formula, evaluate: • We can use the above odd formula since the limits match and n = 7. We stop here since the next coefficient will be zero.

Definite reduction formula • Note that these two formulae do not work for different limits: Different limit! Therefore, formula does NOT work!
06 Integration.pptx