Integration 05 Today s Objectives Integrating products

Integration 05

Today’s Objectives • Integrating products such as: • Integrating [f(x)]n when n is a large, positive integer such as:

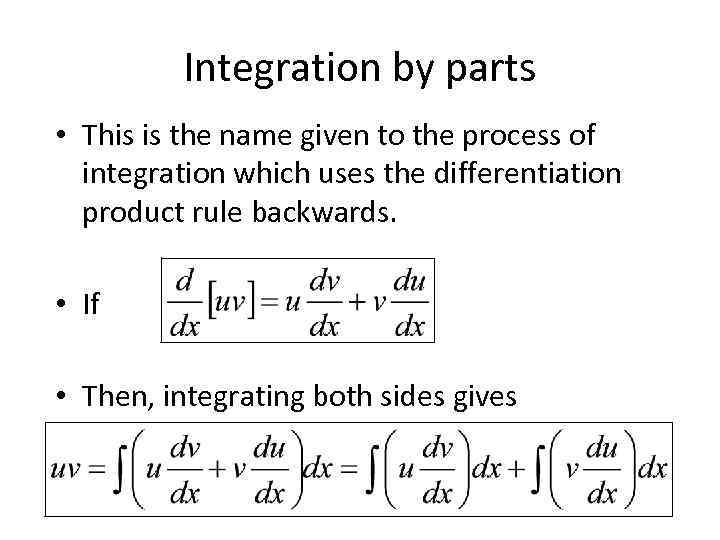
Integration by parts • This is the name given to the process of integration which uses the differentiation product rule backwards. • If • Then, integrating both sides gives

Integration by parts • Since we want a method of integrating a product, we need the integral of a product as the subject of our formula. Rearranging the above we obtain: • Using this formula is called integrating by parts where u and dv/dx are functions of x and form the product we must integrate.

Assigning u and dv • To use this formula we must assign one function to ‘u’ and one function to ‘dv’ – but how do we decide which function is ‘u’ and which function is ‘dv’? • When integrating by parts we will be differentiating ‘u’ and integrating ‘dv’. • So we assign the functions to make the differentiating and integrating as easy as possible for ourselves.

Assigning u and dv • There is a general rule that works in most cases. It is called the LIATE method. • The order of the letters in LIATE tell us which function to differentiate and which to integrate. • LIATE stands for Logarithmic, Inverse, Algebraic, Trigonometric, Exponential

Assigning u and dv • Decide which of these five categories your two functions are. • The function furthest to the left in the order of LIATE is the function to differentiate. • E. g. xcosx • Now, x is Algebraic and cosx is Trigonometric. In LIATE Algebraic is further to the left than Trigonometric so we differentiate x. Therefore u=x and dv=cosx.

Example 1: xcosx • Using LIATE we will assign x and cosx so that we differentiate x and integrate cosx:

Repeating the process • Sometimes it is necessary to integrate by parts more than one in the same question.

Example 2: x 2 cosx • Using LIATE we will assign x 2 and cosx so that we differentiate x 2 and integrate cosx:

Example 2: x 2 cosx • Now we will use integration by parts again for 2 xsinx:

Multiply the function by 1 • Some functions are very difficult to integrate. • Since integration by parts involves differentiating one of the factors, we can treat the difficult function as if it is multiplied by 1. • Therefore, we can differentiate the difficult function and integrate 1. • Using LIATE, 1 is considered Algebraic.

Example 3: lnx • Using LIATE we will assign 1 and lnx so that we differentiate lnx and integrate 1:

Example 4: arcsinx • Using LIATE we will assign 1 and arcsinx so that we differentiate arcsinx and integrate 1:

Example 4: arcsinx • We now use substitution to do the second integral:

Reappearance of original integral • Sometimes after repeating the method of integrating by parts the original integral reappears. • The original integrals can then be gathered together.

Example 5: excosx • Using LIATE we will assign ex and cosx so that we differentiate cosx and integrate ex:

Example 5: excosx • Now we must integrate by parts again:

Example 5: excosx • The original integral has reappeared and they can be gathered together:

Integrating secmxtannx when m is odd and n is even • We said previously that we needed to use integration by parts to integrate secmxtannx when m is odd and n is even. • We factor out a secx and/or a tanx to obtain a factor of secxtanx. • To assign ‘u’ and ‘dv’, LIATE is not helpful since all functions are trigonometric so we can choose how to assign ‘u’ and ‘dv’ to make the differentiating and integrating easier.

Example 6: secxtan 2 x • Since secx is already to the power of 1, we only have to factor out one tanx to obtain a factor of secxtanx:

Example 6: secxtan 2 x • We now have a reappearance of the original integral and so we can gather them together:

Reduction formula • We can use a reduction formula for integrating [f(x)]n where n is a large, positive integer. • We have already seen examples where the original integral reappears. • A reduction formula is when the original integral reappears but the power ‘n’ has been reduced by one or more. • Once you have a general reduction formula in terms of ‘n’, we can replace ‘n’ with any positive integer to find a specific integral.

Establish a reduction formula for • We will use integration by parts. • Since we want to reduce the power of ‘n’, we let ‘u’ equal the function raised to the power of ‘n’ or ‘n-1’, etc. so that when we differentiate ‘u’ the power is reduced.

Establish a reduction formula for • Notice that we take cosx out as a factor rather than considering the function as multiplied by 1 to ensure all of the terms remain trigonometric after differentiating and integrating.

Establish a reduction formula for • Integrating by parts:

Establish a reduction formula for • We now see the reappearance of the original integral exactly and the original integral with a reduced power. We can replace these with the In and In – 2 notation and gather like terms together:

Establish a reduction formula for • This is the reduction formula which can be used for any positive integer value of n.

Use a reduction formula to find

Establish a reduction formula for • The same method can be applied to find the reduction formula for the integral of sinnx. • The resulting reduction formula is:

Establish a reduction formula for • Now using tan 2 x = sec 2 x – 1:

Establish a reduction formula for • Hence the reduction formula for integrating tannx is:

Establish a reduction formula for • We can establish reduction formula for exponential functions too:

Establish a reduction formula for • Using the In – 1 notation we obtain the reduction formula:

Using a reduction formula find • From above:

Using a reduction formula find

Establish a reduction formula for • We can establish reduction formula for logarithmic functions too:

Establish a reduction formula for • Cancelling the x’s and using the In – 1 notation we obtain the reduction formula:

Using a reduction formula find • From above: