Integration 04
Today’s Objectives • Integrating expressions containing: • Integrating polynomial quotients suitable for the partial fraction method.
What have we already done? • Previously we have seen the following:
What have we already done? • We also saw that we could use alternative substitutions:
Another case… • There is a third example in this category:
What next? • Now we consider integrals containing: • Since n is a non-zero integer these terms may appear in the numerator or the denominator. • The integral may include other functions of x. • For example,
What’s the difference? • These examples look similar to the above first examples but the differences mean we cannot use the substitution u=bx/a. Numerators not denominators; Multiplied by another function of x and not of the form g’(x)f(g(x)) or g’(x)/f(g(x))
Which substitution to use? • We use the alternative substitutions mentioned above:
Examples Integrate the following wrt x:
Example 1
Example 2
Example 3
Example 3
Example 4
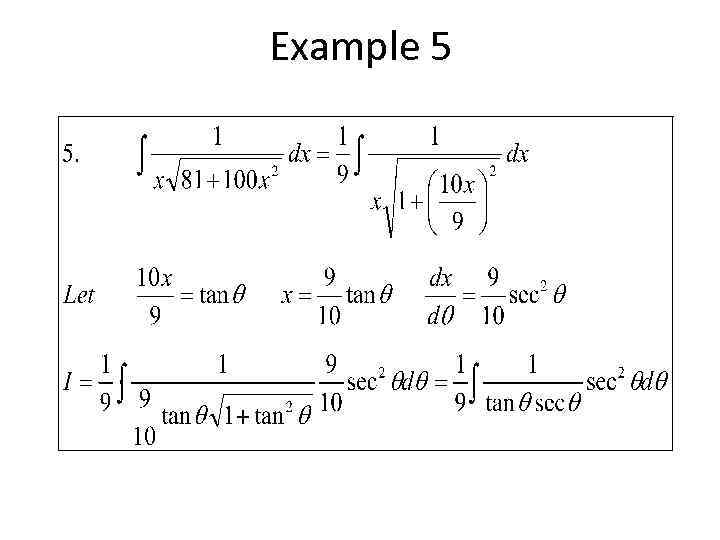
Example 5
Example 5
Example 6
Example 7
Example 8
Partial fractions • If the addition of two fractions can be expressed as a single fraction the reverse is possible. • This is useful when integrating some polynomial fractions. • We will first look at the method of partial fractions and then integrating the result. • The method is best seen by example.
A proper fraction with linear factors in the denominator • Step 1: Factorise the denominator • Step 2: Split into individual fractions • Since the denominators are linear then the numerators are constants.
A proper fraction with linear factors in the denominator • Step 3: We must now find A and B
A proper fraction with linear factors in the denominator • Step 4: Substitute for A and B
A proper fraction with quadratic factors in the denominator • Step 1: Factorise the denominator • Step 2: Split into individual fractions • If the denominator is quadratic then the numerator is linear.
A proper fraction with quadratic factors in the denominator • Step 3: We must now find A, B and C
A proper fraction with quadratic factors in the denominator • Step 3: To find B and C we must multiply out and compare coefficients
A proper fraction with quadratic factors in the denominator • Step 4: Substitute for A, B and C
A proper fraction with repeated factors in the denominator • Step 1: Factorise the denominator • Step 2: Split into individual fractions • The last term is not in its simplest form and so we can manipulate it further
A proper fraction with repeated factors in the denominator • For repeated factors we can move straight to the final line above noting that since the function inside the bracket is linear then the numerator is a constant
A proper fraction with repeated factors in the denominator • Step 3: We must now find A, B and D
A proper fraction with repeated factors in the denominator • Step 3: To find B we must multiply out and compare coefficients
A proper fraction with repeated factors in the denominator • Step 4: Substitute for A, B and D
Improper fractions • If the degree of the numerator is greater than or equal to the degree of the denominator then we must split the fraction into a whole part and a proper fraction. • This can be done by algebraic division or sometimes by algebraic manipulation. For example,
Improper fractions • Once the improper fraction is split into its ‘whole’ part and its proper fraction we can then decide if we need to use the partial fraction method on the proper fraction or not.
Integrating using partial fractions • After you have split the fraction into the individual fractions then you can integrate using one of the methods you already know. • This is best seen by example.
Examples Integrate the following wrt x:
Example 1
Example 2
Example 3
Скачать презентацию Integration 04 Today s Objectives Integrating expressions
04 Integration.pptx