03 Integration.pptx
- Количество слайдов: 49

Integration 03
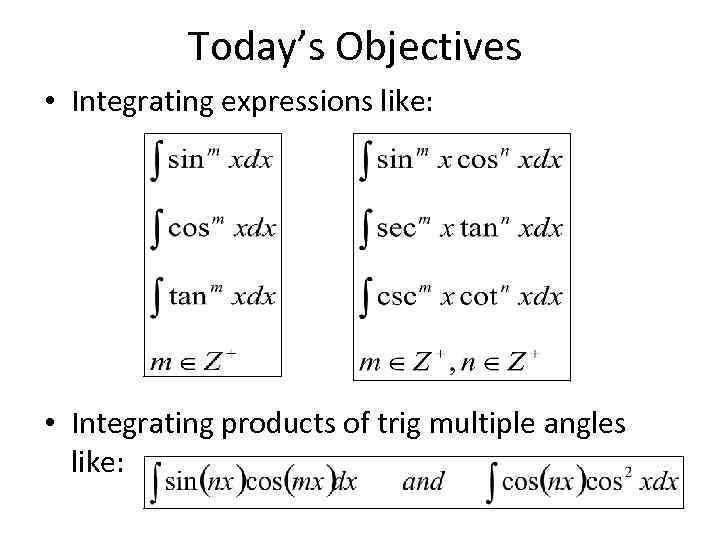
Today’s Objectives • Integrating expressions like: • Integrating products of trig multiple angles like:

What do you know already? • When trying a new problem, think about what you know already. • What do we know about trig and trig integration? • We know: – Trig identities including double angle formulae – Integrating sin(ax + b), cos(ax + b) and tan(ax + b) – Integrating sinxcosnx, cosxsinnx and sec 2 xtannx

What are we trying to do? • When we have a trig function raised to a power, the aim is to convert the expression into a standard form that we know how to integrate such as a polynomial or a standard trig expression. • So we use what we already know to convert the expression into something we can integrate.
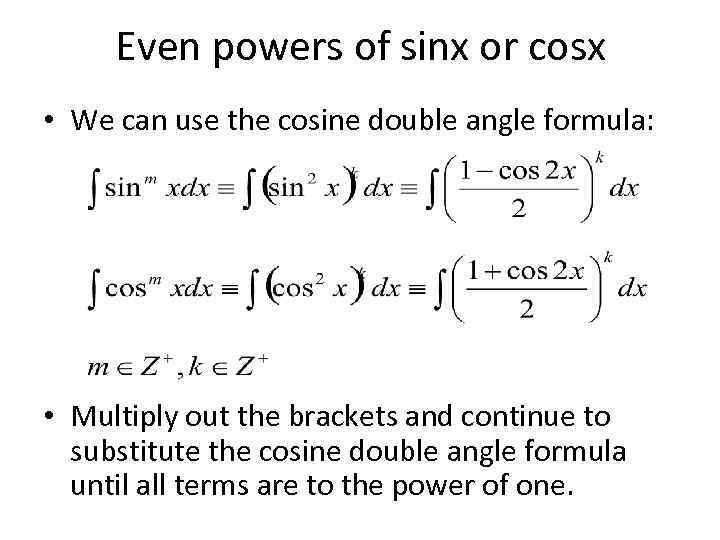
Even powers of sinx or cosx • We can use the cosine double angle formula: • Multiply out the brackets and continue to substitute the cosine double angle formula until all terms are to the power of one.
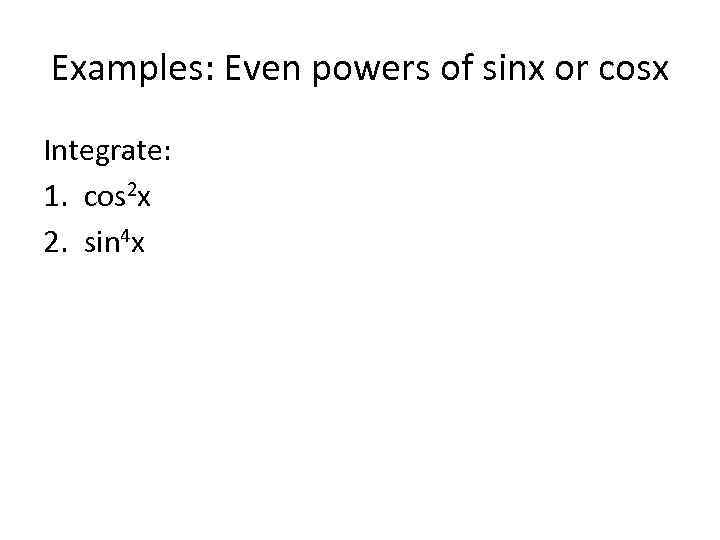
Examples: Even powers of sinx or cosx Integrate: 1. cos 2 x 2. sin 4 x

Solutions
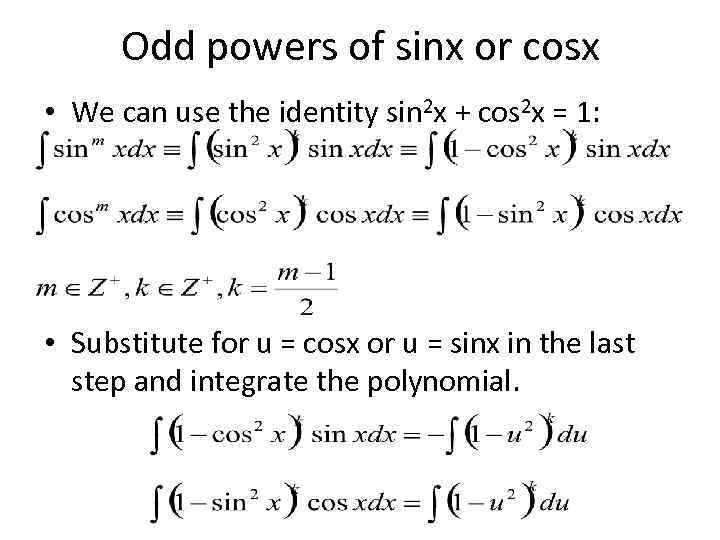
Odd powers of sinx or cosx • We can use the identity sin 2 x + cos 2 x = 1: • Substitute for u = cosx or u = sinx in the last step and integrate the polynomial.
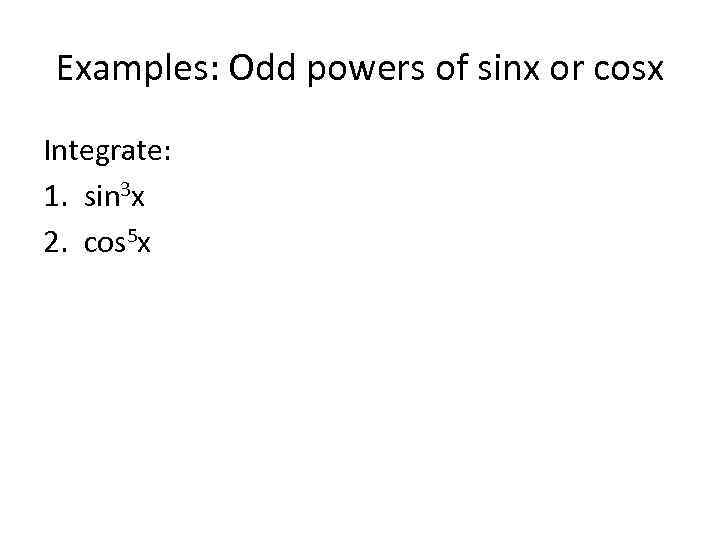
Examples: Odd powers of sinx or cosx Integrate: 1. sin 3 x 2. cos 5 x

Solutions

Odd or even powers of tanx • We can use the identity tan 2 x + 1 = sec 2 x: • Multiply out the bracket. • We can then use previous results found for sec 2 xtannx and repeat the process for tankx. • If m is even, repeat until you obtain tan 2 x as the final term, if m is odd repeat until you obtain tanx as the final term.
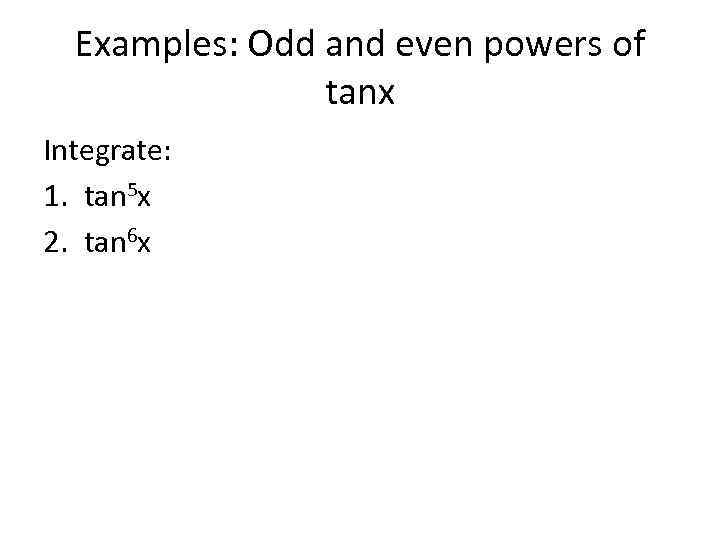
Examples: Odd and even powers of tanx Integrate: 1. tan 5 x 2. tan 6 x

Solutions

Solutions

sinmxcosnx • The method used here depends on whether m and n are odd or even. • There are two cases: – One or both of m and n are odd (both odd, m odd n even or m even n odd) – Both m and n are even • There is a different method for each case.
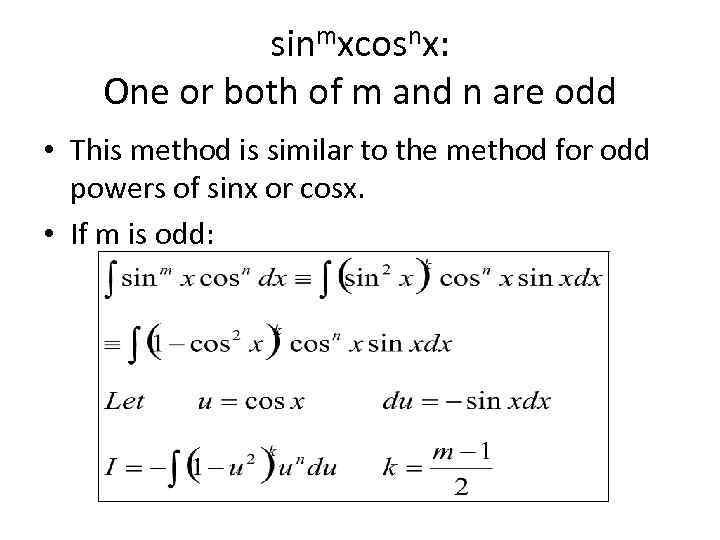
sinmxcosnx: One or both of m and n are odd • This method is similar to the method for odd powers of sinx or cosx. • If m is odd:
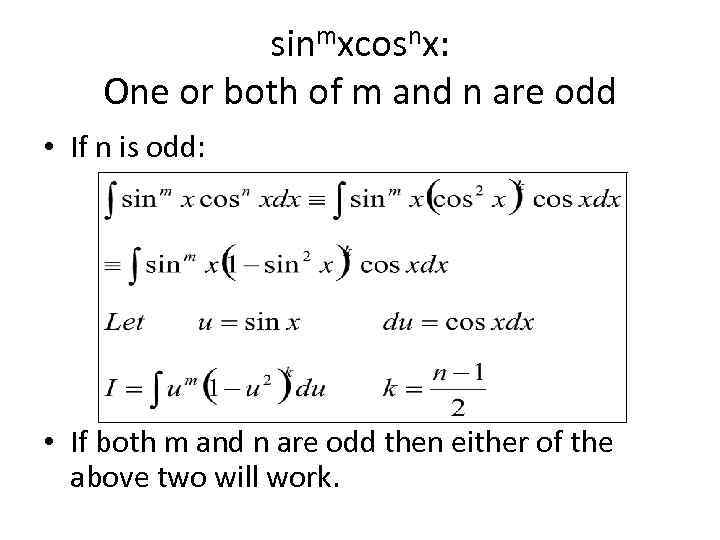
sinmxcosnx: One or both of m and n are odd • If n is odd: • If both m and n are odd then either of the above two will work.
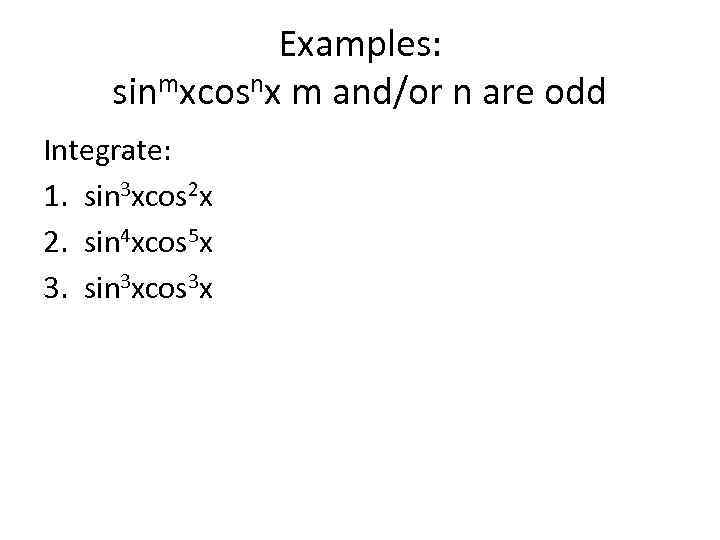
Examples: sinmxcosnx m and/or n are odd Integrate: 1. sin 3 xcos 2 x 2. sin 4 xcos 5 x 3. sin 3 xcos 3 x

Solutions

Solutions

Solutions
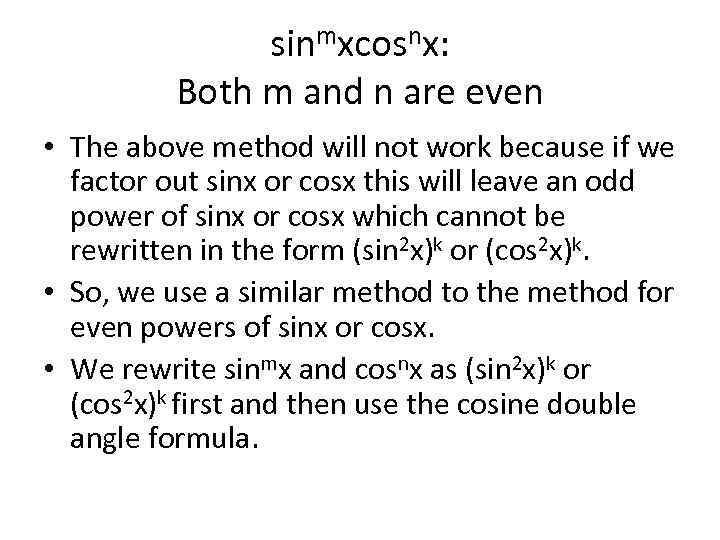
sinmxcosnx: Both m and n are even • The above method will not work because if we factor out sinx or cosx this will leave an odd power of sinx or cosx which cannot be rewritten in the form (sin 2 x)k or (cos 2 x)k. • So, we use a similar method to the method for even powers of sinx or cosx. • We rewrite sinmx and cosnx as (sin 2 x)k or (cos 2 x)k first and then use the cosine double angle formula.
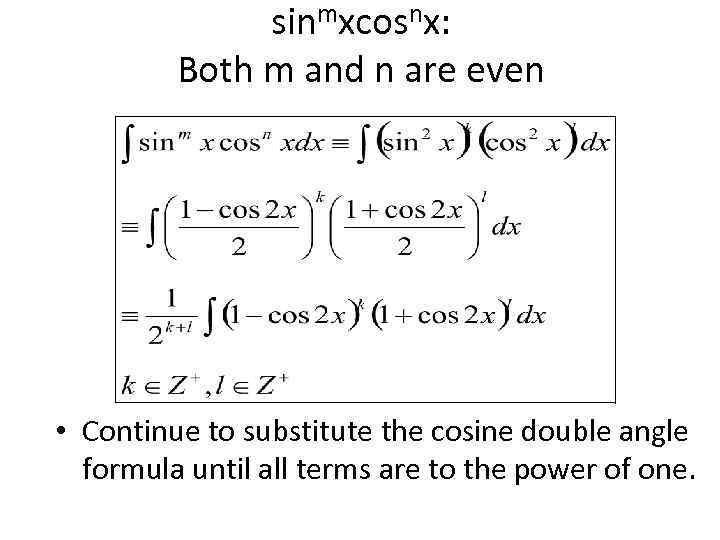
sinmxcosnx: Both m and n are even • Continue to substitute the cosine double angle formula until all terms are to the power of one.
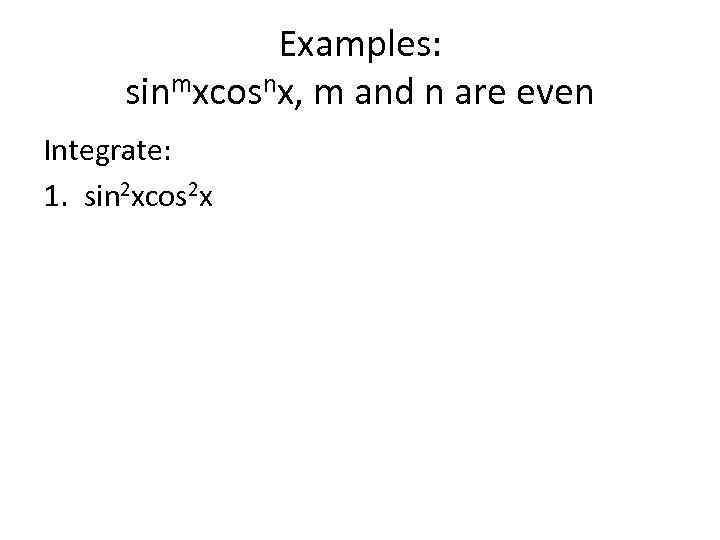
Examples: sinmxcosnx, m and n are even Integrate: 1. sin 2 xcos 2 x

Solutions

secmxtannx • Again the method used here depends on whether m and n are odd or even. • There are three cases: – m is even and n is odd or even – Both m and n are odd – m is odd and n is even • There is a different method for each case.

secmxtannx: m is even and n is odd or even • We will factor out sec 2 x and use the identity tan 2 x + 1 = sec 2 x:

secmxtannx: Both m and n are odd • We will factor out secxtanx and use the identity tan 2 x = sec 2 x – 1:

secmxtannx: m is odd and n is even • We can not use the first method: We can not factor out sec 2 x since this will leave an odd power of secx and this method needs an even power of secx. • We can not use the second method: We can not factor out secxtanx since this will leave an odd power of tanx and this method needs an even power of tanx.

secmxtannx: m is odd and n is even • We can use another method which we have not learnt yet called ‘Integration By Parts’. • We will learn this method later.

Examples: secmxtannx Integrate: 1. sec 4 xtan 2 x 2. sec 6 xtan 3 x 3. sec 3 xtan 3 x

Solutions

Solutions

Solutions

cscmxcotnx • The same three methods used for secmxtannx can be used here. • There are three cases: – m is even and n is odd or even – Both m and n are odd – m is odd and n is even
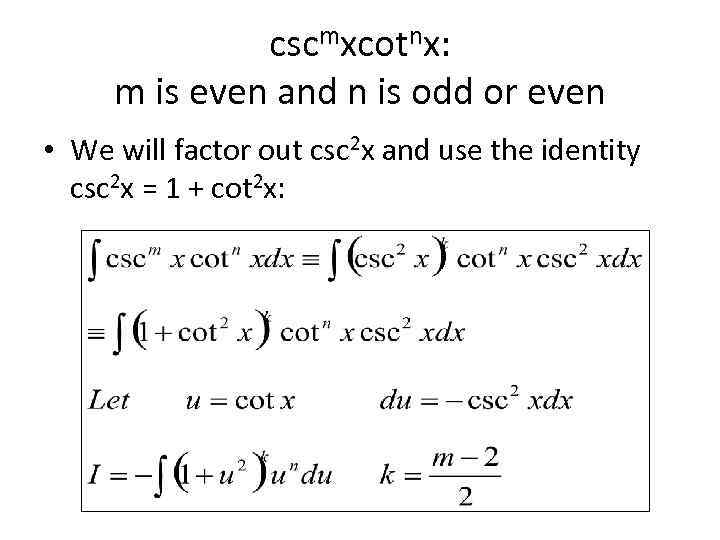
cscmxcotnx: m is even and n is odd or even • We will factor out csc 2 x and use the identity csc 2 x = 1 + cot 2 x:

cscmxcotnx: Both m and n are odd • We will factor out cscxcotx and use the identity cot 2 x = csc 2 x – 1:

cscmxcotnx: m is odd and n is even • Again, we can use ‘Integration By Parts’ which we will learn later.

Examples: cscmxcotnx Integrate: 1. csc 4 xcot 2 x 2. csc 6 xcot 3 x 3. csc 3 xcot 3 x

Solutions

Solutions

Solutions

Products of multiple angles • We use the factor formulae to convert the product into an addition or subtraction:

Products of multiple angles • If one or both of the trig functions are squared we can use the cosine double angle formula first and then the factor formulae to convert the product into an addition or subtraction:

Products of multiple angles • Or if both are squared:

Examples: Multiple angles Integrate: 1. sin(5 x)cos(3 x) 2. cos 2(2 x)cos(5 x) 3. sin 2(3 x)cos 2 (4 x)

Solutions

Solutions

Solutions
03 Integration.pptx