41296790868602e44e3e9e92420059f3.ppt
- Количество слайдов: 41

Integrating Computer Algebra Systems into Algebra and Precalculus Courses Michael Buescher Hathaway Brown School

A Test Question - Algebra 2 Given an arithmetic sequence a with first term t and common difference d, … • Show that a 6 + a 9 = a 3 + a 12 • Show that if m + n = j + k, then am + an = aj + ak Michael Buescher 2004 mbuescher@hb. edu

What are Computer Algebra Systems? 4 Computer-based (Mathematica, Derive, Maple) or Calculator-based (TI-89, TI-92, HP-48, HP-49) Michael Buescher 2004 mbuescher@hb. edu

What are Computer Algebra Systems? 4 Computer-based (Mathematica, Derive, Maple) or Calculator-based (TI-89, TI-92, HP-48, HP-49) 4 Allow Symbolic Manipulation Michael Buescher 2004 mbuescher@hb. edu

What are Computer Algebra Systems? 4 Computer-based (Mathematica, Derive, Maple) or Calculator-based (TI-89, TI-92, HP-48, HP-49) 4 Allow Symbolic Manipulation 4 Capable of solving equations numerically and algebraically Michael Buescher 2004 mbuescher@hb. edu

My Experience 4 Using CAS in Algebra 2 and Precalculus classes for five years 4 TI-89 for all, Mathematica for me 4 Traditional curriculum, heavily influenced by College Board AP Calculus Michael Buescher 2004 mbuescher@hb. edu

Decision to use the TI-89: 4 Some students already had it 4 More students wanted it 4 College Board allowed it for SAT and AP 4 Telling adolescents they can’t do something is always an effective strategy [see session #128 on Dress Code] Michael Buescher 2004 mbuescher@hb. edu

What is your current attitude about Computer Algebra Systems? “Thisgives lots of peoplewon'tlife in “It is madness. They new learn mathematics. It lets off careers in algebra. It will cut them focus more on the problem-solving aspects rather many fields. " than the tedious computations. " -- Richard Askey, University of Wisconsin at Madison -- James Schultz, Ohio University Madness New Life Quotes From: Lisa Black, Robert Channick. “New Algebra: Batteries Required” Chicago Tribune, October 29, 2003 http: //www. chicagotribune. com/news/local/chi-0310290205 oct 29, 1, 3428295. story Michael Buescher 2004 mbuescher@hb. edu

Construction vs. Education 4 You can build a road using shovels and wheelbarrows. 4 You can build a road using a bulldozer. Kutzler, Bernhard. “CAS as Pedagogical Tools for Teaching and Learning Mathematics. ” Computer Algebra Systems in Secondary School Mathematics Education, NCTM, 2003. Michael Buescher 2004 mbuescher@hb. edu

Construction vs. Education 4 Technology allows us to do some things more quickly or more efficiently. 4 Technology allows us to do some things we couldn’t do at all without it. People need to be trained in how to use it! Kutzler, Bernhard. “CAS as Pedagogical Tools for Teaching and Learning Mathematics. ” Computer Algebra Systems in Secondary School Mathematics Education, NCTM, 2003. Michael Buescher 2004 mbuescher@hb. edu

Transportation vs. Computation The Task Go two blocks for a newspaper Appropriate Technology The Task Appropriate Technology Solve 3 x = 21 Go a mile to get vegetables for dinner Solve 3 x + 6 = 21 - 5 x Go to a play downtown Solve. 7 x 3 + 2. 9 x = 17. 3 Kutzler, Bernhard. “CAS as Pedagogical Tools for Teaching and Learning Mathematics. ” Computer Algebra Systems in Secondary School Mathematics Education, NCTM, 2003. Michael Buescher 2004 mbuescher@hb. edu

The High School Student Perspective The Task Buy a sweatshirt at the Exeter Bookstore Appropriate Technology The Task Appropriate Technology Solve 3 x = 21 Buy shampoo at Walgreens Solve 3 x + 6 = 21 - 5 x Take a tour of the New Hampshire coast Solve. 7 x 3 + 2. 9 x = 17. 3 Michael Buescher 2004 mbuescher@hb. edu

Calculator Allowed or Not? Michael Buescher 2004 mbuescher@hb. edu

The Basics 4 Pedagogical Use #1: What I Already Know is True Michael Buescher 2004 mbuescher@hb. edu

The Idea of Function 4 Manipulating Functions 4 Variable vs. Parameter – Variation: y = k∙xn – Gravity Formula: Michael Buescher 2004 mbuescher@hb. edu

Parameters vs. Variables Susan stands on top of a cliff in Portugal and drops a rock into the ocean. It takes 3. 4 seconds to hit the water. Then she throws another rock up; it takes 4. 8 seconds to hit the water. (a) How high is the cliff, to the nearest meter? (b) What was the initial upward velocity of her second rock, to the nearest m/sec? (c) Which ocean did she drop the rock into? Michael Buescher 2004 mbuescher@hb. edu

Idea of Function 4 Manipulating Functions 4 Variable vs. Parameter – Variation: y = k∙xn – Gravity Formula: 4 Functions of several variables – Combinations and Permutations – Distance Formula Michael Buescher 2004 mbuescher@hb. edu

Functions of Multiple Variables For all positive integers x and y, if ‡ is defined by x ‡ y = (x – y) + 1, find (3 ‡ 4) ‡ 5 If f (x, y) = (x – y) + 1, find f (3, 4), 5) Michael Buescher 2004 mbuescher@hb. edu

Powers and Roots 4 Pedagogical Use #2: There seem to be some more truths out there. – Rationalize denominators. • When should denominators be rationalized? • Why should denominators be rationalized? – Imaginary and complex numbers Michael Buescher 2004 mbuescher@hb. edu
![Rationalizing Denominators? [examples from UCSMP Advanced Algebra, supplemental materials, Lesson Master 8. 6 B] Rationalizing Denominators? [examples from UCSMP Advanced Algebra, supplemental materials, Lesson Master 8. 6 B]](https://present5.com/presentation/41296790868602e44e3e9e92420059f3/image-20.jpg)
Rationalizing Denominators? [examples from UCSMP Advanced Algebra, supplemental materials, Lesson Master 8. 6 B] Michael Buescher 2004 mbuescher@hb. edu

Powers and Roots Show that Michael Buescher 2004 mbuescher@hb. edu

Is there something else out there? What are the two things you have to look out for when determining the domain of a function? What does your calculator reply when you ask it the following? a. 9÷ 0 b. Michael Buescher 2004 mbuescher@hb. edu

Polynomials and Rational Functions 4 Change forms for equation 4 What does factored form tell you? 4 What does expanded form tell you? Michael Buescher 2004 mbuescher@hb. edu
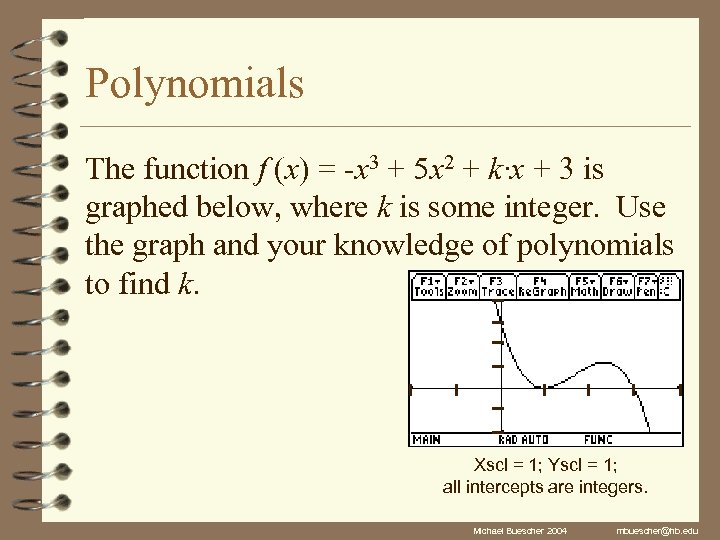
Polynomials The function f (x) = -x 3 + 5 x 2 + k∙x + 3 is graphed below, where k is some integer. Use the graph and your knowledge of polynomials to find k. Xscl = 1; Yscl = 1; all intercepts are integers. Michael Buescher 2004 mbuescher@hb. edu

Rational Functions: The Old Rule 4 Let f be the rational function where N(x) and D(x) have no common factors. – If n < m, the line y = 0 (the x-axis) is a horizontal asymptote. – If n = m, the line is a horizontal asymptote. – If n > m, the graph of f has no horizontal asymptote. 4 Oblique (slant) asymptotes are treated separately. 4 n > m + 1 not dealt with at all. Michael Buescher 2004 mbuescher@hb. edu

Rational Functions 4 Expanded Form: 4 Factored Form: 4 Quotient-Remainder Form: Michael Buescher 2004 mbuescher@hb. edu

Rational Functions: The New Rule 4 Given a rational function f (x), – Find the quotient and remainder. – The quotient is the “macro” picture. – The remainder is the “micro” picture -- it gives details near specific points. Michael Buescher 2004 mbuescher@hb. edu

Rational Functions 4 No need to artificially limit ourselves to expressions where the degree of the numerator is at most one more than the degree of the denominator. 4 Analyze is just as easy as any other rational function. Michael Buescher 2004 mbuescher@hb. edu

Rational Functions 4 Analyze Expanded form: y-intercept is (0, 6) vertical asymptote x = -1 Factored form: x-intercept at (1, 0) Quotient-Remainder form: Approaches f (x) = x 2 - 4 x Michael Buescher 2004 mbuescher@hb. edu

Teaser: Systems of Equations Solve for x and y: Swokowski and Cole, Precalculus: Functions and Graphs. Question #11, page 538 Michael Buescher 2004 mbuescher@hb. edu

Other Extensions of the Curriculum 4 Conic Sections – Solutions to systems of conics – Rotations of conics 4 Exponential and Logarithmic Functions – Logistic Functions – Normal Functions Michael Buescher 2004 mbuescher@hb. edu

Limitations 4 Pedagogical Use #3: The Machine Doesn’t Know Everything 4 “You’ve gotta know the machine, and you’ve gotta know the mathematics. ” 4 Real vs. Complex Numbers – Let – Graph y 2 ( y 1 (x) ) Michael Buescher 2004 mbuescher@hb. edu

Limitations 4 “Solve” can’t always solve algebraically. – Trouble with radicals – Variables both in and out of exponents Michael Buescher 2004 mbuescher@hb. edu

Powers and Roots If , what is the value of ? [Ohio Council of Teachers of Mathematics 2004 Contest, written by Duane Bollenbacher, Bluffton College] Michael Buescher 2004 mbuescher@hb. edu

No exact solution The teachers in the Valley Heights school district receive a starting salary of $30, 000 and a $2000 raise for every year of experience. The teachers in the Lower Hills district also receive a starting salary of $30, 000, but they receive a 5% raise for every year of experience. (a) After how many years of experience will teachers in the two school districts make the same salary (to the nearest year)? (b) Is your answer in (a) the only solution, or are there more? (c) Ms. Jones and Mr. Jacobs graduate from college and begin teaching at the same time, Ms. Jones in the Valley Heights system and Mr. Jacobs in Lower Hills. Will the total amount Mr. Jacobs earns in his career ever surpass the amount Ms. Jones earns? After how many years (to the nearest year)? Michael Buescher 2004 mbuescher@hb. edu

Variables in and out of exponents From a question that arose while studying compound interest: A bank advertises a certificate of deposit that pays 3. 75% interest, with an annual percentage yield (APY) of 3. 80%. How often is the interest compounded? Michael Buescher 2004 mbuescher@hb. edu

Limitations 4 “Solve” can’t always solve algebraically. – Trouble with radicals – Variables both in and out of exponents 4 “Solve” uses inverse functions. – Inverse functions have limitations – Non-linear functions as powers Michael Buescher 2004 mbuescher@hb. edu

Limitations of “Solve” Find all solutions to the equation [Ohio Council of Teachers of Mathematics 2002 Contest, written by Duane Bollenbacher, Bluffton College] Michael Buescher 2004 mbuescher@hb. edu

Teaser: Rational Numbers Is the number rational or irrational? [UCSMP Advanced Algebra, question #19, page 355] Michael Buescher 2004 mbuescher@hb. edu

A Deliberately Provocative Statement “If algebra is useful only for finding roots of equations, slopes, tangents, intercepts, maxima, minima, or solutions to systems of equations in two variables, then it has been rendered totally obsolete by cheap, handheld graphing calculators -- dead -- not worth valuable school time that might instead be devoted to art, music, Shakespeare, or science. ” -- E. Paul Goldenberg Computer Algebra Systems in Secondary Mathematics Education Michael Buescher 2004 mbuescher@hb. edu

Thank You! Michael Buescher Hathaway Brown School For More CAS-Intensive work: The USA CAS conference http: //www 4. glenbrook. k 12. il. us/USACAS/2004. html
41296790868602e44e3e9e92420059f3.ppt