fc39d1a363b63fa734fc864728c1cca9.ppt
- Количество слайдов: 34

ИНТЕГРАЛЬНЫЕ СХЕМЫ ГИГА- И ТЕРАГЕРЦЕВОГО ДИАПАЗОНА: ПРОБЛЕМЫ МОДЕЛИРОВАНИЯ И ПЕРСПЕКТИВЫ РАЗРАБОТКИ ВОЛОЩЕНКО Петр Юрьевич Инженерно-технологическая академия ЮФУ г. Таганрог

Электромагнитное поле (ЭМП) – особая материя, отличающаяся непрерывным распределением в пространстве, характеризующаяся способностью распространяться в виде волн со скоростью света, оказывающая на заряженные частицы силовое воздействие, зависящее от их скорости. Обладающие зарядом элементарные частицы, находящиеся в непрерывном движении, окружены ЭМП. Они представляют единое целое. Электроника – наука о взаимодействии свободных электронов с постоянным и переменным электрическими полем, разработки электронных приборов и устройств, в которых это взаимодействие используется для преобразования и управления электромагнитной энергией (сигналов). Когерентная электроника изучает функционирование множества дискретных электронных приборов (ЭП) СВЧ с кратковременным взаимодействием, направленное на увеличение его КПД и снижение тепловыделения. Электронная волновая цепь – одно- или многомерная совокупность межэлектродных областей пролета электронов и питающих проводников в ЭМП, образующих путь протекания токов проводимости и смещения, наведенного и конвекционного, постоянного и переменного тока. Когерентные процессы в ней могут быть описаны с помощью понятий ЭДС, тока и напряжения. Кластер это объединение ЭП и длинной линии, обладающее новыми электрическими свойствами. Структура есть внутреннее строение чего-либо, скрытое его внешней формой. 2
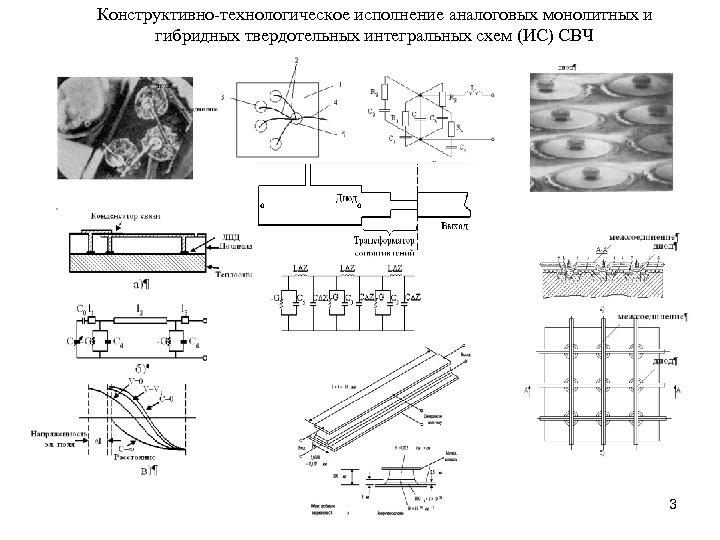
Конструктивно-технологическое исполнение аналоговых монолитных и гибридных твердотельных интегральных схем (ИС) СВЧ 3
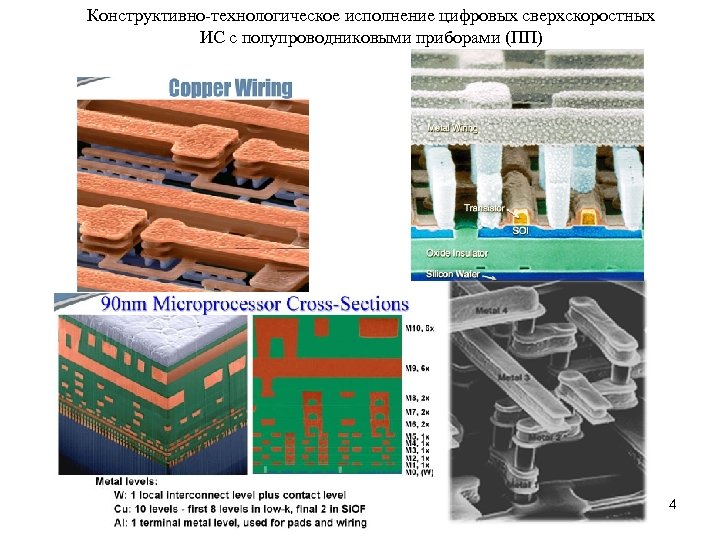
Конструктивно-технологическое исполнение цифровых сверхскоростных ИС с полупроводниковыми приборами (ПП) 4
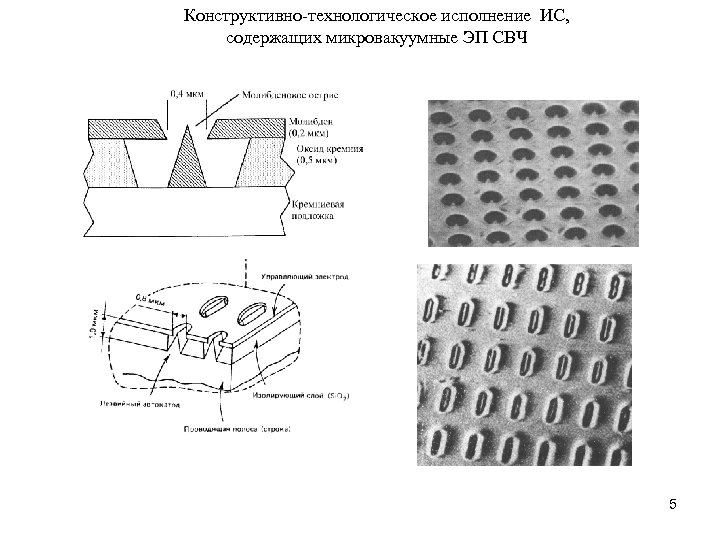
Конструктивно-технологическое исполнение ИС, содержащих микровакуумные ЭП СВЧ 5
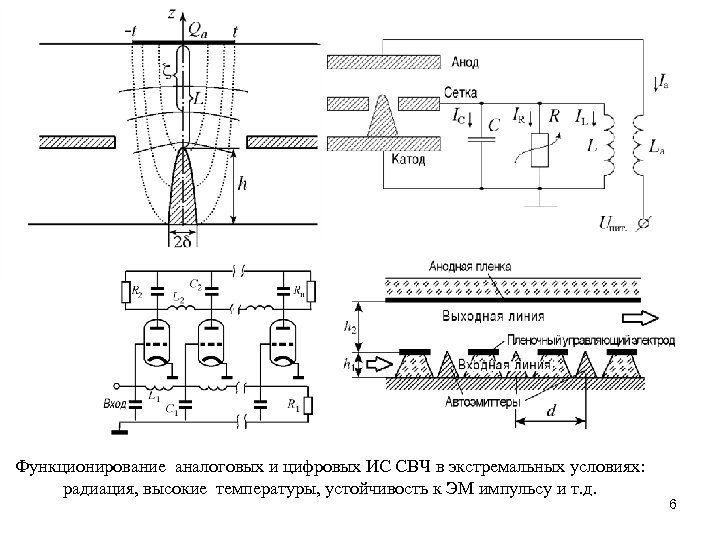
Функционирование аналоговых и цифровых ИС СВЧ в экстремальных условиях: радиация, высокие температуры, устойчивость к ЭМ импульсу и т. д. 6

Использование микровакуумных ЭП с электростатическим управлением без герметично закрытого баллона при конформном размещении на обшивке искусственного космического объекта. В этом случае увеличивается полезный объем несущей платформы, улучшаются условия обитания экипажа летательного аппарата. 7
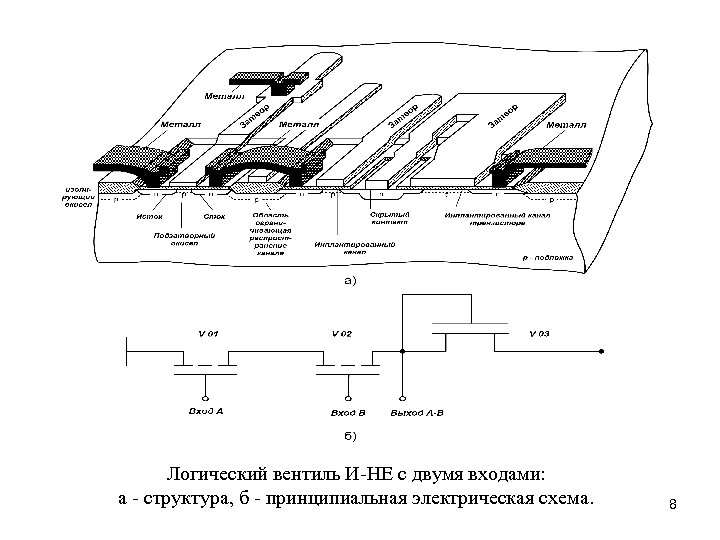
Логический вентиль И-НЕ с двумя входами: а - структура, б - принципиальная электрическая схема. 8
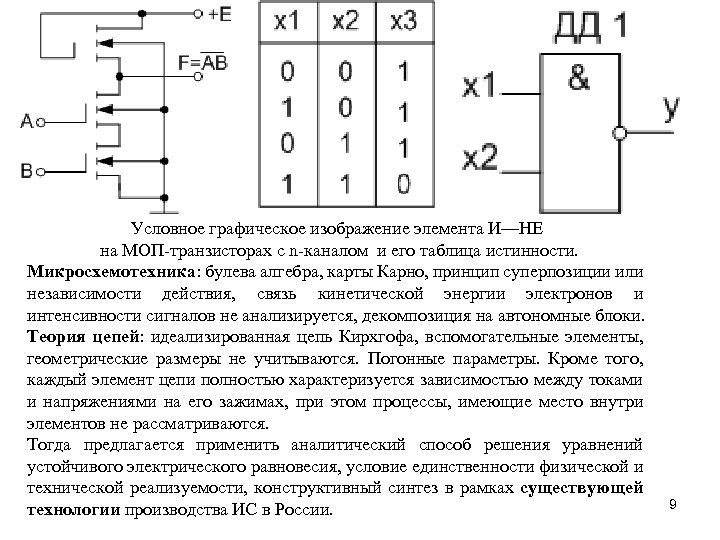
Условное графическое изображение элемента И—НЕ на МОП-транзисторах с n-каналом и его таблица истинности. Микросхемотехника: булева алгебра, карты Карно, принцип суперпозиции или независимости действия, связь кинетической энергии электронов и интенсивности сигналов не анализируется, декомпозиция на автономные блоки. Теория цепей: идеализированная цепь Кирхгофа, вспомогательные элементы, геометрические размеры не учитываются. Погонные параметры. Кроме того, каждый элемент цепи полностью характеризуется зависимостью между токами и напряжениями на его зажимах, при этом процессы, имеющие место внутри элементов не рассматриваются. Тогда предлагается применить аналитический способ решения уравнений устойчивого электрического равновесия, условие единственности физической и технической реализуемости, конструктивный синтез в рамках существующей технологии производства ИС в России. 9

Когда к одному из транзисторов приложено положительное напряжение, он переходит в открытое состояние и образует тем самым путь низкого сопротивления между выходной линией и землей. При последовательном соединении n- канальных нормально закрытых МОП- транзисторов, показанном на предыдущем слайде, получается вентиль И-НЕ. В этом случае, лишь когда оба входа имеют высокий потенциал, последовательно соединенные транзисторы образуют путь со сравнительно низким сопротивлением между выходом и землей. Если хотя бы один вход имеет низкий потенциал, на выходе будет приблизительно равен напряжению источника питания. Поскольку при последовательном соединении сопротивления складываются, количество последовательно соединенных транзисторов ограничено. Мультиплексирование шин. Применение общей шины адресов и данных позволяет сократить число контактов в ИС микропроцессора. Более того, применение модулей памяти с адресными регистраторами приводит к упрощению монтажных соединений между памятью и микропроцессором. Однако производительность микропроцессорной системы при использовании одной шины и для адресов, и для данных в общем случае должна снижаться [4]. 10

Система уравнений Максвелла в дифференциальной форме Уравнение Лоренца (дополнительно применяемое в электронике СВЧ) Уравнение непрерывности обобщенного тока и движения электрона Уравнения Максвелла в интегральной форме (электродинамика) Электро- и радиотехника Теория электрических, радиотехнических и электронных цепей СВЧ 11

Однако в интеграции ЭП любого КТ исполнения невозможно задание начальных и выбор граничных нелинейных условий. В дальнейшем используется 1) методология макромоделирования амплитудно-зависимых инерционных процессов в сверхскоростной ИС корректными инвариантами с учетом явлений композиции и интерференции волн в подобной синергетической системе; 2) способ аналитического расчета механизма дифракции, когерентного функционирования и коллективных «рабочих» режимов совокупности электронных приборов (ЭП), основанный на символьном анализе нелинейных импедансных условий в середине и на краях кластера при монохроматических воздействиях. Математическое моделирование интеграции ЭП базируется на симбиозе методов эквивалентных схем и синусоид, символических (операторном и комплексном), гармонической линеаризации и гармонического баланса в электронной волновой цепи (ЭВЦ). В частности, электрические многомодовые состояния ИС исследуются с помощью законов Кирхгофа, теорем Телледжена и Ланжевена, критериях устойчивости Пирса и Котельникова, с целью повышения ее КПД, минимизации тепловыделения путем оптимизации коэффициента мощности (cos φ). 12
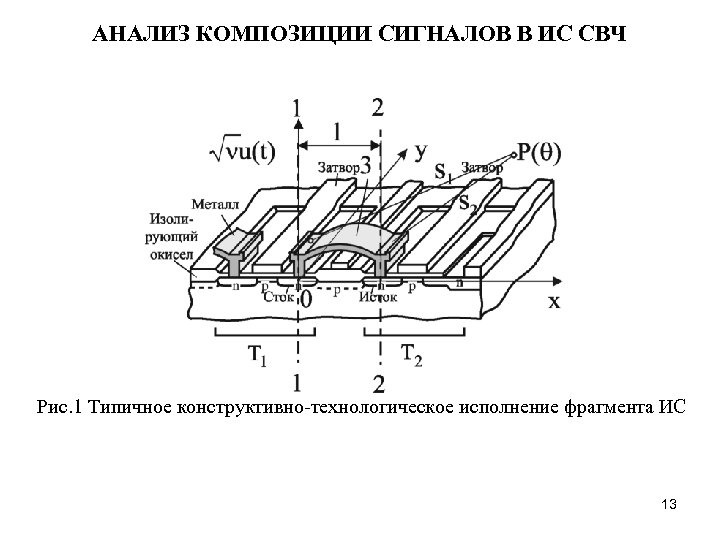
АНАЛИЗ КОМПОЗИЦИИ СИГНАЛОВ В ИС СВЧ Рис. 1 Типичное конструктивно-технологическое исполнение фрагмента ИС 13
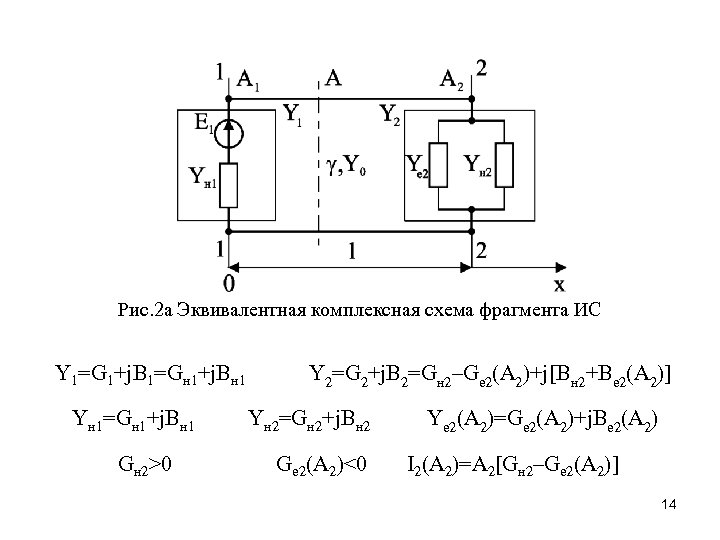
Рис. 2 а Эквивалентная комплексная схема фрагмента ИС Y 1=G 1+j. B 1=Gн 1+j. Bн 1 Yн 1=Gн 1+j. Bн 1 Gн 2>0 Y 2=G 2+j. B 2=Gн 2–Ge 2(A 2)+j[Bн 2+Be 2(A 2)] Yн 2=Gн 2+j. Bн 2 Ge 2(A 2)<0 Ye 2(A 2)=Ge 2(A 2)+j. Be 2(A 2) I 2(A 2)=A 2[Gн 2–Ge 2(A 2)] 14
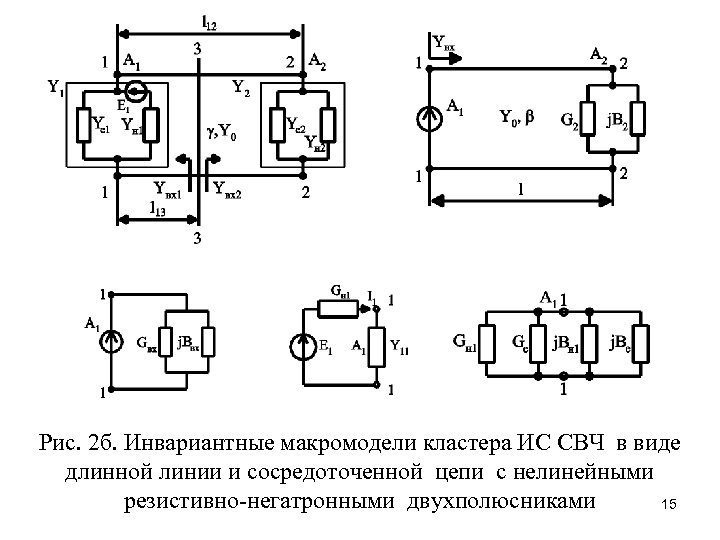
Рис. 2 б. Инвариантные макромодели кластера ИС СВЧ в виде длинной линии и сосредоточенной цепи с нелинейными резистивно-негатронными двухполюсниками 15

g 2(A 2)=Re(I 2/Y 0 A 2)=G 2(A 2)/Y 0 g 2(A 2)=[Gн 2–Ge 2(A 2)]/Y 0=gн 2–ge 2(A 2); b 2(A 2)=Im(I 2/Y 0 A 2)=B 2(A 2)/Y 0 I 2=A 2[Gн 2–Ge 02(1– A 22)]; Модуль и фаза комплексной амплитуды A «смешанной» волны в линии с НЭ: коэффициент n=0, 1, 2, …-соответствует номеру возможной моды СВЧ колебаний. 1. Поиск амплитудно-зависимых граничных условий кластера осуществляем на комплексной плоскости в форме импедансного годографа. 2. Анализ энергоэффективности ЭВЦ проводим с помощью параметров: полная и комплексная, активная и реактивная мощность. 16

В диссипативном режиме фрагмента разность проводимостей теорема Телледжена, а = 1 Gн 2–Ge 02 0, x 2= A 22, y 1= A 12 gн 2–ge 02>0 17
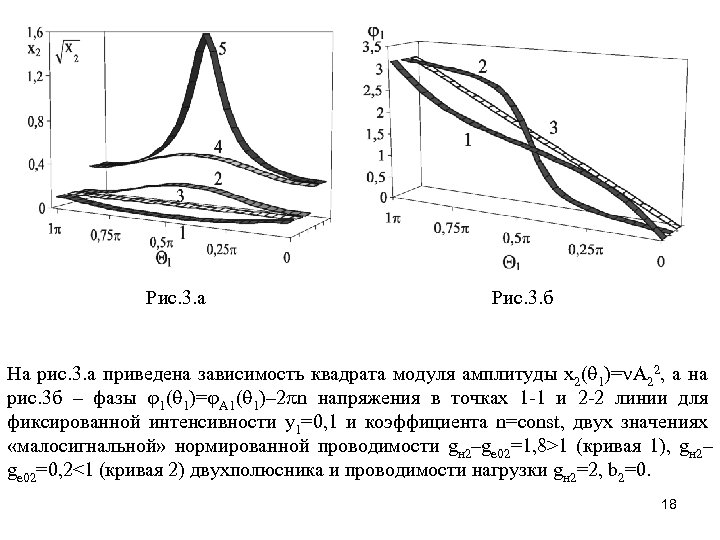
Рис. 3. а Рис. 3. б На рис. 3. а приведена зависимость квадрата модуля амплитуды x 2( 1)= A 22, а на рис. 3 б – фазы 1( 1)= A 1( 1)– 2 n напряжения в точках 1 -1 и 2 -2 линии для фиксированной интенсивности y 1=0, 1 и коэффициента n=const, двух значениях «малосигнальной» нормированной проводимости gн 2–ge 02=1, 8>1 (кривая 1), gн 2– ge 02=0, 2<1 (кривая 2) двухполюсника и проводимости нагрузки gн 2=2, b 2=0. 18

Графики функций x 2( 1), 1( 1) представляют волнообразные кривые, расположенные вдоль прямых x 2=y 1, 1= 1 (отмеченных цифрой 3 на рис. 3 а, б соответственно), максимумы и минимумы которых чередуются. Электрическая цепь фрагмента является одновременно трансформатором модуля и фазы комплексного напряжения с амплитудно-зависимыми свойствами. Поэтому даже в случае «…маломощного сигнала. . » А 1 и проводимости gн 2–ge 02<1 двухполюсника (эквивалентного режиму «холостого хода» на конце линии) в результате наложения волн реализуется амплитуда A 2 напряжения на сосредоточенном НЭ существенно изменяющая его проводимость g 2(A 2) gн 2–ge 02 и рельеф потенциала электрического поля ИС. Таким образом, реакция рядом расположенных ПП в неоднородном электрическом поле ИС на идентичное внешнее или внутреннее воздействие является многозначной. Для иллюстрации достоверности новых результатов рассмотрим характеристики фрагмента при линейных импедансных условиях на его границах и проводимости g 2 f(A 2) двухполюсника не зависящей от напряжения в конце линии. Например, на рис. 3. а приведены графики 4, 5 нормированной амплитуды A 2( 1) колебаний в волновой ветви с НЭ и линейной цепи с распределенными параметрами. Кривая 4 соответствует графику 2 на рис. 3. а, т. к. они построены при идентичных номиналах элементов схемы фрагмента. Эти графики демонстрируют амплитудно-пространственные закономерности и отличия свойств ветвей схем с линейным и нелинейным двухполюсниками. 19 Следовательно, явления дифракции и интерференции волн не позволяют

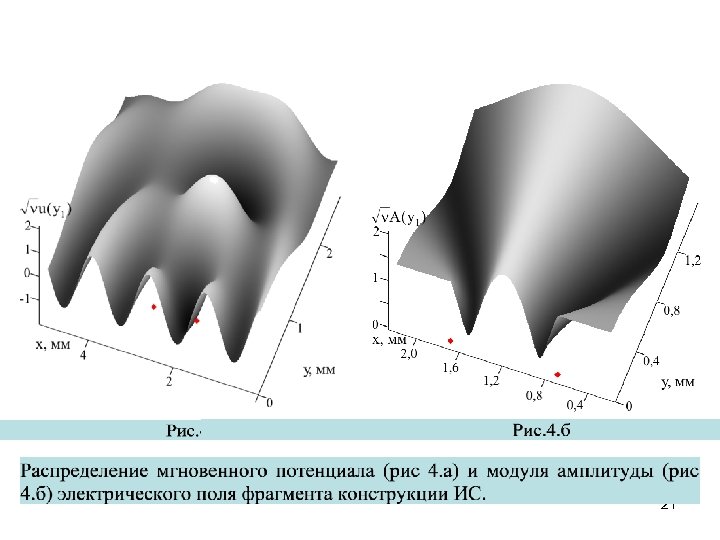
первоначально однозначно отождествить уменьшение или увеличение потока энергии в межсоединении и режимов «малого» либо «большого» сигналов в ИС СВЧ. По мнению автора, на исходном этапе анализа пространственно-временной структуры сверхскоростных цифровых и аналоговых ИС необходимо применять только метод гармонической линеаризации. Волновой и нелинейный характер сверхбыстрых процессов в совокупности ПП, и явлений, происходящих на границе рассматриваемой области, исключает возможность ее предварительного расчета, например, на основе рядов Вольтерра. Используя найденные стационарные значения эквивалентных синусоид A 2, I 2, проводимости g 2(A 2) в уравнениях (1)-(3), рассчитываем мгновенную величину разности потенциалов u 1(t, θ 1, y 1)=A 1( 1, y 1)cos[ t- A 1( 1, y 1)] поля в сечении (1 -1) линии, где t- время, при регулировке параметра y 1= A 12, пропорционального потоку мощности, переносимой бегущей волной от первичного источника в фрагменте ИС, с учетом обратного воздействия ЭВЦ на него. Проведенное теоретическое исследование может быть использовано для оценки нелинейной трансформации низкого и высокого уровней логической амплитуды напряжения цифровой ИС. На рис. 4 а, б приведены результаты первого этапа моделирования электрического поля фрагмента конструкции элемента И–НЕ методом эквивалентных синусоид в произвольной точке P на горизонтальной плоскости (рис. 1), формируемого первичным Т 1 и вторичным Т 2 точечными источниками ЭМ волн. 20
21

Они имеют управляемые ЭДС удовлетворяющие уравнению электрического равновесия, и находятся на расстоянии s 1 и s 2 от точки P наблюдения (рис. 1). ПП излучают равномерно во всех направлениях. Ромбиками на рис. 4 отмечено положение областей стока Т 1 и истока Т 2 (рис. 1). Для построения рис. 4 а, б использованы аналогия между распространением волн вдоль плоскости xz и длинной линией при переносе энергии ЭМ полем, условиями Зоммерфельда в линии и излучения на бесконечности в пространстве. В этом случае, процесс изменения поля в точке P носит характер плоских волн в пространстве или прямолинейных волн на плоскости, бегущих в ту или другую сторону со скоростью u, либо композиции таких волн, имеющих постоянные амплитуды A 1, A 2 и волновое число k= /u. Нормированная интенсивность ЭМ поля фрагмента в точке наблюдения P рассчитывается по формуле Здесь δр - разность фаз между колебаниями y 1, x 2 в точке наблюдения, зависящая от параметров гальванической линии связи и нелинейных свойств ПП, или разность хода волн, приходящих в эту точку, обусловленная длиной s 1 и s 2 ЭМ межсоединений. 22

Расчеты проведены в предположении, что время передачи энергии сигнала по проводнику в полтора раза превышает задержку переключения транзистора с длиной канала- 0, 25 мкм, выполнения условий k= , и потенциальности регистрирующей цепи. Рисунки иллюстрируют коллективное воздействие двух транзисторов СВЧ на потенциал поля фрагмента ИС в окружающем пространстве при t=const (рис. 4 а), возможные направления (рис. 4 б) циркуляции полного тока, в которых формируются дополнительные «сильные» и «слабые» ЭМ связи ПП. На рис. 4 б они характеризуются светлыми и темными участками, соответствующими экстремальным значениям модуля Ap(y 1, θ 1) амплитуды колебаний. 23

ТРАНСФОРМАЦИЯ АМПЛИТУДЫ НАПРЯЖЕНИЯ В ИНТЕГРАЦИИ ЭП СВЧ Считаем, что первичное монохроматическое воздействие, характеризуемое ЭДС E 1 и частотой , локализовано на входе «длинной» линии и обеспечивает в нем амплитуду U 1 напряжения. Тогда ветвь, соединяющую выходные зажимы (2 -2') схемы, рассматриваем как пассивный либо активный НЭ в зависимости от положения его «рабочей» точки и когерентный вторичный источник переменного тока. Решение волнового уравнения для электронной цепи с распределенными параметрами ищем в виде суммы стоячих волн напряжения: (1) Y 0=1/Z 0, l = l=2πl/λ На зажимах 1 -1' и 2 -2' схемы выполняются граничные условия: G 1=Gн 1=Y 0, I 2[U 2(U 1)]=U 2{Gн 2+Ge 2[U 2(U 1)]}=U 2 G 2, Gн 2>0, Ge 2(U 2)<0. Gн 1=Y 0, Gн 2, Ge 2(U 2) - частотно-независимые проводимости источника воздействия и «полезной» нагрузки, замещаемых негатроном и резистором, моделирующих диоды и (или) транзисторы. Тогда уравнение, характеризующее композицию сигналов вдоль линии связи и фронта ЭМ волн в ИС с сверхбыстродействующими ЭП, имеет вид: (2) 24

При величине = n (n=1, 2, 3…) выполняется равенство U 12=U 22, = (n-1/2) взаимосвязь U 12=U 22[g 22(U 22)], 1<g 22(U 22)<1. Параметр n характеризует дискретность спектра собственных ЭМ колебаний и многозначность электрического состояния многомодовой электронной цепи. g 02=gн 2 -ge 02 -малосигнальная элемента. Обозначая x= U 22, y= U 12. проводимость резистивно-негатронного (3) т. к. дискриминант Д = qx 2+px 3>0 при любом y в области значений параметра 0<ge 02/gн 2<1. 25
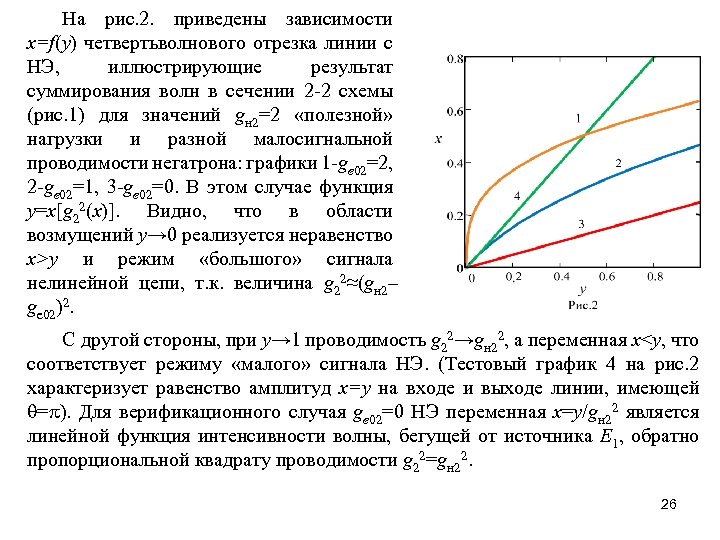
На рис. 2. приведены зависимости x=f(y) четвертьволнового отрезка линии с НЭ, иллюстрирующие результат суммирования волн в сечении 2 -2 схемы (рис. 1) для значений gн 2=2 «полезной» нагрузки и разной малосигнальной проводимости негатрона: графики 1 -ge 02=2, 2 -ge 02=1, 3 -ge 02=0. В этом случае функция y=x[g 22(x)]. Видно, что в области возмущений y→ 0 реализуется неравенство x>y и режим «большого» сигнала нелинейной цепи, т. к. величина g 22≈(gн 2– ge 02)2. С другой стороны, при y→ 1 проводимость g 22→gн 22, а переменная x<y, что соответствует режиму «малого» сигнала НЭ. (Тестовый график 4 на рис. 2 характеризует равенство амплитуд x=y на входе и выходе линии, имеющей = ). Для верификационного случая ge 02=0 НЭ переменная x=y/gн 22 является линейной функция интенсивности волны, бегущей от источника E 1, обратно пропорциональной квадрату проводимости g 22=gн 22. 26

1) Регулировка интенсивности сигналов сопровождается изменением расположения экстремальных значений потенциала электрического поля в конце эквивалентной линии из-за явлений интерференции и дифракции ЭМ волн. Например, для случая gн 2 -ge 02=0, 2) Передача энергии сигнала в идеализированной многомодовой цепи носит однонаправленный характер и наблюдается режим бегущей волны при любой величине gн 2>1, когда произведение 3) Размещение резистивно-негатронного НЭ в минимуме либо максимуме стоячей волны напряжения соответствует принципиально разным устойчивым режимам коллективного взаимодействия смежных ЭП, имеющих разные колебательные характеристики. Структура гальванических соединений должна соответствовать многомодовому распределению поля и резонансному режиму ИС. Отсюда следует: устойчивость ее к электрическим пробоям, не корректность технологии «масштабирования» при современной концепции микроэлектроники о типизации и стандартизации технических решений. 4) На первом этапе моделирования ИС ГГц и ТГц диапазона различного назначения, синтезируемых по технологии когерентной электроники, отсутствует возможность использования численных и аналитических методов расчета мгновенного состояния отдельного диода и (или) транзистора, предполагающих выполнение условия «малых возмущений» или «слабой 27 нелинейности» .

ИССЛЕДОВАНИЕ ВХОДНОГО ИМПЕДАНСА ЭЛЕМЕНТА СВЕРХСКОРОСТНОЙ ИНТЕГРАЛЬНОЙ СХЕМЫ Современные математические модели ИС ГГц и ТГц диапазона, построены на основе сосредоточенных эквивалентных схем полупроводниковых приборов (ПП), в частности, диодов и транзисторов с резонансным туннелированием. Они связаны отрезками длинных линий передачи данных и совместно образуют кластер СВЧ, обладающий одновременно волновыми и нелинейными свойствами. Однако учет интерференционных явлений в общем ЭМ поле, распространяющемся в пространстве диэлектрика, окружающего проводники сверхскоростной ИС, не производится. Вместе с тем, они обуславливают мгновенную вариацию топологии электрической структуры и свойств ПП. Поэтому на практике не удается добиться минимизации токопотребления аналоговой и цифровой аппаратуры, хотя в суперкомпьютерах, стараются обеспечить условие согласования входного импеданса логических элементов по постоянному и переменному току. Тогда компоненты нормированной комплексной входной проводимости yвх(U 2, )=1/zвх(U 2, )=Yвх(U 2, )/Y 0 «длинной» ветви схемы замещения с резистивно -негатронным НЭ, равны: (4) (5) 28

Выражения (1), (2) моделируют связь импедансных условий yвх(y 2), y 2(U 2)=g 2(U 2)+jb 2(U 2) НЭ на границах кластера в волновом масштабе. Знак действительной компоненты gвх(U 2, )=Gвх(U 2, )/Y 0 входной проводимости схемы определяется только результирующей величиной g 2(U 2, ) НЭ. Однако характер ее мнимой составляющей bвх(U 2, ) зависит как от знака проводимости b 2(U 2, ) (емкостной либо индуктивной) НЭ, так и от величин квадрата модуля y 22(U 2)= g 22(U 2)+ b 22(U 2) и параметра tg 2 относительно единицы, соответствующей нормированной волновой проводимости соединения. Следовательно, процесс обмена колебательной энергией линией передачи данных и первичным источником гармонического сигнала, другими ее участками является зависимым от параметра U 22 вторичного воздействия в синергетической системе (рис. 3). Более того, «оптимизация» характеристик кластера возможна в только интервалах, совместно определяемых амплитудой U 1 и величинами Y 0, межсоединений. (а) Рис. 3. Метод неавтономных блоков (б) 29
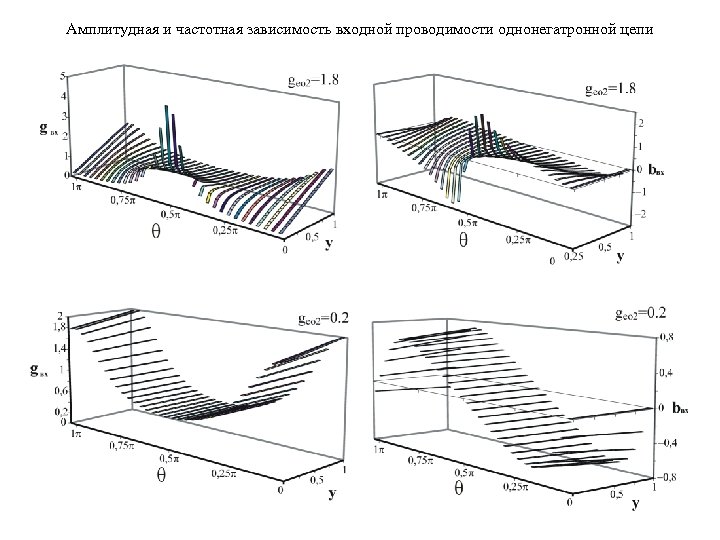
Амплитудная и частотная зависимость входной проводимости однонегатронной цепи 30
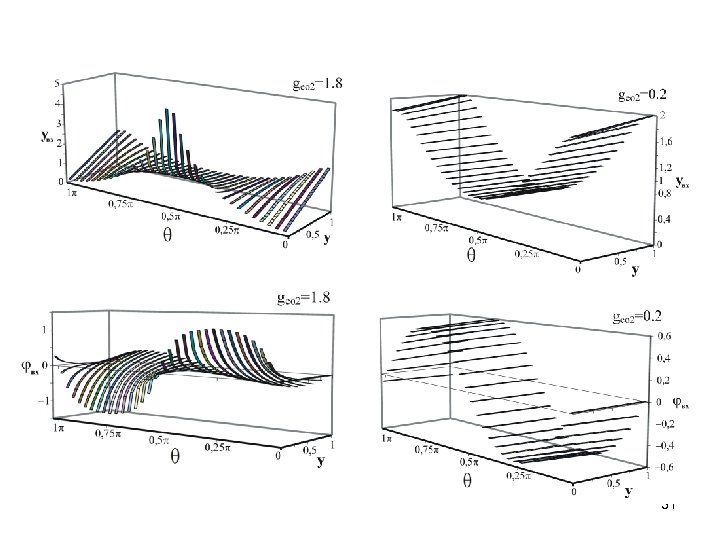
31

Импедансные условия yвх(U 12, ) в начале линии, нагруженной электрически управляемым НЭ меняются периодически при регулировке переменной . Поэтому синергетическая подсистема даже двух наноприборов (рис. 3) обладает множеством собственных резонансных n(U 1) частот колебаний, кратных = n(U 1)/2, при которых реактивная проводимость bвх(U 1) = 0. Причем соответствующие коэффициенты фазы n= n/vф волн в линии образуют бесконечную последовательность, где n- индекс продольной моды колебаний поля вдоль кластера. Таким образом, энергетическое состояние любой пары взаимодействующих соседних ПП ИС, отвечающее ее устойчивому электрическому равновесию, будет меняться дискретным образом (т. е. «квантоваться» ) в соответствии с резонансными свойствами линий связи структуры. При регулировке интенсивности входного сигнала (соответствующей, например, логическому нулю и единице) один и тот же кластер ИС может иметь отличающиеся топологии схемы замещения по переменному току (в виде параллельного, последовательного или смешанного соединения) и номиналу ее идеализированных элементов: отрезка линии, резистора и негатрона, емкости либо индуктивности. В этом случае, для снижения энергопотребления сверхскоростной РЭА и ЭВА условия «согласования» межсоединений и ПП, расположенных в узле или пучности общего ЭМ поля, должны когерентно меняться и определяться нелинейной зависимостью колебаний потенциала и 32 заряда на электродах транзисторов и диодов.

1. Волощенко П. Ю. , Волощенко Ю. П. Методология математического моделирования нелинейных волновых и колебательных электрических процессов в изделиях когерентной радио-, микро- и наноэлектроники. ‒ Таганрог: Изд-во ЮФУ, 2013. ‒ 110 с. 2. Волощенко П. Ю. , Волощенко Ю. П. Основы системного моделирования электрической структуры интеграции сверхбыстродействующих электронных приборов. – Ростов -на- Дону. Изд-во ЮФУ, 2014. – 94 с. 3. Волощенко П. Ю. , Волощенко Ю. П. Основы теории одномерной нелинейной электрической и электронной волновой цепи: учебное пособие. – Таганрог. Изд-во ЮФУ, 2015. – 100 с. 4. Гивоне Д. , Россер Р. Микропроцессоры и микрокомпьютеры. Вводный курс: Пер. с англ. –М. : Мир, 1983. -464 с. 5. Джонсон Г. В. , Грэхем М. Конструирование высокоскоростных цифровых устройств: начальный курс черной магии. : Пер. с англ. -М. : Вильямс, 2006. -624 с. 6. Джонсон Г. В. Высокоскоростная передача цифровых данных: высший курс черной магии. : Пер. с англ. -М. : Вильямс, 2005. -1024 с. 7. Ферри Д. , Эйкерс Л. , Гринч Э. Электроника ультрабольших 33 интегральных схем. –М. : Мир, 1991. -326 с.

9. Абрамов И. И. Методология автоматического синтеза компактных эквивалентных схем полупроводниковых приборов и структур. // Микросистемная техника, 2002, № 6, С. 18 -23. 10. Быстродействующие матричные БИС и СБИС. / Под ред. Б. Н. Файзулаева, И. И. Шагурина. -М. : Радио и связь, 1989. -304 с. 11. Коледов Л. А. Технология и конструкции микросхем, микропроцессоров и микросборок. М. Радио и связь. 1989. 12. Технология СБИС: В 2 х кн. Кн 2. Пер. с англ. / Под ред. С. Зи. М. : Мир, 1986. 453 с. 13. Трубецков Д. И. , Рожнев А. Г. , Соколов Д. В. Лекции по сверхвысокочастотной вакуумной микроэлектронике. Саратов: Изд-во Гос. УНЦ ”Колледж”, 1996. 238 с 14. Трубецков Д. И. , Храмов А. Е. Лекции по сверхвысокочастотной электронике для физиков. В 2 т. Т. 2. -М: ФИЗМАТЛИТ”, 2004. -648 с 34
fc39d1a363b63fa734fc864728c1cca9.ppt