Интегральное исчисление Глава 1.






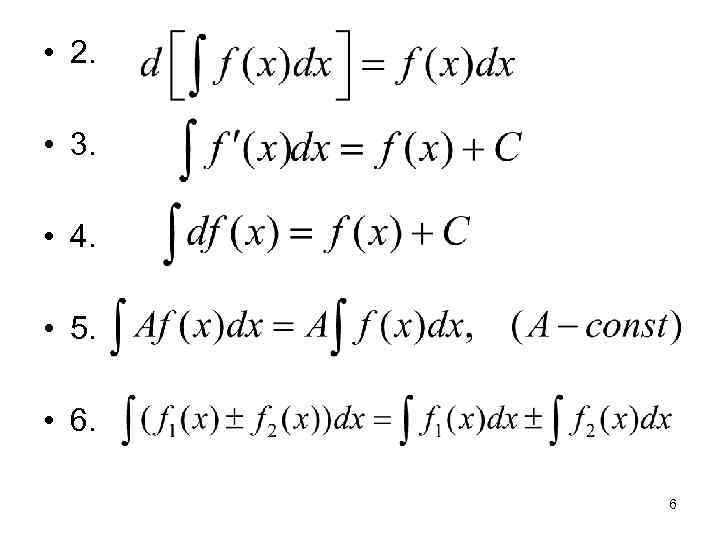

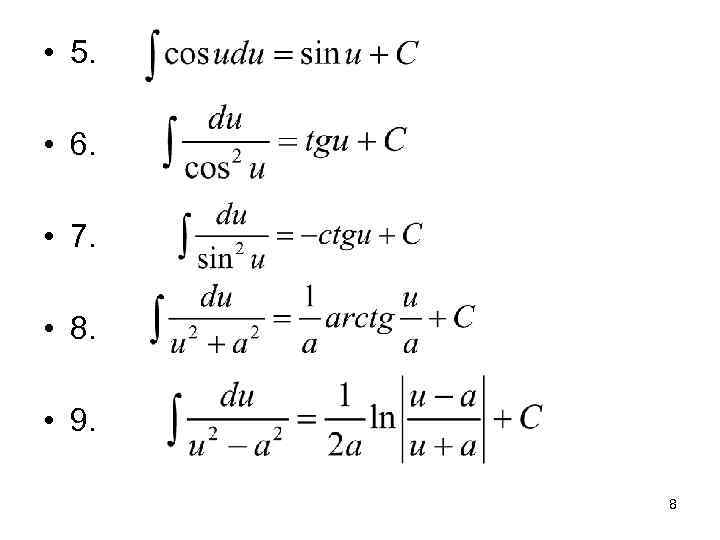





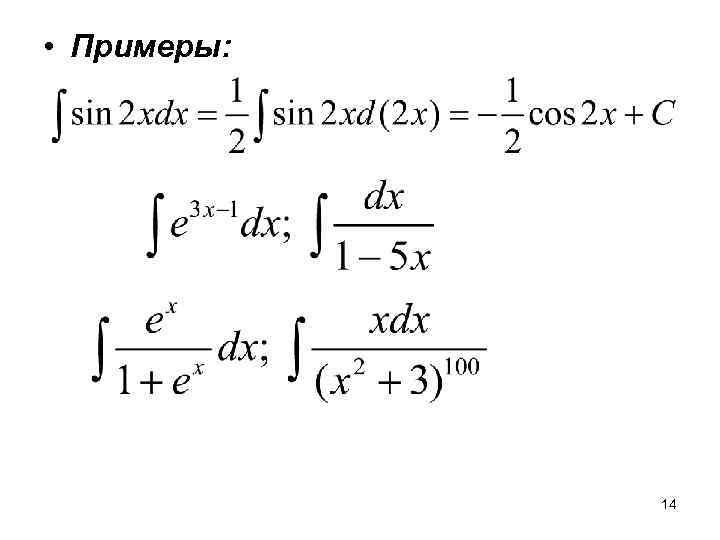


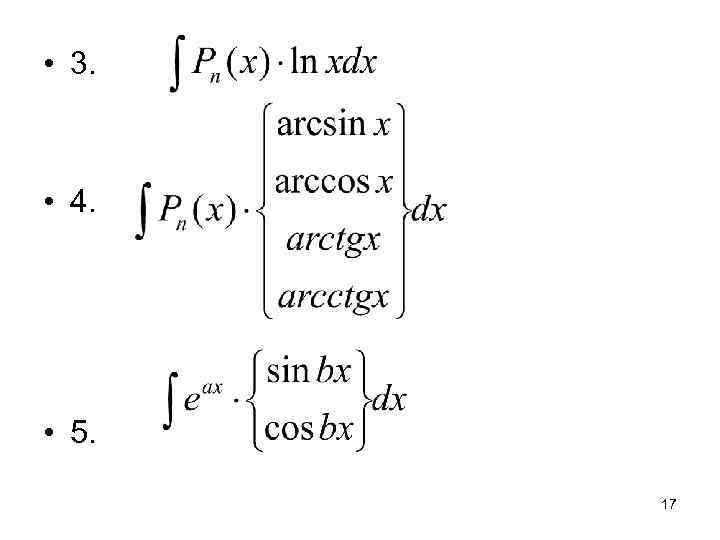




















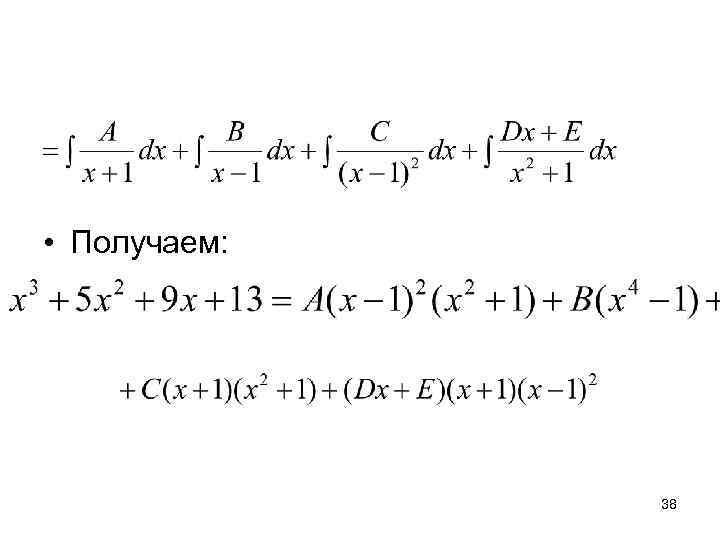




2.1неопредленный интеграл PowerPoint.ppt
- Количество слайдов: 42
 Интегральное исчисление Глава 1. Неопределенный интеграл 1
Интегральное исчисление Глава 1. Неопределенный интеграл 1
 1. 1 Первообразная функция и неопределенный интеграл • Отыскание функции по ее известному дифференциалу • , где • является действием, обратным дифференцированию, и называется интегрированием. 2
1. 1 Первообразная функция и неопределенный интеграл • Отыскание функции по ее известному дифференциалу • , где • является действием, обратным дифференцированию, и называется интегрированием. 2
 • Определение 1. Функция • называется первообразной функцией от (для) функции , если • Примеры: • - первообразная для • так как • - первообразная для 3
• Определение 1. Функция • называется первообразной функцией от (для) функции , если • Примеры: • - первообразная для • так как • - первообразная для 3
 • 1. Для всякой непрерывной функции существует бесчисленное множество первообразных, отличающихся друг от друга постоянным слагаемым. • Если , то • 2. Две различные первообразные для одной и той же функции могут отличаться лишь на постоянное слагаемое. 4
• 1. Для всякой непрерывной функции существует бесчисленное множество первообразных, отличающихся друг от друга постоянным слагаемым. • Если , то • 2. Две различные первообразные для одной и той же функции могут отличаться лишь на постоянное слагаемое. 4
 • Определение. Множество всех первообразных для называется неопределенным интегралом • Терминология. • Свойства неопределенного интеграла: • 1. 5
• Определение. Множество всех первообразных для называется неопределенным интегралом • Терминология. • Свойства неопределенного интеграла: • 1. 5
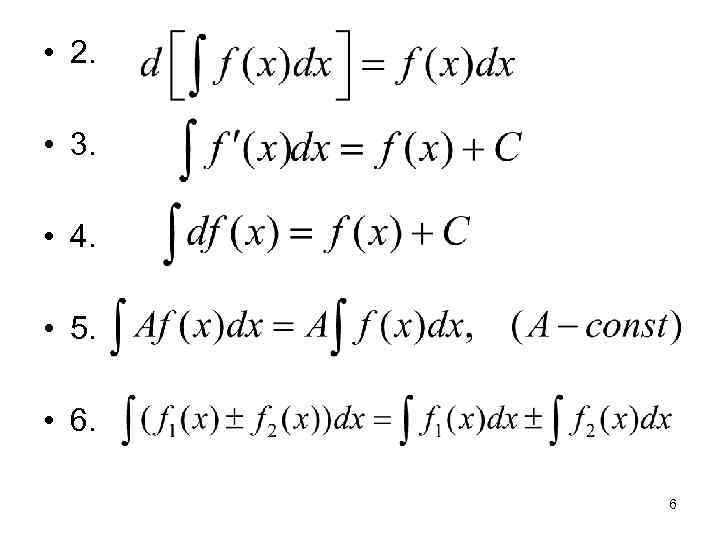 • 2. • 3. • 4. • 5. • 6. 6
• 2. • 3. • 4. • 5. • 6. 6
 1. 2. Таблица основных неопределенных интегралов • 1. • 2. • 3. • 4. 7
1. 2. Таблица основных неопределенных интегралов • 1. • 2. • 3. • 4. 7
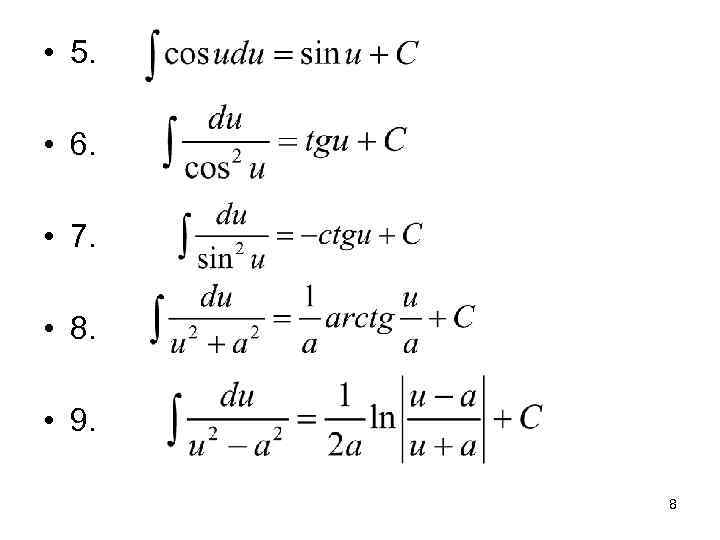 • 5. • 6. • 7. • 8. • 9. 8
• 5. • 6. • 7. • 8. • 9. 8
 • 10. • 11. • U- независимая переменная или любая дифференцируемая функция от независимой переменной. Справедливость приведенных формул интегрирования проверяется путем дифференцирования (свойство 1). • 9
• 10. • 11. • U- независимая переменная или любая дифференцируемая функция от независимой переменной. Справедливость приведенных формул интегрирования проверяется путем дифференцирования (свойство 1). • 9
 1. 3. Основные приемы интегрирования • 3. 1. Непосредственное интегрирование. • • 3. 2. Подведение (внесение функции) под знак дифференциала 10
1. 3. Основные приемы интегрирования • 3. 1. Непосредственное интегрирование. • • 3. 2. Подведение (внесение функции) под знак дифференциала 10
 • В основе метода – определение дифференциала функции • Действительно: • (по сути – это операция интегрирования) • , 11
• В основе метода – определение дифференциала функции • Действительно: • (по сути – это операция интегрирования) • , 11
 • Примеры: • 1. • Здесь использовано соотношение: • 3. 12
• Примеры: • 1. • Здесь использовано соотношение: • 3. 12
 • Полезно запомнить: • Линейное преобразование дифференциала. Так как • , то • • , в частности: • 13
• Полезно запомнить: • Линейное преобразование дифференциала. Так как • , то • • , в частности: • 13
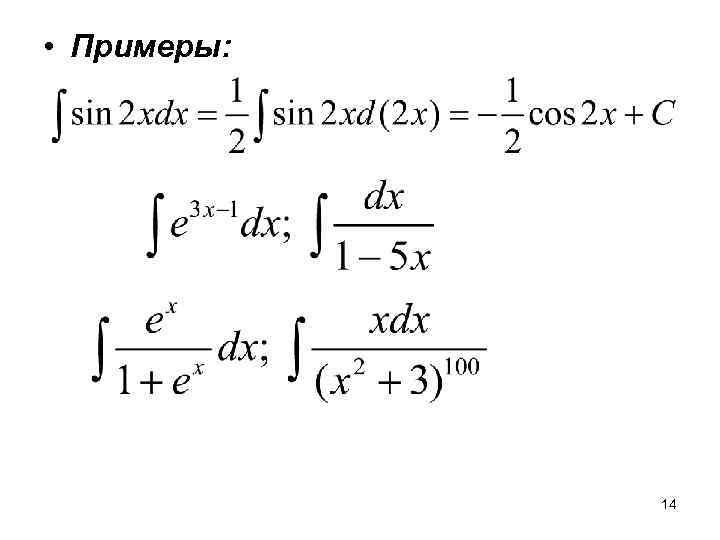 • Примеры: 14
• Примеры: 14
 • 3. 3. Интегрирование по частям. • Если • Примеры 15
• 3. 3. Интегрирование по частям. • Если • Примеры 15
 • Примеры: • Некоторые интегралы вычисляются только с помощью интегрирования по частям, например: • 1. • 2. 16
• Примеры: • Некоторые интегралы вычисляются только с помощью интегрирования по частям, например: • 1. • 2. 16
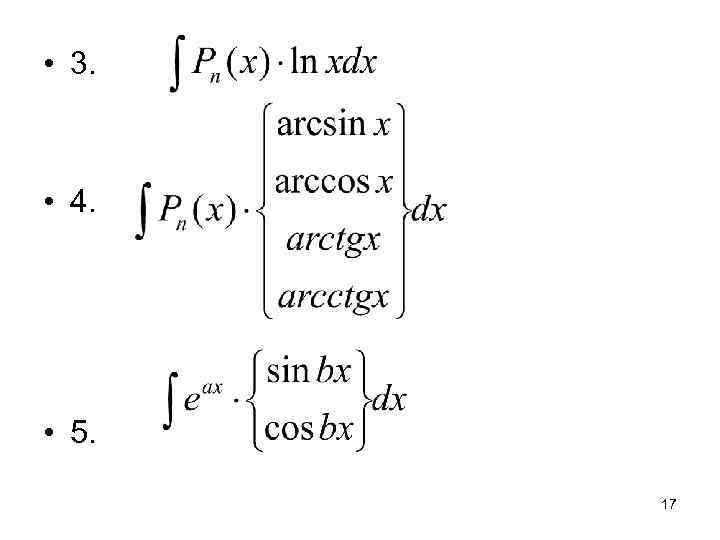 • 3. • 4. • 5. 17
• 3. • 4. • 5. 17
 • В этих формулах - алгебраический многочлен n – й степени относительно х. • В интегралах первых двух типов за U следует принимать многочлен, в 3 и 4 типах – трансцендентную функцию, в интеграле 5 типа – безразлично. 18
• В этих формулах - алгебраический многочлен n – й степени относительно х. • В интегралах первых двух типов за U следует принимать многочлен, в 3 и 4 типах – трансцендентную функцию, в интеграле 5 типа – безразлично. 18
 • 3. 4. Метод замены переменной. • При вычислении интеграла переменную х иногда заменяют новой переменной t, используя формулу • , тогда , и • Вычислим последний интеграл по t, и вернемся к старой переменной. 19
• 3. 4. Метод замены переменной. • При вычислении интеграла переменную х иногда заменяют новой переменной t, используя формулу • , тогда , и • Вычислим последний интеграл по t, и вернемся к старой переменной. 19
 • Например: • Положим • Найдем дифференциал • Отсюда: 20
• Например: • Положим • Найдем дифференциал • Отсюда: 20
 • Подставим в исходный интеграл: • Вернемся к старой переменной: 21
• Подставим в исходный интеграл: • Вернемся к старой переменной: 21
 1. 4. Интегрирование рациональных дробей • Рациональная дробь – это дробь вида • , где , - • многочлены. Если дробь называется правильной, если • то – неправильной. Если дробь неправильная, то нужно разделить числитель на знаменатель , чтобы выделить целую часть и правильную рациональную дробь 22
1. 4. Интегрирование рациональных дробей • Рациональная дробь – это дробь вида • , где , - • многочлены. Если дробь называется правильной, если • то – неправильной. Если дробь неправильная, то нужно разделить числитель на знаменатель , чтобы выделить целую часть и правильную рациональную дробь 22
 • Например: • Правильную рациональную дробь можно представить в виде суммы простейших (простых, элементарных) дробей. • Разложить знаменатель правильной дроби на линейные и квадратичные множители. 23
• Например: • Правильную рациональную дробь можно представить в виде суммы простейших (простых, элементарных) дробей. • Разложить знаменатель правильной дроби на линейные и квадратичные множители. 23
 • Три частных случая. • 1. Знаменатель рациональной дроби имеет n простых (различных) вещественных корней. • - вещественные коэффициенты 24
• Три частных случая. • 1. Знаменатель рациональной дроби имеет n простых (различных) вещественных корней. • - вещественные коэффициенты 24
 • Пример: • Правую часть приводим к общему знаменателю и приравниваем числители. • Найдем коэффициенты А, В, С. 25
• Пример: • Правую часть приводим к общему знаменателю и приравниваем числители. • Найдем коэффициенты А, В, С. 25
 • Подставляя в полученное равенство • последовательно , найдем • Тогда: 26
• Подставляя в полученное равенство • последовательно , найдем • Тогда: 26
 • 2. Знаменатель имеет кратный корень. • Пример: 27
• 2. Знаменатель имеет кратный корень. • Пример: 27
 • Приводим к общему знаменателю, приравниваем числители: • Раскрываем скобки, приравниваем коэффициенты при одинаковых степенях Х. 28
• Приводим к общему знаменателю, приравниваем числители: • Раскрываем скобки, приравниваем коэффициенты при одинаковых степенях Х. 28
 • Знаменатель имеет комплексно- сопряженные корни. • Пример: • Находим коэффициенты методом сравнения. 29
• Знаменатель имеет комплексно- сопряженные корни. • Пример: • Находим коэффициенты методом сравнения. 29
 • Раскрываем скобки, приравниваем коэффициенты при одинаковых степенях Х: 30
• Раскрываем скобки, приравниваем коэффициенты при одинаковых степенях Х: 30
 • Получаем: • В общем случае разложение правильной рациональной дроби на простейшие является комбинацией рассмотренных частных случаев. Способ нахождения неопределенных коэффициентов разложения также комбинированный 31
• Получаем: • В общем случае разложение правильной рациональной дроби на простейшие является комбинацией рассмотренных частных случаев. Способ нахождения неопределенных коэффициентов разложения также комбинированный 31
 Интегрирование простых дробей • 1. • 2. • 3. 32
Интегрирование простых дробей • 1. • 2. • 3. 32
 • Выделим в знаменателе полный квадрат. • Пример: 33
• Выделим в знаменателе полный квадрат. • Пример: 33
 • Пример: • 4. • Выделим в числителе производную знаменателя. 34
• Пример: • 4. • Выделим в числителе производную знаменателя. 34
 • где А и В – некоторые числа. Получим: • Первый интеграл: • Второй – см. случай 3. 35
• где А и В – некоторые числа. Получим: • Первый интеграл: • Второй – см. случай 3. 35
 • Пример. • Так как • То • Интеграл можно записать в виде: 36
• Пример. • Так как • То • Интеграл можно записать в виде: 36
 • Пример: • Общие примеры. 37
• Пример: • Общие примеры. 37
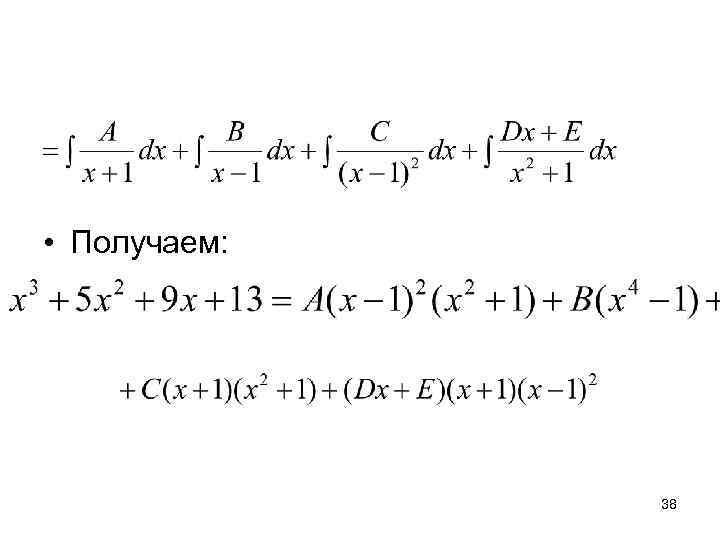 • Получаем: 38
• Получаем: 38
 • Отсюда: • Получаем: 39
• Отсюда: • Получаем: 39
 1. 5. Интегрирование алгебраических иррациональностей • Если подынтегральная функция содержит • • То, обычно, делают подстановку • чтобы избавиться от корня. 40
1. 5. Интегрирование алгебраических иррациональностей • Если подынтегральная функция содержит • • То, обычно, делают подстановку • чтобы избавиться от корня. 40
 • Примеры. • 1. • Положим • В результате подстановки получим интеграл • , 41
• Примеры. • 1. • Положим • В результате подстановки получим интеграл • , 41
 • 2. • Положим: • Далее – самостоятельно. 42
• 2. • Положим: • Далее – самостоятельно. 42

