Інтеграл та його застосування Первісна та її властивості

Інтеграл та його застосування. Первісна та її властивості

Приємного перегляду 2

Диференціювання функції f(x) – операція знаходження її похідної. Наприклад. Знайти похідну функції: а) ; б). Розв’язання а) ; б). Знаходження функції f(x) за даною її похідною називається операцією інтегрування. Операція інтегрування обернена до операції диференціювання. Наприклад. а) Якщо оскільки , то , . будь-якого х з цього проміжку 3 , то оскільки Функція F(x) називається первісною для функції f(x) на даному проміжку, якщо для б) Якщо . Наприклад. Функція , - первісна для функції проміжку на , оскільки при 3

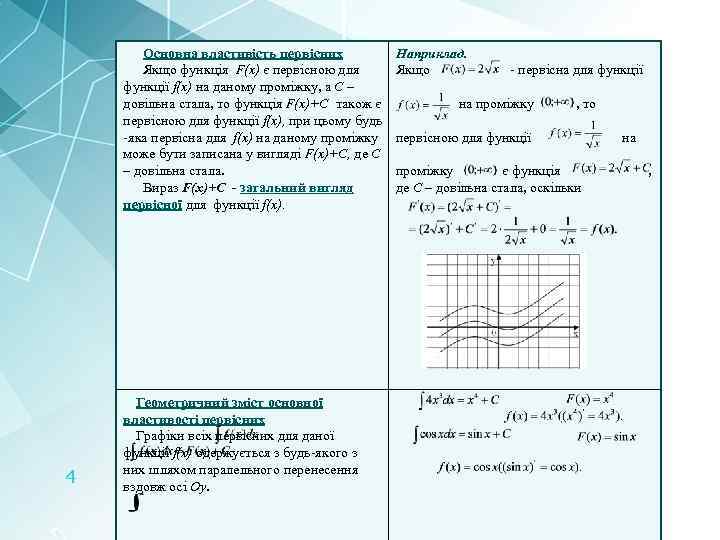Основна властивість первісних Якщо функція F(x) є первісною для функції f(x) на даному проміжку, а С – довільна стала, то функція F(x)+С також є первісною для функції f(x), при цьому будь -яка первісна для f(x) на даному проміжку може бути записана у вигляді F(x)+С, де С – довільна стала. Вираз F(x)+С - загальний вигляд первісної для функції f(x). 4 Геометричний зміст основної властивості первісних Графіки всіх первісних для даної функції f(x) одержується з будь-якого з них шляхом паралельного перенесення вздовж осі Оу. Наприклад. Якщо - первісна для функції на проміжку , то первісною для функції проміжку є функція де С – довільна стала, оскільки на ,

Таблиця первісних (невизначених інтегралів) Функція f(x) Загальний вигляд первісних F(x)+С, де С - стала 0 С 1 Запис за допомогою невизначеного інтеграла х+С 5

Правила знаходження первісних (правила інтегрування) 1. Якщо F - первісна функції , а G – первісна функції , то F+ G – первісна функції Інтеграл від суми дорівнює сумі інтегралів від доданків, тобто Наприклад. Знайти первісну для функції: а) ; б) Розв’язання а) ; б). Наприклад. Обчислити: а) а) б) 6 ; б) Розв’язання . .

Правила знаходження первісних (правила інтегрування) 2. Якщо F - первісна функції сталі, то k. F – первісна для функції , аkіb–. Наприклад. Знайти первісну для функції: а) ; б) Розв’язання а) ; б) Сталий множник інтеграла, тобто виноситься за знак , де k – стала. Наприклад. Обчислити: а) ; б). Розв’язання а) б) 7

Правила знаходження первісних (правила інтегрування) 3. Якщо F - первісна функції , аkіb– сталі , то - первісна для функції. Наприклад. Знайти первісну для функції: а) ; б) Розв’язання . а) ; б) . Наприклад. Обчислити: а) ; б). Розв’язання а) 8 б)

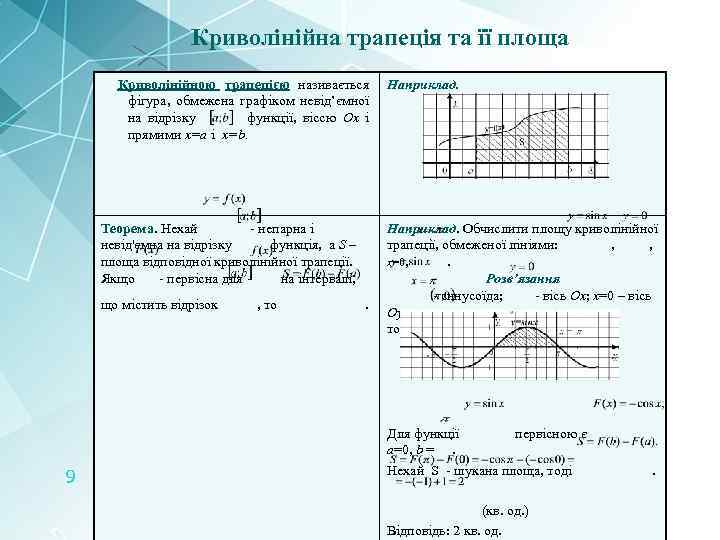Криволінійна трапеція та її площа Криволінійною трапецією називається фігура, обмежена графіком невід’ємної на відрізку функції, віссю Ох і прямими x=a і x=b. Теорема. Нехай - непарна і невід'ємна на відрізку функція, а S – площа відповідної криволінійної трапеції. Якщо - первісна для на інтервалі, що містить відрізок 9 , то . Наприклад. Обчислити площу криволінійної трапеції, обмеженої лініями: , , x=0, . Розв’язання - синусоїда; - вісь Ox; x=0 – вісь Оу; - пряма, що проходить через точку паралельно осі Оу. Для функції первісною є a=0, b =. Нехай S - шукана площа, тоді (кв. од. ) Відповідь: 2 кв. од. .

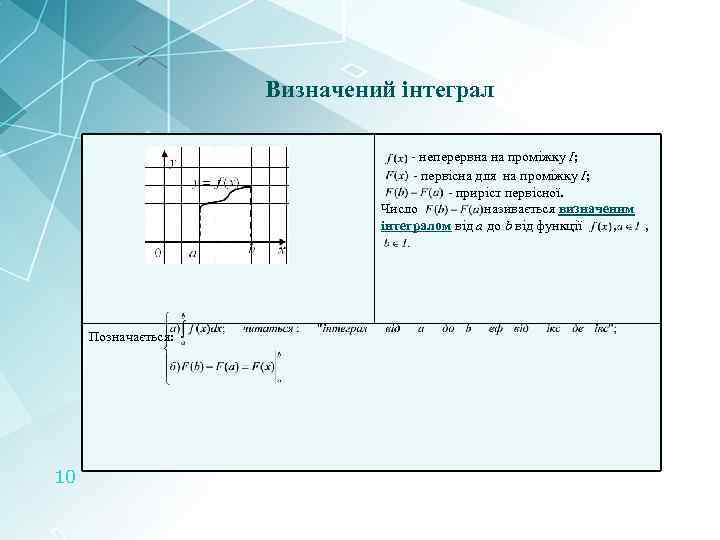Визначений інтеграл - неперервна на проміжку І; - первісна для на проміжку І; - приріст первісної. Число називається визначеним інтегралом від a до b від функції , , Позначається: 10

Формула Ньютона - Лейбніца - підінтегральна функція; - підінтегральний вираз; a - нижня межа інтегрування; b - верхня межа інтегрування; x – змінна інтегрування. Основні властивості визначених інтегралів 1) 2) 11 , (k – стала);

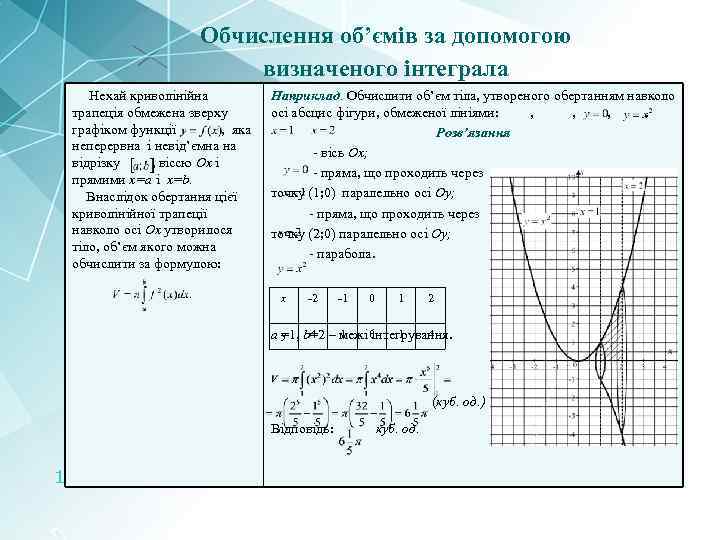Обчислення об’ємів за допомогою визначеного інтеграла Нехай криволінійна трапеція обмежена зверху графіком функції , яка неперервна і невід’ємна на відрізку , віссю Ох і прямими x=a і x=b. Внаслідок обертання цієї криволінійної трапеції навколо осі Ох утворилося тіло, об’єм якого можна обчислити за формулою: Наприклад. Обчислити об’єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої лініями: , , , . Розв’язання - вісь Ох; - пряма, що проходить через точку (1; 0) паралельно осі Оу; - пряма, що проходить через точку (2; 0) паралельно осі Оу; - парабола. х -2 -1 0 1 2 1 1 4 а у b=2 – межі 0 =1, 4 інтегрування. (куб. од. ) Відповідь: 12 куб. од.

Вчимося розв’язувати 1. Знайти загальний вигляд первісної для функції: а) ; б) в) г) Розв’язання: а) 1) Використаємо. 2) Використаємо для функції ( ) первісною є функція Відповідь: б) 1) Використаємо, якщо первісна для функції , то первісна для функції: . 2) Використаємо: для функції - первісною є функція 13 . Відповідь: ; .

в) 1) Використаємо: 2) Для функції первісною є 3) Якщо . ( ) - первісна для функції то (k і b – сталі) – первісна для функції. Відповідь: г) Якщо , то - первісна для функції (k і b – сталі) – первісна для функції . Відповідь: 14

2. Для функції знайти первісну, графік якої проходить через точку А: а) , А(-1; -3); б) , А(1; 2); в) , А . Розв’язання: 1) Для функції запишемо первісну в загальному вигляді. 2) У записану рівність замість х підставимо абсцису точки А і знайдемо значення С. а) А(-1; 3); С=-6. Відповідь: б) А(1; 2); С=4. Відповідь: в) 15 Відповідь: .

3. Обчислити інтеграл: а) ; б) в) ; ; г) Розв’язання: 1) Знайдемо первісну підінтегральної функції. 2) У первісну замість х підставимо спочатку верхню межу інтегрування, потім – нижню та обчислимо різницю одержаних значень. а) б) в) г) Відповідь: а) 16 ; б) 8; в) 1; г) .

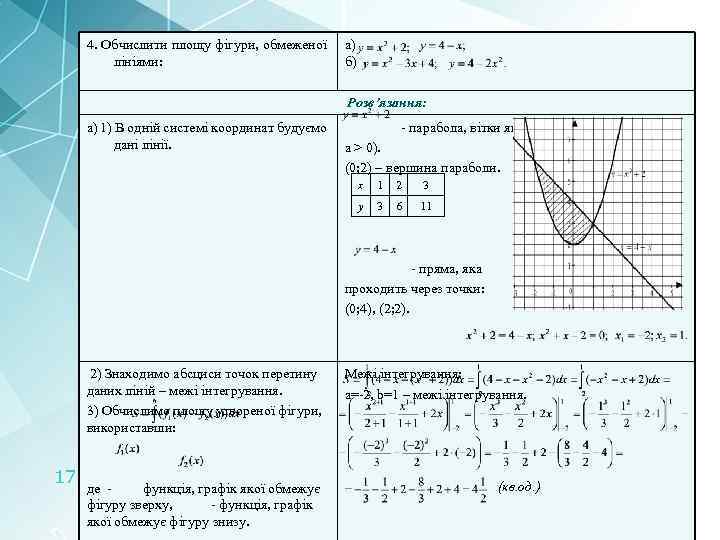4. Обчислити площу фігури, обмеженої лініями: а) б) Вчимося розв’язувати Розв’язання: а) 1) В одній системі координат будуємо дані лінії. - парабола, вітки якої напрямлені вгору (а=1, а > 0). (0; 2) – вершина параболи. х 1 2 3 у 3 6 11 - пряма, яка проходить через точки: (0; 4), (2; 2). 2) Знаходимо абсциси точок перетину даних ліній – межі інтегрування. 3) Обчислимо площу утвореної фігури, використавши: 17 де функція, графік якої обмежує фігуру зверху, - функція, графік якої обмежує фігуру знизу. Межі інтегрування: а=-2, b=1 – межі інтегрування. (кв. од. )

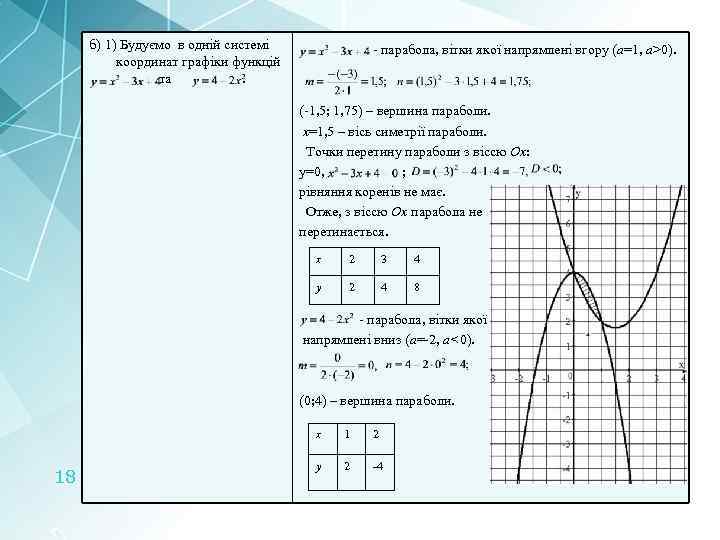б) 1) Будуємо в одній системі координат графіки функцій та. - парабола, вітки якої напрямлені вгору (а=1, a>0). (-1, 5; 1, 75) – вершина параболи. х=1, 5 – вісь симетрії параболи. Точки перетину параболи з віссю Ох: у=0, ; рівняння коренів не має. Отже, з віссю Ох парабола не перетинається. х 2 3 4 у 2 4 8 - парабола, вітки якої напрямлені вниз (а=-2, a<0). (0; 4) – вершина параболи. х 18 1 2 у 2 -4

2) Знаходимо межі інтегрування – розв’язуємо рівняння Межі інтегрування: х=0, х=1. а=0, b=1 – межі інтегрування. 3) Обчислюємо площу фігури, врахувавши, що парабола обмежує фігуру знизу, а парабола - зверху. (кв. од) Відповідь: 0, 5 кв. од. 19

Дякую за увагу Презентацію зробив Учень 11 клсу Каліновський 20 Володимир